Vous êtes ici

Série d'exercices : Triangle rectangle - Théorème de Pythagore 4e

Classe:

Quatrième

Exercice 1 Le théorème de Pythagore

Soit

$ABC$ un triangle rectangle en

$A$ tel que :

$AB=4\;cm\;;\ AC=3\;cm.$

1) Mesurer la distance

$BC.$

2) a) Que représente le segment

$[BC]$ pour le triangle

$ABC$ ? Puis calculer

$BC^{2}.$

b) Que représentent les segments

$[AB]$ et

$[AC]$ pour le triangle

$ABC$ ? Puis calculer

$AB^{2}+AC^{2}.$

c) Comparer

$BC^{2}$ et

$AB^{2}+AC^{2}.$

3) Quelle est la propriété que tu viens de démontrer pour le triangle rectangle ?

Exercice 2 Application du théorème

Soit

$ABC$ un triangle rectangle en

$C$ tel que :

$BC=4\;cm\;;\ AC=3\;cm.$ Calculer

$AB.$

Exercice 3 Application du théorème

Soit

$IJK$ rectangle en

$J$ tel que :

$IJ=8\;cm$ et

$IK=10\;cm.$ Calculer

$JK.$

Exercice 4 Application du théorème

Soit

$RST$ un triangle rectangle en

$R$ tel que :

$TS=2.5\;cm$ et

$RT=1.5\;cm.$ Calculer

$RS.$

Exercice 5 Application du théorème

La figure ci-dessous représente un champ rectangulaire. On donne

$BC=15\;m$ et

$AC=25\;m.$ Calculer le périmètre et l'aire de ce champ.

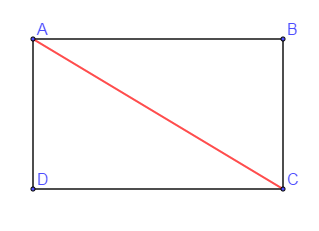
Exercice 6

Tracer un triangle

$AKS$ rectangle en

$S.$

1) Marquer

$M$ , pied de la hauteur relative à l'hypoténuse.

2) Écrire la relation de Pythagore dans chacun des triangles

$AKS\;,\ SMK$ et

$AMS.$

Exercice 7

Soit

$(AB)$ et

$(CD)$ deux droites perpendiculaires en

$M.$

Démontrer que

$AD^{2}+BC^{2}=AC^{2}+DB^{2}.$

Exercice 8 Réciproque du théorème Pythagore

Soit

$ABC$ un triangle rectangle. Dans chacun des cas ci-dessous répondre par vrai ou faux.

1ier cas :

$AB=6\qquad AC=10\qquad BC=8.$

2ième cas :

$AB=4\qquad AC=7\qquad BC=6$

3ime cas :

$AB=6\qquad AC=9\qquad BC=8$

4ième cas :

$AB=9\qquad AC=15\qquad BC=10.$

Exercice 9 Approfondissement

1) Construire un triangle

$OAB$ tel que :

$OA=5\;cm\;;\ OB=3\;cm$ et

$AB=4\;cm.$

2) Démontrer que le triangle

$OAB$ est rectangle.

3) Soit

$D$ le symétrique du point

$A$ par rapport à

$B.$

Soit

$C$ le symétrique de

$O$ par rapport à

$B$ , montrer que le quadrilatère

$OACD$ est un losange.

Exercice 10 Approfondissement

$ABC$ est un triangle isocèle eu

$A$ tel que :

$AB=5\;cm\$ et

$\ BC=8\;cm.$ Soit

$A'$ le symétrique de

$A$ par rapport à

$(BC)$ .

1) Faire une figure.

$I$ est le milieu de

$[BC].$ Calculer

$AI$ et l'aire du triangle

$ACI.$

3) Quelle est la nature du quadrilatère

$ACA'B\ ?$ Puis calculer son aire.

Exercice 11 Relation métrique

1) Soit

$ABC$ un triangle rectangle en

$A$ et

$H$ le pied de la hauteur issue de

$A.$

2) Calculer de deux manières différentes l'aire du triangle

$ABC.$

3) Déduis-en une égalité qui relie :

$AB\;,\ AC\;,\ BC$ et

$AH.$

Exercice 12

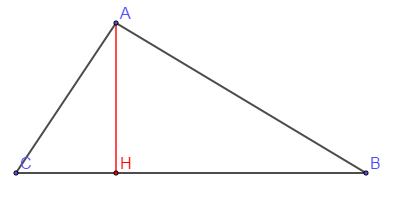
Sur la figure ci-dessus

$ABC$ est un triangle rectangle en

$A$ et

$H$ le pied de la hauteur issue de

$A.$

On donne

$BC=6\;cm\;;\ AC=4.8\;cm$

1) Calculer

$AB.$

2) Calculer l'aire du triangle

$ABC$ . En déduire

$AH$

Exercice 13 Application à la relation métrique

1) Construire un triangle

$ABC$ rectangle en

$A$ tel que :

$AB=3\;cm$ et

$AC=4\;cm.$

Soit

$H$ le pied de la hauteur issue de

$A.$

2) Calculer

$AH.$

Exercice 14 Application à la relation métrique

1) Construire un cercle

$(c)$ de centre

$O$ est de rayon

$5\;cm.$

2) Marque un point

$M$ situé à

$13\;cm$ de

$O.$

3) Soit

$I$ le point de contact d'une tangente à

$(c)$ passant par

$M.$

4) Dans le triangle

$IOM$ , la hauteur passant par

$I$ coupe la droite

$(OM)$ en

$H.$

5) Calculer

$MI$ et

$IH.$

Exercice 15 Approfondissement

$EFG$ est un triangle rectangle en

$E$ tel que :

$EF=8\;cm$ et

$EG=6\;cm.$

1) Calculer

$FG.$

2) Calculer l'aire du triangle

$EFG.$

3) Soit

$H$ le pied de la hauteur issue de

$E.$

Calculer

$EH\;,\ FH$ et

$HG.$

4) Préciser le centre

$M$ du cercle circonscrit au triangle

$EGH$ puis calculer son rayon.

5) Soit

$A$ le point de la demi-droite

$[FE)$ tel que :

$FA=12.5\;cm.$ Calculer

$EA$ et

$GA.$

6) Montrer que

$FGA$ est un triangle rectangle.

Exercice 16 Approfondissement

Soit un triangle

$ABC$ et la hauteur

$[BE]$ avec

$E$ appartenant au segment

$[AC].$

On pose

$AC=12.5\;cm$ et

$AE=4.5\;cm.$ On appel

$x$ la longueur du segment

$[BE].$

1) Calculer

$AB^{2}$ en fonction de

$x$ dans le triangle

$ABE.$

2) Calculer

$BC^{2}$ en fonction de

$x$ dans le triangle

$BCE.$

3) On suppose que

$ABC$ est rectangle en

$B.$ En utilisant les résultats 1) et 2) applique lui le théorème de Pythagore et en déduire que

$2x^{2}=72.$ Calculer

$x.$

4) Calculer

$AB$ et

$BC.$ Déterminer l'aire de

$ABC.$

Exercice 17 Recherche

Soit

$ABC$ un triangle rectangle en

$A$ et

$H$ le pied de la hauteur issue de

$A.$ Montrer que :

$AH^{2}=BH\times CH;$

$AB^{2}=BH\times BC;$

$AC^{2}=BC\times CH.$

Exercice 18

$ABC$ est un triangle rectangle en

$A$ alors, on a :

$AB^{2}+BC^{2}=AC^{2}$

$AB^{2}+AC^{2}=BC^{2}$

$AC^{2}+BC^{2}=AB^{2}$

Écris la lettre qui correspond à la bonne réponse.

Exercice 19

Réponds par vrai ou faux à chacune des affirmations ci-dessous.

1) Dans un triangle rectangle, la somme des cotés de l'angle droit est égale à l'hypoténuse.

2) Dans un triangle rectangle, la somme des carrés des cotés de l'angle droit est égale au carré de l'hypoténuse.

Exercice 20

Recopie puis complète chacune des phrases ci-dessous.

1) Dans un triangle rectangle, la somme des carrés des côtés de l'angle droit est égale

$\ldots\ldots$

2) Dans un triangle rectangle, la somme des

$\ldots\ldots$ est égale au carré de l'hypoténuse.

Exercice 21

$ABC$ est un triangle rectangle en

$A$ tel que,

$AB=4\text{ et }AC=3.$

Calcule

$BC.$

$EFG$ est un triangle rectangle en

$G$ tel que,

$EF=2.5\text{ et }GF=2.$

Calcule

$GE.$

Exercice 22

$ABCD$ est un rectangle de longueur

$4\;cm$ et de largeur

$3\;cm.$

Calcule la diagonale de ce rectangle.

Exercice 23

$ABC$ est un triangle rectangle en

$C$ tel que

$AB=15\;cm$ et

$CB=12\;cm.$

La mesure de la hauteur issue de

$C$ est égale à

$7.2\;cm.$

Calcule

$AC$ sans utiliser le théorème de Pythagore.

Exercice 24

$EGH$ est un triangle rectangle en

$G$ tel que

$GE=4\;cm$ et

$GH=3\;cm.$

La mesure de la hauteur issue de

$G$ est égale à

$2.4\;cm.$

Calcule

$EH$ sans utiliser le théorème de Pythagore.

Exercice 25

On donne trois points

$A$ ,

$B$ et

$C$ tels que :

$AB=5\;cm$ ,

$AC=3\;cm$ et

$BC=4\;cm.$

Montre que le triangle

$ABC$ est rectangle.

Exercice 26

Soit

$M$ ,

$N$ et

$P$ trois points tels que :

$MN=1.5\;cm$ ,

$NP=2.5\;cm$ et

$PM=2\;cm.$

Montre que

$MNP$ est un triangle rectangle.

Exercice 27

On donne trois points

$L$ ,

$M$ et

$N$ tels que :

$LM=2\;cm$ ,

$MN=2\;cm$ et

$NL=3\;cm.$

Le triangle

$LMN$ est-il rectangle ?

Justifie ta réponse.

Exercice 28

On donne trois points

$E$ ,

$F$ et

$G$ tels que :

$EF=2\;cm$ ,

$FG=3.5\;cm$ et

$GE=4\;cm.$

Le triangle

$EFG$ est-il rectangle ?

Justifie ta réponse.

Exercice 29

En Mésopotamie, pendant l'antiquité, on utilisait des cordes à nœuds distants d'un mètre comme indique la figure ci-contre, pour obtenir des angles droits dans les constructions d'autels religieux.

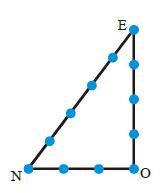
Explique pourquoi cette corde à nœuds bien tendue donne un angle droit.

Exercice 30

On a fixé au mur une étagère

$[ET]$ en la soutenant par un support

$[SP].$

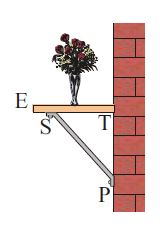
$ST=17.6\;cm\;,\ TP=33\;cm\text{ et }SP=37.4\;cm.$

On suppose que le mur est vertical.

L'étagère est-elle horizontale ?

Justifie.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Commentaires

Elhadji lo (non vérifié)

mar, 12/01/2020 - 21:02

Permalien

Je vous voudrais just De vou

Je vous voudrais just De vou dire Merci beaucoup parce ke vou nous aidez beaucoup De choses surtou aussi la facilité merci bco vraiment

répondre

Anonyme (non vérifié)

jeu, 05/06/2021 - 19:16

Permalien

Oooo la correction

répondre

Anonyme (non vérifié)

ven, 07/09/2021 - 19:04

Permalien

TOUTE LA CORRECTION S'IL VOUS

TOUTE LA CORRECTION S'IL VOUS PLAIT

répondre

Mariama sonko (non vérifié)

jeu, 04/28/2022 - 23:15

Permalien

MAths

Trace un trangLe ABC rectangle en B tel que AB=3 et AC=5 calculé BC 2/La PerPendiculaire a AC passant par B coupe AC en H calculé BH Solutions

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Série d'exercices : Triangle rectangle - Théorème de Pythagore 4e

Formulaire de recherche

Exercice 1 Le théorème de Pythagore

Exercice 2 Application du théorème

Exercice 3 Application du théorème

Exercice 4 Application du théorème

Exercice 5 Application du théorème

Exercice 6

Exercice 7

Exercice 8 Réciproque du théorème Pythagore

Exercice 9 Approfondissement

Exercice 10 Approfondissement

Exercice 11 Relation métrique

Exercice 12

Exercice 13 Application à la relation métrique

Exercice 14 Application à la relation métrique

Exercice 15 Approfondissement

Exercice 16 Approfondissement

Exercice 17 Recherche

Exercice 18

Exercice 19

Exercice 20

Exercice 21

Exercice 22

Exercice 23

Exercice 24

Exercice 25

Exercice 26

Exercice 27

Exercice 28

Exercice 29

Exercice 30

▸Correction des exercices\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}

Commentaires

Je vous voudrais just De vou

Oooo la correction

TOUTE LA CORRECTION S'IL VOUS

MAths

Ajouter un commentaire

Plain text

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$