Solution des exercices : Division des nombres décimaux arithmétiques - 6e
Classe:
Sixième
Exercice 1
1) Posons puis effectuons les opérations suivantes :
a) Soit $6110\div 235$
Le diviseur étant entier alors, en posant et en effectuant l'opération, on obtient :
$$\begin{array}{r} 6110\\-470\ \;\\\hline 1410\\-1410\\\hline 0\\ \\\end{array}\begin{array}{|l} 235\\\hline 26\\ \\\\\\\\\end{array}$$
b) Soit : $734.32\div 26.3$ donc, posons et effectuons l'opération en donnant le résultat avec deux chiffres après la virgule ; c'est à dire à $0.01$ près.
$$\begin{array}{r} 734.32\\\\ \\\end{array}\begin{array}{|l} 26.3\\\hline \\ \\\end{array}$$
Pour effectuer cette opération, on essaie d'abord de rendre le diviseur entier.
Ainsi, on multiplie le diviseur par $10$ pour le rendre entier.
Puis, on multiplie le dividende aussi par le même nombre $10.$ Ce qui revient à déplacer la virgule d'un rang vers sa droite.
Après, on peut effectuer la division, sans oublier de placer la virgule au quotient, au moment d'abaisser le premier nombre après la virgule dans le dividende.
$$\begin{array}{r} 7343.20\ \\-526\quad \;\ \\\hline 2083\ \ \ \\ -1841\ \ \ \\\hline 2422\ \\-2367\ \\\hline 550\\-526\\\hline .24\\\\\end{array}\begin{array}{|l} 263\\\hline 27.92\\ \\\\\\\\\\\\\\\\\end{array}$$
2) Calculons mentalement les quotients suivants.
c) Soit : $2\,009\div 100$
En effet, diviser par $100$, revient à déplacer la virgule de deux rangs vers sa gauche.
Ainsi, $2\,009\div 100=20.09$
d) Soit : $45.37\div 0.1$
On sait que diviser par $0.1$, revient à déplacer la virgule d'un rang vers sa droite.
Donc, $45.37\div 0.1=453.7$
3) Donnons un ordre de grandeur de chacun des quotients.
Pour calculer l'ordre de grandeur (OG) d'un quotient, on choisit d'abord une précision adaptée. Ensuite, on choisira en premier l'ordre de grandeur (OG) du diviseur, puis on choisira pour le dividende, un ordre de grandeur qui permet un calcul rapide et simple.
Enfin, on remplace le diviseur et le dividende par leur ordre de grandeur respectif et on effectue la division de ces ordres de grandeur.
e) Soit : $305\div 19.5$
On choisit une précision à la dizaine près.
Ainsi, $19.5$ est proche de $20$
Par ailleurs, le choix de $300$ comme OG de $305$ permet un calcul simple et rapide.
Par suite, l'ordre de grandeur de $305\div 19.5$ est égal à :
$$300\div 20=30\div 2=15$$
f) Soit : $69\div 6.9$
Pour une précision l'unité près, on a : $6.9$ est proche de $7$ donc, l'OG de $6.9$ est $7.$
En choisissant $70$ comme OG de $69$, on obtient un calcul simple et rapide.
Ainsi, l'ordre de grandeur de $69\div 6.9$ sera donné par :
$$70\div 7=10$$
Exercice 2
1) Donnons le quotient entier approché par défaut de $\dfrac{27}{7}$
Cherchons deux multiples successifs de $7$ qui encadrent l'entier $27.$
On sait que $21\ $ et $\ 28$ sont deux multiples successifs de $7.$
De plus : $21<27<28$
Donc, $\dfrac{21}{7}<\dfrac{27}{7}<\dfrac{28}{7}$
Ce qui donne : $3<\dfrac{27}{7}<4$
Ainsi, le quotient entier approché par défaut de $\dfrac{27}{7}$ est égal à $3.$
2) Donnons le quotient entier approché de la division de $213$ par $13$ à l'unité près par excès.
De la même manière, on a : $208\ $ et $\ 221$ sont deux multiples successifs de $13$ et qui encadrent l'entier $213.$
Donc, $\dfrac{208}{13}<\dfrac{213}{13}<\dfrac{221}{13}$
Par suite, $16<\dfrac{213}{13}<17$
D'où, le quotient entier approché de la division de $213$ par $13$ à l'unité près par excès est le nombre entier $17.$
Exercice 3
1) a) Calculons le quotient au dixième près de $96.4$ par $34$ par défaut.
En arrondissant à un chiffre après la virgule par défaut, on obtient : $\dfrac{96.4}{34}=2.8$
Donc, $2.8$ représente le quotient au dixième près de $96.4$ par $34$ par défaut.
b) En déduisons le reste de la division à $\dfrac{1}{10}$ près.
Soit $r$ le reste de la division alors, on a :
$r=96.4-(34\times 2.8)=96.4-95.2=1.2$
Donc, le reste de la division à $\dfrac{1}{10}$ près est égal à $1.2$
2.a) Calculons le quotient à $\dfrac{1}{100}$ près de $\dfrac{117}{17}$ par excès.
En arrondissant à deux chiffres après la virgule par excès, on obtient : $\dfrac{117}{17}=6.89$
Donc, $6.89$ est le quotient à $\dfrac{1}{100}$ près de $\dfrac{117}{17}$ par excès.
b) En déduisons le reste de la division.
Soit $r$ le reste de la division alors, on a :
$r=117-(17\times 6.88)=117-116.96=0.04$
Ainsi, le reste de la division à $\dfrac{1}{100}$ près est égal à $0.04$
Exercice 4
1) Donnons l'écriture décimale de : $\dfrac{13.5}{6}\ $ et $\ \dfrac{70.2}{26}$
On a : $\dfrac{13.5}{6}=2.25$ donc, $2.25$ est l'écriture décimale de : $\dfrac{13.5}{6}$
On a : $\dfrac{70.2}{26}=2.7$ donc, $2.7$ est l'écriture décimale de : $\dfrac{70.2}{26}$
2) $\dfrac{117}{11}$ n'admet pas une écriture décimale.
En effet, on a : $\dfrac{117}{11}=10.636363\ldots$
Or, $10.636363\ldots$ est un développement décimal illimité périodique de période $63.$
Donc, $\dfrac{117}{11}$ n'est pas un quotient exact.
D'où, $\dfrac{117}{11}$ n'admet pas une écriture décimale.
3) Donnons une écriture fractionnaire de $7.25$
On a : $7.25=\dfrac{725}{100}$
Donc, $\dfrac{725}{100}$ est une écriture fractionnaire de $7.25.$
Exercice 5
1) Donnons l'écriture décimale de $\dfrac{23}{8}$
On a : $\dfrac{23}{8}=2.875$
Donc, $2.875$ est l'écriture décimale de $\dfrac{23}{8}$
2) a) Encadrons $\dfrac{23}{8}$ entre deux entiers naturels consécutifs.
On a : $\dfrac{23}{8}=2.875$
Or, $2<2.875<3$
D'où, un encadrement de $\dfrac{23}{8}$ entre deux entiers naturels consécutifs est donné par :
$$2<\dfrac{23}{8}<3$$
b) Encadrons $\dfrac{23}{8}$ entre deux décimaux consécutifs à $0.01$ près.
On a : $\dfrac{23}{8}=2.875$ alors,
Donc, on peut écrire : $2.87<2.875<2.88$
D'où, un encadrement de $\dfrac{23}{8}$ entre deux décimaux consécutifs à $0.01$ près est donné par :
$$2.87<\dfrac{23}{8}<2.88$$
Exercice 6
1) Donnons le quotient approché par excès à l'unité près de la division de $200.87$ par $49.$
Cherchons alors deux multiples successifs de $49$ qui encadrent l'entier $200.87$
En effet, on sait que : $196\ $ et $\ 245$ sont deux multiples successifs de $49$ et qui encadrent l'entier $200.87$
Donc, $\dfrac{196}{49}<\dfrac{200.87}{49}<\dfrac{245}{49}$
Ce qui donne, $4<\dfrac{200.87}{49}<5$
D'où, le quotient entier approché par excès à l'unité près de la division de $200.87$ par $49$ est le nombre entier $5.$
2) $20.42$ est le quotient approché par défaut au centième près de la division de $347.3$ par $17.$
3) Donner le reste de la division de $75.1$ par $6.3$ aux dixièmes près.
Soit $\dfrac{75.1}{6.3}$
Pour rendre entier le dénominateur, on multiplie par $10$ le numérateur et le dénominateur.
Ce qui donne : $\dfrac{75.1}{6.3}=\dfrac{75.1\times 10}{6.3\times 10}=\dfrac{751}{63}$
Ainsi, aux dixièmes près, on a : $\dfrac{751}{63}=11.9$
Soit $r$ le reste de la division alors, on a :
$r=751-(63\times 11.9)=751-749.7=1.3$
D'où, le reste de la division de $75.1$ par $6.3$ aux dixièmes près est égal à $1.3$
Exercice 7
Écrivons les nombres décimaux suivants sous la forme $\dfrac{a}{b}$ avec $b$ non nul
$$3.5\;;\ 27.04\;;\ 100.001\;;\ 4\;;\ 58.273\;;\ 0.4\;;\ 0.045\;;\ 0.0102\;;\ 0.54321$$
On a :
$3.5=\dfrac{35}{10}$
$27.04=\dfrac{2\,704}{100}$
$100.001=\dfrac{100\,001}{1\,000}$
$4=\dfrac{4}{1}$
$58.273=\dfrac{58\,273}{1\,000}$
$0.4=\dfrac{4}{10}$
$0.045=\dfrac{45}{1\,000}$
$0.0102=\dfrac{102}{10\,000}$
$0.54321=\dfrac{54\,321}{100\,000}$
Exercice 8
a) Exprime ces écritures fractionnaires sous forme de nombres décimaux.
$$\dfrac{14.7}{7}\;;\quad \dfrac{123}{8}\;;\quad \dfrac{154}{11}\;;\quad \dfrac{18.75}{7.5}$$
On a :
$\dfrac{14.7}{7}=2.1$
$\dfrac{123}{8}=15.375$
$\dfrac{154}{11}=14$
$\dfrac{18.75}{7.5}=2.5$
b) Rangeons les écritures fractionnaires dans l'ordre décroissant.
En rangeant dans l'ordre décroissant les nombres décimaux trouvés en a), on a :
$$15.375>14>2.5>2.1$$
Donc, en remplaçant ces nombres décimaux par leur écriture fractionnaire, on obtient :
$$\dfrac{123}{8}>\dfrac{154}{11}>\dfrac{18.75}{7.5}>\dfrac{14.7}{7}$$


Exercice 10
1) Relevons dans cette liste les nombres divisibles : par $2$ ; par $3$ ; par $2$ et $3$
$$12\;;\ 31\;;\ 45\;;\ 810\;;\ 27\;;\ 34\;;\ 312\;;\ 431$$
$-\ $ nombres divisibles par $2$
Un nombre est divisible par $2$ si son dernier chiffre est pair.
Donc, dans cette liste, les nombres divisibles par $2$ sont :
$$12\;;\ 810\;;\ 34\;;\ 312$$
$-\ $ nombres divisibles par $3$
Un nombre est divisible par $3$ si la somme de ses chiffres est un multiple de $3.$
Donc, dans cette liste, les nombres divisibles par $3$ sont :
$$12\;;\ 45\;;\ 810\;;\ 27\;;\ 312$$
Par conséquent les nombres divisibles à la fois par $2$ et par $3$ sont :
$$12\;;\ 810\;;\ 312$$
2) Relevons dans cette liste les nombres divisibles : par $5$ ; par $9$ ; par $5$ et $9$
$$27\;;\ 90\;;\ 45\;;\ 35\;;\ 54\;;\ 792\;;\ 838\;;\ 5$$
$-\ $ nombres divisibles par $5$
Un nombre est divisible par $5$ si son dernier chiffre est $5$ ou $0.$
Donc, dans cette liste, les nombres divisibles par $5$ sont :
$$90\;;\ 45\;;\ 35\;;\ 5$$
$-\ $ nombres divisibles par $9$
Un nombre est divisible par $9$ si la somme de ses chiffres est un multiple de $9.$
Donc, dans cette liste, les nombres divisibles par $9$ sont :
$$27\;;\ 90\;;\ 45\;;\ 54\;;\ 792$$
Ainsi, les nombres divisibles à la fois par $5$ et par $9$ sont :
$$90\;;\ 45$$
Exercice 11
Reproduisons puis complétons le tableau ci-dessous
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline &&\text{Ecriture}&\\a&b&\text{fractionnaire}&\text{Ecriture décimale}\\&&a\text{ sur }b&\\\hline&&&\\ 3&4&\dfrac{3}{4}&0.75\\&&&\\\hline&&&\\ 1&8&\dfrac{1}{8}&0.125\\&&&\\\hline&&&\\ 5&2&\dfrac{5}{2}&2.5\\&&&\\\hline &&&\\0&19&\dfrac{0}{19}=0&0\\&&&\\\hline&&&\\ 1&4&\dfrac{1}{4}&0.25\\&&&\\\hline&&&\\ 2&200&\dfrac{2}{200}&0.01\\&&&\\\hline&&&\\ 1&1&\dfrac{1}{1}=1&1\\&&&\\\hline\end{array}$$
Exercice 12
Calculons : $6\times\dfrac{5}{3}\;;\quad\dfrac{7}{4}\times 12$
On a : $6\times\dfrac{5}{3}=\dfrac{6\times 5}{3}=\dfrac{30}{3}=10$
D'où, $\boxed{6\times\dfrac{5}{3}=10}$
Soit : $\dfrac{7}{4}\times 12=\dfrac{7\times 12}{4}=\dfrac{84}{4}=21$
Ainsi, $\boxed{\dfrac{7}{4}\times 12=21}$
Exercice 13
Un journaliste dispose de $1\;h\;51\;mn$ pour son émission "Wakh sa halate". Il veut accorder à chacun de ses $27$ auditeurs un temps de parole équivalent.
Déterminons temps de chacun des auditeurs.
Comme $1\;h=60\;mn$ alors, en convertissant en minute, on trouve :
$1\;h\;51\;mn=60+51=111\;mn$
Donc, le temps de parole de chaque auditeur est donné par le quotient : $\dfrac{111}{27}$
On sait que $\dfrac{111}{27}$ n'est pas un quotient exact.
Donc, en posant l'opération, on obtient :
$$\begin{array}{r} 111\\-108\\\hline 3\\ \\ \end{array}\begin{array}{|l} 27\\\hline 4\\ \\\\\end{array}$$
Ainsi, chaque auditeur disposera de $4\;mn$ de temps de parole et il restera au journaliste $3\;mn$
Exercice 15
Quatre personnes règlent une facture qui s'élève à $4\,200\;F.$ Les trois premières versent respectivement $\dfrac{1}{3}\;;\ \dfrac{1}{4}\ $ et $\ \dfrac{2}{7}$ de cette somme. La quatrième paye le reste.
Déterminons la somme versée par chacune.
Comme la première personne a versé $\dfrac{1}{3}$ de la facture alors, cela peut encore s'écrire :
$$\text{versement première personne}=\dfrac{1}{3}\times 4\,200$$
En calculant on obtient :
$\begin{array}{rcl}\text{versement première personne}&=&\dfrac{1}{3}\times 4\,200\\\\&=&\dfrac{1\times 4\,200}{3}\\\\&=&\dfrac{4\,200}{3}\\\\&=&1\,400\end{array}$
Donc, la première personne a versé $1\,400\;F$
La deuxième personne a versé $\dfrac{1}{4}$ de la facture. Ce qui se traduit par :
$$\text{versement deuxième personne}=\dfrac{1}{4}\times 4\,200$$
En calculant on obtient :
$\begin{array}{rcl}\text{versement deuxième personne}&=&\dfrac{1}{4}\times 4\,200\\\\&=&\dfrac{1\times 4\,200}{4}\\\\&=&\dfrac{4\,200}{4}\\\\&=&1\,050\end{array}$
D'où, la deuxième personne a versé $1\,050\;F$
Comme la troisième personne a versé $\dfrac{2}{7}$ de la facture alors, cela peut encore s'écrire :
$$\text{versement troisième personne}=\dfrac{2}{7}\times 4\,200$$
En calculant on obtient :
$\begin{array}{rcl}\text{versement troisième personne}&=&\dfrac{2}{7}\times 4\,200\\\\&=&\dfrac{2\times 4\,200}{7}\\\\&=&\dfrac{8\,400}{7}\\\\&=&1\,200\end{array}$
Ainsi, la troisième personne a versé $1\,200\;F$
Par suite, la somme versée par ces trois personnes est égale à :
$$1\,400\;F+1\,050\;F+1\,200\;F=3\,650\;F$$
Comme la quatrième personne paye le reste alors, pour trouver cette sa part on effectue l'opération suivante :
$$\text{versement quatrième personne}=4\,200-3\,650$$
En calculant on trouve : $4\,200-3\,650=550$
D'où, la troisième personne a payé $550\;F$
Déterminons la fraction de la dépense totale versée par la quatrième personne
Soit $\dfrac{1}{3}\;;\ \dfrac{1}{4}\ $ et $\ \dfrac{2}{7}$ la fraction de la dépense totale versée respectivement par les trois premières personnes.
On réduit au même dénominateur. Ce qui donne :
$\dfrac{1}{3}=\dfrac{1\times 4\times 7}{3\times 4\times 7}=\dfrac{28}{84}$
$\dfrac{1}{4}=\dfrac{1\times 3\times 7}{3\times 4\times 7}=\dfrac{21}{84}$
$\dfrac{2}{7}=\dfrac{2\times 4\times 3}{3\times 4\times 7}=\dfrac{24}{84}$
Alors, la fraction de la dépense totale versée en tout par les trois premières personnes est égale :
$$\dfrac{28}{84}+\dfrac{21}{84}+\dfrac{24}{84}=\dfrac{28+21+24}{84}=\dfrac{73}{84}$$
Comme la part totale est égale à $\dfrac{84}{84}$ alors, la part de la quatrième personne est donnée par :
$$\dfrac{84}{84}-\dfrac{73}{84}=\dfrac{84-73}{84}=\dfrac{11}{84}$$
Ainsi, la quatrième personne a versé $\dfrac{11}{84}$ de la somme totale.
Vérification :
$\begin{array}{rcl}\dfrac{11}{84}\times 4\,200&=&\dfrac{11\times 4\,200}{84}\\\\&=&\dfrac{46\,200}{84}\\\\&=&550\end{array}$
Donc, $\dfrac{11}{84}\times 4\,200\;F=550\;F$
Ce qui correspond bien au versement de la quatrième personne.
Exercice 16
a) Considérons les écritures fractionnaires suivantes :
$$\dfrac{10}{2.5}\;;\quad \dfrac{22}{4}\::\quad \dfrac{105}{21}\;;\quad \dfrac{210}{10}$$
Parmi les écritures fractionnaires ci-dessus, celles dont le numérateur est multiple du dénominateur sont :
$$\dfrac{10}{2.5}\::\quad \dfrac{105}{21}\;;\quad \dfrac{210}{10}$$
b) Exprimons ces écritures fractionnaires sous forme de nombres décimaux.
On a :
$\dfrac{10}{2.5}=4$
$\dfrac{22}{4}=5.5$
$\dfrac{105}{21}=5$
$\dfrac{210}{10}=21$
Exercice 17
Reproduisons la figure ci-dessous en utilisant le quadrillage du cahier

a) Recopions et complétons les égalités ci-dessous :
En observant la figure, on peut écrire :
$AB=10\;;\ AC=1\;;\ AD=4\;;\ AE=7$
Ainsi, on a :
$$AC=\dfrac{1}{10}\times AB\;;\quad AD=\dfrac{4}{10}\times AB\;;\quad AE=\dfrac{7}{10}\times AB$$
b) Plaçons $F\ $ et $\ G$ tels que $AF=\dfrac{3}{10}\times AB\ $ et $\ AG=\dfrac{11}{10}\times AB$

Exercice 18
a) Dans une heure il y a $60$ minutes
b) Complétons
$$\dfrac{1}{4}\,h=15\;min\;;\quad\dfrac{1}{2}\,h=30\;min\;;\quad\dfrac{3}{4}\,h=45\;min$$
En effet, on a :
$\dfrac{1}{4}\,h=\dfrac{1}{4}\times 60=\dfrac{60}{4}=15\;min$
$\dfrac{1}{2}\,h=\dfrac{1}{2}\times 60=\dfrac{60}{2}=30\;min$
$\dfrac{3}{4}\,h=\dfrac{3}{4}\times 60\dfrac{3\times 60}{4}=\dfrac{180}{4}=45\;min$
Exercice 19
Le parcours d'un rallye automobile a une longueur totale de $4\,620\;km.$
Déterminons le nombre de postes distants de $140\;km$ les uns des autres que l'on peut installer.
La distance entre deux postes est appelée intervalle.
Alors, le nombre d'intervalles est égal à :
$$\dfrac{4\,620}{140}=33$$
Le nombre de postes est donc donné par :
$$\text{nombre de postes}=\text{nombre d'intervalles}+1$$
Ce qui donne :
$$\text{nombre de postes}=33+1=34$$
D'où, pour ce parcours d'un rallye automobile on peut installer $34$ postes distants de $140\;km$ les uns des autres.
Exercice 20
On considère les nombres de la forme $2\spadesuit 93\spadesuit$, où les $\spadesuit$ remplacent des chiffres. Trouvons tous les nombres de cette forme qui sont divisibles à la fois par $3$ et par $5.$
En effet, on sait que : un nombre est divisible par $5$ si son dernier chiffre est $5$ ou $0.$
Ainsi, les nombres suivants sont divisibles par $5.$
$\begin{array}{cccccccccc} 20\,930&21\,930&22\,930&23\,930&24\,930&25\,930&26\,930&27\,930&28\,930&29\,930\\\\20\,935&21\,935&22\,935&23\,935&24\,935&25\,935&26\,935&27\,935&28\,935&29\,935\end{array}$
Par ailleurs, un nombre est divisible par $3$ si la somme de ses chiffres est un multiple de $3.$
Donc, dans la liste ci-dessus, trouvons les nombres qui sont aussi divisibles par $3.$
On obtient :
$$\begin{array}{cccccc} 21\,930&24\,930&27\,930&22\,935&25\,935&28\,935\end{array}$$
Par conséquent, les nombres de la forme $2\spadesuit 93\spadesuit$, divisibles à la fois par $3$ et par $5$ sont :
$$\begin{array}{cccccc} 21\,930&24\,930&27\,930&22\,935&25\,935&28\,935\end{array}$$
Exercice 21
Une piste d'athlétisme a une longueur de $400\;m.$
a) Déterminons le nombre de tours que doivent effectuer les coureurs de $5\,000\;m$
Comme la piste a une longueur de $400\;m$ alors, le nombre de tours effectués par les coureurs de $5\,000\;m$ est :
$$\text{nombre de tours}=\dfrac{5\,000}{400}$$
En calculant, on trouve : $\dfrac{5\,000}{400}=12.5$
Ce qui signifie que les coureurs de $5\,000\;m$ doivent effectuer $12$ tours et demi.
b) Déterminons le nombre de tours que doivent effectuer les coureurs de $10\,000\;m$
Comme la piste a une longueur de $400\;m$ alors, le nombre de tours effectués par les coureurs de $10\,000\;m$ est :
$$\text{nombre de tours}=\dfrac{10\,000}{400}=25$$
Donc, les coureurs de $10\,000\;m$ doivent effectuer $25$ tours.
Exercice 22
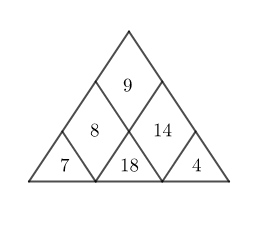
Le triangle ci-dessous est dit magique, car les produits des trois nombres écrits sur les côtés sont égaux.
Son produit magique est :
$$504=7\times 8\times 9=7\times 18\times 4=9\times 14\times 4$$

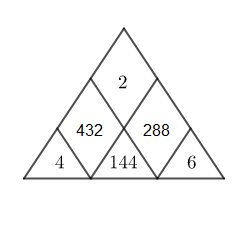
Complétons le triangle ci-dessous pour qu'il soit magique :

On a : $4\times 144\times 6=3\,456$
Donc, pour que le triangle soit magique les produits des trois nombres écrits sur les autres côtés doivent être égaux à $3\,456.$
Ce signifie que :
$4\times\ldots\times 2=3\,456$
$2\times\ldots\times 6=3\,456$
Ainsi, pour trouver la valeur manquante, on divise le nombre $3\,456$ par le produit des deux nombres connus.
On a alors :
$\dfrac{3\,456}{4\times 2}=\dfrac{3\,456}{8}=432$
Donc, pour le côté gauche, le nombre manquant est $432$
De la même manière, on a :
$\dfrac{3\,456}{2\times 6}=\dfrac{3\,456}{12}=288$
Donc, pour le côté droit, le nombre manquant est $288$
Vérification :
$$3\,456=4\times 144\times 6=4\times 432\times 2=2\times 288\times 6$$
Exercice 23
Recopions et complétons les divisions à trous suivantes :
$$\begin{array}{r} 757\\78\\ \\\end{array}\begin{array}{|l} 97\\\hline 7\\ \\\end{array}\qquad\begin{array}{r} 1237\\37\\13\\ \\\end{array}\begin{array}{|l} 24\\\hline 51\\ \\ \\\end{array}$$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
mer, 03/02/2022 - 20:39
Permalien
wouah
Ajouter un commentaire