Solution des exercices : Le rectangle - 5e
Classe:
Cinquième
Exercice 1
1) Traçons deux diamètres $[AB]\ $ et $\ [CD]$ non perpendiculaires d'un cercle $(\mathcal{C}).$
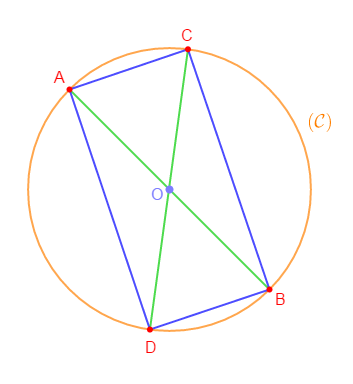
2) Le quadrilatère $ACBD$ est un rectangle.
Justification :
On remarque que les diagonales $[AB]\ $ et $\ [CD]$ ont même milieu $O.$ Donc, le quadrilatère $ACBD$ est un parallélogramme.
Aussi, comme les diagonales non perpendiculaires $[AB]\ $ et $\ [CD]$ sont deux diamètres du cercle $(\mathcal{C})$ alors, elles ont la même longueur.
Or, si un parallélogramme a ses diagonales de même longueur alors c'est un rectangle.
D'où, le quadrilatère $ACBD$ est un rectangle.
Exercice 2
1) Citons deux parmi les propriétés du rectangle.
Dans un rectangle :
$-\ $ les diagonales ont même longueur
$-\ $ deux côtés consécutifs sont perpendiculaire.
2) Reconnaissance d'un rectangle :
$-\ $ Si un quadrilatère a trois angles droits alors c'est un rectangle
$-\ $ Si un parallélogramme a un angle droit alors c'est un rectangle
$-\ $ Si un parallélogramme a ses diagonales de même longueur alors c'est un rectangle
Exemples
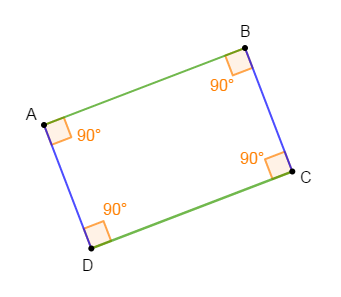
$ABCD$ est un rectangle
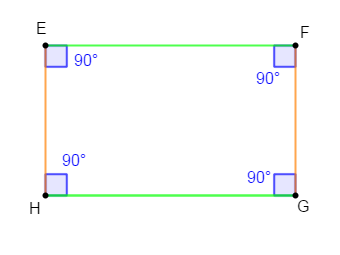
$EFGH$ est un rectangle
Exercice 3
1) Construisons un triangle $ABC$ et la hauteur $(AH)$ tel que $H$ appartient à la droite $(BC).$
2) Construisons les points $M\ $ et $\ N$ pour que les quadrilatères $AHCM\ $ et $\ AHBN$ soient des rectangles.
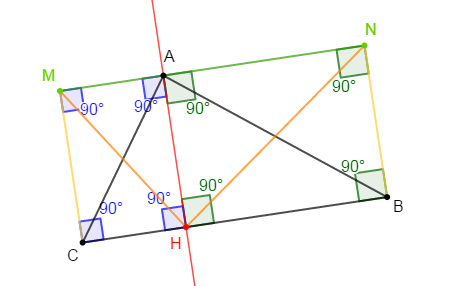
3) Justifions les égalités suivantes :
a) $AC=HM$
On constate que $[AC]\ $ et $\ [HM]$ sont les diagonales du rectangle $AHCM.$
Or, dans un rectangle les diagonales ont même longueur.
Donc, $AC=HM$
b) $AB=HN$
Comme dans un rectangle les diagonales ont même longueur alors, $AB=HN$ car $[AB]\ $ et $\ [HN]$ sont les diagonales du rectangle $AHBN.$
Auteur:
Diny Faye

Commentaires
Souhilta (non vérifié)
dim, 07/04/2021 - 17:59
Permalien
Apprendre mon objectif
Souhilta (non vérifié)
dim, 07/04/2021 - 17:59
Permalien
Apprendre mon objectif
Souhilta (non vérifié)
dim, 07/04/2021 - 17:59
Permalien
Apprendre mon objectif
Souhilta (non vérifié)
dim, 07/04/2021 - 17:59
Permalien
Apprendre mon objectif
Anonyme (non vérifié)
sam, 05/10/2025 - 23:50
Permalien
Exercice le losange
Sambalyon (non vérifié)
mar, 05/20/2025 - 22:56
Permalien
Reussir
Ajouter un commentaire