Devoir n°2 - Physique chimie - 1er S2
Classe:
Première
Exercice 1
La combustion de $1.15\,g$ d'un composé $A$, de formule $C_{x}H_{y}O_{z}$ fournit $2.2\,g$ de dioxyde de carbone et $1.35\,g$ d'eau selon l'équation-bilan suivante :
$$C_{x}H_{y}O_{z}\ +\ aO_{2}\ \Rightarrow\ xCO_{2}\ +\ y/2H_{2}O$$
1.1. Exprimer le coefficient $a$ en fonction de $x$, $y$ et $z.$
1.2. Déterminer la composition centésimale massique de $A.$
1.3. Le volume molaire de $A$ liquide est de $V_{m}=62.2\,mL/mol$ et sa densité par rapport à l'eau est $d=0.74.$
1.4. Calculer la masse molaire de $A.$ On rappelle : et que $\rho_{A}=d\rho_{eau}$ et que $M_{A}=\rho_{A}V_{m}$
1.5. Déterminer la formule brute de $A$ sachant que la masse molaire est égale à $46\,g\cdot mol^{-1}.$
1.6. Écrire sa formule semi-développée sachant que la molécule contient un groupe hydroxyle $(O-H).$
On donne : $C\ :\ 12g/mol$ ; $H\ :\ 1g/mol$ ; $O\ :\ 16g/mol$ ; $\rho_{eau}=1g/mL.$
Exercice 2 Détermination d'un alcane
Un alcane, présent dans le carburant $GPL$, a pour masse molaire $M=86\,g\cdot mol^{-1}.$
2.1. Écrire la formule générale d'un alcane à $n$ atomes de carbone.
2.2. Donner l'expression de la masse molaire de l'alcane en fonction de $n.$
2.3. Déterminer sa formule brute.
2.4. Donner les formules développées possibles de l'alcane et les nommer
Exercice 3
3.1. Une locomotive et son convoi constitue un seul système de masse $M=600$ tonnes. La puissance de la force de traction, constante, a pour valeur $P=24\cdot10^{5}W$ lorsque le train roule à la vitesse constante $V=144km/h$ sur une voie rectiligne et horizontale.

3.1.1. Représenter la force motrice $\overrightarrow{F}$, le poids $\overrightarrow{P}$ de la locomotive, la réaction $\overrightarrow{R}$ des rails et la force de frottement
3.1.2. Calculer la force motrice $\overrightarrow{F}$,
3.1.3. Calculer la force de frottement $\overrightarrow{f}$ qui s'oppose à l'avancement du système.
3.1.4. Quels sont : le travail de la force motrice, le travail du poids, le travail de la réaction et celui de la force de frottement pour un déplacement de $1km$ ?
3.2. Le système {locomotive-convoi} roulant toujours à vitesse constante gravit une voie dont la pente est de $3\%.$
La puissance développée par la nouvelle force motrice est toujours de $24\cdot10^{5}W$ et la résultante des forces de frottement est $f=6\cdot10^{4}N.$
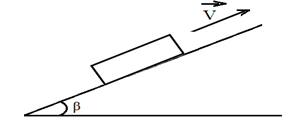
3.2.1. Représenter toutes les forces appliquées au système {locomotive-convoi}
3.2.2. Déterminer l'intensité de la nouvelle force motrice $\overrightarrow{F}.$
3.2.3. Quels sont : le travail de la nouvelle force motrice, le travail du poids et celui de la force de frottement pour un déplacement de $1km$ ?
3.3. Calculer la somme des travaux de toutes les forces appliquées au système et conclure.
Donnée : $g=10N/Kg$
Exercice 4
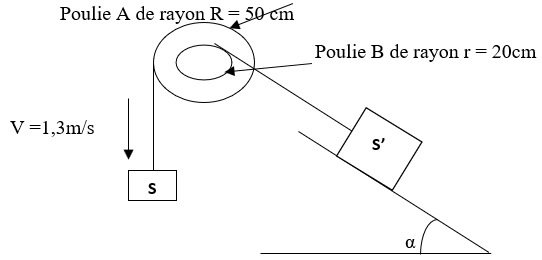
On considère le dispositif de la figure ci-dessous :
Le système $S$ a un poids $P=1000N$ et descend à vitesse constante sans que les câbles ne glissent sur les gorges des poulies $A$ et $B$ solidaires(soudées). Les forces de frottement sur le plan incliné sont représentées par une force unique d'intensité $f=\dfrac{P'}{5}\ ;\ P'=500N$ étant le poids du système $'.$
4.1. Déterminer et représenter la force exercée par le câble sur la poulie $B.$
4.2. Calculer le moment du couple de frottement exercé par l'axe de rotation sur l'ensemble formé par les deux poulies.
4.3. Calculer le travail du poids $\overrightarrow{P}$ sur une durée de $15s$ sachant que la vitesse $V=1.3m/s$
4.4. Calculer le travail du poids $\overrightarrow{P'}$ sur la même durée.
5. Calculer la puissance développée par le couple de frottement ainsi que celle développée par les forces de frottement sur le plan incliné.
N.B :
la bonne présentation de la copie et la rigueur dans la démarche seront prises en compte dans la note des copies
$$\text{Durée : 3 heures}$$

Commentaires
Moussa sow (non vérifié)
dim, 12/19/2021 - 14:03
Permalien
Pc
Nguirane (non vérifié)
lun, 11/27/2023 - 17:31
Permalien
Correction de la devoir
honor (non vérifié)
sam, 01/06/2024 - 23:23
Permalien
réflexion
Amadou Souleyma... (non vérifié)
sam, 03/23/2024 - 21:20
Permalien
Correction de exercice
mouhamed keba seck (non vérifié)
lun, 12/23/2024 - 12:05
Permalien
je veux la correction du devoir
Anonyme (non vérifié)
dim, 12/19/2021 - 14:04
Permalien
Je veux la correction
Elisna (non vérifié)
mer, 10/26/2022 - 16:49
Permalien
Devoir demain
GOUA (non vérifié)
lun, 12/04/2023 - 19:07
Permalien
Bd
kante (non vérifié)
jeu, 02/10/2022 - 12:25
Permalien
etudes
Mohamed Pulisic (non vérifié)
mar, 09/20/2022 - 10:44
Permalien
De recevoir de devoir de physique chimie
Mohamed Pulisic (non vérifié)
mar, 09/20/2022 - 10:45
Permalien
De recevoir de devoir de physique chimie
Bahiba anderson (non vérifié)
mer, 03/09/2022 - 05:34
Permalien
Recherche sur les livres
fallou (non vérifié)
mar, 04/05/2022 - 02:33
Permalien
réussir
Anonyme (non vérifié)
mar, 11/29/2022 - 21:13
Permalien
Excellente
Ousmane Ndiaye (non vérifié)
mer, 11/30/2022 - 18:10
Permalien
Khhkk
Serigne Fallou DEME (non vérifié)
lun, 12/18/2023 - 13:56
Permalien
Non vérifier
Geoffray (non vérifié)
mer, 12/20/2023 - 01:32
Permalien
M'améliorer
Mame bamby (non vérifié)
ven, 12/13/2024 - 14:57
Permalien
J'aimerais avoir la correction de ce devoir svp
Ajouter un commentaire