Série d'exercices : Étude expérimentale des lentilles - 1er s
Classe:
Première
Exercice 1 Obtention de l'image d'un objet $AB$ par une lentille mince
Dans chacun des cas suivant, tracer l'image $A'B'$ du segment $AB$ par la lentille.
Indiquer si l'image est réelle ou virtuelle, droite ou inversée, agrandie ou réduite.
Cas $n^{\circ}1$ :
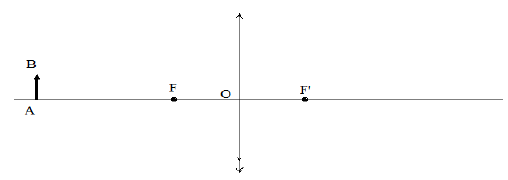
cas $n^{\circ}2$ :
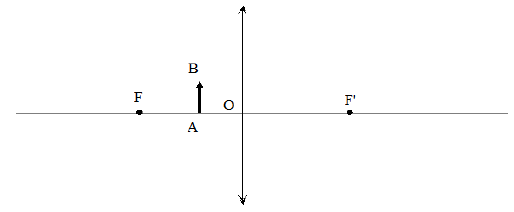
Cas $n^{\circ}3$ :
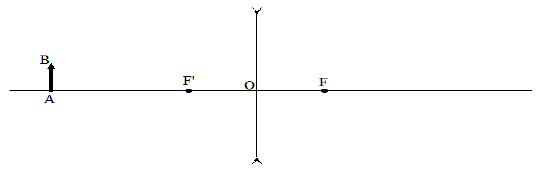
Cas $n^{\circ}4$ :
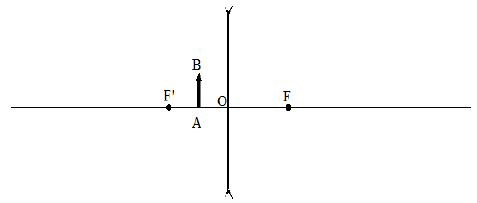
Exercice 2
La distance focale d'une lentille convergente de centre optique $O$ est $4.0\,cm.$
Un objet $AB$ de longueur $2.0\,cm$ est placé perpendiculairement à l'axe de la lentille à $10\,cm$ devant celle-ci.
Le point $A$ est situé sur l'axe optique.
La lumière se propage de gauche à droite.
1) Sur un schéma à l'échelle $1/1$, placer les points $F$, $F'$, $A$ et $B.$
2) Calculer $\overline{OF}$, $\overline{OF'}$ et $\overline{OA}.$
3) Déterminer graphiquement l'image $A'B'$ de $AB$ ; caractériser l'image obtenue.
4) En déduire graphiquement $\overline{OA'}$ et $\overline{A'B'}.$
5) Retrouver $\overline{OA'}$ et $\overline{A'B'}$ en utilisant la formule de conjugaison.
6) Calculer le grandissement de l'image.
Exercice 3
Un objet de grandeur $2.0\,cm$ est placé $4.0\,cm$ d'une loupe, dans un plan perpendiculaire à l'axe principale de celle-ci ; la vergence de cette loupe est $C=20$ dioptries.
1) Calculer la distance focale de cette loupe.
2) Construire l'image de cet objet à travers la loupe à l'échelle $1/2.$
a) Préciser sa nature, réelle ou virtuelle.
b) Préciser son sens.
c) Mesurer sa position par rapport à la loupe.
d) Mesurer sa grandeur ; en déduire le rapport de la grandeur de l'image à celle de l'objet.
Exercice 4
Soit une lentille convergente de distance focale $f'10\,cm$, de centre $O$ et un objet $AB$ placé à $16\,cm$ en avant de $O.$
$A$ est sur l'axe et $AB$ est perpendiculaire à l'axe optique.
1) Calculer la vergence de la lentille et donner son unité.
2) a) Par quelle expérience simple peut-on Vérifier la distance focale de la lentille.
b) Comment peut-on reconnaître une lentille convergente ?
3) a) Donner la relation algébrique de Descartes (relation entre les positions de l'objet et de l'image)
b) Préciser les orientations sur un schéma.
c) calculer numériquement $\overline{OA}$ et $\overline{OA'}.$
4) L'objet est une petite flèche de hauteur $2.0\,cm.$
Donner la formule de Descartes du grandissement $\lambda.$
Calculer $\lambda$ et en déduire la taille de l'image $\overline{A'B'}.$
Exercice 5
Soit une lentille mince convergente de centre optique $O_{1}$ et de distance focale $f=16\,mm.$
(Voir le document ci-dessous à compléter.)
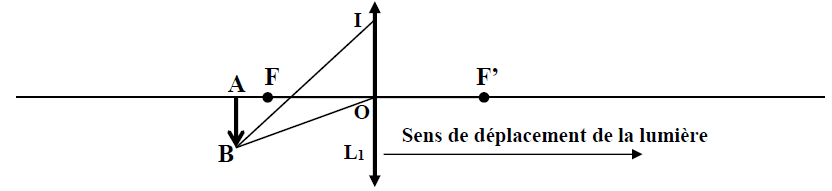
Un objet $AB$ de $5\,mm$ de longueur est placé à $20\,mm$ par rapport au centre optique de la lentille.
1) Calculer : la position de l'image $A'B'$ de $AB$ à travers la lentille $L_{1}$ ;
$-\ $ Le grandissement de la lentille $L_{1}$ dans ces conditions.
$-\ $ La dimension (algébrique) de l'image $A'B'.$
2) L'image $A'B'$ est-elle réelle ou virtuelle, droite ou renversée par rapport à $AB$ ?
Justifier les réponses.
3) Confirmer la position de l'image par une construction.
Exercice 6
Un objet lumineux $AB$ de longueur $5\,cm$ est placé perpendiculairement à l'axe principale d'une lentille mince convergente de distance focale $25\,cm$, le point $A$ est sur l'axe principal.
Déterminer, par le calcul, la position, la nature, le sens et la grandeur de l'image
a) L'objet est réel à $2\,m$ de la lentille
b) L'objet est réel à $50\,cm$ de la lentille
c) l'objet est réel à $20\,cm$ de la lentille
d) L'objet est virtuel à $15,cm$ de la lentille
e) L'objet est virtuel à $1\,cm$ de la lentille
Dans quel cas a-t-on un fonctionnement en loupe ?
Exercice 7
Dans un appareil photographique utilisant une pellicule $24\times36$ (figure 1) ; on dispose d'objectifs assimilables à des lentilles convergentes de distances focales $f'_{1}=24\,mm$ ; $f'_{2}=50\,mm$ ; $f'3=135\,mm.$
L'objectif dit "standard" a une distance focale voisine de la longueur $L$ de la diagonale du rectangle de la pellicule.
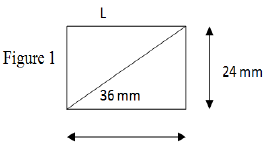
1) Quelle est la distance focale de l'objet standard ?
En déduire parmi les objectifs dont on dispose celui qui s'en approche le plus.
2) Donner la vergence de cet objectif.
3) Construire graphiquement l'image $A'B'$ de $AB.$
Les positions de l'objet, des foyers et de lentille sont celles de la figure ci-jointes, dont l'échelle est arbitraire.
4) Lors d'un défilé de mode on photographie avec le même objectif un mannequin de $1.70\,m$ placé à $7.5\,m$ du centre optique, indiquer :
a) La distance de l'image au centre optique,
b) Le grandissement ainsi que la taille de l'image,
c) Le sens de l'image.
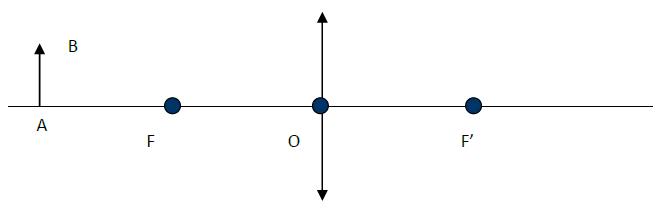
Exercice 8
Un observateur dispose d'une lentille $L$ convergente de distance focale $10\,cm.$
On place un objet réel $AB$ de $1\,cm$ de hauteur, perpendiculaire à l'axe principal de la lentille, à $8\,cm$ avant le centre optique $O$ de la lentille.
Le point $A$ se trouve sur l'axe optique.
A. Étude graphique.
1) Placé sur un schéma
$-\ $ La lentille $L$
$-\ $ Le centre optique $O$
$-\ $ Le foyer objet $F$
$-\ $ Le foyer image $F'$
$-\ $ L'objet $AB$
2) Construire l'image $A'B'$ de l'objet $AB$ donnée par cette lentille.
3) Déterminer graphiquement :
a) La hauteur de l'image $\overline{A'B'}$
b) La position de l'image $\overline{OA'}$
4) En déduire le grandissement $\lambda$
B. Étude théorique
On se propose de vérifier par les calculs les résultats précédents.
On rappelle les formules suivantes :
$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{\overline{OF'}}$
$\lambda=\dfrac{\overline{OA'}}{\overline{OA}}=\dfrac{\overline{A'B'}}{\overline{AB}}$
1) Calculer $\overline{OA'}$
2) Calculer le grandissement $\lambda.$
Interpréter le résultat
Exercice 9
Devant une lentille $L$, de centre optique $O$ et de vergence $C$, on place un objet réel $AB$ perpendiculaire à son axe optique principal tel que et distant de $O$ de $X=1.2\,m.$
Le grandissement de la lentille est $y=-2.$
1) Comment peut distinguer expérimentalement puis théoriquement une lentille divergente d'une lentille convergente ?
2) Établir l'expression de la vergence $C$ de la lentille en fonction $\lambda$ et $x.$
3) Calculer $C$, déduire la nature de la lentille.
4) Déterminer la position de l'image $A'B'$ de l'objet $AB$ donnée par la lentille.
5) Faire un schéma à l'échelle et construire l'image $A'B'$ de $AB$
Échelle $1\,m$ est représenté par $5\,cm.$
(ON prendra $AB=3\,cm)$

Commentaires
Bah Aliou (non vérifié)
ven, 03/14/2025 - 08:00
Permalien
Apprendre
Ajouter un commentaire