Série d'exercices : Dynamique - Ts
Classe:
Terminale
Exercice 1
Dans ce problème on prendra $g=10\,m\cdot s^{-2}.$
Tous les calculs seront effectués à $10^{-2}$ près.
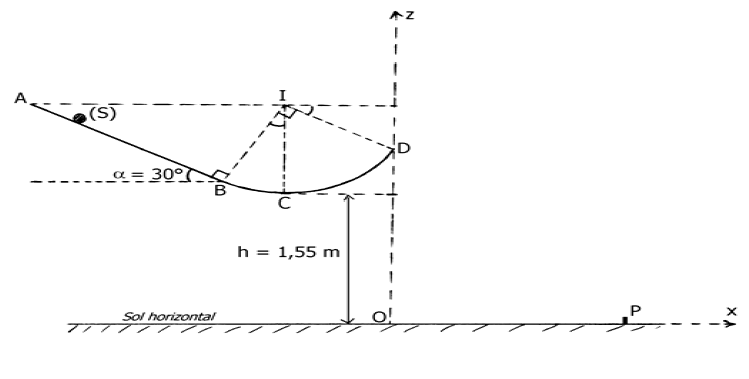
Un solide $(S)$ de masse $m=50\,g$, de dimension négligeable, peut glisser sur une piste $ABCD$ située dans un plan vertical :
$-\ $ $AB$ est la ligne de plus grande pente d'un plan incliné d'un angle $\alpha=30^{\circ}$ par rapport à l'horizontale ; $AB=1.6\,m.$
$-\ $ $BCD$ est le quart d'un cercle de centre $I$ et de rayon $r=0.9\,m$ ; $C$ est situé sur la verticale passant par $I$ (voir figure).
1) On néglige les frottements.
Le solide $(S)$ part du point $A$ sans vitesse.
a) Calculer sa vitesse en $B$, en $C$ et en $D.$
b) Calculer l'intensité de la force $\overrightarrow{R}$ exercée par la piste sur le solide $(S)$ en $C$ et en $D.$
c) Donner les caractéristiques du vecteur vitesse $\overrightarrow{V_{D}}$ du solide $(S)$ au point $D.$
2) On néglige la résistance de l'air.
A partir du point $D$, le solide $(S)$ tombe dans le vide avec la vitesse $\overrightarrow{V_{D}}$ précédente.
Le point $C$ est situé à la hauteur $h=1.55\,m$ du sol horizontal.
a) Donner l'équation cartésienne de la trajectoire du mouvement de $(S)$ à partir du point $D$, dans le repère $(O\;,\ x\;,\ z).$
b) Jusqu'à quelle hauteur $H$ au-dessus du sol horizontal monte le solide $(S)$ ?
c) Calculer la distance $OP$ où $P$ est le point d'impact du solide $(S)$ sur le sol horizontal.
3) Dans cette question, la piste exerce au mouvement du solide $(S)$ une force de frottements $\overrightarrow{f}$ parallèle et de sens contraire à sa vitesse à chaque instant, et d'intensité constante le long de $ABCD.$
Partant de $A$ sans vitesse, le solide $(S)$ s'arrête au point $D.$
a) Établir en fonction de $m$, $g$, $R$ et $\alpha$, l'expression algébrique du travail $W_{\overrightarrow{f}}$ de la force de frottements entre les points $A$ et $D.$
Calculer $W_{\overrightarrow{f}}$
b) En déduire l'intensité de la force $\overrightarrow{f}$
On donne : $\cos 30^{\circ}=0.86.$
Exercice 2
Un avion de guerre supersonique est animé d'un mouvement rectiligne uniforme à la vitesse $V_{0}=400\,m\cdot s^{-1}$ vole à une altitude de $2000\,m$, son radar a détecté un véhicule de transport de soldats ennemis supposé ponctuel, immobile au point $A$, le pilote a décidé de les attaquer, malgré l'interdiction de ce fait par la loi de Genève.
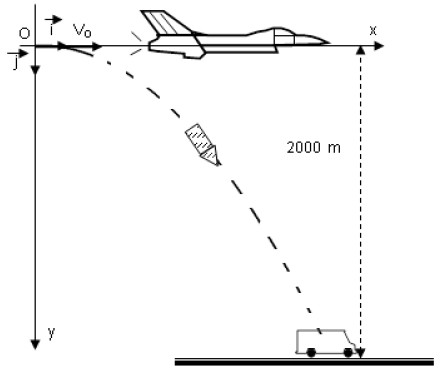
En passant par $O$ origine du repère l'avion $(O\;,\ \vec{i}\;,\ \vec{j})$, a lâché, à une date prise comme origine de temps, une bombe qui après quelques secondes adétériorécomplètement le véhicule et a tué tous les soldats.
En négligeant la force résistance de l'air et en appliquant la relation fondamentale de la dynamique à la bombe déterminer les composantes selon l'axe $(0\;,\ x)$ et selon l'axe $(O\;,\ y)$ de son accélération.
1) Établir les lois horaires de mouvement de la bombe selon les deux axes.
2) En déduire l'équation de la trajectoire de la bombe relativement au repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
3) A quelle distance de la verticale passant par $O$ se trouvait le véhicule ?
Déterminer la date d'arrivée de la bombe au véhicule.
4) Où se trouvait l'avion à la date d'arrivée de la bombe au véhicule ?
Déterminer les caractéristiques du vecteur vitesse de la bombe lorsqu'elle se trouvait à $1000\,m$ au-dessus du sol.
Exercice 3
Dans tout le problème, on néglige les frottements et on prend pour l'intensité de pesanteur $g=10\,m\cdot s^{-2}.$
Un pendule simple est constitué par une bille ponctuelle $M_{1}$ de masse $m_{1}=200\,g$ suspendue au bout d'un fil inextensible de masse négligeable et de longueur $\ell=0.9\,m.$
1) On écarte le pendule d'un angle $\alpha$ par rapport à sa position d'équilibre verticale et on le lâche sans vitesse initiale.
La vitesse de la bille $M_{1}$ lors de son passage à la position
d'équilibre est $v=3\,m\cdot s^{-1}.$
Calculer la valeur de l'angle $\alpha.$
2) Lors de son passage à la position d'équilibre la bille $M_{1}$ heurte, au cours d'un choc parfaitement élastique, une autre bille ponctuelle $M_{2}$ immobile de masse $m_{2}=100\,g.$ (figure)
2) La vitesse de la bille $M_{2}$, juste après le choc, est $v_{A}=4\,m\cdot s^{-1}.$
Calculer la vitesse de la bille $M_{1}$ juste après le choc en appliquant la conservation de la quantité de mouvement.
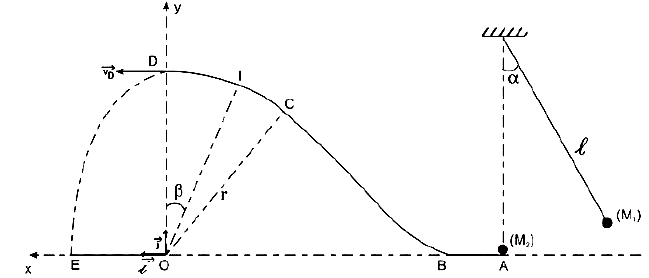
3) La bille $M_{2}$ est propulsée avec la vitesse $V_{A}$ sur une piste qui comporte trois parties :
$-\ $ Une partie horizontale $AB$,
$-\ $ Une certaine courbe $BC$,
$-\ $ Un arc de cercle $CD$, de rayon $r$ et de centre $O.$
Les points $O$, $A$, $B$ et $E$ se trouvent dans un même plan horizontal.
a) Exprimer, en fonction de $g$, $r$, $\beta$ et $v_{A}$, la vitesse de la bille $M_{2}$ au point $I$
b) Exprimer, en fonction de $m_{2}$, $g$, $r$, $\beta$ et $v_{A}$, l'intensité de la réaction de la piste sur la bille $M_{2}$ au point $I.$
c) La bille $M_{2}$ arrive au point $D$ avec une vitesse horizontale de valeur $v_{D}=1\,m\cdot s^{-1}.$
Calculer la valeur de $r.$
4) Arrivée au point $D$, la bille $M_{2}$ quitte la piste avec la vitesse $\overrightarrow{V_{D}}$ précédente et tombe en chute libre.
a) Établir l'équation cartésienne de la trajectoire de la bille $M_{2}$ dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
b) Calculer la distance $OE.$
Exercice 4
Dans tout l'exercice, on suppose que le mouvement des protons a lieu dans le vide.
Et on néglige leur poids devant les autres forces.
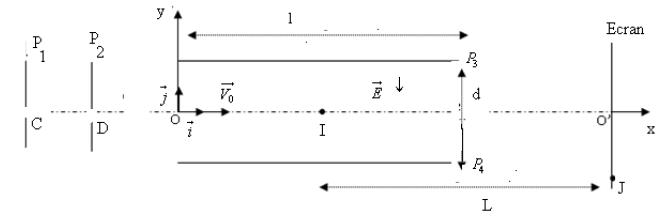
On considère le dispositif de la figure ci-dessous.
Des protons sont émis en $C$ avec une vitesse quasiment nulle, puis accélérés entre les points $C$ et $D$ des plaques $P_{1}$ et $P_{2}$
1. Préciser le signe de la tension $U_{CD}$ pour que les électrons soient accélérés.
Justifier votre réponse.
2. On posera par la suite $|U_{CD}|=U$
2.1 Exprimer la vitesse d'un proton en $D$ en fonction de $U$, $e$ et $m_{p}$
2.2 Calculer cette vitesse.
3. Après la traversée de la plaque $P_{1}$ en $D$, les électrons pénètrent en $O$ entre deux plaques parallèles $P_{3}$ et $P_{4}$ de longueur $l$ et distantes de $d.$
La tension $U'$ appliquée entre ces plaques crée un champ électrostatique $\overrightarrow{E}$ uniforme.
On donne $l=20\,cm$ et $d=7\,cm.$
3.1 Montrer que l'énergie cinétique se conserve entre $D$ et $O.$
3.2 Établir dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ les équations du mouvement d'un proton dans la région limitée par les deux plaques $P_{3}$ et $P_{4}$
3.3 Vérifier que l'équation de la trajectoire peut s'écrire :$$y=-\dfrac{U'}{4dU}x^{2}$$
3.4 Déterminer la condition à laquelle doit satisfaire la tension $U'$ pour que les protons sortent du champ électrostatique $\overrightarrow{E}$ sans heurter la plaque $P_{4}$
3.5 Déterminer $U'$ pour que les protons sortent du champ en passant le point $S$ de coordonnées $\left(l\;,\ -\dfrac{d}{5}\right)$
4. A la sortie du champ électrostatique par le point $S$, les protons sont reçus en $J$ sur un écran plat $E$ placé perpendiculairement à l'axe $Ox$
4.1 Représenter qualitativement la trajectoire d'un proton entre $O$ et $J$
4.2 Établir l'expression littérale de la déviation $O'J$ du spot sur l'écran
4.3 Calculer la distance $O'J.$
On donne :
$L=20\,cm$ ;
$U=10^{3}V$ ;
masse du proton : $m_{p}=1.67\cdot10^{-27}kg$ ;
$OI=\dfrac{l}{2}$
Charge élémentaire : $e=1.6\cdot10^{-19}C$
Exercice 5
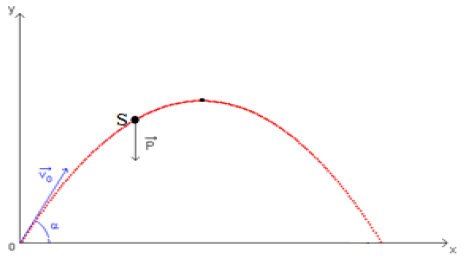
Un dispositif permet de lancer une bille à la vitesse $v_{0}=16\,m\cdot s^{-1}.$
La bille part d'un point $O$, vers le haut, suivant une direction faisant l'angle $\alpha$ avec la verticale.
1) Déterminer les lois horaires du mouvement.
2) Quelle est l'équation de la trajectoire ?
3) a) Pendant combien de temps la bille s'élève-t-elle avant de descendre ?
b) Quelle est sa vitesse à la fin de cette phase ascendante ? $(\alpha=50^{\circ})$
4) Quelle est l'altitude maximale atteinte par la bille, comptée à partir de son point de départ $O$ ?
La bille retombe sur l'axe $Ox$ en $P.$
5) a) Déterminer la distance $OP.$
b) Pour quelle valeur de $\alpha$, $OP$ est-elle maximale ?
Soit $Q$ un point de l'axe $Ox$ d'abscisse $x_{0}=10\,m.$
6) Montrer qu'il y a deux angles de tir $\alpha_{1}$ et $\alpha_{2}$ permettant d'atteindre $Q.$
$$\left(\dfrac{1}{\sin^{2}\alpha}=\dfrac{\sin^{2}\alpha+\cos^{2}\alpha}{\sin^{2}\alpha}=1+cot\,g^{2}\alpha\right)$$
Exercice 6
Une balle $B$ de mini-golf est poussée en $A$ à l'aide d'un club.
La balle, supposée ponctuelle, dévale la pente $AC$ et décolle en $C$ où elle commence alors un mouvement aérien vers le trou noté $T.$
On se propose d'étudier le mouvement de la balle $B$ dans le repère $(O\;,\ x\;,\ z)$ supposé galiléen.
Dans tout l'exercice, on ne considèrera aucune force liée à l'atmosphère.
On précise que $z_{C}=40\,cm$ et $g=9.8\,N\cdot kg^{-1}.$
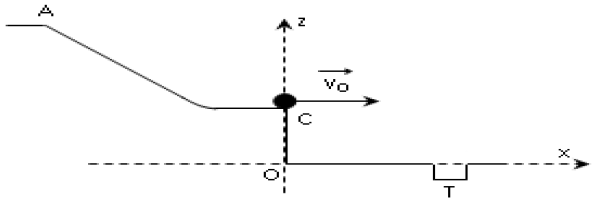
I. La trajectoire balistique de $C$ vers $T.$
La balle quitte le point $C$ de la rampe à la date $t=0s$ avec une vitesse $v_{0}$ horizontale égale à $2.0\,m\cdot s^{-1}.$
a) Qu'est-ce qu'un référentiel galiléen ?
b) Faire le bilan des forces qui s'exercent sur la balle lors de cette phase.
Conclure.
c) Établir les équations horaires de la vitesse et de la position de la balle $B.$
d) En déduire l'équation $z(x)$ de la trajectoire de la balle $B.$
e) Quel doit être alors l'abscisse $x_{T}$ du trou $T$ pour que la balle tombe directement dedans ?
f) Déterminer la date $t_{F}$ à laquelle la balle $B$ tombe dans le trou.
II. Le mouvement sur la rampe
La balle quitte le point $A$ avec une vitesse de $0.80\,m\cdot s^{-1}.$
a) Déterminer la hauteur $z_{A}$ de $A$ nécessaire pour que la balle arrive en $C$ avec la vitesse de $2.0\,m\cdot s^{-1}.$
b) Expliquer pourquoi la vitesse $v_{0}$ est parfaitement horizontale lorsque la balle quitte le point $C.$
Exercice 7
Lors d'un match de basket, pour marquer un panier, il faut que le ballon passe dans un cercle métallique situé dans un plan horizontal, à $3\,m$ du sol.
On assimile le ballon à un point matériel qui doit passer exactement au centre $C$ du cercle métallique.
$xOy$ est un plan vertical contenant le point $C$ ; $xOz$ est le plan du sol supposé horizontal.
1) D'un point $A$ de $Oy$ situé à $2\,m$ du sol, un basketteur, sans adversaire, lance le ballon, avec une vitesse $\overrightarrow{V_{0}}$ contenue dans le plan
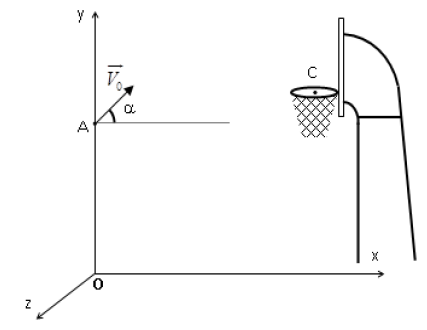
$xOy$ et dont la direction fait un angle $\alpha=45^{\circ}$ avec un plan horizontal.
On négligera l'action de l'air et on prendra $g=10\,m\cdot s^{-2}.$
a) Montrer que la trajectoire est plane.
b) Établir l'équation de cette trajectoire dans le système d'axes indiqué, en fonction de la valeur $V_{0}$ de la vitesse initiale.
c) Quelle doit être la valeur de $V_{0}$ pour que le panier soit réussi, sachant que les verticales de $A$ et de $C$ sont distantes de $7.1\,m$ ?
d) Quelle est la durée du trajet effectué par le ballon du point $A$ au point $C$ ?
2) Voulant arrêter le ballon, un adversaire situé à $0.9\,m$ du tireur, saute verticalement en levant les bras.
La hauteur atteinte alors par ses mains est de $2.7\,m$ au-dessus du sol.
$\alpha$ et $V_{0}$ ayant les mêmes valeurs que précédemment, le panier sera-t-il marqué ?
Exercice 8
Les parties $(A)$ et $(B)$ sont indépendantes.
On donne $g=10\,m\cdot s^{-2}.$
A. Dans cette partie les frottements sont supposés négligeables.
A l'origine des dates, un solide $S_{1}$ supposé ponctuel, de masse $m_{1}=200\,g$ est lâché sans vitesse initiale en un point $A$ d'un plan incliné (fig 1) dont la ligne de plus grande pente fait un angle $\alpha=30^{\circ}$ avec l'horizontale.
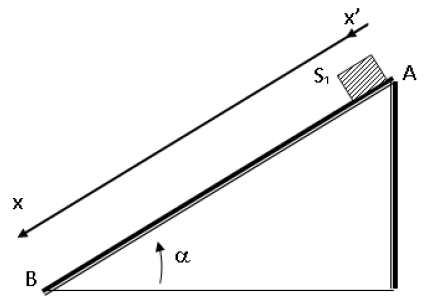
Le solide $(S_{1})$ glisse sans frottement et arrive au point $B$, à la date $t_{B}$, ayant la vitesse $V_{B}.$
1) a) Représenter les forces exercées sur le solide $(S_{1})$
b) Établir l'expression de son accélération $a$, déduire la nature de son mouvement.
Calculer la valeur de $a.$
2) a) Calculer la valeur de la vitesse $V_{B}$ sachant que la distance $AB=2.5\,m.$
b) Calculer la durée $t_{B}$ du trajet $AB.$
B. Dans cette partie les frottements ne sont plus négligeables
Dans cette partie on relie le solide $(S_{1})$ à un solide $(S_{2})$ de masse $m_{2}=m_{1}$ par un fil inextensible, de masse négligeable, qui passe sur la gorge d'une poulie $(P)$ à axe fixe, dont on néglige la masse.
A l'origine des dates $(t=0)$, $(S_{1})$ part de $B$ vers $A$ sans vitesse initiale.
Au cours de son mouvement $(S_{1})$ est soumis à une force de frottement $\overrightarrow{f}$ supposée constante, parallèle à la ligne de plus grande pente du plan incliné et de sens opposé au mouvement. (fig 2)
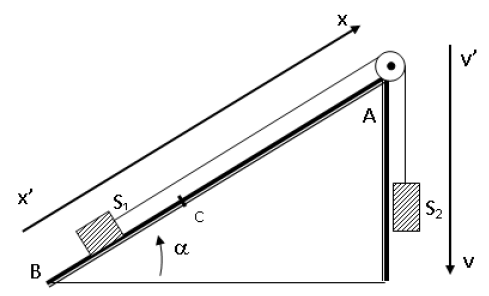
1) a) En appliquant la deuxième loi de Newton $(R.F.D)$ au système, établir l'expression de son accélération $a$ et déduire la nature du mouvement.
b) Sachant que la valeur de $f$ est égale à $0.2\,N$, calculer $a.$
2) A l'instant de date $t_{C}=1\,s$, le solide $(S_{1})$ arrive en $C$ à la vitesse $V_{C}.$
Calculer $V_{C}.$
3) Au passage du solide $(S_{1})$ par le point $C$, le fil est coupé.
a) Donner l'expression de la nouvelle accélération $a_{1}$ du solide $(S_{1})$ après la coupure du fil, déduire la nature de son mouvement.
b) Calculer la distance maximale $($par rapport au point $C)$ parcourue par le solide $(S_{1})$ après la coupure du fil.

Commentaires
Koné Mouhamed (non vérifié)
dim, 01/26/2020 - 14:53
Permalien
Où est la correction des
Hamedi (non vérifié)
mar, 02/09/2021 - 20:59
Permalien
Bac
Mamedy (non vérifié)
mer, 02/07/2024 - 14:33
Permalien
Bac
Hamedi (non vérifié)
mar, 02/09/2021 - 20:59
Permalien
Bac
Moussa gaye (non vérifié)
lun, 03/22/2021 - 16:43
Permalien
Le bac
Mouhamet ndiaye (non vérifié)
jeu, 02/20/2020 - 01:48
Permalien
Reussir
Anonyme (non vérifié)
mer, 04/01/2020 - 14:20
Permalien
Bons exercices
El Hadji Kobar (non vérifié)
ven, 12/04/2020 - 23:42
Permalien
La série
MIAOUAMA (non vérifié)
ven, 01/15/2021 - 10:11
Permalien
Recherche
Lamine Dramé (non vérifié)
mer, 02/17/2021 - 16:32
Permalien
Avoir le bac
Hassan (non vérifié)
jeu, 07/15/2021 - 19:14
Permalien
Réussir
Oumar (non vérifié)
mar, 08/09/2022 - 17:10
Permalien
De maîtriser les exercices pour mon examen
Damba (non vérifié)
sam, 11/26/2022 - 21:51
Permalien
S'il vous plaît je veux la
Miekountima (non vérifié)
ven, 12/30/2022 - 07:13
Permalien
Élève
CAKPO Marius (non vérifié)
mer, 08/14/2024 - 23:02
Permalien
Pct
Kathy (non vérifié)
dim, 12/15/2024 - 18:56
Permalien
Je suis une terminaliste et j
Ajouter un commentaire