Série d'exercices : Propagation des signaux, ondes progressives, interférences mécaniques - 1er s
Classe:
Première
Exercice 1 Ondes le long d'une cordes 1
Un vibreur est le siège d'un mouvement vibratoire périodique de fréquence $f=100\,HZ.$
Les vibrations qu'il crée se propagent le long d'une corde élastique à partir de son extrémité $S$, avec la célébrité $v=8.0\,m\cdot s^{-1}.$
1) Calculer la longueur d'ondes de l'onde qui se propage sur la corde.
2) Comparer le mouvement de la source vibratoire le mouvement d'un point $A$ situé à $32\,cm$ de $S$ et celui d'un point $B$ placé à $40\,cm$ de $S.$
Exercice 2 Ondes le long d'une corde 2
Un vibreur de fréquence $f=100\,HZ$ met en vibration l'extrémité d'une corde élastique.
La figure ci-dessous
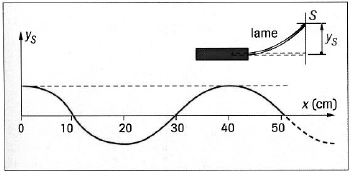
représente l'aspect de la corde à la date $t$ (obtenu par photographie).
1) Combien valent la période, la longueur d'onde et la célérité de l'onde périodique sinusoïdale qui se propage le long de cette corde ?
2) A la date $t$, l'extrémité de la lame est à sa position la plus haute.
Représenter l'aspect de la corde aux dates $t+0.0025\,s$ ; $t+0.0050\,s$ ; $t+0.0075\,s$ et $t+0.010\,s.$
Exercice 3 Ondes rectilignes sur la cuve à ondes 1
On utilise une cuve à ondes.
On crée des ondes rectilignes à la surface de l'eau.
La fréquence de vibration de la réglette est $f=50\,Hz.$
Un enregistrement est réalisé et on dispose d'une image de cet enregistrement.
On voit des lignes claires et noires.
On mesure la distance séparant la crête noire de rang $n$ et la même crête noire de rang $n+4$ ; on trouve $l=16\,cm.$
$–\ $ L'onde est-elle transversale ou longitudinale ?
Justifier la réponse.
$–\ $ Calculer la longueur d'onde des ondes se propageant à la surface de l'eau ;
$–\ $ Calculer la célérité des ondes.
$–\ $ Comparer les mouvements des points $A$ et $B.$
Justifier la réponse.
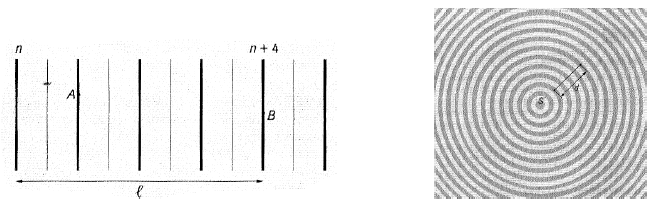
Exercice 4 Ondes circulaires sur la cuve à ondes 2
On utilise une cuve à ondes.
Une pointe $S$ frappe la surface de l'eau de profondeur constante à la fréquence $f=20\,Hz.$
Un enregistrement est réalisé et on dispose d'une image de cet enregistrement.
On voit des cercles clairs et noirs.
On mesure la distance séparant, sur un rayon, le cercle noir de rang $n$ et le cercle noir de rang $n+4$ ; on trouve $d=18\,cm.$
$–\ $ Comment peut-on qualifier l'onde obtenue ?
$–\ $ L'onde est-elle transversale ou longitudinale ?
Justifier la réponse.
$–\ $ Calculer la longueur d'onde des ondes se propageant à la surface de l'eau ;
$–\ $ Calculer la célérité des ondes.
$–\ $ Sur un rayon, on dispose deux petits morceaux de liège en des points $M$ et $N$ tel que $SM=1.5\,cm$ et $SN=10.5\,cm.$
Que peut-on dire des mouvements des points $M$ et $N$ et des mouvements des deux bouchons.
Exercice 5
On considère une corde de longueur $L=120\,cm$ dont l'une des extrémités $S$ est liée à une lame vibrante de fréquence $N=100\,Hz.$
L'autre extrémité est placée de manière à éviter toute réflexion.
L'équation horaire du mouvement de $S$ est $y_{s}(t)=2\cdot10^{-3}\sin(2\pi\,Nt)\;,\ t\geq 0$
Une onde progressive se propage le long de la corde avec une célérité $V$ et une longueur d'onde $\lambda$
1) Déterminer l'équation du mouvement d'un point $P$ de la corde d'abscisse $x=SP.$
2) Exprimer l'abscisse $x$ de $P$ lorsqu'il vibre :
$\bullet\ $ En phase avec $S$ ;
$\bullet\ $ En opposition de phase avec $S.$
3) Au cours de cette propagation on constate que la distance qui sépare le point $M$, $n^{iéme}$ point qui vibre en phase avec $S$ et le point $N$, $(n+2)^{iéme}$ point qui vibre en opposition avec $S$ est $d=50\,cm$
a) Montrer que $d=\dfrac{5\lambda}{2}.$
b) En déduire les valeurs de $\lambda$ et $V$ ;
4) Représenter l'aspect de la corde à l'instant $t_{1}=2\cdot25\cdot10^{-2}s$
Exercice 6
Une lame vibrante est animée d'un mouvement sinusoïdal de fréquence $N.$
Elle est munie d'une pointe qui frappe verticalement la surface libre d'une nappe d'eau au repos en un point $S.$
La source commence à vibrer à l'instant $t=0s.$
On néglige l'amortissement et réflexion des ondes.
1. Définir une onde.
2. Décrire ce qu'on observe a la surface de l'eau, en lumière ordinaire.
3. L'analyse du mouvement d'un point $M_{1}$ situé a la distance $x_{1}$ de $S$, donne le diagramme suivant
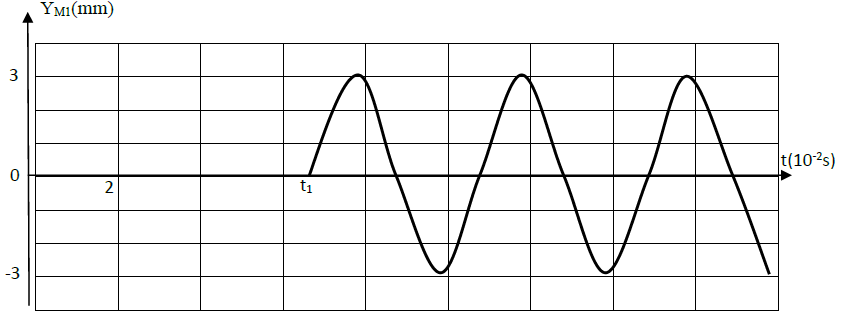
3.1 Déterminer :
$-\ $ La fréquence $N$
$-\ $ L'instant $t_{1}$
$-\ $ La distance $x_{1}$ sachant que la célérité de propagation $V=0.25\,m\cdot s^{-1}.$
3.2 Calculer la longueur d'onde $\lambda.$
3.3 Déterminer l'équation horaire du mouvement du point $M_{1}$
3.4 Déduire l'équation horaire du mouvement de la source $S.$
4. Établir l'équation horaire du mouvement d'un point $M$ de la surface de l'eau situé à la distance $x$ de $S.$
5. Tracer l'aspect d'une coupe de la surface de l'eau par un plan vertical passant par S a un instant $t_{2}=9\cdot10^{-2}s$
6. On éclaire la surface d'eau à l'aide d'un stroboscope de fréquence réglable $N_{e}.$
$10\,Hz\leq N_{e}\leq 100\,Hz$
6.1 Qu'observe-t-on en immobilité apparente.
6.2 Déterminer les fréquences $N_{e}$ pour lesquelles on observe l'immobilité apparente de la surface de l'eau.
Exercice 7
Une corde élastique de longueur $L=40\,cm$, tendue horizontalement et reliée par l'une de ces extrémité $(S)$ à un vibreur qui lui impose des vibrations rectilignes sinusoïdales d'amplitude $a=2\,mm$ et de fréquence $N=50\,Hz.$
La célérité des ondes le long de la corde est $V=5m\cdot s^{-1}.$
1. Dire pourquoi on utilise des absorbants d'énergie au niveau des supports fixes.
2. Décrire l'aspect de la corde :
$-\ $ En lumière ordinaire.
$-\ $ En lumière stroboscopique pour une fréquence du stroboscope $N_{e}=25\,Hz$
3. Calculer la longueur d'onde $\lambda.$
4. Écrire l'équation du mouvement de la source $(S)$ sachant qu'elle débute son mouvement a la date $t=0s$ dans le sens négatif.
5. Établir l'équation de mouvement d'un point $M$ de la corde d'abscisse $x=SM.$
6.1 Déduire l'équation de mouvement d'un point $M_{1}$ de la corde d'abscisse $x_{1}=17.5\,cm$
6.2 Représenter sue le même système d'axes $y_{s}(t)$ et $y_{M_{1}}(t).$
Comparer les mouvements des points $S$ et $M_{1}.$
7. Écrire l'équation traduisant l'aspect de la corde à la date $t_{2}=0.035s.$
Représenter l'aspect de la corde à cette date.
8. Déterminer le nombre et les positions des points qui vibrent en opposition de phase par rapport à la source à l'instant $t_{2}.$
Exercice 8
Une pointe excite verticalement un point $O$ de la surface libre d'un liquide homogène à la fréquence $N=25\,Hz.$
L'origine des temps $(t=0s)$ est choisie à l'instant où $O$ commence à vibrer en se déplaçant vers le haut, sens choisis comme sens positif des élongations.
Le mouvement de $O$ est supposé sinusoïdal d'amplitude $a=5\,mm.$
On appellera $V$ la célérité de propagation des déformations à la surface du liquide et on négligera la diminution d'amplitude due à l'amortissement et la dilution de l'énergie.
1.1 Le phénomène résultant de la propagation des déformations à la surface du liquide est appelé onde mécanique transversale.
Justifier cette appellation.
1.2 Décrire l'aspect de la surface libre du liquide en lumière ordinaire.
2. Établir l'équation horaire $y_{O}(t)$ du mouvement de $O.$
3.1 Définir la longueur d'onde $\lambda.$
3.2 Sachant qu'à l'instant de date $t_{1}=0.02s$, le front d'onde est à $8\cdot10^{-3}m$ de $O.$
Calculer les valeurs de $\lambda$ et $V.$
4. On considère un point quelconque $M$ de la surface du liquide à une distance $r=OM$ de $O.$
4.1 Établir l'équation horaire $y_{M}(t)$ du mouvement de $M$ en fonction de $r$, $t$ et $\lambda.$
4.2 Déterminer l'expression donnant les valeurs de $r$ pour lesquelles le mouvement de $M$ est en opposition de phase avec celui de $O.$
5.1 Représenter, en justifiant, une coupe transversale de la surface du liquide suivant un plan vertical passant par $O$, à l'instant de date $t_{2}=7\cdot10^{-2}s$ de $O.$
5.2 Soit $P$ un point de la surface libre du liquide situé à $r=2\cdot10^{-2}m$ de $O.$
5.2.1 Déterminer la valeur de la vitesse de ce point à l'instant de date $t_{2}$
5.2.2 Déterminer le déphasage du mouvement de $P$ avec celui de $O.$
Préciser, en justifiant, si ce déphasage évolue ou non au cours du temps.
Exercice 9
Une corde élastique de longueur infinie, tendue horizontalement, est attachée par son extrémité $S$ à une lame vibrante qui lui communique, à partir de l'instant de date $t_{0}=0\,s$, des vibrations sinusoïdales de fréquence $N.$
On suppose qu'il n'y a aucun amortissement.
1. Décrire brièvement ce qu'on observe :
1.1 En lumière ordinaire.
1.2 En lumière stroboscopique, pour une période $Te$ légèrement supérieure à la période $T$ du vibreur.
2. L'une des courbes de la figure 3 représente le diagramme du mouvement d'un point $A$ de la corde situé à une distance $x_{A}$ de l'extrémité source.
L'autre représente l'aspect de la corde à un instant de date $t_{1}.$
Figure 3
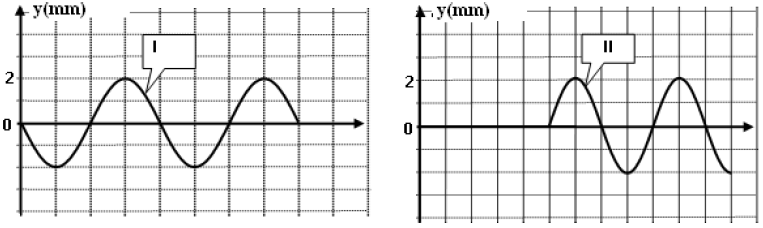
Échelle :
des abscisses : $1\text{ div }\ \rightarrow\ t=2\cdot10^{-3}s$
des ordonnées : $1\text{ div }\ \rightarrow\ x=2\,cm$
Identifier les courbes $(I)$ et $(II)$ en justifiant la réponse.
En déduire les valeurs de la période temporelle $T$ et spatiale $l$ de l'onde, ainsi que celle de son amplitude $a.$
3. Déterminer graphiquement la célérité de l'ébranlement, la distance $x_{A}$ et l'instant de date $t_{1}.$
4. Établir l'équation horaire des vibrations du point $A$ de la corde et déduire celle de la source $S.$
5. Représenter l'aspect de la corde à l'instant de date $t_{2}=2.8\cdot10^{-2}s.$
6. Déterminer la distance parcourue par la source $S$ entre les dates $t_{0}=0\,s$ et $t_{2}=2.8\cdot10^{-2}s.$
Exercice 10
1) Un vibreur $S_{1}$ est animé d'un mouvement oscillatoire sinusoïdal vertical de fréquence $30\,Hz$ et d'amplitude $2\,cm.$
Il est mis en route à la date $t=0$ à partir de sa position la plus basse.
Écrire l'équation horaire de $S_{1}$ dans un repère $Oy$ orienté vers le haut.
2) $S_{1}$ est relié à une corde élastique horizontale de longueur $52\,cm$ sur laquelle prend naissance une onde qui progresse à la célérité de $2.4m/s.$
Écrire l'équation du mouvement d'un point $M$ situé à la distance de $20\,cm$ de $S_{1}.$
Comparer $I$ l'état vibratoire de $S_{1}$ et de $M.$
3) A l'autre extrémité de la corde se trouve un deuxième vibreur $S_{2}$, identique a $S_{1}$ mais qui est mis en route à la date $t=0$ à partir de sa position la plus haute.
Écrire l'équation horaire de $S_{2}.$
4) Écrire l'équation horaire du mouvement du même point $M$ qu'en 2) sous $I$ l'effet de l'onde progressive issue de $S_{2}.$
5) Quel est l'état vibratoire du point $M$ sous l'effet des ondes issues de $S_{1}$ et $S_{2}$ ensemble ?
6) Comment peut-on qualifier les $2$ sources $S_{1}$ et $S_{2}$ ?
Peuvent-elles donner naissance à un phénomène d'interférences ?
Exercice 11
Sur une nappe d'eau, à l'aide de deux pointes reliées a un même vibreur, on produit des vibrations de même amplitude $A=0.3\,cm$ et dont la fréquence est égalé à $10\,Hz.$
Les ondes se déplacent a une vitesse de $50cm/s.$
La distance entre les pointes $P_{1}$ et $P_{2}$ vaut $10\,cm.$
1) Expliquer pourquoi, pour observer le phénomène d'interférences, il est important que ces pointes soient reliées au même vibreur.
2) Calculer la longueur d'onde.
3) Écrire l'équation horaire des deux pointes $P_{1}$ et $P_{2}$, sachant qu'à l'instant $t=0\,s$, les pointes passent par la position la plus basse.
4) Établir l'expression générale de l'équation d'onde pour un point qui se situe a une distance $x$ d'une des deux pointes.
Soit un point $M$ qui se situe à $15\,cm$ de $P_{1}$ et à $17.5\,cm$ de $P_{2}.$
5) Déterminer les $2$ équations d'ondes arrivant au point $M$ et issues respectivement de $P_{1}$ et $P_{2}.$
6) En déduire l'équation horaire de $M$, sous l'effet des deux ondes issues de $P_{1}$ et $P_{2}$ ensemble.
Quelle est l'amplitude du point $M$ ?
7) Énoncer et expliquer la condition générale sur la différence de marche $\delta$ pour obtenir une interférence destructives
Exercice 12 Interférences à la surface de l'eau
Diverses expériences sont réalisées dans une cuve à ondes, afin de déterminer certaines caractéristiques de l'onde.
1. On produit des ondes progressives circulaires à la surface de l'eau en utilisant une cuve à ondes.
La célérité $c$ de l'onde est mesurée et vaut : $c=40\,cm\cdot s^{-1}.$
Le point source $S$ de la surface du liquide contenu dans la cuve à ondes est animé d'un mouvement vertical sinusoïdal de fréquence : $f=20\,Hz$ et d'amplitude $a$ supposée constante : $a=2.0\,mm.$
On néglige l'amortissement dû aux forces de frottement.
1.1 Calculer la longueur d'onde $\lambda$ de l'onde progressive.
1.2 On considère un point $M$ de la surface de l'eau situé à : $d=12\,cm$ du point $S.$
Le point $M$ vibre-t-il en phase ou en opposition de phase avec le point source $S$ ?
Justifier.
2. On réalise maintenant des interférences à la surface de l'eau.
Deux points sources synchrones, notés $S_{1}$ et $S_{2}$, vibrant en phase et ayant même amplitude $a=2.0\,mm$, émettent chacun une onde progressive de fréquence : $f=20\,Hz.$
On s'intéresse à la zone où les deux ondes interfèrent.
En un point $P$ de la région où se superposent les ondes issues des deux sources, $\delta=S_{2}P-S_{1}P$ représente la différence de marche entre les deux ondes qui arrivent en $P.$
2.1 Donner l'état vibratoire d'un point noté $P_{1}$ de la surface de l'eau tel que $S_{1}P_{1}=8.0\,cm$ et $S_{2}P_{1}=17\,cm$ en justifiant la réponse.
2.2 On considère le segment $S_{1}S_{2}$ de longueur $S_{1}S_{2}=11\,cm.$
Déterminer l'amplitude $A$ du mouvement du point $O$ milieu de ce segment.
2.3 Montrer que, sur le segment $S_{1}S_{2}$, deux points consécutifs d'amplitude maximale sont distants de $\dfrac{\lambda}{2}.$
2.4 Combien y a-t-il de points d'amplitude maximale sur le segment $S_{1}S_{2}$ ?
Répondre en s'aidant d'un schéma explicatif.
Exercice 13 Ondes dans un liquide
L'extrémité $S$ d'une corde élastique, tendue horizontalement, est mise en mouvement vibratoire vertical et sinusoïdal à l'aide d'un vibreur.
La corde est alors le siège d'une onde progressive sinusoïdale.
Le mouvement de l'extrémité $S$ débute à l'origine du temps $(t=0s)$ et est caractérisé par une fréquence $N$ et une amplitude $a.$
Dans la suite, on suppose absent tout phénomène d'amortissement ou de réflexion des ébranlements.
L'analyse du mouvement d'un point $A$ de la corde, situé à la distance $x_{A}=3\,cm$ de la source d'onde $S$, a fourni le diagramme de la figure 6.a (voir page 4/4 à rendre avec la copie).
La figure 6.b (voir page 4/4 à rendre avec la copie) représente une photo de la corde prise à l'instant de date $t_{1}.$
1. Déterminer, en se référant aux deux figures (6.a et 6.b) :
1.1 La période temporelle $T$ et la fréquence $N$ de l'onde progressive dans la corde.
1.2 La date $\theta$ à laquelle le point $A$ a commencé son mouvement vibratoire et son amplitude $a.$
1.3 La vitesse $V$ de propagation de l'onde dans cette corde.
En déduire sa longueur d'onde $\lambda.$
1.4 La date $t_{1}$ à laquelle a été prise la photo de la corde (figure 6.b).
2.1 Déterminer l'équation horaire $y_{A}(t)$ du mouvement du point $A.$
En déduire celle de la source d'onde $y_{S}(t).$
$($On pourra appliquer le principe de propagation entre $A$ et $S)$
2.2 Représenter alors, sur la même figure 6.a, le diagramme du mouvement de la source $S.$
Exercice 14
A l'extrémité $S$ d'une lame vibrante à la fréquence $N$, on fixe l'une des extrémités d'une corde élastique de longueur $L$, l'autre extrémité étant fixée à un solide de masse $M=50\,g$ qui plonge dans un liquide pour empêcher les phénomènes des réflexions des ondes.
Au cours de cette étude on néglige les amortissements.
Sur la figure ci-dessous on donne les graphes suivants :
1) La courbe A représente la variation de l'élongation d'un point $M_{1}$ de la corde d'abscisse $x_{1}$, en fonction du temps.
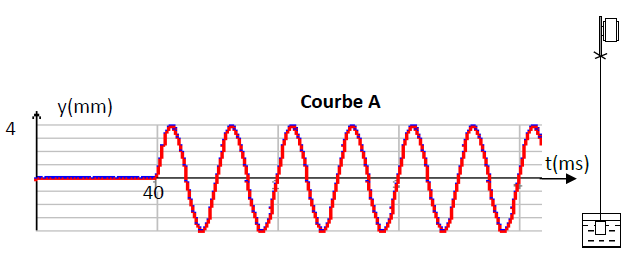
Déduire à partir de cette courbe :
$-\ $ La fréquence $N$ de la lame vibrante.
$-\ $ L'équation donnant la variation de l'élongation du point $M_{1}$ en fonction du temps, sachant que $S$ débute son mouvement à l'origine des dates $t=0\,s.$
$-\ $ Le retard temporel mis par l'onde pour atteindre le point $M_{1}.$
$-\ $ L'équation donnant la variation de l'élongation du point $S$ en fonction du temps
2) La courbe B représente l'aspect de la corde à une date $t_{1}.$
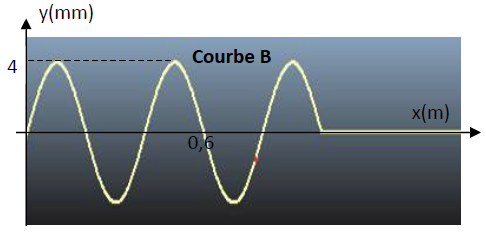
Déterminer :
$-\ $ La longueur d'onde $\lambda.$
Déduire la célérité de l'onde.
$-\ $ La masse linéique $\mu$ de la corde.
On donne l'expression de la célérité d'une onde le long d'une corde élastique $v=\sqrt{\dfrac{T}{\mu}}$ avec $T$ :
tension de la corde et $\mu=\dfrac{\text{masse de la corde}}{\text{longueur de la corde}}$
$-\ $ La date $t_{1}.$
$-\ $ L'aspect de la corde à la date $t_{2}=t_{1}+0.5T.$
$($On suppose qu'a la date $t_{2}$ l'onde n'as pas encore atteint l'extrémité de la corde$).$
$-\ $ L'abscisse $x_{1}$ du point $M_{1}.$
3) Pour observer l'aspect de la corde à la date $t_{1}$ on utilise un stroboscope dont les fréquences des éclaires varient de $20$ à $240\,Hz.$
Déterminer les fréquences du stroboscope qui peuvent donner l'immobilité apparente observée à la date $t_{1}.$
4) Déterminer à la date $t_{1}$ le nombre et les positions des points ayant une vitesse de valeur algébrique positive et une élongation de $2\,mm$ :
$-\ $ Par calcul.
$-\ $ A partir de l'une des courbes.
5) Déterminer à la date $t_{1}$, par calcul et à partir de l'une des courbes, le nombre et les positions des points de la corde qui vibrent en quadrature retard de phase par rapport à un point $M_{2}$ d'abscisse $x_{2}=20\,cm.$

Commentaires
Hasna (non vérifié)
dim, 10/18/2020 - 09:29
Permalien
Correction please de exercice
Maman (non vérifié)
dim, 07/18/2021 - 17:04
Permalien
Tout les exos
Hasina (non vérifié)
mar, 11/23/2021 - 14:56
Permalien
Correction de exo 1
Koupékimissa (non vérifié)
sam, 06/10/2023 - 08:14
Permalien
Obtention des corrigés
Jaafar (non vérifié)
jeu, 08/10/2023 - 13:13
Permalien
Vu correction exercice
Jaafar (non vérifié)
jeu, 08/10/2023 - 13:14
Permalien
Vu correction exercice
Souma (non vérifié)
dim, 10/08/2023 - 23:28
Permalien
Correction
Lmotakhalif (non vérifié)
jeu, 11/09/2023 - 09:20
Permalien
...
Chahouani nourdine (non vérifié)
ven, 08/23/2024 - 17:53
Permalien
Exercices
Chahouani nourdine (non vérifié)
ven, 08/23/2024 - 17:55
Permalien
Preparation
Anonyme (non vérifié)
ven, 08/23/2024 - 17:55
Permalien
Pour voir correction
Ajouter un commentaire