Solution des exercices : Gravitation universelle - Ts
Classe:
Terminale
Exercice 1
1) Calcul de la valeur de l'intensité $g$ du champ de pesanteur à l'altitude $h$
$\begin{array}{rcl} g&=&g_{0}\dfrac{R^{2}}{(R+h)^{2}}\\\\&=&9.8\times\dfrac{(6.4\cdot 10^{6})^{2}}{(6.4\cdot 10^{6}+3.6\cdot 10^{7})^{2}}\\\\\Rightarrow\;g&=&0.22\,m\cdot s^{-2} \end{array}$
2) Bilan des forces appliquées au satellite
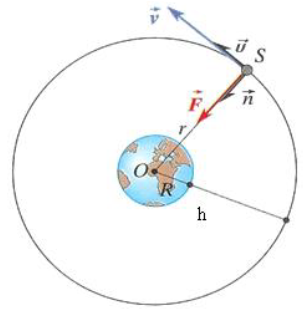
Le satellite est soumis à la force de gravitation :
$\overrightarrow{F}=k\dfrac{Mm}{r^{2}}\overrightarrow{n}$
La vitesse du satellite
La deuxième loi de Newton s'écrit :
$\begin{array}{rcl} \overrightarrow{F}=m\overrightarrow{a}&\Rightarrow&k\dfrac{Mm}{r^{2}}\overrightarrow{n}=m\overrightarrow{a}\\\\&\Rightarrow&\overrightarrow{a}=k\dfrac{M}{r^{2}}\overrightarrow{n} \end{array}$
En projetant la relation dans le repère de Frenet $\left(S\;,\ \overrightarrow{u}\;,\ \overrightarrow{n}\right)$
$\begin{array}{rcl} k\dfrac{Mm}{r^{2}}&=&m\,a_{n}\\\\&=&m\dfrac{v^{2}}{r}\\ \\\Rightarrow\;v&=&\sqrt{k\dfrac{M}{r}}\\\\\Rightarrow\;v&=&\sqrt{6.67\cdot 10^{-11}\times\dfrac{5.97\cdot 10^{24}}{6.4\cdot 10^{6}+3.6\cdot 10^{7}}}\\\\\Rightarrow\;v&=&3.1\cdot 10^{3}m\cdot s^{-1} \end{array}$
3) Détermination de la période du mouvement
$\begin{array}{lcl} T&=&\dfrac{2\pi(R+h)}{v}\\\\&=&\dfrac{2\pi(6.4\cdot 10^{6}+3.6\cdot 10^{7})}{3.1\cdot 10^{3}}\\ \\\Rightarrow\;T&=&86\cdot 10^{3}s \end{array}$
Exercice 2
1.1.1 Expression de l'intensité $F_{0}$ de la force exercée par la Terre sur un corps ponctuel de masse $m=1Kg$ placé à surface
$F_{0}=G\dfrac{mM_{T}}{R_{T}^{2}}$
1.1.2 a) Expression de la masse $M_{T}$ de la Terre en fonction de $g_{0}$, $R_{T}$ et $G$
$\begin{array}{rcl} F_{0}&=&G\dfrac{mM_{T}}{R_{T}^{2}}\\\\&=&m g_{0}\\\\\Rightarrow\;M_{T}&=&\dfrac{g_{0}R_{T}^{2}}{G} \end{array}$
b) Calcul de la masse de la Terre
$\begin{array}{rcl} M_{T}&=&\dfrac{g_{0}R_{T}^{2}}{G}\\\\&=&\dfrac{9.8\times(6370\cdot 10^{3})^{2}}{6.67\cdot 10^{-11}}\\\\\Rightarrow\;M_{T}&=&5.96\cdot 10^{24}kg \end{array}$
1.2 Montrons qu'a l'altitude $h$ au-dessus de la Terre, l'intensité du champ de gravitation est donnée par la relation :
$g=g_{0}\dfrac{R_{T}^{2}}{(R_{T}+h)^{2}}$
A la distance $r$ :
$g=G\dfrac{M_{T}}{r_{2}}$
A la surface de la Terre :
$g_{0}=G\dfrac{M_{T}}{R_{T}^{2}}\Rightarrow\;GM_{T}=g_{0}R_{T}^{2}$
A l'altitude $h$ :
$g=G\dfrac{M_{T}}{(R_{T}+h)^{2}}\Rightarrow\;g=\dfrac{g_{0}R_{T}^{2}}{(R_{T}+h)^{2}}$
2.1 Montrons que le mouvement du satellite est uniforme
$-\ $ Système : le satellite
$-\ $ Référentiel d'étude : terrestre
$-\ $ Bilan des forces appliquées : la Force gravitationnelle $\overrightarrow{F}$
La deuxième loi de Newton
$\overrightarrow{F}=m\overrightarrow{a}\Rightarrow-G\dfrac{Mm}{r^{2}}\overrightarrow{u}=m\overrightarrow{a}$
$\Rightarrow\overrightarrow{a}=-G\dfrac{M}{r^{2}}\overrightarrow{u}$
En projetant la relation dans le repère $\left(S\;,\ \overrightarrow{u_{t}}\;,\ \overrightarrow{u_{n}}\right)$
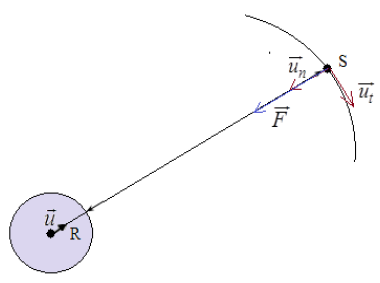
$a=a_{n}\Rightarrow\;a_{t}=\dfrac{\mathrm{d}v}{\mathrm{d}t}=0\Rightarrow\;v=cte$
Le mouvement du satellite est donc uniforme
2.2 Établissement en fonction $g_{0}$, $R_{T}$ et $h$
2.2.1 de l'expression de la vitesse $v$ du satellite ;
$\begin{array}{rcl} a=a_{n}&\Rightarrow&G\dfrac{M}{r^{2}}=\dfrac{v^{2}}{r}\\\\&\Rightarrow&v^{2}=\dfrac{GM}{r}\\\\&\Rightarrow&v^{2}=\dfrac{g_{0}R_{T}^{2}}{R_{T}+h}\\ \\&\Rightarrow&v=\sqrt{\dfrac{g_{0}R_{T}^{2}}{R_{T}+h}} \end{array}$
2.2.2 de l'expression de la période $T$ du satellite ;
$\begin{array}{rcl} T&=&\dfrac{2\pi r}{v}\\\\&=&2\pi(R_{T}+h)\sqrt{\dfrac{R_{T}+h}{g_{0}R_{T}^{2}}}\\\\&=&2\pi\sqrt{\dfrac{(R_{T}+h)^{3}}{g_{0}R_{T}^{2}}} \end{array}$
2.3 Calcul de $v$ et $T$
$\begin{array}{rcl} v&=&\sqrt{\dfrac{g_{0}R_{T}^{2}}{R_{T}+h}}\\\\&=&\sqrt{\dfrac{9.8\times (6370\cdot 10^{3})^{2}}{6370\cdot 10^{3}+300\cdot 10^{3}}}\\\\\Rightarrow\;v&=&7.7\cdot 10^{2}m\cdot s^{-1} \end{array}$
$\begin{array}{rcl} T&=&\dfrac{2\pi(R_{T}+h)}{v}\\\\&=&\dfrac{2\pi(6370\cdot 10^{3}+300\cdot 10^{3})}{7.7\cdot 10^{2}}\\\\\Rightarrow\;T&=&54\cdot 10^{3}s \end{array}$
2.4.1 Montrons que le rapport $\dfrac{T^{2}}{r^{3}}$ est égal à un constante .
$T=2\pi\sqrt{\dfrac{(R_{T}+h)^{3}}{g_{0}R_{T}^{2}}}$ or, $\ r=R_{T}+h$ donc,
$\begin{array}{rcl} T=2\pi\sqrt{\dfrac{r^{3}}{g_{0}R_{T}^{2}}}&\Rightarrow&T^{2}=4\pi^{2}\times\dfrac{r^{3}}{g_{0}R_{T}^{2}}\\\\&\Rightarrow&\dfrac{T^{2}}{r^{3}}=\dfrac{4\pi^{2}}{g_{0}R_{T}^{2}}\ =\ cte \end{array}$
2.4.2 Exprimer le rapport $\dfrac{T^{2}}{r^{3}}$ en fonction de $M_{T}$ et $G$
$T=2\pi\sqrt{\dfrac{r^{3}}{g_{0}R_{T}^{2}}}$ or $GM_{T}=g_{0}R_{T}^{2}$
$\Rightarrow\dfrac{T^{2}}{r^{3}}=\dfrac{4\pi^{2}}{GM_{T}}=cte$
2.4.3 Calculer la masse $M_{T}$ de la Terre.
$\begin{array}{rcl} \dfrac{T^{2}}{r^{3}}&=&\dfrac{4\pi^{2}}{GM_{T}}\\\\\Rightarrow\;M_{T}&=&\dfrac{4\pi^{2}r^{3}}{GT^{2}}\\\\&=&\dfrac{4\pi^{2}(R_{T}+h)^{3}}{GT^{2}}\\\\&=&\dfrac{4\pi^{2}(6370\cdot 10^{3}+300\cdot 10^{3})^{3}}{6.67\cdot 10^{-11}\times(54\cdot 10^{3})^{2}} \end{array}$
Cette valeur n'est pas compatible avec celle de la question 1.1.2
Exercice 3
1.1 Expression de la vitesse $V$ de $(S)$ en fonction de l'intensité $G_{0}$ du champ de gravitation du sol, de $R$ et $r$
$\begin{array}{rcl} a_{n}&=&\dfrac{GM}{r^{2}}\\\\&=&\dfrac{v^{2}}{r}\\\\\Rightarrow\;v&=&\sqrt{\dfrac{GM}{r}}\text{ or }\;G_{0}R^{2}&=&GM\\\\\Rightarrow\;v&=&\sqrt{\dfrac{G_{0}R^{2}}{r}} \end{array}$
1.2 Expression de la période $T$ du mouvement.
$\begin{array}{lcl} vT=2\pi r&\Rightarrow&T=\dfrac{2\pi r}{v}\\\\&\Rightarrow&T=2\pi r\sqrt{\dfrac{r}{G_{0}R^{2}}}\\\\&\Rightarrow&T=2\pi\sqrt{\dfrac{r^{3}}{G_{0}R^{2}}} \end{array}$
Calculer de $T$
$\begin{array}{rcl} T&=&2\pi\sqrt{\dfrac{r^{3}}{G_{0}R^{2}}}\\\\&=&2\pi\sqrt{\dfrac{(8\,000\cdot 10^{3})^{3}}{9.8\times(6\,400\cdot 10^{3})^{2}}}\\\\\Rightarrow\;T&=&7.1\cdot 10^{3}s \end{array}$
2.1 Montrons que le travail de la force gravitation lors du déplacement du sol jusqu'à l'orbite de rayon $r$ est donné par :
$W=mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)$
$\begin{array}{rcl} \mathrm{d}w&=&-f\mathrm{d}r\\\\&=&-\dfrac{GmM}{r^{2}}\mathrm{d}r\\\\\Rightarrow\;W&=&-\int_{R}^{r}\dfrac{GmM}{r^{2}}\mathrm{d}r\\\\&=&\left[\dfrac{GmM}{r}\right]_{R}^{r}\\\\\Rightarrow\;W&=&mGM\left(\dfrac{1}{r}-\dfrac{1}{R}\right)\\\\&=&mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right) \end{array}$
avec $G_{0}R^{2}=GM$
2.2 Expression de l'énergie potentielle du système Terre-satellite en fonction de $G_{0}$, $m$, $r$
$\begin{array}{rcl} \Delta E_{p}=-W&\Rightarrow&E_{p}(r)-E_{p}(R)=-mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)\\\\&\Rightarrow&E_{p}(r)=-mG_{0}R^{2}\dfrac{1}{r}+cte \end{array}$
$\begin{array}{rcl} E_{p}(R)=-mG_{0}R^{2}\dfrac{1}{R}+cte&\Rightarrow&cte=mG_{0}R^{2}\dfrac{1}{R}\\\\&\Rightarrow&E_{p}(r)=-mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right) \end{array}$
2.3 Expression de l'énergie cinétique de $(S)$ en fonction de $G_{0}$, $m$, $r$ et $R$
$\begin{array}{rcl} E_{C}&=&\dfrac{1}{2}mv^{2}\\\\&=&\dfrac{1}{2}m\left(\sqrt{\dfrac{G_{0}R^{2}}{r}}\right)^{2}\\\\&=&\dfrac{1}{2}\dfrac{mG_{0}R^{2}}{r} \end{array}$
Expression de l'énergie mécanique $E$
$\begin{array}{rcl} E_{m}&=&E_{C}+E_{p}\\\\&=&\dfrac{1}{2}\dfrac{mG_{0}R^{2}}{r}-mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)\\\\\Rightarrow\;E_{m}&=&mG_{0}R^{2}\left(\dfrac{1}{R}-\dfrac{1}{2r}\right) \end{array}$
3.1 Expression de la variation $\mathrm{d}v$ de la vitesse et montrons que $\mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r$
$\begin{array}{rcl} T=2\pi\sqrt{\dfrac{r^{3}}{G_{0}R^{2}}}&\Rightarrow&\dfrac{T^{2}}{4\pi^{2}}=\dfrac{r^{3}}{G_{0}R^{2}}\\\\&\Rightarrow&\dfrac{4\pi^{2}}{T^{2}}=\dfrac{G_{0}R^{2}}{r^{3}}\\\\&\Rightarrow&v^{2}=\dfrac{G_{0}R^{2}}{r}\\\\&\Rightarrow&\dfrac{\mathrm{d}v^{2}}{\mathrm{d}r}=\dfrac{\mathrm{d}}{\mathrm{d}r}\left(\dfrac{G_{0}R^{2}}{r}\right)\\\\&\Rightarrow&2v\dfrac{\mathrm{d}v}{\mathrm{d}r}=-\dfrac{G_{0}R^{2}}{r^{2}}\\\\&\Rightarrow&2\dfrac{2\pi r}{T}\dfrac{\mathrm{d}v}{\mathrm{d}r}=-\dfrac{G_{0}R^{2}}{r^{2}}\\\\&\Rightarrow&\dfrac{4\pi}{T}\mathrm{d}v=-\dfrac{G_{0}R^{2}}{r^{3}}\mathrm{d}r\\\\&\Rightarrow&\dfrac{4\pi}{T}\mathrm{d}v=-\dfrac{4\pi^{2}}{T^{2}}\mathrm{d}r\\\\&\Rightarrow&\mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r \end{array}$
3.2 La variation de $\mathrm{d}r$ est en réalité due au travail $\mathrm{d}w_{f}$ des forces de frottements exercées par les couches raréfiées de l'atmosphère pendant le déplacement.
Du signe de $\mathrm{d}w_{f}$, déduire l'effet de ces forces sur l'altitude et la vitesse de $(S).$
$\begin{array}{rcl} \mathrm{d}w_{f}=-f\mathrm{d}r&\Rightarrow&\mathrm{d}r=-\dfrac{\mathrm{d}w_{f}}{f} \end{array}$
$\mathrm{d}w_{f}>0$ $\Rightarrow\mathrm{d}r<0$ L'altitude diminue.
$\begin{array}{rcl} \mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r&\Rightarrow&\mathrm{d}r=-\dfrac{\pi}{T}\mathrm{d}v\\\\&\Rightarrow&\mathrm{d}w_{f}=f\dfrac{\pi}{T}\mathrm{d}v\\\\&\Rightarrow&\mathrm{d}v=\dfrac{T}{\pi}\dfrac{\mathrm{d}w_{f}}{f} \end{array}$
$\mathrm{d}w_{f}>0$ $\Rightarrow\mathrm{d}v>0$ La vitesse augmente.
Exercice 4
1. Expression littérale du champ de gravitation $G_{0}S$ à la surface du Soleil.
$G_{0S}=\dfrac{GM_{S}}{R_{S}^{2}}$
Calcul de la valeur numérique du champ de gravitation $G_{0S}.$
$G_{0S}=\dfrac{GM_{S}}{R_{S}^{2}}=\dfrac{6.67\cdot 10^{-11}\times 2.0\cdot 10^{30}}{(7.0\cdot 10^{8})^{2}}$
$\Rightarrow\;G_{0S}=2.72\cdot 10^{2}m\cdot s^{-2}$
2. Expression littérale du champ de gravitation $G_{S}$ en un point de l'orbite terrestre autour du Soleil.
$G_{S}=\dfrac{GM_{S}}{r^{2}}$
Calcul de la valeur du champ de gravitation $G_{0S}$
$G_{S}=\dfrac{GM_{S}}{r^{2}}=\dfrac{6.67\cdot 10^{-11}\times 2.0\cdot 10^{30}}{(1.5\cdot 10^{8})^{2}}$
$\Rightarrow\;G_{S}=59.3\cdot 10^{2}m\cdot s^{-2}$
3. Comparons la valeur du champ de gravitation $G_{S}$ à celle $G_{0T}$ du champ de gravitation terrestre au niveau du sol.
$\dfrac{G_{S}}{G_{0S}}=\dfrac{59.3\cdot 10^{2}}{2.72\cdot 10^{2}}\Rightarrow\dfrac{G_{S}}{G_{0S}}\approx 22$
$\Rightarrow\;G_{S}\approx 22G_{0S}$
Conclusion :
L'intensité du champ de gravitation augmente lorsque l'altitude diminue
4. Calcul de la valeur du champ de gravitation lunaire $G_{0L}$ au niveau de son sol
$G_{OL}=\dfrac{GM_{L}}{R_{OL}^{2}}$
$G_{0L}=\dfrac{GM_{L}}{R_{0L^{2}}}$ ;
$G_{0T}=\dfrac{GM_{T}}{R_{0T}^{2}}$
\begin{eqnarray} \dfrac{G_{0L}}{G_{0T}}&=&\dfrac{\dfrac{GM_{L}}{R_{0L^{2}}}}{\dfrac{GM_{T}}{R_{0T}^{2}}}\nonumber\\\\&=&\dfrac{M_L}{M_{T}}\times\dfrac{R_{0T}^{2}}{R_{0L}^{2}}&=&\dfrac{1}{81}\times(\dfrac{11}{3})^{2}\nonumber\\\\Rightarrow G_{0L}&=&\dfrac{1}{81}\times(\dfrac{11}{3})^{2}\times 9.8\nonumber\\\\\Rightarrow G_{0L}&=&1.62NKg^{-1} \end{eqnarray}
5) a calcul de la distance $d$ du point $M$ remarquable au centre de la terre.
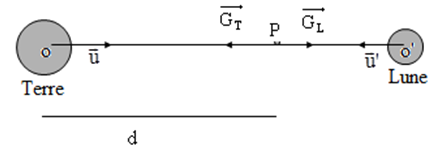
$G_{T}=\dfrac{GM_{T}}{d^{2}}$ ;
$G_{L}=\dfrac{GM_{L}}{(D-d)^{2}}$
\begin{eqnarray} G_{T}=G_{L}\nonumber\\\\\Rightarrow\dfrac{GM_{T}}{d^{2}}&=&\dfrac{GM_{L}}{(D-d)^{2}}\nonumber\\\\\Rightarrow\dfrac{(D-d)^{2}}{d^{2}}&=&\dfrac{M_{L}}{M_{T}}\nonumber\\\\\Rightarrow\dfrac{D-d}{d}&=&\sqrt{\dfrac{M_{L}}{M_{T}}}\nonumber\\\\\Rightarrow d\sqrt{\dfrac{M_{L}}{M_{T}}}&=&D-d\nonumber\\\\d(1+\sqrt{\dfrac{M_{L}}{M_{T}}})&=&D\nonumber\\\\\Rightarrow d&=&\dfrac{D}{(1+\sqrt{\dfrac{M_{L}}{M_{T}}}})&=&\dfrac{380000}{1+\sqrt{\dfrac{1}{81}}}\nonumber\\\\\Rightarrow d&=&342000km \end{eqnarray}
b) Domaine ou l'action gravitationnelle d'un des deux astres est prépondérante $x<d$ l'action gravitationnelle terrestre est prépondérante
Exercice 5
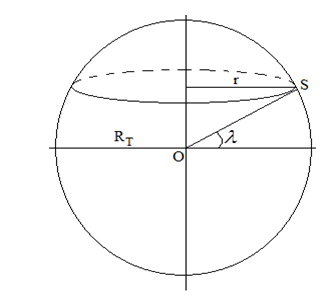
1) Lancement d'un satellite
1)a) Établissement de l'expression de la vitesse du point $S$ de la surface de la surface terrestre en fonction de la vitesse angulaire $\omega$ de rotation de la terre, du rayon terrestre $R_{T}$ et de la latitude $\lambda$ du lieu du lancement.
\begin{eqnarray} v&=&r\lambda\nonumber\\\\&=&R_{T}\lambda\cos\lambda \end{eqnarray}
1)b) Le champ de tir le plus favorable pour le lancement du satellite.
Baikonour au Kazakhstan est le champ de tir le plus favorable car la vitesse de lancement du satellite est minimale.
1)c) Expression de l'énergie potentielle de gravitation d'un satellite en fonction de son altitudez
$E_{P}(r)=-\dfrac{GmM_{T}}{r}+cte$
\begin{eqnarray} E_{p}(r=\infty)&=&-\dfrac{GmM_{T}}{\infty}+cte&=&0\nonumber\\\\\Rightarrow cte&=&0\nonumber\\\\\Rightarrow E_{p}(r)&=&-\dfrac{GmM_{T}}{r} \end{eqnarray}
A l'altitude $z$
\begin{eqnarray} r&=&R_{T}+Z\nonumber\\\\\Rightarrow\,E_{P_{{Z}}&=&\dfrac{GmM_{T}}{R_{T}+Z} \end{eqnarray}
Expression de l'énergie mécanique du satellite sur sa base de lancement dans le référentiel géocentrique
\begin{eqnarray} E_{m}&=&E_{c}+E_{p}\nonumber\\\\&=&\dfrac{1}{1}mV^{2}-\dfrac{GmM_{T}}{r}\nonumber\\\\&=&\dfrac{1}{2}m(R_{T}\Omega\cos\lambda)^{2}-\dfrac{GmM_{T}}{R_{T}\cos\lambda} \end{eqnarray}
1)d) Expression de la vitesse de libération $V_{1}$
Elle correspond à la vitesse minimale pour le satellite quitte l'attraction terrestre avec une énergie mécanique nulle dans le cas limite
\begin{eqnarray} E_{m}&=&\dfrac{1}{2}mV_{L}^{2}-\dfrac{GmM_{T}}{R_{T}\cos\lambda}\nonumber\\\\\Rightarrow V_{L}\nonumber\\\\&=&\sqrt{\dfrac{2GM_{T}}{R_{T}\cos}\lambda} \end{eqnarray}
Calcul de la vitesse de libération $v_{1}$
\begin{eqnarray} V_{L}&=&\sqrt{\dfrac{2GM_{T}}{R_{T}\cos\lambda}}\nonumber\\\\&=&\sqrt{\dfrac{2\times 6.67\cdot 10^{-11}\times 5.97\cdot 10^{24}}{6.38\cdot 10^{6}\times\cos 5.23^{\circ}}}\nonumber\\\\\Rightarrow\,V_{L}&=&11.2\cdot 10^{3}m\cdot s^{-1} \end{eqnarray}
2) Satellite artificiel en orbite
2) a) Montrons que le mouvement du satellite est uniforme
Système : le satellite
Référentiel d'étude : terrestre
Bilan des forces appliquées : la Force gravitationnelle $\overrightarrow{F}$
La deuxième loi de Newton s'écrit :
$\begin{array}{lcl} \overrightarrow{F}&=&m\vec{a}\\\\\Rightarrow-G\dfrac{Mm}{r^{2}}\vec{u}&=&m\vec{a}\\\\\Rightarrow\vec{a}&=&-G\dfrac{M}{r^{2}}\vec{u} \end{array}$
En projetant la relation dans le repère $\left(S\;,\ \overrightarrow{u_{t}}\;,\ \overrightarrow{u_{n}}\right).$
$\begin{array}{lcl} a&=&a_{n}\\\\\Rightarrow\,a_{t}&=&\dfrac{\mathrm{d}v}{\mathrm{d}t}\\\\&=&0\\\\\Rightarrow\,v&=&\text{cte} \end{array}$
Le mouvement du satellite est donc uniforme.
Établissement de l'expression de la vitesse du satellite en fonction de son altitude.
$\begin{array}{lcl} a_{n}&=&\dfrac{GM}{r^{2}}\\\\&=&\dfrac{v^{2}}{r}\\\\\Rightarrow\,v&=&\sqrt{\dfrac{GM}{r}}\\\\\text{or à l'altitude }z\ r&=&R_{T}+z\\\\\Rightarrow\,v&=&\sqrt{\dfrac{GM}{R_{T}}+z} \end{array}$
La troisième loi de Kepler liant la période de rotation $T$ du satellite au rayon $r$ de sa trajectoire
$\begin{array}{lcl} T&=&\dfrac{2\pi r}{v}\\\\&=&2\pi r\sqrt{\dfrac{r}{GM_{T}}}\\\\\Rightarrow\,T^{2}&=&4\pi^{2}\dfrac{r^{3}}{GM_{T}}\\\\\Rightarrow\dfrac{T^{2}}{r^{3}}\\\\&=&\dfrac{4\pi^{2}}{GM_{T}} \end{array}$
2) b) Calcul du rayon de l'orbite d'un satellite géostationnaire
$\begin{array}{lcl} \dfrac{T^{2}}{r^{3}}&=&\dfrac{4\pi^{2}}{GM_{T}}\\\\\Rightarrow\,r&=&\sqrt[3]{\dfrac{GM_{T}T^{2}}{4\pi^{2}}}\\\\&=&\sqrt[3]{\dfrac{6.67\cdot 10^{-11}\times 5.97\cdot 10^{24}\times\left(24\times 3600\right)^{2}}{4\pi^{2}}}\\\\\Rightarrow\,r&=&4.2\cdot 10^{7}m \end{array}$
2) c) Expression du rayon $r$ et de la vitesse $v$ du satellite en fonction du temps
$\begin{array}{lcl} E_{m}&=&E_{C}+E_{P}\\\\&=&\dfrac{1}{2}mv^{2}-\dfrac{GmM_{T}}{r}\\\\&=&\dfrac{1}{2}m\left(\sqrt{\dfrac{GM_{T}}{r}}\right)^{2}-\dfrac{GmM_{T}}{r}\\\\&=&\dfrac{1}{2}\dfrac{GmM_{T}}{r}-\dfrac{GmM_{T}}{r}\\\\&=&-\dfrac{GmM_{T}}{2r}\\\\\Rightarrow\,E_{m}&=&-\dfrac{GmM_{T}}{2r}\\\\&=&E_{m}0(1+bt)\\\\\Rightarrow\,r&=&-\dfrac{GmM_{T}}{E_{m0}(1+bt)} \end{array}$
$\begin{array}{lcl} E_{C}&=&-E_{m}\\\\&=&-E_{m0}(1+bt)\\\\\Rightarrow\dfrac{1}{2}mv^{2}\\\\&=&-E_{m0}(1+bt)\\\\\Rightarrow\,v&=&\sqrt{\dfrac{-2E_{m0}(1+bt)}{m}} \end{array}$
Le rayon $r$ diminue lorsque le temps s'écoule ; par contre la vitesse augmente avec le temps
$\begin{array}{lcl} E_{C}&=&-E_{m}\\\\&=&-E_{m0}(1+bt) \end{array}$
$\begin{array}{lcl} E_{P}&=&2E_{m}\\\\&=&2E_{m0}(1+bt) \end{array}$
L'énergie cinétique augmente ; tandis que l'énergie potentielle diminue.
L'énergie perdue se trouve sous forme d'énergie thermique.
Exercice 6
1) L'accélération de la fusée
$\begin{array}{lcl} F&=&ma\\\\\Rightarrow\,a&=&\dfrac{F}{m}\\\\&=&\dfrac{7.5\cdot 10^{5}}{40\cdot 10^{3}}\\\\\Rightarrow\,a&=&18.75m\cdot s^{-2} \end{array}$
2) Expression la vitesse $v$ et la période $T$ du mouvement du satellite en fonction de $K$, $r$ et $M.$
$\begin{array}{lcl} a_{n}&=&\dfrac{KM}{r^{2}}\\\\&=&\dfrac{v^{2}}{r}\\\\\Rightarrow\,v&=&\sqrt{\dfrac{KM}{r}} \end{array}$
$\begin{array}{lcl} T&=&\dfrac{2\pi r}{v}\\\\&=&2\pi r\sqrt{\dfrac{r}{KM}}\\\\\Rightarrow\,T&=&2\pi\sqrt{\dfrac{r^{3}}{KM}} \end{array}$
Déduisons que $\dfrac{T^{2}}{R^{3}}=$ constante
$\begin{array}{lcl} T&=&2\pi\sqrt{\dfrac{r^{3}}{KM}}\\\\\Rightarrow\,T^{2}&=&4\pi^{2}\dfrac{r^{3}}{KM}\\\\\Rightarrow\dfrac{T^{2}}{r^{3}}&=&\dfrac{4\pi^{2}}{KM} \end{array}$
3) La valeur de la masse de la Terre.
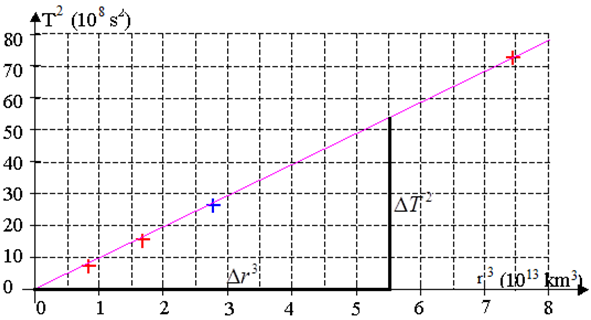
Le graphe représentant $T^{2}=f\left(r^{3}\right)$ est une droite linéaire de pente :
$\begin{array}{lcl} a&=&\dfrac{\Delta T^{2}}{\Delta r^{3}}\\\\&=&\dfrac{4\pi^{2}}{KM}\\\\\Rightarrow\,M&=&4\pi^{2}\dfrac{\Delta r^{3}}{K\Delta T^{2}}\\\\&=&4\pi^{2}\dfrac{5.5\cdot 10^{22}-0}{6.67\cdot 10^{-11}\left(55\cdot 10^{8}-0\right)} \end{array}$
$M=5.92\cdot 10^{24}kg$
4) a) Expression des énergies potentielles $E_{P}$, EC et totale ET du satellite en fonction de la masse M de la Terre, de la masse m du satellite et de r.

Commentaires
Thioune (non vérifié)
mer, 02/03/2021 - 14:21
Permalien
Élève
Diatta (non vérifié)
sam, 02/27/2021 - 23:32
Permalien
Merci beaucoup
Anonyme (non vérifié)
lun, 03/22/2021 - 14:55
Permalien
Comment telecharger la
Anonyme (non vérifié)
mer, 03/24/2021 - 23:24
Permalien
Vraiment j'aime votre page ..
seynabou (non vérifié)
jeu, 03/25/2021 - 09:14
Permalien
Télécharger la correction
Diaw// (non vérifié)
ven, 01/14/2022 - 23:56
Permalien
Question
Diambodji Camara (non vérifié)
jeu, 02/22/2024 - 10:16
Permalien
Corrections des exercices
Diambodji Camara (non vérifié)
jeu, 02/22/2024 - 10:16
Permalien
Corrections des exercices
Diambodji Camara (non vérifié)
jeu, 02/22/2024 - 10:16
Permalien
Corrections des exercices
Diambodji Camara (non vérifié)
jeu, 02/22/2024 - 10:16
Permalien
Corrections des exercices
Diambodji Camara (non vérifié)
jeu, 02/22/2024 - 10:16
Permalien
Corrections des exercices
Ajouter un commentaire