Solution des exercices : Oscillations Mécaniques - Ts
Classe:
Terminale
Exercice 1
I.
1) Équation différentielle du mouvement du corps $M$
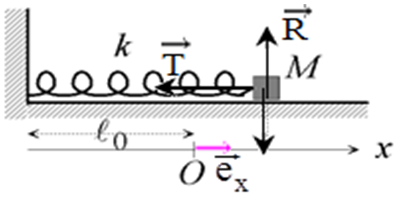
Système étudié : le corps
Référentiel d'étude : terrestre supposé galiléen
Bilan des forces extérieurs appliquées : le poids $\overrightarrow{P}$ ; la tension $\overrightarrow{T}$ ; la réaction $\overrightarrow{R}$ ; du plan horizontal
Le Théorème du centre d'inertie s'écrit : $\overrightarrow{P}+\overrightarrow{T}+\overrightarrow{R}=m\vec{a}$
En projetant suivant l'axe $(Ox)$ ; il vient :
\begin{eqnarray} 0-kx &=& m\ddot{x}\nonumber\\\\\Rightarrow\ddot{x}+\dfrac{k}{m}x&=&0 \end{eqnarray}
est l'équation différentielle du mouvement de $M$ où $\ddot{x}+\omega^{2}x=0\text{ avec }\omega=\sqrt{\dfrac{k}{m}}$
2) Détermination de l'équation horaire du mouvement du corps $M$
a) Cas : $t=0$ ; $x=x_{0}>0$ et la vitesse initiale de $M$ est nulle
L'équation différentielle admet comme solution : $x=x_{m}\cos\left(\omega t\varphi\right)$
\begin{eqnarray} \text{A}\quad t&=&0\nonumber\\\\\Rightarrow x(0)&=& x_{m}\cos\left(\omega\times 0+\varphi\right)\nonumber\\\\ &=& x_{m}\cos\varphi\nonumber\\\\ &=& x_{0}>0 \end{eqnarray}
$x=-\omega x_{m}\sin\left(\omega t+\varphi\right)$
\begin{eqnarray} \dot{x}(0)&=& -\omega x_{m}\sin\left(\omega\times 0+\varphi\right)\nonumber\\\\&=& -\omega x_{m}\sin\varphi\nonumber\\\\&=&0\nonumber\\\\\Rightarrow\varphi &=&0\nonumber\\\\\text{ou}\quad\varphi &=&\pi\nonumber\\\\\text{or à}\quad t=0\ ;\ \cos\varphi>0\nonumber\\\\\Rightarrow\varphi &=&0\nonumber\\\\\Rightarrow x_{m}\cos 0 &=& x_{0}\nonumber\\\\\Rightarrow x_{m}&=& x_{0}\nonumber\\\\\text{d'où}\quad x&=& x_{0}\cos\omega t \end{eqnarray}
b) cas : $t=0$ le corps $M$ est en $x=x_{0}$ et la vitesse de $M$ est $\vec{v}=v_{0}\vec{e}_{x}$ avec $v_{0}>0$
$\begin{array}{lcr} \text{A}\quad t=0\Rightarrow\;x(0)&=&x_{m}\cos\left(\omega\times 0+\varphi\right)\\\\&=&x_{m}\cos\varphi\\\\&=&x_{0} \end{array}$
$\begin{array}{lcr} \dot{x}(0)&=&-\omega\,x_{m}\sin\left(\omega\times 0+\varphi\right)\\\\&=&-\omega\,x_{m}\sin\varphi\\\\&=&v_{0}>0\\\\\Rightarrow\sin\varphi&<&0\\\\\dfrac{-\omega\,x_{m}\sin\varphi}{x_{m}\cos\varphi}&=&\dfrac{v_{0}}{x_{0}}\\\\\Rightarrow\tan\varphi&=&-\dfrac{v_{0}}{\omega\,x_{0}}\\\\\Rightarrow\varphi&=&\tan^{-1}\left(-\dfrac{v_{0}} {\omega\,x_{0}}\right)\\\\\Rightarrow\,x&=&x_{m}\cos\left(\omega\,t+\tan^{-1}\left(-\dfrac{v_{0}}{\omega\,x_{0}}\right)\right) \end{array}$
II.
1) Détermination de la position d'équilibre du corps $M.$
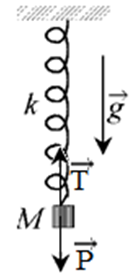
Système étudier : le corps
Référentiel d'étude : terrestre supposé galiléen
Bilan des forces extérieurs appliqués : le poids $\overrightarrow{P}$ ; la tension $\overrightarrow{T}$
La condition d'équilibre s'écrit :
$\begin{array}{lcr} \overrightarrow{P}+\overrightarrow{T}&=&\overrightarrow{0}\\\\\Rightarrow\;mg-k\left(l-l_{0}\right)&=&0 \end{array}$
2) Équation différentielle du mouvement de $M$
En mouvement :
$\begin{array}{lcr} \overrightarrow{P}+\overrightarrow{T}&=&m\vec{a}\\\\\Rightarrow\;mg-k\left(l+x-l_{0}\right)&=&m\ddot{x}\\\\\Rightarrow\;mg-k\left(l-l_{0}\right)-kx&=&m\ddot{x}\\\\\Rightarrow\;\ddot{x}+\dfrac{k}{m}x&=&0 \end{array}$
Exercice 2 : Oscillations d'un pendule simple
1) Conservation de l'énergie
a) Expression de l'énergie cinétique $E_{C}(\dot{\theta})$, de l'énergie potentielle de pesanteur $E_{P}(\theta)$ et de l'énergie totale $E.$
$E_{P}(\theta)=mg\left(l-\cos\theta\right)$
$\begin{array}{lcr} E_{C}(\dot{\theta})&=&\dfrac{1}{2}mv^{2}\\\\\text{or }v&=&1\dot{\theta}\\\\\Rightarrow\;E_{C}(\dot{\theta})&=&\dfrac{1}{2}ml^{2}\dot{\theta}^{2} \end{array}$
$\begin{array}{lcr} E_{m}&=&E_{P}(\theta)+E_{C}(\dot{\theta})\\\\&=&mg\left(l-\cos\theta\right)+\dfrac{1}{2}ml^{2}\dot{\theta}^{2} \end{array}$
$\begin{array}{lcr} \text{A}\quad t=0\quad E_{m0}&=&E_{P}\left(\theta_{0}\right)+E_{C}\left(\dot{\theta_{0}}\right)\\\\&=&mg\left(l-\cos\theta_{0}\right)\\\\&=&mg\left(l-\cos\theta_{0}\right)\\\\&=&\text{cte} \end{array}$

Commentaires
Anonyme (non vérifié)
lun, 03/20/2023 - 21:08
Permalien
Je voudrais la correction de l exercice 6
Anonyme (non vérifié)
ven, 04/14/2023 - 11:19
Permalien
Solution de l'exercice 10
habibmoussoulou... (non vérifié)
sam, 04/22/2023 - 19:50
Permalien
Corrigé exo 10
Atté (non vérifié)
lun, 12/18/2023 - 14:23
Permalien
Correction
Elmekkaoui (non vérifié)
mar, 05/07/2024 - 17:20
Permalien
Correction en pdf
Atté (non vérifié)
lun, 12/18/2023 - 14:25
Permalien
Correction
Atté (non vérifié)
lun, 12/18/2023 - 14:29
Permalien
Correction
Berté (non vérifié)
ven, 12/29/2023 - 17:54
Permalien
Je voudrai la correction de l'exercice 7
Berté (non vérifié)
ven, 12/29/2023 - 17:54
Permalien
Je voudrai la correction de l'exercice 7
Baal (non vérifié)
lun, 02/05/2024 - 03:33
Permalien
Je voudrais la correction de
Fallou (non vérifié)
sam, 02/17/2024 - 02:13
Permalien
La correction
Camara (non vérifié)
jeu, 02/22/2024 - 14:59
Permalien
Exercice
Abdourahmane sow (non vérifié)
jeu, 02/13/2025 - 01:06
Permalien
Je voudrais la correction de l'exercice 12
Aïcha (non vérifié)
sam, 02/22/2025 - 09:11
Permalien
Apprendre
Sangotte (non vérifié)
sam, 02/22/2025 - 09:14
Permalien
Apprendre
Sangotte (non vérifié)
sam, 02/22/2025 - 09:15
Permalien
Apprendre
Sangotte (non vérifié)
sam, 02/22/2025 - 09:17
Permalien
Apprendre
Ajouter un commentaire