Solution des exercices : Solutions acides - solutions basiques - 3e
Classe:
Troisième
Exercice 1
Le $BBT$ qui change de couleur suivant la nature de la solution est un indicateur Coloré.
Une solution acide fait virer le $BBT$ au jaune. Le $BBT$ reste vert dans une solution neutre. Le vert est la zone de virage du $BBT$. Une solution est basique quand elle fait virer le $BBT$ au bleu.
Dans une réaction acido-basique, l'élévation de la température notée par le thermomètre montre que la réaction est exothermique. La réaction entre un acide et une base donne du dioxyde de carbone $(CO_{2})$ et de l'eau. La réaction permet d'obtenir une solution neutre ; elle se produit quand le nombre de mols de base est égal à celui de l'acide. A ce moment précis, l'indicateur coloré change de coloration, le point équivalent est atteint. Le dosage ou titrage d'une solution est la détermination de la quantité de matière (titre) inconnue d'une solution à partir de celle (titre) connue d'une autre solution : c'est une application de la réaction acido-basique. Dans un dosage, la solution titrante est dans la burette ; sa concentration est connue alors que la solution titrée dont la concentration est inconnue est dans le bêcher.
Exercice 2
Au laboratoire, on dose souvent une solution acide (ou basique) par une solution basique (ou acide) en présence d'un indicateur coloré.
1) L'utilité de ce dosage est de déterminer la concentration (inconnue) d'une solution (acide ou basique) par une autre solution (basique ou acide) dont la concentration est connue.
2) L'indicateur coloré permet d'indiquer l'équivalence acido-basique.
3) L'équivalence acido-basique c'est lorsque l'acide et la base ont les mêmes quantités de matières.
Exercice 3
1) Cette expérience est un dosage d'un acide par une base.
2) Complétons le tableau expérimental joint.
$$\begin{array}{|l|l|}\hline\text{Annotation}&\text{Fonction expérimentale} \\ \hline\text{1 : burette}&\text{contient la solution titrante} \\ \hline\text{2 : robinet}&\text{permet de controler le volume de la} \\ &\text{solution titrante à verser pour ne pas} \\ &\text{dépasser l'équivalence} \\ \hline\text{3 : bêcher}&\text{il contient la solution à titrer} \\ \hline\text{4 : solution acide}&\text{c'est la solution dont la concentration} \\ &\text{est inconnue} \\ \hline\text{5 : solution basique}&\text{c'est la solution dont la concentration} \\ &\text{est connue} \\ \hline\end{array}$$
Exercice 4
Masse d'hydroxyde de sodium $NaOH$ à dissoudre dans $500\;mL$ d'une solution d'acide chlorhydrique décimolaire pour la neutraliser.
Soit $n_{B}$ le nombre de mols de la base et $n_{A}$ le nombre de mols de l'acide.
A l'équivalence on a : $n_{A}=n_{B}\ $ or, $\ n_{A}=c_{A}\times V_{A}\ $ et $\ n_{B}=\dfrac{m_{B}}{M_{B}}$
Ainsi, $c_{A}\times V_{A}=\dfrac{m_{B}}{M_{B}}$
Par suite, $m_{B}=c_{A}\times V_{A}\times M_{B}\ $ avec $M_{B}=M_{NaOH}=40\;g.mol^{-1}$
A.N : $m_{B}=0.1\times 500\;10^{-3}\times 40=2$
Donc, $\boxed{m_{B}=2\;g}$
Exercice 5
Pour doser une solution d'acide chlorhydrique, $30\;mL$ de soude de concentration $0.25\;mol\cdot L^{-1}$ ont été versés pour neutraliser $20\;cm^{3}$ de cet acide.
1) Schéma annoté de l'expérience.
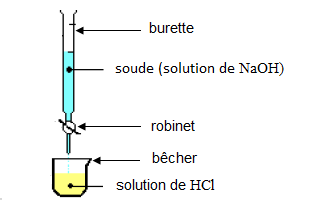
2) Trouvons la concentration molaire de $HCl$
Soit $n_{A}$ le nombre de mols de $HCl\ $ et $\ n_{B}$ le nombre de mols de $NaOH.$
A l'équivalence on a : $n_{A}=n_{B}\ $ or, $\ n=c\times V$
Donc, $c_{A}\times V_{A}=c_{B}\times V_{B}$
Par suite, $c_{A}=\dfrac{c_{B}\times V_{B}}{V_{A}}$
A.N : $c_{A}=\dfrac{0.25\times 30}{20}=0.375$
Ainsi, $\boxed{c_{A}=0.375\;mol\cdot l^{-1}}$
Déduisons sa concentration massique.
On a $c_{m}=c\times M$ avec $M_{(HCl)}=36.5\;g\cdot mol^{-1}$
A.N : $c_{m}=0.375\times 36.5=13.687$
Donc, $\boxed{c_{m}=13.687\;g\cdot l^{-1}}$
3) Calculons la masse de sel et d'eau produit par ce dosage.
Soit l'équation de la réaction suivante :
$$HCl\ +\ NaOH\ \longrightarrow\ NaCl\ +\ H_{2}O$$
On a : $n_{(HCl)}=n_{(NaCl)}=n_{(H_{2}O)}$
or, $c_{A}\times V_{A}=n_{(NaCl)}$ et que $n=\dfrac{m}{M}$
Donc, $c_{A}\times V_{A}=\dfrac{m}{M}\ \Rightarrow\ m=c_{A}\times V_{A}\times M$
A.N : pour $NaCl$, on a : $M_{(NaCl)}=58.5\;g\cdot mol^{-1}$
$m_{(NaCl)}=0.375\times 20\;10^{-3}\times 58.5=0.438$
Par suite, $\boxed{m_{(NaCl)}=0.438\;g}$
pour $H_{2}O$, on a : $M_{(H_{2}O)}=18\;g\cdot mol^{-1}$
$m_{(H_{2}O)}=0.375\times 20\;10^{-3}\times 18=0.135$
Donc, $\boxed{m_{(H_{2}O)}=0.135\;g}$
Exercice 6
Une solution de soude de concentration inconnue est dosée par une solution d'acide chlorhydrique de concentration $0.10\;mol\cdot L^{-1}$. Pour une prise d'essai de $10.0\;cm^{3}$ de la solution basique, il faut verser $8.2\;cm^{3}$ de la solution d'acide pour le virage du $BBT.$
Trouvons la concentration molaire et massique.
Au virage du $BBT$ on a : $n_{A}=n_{B}$ avec $n_{A}$ le nombre de mols de l'acide et $n_{B}$ le nombre de mols de la base.
$c_{A}\times V_{A}=c_{B}\times V_{B}\ \Rightarrow\ c_{B}=\dfrac{c_{A}\times V_{A}}{V_{B}}$
A.N : $c_{B}=\dfrac{0.10\times 8.2}{10}=0.082$
Donc, $\boxed{c_{B}=0.082\;mol/l}$
$c_{m_{B}}=c_{B}\times M\ $ avec, $M_{(NaOH)}=40\;g\cdot mol^{-1}$
A.N : $c_{m_{B}}=0.082\times 40=3.28$
D'où, $\boxed{c_{m_{B}}=3.28\;mol\cdot l^{-1}}$
Exercice 7
Dans un bécher, on met $100\;mL$ d'eau pure dans lesquelles on dissout $2\;g$ d'hydroxyde de sodium $NaOH.$
1) Calculons la molarité de la solution obtenue.
On a : $c=\dfrac{n}{V}$ or $n=\dfrac{m}{M}$
Alors, $c=\dfrac{m}{M\times V}$ avec $M_{NaOH}=40\;g\cdot mol^{-1}$
A.N : $c=\dfrac{2}{40\times 100\;10^{-3}}=0.5$
Donc, $\boxed{c=0.5\;mol\cdot l^{-1}}$
2-1) Trouvons la masse de chacun des produits obtenus.
Soit l'équation de la réaction :
$$HCl\ +\ NaOH\ \longrightarrow\ NaCl\ +\ H_{2}O$$
On a : $n_{HCl}=n_{NaCl}=n_{H_{2}O}$
Or, $c\times V=n=\dfrac{m}{M}$
Donc, $m=c\times V\times M$
A.N : pour $NaCl$, on a : $M_{(NaCl)}=58.5\;g\cdot mol^{-1}$
$m_{(NaCl)}=0.5\times 100\;10^{-3}\times 58.5=2.925$
Ainsi, $\boxed{m_{(NaCl)}=2.925\;g}$
pour $H_{2}O$, on a : $M_{(H_{2}O)}=18\;g\cdot mol^{-1}$
$m_{(H_{2}O)}=0.5\times 100\;10^{-3}\times 18=0.9$
Donc, $\boxed{m_{(H_{2}O)}=0.9\;g}$
2-2) Concentration molaire de la solution acide.
On a : $c_{(NaOH)}\times V=c_{(HCl)}\times V$
Alors, $c_{(HCl)}=\dfrac{c_{(NaOH)}\times V_{NaOH}}{V_{HCl}}$
A.N : $c_{(HCl)}=\dfrac{0.5\times 100}{50}=1$
Donc, $\boxed{c_{(HCl)}=1\;mol\cdot l^{-1}}$
Exercice 8
Un bécher contient $30\;ml$ d'une solution d'hydroxyde de sodium de concentration molaire $C_{B}.$ On y ajoute quelques gouttes de bleu de bromothymol $(B.B.T.).$ Cette solution est dosée par une solution d'acide chlorhydrique de concentration $C_{A}=1.5\;mol\cdot l^{-1}$. On obtient le point d'équivalence après avoir versé $20\;ml$ de la solution acide dans le bécher.
1) Calculons la concentration massique de la solution acide.
On a : $c_{m}=c\times M\ $ avec, $M_{(HCl)}=36.5\;g\cdot mol^{-1}$
A.N : $c_{m}=1.5\times 36.5=54.75$
Donc, $\boxed{c_{m}=54.75\;g\cdot l^{-1}}$
2) Calculons la concentration molaire $C_{B}$ de la solution basique.
A l'équivalence on a : $n_{A}=n_{B}\ $ or, $\ n=cV$
Donc, $c_{A}\times V_{A}=c_{B}\times V_{B}$
Par suite, $c_{B}=\dfrac{c_{A}\times V_{A}}{V_{B}}$
A.N : $c_{B}=\dfrac{1.5\times 20}{30}=1$
Ainsi, $\boxed{c_{B}=1\;mol\cdot l^{-1}}$
3) On ajoute $10\;ml$ d'acide dans le bécher. La nouvelle solution vire au jaune.
3-1) La couleur jaune indique que la nouvelle solution est une solution acide.
3-2) Calculons sa concentration molaire.
On a : $c'_{A}=\dfrac{n'_{A}}{V'_{A}}\ $ or, $\ n'_{A}=c_{A}\times V_{\text{ajouté}}\ $ et $\ V'_{A}=V_{s}+V_{\text{ajouté}}$
Donc, $c'_{A}=\dfrac{c_{A}\times V_{\text{ajouté}}}{V_{s}+V_{\text{ajouté}}}\ $ avec $\ V_{s}=V_{A}+V_{B}$
Ainsi, $c'_{A}=\dfrac{c_{A}\times V_{\text{ajouté}}}{V_{A}+V_{B}+V_{\text{ajouté}}}$
A.N : $c'_{A}=\dfrac{1.5\times 10}{20+30+10}=0.25$
Donc, $\boxed{c'_{A}=0.25\;mol\cdot l^{-1}}$
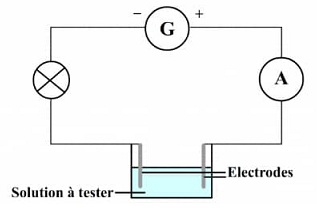
Activité
1) On verse une goutte de $BBT$ dans chacune des solutions et on note la teinte correspondante (voir tableau ci-dessous)
Complétons le tableau en précisant la nature acide, basique ou neutre de chaque solution.
Pour rappel : en présence de $BBT$, une solution est jaune si elle est acide, bleue si elle est basique et verte si elle est neutre.
$$\begin{array}{|l|c|l|}\hline\text{Solution}&\text{Teinte}&\text{Nature}\\ \hline\text{Jus d'orange}&\text{Jaune}&\text{acide}\\ \hline\text{Eau pure}&\text{Verte}&\text{neutre}\\ \hline \text{Eau savonneuse}&\text{Bleue}&\text{basique}\\ \hline\text{Jus de tomate}&\text{Jaune}&\text{acide}\\ \hline\text{Jus de pamplemousse}&\text{Jaune}&\text{acide}\\ \hline \text{Eau de mer}&\text{Bleue}&\text{basique}\\ \hline\text{Lait}&\text{Jaune}&\text{acide}\\ \hline\text{Solution de cendre}&\text{Bleue}&\text{basique}\\ \hline\end{array}$$
2)Schématisons un montage électrique qui permet de tester le caractère conducteur d'une solution.

Exercice 9
Recopions et complétons le texte suivant en ajoutant les mots ou groupe de mots manquants.
Une solution acide donne une coloration jaune en présence de BBT, tandis qu'une solution basique donnera une coloration bleue.
Une solution dans laquelle le $BBT$ vire au vert est neutre.
Une solution d'acide contient toujours des ions $H^{+}$, tandis qu'une solution basique contient toujours des ions $OH^{-}.$
Exercice 10
L'acidité du sol joue un rôle important dans l'agriculture.
Proposons une méthode expérimentale permettant de vérifier le caractère acide ou basique d'un sol.
Vérifier le caractère acide ou basique d'un sol revient à mesurer le $pH$ de ce sol. Pour ce faire, il faut creuser le sol jusqu'à $20$ voire $30\;cm$ de profondeur.
On prélève un échantillon de ce sol qui est ensuite séché et tamisé.
On mélange l'échantillon de sol avec de l'eau distillée, de $pH$ connu jusqu'à ce que le sol et le liquide soient en équilibre. La valeur du $pH$ de l'eau distillée doit être précisée pour déterminer si l'eau distillée a affecté les mesures.
Remuer le mélange avec une cuillère jusqu'à ce qu'il soit totalement mélangé.
Remuer le mélange pendant $30\;s$ puis attendre pendant $3\;mn$ et répéter 5 fois ce cycle (remuer/attendre).
Ensuite, laisser le mélange jusqu'à ce qu'une couche surnageante se forme.
A l'aide d'un $\text{pH-mètre}$, mesurer le $pH$ de la couche surnageante.
Pour des mesures de précision, prendre trois échantillons dans des endroits différents et répéter la même expérience.
Alors, ces valeurs correspondent au $pH$ de ce sol.
Exercice 11
Après avoir préparé diverses solutions, on verse dans chacune d'elles quelques gouttes de $BBT.$
1) En milieu acide le $BBT$ donne une coloration jaune, tandis qu'en milieu basique il donne une coloration bleue et une coloration verte en milieu neutre.
2) Recopions et remplissons le tableau ci-dessous :
$$\begin{array}{|l|c|l|}\hline\text{Solution}&\text{Teinte}&\text{Nature}\\ \hline\text{Jus de tamarin}&\text{jaune}&\text{acide}\\ \hline\text{Liquide vaisselle}&\text{bleu}&\text{basique}\\ \hline\text{Jus de citron}&\text{jaune}&\text{acide}\\ \hline\text{vinaigre}&\text{jaune}&\text{acide}\\ \hline\text{Eau de mer}&\text{bleu}&\text{basique}\\ \hline\text{Chlorure de sodium}&\text{verte}&\text{neutre}\\ \hline\end{array}$$
Exercice 12
On mélange un volume $V_{a}=25\;cm^{3}$ de solution d'acide chlorhydrique de concentration $C_{a}=10^{-1}mol\cdot l^{-1}$ et un volume $V_{b}=20\;cm^{3}$ d'une solution d'hydroxyde de sodium de concentration $C_{b}=1.5\cdot 10^{-1}mol\cdot l^{-1}.$
1) Déterminons la nature du mélange (acide ou basique)
En effet, le mélange est acide si le nombre de moles d'acide est supérieur à celle de la base. Et vice versa.
Comparaison des nombres de moles :
On a : $C=\dfrac{n}{V}\ $ donc, $\ n=C\times V.$ Ainsi :
$\blacktriangleright$ Pour l'acide, on obtient alors :
$n_{a}=10^{-1}\times 25\cdot 10^{-3}=2.5\cdot10^{-3}$
D'où, $\boxed{n_{a}=2.5\cdot10^{-3}}$
$\blacktriangleright$ Pour la base, on a :
$n_{b}=1.5\cdot10^{-1}\times 20\cdot 10^{-3}=3\cdot 10^{-3}$
Donc, $\boxed{n_{b}=3\cdot 10^{-3}}$
On remarque que : $n_{b}>n_{a}.$ Ce qui signifie qu'il y a excès de la base par rapport à l'acide.
Par conséquent, le mélange est basique.
2) Calculons alors le volume d'acide à ajouter pour neutraliser la solution.
Soit $V_{a'}$ le volume total d'acide alors, $V_{a'}=V_{a}+V_{\text{ajouté}}.$
A l'équivalence (neutralisation), on a : $n_{a}=n_{b}$
Or, $n_{a}=C_{a}\times V_{a'}\ $ et $\ n_{b}=C_{b}\times V_{b}$
Donc, $C_{a}\times V_{a'}=C_{b}\times V_{b}$
Par suite, $V_{a'}=\dfrac{C_{b}\times V_{b}}{C_{a}}$
A.N : $V_{a'}=\dfrac{1.5\cdot 10^{-1}\times 20}{10^{-1}}=30\,cm^{3}$
Donc, $V_{a'}=30\;cm^{3}$
Comme $V_{a'}=V_{a}+V_{\text{ajouté}}\ $ alors, $V_{\text{ajouté}}=V_{a'}-V_{a}$
A.N : $V_{\text{ajouté}}=30-25=5$
D'où, $\boxed{V_{\text{ajouté}}=5\;cm^{3}}$
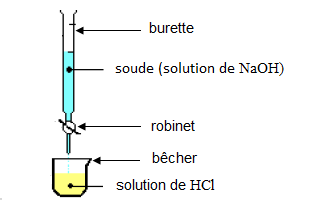
Exercice 13
1) Schéma annoté du dispositif expérimental :

2) Écrivons l'équation globale de la réaction de dosage :
$$(H^{+}+ Cl^{-})\ +\ (Na^{+}+OH^{-})\ \ \longrightarrow\ \ (Na^{+}+Cl^{-})\ +\ (H^{+}+OH^{-})$$
3) Le $BBT$ prend une coloration verte à l'équivalence.
En effet, à l'équivalence, les quantités de matière d'acide et de base sont égales : $n_{a}=n_{b}.$
Ce qui fait que la solution est neutre en ce point. D'où, le $BBT$ prend la coloration verte qui caractérise la neutralité de la solution.
4) Déterminons la concentration $C_{a}$ de la solution d'acide.
A l'équivalence, on a : $n_{a}=n_{b}\ $ or, $\ n_{a}=C_{a}\times V_{a}\ $ et $n_{b}=C_{b}\times V_{b}$
Donc, $C_{a}\times V_{a}=C_{b}\times V_{b}$
D'où $C_{a}=\dfrac{C_{b}\times V_{b}}{V_{a}}$
A.N : $C_{a}=\dfrac{0.05\times20}{10}=0.1$
Ainsi, $\boxed{C_{a}=0.1\;mol\cdot l^{-1}}$
5) Si l'on continuait à verser la soude, la solution prendrait une couleur bleue.
Justification : si on continuait à verser la soude, cette dernière serait en excès par rapport à l'acide. Ce qui rendrait la solution basique. D'où sa coloration en bleue.
Exercice 14
Pour déterminer la concentration $C_{a}$ de l'acide chlorhydrique, lors d'un compte rendu de TP, un élève de $3^{e}$ utilise la démarche suivante :
$\dfrac{C_{a}}{V_{a}}=\dfrac{C_{b}}{V_{b}}\ \Rightarrow\ C_{a}=\dfrac{V_{a}\times C_{b}}{V_{b}}=\boxed{\dfrac{(10\times 0.010)}{20}}$
Rectifions les erreurs de cet élève de $3^{e}$
Il doit d'abord se rappeler qu'à l'équivalence, on a : $n_{a}=n_{b}\ $ avec, $C_{a}\times V_{a}\ $ et $\ n_{b}=C_{b}\times V_{b}$
Ce qui lui permet donc d'écrire :
$\begin{array}{rcl} C_{a}\times V_{a}=C_{b}\times V_{b}&\Rightarrow&C_{a}=\dfrac{C_{b}\times V_{b}}{V_{a}}\\ \\&\Rightarrow&C_{a}=\dfrac{0.10\times20}{10}\\ \\&\Rightarrow&C_{a}=0.2\;mol\cdot l^{-1}\end{array}$
Exercice 15
Lors d'une séance de travaux pratiques, un groupe d'élèves, a préparé dans des erlenmeyers $30\;ml$ de solution d'hydroxyde de sodium, $30\;ml$ d'acide chlorhydrique et $30\;ml$ de chlorure de sodium ayant chacune une concentration de $1\;mol\cdot l^{-1}.$
Ces élèves se trouvent ensuite dans l'impossibilité de distinguer les trois solutions.
1) Afin de reconnaitre les trois solutions, ces élèves peuvent mettre quelques gouttes de $BBT$ dans chaque erlenmeyer.
En effet, en présence de $BBT$, une solution acide donne une coloration jaune, tandis qu'une solution basique donne une coloration bleue et une solution neutre donne une coloration verte.
Sachant que la solution d'hydroxyde de sodium est basique, celle d'acide chlorhydrique est acide et celle de chlorure de sodium est neutre alors, quelques gouttes de $BBT$ dans chaque erlenmeyer permettront de distinguer les trois solutions.
2) Pour éviter une telle mésaventure à l'avenir, ils doivent les étiquetées afin de pouvoir les distinguer.
Exercice 16
On prélève $100\;ml$ de solution d'hydroxyde de sodium ou soude $\left(Na^{+}+OH^{-}\right)$ de concentration molaire $0.5\;mol\cdot l^{-1}$
1) Calculons la quantité de matière de soluté $NaOH$ dissoute dans cette solution.
Soit $n_{(NaOH)}$ la quantité de matière dissoute alors, on a :
$C=\dfrac{n_{(NaOH)}}{V}\ \Rightarrow\ n_{(NaOH)}=C\times V$
A.N : $n_{(NaOH)}=0.5\times 100\cdot 10^{-3}=0.05$
Donc, $\boxed{n_{(NaOH)}=0.05\;mol}$
2) Calculons sa concentration massique
Soit : $C_{m}=C\times M_{(NaOH)}$ avec,
$\begin{array}{rcl} M_{(NaOH)}&=&M_{(Na)}+M_{(O)}+M_{(H)}\\&=&23+16+1\\&=&40\end{array}$
Donc, $M_{(NaOH)}=40\;g\cdot mol^{-1}$
Par suite, $C_{m}=0.5\times 40=20$
D'où, $\boxed{C_{m}=20\;g\cdot l^{-1}}$
3) Cette solution est utilisée pour doser une solution d'acide chlorhydrique $\left(H^{+}+Cl^{-}\right)$ de volume $10\;ml.$
a) Écrivons l'équation bilan de la réaction de dosage
$$(H^{+}+Cl^{-})\ + \ (Na^{+}+OH^{-})\ \longrightarrow\ (Na^{+}+Cl^{-})\ +\ (H^{+}+OH^{-})$$
b) Calculons la concentration molaire de l'acide
A l'équivalence, on a : $n_{a}=n_{b}\ $ or, $\ n_{a}=C_{a}\times V_{a}\ $ et $\ n_{b}=C_{b}\times V_{b}$
Donc,
$\begin{array}{rcl} n_{a}=n_{b}&\Rightarrow&C_{a}\times V_{a}=C_{b}\times V_{b}\\ \\&\Rightarrow&C_{a}=\dfrac{C_{b}\times V_{b}}{V_{a}}\end{array}$
A.N : $C_{a}=\dfrac{0.5\times 15}{10}=0.75$
Ainsi, $\boxed{C_{a}=0.75\;mol\cdot l^{-1}}$
Exercice 17
Pour préparer une solution $S$ d'hydroxyde de sodium $\left(Na^{+}+OH^{-}\right)$ de concentration $C_{b}=5\cdot 10^{-2}\;mol\cdot l^{-1}$, on pèse une masse $m$ d'hydroxyde de sodium que l'on fait dissoudre dans un volume $V=1200\;ml$ d'eau pure.
On considère que la dissolution a lieu sans variation de volume.
1) Calculons la concentration massique de la solution $S.$
Soit $C_{m}=C\times M_{(NaOH)}$ avec,
$\begin{array}{rcl} M_{(NaOH)}&=&M_{(Na)}+M_{(O)}+M_{(H)}\\&=&23+16+1\\&=&40\end{array}$
Donc, $M_{(NaOH)}=40\;g\cdot mol^{-1}$
Ainsi, $C_{m}=5\cdot 10^{-2}\times 40=2$
Par suite, $\boxed{C_{m}=2\;g\cdot l^{-1}}$
En déduisons la valeur de la masse $m$
On a : $C_{m}=\dfrac{m}{V}\ \Rightarrow\ m=C_{m}\times V$
A.N : $m=2\times 1200\cdot 10^{-3}=2.4$
D'où, $\boxed{m=2.4\;g}$
2) On répartit la solution $S$ en trois parties $A\;,\ B\ $ et $\ C$ de volumes $V_{A}=400\;ml\;,\ V_{B}=300\;ml\ $ et $\ V_{C}=500\;ml.$
a) Déterminons la quantité de matière d'hydroxyde de sodium présente dans chaque partie.
Soit : $n=C\times V$
$-\ $ Partie $A\ :$
$n_{A}=5\cdot 10^{-2}\times 400\cdot 10^{-3}=0.02$
Donc, $\boxed{n_{A}=0.02\;mol}$
$-\ $ partie $B\ :$
$n_{B}=5\cdot 10^{-2}\times 300\cdot 10^{-3}=0.015$
Ainsi, $\boxed{n_{B}=0.015\;mol}$
$-\ $ Partie $C\ :$
$n_{C}=5\cdot 10^{-2}\times 500\cdot 10^{-3}=0.025$
Pars suite, $\boxed{n_{C}=0.025\;mol}$
b) Dans chaque partie, on ajoute $200\;ml$ d'une solution d'acide chlorhydrique de concentration $1\cdot 10^{-2}\;mol\cdot l^{-1}.$
Indiquons le caractère acide, basique ou neutre de ces solutions.
Pour cela, cherchons d'abord le nombre de moles d'acide $n_{a}$ ajouté.
Soit : $n_{a}=1\cdot 10^{-2}\times 200\cdot 10^{-3}=0.002$
Donc, $n_{a}=0.002\;mol$
Ensuite, comparons avec la quantité de matière d'hydroxyde de sodium présente dans chaque partie pour enfin conclure.
$-\ $ Pour la solution $A$, on a :
$n_{A}>n_{a}$ donc, la solution est basique car la base est en excès par rapport à l'acide.
$-\ $ Pour la solution $B$, on a : $n_{B}>n_{a}$ donc, la solution est basique.
$-\ $ Pour la solution $C$, on a : $n_{C}>n_{a}$ alors, la solution est basique.

Commentaires
Anonyme (non vérifié)
mer, 12/12/2018 - 18:40
Permalien
Je voulais être ancien tu
Soda diaw (non vérifié)
mar, 12/27/2022 - 22:48
Permalien
Apprendre
Soda diaw (non vérifié)
mar, 12/27/2022 - 22:48
Permalien
Apprendre
Anonyme (non vérifié)
jeu, 12/28/2023 - 08:11
Permalien
Qu'est-ce qu'un indicateur
Amina (non vérifié)
mar, 01/16/2024 - 19:49
Permalien
Personne
Mour Talla Gueye (non vérifié)
mar, 03/12/2019 - 00:38
Permalien
Commentaire
Mour Talla Gueye (non vérifié)
mar, 03/12/2019 - 00:38
Permalien
Commentaire
Pierre (non vérifié)
ven, 05/22/2020 - 13:45
Permalien
Sambou
fdini
sam, 05/23/2020 - 00:26
Permalien
Bjr M. Sambou, c'est bien ça,
Bjr M. Sambou, c'est bien ça,
vous avez surement oublié que la solution s'était d'abord neutralisée avant qu'on y ajoute à nouveau les 10 ml.
Donc c'est comme si les quantités de manière ont totalement réagi avant que l'on ajoute les 10 ml d'acide.
Pierre (non vérifié)
sam, 05/23/2020 - 15:01
Permalien
Ah ok je vois. Merci
MOHAMED FALL (non vérifié)
ven, 06/19/2020 - 15:43
Permalien
commentaire
Mame diarra fall (non vérifié)
mar, 01/17/2023 - 21:23
Permalien
Savoir
abass ndiaye (non vérifié)
mer, 01/25/2023 - 14:56
Permalien
scientifiques
Anonyme (non vérifié)
mer, 12/09/2020 - 17:54
Permalien
travail exceptionnel,, merci
Cheikh Toure (non vérifié)
dim, 04/25/2021 - 00:07
Permalien
travail exeptionnel
Diadié (non vérifié)
jeu, 01/11/2024 - 18:06
Permalien
Élève
queenk (non vérifié)
jeu, 05/20/2021 - 22:53
Permalien
amen
queenk (non vérifié)
jeu, 05/20/2021 - 22:53
Permalien
amen
Fatou (non vérifié)
dim, 01/29/2023 - 20:50
Permalien
Éleve
Fatou (non vérifié)
dim, 01/29/2023 - 20:51
Permalien
Éleve
Fatou (non vérifié)
dim, 01/29/2023 - 20:51
Permalien
Éleve
Nafissatou séne (non vérifié)
ven, 03/04/2022 - 22:18
Permalien
Slt je voudrai que tu m'aide sur les leçon de physique et chimie
Mouhamadou Ndiaye (non vérifié)
mer, 12/28/2022 - 11:44
Permalien
Voudrais cour en ligne
Momodou (non vérifié)
ven, 01/20/2023 - 22:23
Permalien
Pc
Khoudia arame n... (non vérifié)
dim, 01/08/2023 - 19:08
Permalien
Demande d'aide
leyemame (non vérifié)
mar, 03/22/2022 - 17:39
Permalien
approche
Fatou samb (non vérifié)
mar, 04/05/2022 - 22:45
Permalien
Slt je voudrait participer
Kiné diongue (non vérifié)
mer, 01/25/2023 - 20:43
Permalien
Matière
Djiby Diallo (non vérifié)
jeu, 02/09/2023 - 21:40
Permalien
Apprendre
Djiby Diallo (non vérifié)
jeu, 02/09/2023 - 21:40
Permalien
Apprendre
Aliou ba (non vérifié)
sam, 01/07/2023 - 18:22
Permalien
Chimie
Aliou ba (non vérifié)
sam, 01/07/2023 - 18:22
Permalien
Chimie
Aliou ba (non vérifié)
sam, 01/07/2023 - 18:22
Permalien
Chimie
Anonyme (non vérifié)
jeu, 01/12/2023 - 07:11
Permalien
Merci
Bineta Basse (non vérifié)
mer, 02/22/2023 - 19:57
Permalien
Réussir mon examen BFM
Bineta Basse (non vérifié)
mer, 02/22/2023 - 20:04
Permalien
Réussir mon examen aider moi surtout en svt et PC stp
Jc mayouma (non vérifié)
sam, 10/28/2023 - 19:27
Permalien
Approfondir les connaissances
soda (non vérifié)
mer, 01/10/2024 - 00:07
Permalien
ah c est bon
soda (non vérifié)
mer, 01/10/2024 - 00:07
Permalien
ah c est bon
soda (non vérifié)
mer, 01/10/2024 - 00:07
Permalien
ah c est bon
halimata (non vérifié)
mer, 01/17/2024 - 17:16
Permalien
éléve
Anonyme (non vérifié)
sam, 01/11/2025 - 23:01
Permalien
A
Daba diakhoumpa (non vérifié)
mar, 01/06/2026 - 18:26
Permalien
Exo 6 Cm c'est g/l
Ajouter un commentaire