Solution des exercices : Tension électrique - 2nd S
Classe:
Seconde
Exercice 1
Considérons le circuit ci-dessous
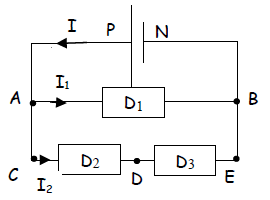
1) Représentons les tensions $$U_{PN}\;,\ U_{AB}\;,\ U_{DC}\ \text{ et }\ U_{DE}$$
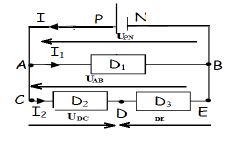
2) Déterminons la valeur de $U_{AB}$
Soit : $U_{AB}=U_{PN}$
Alors, $\boxed{U_{AB}=20\;V}$
3) Déduction de la valeur de $I_{1}$
D'après la loi des nœuds, on a :
$$I=I_{1}+I_{2}\ \Rightarrow\ I_{1}=I-I_{2}$$
Donc, $I_{1}=300-200=100$
Ainsi, $\boxed{I_{1}=100\;mA}$
4) Déterminons la valeur de $U_{DC}$
La loi d'additivité des tensions permet d'écrire :
$U_{AB}=U_{CD}+U_{DE}\ $ or, les dipôles $D_{3}\ $ et $\ D_{2}$ sont identiques donc, $U_{DE}=U_{CD}$
Par suite, $U_{AB}=2U_{CD}$
Par ailleurs, $U_{CD}=-U_{DC}$
Donc, $U_{AB}=-2U_{CD}\ \Rightarrow\ U_{CD}=-\dfrac{U_{AB}}{2}$
A.N : $U_{CD}=-\dfrac{20}{2}=-10$
D'où, $\boxed{U_{CD}=-10\;V}$
5) Déterminons la valeur de $U_{DE}$
Soit : $U_{DE}=-U_{DC}$
Donc, $\boxed{U_{DE}=10\;V}$
Exercice 2
1) Nommons dans chaque cas la tension mesurée par l'oscillographe.
L'oscillographe mesure respectivement les tensions $U_{AB}\ $ et $\ U_{CD}$
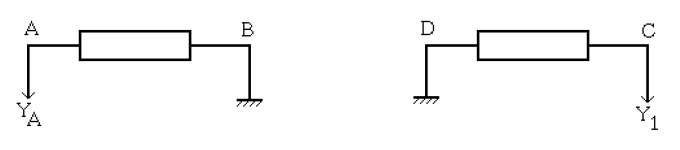
2) On fournit un écran d'oscillographe
Les réglages initiaux de l'oscillographe sont tels que la ligne médiane horizontale corresponde à une tension nulle
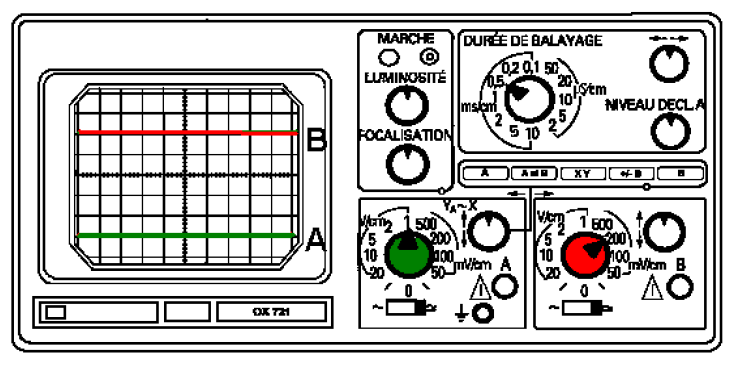
2.1) Sur la voie $A$ la sensibilité utilisée est $1\;V/cm$
2.2) Sur la voie $B$ la sensibilité utilisée est $200\;mV/cm$
2.3) La tension mesurée sur la voie $A$ est négative
2.4) La tension mesurée sur la voie $B$ est positive
2.5) La déviation observée sur la voie $A$ est 3 divisions
Déduisons la valeur de la tension mesurée sur la voie $A$
$U_{Y_{A}}=1\times 3 \Rightarrow\ U_{Y_{A}}=3\;V$
2.6) La déviation observée sur la voie $B$ est $2$ divisions
Déduisons la valeur de la tension mesurée sur la voie $B$
$U_{Y_{B}}=200\times 2 \Rightarrow\ U_{Y_{B}}=400\;mV$
Exercice 3
On a visualisé ci-dessous diverses tensions. La sensibilité verticale est de $2\;V/div$ et la sensibilité horizontale de $2\;ms/div.$
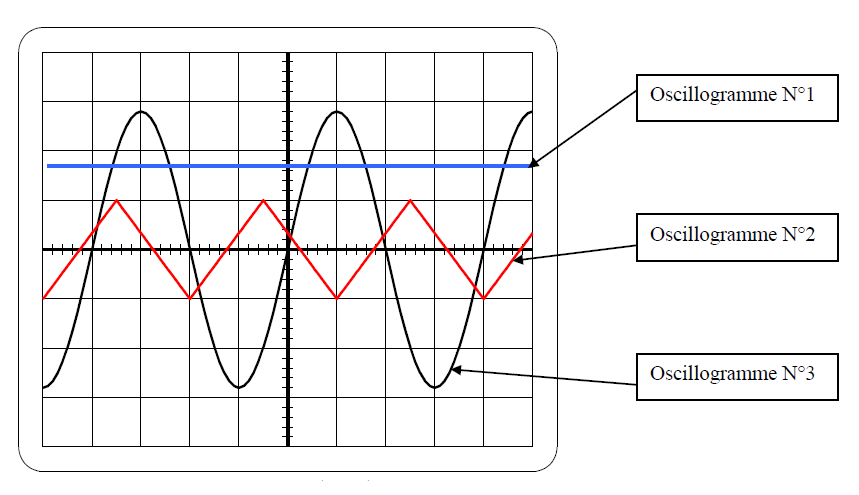
1) Indiquons l'oscillogramme qui correspond à une tension continue et celui qui correspond à une tension alternative sinusoïdale.
L'oscillogramme correspond $N^{\circ}1$ correspond à une tension continue , l'oscillogramme $N^{\circ}3$ à une tension alternative sinusoïdale.
2) Pour l'oscillogramme représentant une tension continue, calculons la valeur de la tension qui a été mesurée
Soit : $U_{1}=8.5\times 2 \Rightarrow U_{1}=17\;V$
3) Pour l'oscillogramme représentant une tension alternative sinusoïdale,
a) Déterminons $U_{max}$
On a : $U_{max}=2\times 14 \Rightarrow U_{max}=28\;V$
b) Calculons la valeur efficace de la tension.
Soit : $U_{eff}=\dfrac{U_{max}}{\sqrt{2}}$
A.N : $U_{eff}=\dfrac{28}{\sqrt{2}}=19.8$
Ainsi, $\boxed{U_{eff}=19.8\;V}$
4) Pour l'oscillogramme représentant une tension alternative sinusoïdale, déterminons la période du courant et sa fréquence.
Soit : $T=2\times 20.10^{-3}\Rightarrow T=40.10^{-3}s$
On a : $N=\dfrac{1}{T}=\dfrac{1}{40.10^{-3}}$ donc, $N=25\;Hz$
Exercice 4
On considère le circuit électrique ci-dessous comportant sept dipôles passifs comme l'indique la figure ci-dessous.
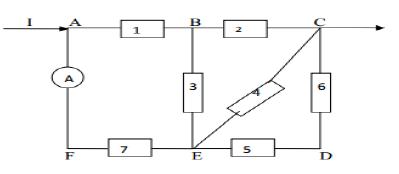
1) Calcul des tensions électriques suivantes :
$$U_{BE}\;;\ U_{CE}\;;\ U_{DC}$$
Soit :
$\begin{array}{rcl} U_{BE}&=&U_{BA}+U_{AF}+U_{FE}\quad\text{or, }U_{BA}=-U_{AB}\\\\&=&-U_{AB}+U_{AF}+U_{FE}\\\\&=&-4+0+2\\\\&=&-2\;V\end{array}$
Donc, $\boxed{U_{BE}=-2\;V}$
$\begin{array}{rcl} U_{CE}&=&U_{BE}+U_{CB}\\\\&=&U_{BE}+U_{BC}\\\\&=&-2-1\\\\&=&-3\;V\end{array}$
Ainsi, $\boxed{U_{CE}=-3\;V}$
$\begin{array}{rcl} U_{DC}&=&U_{EC}+U_{DE}\\ \\&=&U_{EC}-\dfrac{3}{2U_{BC}}\\ \\&=&-(-3)-\dfrac{3}{2}\times 1\\ \\&=&1.5\;V\end{array}$
Ainsi, $\boxed{U_{DC}=1.5\;V}$
2) Déduisons le sens du courant dans la branche $(BE).$
La tension $U_{BE}$ est négative, le courant circule branche $(BE)$ de $E$ vers $B$
3) Détermination des intensités électriques $I_{2}\;;\ I_{4}\;;\ I_{6}\ $ et $\ I_{7}.$
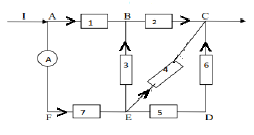
En utilisant la loi des nœuds, on obtient :
$\begin{array}{rcl} I=I_{1}+I_{7}&\Rightarrow&I_{7}=I-I_{1}\\\\&\Rightarrow&I_{7}=5-2\\\\&\Rightarrow&I_{7}=3\;A\end{array}$
Donc, $\boxed{I_{7}=3\;A}$
$\begin{array}{rcl} I_{2}&=&I_{1}+I_{3}\\\\&=&2+3\\\\&=&5\;A\end{array}$
Ainsi, $\boxed{I_{2}=5\;A}$
$\begin{array}{rcl} I=I_{2}+I_{4}+I_{6}&\Rightarrow&I=I_{2}+2I_{4}\quad\text{car, }\ I_{4}=I_{5}=I_{6}\\ \\&\Rightarrow&I_{4}=\dfrac{I-I_{2}}{2}\\ \\&\Rightarrow&I_{4}=\dfrac{5-5}{2}\\ \\&\Rightarrow &I_{4}=0\;A\\ \\&\Rightarrow&I_{6}=0\;A\end{array}$
D'où, $\boxed{I_{6}=0\;A}$
4) L'ampèremètre du circuit est de classe 2. Il comporte $100$ divisions et porte les calibres
$$1\;A\;;\ 5\;A\;;\ 10\;A\ \text{ et }\ 15\;A$$
a) Déterminons le calibre le mieux adapté à la mesure.
Le calibre le mieux adapté à la mesure $5\;A$ est le calibre.
Déduisons l'indication $n$ de l'aiguille.
On sait que : $I_{7}=\dfrac{C\times n}{N}\Rightarrow n=\dfrac{I_{7}\times N}{C}$
Donc, $n=\dfrac{3\times 100}{5}=60$ d'où, $\boxed{ n=60\text{ divisions}}$
b) Donnons un encadrement de l'intensité mesurée
Soit : $\Delta I_{7}=\dfrac{C\times 1}{N}=\dfrac{5\times 1}{00}\Rightarrow \Delta I_{7}=0.05\;A$
On a :
$\begin{array}{rcrcccl} I_{7}-\Delta I_{7}\leq I_{7}\leq I_{7}+\Delta I_{7}&\Rightarrow&3-0.05&\leq&I_{7}&\leq&3+0.05\\\\&\Rightarrow&2.95\;A&\leq&I_{7}&\leq&3.05\;A\end{array}$

Commentaires
Bechara (non vérifié)
lun, 11/09/2020 - 15:31
Permalien
Enseignant
ntsanidorcelin@... (non vérifié)
jeu, 12/24/2020 - 03:42
Permalien
Tension
Mbeng Atome (non vérifié)
sam, 01/09/2021 - 23:21
Permalien
J'ai besoin d'aide en
Gabriella christy (non vérifié)
ven, 01/15/2021 - 07:40
Permalien
Avoir des bonnes notes
Folly (non vérifié)
jeu, 11/23/2023 - 17:52
Permalien
Tension électrique
Anonyme (non vérifié)
ven, 01/15/2021 - 07:38
Permalien
J'ai beaucoup aimé cette
mouinba (non vérifié)
lun, 03/08/2021 - 12:06
Permalien
physigue
Jacques (non vérifié)
sam, 05/29/2021 - 12:53
Permalien
jai une eval dans 3jours
Anonyme (non vérifié)
ven, 06/18/2021 - 17:34
Permalien
J'ai besoin de celles de la
Anonyme (non vérifié)
mer, 04/06/2022 - 10:54
Permalien
Exercice 11
M. BAKAYOKO MOULAYE (non vérifié)
lun, 04/15/2024 - 14:40
Permalien
avoir la correction de l'exercice 11
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:26
Permalien
Exercice 13
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Riyan (non vérifié)
dim, 04/24/2022 - 02:02
Permalien
Kong
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Fousseni D keïta (non vérifié)
mer, 04/20/2022 - 21:28
Permalien
Exercice 13
Hyam (non vérifié)
dim, 04/24/2022 - 02:02
Permalien
Saaab
Anonyme (non vérifié)
dim, 04/24/2022 - 02:03
Permalien
Correction d’exercice6
Anonyme (non vérifié)
dim, 04/24/2022 - 13:02
Permalien
Hyper bien
Keita Lansané (non vérifié)
dim, 04/24/2022 - 13:03
Permalien
Très intéressant
Anonyme (non vérifié)
dim, 04/24/2022 - 13:04
Permalien
Effectivement Dr
Boubacare (non vérifié)
mar, 04/26/2022 - 16:07
Permalien
Exo physique 3em
Boubacare (non vérifié)
mar, 04/26/2022 - 16:08
Permalien
Exo physique 3em
Boubacare (non vérifié)
mar, 04/26/2022 - 16:08
Permalien
Exo physique 3em
Raissa (non vérifié)
jeu, 02/23/2023 - 21:40
Permalien
Tension électrique
diabagate el ha... (non vérifié)
mer, 03/22/2023 - 22:07
Permalien
aidez moi
HAli (non vérifié)
ven, 04/14/2023 - 23:00
Permalien
Aide
Koudougou (non vérifié)
jeu, 05/11/2023 - 08:20
Permalien
Exercice seconde
Koudougou (non vérifié)
jeu, 05/11/2023 - 08:22
Permalien
Exercice seconde
Ayena (non vérifié)
lun, 11/13/2023 - 16:49
Permalien
Phisique
Ndiaye (non vérifié)
jeu, 04/18/2024 - 17:58
Permalien
Les autres exercices
clowi paterson (non vérifié)
ven, 04/19/2024 - 15:35
Permalien
Je n' ai pas trouvé l
Anonyme (non vérifié)
jeu, 05/30/2024 - 13:59
Permalien
Le reste
Anonyme (non vérifié)
dim, 06/02/2024 - 16:35
Permalien
Suite bi
Ella (non vérifié)
mer, 12/04/2024 - 16:37
Permalien
Svp la suite
Ganou Zacky (non vérifié)
jeu, 03/13/2025 - 01:58
Permalien
C'est super
Onmar (non vérifié)
sam, 04/12/2025 - 20:20
Permalien
Étudier la physique chimie
Ajouter un commentaire