Solution des exercices : Travail et puissance mécaniques - 1er s
Classe:
Première
Exercice 1
Un système constitué de deux blocs reliés par un fil $AB$ de masse négligeable est tiré avec une force constante $F$, d'intensité $300\,N$, sur un plan horizontal rugueux.
On donne $\alpha=60^{\circ}$
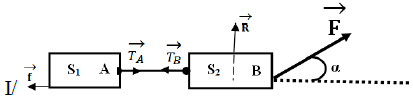
1. Calcul du travail de la force $\vec{F}$ lorsque le système s'est déplacé de $CD=20\,m.$ On a :
$\begin{array}{rcl} W_{CD}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{CD}\\ \\&=&F\times CD\cos\alpha\\ \\&=&300\times 20\cos 60^{\circ}\\ \\&=&3.0\cdot10^{3}\end{array}$
Ainsi, $\boxed{W_{CD}\left(\vec{F}\right)=3.0\cdot 10^{3}\;J}$
2. La vitesse étant constante, la tension du fil horizontal $AB$ qui relie les deux blocs est alors constante et égale à $120\,N.$
Calculons le travail au cours du trajet de la tension du fil appliqué au bloc $S_{2}$ et le travail de la tension du fil appliqué au bloc $S_{1}.$ Soit :
$\begin{array}{rcl} W_{CD}\left(\overrightarrow{T_{B}}\right)&=&\overrightarrow{T_{B}}\cdot\overrightarrow{CD}\\ \\&=&-T_{B}\times CD\\ \\&=&-120\times 20\\ \\&=&-2.4\cdot10^{3}\end{array}$
Donc, $\boxed{W_{CD}\left(\overrightarrow{T_{B}}\right)=-2.4\cdot 10^{3}\;J}$
Par ailleurs, comme $\overrightarrow{T_{B}}+\overrightarrow{T_{A}}=\vec{0}$ alors, $T_{A}=T_{B}$
Par suite,
$\begin{array}{rcl} W_{CD}\left(\overrightarrow{T_{A}}\right)&=&\overrightarrow{T_{A}}\cdot\overrightarrow{CD}\\ \\&=&T_{A}\times CD\\ \\&=&T_{B}\times CD\\ \\&=&-W_{CD}\left(\overrightarrow{T_{B}}\right)\\ \\&=&2.4\cdot 10^{3}\end{array}$
D'où, $\boxed{W_{CD}\left(\overrightarrow{T_{A}}\right)=2.4\cdot 10^{3}\;J}$
Calcul du travail total des forces de frottement exercées par le plan sur $S_{1}$ et $S_{2}.$
La vitesse est constante, le principe de l'inertie appliqué au système constitué du bloc $S_{1}$ et du bloc $S_{2}$ s'écrit :
$\begin{array}{rcl} \vec{F}+\vec{f}=\vec{0}&\Rightarrow&F\cos\alpha-f=0\\\\&\Rightarrow&f=F\cos\alpha \end{array}$
Par suite :
$\begin{array}{rcl} W_{CD}\left(\vec{f}\right)&=&\vec{f}\cdot\overrightarrow{CD}\\\\&=&-f\times CD\\\\&=&-F\times CD\cos\alpha\\\\&=&-3.0\cdot10^{3}\end{array}$
D'où, $\boxed{W_{CD}\left(\vec{f}\right)=-3.0\cdot10^{3}\;J}$
3. On envisage maintenant le cas où la vitesse n'est plus constante ; la tension du fil varie au cours du mouvement.
Dans ce contexte, les travaux de la tension $\overrightarrow{T_{B}}$ appliquée en $B$ et de la tension $\overrightarrow{T_{A}}$ appliquée en $A$ dépendent du chemin suivi.
Exercice 2
Alpha tire, à vitesse constante, une luge de masse $m=6.00\,kg$ sur un sol horizontal ; la distance parcourue est $d=AB=100\,m.$
La force $\vec{F}$ exercée sur la luge par l'intermédiaire de la corde est constante sur la distance $d$ ; la corde fait un angle $\alpha=30.0^{\circ}$ avec le sol.
On suppose que la valeur $f$ des forces de frottements vaut le cinquième du poids $P$ de la luge.
1. Inventaire des forces qui s'exercent sur le système $\{\text{Alpha+luge}\}.$
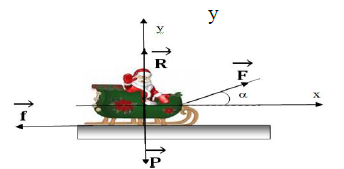
2. Calcul de la valeur de la force de traction qu'exerce Alpha sur sa luge.
Système : $\{\text{Alpha} + \text{luge}\}$
Bilan des forces appliquées : $\vec{F}\ :\ \vec{P}\ :\ \vec{R}\ :\ \vec{f}$
Le système évolue à vitesse constante, le principe de l'inertie s'écrit :
$$\vec{F}+\vec{P}+\vec{R}+\vec{f}=\vec{0}$$
En projetant la relation vectorielle suivant l'axe des $x$, il vient :
$\begin{array}{rcl} F\cos\alpha+0+0-f=0&\Rightarrow&F\cos\alpha=f\\ \\&\Rightarrow&F =\dfrac{f}{\cos\alpha}\quad\text{or }f=\dfrac{P}{5}=\dfrac{mg}{5}\\ \\&\Rightarrow&F=\dfrac{mg}{5\cos\alpha}\\ \\&\Rightarrow&F=\dfrac{6.00\times 9.81}{5\cos 30.0^{\circ}}\\ \\&\Rightarrow&F=13.6\;N \end{array}$
D'où, $\boxed{F=13.6\;N}$
3. Calcul du travail de chacune des forces le long du trajet.
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&\overrightarrow{F}\cdot\overrightarrow{AB}\\\\&=&Fd\cos\alpha\\\\&=&13.6\times 100\cos 30.0^{\circ}\\\\&=&11.8\cdot 10^{2}\end{array}$
D'où, $\boxed{W_{AB}\left(\vec{F}\right) =11.8\cdot 10^{2}\;J}$
$W_{AB}\left(\vec{P}\right)=\vec{P}\cdot\overrightarrow{AB}=0$
Or, $\overrightarrow{P}\perp\overrightarrow{AB}$ donc, $\vec{P}\cdot\overrightarrow{AB}=0$
D'où, $\boxed{W_{AB}\left(\vec{P}\right)=0\;J}$
$\begin{array}{rcl} W_{AB}\left(\vec{f}\right)&=&\vec{f}\cdot\overrightarrow{AB}\\\\&=&-fd\\\\&=&-\dfrac{P}{5}d\\\\&=&-\dfrac{mg}{5}d\\\\&=&-\dfrac{6.00\times 9.81}{5}\times 100\\\\&=&-11.8\cdot 10^{2}J \end{array}$
Ainsi, $\boxed{ W_{AB}\left(\vec{f}\right) =-11.8\cdot 10^{2}\;J}$
$W_{AB}\left(\vec{R}\right)=\vec{R}\cdot\overrightarrow{AB}=0\;J$ car $\vec{R}\perp\overrightarrow{AB}$
Alpha aborde maintenant la piste de luge (de longueur $l=100\,m$) qui forme un plan incliné d'un angle $\beta=15.0^{\circ}$ avec l'horizontale.
Elle tire toujours rectilignement et à vitesse constante ; l'angle entre la corde et la pente est toujours de $30.0^{\circ}.$
On suppose que la force de frottements garde la même valeur $f$ que précédemment.
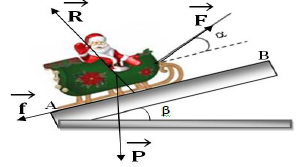
4. Le travail de la somme des forces est nul.
En effet,
$\begin{array}{rcl} \vec{v}=\overrightarrow{cte}&\Rightarrow&\vec{F}+\vec{P}+\vec{R}+\vec{f}=\vec{0}\\ \\&\Rightarrow&\vec{F}\cdot\overrightarrow{AB}+\vec{P}\cdot\overrightarrow{AB}+\vec{R}\cdot\overrightarrow{AB}=\vec{0}\cdot\overrightarrow{AB}\\\\&\Rightarrow&W_{AB}\left(\vec{F}\right)+W_{AB}\left(\vec{P}\right)+W_{AB}\left(\vec{R}\right)+W_{AB}\left(\vec{f}\right)=0\end{array}$
5. Donnons l'expression du travail de chacune des forces s'exerçant sur la luge.
$W_{AB}\left(\vec{F}\right)=\vec{F}\cdot\overrightarrow{AB}=Fl\cos\beta$
$W_{AB}\left(\vec{P}\right)=\vec{P}\cdot\overrightarrow{AB}=-Pl\sin\beta$
$W_{AB}\left(\vec{R}\right)=\vec{R}\cdot\overrightarrow{AB}=0$ car $\vec{R}\perp\overrightarrow{AB}$
$W_{AB}\left(\vec{f}\right)=\vec{f}\cdot\overrightarrow{AB}=-fl$
6. Comparons les valeurs de la force de traction sur la partie plane et sur la pente.
Sur la partie pente :
$\begin{array}{rcl} W_{AB}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{AB}\\\\&=&Fl\cos\beta\\\\&=&13.6\times 100\times\cos 15.0^{\circ}\\\\&=&13.1\cdot 10^{2} \end{array}$
Donc, sur la pente : $W_{AB}\left(\vec{F}\right)=13.1\cdot 10^{2}\;J$
Sur la partie rectiligne : $W_{AB}\left(\vec{F}\right)=11.8\cdot 10^{2}\;J$
Sur la partie pente, Alpha fournit plus d'efforts.
C'est pourquoi $W_{AB}\left(\vec{F}\right)=13.1\cdot 10^{2}\;J>W_{AB}\left(\vec{F}\right)=11.8\cdot 10^{2}\;J$
7. Le déplacement est effectué en $2.0\,min.$
Calculons la puissance moyenne du travail du poids.
On a :
$\begin{array}{rcl} P_{m}\left(\vec{P}\right)&=&\dfrac{W_{AB}\left(\vec{P}\right)}{\Delta t}\\\\&=&\dfrac{-Pl\sin\beta}{\Delta t}\\\\&=&\dfrac{-6.00\times 9.81\times 100\times\sin 15.0}{2.0\times 60}\\\\&=&-12.7\end{array}$
D'où, $\boxed{P_{m}\left(\vec{P}\right)=-12.7\;W}$
Exercice 3
Un chariot de masse $M=20\,Kg$ tiré le long d'une piste horizontale $AB$ de longueur $L=4\,m$ par une force $\vec{F}$ inclinée d'un angle $\alpha=60^{\circ}$ par rapport au déplacement et de valeurs $F=120\,N$ (voir fig).
On néglige tous les frottements.
Le long du trajet $AB$, le chariot est tiré avec une vitesse constante $=1\,m\cdot s^{-1}.$
1. Expression et calcul du travail effectué par $\vec{F}$ le long du trajet $AB.$
On a :
$\begin{array}{rcl} W_{AB}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{AB}\\\\&=&Fl\cos\alpha\\\\&=&120\times 4\times\cos 60^{\circ}\\\\&=&240\end{array}$
D'où, $\boxed{W_{AB}\left(\vec{F}\right) =240\;J}$
2. Expression et calcul de la puissance moyenne développée par cette force
On a :
$\begin{array}{rcl} P_{m}\left(\vec{F}\right)&=&\vec{F}\vec{v}\\\\&=&Fv\\\\&=& 120\times 1\\\\&=&-120\end{array}$
Ainsi, $\boxed{P_{m}\left(\vec{F}\right)=-120\;W}$
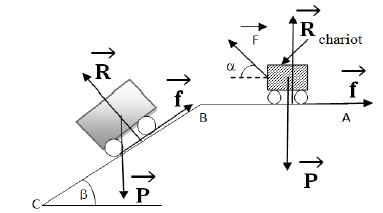
3. En arrivant au point $B$, on supprime la force motrice $\vec{F}$ et le chariot aborde une piste $BC$ de longueur $L'$ incliné par rapport à l'horizontale passant par $C$ d'un angle $\beta=30^{\circ}.$
Le long du trajet $BC$, le chariot est soumis à des forces de frottement équivalente à une force $\vec{f}$ constamment opposé au déplacement et de valeur $f=30\,N.$
La différence d'altitude entre les points $B$ et $C$ est $h=2\,m.$
a) Expression et calcul du travail du poids $\vec{P}$ du chariot.
Soit :
$\begin{array}{rcl} W_{BC}\left(\vec{P}\right)&=&\vec{P}\cdot\overrightarrow{BC}\\\\&=&Mgh\\\\&=&20\times 10\times 2\\\\ &=&4\cdot 10^{2}\end{array}$
Alors, $\boxed{W_{AB}\left(\vec{P}\right)=4\cdot 10^{2}\;J}$
b) Expression et calcul du travail de la force de frottement.
On a :
$\begin{array}{rcl} W_{BC}\left(\vec{f}\right) &=&\vec{f}\cdot\overrightarrow{BC}\\\\&=&-Fl \\\\&=&-f\dfrac{h}{\sin\beta}\\\\&=&-30\times\dfrac{2}{\sin 30^{\circ}}\\\\ &=&4-120\end{array}$
D'où, $\boxed{W_{AB}\left(\vec{f}\right) =4-120\;J}$
c) Expression et calcul du travail de la réaction $\vec{R}$ du plan
Soit : $W_{AB}\left(\vec{R}\right)=\vec{R}\cdot\overrightarrow{AB}=0$ car $\vec{R}\perp\overrightarrow{AB}$
Exercice 4
Une barre est maintenue horizontale par l'intermédiaire d'un fil métallique et un fil de coton fixés en son milieu.
Les deux fils sont verticaux, le fil métallique est au-dessus de la barre, le fil de coton en dessous.
Le fil métallique a une constante de torsion $C=4.0\cdot10^{-2}N\cdot m\cdot rad^{-1}.$
Le fil de coton exerce un couple négligeable.
1. Schéma du dispositif.
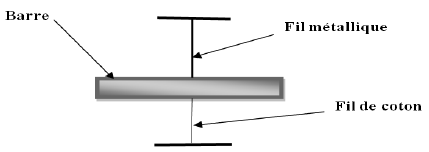
2. Calcul du travail du couple de torsion dans les situations suivantes :
2.1. La barre écartée de $90^{\circ}$ par rapport à sa position d'équilibre. Alors, on a :
$\begin{array}{rcl} W_{C}&=&-C\left(\mathcal{g_{f}}-\mathcal{g_{i}}\right)\\\\&=&-4.0\cdot 10^{-2}\left(\dfrac{\pi}{2}-0\right)\\\\&=&-6.28\cdot 10^{-2}\end{array}$
Donc, $\boxed{W_{C}=-6.28\cdot 10^{-2}\;J}$
2.2 Lorsque la barre passe de la position précédente à la position où elle fait un angle de $45^{\circ}$ par rapport à sa position d'équilibre.
Soit alors :
$\begin{array}{rcl} W_{C}&=&-C\left(\mathcal{g}_{f}-\mathcal{g}_{i}\right)\\\\&=&-4.0\cdot 10^{-2}\left(\dfrac{\pi}{4}-\dfrac{\pi}{2}\right)\\\\&=& 3.14\cdot 10^{-2}\end{array}$
D'où, $\boxed{W_{C}=3.14\cdot 10^{-2}\;J}$
2.3 Lorsque la barre passe de cette dernière position à la position où elle est écartée d'un angle de $30^{\circ}$ de l'autre côté de sa position d'équilibre.
$\begin{array}{rcl} W_{C} &=&-C\left(\mathcal{g}_{f}-\mathcal{g}_{i}\right)\\\\&=&-4.0\cdot 10^{-2}\left(-\dfrac{\pi}{6}-\dfrac{\pi}{4}\right) \\\\&=&5.24\cdot 10^{-2}\end{array}$
Ainsi, $\boxed{W_{C}=5.24\cdot 10^{-2}\;J}$
Exercice 5
Pour hisser, à vitesse constante, un corps sur une plateforme on utilise un treuil entraîné par un moteur (fig 1).
La masse du corps $M=1\,000\;kg$, la hauteur $h=2\;m$ et les frottements créent une force $f$ de direction opposée au déplacement.
La force motrice $F=10\,000\;N$ pour un angle $\alpha=30^{\circ}.$
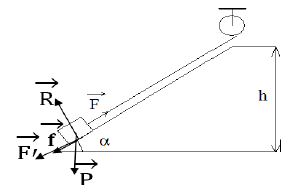
1. Calculons la force résistante $\left(\vec{F}'\right)$ présentée par le poids : $F'=P\cdot\sin\alpha$ (sens opposé au déplacement) et la force de frottement.
Soit :
$\begin{array}{rcl}\vec{F'} &=& P\cdot\sin\alpha\\\\&=&Mg\sin\alpha\\\\&=&1\,000\times 10\times\sin 30^{\circ}\\\\&=&5.0\cdot 10^{3}\end{array}$
Donc, $\boxed{F'=5.0\cdot 10^{3}\;N}$
Le corps se déplace à vitesse constante, le principe de l'inertie s'écrit :
$$\vec{F}+\vec{P}+\vec{R}+\vec{f}=\vec{0}$$
En projetant suivant le sens de la force motrice, il vient :
$\begin{array}{rcl} F-F'+0-f=0&\Rightarrow& f=F-F'\\\\&\Rightarrow&f=1\,000-5.0\cdot 10^{5}\\\\&\Rightarrow&f=5.0\cdot 10^{5}\end{array}$
D'où, $\boxed{f=5.0\cdot 10^{5}\;N}$
2. Calculons le travail de la force $\vec{F}$ et la puissance correspondante si la masse se déplace à $0.2\;m/s.$
Soit :
$\begin{array}{rcl} W\left(\vec{F}\right) &=&F\dfrac{h}{\sin\alpha}\\\\&=&10\,000\times\dfrac{2}{\sin 30^{\circ}}\\\\&=&4.0\cdot 10^{4}\end{array}$
Alors, $\boxed{W\left(\vec{F}\right)= 4.0\cdot 10^{4}\;J}$
Pour la puissance, on obtient :
$\begin{array}{rcl} P\left(\vec{F}\right)&=&\vec{F}\cdot\vec{v}\\\\&=&Fv\\\\&=&10\,000\times 0.2\\\\&=&2.0\cdot 10^{3}\end{array}$
Ainsi, $\boxed{P\left(\vec{F}\right)=2.0\cdot 10^{3}\;W}$
Le treuil ayant un diamètre de $20\;cm$ et un rendement de $0.85$
3. Calculons :
$-\ $ la puissance mécanique du moteur nécessaire
On a :
$\begin{array}{rcl} \dfrac{P\left(\vec{F}\right)}{P_{M}}=0.85&\Rightarrow&P_{M}=\dfrac{P\left(\vec{F}\right)}{0.85}\\ \\&\Rightarrow&P_{M}=\dfrac{2.0\cdot 10^{3}}{0.85}\\\\&\Rightarrow&P_{M}=2.4\cdot 10^{3}\end{array}$
Donc, $\boxed{P_{M}=2.4\cdot 10^{3}\;W}$
$-\ $ la vitesse angulaire de rotation,
Soit :
$\begin{array}{rcl} \omega&=&\dfrac{v}{r}\\\\&=&\dfrac{v}{\dfrac{d}{2}}\\\\&=&\dfrac{2v}{d}\\\\&=&\dfrac{2\times 0.2}{20\cdot 10^{-2}}\\\\&=&20\end{array}$
Ainsi, $\boxed{\omega=20\;rad\cdot s^{-1}}$
$-\ $ la fréquence de rotation $(tr/min)$
On a :
$\begin{array}{rcl} \omega=2\pi N&\Rightarrow&N=\dfrac{\omega}{2\pi}\\\\&\Rightarrow&N=\dfrac{20}{2\pi}\\\\&\Rightarrow&N=3\;Hz\end{array}$
En convertissant, on obtient :
$N=3\;Hz=3\times 60=180\;tr/mn$
D'où, $\boxed{N=180\;tr/mn}$
$-\ $ le moment du couple moteur
Soit :
$\begin{array}{rcl} P_{M}=M_{C}\omega&\Rightarrow&M_{C}=\dfrac{P_{M}}{\omega}\\\\&\Rightarrow&M_{C}=\dfrac{2.4\cdot 10^{3}}{20}\\\\&\Rightarrow&M_{C}=1.2\cdot 10^{2}Nm \end{array}$
Par suite, $\boxed{M_{C}=1.2\cdot 10^{2}\;Nm }$
Exercice 6
Une tige de cuivre supporte deux boules de fer $(m_{1}=m_{2}=m).$
L'ensemble est mobile sans frottement autour d'un axe horizontal $\Delta$, qui est perpendiculaire en $O$, au plan de la figure.
Le centre d'inertie de la barre de masse $(M)$ est à la distance $OG=a$ de l'axe.
Un aimant attire la boule de fer en $A_{1}$, avec une force horizontale $F_{1}$ ; un deuxième aimant attire la boule de fer $A_{2}$ avec une force $F_{2}.$
On pose $OA_{1}=\ell_{1}\ $ et $\ OA_{2}=\ell_{2}$
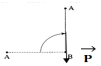
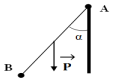
1. La tige fait un angle $\alpha$ avec la verticale.
a) Représentons les forces extérieures appliquées sur le système (tige + boules)
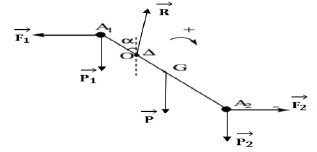
b) Exprimons littéralement les moments de ces forces par rapport à l'axe $\Delta$ en fonction des données.
On a :
$\begin{array}{rcl} M_{\Delta}\left(\vec{F}_{1}\right)&=&-F_{1}OA_{1}\cos\alpha\\\\&=&-F_{1}l_{1}\cos\alpha \end{array}$
Soit : $\boxed{M_{\Delta}\left(\vec{F}_{1}\right)=-F_{1}l_{1}\cos\alpha}$
On a :
$\begin{array}{rcl} M_{\Delta}\left(\vec{F}_{2}\right)&=&-F_{2}OA_{2}\cos\alpha\\\\&=& -F_{2}l_{2}\cos\alpha\end{array}$
Soit alors : $\boxed{M_{\Delta}\left(\vec{F}_{2}\right)=-F_{2}l_{1}\cos\alpha}$
On a :
$\begin{array}{rcl} M_{\Delta}\left(\vec{P}\right)&=&POG\cos\alpha\\\\&=&Mga\cos\alpha \end{array}$
Ainsi, $\boxed{M_{\Delta}\left(\vec{P}\right)=Mga\cos\alpha}$
Soit :
$\begin{array}{rcl} M_{\Delta}\left(\vec{P}_{1}\right)&=&-P_{1}OA_{1}\sin\alpha\\\\&=& -mgl_{1}\sin\alpha\end{array}$
Donc, $\boxed{M_{\Delta}\left(\vec{P}_{1}\right)=-mgl_{1}\sin\alpha}$
On a :
$\begin{array}{rcl} M_{\Delta}\left(\vec{P}_{2}\right)&=&P_{2}OA_{2}\sin\alpha\\\\&=& mgl_{2}\sin\alpha\end{array}$
D'où, $\boxed{M_{\Delta}\left(\vec{P}_{2}\right)=mgl_{2}\sin\alpha}$
Enfin, $M_{\Delta}\left(\vec{R}\right)=0$
2. Pour la valeur de $=\alpha=20^{\circ}$, l'ensemble est en équilibre.
Déterminons alors l'intensité commune $F$ des forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$
Soit :
$$M_{\Delta}\left(\vec{F}_{1}\right)+M_{\Delta}\left(\vec{F}_{2}\right)+M_{\Delta}\left(\vec{P}\right)+M_{\Delta}\left(\vec{P}_{1}\right)+M_{\Delta}\left(\vec{P}_{2}\right)+M_{\Delta}\left(\vec{R}\right)=0$$
Ce qui donne : $F_{1}l_{1}\cos\alpha-F_{2}l_{2}\cos\alpha+Mga\cos\alpha-mgl_{1}\sin\alpha+mgl_{2}\sin\alpha+0=0$
Or, $F_{1}=F_{2}=F$ donc, $Fl_{1}\cos\alpha-Fl_{2}\cos\alpha+Mga\cos\alpha+mg\sin\alpha(l_{2}-l_{1})=0$
$\Rightarrow\ F\cos\alpha(l_{1}-l_{2})+Mga\cos\alpha+mg\sin\alpha(l_{2}-l_{1})=0$
$\Rightarrow\ F=\dfrac{Mga\cos\alpha+mg\sin\alpha\times\left(l_{2}-l_{1}\right)}{\left(l_{2}-l_{1}\right)\cos\alpha}$
$\Rightarrow\ F=9.8\dfrac{300\cdot 10^{-3}\times 6.0\cos 20^{\circ}+100\cdot 10^{-3}\times\sin 20^{\circ}\times(24-12)}{(12+24)\cos 20^{\circ}}$
$\Rightarrow F=0.61\;N$
D'où, $\boxed{F=0.61\;N}$
3. Détermination du travail effectué par chaque force pendant deux tours $\theta=2\pi$
Soit :
$\begin{array}{rcl} W\left(\vec{F}\right)&=&M_{\Delta}\left(\vec{F}\right)\theta\\\\&=&F\left(l_{1}+l_{2}\right)\times 2\pi\\\\&=&0.61(12+24)10^{-2}\times 2\pi\\\\&=&1.38\end{array}$
Donc, $\boxed{W\left(\vec{F}\right)= 1.38\;J}$
On a :
$\begin{array}{rcl} W\left(\vec{P}\right)&=&M_{\Delta}\left(\vec{P}\right)\theta\\\\&=&Mga\cos\alpha \times 2\pi\\\\&=&300\cdot 10^{-2}\times 9.8\times6.0\cdot 10^{-2}\cos 20^{\circ}\times 2\pi\\\\&=& 1.04\end{array}$
Donc, $\boxed{W\left(\vec{P}\right)=1.04\;J}$
Soit :
$\begin{array}{rcl} W\left(\vec{P}_{1}\right)&=&M_{\Delta}\left(\vec{P}_{1}\right)\theta\\\\&=&-100\cdot 10^{-3}\times 9.8\times 12\cdot 10^{-2}\sin 20^{\circ}\times 2\pi\\\\&=&0.25\end{array}$
Ainsi, $\boxed{W\left(\vec{P}_{1}\right)=0.25\;J}$
On a :
$\begin{array}{rcl} W\left(\vec{P}_{2}\right) &=& M_{\Delta}\left(\vec{P}_{2}\right)\theta\\\\&=& 100\cdot 10^{-3}\times 9.8\times 24\cdot 10^{-2}\sin 20^{\circ}\times 2\pi\\\\&=&0.51\end{array}$
Donc, $\boxed{W\left(\vec{P}_{2}\right)=0.51\;J}$
Soit :
$\begin{array}{rcl} W\left(\vec{R}\right) &=&M_{\Delta}\left(\vec{R}\right)\theta\\\\ &=&0\times 2\pi\\\\&=&0\end{array}$
D'où, $\boxed{W\left(\vec{R}\right)=0\;J}$
Exercice 7
Un solide ponctuel $S$, de masse $m$, se déplace dans un plan vertical le long d'un trajet $ABCD$ qui comporte deux phases.
$-\ $ Une partie horizontale $AB$ rectiligne de longueur $8\;m.$
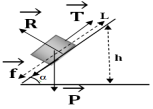
Le long de cette partie, le solide est soumis à une force constante $\vec{F}$, faisant un angle $\alpha=60^{\circ}$ avec l'horizontale et développant une puissance $P=6\;W$ en plus d'une force de frottement $\vec{f}$, opposée au déplacement de valeur constante $f=3\;N.$
$-\ $ Une demi sphère $BCD$, de centre $O$ et de rayon $R=0.5\;m$ où le solide est soumis uniquement à son poids $\vec{P}.$
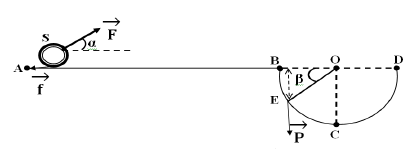
1. Sachant que pendant la partie $AB$ le mouvement est rectiligne uniforme de vitesse $V=2\;m\cdot s^{-1}$,
a) Exprimons la puissance moyenne $P$ développée par $\vec{F}$ en fonction de $F\;,\ V\ $ et $\ \alpha.$
Soit :
$$P_{m}\left(\vec{F}\right)=\vec{F}\cdot\vec{V}=FV\cos\alpha$$
b) Déduction de la valeur de la force $F.$
On a :
$\begin{array}{rcl} P_{m}\left(\vec{F}\right)=FV\cos\alpha&\Rightarrow&F=\dfrac{P_{m}\left(\overrightarrow{F}\right)}{V\cos\alpha}\\\\&\Rightarrow&F=\dfrac{6}{2\times\cos 60^{\circ}}\\\\&\Rightarrow&F =6\;N\end{array}$
Donc, $\boxed{F=6\;N}$
c) Calcul du travail de la force $\vec{F}$ pendant le déplacement $AB.$
Soit :
$\begin{array}{rcl} W_{AB}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{AB}\\\\&=&F\cdot AB\cos\alpha\\\\&=& 6\times 8\times\cos 60^{\circ}\\\\&=&24\end{array}$
D'où, $\boxed{W_{AB}\left(\vec{F}\right) =24\;J}$
2. Détermination du travail de la force de frottement $\vec{f}$ au cours du déplacement de $AB.$
On a :
$\begin{array}{rcl} W_{AB}\left(\vec{f}\right)&=&\vec{f}\cdot\overrightarrow{AB}\\\\ &=& -f\cdot AB\cos\alpha\\\\ &=& -3\times 8\\\\&=&-24\end{array}$
Ainsi, $\boxed{W_{AB}\left(\vec{f}\right) =-24\;J}$
3. Arrivant au point $B$, on annule les forces $\vec{F}\ $ et $\ \vec{f}.$
Sachant que le travail du poids de $S$ lorsqu'il glisse de $B$ vers $C$ est $W_{B\rightarrow C}\left(\vec{P}\right)=0.5\;J$
a) Déterminons la masse du solide $S.$
On a :
$\begin{array}{rcl} W_{B\rightarrow C}\left(\overrightarrow{P}\right)=mgR&\Rightarrow&m=\dfrac{W_{B\rightarrow C}\left(\overrightarrow{P}\right)}{gR}\\\\&\Rightarrow&m=\dfrac{0.5}{10\times 0.5}\\\\&\Rightarrow&m=0.1\;kg \end{array}$
D'où, $\boxed{m=0.1\;kg}$
b) Donnons l'expression du travail du poids de $S$ lorsqu'il passe de $B$ vers $E$ en fonction de $m\;,\ g\;,\ R\ $ et $\ \beta.$
Soit : $W_{B\rightarrow E}\left(\vec{P}\right)=mgR\sin\beta$
Calcul de sa valeur : $W_{B\rightarrow E}\left(\vec{P}\right)= 0.1\times 10\times 0.5\times\sin 30^{\circ}=0.25$
Ainsi, $\boxed{W_{B\rightarrow E}\left(\vec{P}\right)=0.25\;J}$
c) Déduisons du travail du poids de $S$ lors du déplacement de $E$ vers $C.$
Soit :
$\begin{array}{rcl} W_{E\rightarrow C}\left(\vec{P}\right)&=&W_{B\rightarrow C}\left(\vec{P}\right)-W_{B\rightarrow E}\left(\vec{P}\right)\\\\&=&mgR-mgR\sin\beta\\\\&=&0.1\times 10\times 0.5(1-\sin 30^{\circ})\\\\&=&0.25\end{array}$
Alors, $\boxed{W_{E\rightarrow C}\left(\vec{P}\right)=0.25\;J}$
4. Détermination du travail du poids de $S$ lors du déplacement de $C$ vers $D.$
Soit : $W_{C\rightarrow D}\left(\vec{P}\right)=-W_{B\rightarrow C}\left(\vec{P}\right)$
Donc, $\boxed{W_{C\rightarrow D}\left(\vec{P}\right)=-0.5\;J}$
Exercice 8
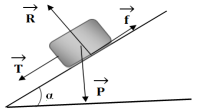
a. Bilan des forces extérieurs s'appliquant au traîneau
$\overrightarrow{T}$ : force des traction exercée par les chiens,
$\overrightarrow{R}$ : réaction du plan inclinée,
$\overrightarrow{f}$ : force de frottement
et $\overrightarrow{P}$ : Poids du traîneau
Représentation des forces sur un schéma

b. Résultante de ces forces
Le système évolue à vitesse constante, le principe de l'inertie s'écrit :
$$\overrightarrow{T}+\overrightarrow{P}+\overrightarrow{R}+\overrightarrow{f}=\overrightarrow{O}$$
La résultante de ces forces est donc nulle
c. Calcule du travail du poids $\overrightarrow{P}$ et du travail de la force de frottement $\overrightarrow{f}$
$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&-mgh\\ &=&-mgL\sin\alpha\\&=&-110\times 500\times\dfrac{6.0}{100}\\\Rightarrow\; W\left(\overrightarrow{P}\right)&=&-33.10^{3}J \end{array}$
$\begin{array}{rcl} W\left(\overrightarrow{f}\right)&=&-70\times 500\\\Rightarrow\;W\left(\overrightarrow{f}\right)&=&-35\cdot 10^{3}J \end{array}$
d. Déduction du travail de la force de traction $\overrightarrow{T}$ exercée par les chiens sur le traîneau pour un déplacement de longueur $L$
$\begin{array}{rcl} \overrightarrow{T}+\overrightarrow{P}+\overrightarrow{R}+\overrightarrow{f}&=&0\\\Rightarrow\overrightarrow{T}\overrightarrow{L}+\overrightarrow{P}\overrightarrow{L}+\overrightarrow{R}\overrightarrow{L}+\overrightarrow{f}\overrightarrow{L}&=&\overrightarrow{O}\overrightarrow{L}\\ \Rightarrow\;W(T)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{R}\right)+W\left(\overrightarrow{f}\right)&=&0 \end{array}$
Or
$\begin{array}{rcl} W\left(\overrightarrow{T}\right)&=&0\\\Rightarrow\;W\left(\overrightarrow{T}\right)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{f}\right)&=&\\\Rightarrow\;W\left(\overrightarrow{T}\right)&=&-W\left(\overrightarrow{P}\right)-W\left(\overrightarrow{f}\right)\\&=&-\left(-33\cdot10^{3}\right)-\left(-35\cdot10^{3}\right)\\\Rightarrow\;W\left(\overrightarrow{T}\right)&=&68\cdot10^{3}\,J \end{array}$
Puissance moyenne de cette force
$\begin{array}{rcl}P_{m}\left(\overrightarrow{T}\right)&=&\overrightarrow{T}\overrightarrow{V}\\&=&TV\text{ or }T=\dfrac{W(T)}{L}\\\Rightarrow\;P_{m}\left(\overrightarrow{T}\right)&=&\dfrac{W(T)}{L}V&=&\dfrac{68\cdot10^{3}}{500}\times 6.94\\\Rightarrow\;P_{m}\left(\overrightarrow{T}\right)&=&9.4\cdot10^{2}W\end{array}$
Exercice 9


a. Calculer du travail du poids de l'échelle lors de cette opération.
$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&-mg\dfrac{L}{2}\\&=&-10\times10\times\dfrac{3.0}{2}\\\Rightarrow\;W\left(\overrightarrow{P}\right) &=&-1.5\cdot10^{2}J \end{array}$
b. Calcul du travail du poids de l'échelle lors de cette opération.
$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&-mg\dfrac{L}{2}\cos\alpha\\&=&-10\times10\times\dfrac{3.0}{2}\cos 30^{\circ}\\\Rightarrow\;w\left(\overrightarrow{P}\right)&=&-1.3\cdot10^{2}J \end{array}$
Exercice 10

a. Bilan des forces extérieures s'appliquant à la caravane et représentation de ces forces
$\overrightarrow{T}$ : force de traction exercée par la voiture
$\overrightarrow{R}$ : réaction du plan incliné
$\overrightarrow{f}$ : Force de frottement
$\overrightarrow{P}$ : poids de la caravane
b. Résultante de ces forces
Le système évolue à vitesse constante, le principe de l'inertie s'écrit :
$\overrightarrow{T}+\overrightarrow{P}+\overrightarrow{R}+\overrightarrow{f}=\overrightarrow{O}$
La résultante de ces forces est donc nulle
c. Calcul du travail du poids $\overrightarrow{P}$ et du travail de la force de frottement $\overrightarrow{f}$ pour un déplacement de longueur $L$
$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&mgL\sin\alpha\\&=&500\times10\times200\times\dfrac{6.0}{100}\\&=&0\\\Rightarrow\;W\left(\overrightarrow{P}\right)&=&6\cdot10^{4}J \end{array}$
or
$\begin{array}{rcl} W\left(\overrightarrow{R}\right)&=&0\\\Rightarrow\;W\left(\overrightarrow{T}\right)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{f}\right)&=&0\\\Rightarrow\;W\left(\overrightarrow{T}\right)&=&-W\left(\overrightarrow{P}\right)-W\left(\overrightarrow{f}\right)\\&=&-6\cdot10^{4}J-\left(-2.0\cdot10^{5}J\right)\\\Rightarrow\;W\left(\overrightarrow{R}\right)&=&14\cdot10^{4}J \end{array}$
$\begin{array}{rcl} W\left(\overrightarrow{f}\right)&=&-fT\\&=&-1.0\cdot10^{3}\times200\\\Rightarrow\;W\left(\overrightarrow{f}\right)&=&-2.0\cdot10^{5}J \end{array}$
d. Déduction du travail de la force de la force de traction $\overrightarrow{T}$ exercée par la voiture sur la caravane
$W\left(\overrightarrow{T}\right)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{R}\right)+W\left(\overrightarrow{f}\right)=0$
La puissance moyenne de cette force
$\begin{array}{rcl} P_{m}\left(\overrightarrow{T}\right)&=&\overrightarrow{T}\overrightarrow{V}\\&=&TV\text{ or }T&=&\dfrac{W\left(\overrightarrow{T}\right)}{L}\\\Rightarrow\;P_{m}\left(\overrightarrow{T}\right)&=&\dfrac{W\left(\overrightarrow{T}\right)}{L}V\\&=&\dfrac{14\cdot10^{4}}{200}\times19.4\\\Rightarrow\;P_{m}\left(\overrightarrow{T}\right)&=&1.36\cdot10^{2}W \end{array}$
e. La pente de la côte devrait être montante pour que le travail de $\overrightarrow{T}$ change de signe
La signification physique de ce changement de signe permet de préciser la nature du travail de $\overrightarrow{T}$

Commentaires
Anonyme (non vérifié)
mer, 12/30/2020 - 23:22
Permalien
Bien
Abou (non vérifié)
mar, 10/12/2021 - 12:12
Permalien
Exercice 11 sur travail et puissance d'une force en 1ere
JEAN
sam, 01/06/2024 - 16:39
Permalien
Travail et puissance
Dione (non vérifié)
lun, 11/18/2024 - 17:58
Permalien
Correction des exercices
Ibrahim (non vérifié)
ven, 12/19/2025 - 02:11
Permalien
Solution de l'exercice 11
Ndiaye (non vérifié)
dim, 11/10/2024 - 17:21
Permalien
Merci beaucoup
amine (non vérifié)
lun, 01/04/2021 - 23:30
Permalien
Correction d’autres exercices
Dione (non vérifié)
mer, 01/20/2021 - 18:11
Permalien
Correction de l'exercice 11
Dozzh NGB (non vérifié)
mar, 11/09/2021 - 06:39
Permalien
Faire des Travaux dirigés
Dozzh NGB (non vérifié)
mar, 11/09/2021 - 06:39
Permalien
Faire des Travaux dirigés
Ngom (non vérifié)
mar, 11/07/2023 - 07:57
Permalien
Étude
Djafarou (non vérifié)
sam, 02/06/2021 - 22:18
Permalien
Physique
Anonyme (non vérifié)
dim, 01/22/2023 - 16:12
Permalien
C'est très bien votre site
Aly diop (non vérifié)
dim, 11/14/2021 - 23:34
Permalien
J’aimerais avoir le reste de
Fabiana (non vérifié)
mar, 11/19/2024 - 18:34
Permalien
Étude
Birahim fall (non vérifié)
jeu, 01/07/2021 - 07:19
Permalien
Regarder les autres corrections
Anonyme (non vérifié)
mar, 01/12/2021 - 22:55
Permalien
le probleme est que ont nous
Cheikh Diagne (non vérifié)
mer, 01/13/2021 - 13:39
Permalien
reussite
Elhadji (non vérifié)
mer, 11/01/2023 - 21:48
Permalien
Il m'a permis de mieux
Abdourahmane (non vérifié)
ven, 01/15/2021 - 01:10
Permalien
Eleve en première s2
ibrahima seck (non vérifié)
mer, 01/20/2021 - 20:55
Permalien
demande d'aide sur la science
Djafarou (non vérifié)
sam, 02/06/2021 - 22:20
Permalien
physique
Anonyme (non vérifié)
ven, 09/17/2021 - 16:01
Permalien
Ok
Djariatougassama (non vérifié)
ven, 10/29/2021 - 19:39
Permalien
Suivre les cours
Anonyme (non vérifié)
lun, 11/01/2021 - 18:43
Permalien
Salut
Divine (non vérifié)
lun, 11/01/2021 - 18:45
Permalien
Poids
Anonyme (non vérifié)
lun, 11/01/2021 - 18:47
Permalien
Salut
Anonyme (non vérifié)
mer, 09/21/2022 - 18:24
Permalien
Etude
Anonyme (non vérifié)
jeu, 09/22/2022 - 22:02
Permalien
La correction de l exo 5 me
Anonyme (non vérifié)
dim, 08/25/2024 - 23:56
Permalien
la correction de l exo 5
Anonyme (non vérifié)
dim, 08/25/2024 - 23:58
Permalien
La correction de l exo 5
Inass elfarouki (non vérifié)
dim, 09/25/2022 - 10:10
Permalien
Exercice corrige
Anonyme (non vérifié)
mar, 09/27/2022 - 18:22
Permalien
intéressant
Khady Ndiaye (non vérifié)
mar, 11/15/2022 - 21:37
Permalien
Sciences physiques
Hicham (non vérifié)
ven, 12/09/2022 - 19:27
Permalien
Ex:9
Anonyme (non vérifié)
mer, 11/01/2023 - 21:44
Permalien
C'est bonne
Anonyme (non vérifié)
mer, 11/01/2023 - 21:44
Permalien
C'est bonne
Anonyme (non vérifié)
mar, 08/01/2023 - 15:38
Permalien
Bonjour
Fatou seck (non vérifié)
dim, 11/12/2023 - 23:28
Permalien
Jeveux la c
KENE (non vérifié)
lun, 08/26/2024 - 00:02
Permalien
CORRECTION DE L EXO 5
Ajouter un commentaire