Solutions des exercices : Oscillations électriques libres et forcées - Ts
Classe:
Terminale
Exercice 1
1) a) Expression de $Q_{0}$ en fonction de $U_{0}$ et $C.$
$Q_{0}=CU_{0}$
b) Expression de $E_{0}$ en fonction de $Q_{0}$ et $C.$
$E_{0}=\dfrac{1}{2}CU_{0}$
2) a) Expression de l'énergie électromagnétique $E$ en fonction de $L$, $C$, $q$ et $i.$
$E=\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}Li^{2}$
b) Montrons que l'énergie électromagnétique se conserve et elle est égale à $\dfrac{Q_{0}^{2}}{2C}$
Le circuit électrique ne comporte que des dipôles non dissipatifs (condensateur et bobine) ; donc l'énergie électromagnétique se conserve et est égale à l'énergie initialement emmagasinée par le condensateur : $E_{0}=\dfrac{1}{2}\dfrac{Q_{0}^{2}}{C}$
Équation différentielle des oscillations électriques.
$\begin{array}{rcl} E_{0}&=&E\\\\&=&\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}Li^{2}\\\\\Rightarrow\dfrac{\mathrm{d}E_{0}}{\mathrm{d}t}&=&\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{1}{2}+\dfrac{1}{2}Li^{2}\right)\\\\&=&0\\\\\Rightarrow\dfrac{1}{2C}\times 2q\dfrac{\mathrm{d}q}{\mathrm{d}t}+\dfrac{1}{2}L\times 2i\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&0\\\\\text{or }\dfrac{\mathrm{d}q}{\mathrm{d}t}&=&i\\\\&=&\dot{q}\\\\\text{et }\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&\ddot{q}\\\\\Rightarrow\dot{q}\left(\dfrac{q}{C}+L\ddot{q}\right)&=&0\\\\\text{comme }\dot{q}\text{ n'est pas toujours nul}\\\\\Rightarrow\dfrac{q}{C}+L\ddot{q}&=&0 \end{array}$
c) Détermination de l'expression de la période propre $T_{0}$ en fonction de $L$ et $C.$
$T_{0}=2\pi\sqrt{LC}$
d) Expression de la charge $q$ en fonction du temps.
$\begin{array}{rcl} q&=&q_{m}\cos\left(\omega_{0}t+\varphi\right)\\\\&=&q_{m}\cos\left(\dfrac{2\pi}{T_{0}}t+\varphi\right) \end{array}$
$\begin{array}{rcl} \text{A }q&=&q_{m}\cos\varphi\\\\&=&q_{m}\\\\&=&Q_{0}\\\\\Rightarrow\cos\varphi&=&1\\\\\Rightarrow\varphi&=&0\\\\\Rightarrow\,q&=&Q_{0}\cos\dfrac{2\pi}{T_{0}}t \end{array}$
3. Montrons que l'expression l'énergie $E_{L}$ en fonction du temps s'écrit :
$\begin{array}{rcl} E_{L}&=&\dfrac{E_{0}}{2}\left[1+\cos\left(\dfrac{4\pi}{T_{0}}t+\pi\right)\right]\\\\\,E_{L}&=&\dfrac{1}{2}Li^{2}\\\\&=&\dfrac{1}{2}L\ddot{q}^{2}\\\\&=&\dfrac{1}{2}L\left(-\dfrac{2\pi}{T_{0}}Q_{0}\sin\dfrac{2\pi}{T_{0}}t\right)^{2}\\\\&=&\dfrac{1}{2}L\dfrac{4\pi^{2}}{T_{0}^{2}}Q_{0}^{2}\sin^{2}\dfrac{2\pi}{T_{0}}t\sin^{2}\alpha\\\\&=&\dfrac{1-\cos 2\alpha}{2}\\\\\Rightarrow\,E_{L}&=&\dfrac{1}{2}L\dfrac{4\pi^{2}}{T_{0}^{2}}Q_{0}^{2} \end{array}$
4) a) Valeurs de $L$ et de $_{E0}.$
$\begin{array}{rcl} E_{0}&=&2\cdot 10^{-3}J\\\\ E8{0}&=&2\cdot 10^{-3}J\\\\\Rightarrow\,E_{0}&=&\dfrac{1}{2}Li^{2}\\\\\Rightarrow\,L&=&\dfrac{2E_{0}}{i^{2}}\\\\&=&\dfrac{2\times 2\cdot 10^{-3}}{(0.2)^{2}}\\\\\Rightarrow\,L&=&10^{-1}H \end{array}$
b) Valeur de $T_{0}.$
$T_{0}=2\pi\cdot 10^{-4}s$
5) Détermination de $C$, $Q_{0}$ et $U_{0}.$
$\begin{array}{rcl} T_{0}&=&2\pi\sqrt{LC}\\\\\Rightarrow\,LC&=&\dfrac{T_{0}^{2}}{4\pi^{2}}\\\\\Rightarrow\,C&=&\dfrac{T_{0}^{2}}{4\pi^{2}L}\\\\&=&\dfrac{\left(2\pi\cdot 10^{-4}\right)^{2}}{4\pi^{2}\times 2\cdot 10^{-2}}\\\\\Rightarrow\,C&=&5\cdot 10^{-5}F \end{array}$
$\begin{array}{rcl} E_{0}&=&\dfrac{1}{2}L\dfrac{4\pi^{2 }}{T_{0}^{2}}Q_{0}^{2}\\\\\Rightarrow\,Q_{0}&=&\sqrt{\dfrac{2E_{0}T_{0}^{2}}{4\pi^{2}}L}\\\\&=&\sqrt{\dfrac{2\times 2\cdot 10^{-3}\times\left(2\pi 10^{-4}\right)^{2}}{4\pi^{2}\times 2\cdot 10^{-2}}}\\\\\Rightarrow\,Q_{0}&=&4.47\cdot 10^{-5}C \end{array}$
$\begin{array}{rcl} U_{0}&=&\dfrac{Q_{0}}{C}\\\\&=&\dfrac{4.47\cdot 10^{-5}}{5\cdot 10^{-7}}\\\\\Rightarrow\,U_{0}&=&89.4V \end{array}$
Exercice 2
A. L'interrupteur $K$ est dans la position (1)
1) Le phénomène observé est la charge du condensateur
2) Allure de la courbe de variation de la tension aux bornes du condensateur en fonction du temps.
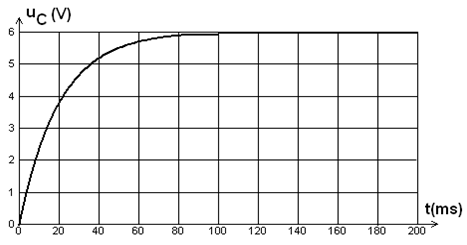
B. L'interrupteur $K$ est basculé dans la position (2)
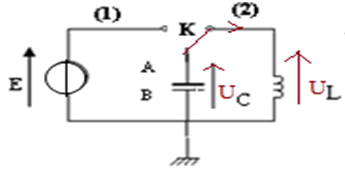
1) a) Établissement de l'équation différentielle qui régit les oscillations de la charge $q(t).$
La loi d'additivité des tensions s'écrit : $U_{C}+U_{L}=0$
$\begin{array}{rcl} U_{C}&=&\dfrac{q}{C}\ ;\\\\ U_{L}&=&L\dfrac{\mathrm{d}i}{\mathrm{d}t}\ ;\\\\ i&=&\dfrac{\mathrm{d}q}{\mathrm{d}t}\\\\&=&\dot{q}\ ;\\\\\dfrac{\mathrm{d}i}{\mathrm{d}t}\\\\&=&\ddot{q}\\\\\Rightarrow\dfrac{q}{C}+L\ddot{q}\\\\&=&0\\\\\Rightarrow\ddot{q}+\dfrac{q}{LC}\\\\&=&0 \end{array}$
b) Montrons que $q(t)=Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)$ peut être une solution de l'équation différentielle
$\begin{array}{rcl} q(t)&=&Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\\\\\Rightarrow\,q(t)&=&\omega_{0}Q_{m}\cos\left(\omega_{0}t+\varphi_{q}\right)\\\\\Rightarrow\ddot{q}t&&=&-\omega_{0}^{2}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\\\\\ddot{q}+\dfrac{q}{LC}&=&0\\\\\Rightarrow-\omega_{0}^{2}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)+\dfrac{1}{LC}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\\\\&=&0\\\\\Rightarrow\left(-\omega_{0}^{2}+\dfrac{1}{LC}\right)Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)&=&0\\\\\Rightarrow-\omega_{0}^{2}+\dfrac{1}{LC}&=&0\\\\\Rightarrow-\omega_{0}^{2}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)&=&0\\\\\Rightarrow-\omega_{0}^{2}+\dfrac{1}{LC}&=&0\\\\\Rightarrow\omega_{0}^{2}&=&\dfrac{1}{LC}\\\\\Rightarrow\omega_{0}&=&\sqrt{\dfrac{1}{LC}} \end{array}$
2) a) Montrons que le circuit $(L\;,\ C)$ est conservatif
$\begin{array}{rcl} E_{C}+E_{L}&=&\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}Li^{2}\\\\&=&\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}L\dot{q^{2}}\\\\&=&\dfrac{1}{2}\dfrac{\left(Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\right)^{2}}{C}+\dfrac{1}{2}L\left(\omega_{0}Q_{m}\cos\left(\omega_{0}t+\varphi_{q}\right)\right)^{2}\\\\\Rightarrow\,E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\sin^{2}\left(\omega_{0}t+\varphi_{q}\right)+\dfrac{1}{2}L\omega_{0}^{2}Q_{m}^{2}\cos^{2}\left(\omega_{0}t+\varphi_{q}\right)\\\\\text{or}\quad \omega_{0}^{2}&=&\dfrac{1}{LC}\\\\\Rightarrow\,E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\sin^{2}\left(\omega_{0}t+\varphi_{q}\right)+\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\cos^{2}\left(\omega_{0}t+\varphi_{q}\right)\\\\&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\left(\sin^{2}\left(\omega_{0}t+\varphi_{q}\right)+\cos^{2}\left(\omega_{0}t+\varphi_{q}\right)\right)\\\\\Rightarrow\,E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C} \end{array}$
Et l'énergie totale est constante ; le circuit $(L\;,\ C)$ est donc conservatif
b) Montrons que l'énergie électrique emmagasinée dans le condensateur en fonction de $i^{2}$ est de la forme $E_{e}= Q_{m}^{2}-\dfrac{1}{2} L\cdot i^{2}$
$\begin{array}{rcl} E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\\\\&=&E_{e}+E_{L}\\\\\Rightarrow\,E_{e}&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}-E_{L}\\\\\Rightarrow\,E_{e}&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}-\dfrac{1}{2}Li^{2} \end{array}$
c) Justifions théoriquement l'allure de la courbe
D'après la loi d'additivité des tensions : $U_{C}+U_{L}=0$
$\Rightarrow\,U_{L}=-U_{C}\Rightarrow\,U_{L}=-\dfrac{q}{C}$
La courbe représentant la tension $U_{L}$ aux bornes de la bobine en fonction de la charge $q$ une droite passant par l'origine de pente négative. Ce que l'allure de la courbe confirme
3) Détermination :
a) L'inductance $L$ de la bobine.
$\begin{array}{rcl} E_{e}&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}-\dfrac{1}{2}Li^{2}\\\\\Rightarrow\dfrac{\Delta E_{e}}{\Delta i^{2}}&=&-\dfrac{1}{2}L\\\\\Rightarrow\,L&=&-\dfrac{2\Delta E_{e}}{\Delta i^{2}}\\\\&=&-\dfrac{2\left(0-5\cdot 10^{-4}\right)}{(10-0)\cdot 10^{-4}}\\\\\Rightarrow\,L&=&1H \end{array}$
b) La capacité C du condensateur.

Commentaires
Iris medeho (non vérifié)
lun, 04/10/2023 - 18:50
Permalien
Corrigé exercice
ORPHÉE tu (non vérifié)
sam, 04/20/2024 - 04:14
Permalien
Je veus le reste de la
Mame Diarra (non vérifié)
ven, 06/06/2025 - 06:26
Permalien
Je veux le reste de la
Ajouter un commentaire