Physique

Équilibre d'un solide soumis à des forces non parallèles - 2nd S

Classe: 
Seconde
 

I. Équilibre d'un solide soumis à deux forces

1. Étude expérimentale 

1.1. Expérience

Un morceau de polystyrène est soumis aux actions de deux fils tendus.
 
Ces fils exercent sur le solide $(S)$ la force appliquée au point $A$ et la force au point $B.$
 
Le poids du solide est peut être négligé devant ces deux forces beaucoup plus importantes.
 
Deux dynamomètres permettent de mesurer les valeurs de ces deux forces 
 
 

1.2. Observations

On constate que, lorsque le solide est immobile, c'est-à-dire en équilibre : 
 
$-\ $ les fils sont dans le prolongement de l'un de l'autre
 
$-\ $ les dynamomètres donnent la même indication 
 
 

1.3. Interprétation

$-\ $ les fils dans le prolongement de l'un de l'autre impliquent que les deux forces aient la même d'action. 
 
On qu'elles sont colinéaires  
 
$-\ $ les deux forces ont la même valeur. Les deux forces sont représentées par deux segments fléchés de même longueur mais de sens opposés

2. Conditions d'équilibre

Si un corps soumis à deux forces $F_{1}\ $ et $\ F_{2}$ est en équilibre, ces forces ont :
 
$-\ $ la même droite d'action ;
 
$-\ $ des sens contraires ;
 
$-\ $ la même intensité : $F_{1}=F_{2}.$
 
Les deux vecteurs force sont donc opposés :  
$$\vec{F}_{1}=-\vec{F}_{2}\quad\text{ou}\quad\vec{F}_{1}+\vec{F}_{2}=\vec{0}$$

Remarque :

La somme vectorielle des deux forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ nulle est une condition nécessaire mais pas suffisante.
 
Les deux forces peuvent avoir la même intensité et des sens contraires, mais pas la même droite d'action ; le corps n'est pourtant pas en équilibre car, il tourne.
 
 

3. Applications

3.1. Solide suspendu à l'extrémité d'un fil

Système étudié : le solide $(S)$
 
Référentiel d'étude : référentiel terrestre 
 
Bilan des forces appliquées : $\vec{P}\ $ et $\ \vec{T}$  
 
La condition d'équilibre s'écrit : $\vec{P}+\vec{T}=\vec{0}$
 
En projetant la relation vectorielle suivant le sens de $\vec{T}$ , il vient :
$$-P+T=0\Rightarrow\,T=P$$ 
 
 

3.2. Solide sur un plan lisse horizontal

Le solide est soumis à deux forces :
 
$-\ $ la réaction du support $\vec{R}$ et le poids $\vec{P}$
 
$-\ $ Il est en équilibre.
 
$-\ $ La condition nécessaire d'équilibre permet d'écrire que :
$$\vec{P}+\vec{R}=\vec{0}$$
En projetant la relation vectorielle suivant le sens de $\vec{R}$, il vient :
$$-P+R=0\Rightarrow\,R=P$$
 
 

II. Équilibre d'un solide soumis à trois forces non parallèles

1. Étude expérimentale 

1.1. Expérience

Une plaque $S$ est soumise aux actions de trois fils tendus.
 
Ces fils exercent sur le solide $(S)$ trois forces aux différents points d'attache.
 
 
Le poids du solide est peut être négligé devant ces deux forces beaucoup plus importantes.
 
Trois dynamomètres permettent de mesurer les valeurs de ces trois forces.
 
De plus, on peut relever sur papier, les directions des trois fils, c'est-à-dire les directions des forces.

1.2. Observations

L'expérience est répétée plusieurs fois en changeant les directions et les intensités des forces.
 
On constate si le corps est à l'équilibre,
 
$-\ $ les trois forces $\vec{F}_{1}\;,\ \vec{F}_{2}\ $ et $\ \vec{F}_{3}$ se trouvent dans un même plan : on dit qu'elles sont coplanaires.
 
$-\ $ les lignes d'action ou droites qui portent les vecteurs forces passent par un même point : on dit les forces sont concourantes.
 
$-\ $ En général les intensités des trois forces sont différentes
 
 

1.3. Interprétation

Déterminons la résultante de ces trois forces.
 
$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{AC}+\overrightarrow{CA}=\vec{0}$
 
$\Rightarrow\ \vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}=\vec{0}$
 
 
$-\ $ Les vecteurs forces $\vec{F}_{1}\;,\ \vec{F}_{2}\ $ et $\ \vec{F}_{3}$ forment un triangle (le dynamique des forces) fermé.
 
La somme vectorielle des forces est égale au vecteur nul :  
$$\vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}=\vec{0}$$

2. Condition d'équilibre 

Si un corps soumis à trois forces $\vec{F}_{1}\;,\ \vec{F}_{2}\ $ et $\ \vec{F}_{3}$ est en équilibre :
 
$-\ $ les trois forces sont coplanaires et concourantes ;
 
$-\ $ la somme vectorielle des trois forces est nulle.
 
La deuxième condition s'exprime par la relation vectorielle :
$$\vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}=\vec{0}$$ 

3.  Exercice d'application                                                                                                         

On attache une bille de fer $(S)$ de masse $m=300g$ à l'extrémité d'un ressort de raideur $k=100N\cdot m^{-1}$ et on applique une force horizontale   par un aimant. 
 
La bille de fer $(S)$ est en équilibre lorsque l'axe du ressort constitue $\alpha=30^{\circ}$ avec le Vertical.
 
1. Faire l'inventaire des forces appliquées à la bille de fer $(S).$
 
2. Énoncer la condition d'équilibre
 
3. Trouver l'expression de $T$ et $F$ en fonction de $m$, $g$ et $\alpha$, puis calculer leurs valeurs.
 
4. En déduire l'allongement du ressort
 
 
On donne : $g=10N\cdot kg^{-1}$

Résolution

1. Inventaire des forces appliquées au solide $(S)$
 
 
Le solide $(S)$ soumis à :
 
$-\ $ son poids $\vec{P}$  
 
$-\ $ la tension $\vec{T}$ du ressort
 
$-\ $ la force magnétique $\vec{F}$
 
2. Énoncé la condition d'équilibre 
 
Lorsqu'un solide est soumis trois forces est en équilibre alors la somme vectorielle de ces trois forces est nulle.
 
3. Expression de $T\ $ et $\ F$ en fonction de $m$, $g$ et $\alpha$ et calcul de leurs valeurs.
 
La condition d'équilibre, appliquée au solide $(S)$, s'écrit : 
$$\vec{P}+\vec{T}+\vec{F}=\vec{0}$$
En projetant suivant l'axe $y'y$, il vient : 
   
$\begin{array}{rcl} -P+T\cos\alpha+0=0&\Rightarrow&T\cos\alpha =P=mg\\ \\&\Rightarrow&T=\dfrac{mg}{\cos\alpha}\\ \\&\Rightarrow&T=\dfrac{300\cdot 10^{-3}\times 10}{\cos 30^{\circ}}\\ \\&\Rightarrow&T=3.5N\end{array}$  
 
En projetant suivant l'axe $x'x$, il vient : 
 
$\begin{array}{rcl} 0+T\sin\alpha-F=0&\Rightarrow&F=T\sin\alpha\\ \\&\Rightarrow&F=3.5\sin\alpha 30^{\circ}\\ \\&\Rightarrow&F=1.75N\end{array}$
 
4. Déduction de l'allongement du ressort
 
$\begin{array}{rcl} T=K\Delta l&\Rightarrow&\Delta l=\dfrac{T}{K}=\dfrac{3.5}{100}\\ \\&\Rightarrow&\Delta l=3.5\cdot10^{-2}m\\ \\&\Rightarrow&\Delta l= 3.5\,cm\end{array}$

 

 
Auteur: 
Sidy Mouhamed Ndiaye

Poids - Masse : Relation entre poids et masse - 2nd S

Classe: 
Seconde
 

I. Masse d'un corps

1. Observations

Soit, par exemple, un sac rempli de riz : on dit que ce sac contient une certaine quantité de riz ou encore une certaine masse de riz.
 
Considérons maintenant un sac $A$ de riz et un sac $B$ de riz : on dit que le sac $A$ contient une quantité de riz qui est importante de celle qui est contenue dans le sac $B$ ou bien qu'il contient une masse plus grande de celle contenue dans le sac rempli à demi.
 
 

2. Définition

La masse d'un corps est une grandeur physique représentant la quantité de matière contenue dans ce corps.

3. Caractéristiques de la masse d'un corps

La masse d'un corps est une grandeur scalaire positive, extensive, invariable, et indépendante du lieu.

4. Mesures et unités

4.1. Mesures

4.1.1. Appareil de mesure 

La masse d'un corps est mesurée à l'aide d'une balance.

Exemples de balance

Balance Roberval
 
 
Balance monoplateau
 
Balance médicale

4.1.2. Types de mesure 

4.1.2.1. Mesure par la simple pesée 

La simple est réalisée lorsqu'une grande pesée n'est pas nécessaire
 
On utilise, par exemple une balance de Roberval. 
 
Sur l'un des plateaux, on place l'objet dont on veut mesurer sa masse et on met sur l'autre plateau des masses marquées jusqu'à ce que la balance soit équilibrée.

4.1.2.2. Mesure par la double pesée 

La double pesée permet de mesurer des masses même si la balance utilisée n'est pas juste.
 
On utilise, une balance précise, par exemple, un trébuchet.
 
Pour peser l'objet dont on cherche la masse $m$, on effectue deux pesées avec la même tare $T$ (double pesée à tare constante). 
 
La tare est un objet quelconque, par exemple une masse marquée dont la masse est supérieure à la masse $m$ à mesurer.
 
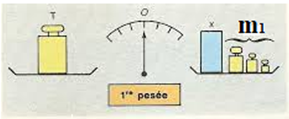
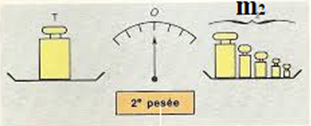
Première pesée : la tare est placée dans l'un des plateaux, l'objet à peser $($masse $m)$ dans l'autre plateau et on équilibre la balance au zéro avec des masses marquées $(m_{1})$ à côté de l'objet dont on cherche la masse
 
Deuxième pesée : on conserve la tare et on équilibre la balance au zéro en plaçant des masses marquées dans le plateau contenant l'objet après avoir vidé de son contenu
 
La valeur cherchée $m$ s'obtient par la relation :    
$$m+m_{1}=m_{2}\Leftrightarrow\boxed{m=m_{2}-m_{1}}$$

4.2. Unité de la masse 

L'unité de masse dans le Système International $(S.I)$ est le kilogramme $($symbole : $kg)$
 
On utilise également les multiples et les sous-multiples du kilogramme
$$\begin{array}{|l|l|l|l|} \hline &\text{Unité et symbole}&\text{Valeur}&\text{Valeur}\\ & &\text{en kilogramme}&\text{en gramme}\\\hline &\text{La tonne }(t)&10^{3}kg&10^{6}g\\ \text{Multiples}&\text{Le quintal }(q)&10^{2}kg&10^{5}g\\ &\text{Dizaine du kilogramme }(10)&10^{1}kg&10^{4}g\\ \hline &\text{Hectogramme }(hg)&10^{-1}kg&10^{3}g\\ &\text{Décagramme }(dag)&10^{-2}kg&10^{2}g\\ &\text{Gramme }(g)&10^{-3}kg&1g\\ \text{Sous-multiples}&\text{Décigramme }(dg)&10^{-4}kg&10^{-1}g\\ &\text{Centigramme }(cg)&10^{-5}kg&10^{-2}g\\ &\text{Miligramme }(mg)&10^{-6}kg&10^{-3}g\\ &\text{Microgramme }(\mu)&10^{-9}kg&10^{-6}g\\ &\text{Nanogramme }(n)&10^{-12}kg&10^{-9}g\\ \hline \end{array}$$
 
Quelques ordres de grandeurs de masses quelques corps ou particules.
 
masse du proton : $m_{p}=1.672\cdot10^{-27}kg$ ; 
 
masse du neutron : $m_{n}=1.674\cdot10^{-27}kg$ ; 
 
masse de la Terre : $m_{T}=6\cdot10^{24}kg$ ; 
 
masse du Soleil : $m_{S}=2\cdot10^{30}kg$

Définition du kilogramme

Le kilogramme est la masse de l'objet dénommé kilogramme-étalon et conservé au Pavillon de Breteuil à Sèvres

II. Masse volumique et densité d'un corps

1. Masse volumique d'un corps 

Des corps ayant le même volume ont généralement des masses différentes. 
 
Pour caractériser un corps, on peut utiliser une grandeur physique appelée masse volumique.

1.1. Définition

La masse volumique d'un corps, à température donnée, est la masse de l'unité de volume de ce corps à cette température.

Remarque :

La masse volumique d'une substance dépend des conditions dans lesquelles elle se trouve, elle varie en fonction de la température et de la pression, surtout pour les gaz, mais aussi pour les liquides et les solides.

1.2. Unités de la masse volumique

La masse volumique s'exprime, dans le Système International, en kilogrammes par mètre cube $($symbole : $kg\cdot m^{-3})$
 
Les unités usuelles sont : 
 
le gramme par centimètre cube $(g\cdot cm^{-3})$ ; le kilogramme par décimètre cube $(kg\cdot dm^{-3})$ ; la tonne par mètre cube $(t\cdot m^{-3})$

Remarque :

$-\ $ Le kilogramme par litre $(kg/L)$, le gramme par millilitre $(g/mL)$, le kilogramme par décimètre cube $(kg/dm^{3})$ et le gramme par centimètre cube $(g/cm^{3})$ sont équivalents :
$$1kg/L=1g/L=1kg/dm^{3}=1g/cm^{3}$$
 
$-\ $ Le gramme par litre $(g/L)$, le milligramme par millilitre $(mg/mL)$, gramme par décimètre cube $(kg/dm^{3})$ et le milligramme par centimètre cube $(g/cm^{3})$ sont équivalents :
$$1g/L=1mg/mL=1g/dm^{3}=1mg/cm^{3}$$

1.3. Mesure de la masse volumique d'un corps

Pour déterminer la masse volumique d'une substance, il faut en mesurer la masse d'un volume donné.
 
Si le corps a une forme géométrique simple, la mesure des dimensions et un calcul permettent d'obtenir son volume. 
 
Sinon, la méthode est à adapter à la nature de la substance et à son état physique.
 
Pour mesurer la masse, on utilise une balance et des masses marquées.

1.3.1. Masse volumique d'un solide 

$\blacktriangleright\ $Pour un solide à forme géométrique simple on détermine :
 
$-\ $ sa masse par pesée : simple ou double
 
$-\ $ son volume calculé à partir des dimensions : 
 
par exemple : $V=\pi R^{2}h\quad \text{(cylindre)}$
 
$\blacktriangleright\ $Solide à forme géométrique quelconque : 
 
$-\ $La masse est déterminée par pesée : simple ou double.
 
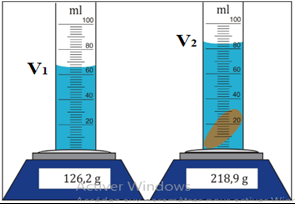
$-\ $Le volume est déterminé par immersion : $V=V_{2}-V_{1}$
 
On détermine la masse volumique du solide par la relation :
$$\rho=\dfrac{m}{V}$$
 
 

1.3.2. Masse volumique de liquide 

La masse de liquide se détermine par double-pesée avec une balance et le volume peut se lire avec une fiole jaugée 
 
La masse volumique du liquide est déterminée par la relation : 
$$\rho=\dfrac{m_{2}-m_{1}}{V}$$
 
Première pesée
 
Deuxième pesée

1.3.3. Masse volumique des gaz 

Tout comme pour les liquides et les solides, il est possible de calculer la masse volumique d'un gaz en divisant la mesure de sa masse par celle de son volume.
$$\rho=\dfrac{m}{V}$$

1.3.4. Masse volumique de quelques substances 

$$\begin{array}{|l|l|l|l|l|l|l|l|} \hline \text{Métal}&\text{Aluminium}&\text{Argent}&\text{Laiton (alliage)}&\text{Cuivre}&\text{Fer}&\text{Plomb}&\text{Or}\\ \hline \rho\text{ en }g\cdot cm^{-3}&2.7&10.5&7.3\;-\;8.4&8.9&7.9&11.4&19.3\\\hline \end{array}$$

2. Densité d'un corps

2.1.Observations

Un glaçon flotte sur l'eau, un tronc d'arbre flotte sur la rivière. 
 
Au contraire une roche, un morceau de fer, une bille de plomb tombent au fond de l'eau. 
 
Celles qui coulent ont une masse volumique plus grande que la masse volumique de l'eau. 
 
Au contraire, les substances qui flottent ont une masse volumique plus petite que celle de l'eau.
 
Comparer la masse volumique d'une substance à celle de l'eau permet donc de faire des prévisions pour savoir si la substance flotte ou non.
 
Il est pratique d'introduire une notion : la densité.

2.2 .Définition 

$\blacktriangleright\ $La densité d'un corps est le rapport de la masse de ce corps à la masse d'un égal volume d'un corps pris comme référence pris à la même température
$$d=\dfrac{m}{m_{ref}}$$
 
Comme $m=\rho V\text{ et }m_{ref}=\rho_{ref}V$
 
$\blacktriangleright\ $La densité d'un corps est le rapport de sa masse volumique à la masse volumique d'un corps pris comme référence
$$d=\dfrac{\rho}{\rho_{ref}}$$
 
$-\ $ Pour les solides et les liquides, le corps de référence est l'eau : 
$$d=\dfrac{\rho}{\rho_{eau}}$$
 
$-\ $ Pour les gaz, le corps de référence est l'air : 
$$d=\dfrac{\rho}{\rho_{air}}$$

2.3. Densité de quelques substances 

Le tableau ci-dessous résume la densité de quelques substances
$$\begin{array}{|l|l|l|l|l|l|l|} \hline \text{Substance}&\text{Fer}&\text{Aluminium}&\text{Cuivre}&\text{Ethanol}&\text{Caoutchouc}&\text{Glace}\\ \hline \text{Densité}&7.86&2.7&8.92&0.798&0.92\text{ à }0.99&0.917\\ \hline \end{array}$$
 
L'acier a une densité de l'ordre de celle du fer suivant sa composition.

Remarque :

Un corps flotte dans l'eau lorsque la densité est inférieure à $1$ et coule lorsque la densité est supérieure à $1$

III. Le poids d'un corps

1. Observations

Un objet lâché sans vitesse initiale tombe et se dirige vers la Terre.
 
Une balle lancée verticalement vers le haut atteint une hauteur limite puis retombe.
 
Un projectile lancé de façon quelconque décrit une trajectoire courbe et finit par atteindre le sol.
 
Ces observations montrent que la Terre exerce une force sur tout objet placé dans son environnement immédiat.

2. Définition 

Le poids d'un corps est la force d'attraction que la Terre exerce sur ce corps.

3. Caractéristiques du poids

Les caractéristiques du poids d'un corps sont :
 
$-\ $ Son point d'application
 
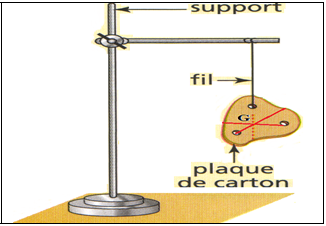
Son point d'application est le centre de gravité $G.$ 
 
Toutes les verticales passant par un point quelconque de suspension $S$ du corps concourent en point G appelé centre de gravité. 
 
Le point $G$ dépend de la répartition de la matière dans le volume de l'objet 
 
 
$-\ $ Sa direction
 
La verticale du lieu où se trouve le corps
 
$-\ $ Son sens
 
Le sens est du haut vers le bas
 
$-\ $ Son intensité
 
C'est sa grandeur poids $P$

4. Mesure et unité 

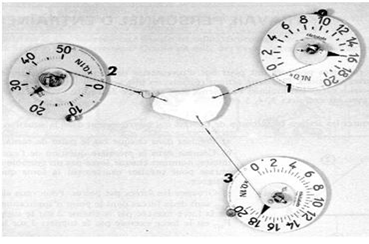
L'appareil servant à la mesure du poids d'un corps est le dynamomètre 
 
Le poids $P$ s'exprime en newtons $(N)$

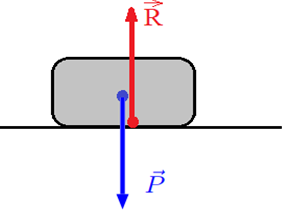
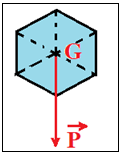
5. Représentation vectorielle 

Le poids est une grandeur vectorielle. 
 
On le représente par un vecteur en respectant ses caractéristiques
 
 

IV. Relation entre corps et masse 

1. Expérience

A l'aide d'une balance et d'un dynamomètre, mesurons respectivement la masse et le poids de différents objets. 
 
On obtient le tableau de valeurs suivantes :
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|} \hline \text{Masse }m\ (kg)&0.1&0.2&0.3&0.4&0.5&0.6&0.7&0.8&0.9&1\\ \hline \text{Poids }P(N)&0.98&1.96&2.94&3.92&4.9&5.88&6.86&7.84&8.82&9.8\\ \hline P/m\ (N/kg)&9.8&9.8&9.8&9.8&9.8&9.8&9.8&9.8&9.8&9.8\\\hline \end{array}$$
 
$\blacktriangleright\ $Déterminons le rapport $\dfrac{P}{m}$
 
On constate en un lieu donné, le poids d'un objet est proportionnel à sa masse.
 
Ce rapport est constant : $\dfrac{P}{m}=9.8N\cdot kg^{-1}$
  
Cette constante ou coefficient de proportionnalité est égale à l'intensité $g$ du champ de pesanteur au lieu considéré.
$$\dfrac{P}{m}=g\Rightarrow\begin{array}{|}\hline\\&P\text{ en }N\\P=mg&m\text{ en }kg\\&(N\cdot kg^{-1})\\\hline\end{array}$$
 
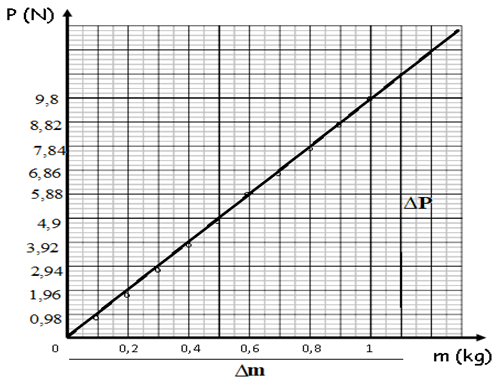
$\blacktriangleright\ $Traçons la courbe représentant les variations du poids $P$ en fonction de la masse $m$
 
 
Le graphe représentant le poids $P$ en fonction de la masse $m$ est une droite passant par l'origine de la forme
 
$P=am\text{ avec : }a=\dfrac{\Delta P}{\Delta m}=\dfrac{10.8-0}{1.1-0}=9.8N\cdot kg^{-1}=g$ étant le coefficient directeur de la droite
$$a=g\Rightarrow\,P=mg$$

2. Caractéristiques du vecteur champ de pesanteur 

Le poids est une grandeur vectorielle et la masse une grandeur scalaire.
 
Le champ de pesanteur est donc une grandeur vectorielle
$$\overrightarrow{P}=m\overrightarrow{g}$$
 
Le champ de pesanteur $\overrightarrow{g}$ a les caractéristiques suivantes :
 
$-\ $ Direction : la verticale du lieu
 
$-\ $ Sens : vers le bas

3. Variation de l'intensité de la pesanteur

Considérons les tableaux de mesures ci-dessous
$$\begin{array}{|c|c|c|c|} \hline \text{Latitude}&\text{Paris}&\text{Pole Nord}&\text{Equateur}\\ \hline g(N\cdot kg^{-1})&9.81&9.83&9.78\\ \hline \end{array}$$ $$\begin{array}{|c|c|c|} \hline \text{Altitude}&\text{Chamonix}&\text{Mont Blanc}\\ \hline g(N\cdot kg^{-1})&9.809&9.806\\ \hline \end{array}$$
 
On constate que l'intensité de la pesanteur varie :
 
$-\ $ la latitude du lieu considéré
 
$-\ $ l'altitude considéré

4. Différences entre le poids et la masse 

Il ne faut pas confondre le poids et la masse.
 
La masse d'un corps est indépendante du lieu. 
 
Le poids d'un corps dépend du lieu où trouve ce corps.
 
Le poids est une grandeur vectorielle. 
 
La masse est une grandeur scalaire positive.
 
La masse s'exprime en kilogramme. 
 
Le poids s'exprime en newton.

5. Étalonnage d'un ressort

Étalonner un appareil revient après tout à y adjoindre (ajouter) des repères permettant de le mettre à niveau pour jouer le rôle d'instrument de mesure.

5.1. Protocole expérimentale : 

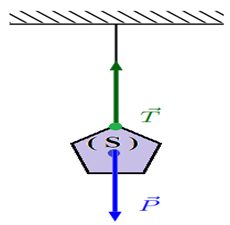
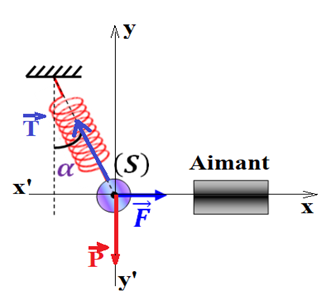
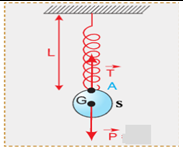
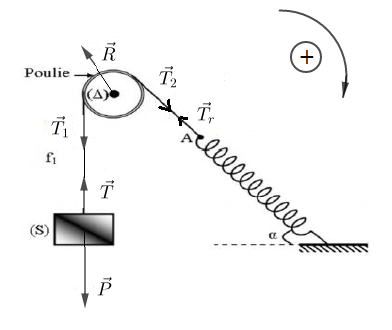
Le solide $S$ exerce sur le ressort une force notée $\overrightarrow{P}.$
 
De même le ressort exerce une force sur le solide notée $\overrightarrow{T}.$
  
D'après le principe d'interaction : $\overrightarrow{P}=-\overrightarrow{T}$
  
En module : $P=T$
 
Comme $P=mg\Rightarrow\,T=mg$ 
 
 

5.2. Tableau de valeurs

On accroche l'une des extrémités d'un ressort à un support et on le laisse pendre verticalement, le ressort prend une longueur initiale $L_{0}.$
 
On suspend une masse marquée $M$ à l'extrémité libre du ressort. 
 
Le ressort s'allonge et prend une longueur finale $L.$
 
Le ressort sera alors allongé de : $\Delta L=L-L_{0}.$

N.B : 

Le cas de la compression du ressort : $\Delta L=L_{0}-L$
 
On accroche des masses différentes successivement.
 
Les résultats des mesures sont reportés dans un tableau
 
Tableau de variation de $\Delta L$ avec la masse $m$ 
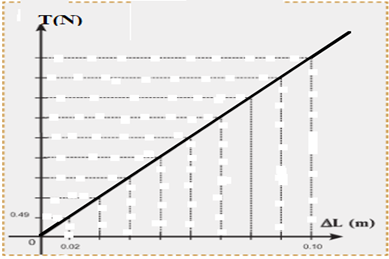
$$\begin{array}{|c|c|c|c|c|c|} \hline m(g)&50&100&150&200&250\\ \hline P(N)&0.49&0.98&1.47&1.96&2.45\\ \hline L(m)&0.22&0.24&0.26&0.28&0.30\\ \hline \Delta L(m)&0.02&0.04&0.06&0.08&0.10\\ \hline P/\Delta L(N/m)&24.5&24.5&24.5&24.5&24.5\\ \hline \end{array}$$

5.2. Exploitation 

Le graphique donnant la variation de $T$ avec $\Delta L$, montre que la courbe obtenue est une demi-droite croissante passant par l'origine.
 
Donc l'intensité $T$ de la tension est proportionnelle à $\Delta L.$
 
La constante de proportionnalité est note $K$ et s'appelle constante de raideur du ressort et s'exprime en newtons par mètre $(N\cdot m^{-1})$
 
D'où la relation : 
$$T= K\Delta L\quad\text{ou}\quad T=Kx\quad\text{où}\quad x=\Delta L$$
 
$T$ en $N$, $\Delta L$ ou $x$ en $m$ et $K$ en $N\cdot m^{-1}$
 

 
Auteur: 
Sidy Mouhamed Ndiaye

Généralités sur les forces - 2nd S

Classe: 
Seconde
 

I. Les effets d'une force

1. Les effets dynamiques d'une force

Au cours d'un match de football entre deux équipes $A$ et $B$, un joueur de l'équipe de $A$ tire un coup franc.
 
Le gardien de but de l'équipe $B$ peut, soit arrêter la balle, soit la dévier. 
 
Le joueur met ainsi en mouvement et le gardien de but modifie ce mouvement. 
 
Tous les deux ont exercé une action mécanique sur la balle.

2. Les effets statiques d'une force

Un objet accroché à un ressort le déforme. 
 
Le ressort, quant à lui, maintient l'objet au repos.
 
Le ressort exercice une action mécanique sur l'objet. 
 
Il en va de même de l'objet sur le ressort.

Remarque :

La déformation peut ne pas être visible. 
 
C'est le cas, par exemple, d'un livre posé sur la table.

3. Notion de force

Nous attribuerons tous les effets observés lors des situations précédentes, effets dynamiques et effets statiques à la même cause. 
 
Cette cause commune est appelée force.

3.1. Définition

Une force est toute cause capable :
 
$-\ $ de mettre un corps en mouvement ou de modifier le mouvement d'un corps (effets dynamiques)
 
$-\ $ de déformer un corps ou de le maintenir au repos (effets statiques) 

3.2. Les caractéristiques et représentations d'une force

3.2.1. Les caractéristiques d'une force

On peut déterminer les caractéristiques d'une force en étudiant les effets qu'elle produit.
 
Les quatre caractéristiques d'une force sont :
 
$-\ $ Point d'application : C'est le point sur lequel la force exercice.
 
$-\ $ La direction ou la droite d'action : C'est la droite suivant laquelle la force agit
 
$-\ $ Le sens : Le sens d'une force est le sens de déplacement que cette force tend à produire.
 
$-\ $ L'intensité : C'est la grandeur de la force.
 
L'intensité ou la norme est d'autant plus grande que ses effets sur le déplacement ou la déformation d'un corps sont plus importants.
 
Dans le Système International, l'unité de la force est le newton $($symbole : $N)$
 
L'intensité de la force se mesure à l'aide d'un appareil appelé dynamomètre.
 
Il existe deux de dynamomètres : un dynamomètre simple et un dynamomètre circulaire.
 
Dynamomètre simple et symbole
 
Dynamomètre circulaire avec support magnétique et symbole

3.2.2. Représentation d'une force

Les caractéristiques d'une force sont celles d'un vecteur : la force est une grandeur vectorielle.

Exemple : 

représentation d'une force
 
 

II. Exemples de forces

1. Forces de contact et forces à distance

1.1. Forces de contact

Elles se manifestent lorsqu'un corps est contact avec un autre corps

1.1.1. Les tensions

 
C'est la force exercée par ce fil sur un solide accroché à l'une de ses extrémités. 
 
$-\ $Point d'application : point d'attache
 
$-\ $Direction : celle du fil tendu.
 
$-\ $Sens : du point d'attache vers le fil
 
$-\ $Intensité : égale à celle de la force exercée par l'objet accroché sur le fil.
 
 
C'est la force exercée par ce ressort sur un solide accroché à l'une de ses extrémités.
 
$-\ $Point d'application : point d'attache
 
$-\ $Direction : celle du ressort tendu.
 
$-\ $Sens : du point d'attache vers le ressort
 
$-\ $Intensité : égale à celle de la force exercée par l'objet accroché sur le ressort. 
 
$T=k\left|l_{0}-l\right|$ Avec $k$ : constante de raideur du ressort en newtons $(N)$ ; $l$ : allongement du ressort et $l_{0}$ longueur à vide du ressort en mètres $(m).$

1.1.2. Les réactions 

Dans le cas d'un objet posé sur un support, le support exerce une force sur l'objet (la réaction du support).
 
 
 
 
 

1.2. Forces de contact

On appelle forces à distances des forces qui exercent entre objets séparés par une distance.

Exemples : 

les forces de gravitation, les forces magnétiques, les forces électriques
 
 
 
 

2. Forces localisées et forces réparties

2.1. Forces localisées

Une force est localisée sur un corps qu'on connait la position exacte à partir de laquelle elle exerce.

Exemples : 

les tensions, la réaction d'un crochet

2.2. Forces réparties

Une force est dite répartie si elle n'agit pas en un point, mais sur une surface.

Exemples : 

l'action du vent sur la voile d'un bateau ; ou celle de la Terre sur un corps (elle s'exerce sur toutes les parties du corps).

Remarque :

Il est souvent possible de remplacer une force répartie par une force localisée ayant le même effet.

III. Principe d'interaction

1. Interaction entre deux solides

 
Le livre exerce une force  sur la table appelée action.
 
La table réagit en exerçant une force  sur le livre appelée réaction.

2. Énoncé

Lorsqu'un solide $S_{1}$ est en interaction avec un solide $S_{2}$, la force  exercée par le solide $S_{1}$ sur le solide $S_{2}$ (action) est égale à l'opposée de la force exercée par le solide $S_{2}$ sur le solide $S_{1}$ (réaction).
 
Les deux forces $\overrightarrow{F_{1}}$ et $\overrightarrow{F_{2}}$ ont la même droite d'action.
$$\overrightarrow{F_{1}}=-\overrightarrow{F_{2}}\quad\text{ ou }\quad\overrightarrow{F_{1}}+\overrightarrow{F_{2}}=0$$

IV. Forces intérieures et forces extérieures

1. Le système

Un système est un corps ou un ensemble de corps sur lequel porte l'étude.
 
Tout ce qui n'appartient pas au système est appelé milieu extérieur.

2. Forces extérieures

Les forces extérieures sont des forces exercées par l'extérieur sur le système.

Exemple : 

Un camion $(C)$ tire une remorque $(R)$ par l'intermédiaire d'un câble
 
 
$\overrightarrow{F}$ : la force motrice exercée sur le camion 
 
$\overrightarrow{T_{1}}$ : la force exercée par la remorque sur le camion
 
$\overrightarrow{T_{2}}$ : la force exercée par le camion sur la remorque
 
Si on considère la remorque comme système : $\overrightarrow{T_{2}}$ est une force extérieure 
 
De même, en considérant le camion comme système : $\overrightarrow{F}$ et $\overrightarrow{T_{1}}$ sont des forces extérieures  

3. Forces intérieures

Les forces intérieures sont des forces sur une partie du système sur une autre partie du système.
 

 
En considérant le système constitué du camion et de la remorque, $\overrightarrow{T_{1}}$ et $\overrightarrow{T_{2}}$ sont des forces intérieures.
 
Auteur: 
Sidy Mouhamed Ndiaye

Généralités sur le mouvement - vitesse - 2nd S

Classe: 
Seconde
 

I. Mouvement

1. Notion de mouvement

 
Lorsqu'une voiture démarre, ses roues tournent, sa carrosserie se déplace par rapport à la route et les tous objets fixes sur la terre.
 
Un corps est en mouvement lorsqu'il change de position dans le temps par rapport à d'autres corps.

2. Relativité du mouvement

Le mouvement et l'immobilité sont des notions toutes relatives.
 
Un objet $A$ peut être en mouvement par rapport à un objet $B$ mais immobile par rapport à un objet $C.$
 
Ces observations montrent bien que l'état de mouvement ou de repos d'un corps dépend de l'objet de référence choisi appelé référentiel. 
 
On dit que le mouvement a un caractère relatif : C'est la relativité du mouvement.

II. Référentiels et repères

1. Référentiels

1.1. Définition

Un référentiel est un solide (ou un ensemble de solides) par rapport auquel le mouvement est étudié.

1.2. Exemples de référentiels

1.2.1. Référentiel héliocentrique

Il a pour origine le centre du système solaire et trois axes dirigés vers trois étoiles fixes.
 
Il est généralement utilisé des astres ou des planètes du système solaire 
 
 

1.2.2. Référentiel géocentrique

Il a pour origine le centre de la Terre et comprend trois axes dirigés vers trois étoiles fixes, parallèles à ceux du référentiel héliocentrique. 
 
Il est généralement utilisé pour l'étude du mouvement d'un satellite de la Terre.
 
 

1.2.3. Référentiel terrestre
 

Le solide de référence est la Terre. 
 
Il est utilisé dans le cadre des études mécaniques effectuées dans un laboratoire ou à partir du sol.
 
L'objet de référence peut être un arbre, un mur, une table d'expérience... etc 
 
Le référentiel terrestre est encore appelé référentiel de laboratoire
 
 

2. Repères d'espace et de temps

Pour décrire le mouvement d'un point mobile, il faut le situer dans l'espace et dans le temps ; d'où la nécessité de choisir un repère d'espace et repère de temps 

2.1. Notion de point mobile

Tout objet en mouvement est appelé objet mobile. 
 
Cet objet est considéré comme point mobile si l'étude, sur une distance grande par rapport à ses dimensions porte sur son mouvement global

2.2. Repères d'espaces

Le repère d'espace permet de repérer d'un mobile.
 
Il est lié au référentiel d'étude
 
Le choix du repère d'espace se ramène au choix d'un système d'axes liés à la référence
 
Le repère d'espace peut être :

2.2.1. Le repère cartésien

Dans l'espace tout point $M$ est repéré par ses coordonnées ou ses composantes $x$, $y$ et $z$ ; le vecteur position est : 
$$\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}$$
 
 
Dans le plan, le point $M$ est repéré par ses coordonnées $x$ et $y$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}+y\vec{j}$$
 
 
Sur un axe, le point $M$ est repéré par sa coordonnée $x$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}$$
 
 

2.2.2. Le repère curviligne

Le mobile est repéré par son abscisse curviligne $S=\overset{\displaystyle\frown}{OM}$
 
 

2.2.3. Le repère angulaire

Le repère est constitué par un point origine $O$ associé à une base $\vec{i}$
 
 
La position du mobile est déterminé par :
 
$-\ $ la norme $S$ du vecteur  :   
 
$-\ $ l'angle polaire 

2.3. Repère de temps

$\blacktriangleright\ $ On peut distinguer deux aspects du temps :
 
$-\ $ l'instant, la date où se produit l'événement. 
 
Chaque instant est caractérisé par un nombre algébrique $t$ appelée date
 
$-\ $ la durée du phénomène qui mesure l'intervalle de temps entre le début et la fin du phénomène 
 
Deux évènements liant lieu à des dates $t_{i}$ et $t_{f}$ sont séparés par une durée ou intervalle de temps que l'on note : 
 
Dans le système l'unité de temps est la seconde $($symbole : $s)$
 
$\blacktriangleright\ $ Le repère de temps est l'association :
 
$-\ $ d'un instant origine ou origine des temps que l'on choisit arbitrairement
 
$-\ $ d'une unité de temps associé à un compteur de temps : le chronomètre ou l'horloge

3. Trajectoire

Dans un référentiel donné, la trajectoire d'un point mobile est l'ensemble des positions successivement occupées par ce point mobile

Remarque :

$\blacktriangleright\ $ Si la trajectoire est :
 
$-\ $ une droite, le mouvement est rectiligne ;
 
$-\ $ un cercle, le mouvement est circulaire ;
 
$-\ $ une courbe quelconque, le mouvement est curviligne
 
$\blacktriangleright\ $ La trajectoire d'un point mobile est relatif à un référentiel c'est-à-dire, elle dépend du référentiel 
 
Par exemple, la valve d'un vélo en mouvement décrit par rapport au sol, une courbe appelée cycloïde alors que, par rapport à l'axe de la roue, elle décrit un mouvement circulaire
 
Par rapport à la roue, elle est immobile

 
 

III. Vitesse

Dans la vie courante, la distance parcourue et la durée du parcours sont toujours associées

1. Vitesse moyenne

Dans un référentiel donné, la vitesse moyenne d'un point ou d'un objet entre deux instants $t_{i}$ et $t_{f}$ est le rapport de la distance $d$ parcourue par ce point par la durée du parcours $\Delta\,t=t_{f}-t_{i}$ :
$$\begin{array}{l|l} &d=\text{distance parcourue (en m)}\\ \boxed{V_{M}=\dfrac{d}{\Delta\,t}=\dfrac{d}{t_{f}-t_{i}}}&\Delta\,t=t_{f}-t_{i}=\text{durée du parcours (en s)}\\ &V_{M}=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$
$\blacktriangleright\ $ Si la vitesse augmente, le mouvement est accéléré ;
 
$\blacktriangleright\ $ Si la vitesse diminue, le mouvement est ralenti ou décéléré ou retard 
 
$\blacktriangleright\ $ Si la vitesse est constante, le mouvement est uniforme.

Remarque : 

$\blacktriangleright\ $ Il est fréquent d'exprimer une vitesse en kilomètre par heure
$$V(\text{en }m\cdot s^{-1})\stackrel{\times 3.6}{\longrightarrow}V(\text{en }km\cdot h^{-1})$$
$$V(\text{en }m\cdot s^{-1})\stackrel{\div 3.6}{\longleftarrow}V(\text{en }km\cdot h^{-1})$$
$\blacktriangleright\ $ La vitesse moyenne donne une information globale sur le parcours mais ne permet pas de savoir comment il a été : freinage, accélération, arrêt 

2. Vitesse instantanée 

2.1. Définition 

La vitesse instantanée d'un point mobile $M$ est la vitesse à l'instant $t$
 
Pratiquement cette vitesse instantanée du point mobile, à la date $t$, est égale à sa vitesse moyenne calculée pendant un intervalle très court encadrant l'instant $t$ considérée
$$\begin{array}{l|l} &i\neq 0\\ \boxed{V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}}&t_{i+1}-t_{i-1}=\text{durée du parcours (en s)}\\& V_{i}(t_{i})=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$

2.2. Détermination pratique

Le document ci-dessous est une production de l'enregistrement, à intervalle de temps réguliers $\tau$ du mouvement d'un mobile $M$
 
 
Déterminons les expressions des vitesses instantanées $V_{1}\;,\ V_{2}\;,\ V_{3}\ $ et $\ V_{6}$
 
De manière générale :
$$V_{i}=V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$$
 
$V_{1}=V_{1}(t_{1})=\dfrac{M_{0}M_{2}}{t_{2}-t_{0}}=\dfrac{M_{0}M_{2}}{2\tau}$ ;
 
$V_{2}=V_{2}(t_{2})=\dfrac{M_{1}M_{3}}{t_{3}-t_{1}}=\dfrac{M_{1}M_{3}}{2\tau}$ ;
 
$V_{3}=V_{3}(t_{3})=\dfrac{M_{2}M_{4}}{t_{4}-t_{2}}=\dfrac{M_{2}M_{4}}{2\tau}$ ;
 
$V_{6}=V_{6}(t_{6})=\dfrac{M_{5}M_{7}}{t_{7}-t_{5}}=\dfrac{M_{5}M_{7}}{2\tau}$ 

3. Vecteur vitesse instantanée

La valeur de la vitesse instantanée est insuffisante pour caractériser le mouvement d'un point mobile 
 
Elle n'indique pas la direction du mouvement, le sens du mouvement 
 
Pour ces informations, il faut introduire le vecteur vitesse instantanée 

3.1. Définition 

Le vecteur vitesse instantanée est pratiquement définie par la relation : 
$$\overrightarrow{V}_{i}=\overrightarrow{V}_{i}(t_{i})=\dfrac{\overrightarrow{M_{i-1}M_{i+1}}}{t_{i+1}-t_{i-1}}\quad\text{ avec }i\neq 0$$

Exemple :

3.2. Caractéristiques du vecteur vitesse instantanée

Les caractéristiques du vecteur vitesse instantanée au point $M$ sont 
 
$\surd\ $ le point $M$
 
$\surd\ $ tangente à la trajectoire au point $M$
 
$\surd\ $ Sens : celui du mouvement
 
$\surd\ $ Norme : la valeur $V_{i}=V_{i}(t)=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$
 
 

IV. Étude de quelques mouvements

1. Mouvement rectiligne

1.1. Définition

$-\ $ Un mobile est en mouvement rectiligne uniforme s'il se déplace sur une droite avec un vecteur vitesse constant.

Remarque :

Un mobile est en mouvement rectiligne si le mobile parcourt des distances égales pendant des durées égales.
 
 

1.2. Loi horaire

Par définition :
 
$\begin{array}{rcrcl} V=\dfrac{MM_{0}}{t-t_{0}}=\dfrac{x-x_{0}}{t-t_{0}}&\Rightarrow&x-x_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&x&=&V(t-t_{0})+x_{0} \end{array}$
 
Si $t_{0}=0$ alors, $x=V(t-0)+x_{0}$
 
Par suite, $x=Vt+x_{0}$
 
Ainsi, $x$ est une fonction affine du temps

2. Mouvement rectiligne varié

2.1. Définition

$-\ $ Un mobile est en mouvement rectiligne varié s'il se déplace sur une droite avec un vecteur vitesse de module variable.

2.2. Mouvement accéléré et mouvement décéléré 

Le mouvement est accéléré si le module du vecteur vitesse croit ; le mouvement est décéléré ou retardé si le module du vecteur vitesse décroit.

Remarque :

$-\ $ Un mobile est en mouvement rectiligne accéléré si le mobile parcourt des distances de plus en plus grandes pendant des durées égales 
 
 
$-\ $ Un mobile est en mouvement rectiligne décéléré ou retardé si le mobile parcourt des distances de plus en plus petites pendant des durées égales
 
 
Le mouvement est uniformément varié si la vitesse est une fonction affine du temps.

3. Mouvement circulaire uniforme

3.1. Définition

$-\ $ Un mobile est en mouvement circulaire uniforme s'il se déplace sur un cercle avec un vecteur vitesse de module constant.
 

 
Le vecteur vitesse varie en direction et en sens.

3.2. Loi horaire

Par définition :
 
$\begin{array}{rcrcl} V=\dfrac{\overset{\displaystyle\frown}{M_{0}M}}{t-t_{0}}=\dfrac{S-S_{0}}{t-t_{0}}&\Rightarrow&S-S_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&S&=&V(t-t_{0})+S_{0}\end{array}$
 
Par suite, si $t_{0}=0$ alors, $S=Vt+S_{0}$
 
Il est une relation entre l'abscisse curviligne et l'angle : $S=R\theta$

3.3. La période du mouvement

La durée pour effectuer un tour est appelée période que l'on note $T.$
 
Le mouvement étant uniforme 
$$V=\dfrac{d}{\Delta t}=\dfrac{2\pi R}{T}\Rightarrow T=\dfrac{2\pi R}{V}$$
 
$T$ est constant, car $R$ est fixe et $V$ est constant

3.3. La fréquence du mouvement

La fréquence du mouvement représente le nombre de périodes par seconde 
$$N=\dfrac{1}{T}\quad\text{ ou }\quad N=\dfrac{V}{2\pi R}$$
La fréquence $N$ s'exprime en hertz $($symbole : $Hz)$

V. Mouvement de translation et de rotation d'un solide

1. Mouvement de translation d'un solide

1.1. Définition

Un solide (ou objet indéformable) effectue un mouvement de translation lorsque n'importe quel segment de ce solide se déplace en conservant sa direction. 

1.2. Les différents types de translation

La translation peut être :
 
$-\ $ rectiligne : chaque point du solide décrit une droite
 
$-\ $ curviligne : chaque du solide décrit une courbe
 
$-\ $ circulaire : chaque du solide décrit un cercle  

2. Mouvement de rotation d'un solide

2.1. Définition

Un solide est un mouvement de rotation si les points d'un mobile en rotation décrivent des cercles ou des arcs de cercle centrés sur la même droite, appelée axe de rotation. 
 
Cet axe est perpendiculaire aux plans du cercle.

2.2. Vitesse angulaire

La vitesse angulaire est l'angle balayé par seconde
$$\begin{array}{l|l} &\alpha\text{ angle radians (rad)}\\\boxed{\omega=\dfrac{\alpha}{\Delta t}}&\Delta t=t_{f}-t_{i}=\text{durée en seconde (s)}\\&\omega=\text{vitesse angulaire en radians par seconde }(rad\cdot s^{-1}) \end{array}$$

2.3. Relation entre vitesse d'un point et vitesse angulaire

Par définition :
 
$v=\dfrac{S}{\Delta t}=\dfrac{R\alpha}{\Delta t}=R\dfrac{\alpha}{\Delta t}$
 
Or, $\omega=\dfrac{\alpha}{\Delta t}$ donc, $v=R\omega$
 
Auteur: 
Sidy Mouhamed Ndiaye

Exercice sur la Régulation de la pression artérielle - Ts

Classe: 
Terminale

Sujet 4 

Chez un sujet sain au repos, la pression artérielle est maintenue à une valeur relativement constante en dépit de l’existence de plusieurs facteurs pouvant provoquer sa variation. Par un exposé concis et structuré, vous rappellerez l’influence de chacun des trois principaux facteurs de variation de la pression artérielle, puis vous expliquerez comment le système rénine – angiotensine – aldostérone corrige une baisse de pression artérielle.

Correction  sujet 4

Introduction

L’irrigation correcte des organes et l’approvisionnement de leurs cellules en dioxygène et en nutriments nécessitent une pression artérielle convenable. La pression artérielle st la pression exercée par le sang sur la paroi des artères. Quels sont les principaux facteurs responsables d’une variation de la pression artérielle ? Comment une baisse de a pression artérielle est-elle corrigée par le système rénine-angiotensine-aldostérone ? Pour répondre à ces questions nous rappellerons les trois principales causes d’une perturbation de la pression artérielle puis nous expliquerons le mécanisme de la correction d’une hypotension par les hormones.  

I. Les trois principales causes d'une variation de la pression artérielle

La pression artérielle varie en fonction du débit cardiaque, de la vasomotricité et de la volémie. Une augmentation du débit cardiaque ou de la volémie élève la pression artérielle tandis que leur baisse entraine une diminution de la pression artérielle. Une vasodilatation abaisse la pression artérielle alors qu’une vasoconstriction provoque une hausse de la pression artérielle.

II. La correction d'une hypotension par le système rénine - angiotensine - aldostérone

Une chute de la pression artérielle stimule la sécrétion de rénine par le rein. La rénine catalyse la conversion de l’angiotensinogène provenant du foie en angiotensine. L’angiotensine provoque d’une part une vasoconstriction des vaisseaux sanguins d’où une élévation de la pression artérielle, et d’autre part une stimulation de la corticosurrénale qui secrète l’aldostérone. L’aldostérone stimule la rétention de sodium et d’eau par le rein. Il en résulte une hausse de la pression artérielle qui corrige l’hypotension.

Conclusion

Le débit cardiaque, la vasomotricité et la volémie sont les trois principales causes d’une variation de la pression artérielle. Une hypotension peut être corrigée par le système rénine-angiotensine-aldostérone qui provoque une vasoconstriction des artères et une hausse de la volémie.
Auteur: 
Daouda Tine

Exercice sur l'Etude d'un réflexe inné - Ts

Classe: 
Terminale

Sujet 3 

Par un texte illustré de schémas clairs et soigneusement annotés, expliquez le mécanisme de la propagation du message nerveux sur une fibre nerveuse puis rappelez les facteurs qui font varier sa vitesse de propagation.  

Correction sujet 3

Introduction

La fibre nerveuse est conductrice et excitable. Une stimulation efficace crée une inversion momentanée de sa polarité membranaire qui correspond à un potentiel d'action, signal élémentaire du message nerveux. Comment cette dépolarisation se propage-t-elle le long de la fibre et à quelle vitesse ? Pour répondre à cette interrogation, nous expliquerons le mécanisme de la propagation du message nerveux le long de la fibre nerveuse puis nous rappellerons les facteurs qui font varier sa vitesse.  Développement

I. Le mécanisme de la production

Une stimulation efficace portée sur la fibre nerveuse crée un potentiel d'action au niveau de la zone excitée. Des charges migrent de part et d'autre du point stimulé et dépolarisent la portion de membrane voisine jusqu'au seuil permettant l'ouverture des canaux à  voltage-dépendants. Un nouveau potentiel d'action identique au précédent est donc généré. Les canaux à  venant de se refermer sont momentanément inactivés, ce qui empêche le retour en arrière de l'onde de dépolarisation. Ainsi, le potentiel d'action engendré se propage de proche en proche sur une fibre amyélinique grâce aux courants locaux
Dans les fibres nerveuses myélinisées, la couche de myéline a un rôle isolant et les canaux à  voltage-dépendants ne sont présents qu'au niveau des nœuds de Ranvier. Ainsi le potentiel d'action "saute" d'un nœud de Ranvier au suivant : c'est la conduction saltatoire qui est plus rapide.
Dans les conditions expérimentales, le potentiel d'action se propage dans les deux sens à partir du point excité.

II. Les facteurs qui font varier la vitesse de propagation

La vitesse de propagation du message nerveux varie en fonction du diamètre de la fibre nerveuse, de la présence ou de l'absence de myéline, et de la température. Elle augmente avec la température. Les fibres à gros diamètre conduisent l'influx nerveux plus vite que celles à petit diamètre. A diamètre égal, une fibre nerveuse myélinisée conduit l'influx nerveux plus rapidement qu'une fibre sans myéline.

Conclusion

La présence d'un potentiel d'action en un point de la membrane dépolarise celle-ci au voisinage et crée un nouveau potentiel d'action identique à celui qui est en train de disparaître. Sa propagation s'effectue de proche en proche ou par conduction saltatoire avec une vitesse variant selon la nature de la fibre, son calibre et en fonction de la température.

Auteur: 
Daouda Tine

Exercice sur Synapses - Ts

Classe: 
Terminale

Sujet 2  

En prenant l'exemple d'une synapse à acétylcholine, exposez la succession des événements qui permettent la transmission de l'influx nerveux d'un motoneurone à la fibre musculaire, puis expliquez comment une substance chimique mimétique comme le curare peut perturber la transmission synaptique du message nerveux. Votre exposé sera structuré et illustré par des schémas annotés.

Correction sujet 2

Introduction

Dans l'organisme, les muscles squelettiques sont sous la commande des nerfs moteurs. Le message nerveux qui parcourt le motoneurone traverse la plaque motrice puis déclenche la contraction musculaire. Une synapse neuromusculaire est une jonction entre l'arborisation terminale d'un neurone moteur et une cellule musculaire. Le franchissement de la synapse neuromusculaire par l'influx nerveux nécessite la libération d'un neurotransmetteur excitateur : l'acétylcholine. La molécule de curare qui a la même conformation spatiale que l'acétylcholine occupe ses récepteurs sur l'appareil sous-neural. Comment fonctionne la plaque motrice? Comment un poison comme le curare peut-il perturber la transmission synaptique de l'influx nerveux à travers la synapse neuromusculaire ? C’est à ces questions que nous tenterons de répondre dans notre exposé.

I. Le fonctionnement de la plaque motrice

L'arrivée du potentiel d'action au niveau de la membrane pré-synaptique déclenche la succession des événements suivants :
$-\ $ Entée d'ions $Ca^{++}$ dans la terminaison nerveuse qui entraine la libération d'acétylcholine dans la fente synaptique.
$-\ $ L'acétylcholine libéré se fixe sur les récepteurs de la membrane post-synaptique qui sont des canaux à $Na^{+}$ chimio-dépendants.
$-\ $ Les canaux à $Na^{+}$ chimio-dépendants s'ouvrent d'où une entée d'ions $Na^{+}$ dans la fibre musculaire dont la membrane se dépolarise.
$-\ $ Une enzyme l'acétylcholinestérase hydrolyse l'acétylcholine.
$-\ $ Choline issue de cette inactivation de l'acétylcholine est réabsorbée au niveau de la membrane pré-synaptique.

II. Perturbation par le curare de la transmission synaptique de l'influx nerveux

La molécule de curare, poison d'origine végétale, mime grossièrement à ses deux extrémités, une molécule d'acétylcholine. Elle se fixe sur les récepteurs à acétylcholine de l'appareil sous-neural et provoque la paralysie.

Conclusion

L'arrivée du potentiel d'action au niveau du bouton synaptique déclenche la libération de l'acétylcholine dans la fente synaptique. L'acétylcholine se fixe sur les récepteurs de la membrane post synaptique d'où une entrée de Na+ provoquant la dépolarisation de la fibre musculaire. Le curare occupe les récepteurs à acétylcholine de la membrane musculaire, bloquant ainsi la transmission synaptique de l'influx nerveux

Auteur: 
Daouda Tine

Exercice sur le potentiel de repos - Ts

Classe: 
Terminale

Sujet 1 

Par un exposé clair et illustré, décrire une expérience de mise en évidence du potentiel de repos d’une cellule nerveuse, puis expliquer son origine et son maintien

Correction sujet 1

Introduction

La cellule nerveuse ou neurone est une cellule hautement spécialisée tant du point de vue de son architecture que de son fonctionnement. Elle est en effet formée d’un corps cellulaire de forme étoilée, avec plusieurs prolongements courts appelés dendrite et d’un unique prolongement long appelé axone. Elle assure grâce au message nerveux qu’elle peut conduire, la communication entre les différents organes et le système nerveux central : c’est donc une cellule excitable. Elle est à l’image de la plupart des cellules de l’organisme, une cellule polarisée dans les conditions naturelles. Cette polarité correspond à une différence de potentiel (ddp) entre le milieu intracellulaire et le milieu extracellulaire, ou potentiel de repos (pr). Comment peut-on mettre en évidence ce PR ? Qu’est-ce qui est à l’origine de ce PR ? Comment est-il maintenu au niveau du neurone ? C’est à ces trois principales questions que nous tenterons de répondre dans notre exposé.

I. Mise en évidence de PR

Lorsqu’on place deux électrodes réceptrices à la surface de l’axone d’un neurone, le spot d’électrons de l’oscilloscope sur lequel les ER sont branchées balaie horizontalement à partir de zéro. Ce résultat ne s’explique que si l’on admet que deux point de la surface d’un axone ont la même charge : ils sont équipotentiels.
    Avec le même dispositif expérimental, on constate que dès qu’on enfonce la deuxième ER, le spot d’électrons balaie horizontalement mais à partir d’une valeur négative. Compte tenu de la valeur négative des électrons et du branchement conventionnel des ER aux plaques horizontales de l’oscilloscope, nous en déduisons que l’axoplasme est négativement chargé par rapport au milieu extracellulaire correspondant au PR. Ce PR est environ de l’ordre de $– 70 mv$ à $– 60mv$ selon la cellule.

II. Origine et maintien du PR

1. Origine du PR

Les analyses chimiques ont révélé que la concentration en $Na^{+}$ est plus importante dans le milieu extracellulaire que dans l’axoplasme alors que celle de $K^{+}$ est plus importante dans l’axoplasme. Selon le principe de la dialyse, les ions $K^{+}$ diffusent de l’axoplasme vers le milieu extracellulaire alors que les ions $Na^{+}$ diffusent de l’extérieur vers l’axoplasme. L’utilisation d’isotopes radioactifs de ces ions a révélé que l’axolemme est plus perméable aux ions $K^{+}$ qu’aux ions $Na^{+}$.
Il en résulte alors un excès de cation à l’extérieur et donc un déficit de ces mêmes cations de part et d’autre de la membrane axonique. Ce PR étant maintenu en permanence au niveau d’un neurone vivant, nous devons donc admettre qu’en plus de la dialyse simple, un autre type d’échange de ces cations à travers l’axolemme intervient.

2. Le maintient du PR.

L’utilisation d’isotopes radioactifs du sodium, a révélé que parallèlement à l’échange de ce soluté par le biais de la diffusion simple, il est également échangé contre le gradient de concentration. Ce phénomène disparaissant lorsqu’on bloque la respiration cellulaire (phénomène producteur d’énergie) à l’aide de poisons respiratoires comme le $DNP$ ou le cyanure. Ces résultats montrent que parallèlement à l’échange passif des ions $Na^{+}$ et $K^{+}$ à travers l’axolemme, un échange actif de ces mêmes cations a également lieu, mais dans le sens opposé. Ce dernier correspond à la pompe $Na^{+}$/$K^{+}$ ATPase qui fait sortir théoriquement à chaque tour de « rotation » $3Na^{+}$ et fait entrer $2K^{+}$ dans l’axoplasme. Au final, par la diffusion simple et l’échange actif, la quantité de cations sortant s’équilibre avec celle entrant ; d’où le maintient du déficit de cations dans l’axoplasme ; et donc du PR.

Conclusion

Le potentiel de repos correspond donc à un déséquilibre ionique de part et d’autre de la membrane axonique. C’est un phénomène purement biochimique qu’on observe d’ailleurs au niveau de la plupart des cellules vivantes. En outre, il est pour l’essentiel, à l’origine de l’excitabilité de la cellule nerveuse.
Auteur: 
Daouda Tine

Solution des exercices : Gravitation universelle - Ts

Classe: 
Terminale
 

Exercice 1

1) Calcul de la valeur de l'intensité $g$ du champ de pesanteur à l'altitude $h$
 
$\begin{array}{rcl} g&=&g_{0}\dfrac{R^{2}}{(R+h)^{2}}\\\\&=&9.8\times\dfrac{(6.4\cdot 10^{6})^{2}}{(6.4\cdot 10^{6}+3.6\cdot 10^{7})^{2}}\\\\\Rightarrow\;g&=&0.22\,m\cdot s^{-2} \end{array}$
 
2) Bilan des forces appliquées au satellite
 
 
Le satellite est soumis à la force de gravitation :
 
$\overrightarrow{F}=k\dfrac{Mm}{r^{2}}\overrightarrow{n}$
 
La vitesse du satellite
 
La deuxième loi de Newton s'écrit :
 
$\begin{array}{rcl} \overrightarrow{F}=m\overrightarrow{a}&\Rightarrow&k\dfrac{Mm}{r^{2}}\overrightarrow{n}=m\overrightarrow{a}\\\\&\Rightarrow&\overrightarrow{a}=k\dfrac{M}{r^{2}}\overrightarrow{n} \end{array}$
 
En projetant la relation dans le repère de Frenet $\left(S\;,\ \overrightarrow{u}\;,\ \overrightarrow{n}\right)$
 
$\begin{array}{rcl} k\dfrac{Mm}{r^{2}}&=&m\,a_{n}\\\\&=&m\dfrac{v^{2}}{r}\\ \\\Rightarrow\;v&=&\sqrt{k\dfrac{M}{r}}\\\\\Rightarrow\;v&=&\sqrt{6.67\cdot 10^{-11}\times\dfrac{5.97\cdot 10^{24}}{6.4\cdot 10^{6}+3.6\cdot 10^{7}}}\\\\\Rightarrow\;v&=&3.1\cdot 10^{3}m\cdot s^{-1} \end{array}$
 
3) Détermination de la période du mouvement
 
$\begin{array}{lcl} T&=&\dfrac{2\pi(R+h)}{v}\\\\&=&\dfrac{2\pi(6.4\cdot 10^{6}+3.6\cdot 10^{7})}{3.1\cdot 10^{3}}\\ \\\Rightarrow\;T&=&86\cdot 10^{3}s \end{array}$

Exercice 2

1.1.1 Expression de l'intensité $F_{0}$ de la force exercée par la Terre sur un corps ponctuel de masse $m=1Kg$ placé à surface
 
$F_{0}=G\dfrac{mM_{T}}{R_{T}^{2}}$
 
1.1.2 a) Expression de la masse $M_{T}$ de la Terre en fonction de $g_{0}$, $R_{T}$ et $G$
 
$\begin{array}{rcl} F_{0}&=&G\dfrac{mM_{T}}{R_{T}^{2}}\\\\&=&m g_{0}\\\\\Rightarrow\;M_{T}&=&\dfrac{g_{0}R_{T}^{2}}{G} \end{array}$
 
b) Calcul de la masse de la Terre
 
$\begin{array}{rcl} M_{T}&=&\dfrac{g_{0}R_{T}^{2}}{G}\\\\&=&\dfrac{9.8\times(6370\cdot 10^{3})^{2}}{6.67\cdot 10^{-11}}\\\\\Rightarrow\;M_{T}&=&5.96\cdot 10^{24}kg \end{array}$
 
1.2 Montrons qu'a l'altitude $h$ au-dessus de la Terre, l'intensité du champ de gravitation est donnée par la relation :
 
$g=g_{0}\dfrac{R_{T}^{2}}{(R_{T}+h)^{2}}$
 
A la distance $r$ :
 
$g=G\dfrac{M_{T}}{r_{2}}$
 
A la surface de la Terre :
 
$g_{0}=G\dfrac{M_{T}}{R_{T}^{2}}\Rightarrow\;GM_{T}=g_{0}R_{T}^{2}$
 
A l'altitude $h$ :
 
$g=G\dfrac{M_{T}}{(R_{T}+h)^{2}}\Rightarrow\;g=\dfrac{g_{0}R_{T}^{2}}{(R_{T}+h)^{2}}$
 
2.1 Montrons que le mouvement du satellite est uniforme
 
$-\ $ Système : le satellite
 
$-\ $ Référentiel d'étude : terrestre
 
$-\ $ Bilan des forces appliquées : la Force gravitationnelle $\overrightarrow{F}$
 
La deuxième loi de Newton
 
$\overrightarrow{F}=m\overrightarrow{a}\Rightarrow-G\dfrac{Mm}{r^{2}}\overrightarrow{u}=m\overrightarrow{a}$
 
$\Rightarrow\overrightarrow{a}=-G\dfrac{M}{r^{2}}\overrightarrow{u}$
 
En projetant la relation dans le repère $\left(S\;,\ \overrightarrow{u_{t}}\;,\ \overrightarrow{u_{n}}\right)$
 
 

$a=a_{n}\Rightarrow\;a_{t}=\dfrac{\mathrm{d}v}{\mathrm{d}t}=0\Rightarrow\;v=cte$

 
Le mouvement du satellite est donc uniforme
 
2.2 Établissement en fonction $g_{0}$, $R_{T}$ et $h$
 
2.2.1 de l'expression de la vitesse $v$ du satellite ;
 
$\begin{array}{rcl} a=a_{n}&\Rightarrow&G\dfrac{M}{r^{2}}=\dfrac{v^{2}}{r}\\\\&\Rightarrow&v^{2}=\dfrac{GM}{r}\\\\&\Rightarrow&v^{2}=\dfrac{g_{0}R_{T}^{2}}{R_{T}+h}\\ \\&\Rightarrow&v=\sqrt{\dfrac{g_{0}R_{T}^{2}}{R_{T}+h}} \end{array}$
 
2.2.2 de l'expression de la période $T$ du satellite ;
 
$\begin{array}{rcl} T&=&\dfrac{2\pi r}{v}\\\\&=&2\pi(R_{T}+h)\sqrt{\dfrac{R_{T}+h}{g_{0}R_{T}^{2}}}\\\\&=&2\pi\sqrt{\dfrac{(R_{T}+h)^{3}}{g_{0}R_{T}^{2}}} \end{array}$
 
2.3 Calcul de $v$ et $T$
 
$\begin{array}{rcl} v&=&\sqrt{\dfrac{g_{0}R_{T}^{2}}{R_{T}+h}}\\\\&=&\sqrt{\dfrac{9.8\times (6370\cdot 10^{3})^{2}}{6370\cdot 10^{3}+300\cdot 10^{3}}}\\\\\Rightarrow\;v&=&7.7\cdot 10^{2}m\cdot s^{-1} \end{array}$
 
$\begin{array}{rcl} T&=&\dfrac{2\pi(R_{T}+h)}{v}\\\\&=&\dfrac{2\pi(6370\cdot 10^{3}+300\cdot 10^{3})}{7.7\cdot 10^{2}}\\\\\Rightarrow\;T&=&54\cdot 10^{3}s \end{array}$
 
2.4.1 Montrons que le rapport $\dfrac{T^{2}}{r^{3}}$ est égal à un constante .
 
$T=2\pi\sqrt{\dfrac{(R_{T}+h)^{3}}{g_{0}R_{T}^{2}}}$ or, $\ r=R_{T}+h$ donc,
 
$\begin{array}{rcl} T=2\pi\sqrt{\dfrac{r^{3}}{g_{0}R_{T}^{2}}}&\Rightarrow&T^{2}=4\pi^{2}\times\dfrac{r^{3}}{g_{0}R_{T}^{2}}\\\\&\Rightarrow&\dfrac{T^{2}}{r^{3}}=\dfrac{4\pi^{2}}{g_{0}R_{T}^{2}}\ =\ cte \end{array}$
 
2.4.2 Exprimer le rapport $\dfrac{T^{2}}{r^{3}}$ en fonction de $M_{T}$ et $G$
 
$T=2\pi\sqrt{\dfrac{r^{3}}{g_{0}R_{T}^{2}}}$ or $GM_{T}=g_{0}R_{T}^{2}$
 
$\Rightarrow\dfrac{T^{2}}{r^{3}}=\dfrac{4\pi^{2}}{GM_{T}}=cte$
 
2.4.3 Calculer la masse $M_{T}$ de la Terre.
 
$\begin{array}{rcl} \dfrac{T^{2}}{r^{3}}&=&\dfrac{4\pi^{2}}{GM_{T}}\\\\\Rightarrow\;M_{T}&=&\dfrac{4\pi^{2}r^{3}}{GT^{2}}\\\\&=&\dfrac{4\pi^{2}(R_{T}+h)^{3}}{GT^{2}}\\\\&=&\dfrac{4\pi^{2}(6370\cdot 10^{3}+300\cdot 10^{3})^{3}}{6.67\cdot 10^{-11}\times(54\cdot 10^{3})^{2}} \end{array}$
 
Cette valeur n'est pas compatible avec celle de la question 1.1.2

Exercice 3

1.1 Expression de la vitesse $V$ de $(S)$ en fonction de l'intensité $G_{0}$ du champ de gravitation du sol, de $R$ et $r$
 
$\begin{array}{rcl} a_{n}&=&\dfrac{GM}{r^{2}}\\\\&=&\dfrac{v^{2}}{r}\\\\\Rightarrow\;v&=&\sqrt{\dfrac{GM}{r}}\text{ or }\;G_{0}R^{2}&=&GM\\\\\Rightarrow\;v&=&\sqrt{\dfrac{G_{0}R^{2}}{r}} \end{array}$
 
1.2 Expression de la période $T$ du mouvement.
 
$\begin{array}{lcl} vT=2\pi r&\Rightarrow&T=\dfrac{2\pi r}{v}\\\\&\Rightarrow&T=2\pi r\sqrt{\dfrac{r}{G_{0}R^{2}}}\\\\&\Rightarrow&T=2\pi\sqrt{\dfrac{r^{3}}{G_{0}R^{2}}} \end{array}$
 
Calculer de $T$
 
$\begin{array}{rcl} T&=&2\pi\sqrt{\dfrac{r^{3}}{G_{0}R^{2}}}\\\\&=&2\pi\sqrt{\dfrac{(8\,000\cdot 10^{3})^{3}}{9.8\times(6\,400\cdot 10^{3})^{2}}}\\\\\Rightarrow\;T&=&7.1\cdot 10^{3}s \end{array}$
 
2.1 Montrons que le travail de la force gravitation lors du déplacement du sol jusqu'à l'orbite de rayon $r$ est donné par :
 
$W=mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)$
$\begin{array}{rcl} \mathrm{d}w&=&-f\mathrm{d}r\\\\&=&-\dfrac{GmM}{r^{2}}\mathrm{d}r\\\\\Rightarrow\;W&=&-\int_{R}^{r}\dfrac{GmM}{r^{2}}\mathrm{d}r\\\\&=&\left[\dfrac{GmM}{r}\right]_{R}^{r}\\\\\Rightarrow\;W&=&mGM\left(\dfrac{1}{r}-\dfrac{1}{R}\right)\\\\&=&mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right) \end{array}$
 
avec $G_{0}R^{2}=GM$
 
2.2 Expression de l'énergie potentielle du système Terre-satellite en fonction de $G_{0}$, $m$, $r$
 
$\begin{array}{rcl} \Delta E_{p}=-W&\Rightarrow&E_{p}(r)-E_{p}(R)=-mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)\\\\&\Rightarrow&E_{p}(r)=-mG_{0}R^{2}\dfrac{1}{r}+cte \end{array}$
 
$\begin{array}{rcl} E_{p}(R)=-mG_{0}R^{2}\dfrac{1}{R}+cte&\Rightarrow&cte=mG_{0}R^{2}\dfrac{1}{R}\\\\&\Rightarrow&E_{p}(r)=-mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right) \end{array}$
 
2.3 Expression de l'énergie cinétique de $(S)$ en fonction de $G_{0}$, $m$, $r$ et $R$
 
$\begin{array}{rcl} E_{C}&=&\dfrac{1}{2}mv^{2}\\\\&=&\dfrac{1}{2}m\left(\sqrt{\dfrac{G_{0}R^{2}}{r}}\right)^{2}\\\\&=&\dfrac{1}{2}\dfrac{mG_{0}R^{2}}{r} \end{array}$
 
Expression de l'énergie mécanique $E$
 
$\begin{array}{rcl} E_{m}&=&E_{C}+E_{p}\\\\&=&\dfrac{1}{2}\dfrac{mG_{0}R^{2}}{r}-mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)\\\\\Rightarrow\;E_{m}&=&mG_{0}R^{2}\left(\dfrac{1}{R}-\dfrac{1}{2r}\right) \end{array}$
 
3.1 Expression de la variation $\mathrm{d}v$ de la vitesse et montrons que $\mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r$
 
$\begin{array}{rcl} T=2\pi\sqrt{\dfrac{r^{3}}{G_{0}R^{2}}}&\Rightarrow&\dfrac{T^{2}}{4\pi^{2}}=\dfrac{r^{3}}{G_{0}R^{2}}\\\\&\Rightarrow&\dfrac{4\pi^{2}}{T^{2}}=\dfrac{G_{0}R^{2}}{r^{3}}\\\\&\Rightarrow&v^{2}=\dfrac{G_{0}R^{2}}{r}\\\\&\Rightarrow&\dfrac{\mathrm{d}v^{2}}{\mathrm{d}r}=\dfrac{\mathrm{d}}{\mathrm{d}r}\left(\dfrac{G_{0}R^{2}}{r}\right)\\\\&\Rightarrow&2v\dfrac{\mathrm{d}v}{\mathrm{d}r}=-\dfrac{G_{0}R^{2}}{r^{2}}\\\\&\Rightarrow&2\dfrac{2\pi r}{T}\dfrac{\mathrm{d}v}{\mathrm{d}r}=-\dfrac{G_{0}R^{2}}{r^{2}}\\\\&\Rightarrow&\dfrac{4\pi}{T}\mathrm{d}v=-\dfrac{G_{0}R^{2}}{r^{3}}\mathrm{d}r\\\\&\Rightarrow&\dfrac{4\pi}{T}\mathrm{d}v=-\dfrac{4\pi^{2}}{T^{2}}\mathrm{d}r\\\\&\Rightarrow&\mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r \end{array}$
 
3.2 La variation de $\mathrm{d}r$ est en réalité due au travail $\mathrm{d}w_{f}$ des forces de frottements exercées par les couches raréfiées de l'atmosphère pendant le déplacement. 
 
Du signe de $\mathrm{d}w_{f}$, déduire l'effet de ces forces sur l'altitude et la vitesse de $(S).$
 
$\begin{array}{rcl} \mathrm{d}w_{f}=-f\mathrm{d}r&\Rightarrow&\mathrm{d}r=-\dfrac{\mathrm{d}w_{f}}{f} \end{array}$
 
$\mathrm{d}w_{f}>0$ $\Rightarrow\mathrm{d}r<0$ L'altitude diminue.
 
$\begin{array}{rcl} \mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r&\Rightarrow&\mathrm{d}r=-\dfrac{\pi}{T}\mathrm{d}v\\\\&\Rightarrow&\mathrm{d}w_{f}=f\dfrac{\pi}{T}\mathrm{d}v\\\\&\Rightarrow&\mathrm{d}v=\dfrac{T}{\pi}\dfrac{\mathrm{d}w_{f}}{f} \end{array}$
 
$\mathrm{d}w_{f}>0$ $\Rightarrow\mathrm{d}v>0$ La vitesse augmente.

Exercice 4

1. Expression littérale du champ de gravitation $G_{0}S$ à la surface du Soleil.
 
$G_{0S}=\dfrac{GM_{S}}{R_{S}^{2}}$
 
Calcul de la valeur numérique du champ de gravitation $G_{0S}.$
 
$G_{0S}=\dfrac{GM_{S}}{R_{S}^{2}}=\dfrac{6.67\cdot 10^{-11}\times 2.0\cdot 10^{30}}{(7.0\cdot 10^{8})^{2}}$
 
$\Rightarrow\;G_{0S}=2.72\cdot 10^{2}m\cdot s^{-2}$
 
2. Expression littérale du champ de gravitation $G_{S}$ en un point de l'orbite terrestre autour du Soleil.
 
$G_{S}=\dfrac{GM_{S}}{r^{2}}$
 
Calcul de la valeur du champ de gravitation $G_{0S}$
 
$G_{S}=\dfrac{GM_{S}}{r^{2}}=\dfrac{6.67\cdot 10^{-11}\times 2.0\cdot 10^{30}}{(1.5\cdot 10^{8})^{2}}$
 
$\Rightarrow\;G_{S}=59.3\cdot 10^{2}m\cdot s^{-2}$
 
3. Comparons la valeur du champ de gravitation $G_{S}$ à celle $G_{0T}$ du champ de gravitation terrestre au niveau du sol.
 
$\dfrac{G_{S}}{G_{0S}}=\dfrac{59.3\cdot 10^{2}}{2.72\cdot 10^{2}}\Rightarrow\dfrac{G_{S}}{G_{0S}}\approx 22$
 
$\Rightarrow\;G_{S}\approx 22G_{0S}$

Conclusion :

L'intensité du champ de gravitation augmente lorsque l'altitude diminue
 
4. Calcul de la valeur du champ de gravitation lunaire $G_{0L}$ au niveau de son sol
$G_{OL}=\dfrac{GM_{L}}{R_{OL}^{2}}$
 
$G_{0L}=\dfrac{GM_{L}}{R_{0L^{2}}}$ ; 
 
$G_{0T}=\dfrac{GM_{T}}{R_{0T}^{2}}$
 
\begin{eqnarray} \dfrac{G_{0L}}{G_{0T}}&=&\dfrac{\dfrac{GM_{L}}{R_{0L^{2}}}}{\dfrac{GM_{T}}{R_{0T}^{2}}}\nonumber\\\\&=&\dfrac{M_L}{M_{T}}\times\dfrac{R_{0T}^{2}}{R_{0L}^{2}}&=&\dfrac{1}{81}\times(\dfrac{11}{3})^{2}\nonumber\\\\Rightarrow G_{0L}&=&\dfrac{1}{81}\times(\dfrac{11}{3})^{2}\times 9.8\nonumber\\\\\Rightarrow G_{0L}&=&1.62NKg^{-1} \end{eqnarray}
 
5) a calcul de la distance $d$ du point $M$ remarquable au centre de la terre.
 
 
$G_{T}=\dfrac{GM_{T}}{d^{2}}$ ;
 
$G_{L}=\dfrac{GM_{L}}{(D-d)^{2}}$
 
\begin{eqnarray} G_{T}=G_{L}\nonumber\\\\\Rightarrow\dfrac{GM_{T}}{d^{2}}&=&\dfrac{GM_{L}}{(D-d)^{2}}\nonumber\\\\\Rightarrow\dfrac{(D-d)^{2}}{d^{2}}&=&\dfrac{M_{L}}{M_{T}}\nonumber\\\\\Rightarrow\dfrac{D-d}{d}&=&\sqrt{\dfrac{M_{L}}{M_{T}}}\nonumber\\\\\Rightarrow d\sqrt{\dfrac{M_{L}}{M_{T}}}&=&D-d\nonumber\\\\d(1+\sqrt{\dfrac{M_{L}}{M_{T}}})&=&D\nonumber\\\\\Rightarrow d&=&\dfrac{D}{(1+\sqrt{\dfrac{M_{L}}{M_{T}}}})&=&\dfrac{380000}{1+\sqrt{\dfrac{1}{81}}}\nonumber\\\\\Rightarrow d&=&342000km \end{eqnarray}
 
b) Domaine ou l'action gravitationnelle d'un des deux astres est prépondérante $x<d$ l'action gravitationnelle terrestre est prépondérante

Exercice 5

 
1) Lancement d'un satellite
 
1)a) Établissement de l'expression de la vitesse du point $S$ de la surface de la surface terrestre en fonction de la vitesse angulaire $\omega$ de rotation de la terre, du rayon terrestre $R_{T}$ et de la latitude $\lambda$ du lieu du lancement.
 
\begin{eqnarray} v&=&r\lambda\nonumber\\\\&=&R_{T}\lambda\cos\lambda \end{eqnarray}
 
1)b) Le champ de tir le plus favorable pour le lancement du satellite.
 
Baikonour au Kazakhstan est le champ de tir le plus favorable car la vitesse de lancement du satellite est minimale.
 
1)c) Expression de l'énergie potentielle de gravitation d'un satellite en fonction de son altitudez
 
$E_{P}(r)=-\dfrac{GmM_{T}}{r}+cte$
 
\begin{eqnarray} E_{p}(r=\infty)&=&-\dfrac{GmM_{T}}{\infty}+cte&=&0\nonumber\\\\\Rightarrow cte&=&0\nonumber\\\\\Rightarrow E_{p}(r)&=&-\dfrac{GmM_{T}}{r} \end{eqnarray}
 
A l'altitude $z$
 
\begin{eqnarray} r&=&R_{T}+Z\nonumber\\\\\Rightarrow\,E_{P_{{Z}}&=&\dfrac{GmM_{T}}{R_{T}+Z} \end{eqnarray}
 
Expression de l'énergie mécanique du satellite sur sa base de lancement dans le référentiel géocentrique
 
\begin{eqnarray} E_{m}&=&E_{c}+E_{p}\nonumber\\\\&=&\dfrac{1}{1}mV^{2}-\dfrac{GmM_{T}}{r}\nonumber\\\\&=&\dfrac{1}{2}m(R_{T}\Omega\cos\lambda)^{2}-\dfrac{GmM_{T}}{R_{T}\cos\lambda} \end{eqnarray}
                                                                                                                                                                                                                                                                                                                                                                                                                                                                          
1)d) Expression de la vitesse de libération $V_{1}$
 
Elle correspond à la vitesse minimale pour le satellite quitte l'attraction terrestre avec une énergie mécanique nulle dans le cas limite
 
\begin{eqnarray} E_{m}&=&\dfrac{1}{2}mV_{L}^{2}-\dfrac{GmM_{T}}{R_{T}\cos\lambda}\nonumber\\\\\Rightarrow V_{L}\nonumber\\\\&=&\sqrt{\dfrac{2GM_{T}}{R_{T}\cos}\lambda} \end{eqnarray}
 
Calcul de la vitesse de libération $v_{1}$
 
\begin{eqnarray} V_{L}&=&\sqrt{\dfrac{2GM_{T}}{R_{T}\cos\lambda}}\nonumber\\\\&=&\sqrt{\dfrac{2\times 6.67\cdot 10^{-11}\times  5.97\cdot 10^{24}}{6.38\cdot 10^{6}\times\cos 5.23^{\circ}}}\nonumber\\\\\Rightarrow\,V_{L}&=&11.2\cdot 10^{3}m\cdot s^{-1} \end{eqnarray}
 
2) Satellite artificiel en orbite
 
2) a) Montrons que le mouvement du satellite est uniforme
 
Système : le satellite
 
Référentiel d'étude : terrestre
 
Bilan des forces appliquées : la Force gravitationnelle $\overrightarrow{F}$
 
La deuxième loi de Newton s'écrit :
 
$\begin{array}{lcl} \overrightarrow{F}&=&m\vec{a}\\\\\Rightarrow-G\dfrac{Mm}{r^{2}}\vec{u}&=&m\vec{a}\\\\\Rightarrow\vec{a}&=&-G\dfrac{M}{r^{2}}\vec{u} \end{array}$
 
En projetant la relation dans le repère $\left(S\;,\ \overrightarrow{u_{t}}\;,\ \overrightarrow{u_{n}}\right).$
 
$\begin{array}{lcl} a&=&a_{n}\\\\\Rightarrow\,a_{t}&=&\dfrac{\mathrm{d}v}{\mathrm{d}t}\\\\&=&0\\\\\Rightarrow\,v&=&\text{cte} \end{array}$
 
Le mouvement du satellite est donc uniforme.
 
Établissement de l'expression de la vitesse du satellite en fonction de son altitude.
 
$\begin{array}{lcl} a_{n}&=&\dfrac{GM}{r^{2}}\\\\&=&\dfrac{v^{2}}{r}\\\\\Rightarrow\,v&=&\sqrt{\dfrac{GM}{r}}\\\\\text{or à l'altitude }z\ r&=&R_{T}+z\\\\\Rightarrow\,v&=&\sqrt{\dfrac{GM}{R_{T}}+z} \end{array}$
 
La troisième loi de Kepler liant la période de rotation $T$ du satellite au rayon $r$ de sa trajectoire
 
$\begin{array}{lcl} T&=&\dfrac{2\pi r}{v}\\\\&=&2\pi r\sqrt{\dfrac{r}{GM_{T}}}\\\\\Rightarrow\,T^{2}&=&4\pi^{2}\dfrac{r^{3}}{GM_{T}}\\\\\Rightarrow\dfrac{T^{2}}{r^{3}}\\\\&=&\dfrac{4\pi^{2}}{GM_{T}} \end{array}$
 
2) b) Calcul du  rayon de l'orbite d'un satellite géostationnaire
 
$\begin{array}{lcl} \dfrac{T^{2}}{r^{3}}&=&\dfrac{4\pi^{2}}{GM_{T}}\\\\\Rightarrow\,r&=&\sqrt[3]{\dfrac{GM_{T}T^{2}}{4\pi^{2}}}\\\\&=&\sqrt[3]{\dfrac{6.67\cdot 10^{-11}\times 5.97\cdot 10^{24}\times\left(24\times 3600\right)^{2}}{4\pi^{2}}}\\\\\Rightarrow\,r&=&4.2\cdot 10^{7}m \end{array}$
 
2) c) Expression du rayon $r$ et de la vitesse $v$ du satellite en fonction du temps
 
$\begin{array}{lcl} E_{m}&=&E_{C}+E_{P}\\\\&=&\dfrac{1}{2}mv^{2}-\dfrac{GmM_{T}}{r}\\\\&=&\dfrac{1}{2}m\left(\sqrt{\dfrac{GM_{T}}{r}}\right)^{2}-\dfrac{GmM_{T}}{r}\\\\&=&\dfrac{1}{2}\dfrac{GmM_{T}}{r}-\dfrac{GmM_{T}}{r}\\\\&=&-\dfrac{GmM_{T}}{2r}\\\\\Rightarrow\,E_{m}&=&-\dfrac{GmM_{T}}{2r}\\\\&=&E_{m}0(1+bt)\\\\\Rightarrow\,r&=&-\dfrac{GmM_{T}}{E_{m0}(1+bt)} \end{array}$
 
$\begin{array}{lcl} E_{C}&=&-E_{m}\\\\&=&-E_{m0}(1+bt)\\\\\Rightarrow\dfrac{1}{2}mv^{2}\\\\&=&-E_{m0}(1+bt)\\\\\Rightarrow\,v&=&\sqrt{\dfrac{-2E_{m0}(1+bt)}{m}} \end{array}$
 
Le rayon $r$ diminue lorsque le temps s'écoule ; par contre la vitesse augmente avec le temps 
 
$\begin{array}{lcl} E_{C}&=&-E_{m}\\\\&=&-E_{m0}(1+bt) \end{array}$
 
$\begin{array}{lcl} E_{P}&=&2E_{m}\\\\&=&2E_{m0}(1+bt) \end{array}$
 
L'énergie cinétique augmente ; tandis que l'énergie potentielle diminue.
 
L'énergie perdue se trouve sous forme d'énergie thermique.

Exercice 6

1) L'accélération de la fusée 
 
$\begin{array}{lcl} F&=&ma\\\\\Rightarrow\,a&=&\dfrac{F}{m}\\\\&=&\dfrac{7.5\cdot 10^{5}}{40\cdot 10^{3}}\\\\\Rightarrow\,a&=&18.75m\cdot s^{-2} \end{array}$
 
2) Expression la vitesse $v$ et la période $T$ du mouvement du satellite en fonction de $K$, $r$ et $M.$
 
$\begin{array}{lcl} a_{n}&=&\dfrac{KM}{r^{2}}\\\\&=&\dfrac{v^{2}}{r}\\\\\Rightarrow\,v&=&\sqrt{\dfrac{KM}{r}} \end{array}$
 
$\begin{array}{lcl} T&=&\dfrac{2\pi r}{v}\\\\&=&2\pi r\sqrt{\dfrac{r}{KM}}\\\\\Rightarrow\,T&=&2\pi\sqrt{\dfrac{r^{3}}{KM}} \end{array}$
 
Déduisons que $\dfrac{T^{2}}{R^{3}}=$ constante
 
$\begin{array}{lcl} T&=&2\pi\sqrt{\dfrac{r^{3}}{KM}}\\\\\Rightarrow\,T^{2}&=&4\pi^{2}\dfrac{r^{3}}{KM}\\\\\Rightarrow\dfrac{T^{2}}{r^{3}}&=&\dfrac{4\pi^{2}}{KM} \end{array}$
 
3) La valeur de la masse de la Terre.
 
 
Le graphe représentant $T^{2}=f\left(r^{3}\right)$ est une droite linéaire de pente :
 
$\begin{array}{lcl} a&=&\dfrac{\Delta T^{2}}{\Delta r^{3}}\\\\&=&\dfrac{4\pi^{2}}{KM}\\\\\Rightarrow\,M&=&4\pi^{2}\dfrac{\Delta r^{3}}{K\Delta T^{2}}\\\\&=&4\pi^{2}\dfrac{5.5\cdot 10^{22}-0}{6.67\cdot 10^{-11}\left(55\cdot 10^{8}-0\right)} \end{array}$
 
$M=5.92\cdot 10^{24}kg$
 
4) a) Expression des énergies potentielles $E_{P}$, EC et totale ET du satellite en fonction de la masse M de la Terre, de la masse m du satellite et de r. 

 

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Solution des exercices : Équilibre d'un solide mobile autour d'un axe - 2nd S

Classe: 
Seconde
 

Exercice 1

Un chemin forestier est fermé par une barrière constituée d'une poutre (1) et d'un contre-poids (2).
 
La barrière peut tourner autour d'un axe $\Delta$ perpendiculaire en $O$ au plan de la figure
 
 
Les cotes sont en mètres. La masse de la barrière est $60\;kg\;;\ G$ est son centre de gravité.
 
Un promeneur veut la soulever en exerçant en $A$ une force $\vec{F}$ d'intensité $100\;N.$
 
1) a) Calculons l'intensité du poids $\vec{P}$ de la barrière.
 
Soit : $P=m.g\ $ avec, $g=10\;N.kg^{-1}.$
 
A.N : $P=60\times 10=600$
 
Donc, $\boxed{P=600\;N}$
 
b) Calculons le moment de $\vec{P}$ par rapport à $\Delta.$
 
On a : $\mathcal{M}_{\Delta}(\vec{P})=P\cdot OG$
 
A.N : $\mathcal{M}_{\Delta}(\vec{P})=600\times 0.5=300$
 
Ainsi, $\boxed{\mathcal{M}_{\Delta}(\vec{P})=300\;Nm}$
 
c) Calculons le moment de $\vec{F}$ par rapport à $\Delta.$
 
L'expression du moment de $\vec{F}$ par rapport à $\Delta$ est donnée par : $\mathcal{M}_{\Delta}(\vec{F})=P\cdot OA$
 
A.N : $\mathcal{M}_{\Delta}(\vec{F})=100\cdot 4=400$
 
D'où, $\boxed{\mathcal{M}_{\Delta}(\vec{F})=400\;Nm}$
 
2) Le promeneur peut soulever la barrière car $\mathcal{M}_{\Delta}(\vec{F})>\mathcal{M}_{\Delta}(\vec{P})$
 

Exercice 2

Le chargeur représenté ci-dessous se compose :
 
$-\ $ d'un châssis et du conducteur de masse $400\;kg$ ;
 
$-\ $ de son chargement de masse $420\;kg$ ;
 
$-\ $ d'un système de levage et du godet de masse $150\;kg.$
 
Le poids du châssis s'applique au point $G_{1}$
 
Le poids du chargement au poing $G_{2}$
 
Le poids du système de levage au poing $G_{3}$
 
 
1) Calculons les intensités des poids $P_{1}\;,\ P_{2}\ $ et $\ P_{3}$ du châssis, du chargement et du système de levage
 
Soit alors :
 
$P_{1}=m_{1}.g=400\times 10=40\cdot 10^{2}$
 
Donc, $\boxed{P_{1}=40\cdot 10^{2}\;N}$
 
$P_{2}=m_{2}.g=420\times 10=42\cdot 10^{2}$
 
Ainsi, $\boxed{P_{2}=42\cdot 10^{2}\;N}$
 
$P_{3}=m_{3}.g=150\times 10=15\cdot 10^{2}$
 
Par suite, $\boxed{P_{3}=15\cdot 10^{2}\;N}$
 
2) Calcul du moment du poids $P_{1}$ par rapport à l'axe $\Delta$ de la roue avant.
 
Choisissons un sens positif de rotation (voir figure)
 
Soit : $\mathcal{M}_{\Delta}(\vec{P}_{1})=P_{1}\cdot d_{1}$
 
A.N : $\mathcal{M}_{\Delta}(\vec{P}_{1})=40\cdot 10^{2}\cdot 2.40=96\cdot 10^{2}$
 
D'où, $\boxed{\mathcal{M}_{\Delta}(\vec{P}_{1})=96\cdot 10^{2}\;Nm}$
 
3) Calculons le moment du poids $P_{2}$ par rapport à l'axe $\Delta$ de la roue avant.
 
On a : $\mathcal{M}_{\Delta}(\vec{P}_{2})=-P_{2}\cdot d_{2}$
 
Donc, $\mathcal{M}_{\Delta}(\vec{P}_{2})=-42\cdot 10^{2}\cdot 1.75=-73.5\cdot 10^{2}$
 
Par suite, $\boxed{\mathcal{M}_{\Delta}(\vec{P}_{2})=-73.5\cdot 10^{2}\;Nm}$
 
4) Calcul du moment du poids $P_{3}$ par rapport à l'axe $\Delta$ de la roue avant.
 
Soit : $\mathcal{M}_{\Delta}(\vec{P}_{3})=-P_{3}\cdot d_{3}$
 
A.N : $\mathcal{M}_{\Delta}(\vec{P}_{3})=-15\cdot 10^{2}\cdot 1.20=-18\cdot 10^{2}$
 
D'où, $\boxed{\mathcal{M}_{\Delta}(\vec{P}_{3})=-18\cdot 10^{2}\;Nm}$
 
5) Vérifions si le chargeur ainsi chargé pivote autour de l'axe $\Delta$
 
On a :
 
$\begin{array}{rcl}\left|\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})\right|&=&\left|-73.5\cdot 10^{2}-18\cdot 10^{2}\right|\\ \\&=&91.5\end{array}$
 
Donc, $\left|\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})\right|=91.5\;Nm$
 
Comme $\mathcal{M}_{\Delta}(\vec{P}_{})=96\cdot 10^{2}\;Nm$ alors, $\mathcal{M}_{\Delta}(\vec{P}_{})>\left|\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})\right|$
 
Par conséquent, le chargeur ainsi chargé pivote autour de l'axe $\Delta.$
 
6) Déterminons la charge maximale que peut transporter le godet
 
Soit : $\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})=0$ alors,
 
$\begin{array}{rcl}\mathcal{M}_{\Delta}(\vec{P}_{2})=-\mathcal{M}_{\Delta}(\vec{P}_{1})-\mathcal{M}_{\Delta}(\vec{P}_{3})&\Rightarrow&-P_{2}.d_{2}=-\mathcal{M}_{\Delta}(\vec{P}_{1})-\mathcal{M}_{\Delta}(\vec{P}_{3})\\ \\&\Rightarrow&P_{2}=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}}\\ \\&\Rightarrow&M_{2}.g=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}}\\ \\&\Rightarrow&M_{2}=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}.g}\end{array}$
 
Donc, $M_{2}=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}.g}$
 
A.N : $M_{2}=\dfrac{96\cdot 10^{2}-18\cdot 10^{2}}{1.75\times 10}=446$
 
D'où, $\boxed{M_{2}=446\;kg}$

Exercice 3

Un solide $(S)$ de masse $m=200\;g$ est relié à un fil de masse négligeable passant par la gorge d'une poulie à axe fixe $(\Delta)$, de masse négligeable et de rayon $r.$
 
L'autre extrémité du fil est attachée à un ressort de raideur $k$ et de masse négligeable. 
 
A l'équilibre, l'axe du ressort fait un angle $\alpha=30^{\circ}$ avec l'horizontale et le ressort est allongé de $\Delta l=4\;cm.$ On néglige tout type de frottement.
 
1) a) Représentons les forces exercées sur le solide $(S).$
 
 
b) Écrivons la condition d'équilibre de $(S)$
$$\vec{P}+\vec{T}=\vec{0}$$
Déterminons l'expression de la tension du fil $f_{1}.$
 
On a : 
 
$\begin{array}{rcl}\vec{P}+\vec{T}=\vec{0}&\Rightarrow&m.g-T=0\\ \\&\Rightarrow&T=m.g\end{array}$
 
Calcul de sa valeur.
 
$T=m.g=200.10^{-3}\times 10=2$
 
Donc, $\boxed{T=2\;N}$
 
2) a) Représentons les forces exercées sur la poulie.
 
Voir figure
 
b) Détermination de la tension du fil $f_{2}$
 
Le théorème des moments s'écrit :
 
$\begin{array}{rcl} M_{\Delta}(\vec{T_{1}})+M_{\Delta}(\vec{T_{2}})+M_{\Delta}(\vec{R})=0&\Rightarrow&-T_{1}r+T_{2}r+0=0\\ \\&\Rightarrow&T_{2}r=T_{1}r\\ \\&\Rightarrow&T_{2}=T_{1}\end{array}$
 
Le fil transmet les forces donc :
 
$\begin{array}{rcl} T_{1}=T&\Rightarrow&T_{2}=T\\ \\&\Rightarrow& T_{2}=2\;N\end{array}$
 
c) Déduction de la tension du fil $f_{2}$ au point $A.$
 
Le fil transmet les forces alors : 
$$T_{r}=T_{2}\ \Rightarrow\ T_{r}=2\;N$$
3) Déterminons la valeur de la raideur du ressort $k.$
 
On a : $T_{r}=k\Delta l\ \Rightarrow\ k=\dfrac{T_{r}}{\Delta l}$
 
A.N : $k=\dfrac{2.0}{4.10^{-2}}=25$
 
Ainsi, $\boxed{k=25\;N.m^{-1}}$
 
4) Par projection de la relation vectorielle, traduisant l'équilibre de la poulie, dans un repère orthonormé, montrons que la valeur de la réaction R de l'axe $(\Delta)$ est $R=mg\sqrt{2(1+\sin \alpha)}$
 
La condition d'équilibre s'écrit :
$$\vec{T_{1}}+\vec{T_{2}}+\vec{R}=\vec{0}$$
 
 
En projetant la relation vectorielle suivant les axes $x’x\ $ et $\ y’y$, il vient :
 
$0+T_{2}\cos \alpha-R_{x}=0\ \Rightarrow\ R_{x}=T_{2}\cos \alpha=mg\cos \alpha$
 
$\begin{array}{rcl} T_{1}+T_{2}\sin \alpha-R_{y}=0&\Rightarrow&R_{y}=T_{1}+T_{2}\sin \alpha\quad\text{or, }\ T_{1}=T_{2}=mg\\ \\&\Rightarrow&R_{y}=mg(1+\sin \alpha)\end{array}$
 
Soit alors :
 
$\begin{array}{rcl}  R&=&\sqrt{R_{x}^{2}+R_{y}^{2}}\\ \\&=&\sqrt{(m.g\cos \alpha)^{2}+(m.g(1+\sin \alpha))^{2}}\\ \\&=&m.g\sqrt{(\cos \alpha)^{2}+(1+\sin \alpha)^{2}}\\ \\&=&m.g\sqrt{\cos^{2}\alpha+1+2\sin \alpha+\sin^{2}\alpha}\\ \\&=&m.g\sqrt{2+2\sin \alpha}\\ \\&=&m.g\sqrt{2(1+\sin \alpha)}\end{array}$
 
Calcul de sa valeur
 
$\begin{array}{rcl} R&=&m.g\sqrt{2(1+\sin \alpha)}\\ \\&=&200.10^{-3}\times 10\sqrt{2(1+\sin 30^{\circ})}\\ \\&=&0.34\end{array}$
 
D'où, $\boxed{R=0.34\;N}$

Exercice 4

On dispose d'une règle homogène, de masse négligeable, pouvant tourner autour d'un axe horizontal $\Delta$ passant par son centre d'inertie $O.$ On veut connaître le comportement de la règle dans les situations suivantes :
 
1) La règle, initialement au repos, est soumise à un seul couple de forces $(\vec{F}\;,\ \vec{F'})\ :$, indiquons quel est le comportement de la règle et donnons le signe du moment du couple de forces.
 
 
Le couple de forces fait tourner la règle dans un sens opposé à celui du sens positif choisi. Le signe du moment du couple est donc négatif.
 
 
2.1) Calcul du moment de chaque couple.
 
Soit : $F_{1}=F_{2}=2.5\times 2\ \Rightarrow\ F_{1}=F_{2}=5\;N$
 
$d=1.6\times 10\ \Rightarrow\ d=16\;cm$
 
$F_{3}=F_{4}=2\times 2\ \Rightarrow\ F_{3}=F_{4}=4\;N$
 
$d'=3.0\times 10\ \Rightarrow\ d'=30\;cm$
 
Alors, 
 
$M_{\Delta}(F_{1}\;,\ F_{2})=F_{1}.d=5\times 16.10^{-2}$
 
Donc, $\boxed{M_{\Delta}(F_{1}\;,\ F_{2})=0.80\;Nm}$
 
$M_{\Delta}(F_{1}\;,\ F_{2})=F_{1}.d=5\times 16.10^{-2}$
 
Ainsi, $\boxed{M_{\Delta}(F_{1}\;,\ F_{2})=0.80\;Nm}$
 
$M_{\Delta}(F_{3}\;,\ F_{4})=-F_{3}.d'=4\times 30.10^{-2}$
 
D'où, $\boxed{M_{\Delta}(F_{3}\;,\ F_{4})=-1.20\;Nm}$
 
2.2) Exprimons la condition d'équilibre de la règle.
$$M_{\Delta}(F_{1}\;,\ F_{2})+M_{\Delta}(F_{3}\;,\ F_{4})=0$$
Montrons alors que la règle n'est pas en équilibre mais en rotation non uniforme.
 
On a :
$$\left|M_{\Delta}(F_{3}\;,\ F_{4})\right|>M_{\Delta}(F_{1}\;,\ F_{2})$$
Donc, la règle n'est pas équilibre mais en rotation non uniforme.
 
Cette rotation se fait dans le sens négatif.
 
2.3) On veut obtenir l'équilibre de cette règle :
 
2.3.1) Pour cela, on déplace le point d'application $A_{3}$ de la force $\vec{F}_{3}$, déterminons la position de $A_{3}$ par rapport à $O$ pour que la règle soit en équilibre.
 
On sait que : $M_{\Delta}(F_{1}\;,\ F_{2})+M_{\Delta}(F_{3}\;,\ F_{4})=0$
 
Donc,
 
$\begin{array}{rcl} M_{\Delta}(F_{3}\;,\ F_{4})=-M_{\Delta}(F_{1}\;,\ F_{2})&\Rightarrow&-F_{3}.d=-M_{\Delta}(F_{1}\;,\ F_{2})\\ \\&\Rightarrow&d=\dfrac{M_{\Delta}(F_{1}\;,\ F_{2})}{F_{3}}\\ \\&\Rightarrow&d=\dfrac{0.80}{4}\\ \\&\Rightarrow&d=0.20\;m\end{array}$
 
2.3.2) Donnons l'expression du moment du couple $(\vec{F_{3}}\;,\ \vec{F_{4}})$ en fonction de $\alpha\;,\ F_{3}\;,\ A_{3}A_{4}$
 
 
On a :
$$M_{\Delta}(F_{3}\;,\ F_{4})=-F_{3}.A_{3}A_{4}.\cos\alpha$$
 
Détermination de la valeur de $\alpha$ pour laquelle la règle est en équilibre.
 
On a : $M_{\Delta}(F_{1}\;,\ F_{2})+M_{\Delta}(F_{3}\;,\ F_{4})=0\ \Rightarrow\ M_{\Delta}(F_{3}\;,\ F_{4})=-M_{\Delta}(F_{1}\;,\ F_{2})$
 
Alors,
 
$\begin{array}{rcl} -F_{3}.A_{3}A_{4}.\cos\alpha=-M_{\Delta}(F_{1}\;,\ F_{2})&\Rightarrow&\cos\alpha=\dfrac{M_{\Delta}(F_{1}\;,\ F_{2})}{F_{3}.A_{3}A_{4}}\\ \\&\Rightarrow&\alpha=\cos^{-1}\left(\dfrac{(M_{\Delta}(F_{1}\;,\ F_{2})}{F_{3}.A_{3}A_{4}}\right)\\ \\&\Rightarrow&\alpha=\cos^{-1}\left(\dfrac{0.80}{4\times 0.30}\right)\\ \\&\Rightarrow&\alpha=48.2^{\circ}\end{array}$
 
Donc, $\boxed{\alpha=48.2^{\circ}}$

 

 

 

Pages