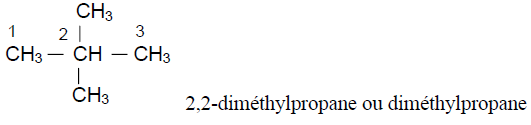Physique

Corrigé Devoir n° 1 - Physique Chimie - 4e

Classe: 
Quatrième
 

Exercice 1

1.1. Donnons la définition d'un phénomène physique et d'un phénomène chimique.
 
$-\ $ Un phénomène physique est une transformation au cours de laquelle les corps ne changent pas de nature.
 
$-\ $ Un phénomène chimique est une transformation au cours de laquelle les corps changent de nature.
 
1.2. Reproduisons le tableau ci-dessous et mettons une croix dans la case qui convient.
$$\begin{array}{|l|c|c|}\hline\text{Phénomènes}&\text{Phénomènes}&\text{Phénomènes}\\&\text{physiques}&\text{chimiques}\\ \hline\text{Mouvement d'un objet}&\times&\\ \hline\text{Action de l'acide sur le cuivre}&&\times\\ \hline\text{Effet du jus de citron sur le calcaire}&&\times\\ \hline\text{Déformation d'un ressort}&\times&\\ \hline\end{array}$$

Exercice 2

2.1. Les différents états de la matière sont :
 
$-\ $ Etat solide
 
$-\ $ Etat liquide
 
$-\ $ Etat gazeux
 
2.2. Recopions et complétons ce texte qui décrit les propriétés caractéristiques des états de la matière.
 
Les solides sont durs, résistants à la déformation et ayant une forme et un volume propres. 
 
Les liquides sont des fluides, ils prennent la forme du récipient qui les contient, au repos, leur surface libre est plane et horizontale.
 
Les gaz sont expansibles, compressibles et élastiques.
 
2.3. Complétons le schéma suivant :
$$\begin{array}{rclcl}&\underrightarrow{\quad\text{fusion}\quad}&&\underrightarrow{\text{vaporisation}}&\\ \boxed{\text{Etat solide}}&&\boxed{\text{Etat liquide}}&&\boxed{\text{Etat gazeux}}\\&\overleftarrow{\text{solidification}}&&\overleftarrow{\text{condensation}}&\end{array}$$

Exercice 3

3.1. Donnons la définition d'un mélange homogène et d'un mélange hétérogène.
 
$-\ $ Un mélange est dit homogène si on ne peut pas distinguer à l'œil nu ses différentes parties.
 
$-\ $ Un mélange est dit hétérogène si on peut distinguer à l'œil nu ses différentes parties.
 
3.2. Reproduisons le tableau ci-dessous et mettons une croix dans la case qui convient.
$$\begin{array}{|l|c|c|}\hline\text{Mélanges}&\text{Mélange}&\text{Mélange}\\&\text{homogène}&\text{hétérogène}\\ \hline\text{Eau sallée}&\times&\\ \hline\text{Eaux de ruissellement}&&\times\\ \hline\text{Jus de bissap (oseille)}&\times&\\ \hline\text{Poignée de sable}&&\times\\ \hline\end{array}$$

Exercice 4

L'électrolyse d'un volume d'eau a donné un dégagement de $10\;cm^{3}$ d'un gaz à l'anode.
 
4.1. Le gaz dégagé à l'anode est du dioxygène.
 
4.2. Pour mettre en évidence ce gaz, on approche une bûchette en incandescence à l'anode. On constate alors que la bûchette se rallume. Ce qui caractérise la présence du dioxygène.
 
4.3. On sait que dans une expérience d'électrolyse de l'eau, le volume du gaz recueilli à la cathode est le double de celui dégagé à l'anode.
 
Ce qui se traduit par : $V_{\text{cathode}}=2V_{\text{anode}}$
 
Comme le gaz qui se dégage à l'anode est du dioxygène alors, on a :
 
$V_{\text{anode}}=V_{O_{2}}=10\;cm^{3}$
 
Par suite, $V_{\text{cathode}}=2\times 10\;cm^{3}=20\;cm^{3}$
 
4.4. Le gaz qui se dégage au niveau de la cathode est du dihydrogène

 

Auteur: 
Diny Faye

Solution des exercices : Énergie cinétique - 1er s

Classe: 
Première
 

Exercice 1

 
1. Exprimons, puis calculons l'énergie cinétique de l'autoporteur en $A.$
 
$\begin{array}{rcl} E_{C_{A}} &=&\dfrac{1}{2}mV_{A}^{2}\\ &=&\dfrac{1}{2}\times 600\cdot 10^{-3}\times 6^{2} \\\Rightarrow E_{C_{A}} &=&10.8J \end{array}$
 
2. Inventaire des forces extérieures agissant sur l'autoporteur au cours de la phase $AB.$
 
Les forces extérieures sont : $\overrightarrow{P}$ et $\overrightarrow{R}$
 
3. a) Définition d'un système pseudo-isolé ;
 
Un système pseudo-isolé est un système soumis à des forces qui se compensent.
 
b) L'autoporteur est pseudo-isolé au cours de la phase $AB$, car, pendant cette phase les forces se compensent.
 
Par contre, pendant la phase $BD$, les forces ne se compensent plus, et le système n'est plus pseudo-isolé
 
c) Déduction de la vitesse du centre d'inertie du mobile en $B$
 
Le théorème de l'énergie cinétique s'écrit :
 
$\begin{array}{rcl} \Delta BC &=& \sum\,W\left(\overrightarrow{F}_{extérieurs}\right)\\\Rightarrow\;E_{CB}-E_{CA}&=&W_{AB}\left(\overrightarrow{P}\right)+W_{AB}\left(\overrightarrow{R}\right) \\\Rightarrow\dfrac{1}{2}mV_{B}^{2}-\dfrac{1}{2}mV_{A}^{2}&=&0+0\\\Rightarrow\dfrac{1}{2}mV_{A}^{2}&=&\dfrac{1}{2}mV_{B}^{2}\\\Rightarrow\;V_{B}^{2}&=&V_{A}^{2}\\\Rightarrow\;V_{B}&=&V_{A}\\ \Rightarrow\;V_{B}&=&6m\cdot s^{-1} \end{array}$
 
4. Calcul du travail du poids de l'autoporteur et le travail de l'action $R$ du plan sur l'autoporteur au cours du déplacement $BC_{1}$
 
$\begin{array}{rcl} W_{BC_{1}}\left(\overrightarrow{P}\right) &=&\overrightarrow{P}\cdot\overrightarrow{BC_{1}}\\ &=&-mgBC_{1}\sin\alpha\nonumber\\ &=&-600\cdot 10^{-3}\times 10\times 1\times\sin 30^{\circ} \\ \Rightarrow\;W_{BC_{1}}\left(\overrightarrow{P}\right) &=&-3.0J \end{array}$
 
$W_{BC_{1}}\left(\overrightarrow{R}\right)=\overrightarrow{R}\cdot\overrightarrow{BC_{1}}=0\left(\overrightarrow{R}\perp\overrightarrow{BC_{1}}\right)$
 
5. Déduction de $V_{c_{1}}$
 
Le théorème de l'énergie cinétique au solide entre les instants $t_{B}$ et $t_{C_{1}}$ s'écrit :
 
$\begin{array}{rcl} E_{C_{c_{1}}}-E_{C_{B}}&=&W_{BC_{1}}\left(\overrightarrow{P}\right)+W_{BC_{1}}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{C_{1}}^{2}-\dfrac{1}{2}mV_{B}^{2}&=&-mgBC_{1}\sin\alpha+0\\\Rightarrow\;V_{C_{1}}^{2}-V_{B}^{2}&=&-2gBC_{1}\sin\alpha\\\Rightarrow\; V_{C_{1}}^{2}&=&V_{B}^{2}-2gBC_{1}\sin\alpha\\\Rightarrow\; V_{C_{1}} &=&\sqrt{V_{B_{1}}-2gBC_{1}\sin\alpha}\\ \Rightarrow\; V_{C_{1}}&=&\sqrt{6^{2}-2\times 10\times 1\times\sin 30^{\circ}}\\\Rightarrow\;V_{C_{1}} &=&5.1\,m\cdot s^{-1} \end{array}$
 
6. Déduction de $BC_{2}$ la distance parcourue par le mobile avant de rebrousser chemin en $C_{2}.$
 
$\begin{array}{rcl} E_{C_{c_{1}}}-E_{C_{B}} &=& W_{BC_{2}}\left(\overrightarrow{P}\right)+W_{BC_{2}}\left(\overrightarrow{R}\right)\\\Rightarrow\;0-\dfrac{1}{2}mV_{B}^{2} &=&-mgBC_{2}\sin\alpha+0 \\\Rightarrow \;-V_{B}^{2} &=& -2gBC_{2}\sin\alpha\\\Rightarrow\; 2gBC_{2}\sin\alpha &=&V_{B}^{2} \\\Rightarrow\;  BC_{2} &=&\dfrac{V_{B}^{2}}{2g\sin\alpha}\\\Rightarrow\;BC_{2} &=&\dfrac{6^{2}}{2\times 10\sin 30^{\circ}}\\\Rightarrow \;BC_{2} &=&3.6\,m \end{array}$

Exercice 2

 
1.1. Bilan des forces qui s'appliquant sur le mobile au point $M$ sont : $\overrightarrow{P}$ et $\overrightarrow{R}.$
 
1.2. Expression du travail de chacune des forces, au point $M$, en fonction de $m$, $g$, $r$ et $\theta.$
$W_{AM}\left(\overrightarrow{P}\right)=\overrightarrow{P}\cdot\overrightarrow{AM}=mgr\cos\theta$
 
$W_{AM}\left(\overrightarrow{R}\right)=\overrightarrow{R}\cdot\overrightarrow{AB}=0\quad\text{car}\quad\overrightarrow{R}\perp\overrightarrow{AB}$
 
1.3. Établissement de l'expression littérale de la vitesse $V_{M}$ du mobile en fonction de $V_{A}$, $g$, $r$ et $\theta.$
 
Appliquons le théorème de l'énergie cinétique au point $M$ et
 
$\begin{array}{rcl} E_{C_{M}}-E_{C_{A}} &=& W_{AM}\left(\overrightarrow{P}\right)+W_{AM}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{M}^{2} &=&mgr\cos\theta+0\\\Rightarrow\dfrac{1}{2}mV_{M}^{2} &=&\dfrac{1}{2}mV_{A}^{2}+mgr\cos\theta\\\Rightarrow \;V_{M}^{2} &=&V_{A}^{2}+2gr\cos\theta\\\Rightarrow\; V_{M} &=&\sqrt{V_{A}^{2}+2gr\cos\theta} \end{array}$
 
1.4. Calcul de $V_{M}$ en $B$ $($pour $\theta=0).$
 
$\begin{array}{rcl} V_{M} &=&\sqrt{V_{A}^{2}+2gr\cos\theta}\ ;\ \text{pour }\theta=0\\\Rightarrow\; V_{M} &=& \sqrt{V_{A}^{2}+2gr\cos 0}\\\Rightarrow \;V_{B} &=&\sqrt{V_{A}^{2}+2gr}\\\Rightarrow \;V_{B} &=&\sqrt{5^{2}+2\times 10\times 1}\\\Rightarrow \;V_{B} &=&6.71\,m\cdot s^{-1} \end{array}$
 
2. Détermination de l'expression littérale et numérique de $f.$
 
$\begin{array}{rcl} E_{C_{C}}-E_{C_{B}} &=& W_{BC}\left(\overrightarrow{P}\right)+W_{BC}\left(\overrightarrow{R}\right)+W_{BC}\left(\overrightarrow{f}\right)\\\Rightarrow\dfrac{1}{2}mV_{C}^{2}-\dfrac{1}{2}mV_{B}^{2} &=&0+0-f\times BC\\\Rightarrow \;f &=&\dfrac{m\left(V_{B}^{2}\right)}{2BC}\\\Rightarrow\; f &=&\dfrac{0.1\times\left(6.71^{2}-5\right)}{2\times 1} \\\Rightarrow \;f &=& 1N \end{array}$

Exercice 3 Voiture tremplin

 
1. Dans le référentiel terrestre supposé galiléen, les forces s'exerçant sur le système {ensemble automobile-pilote} sont :
 
$-\ $dans la phase $BO$ : son poids $\overrightarrow{P}$, la réaction $\overrightarrow{R}$ du support, les frottements $\overrightarrow{f}$ et la traction $\overrightarrow{T}$ du système.
 
$-\ $dans la phase $OE$ : son poids $\overrightarrow{P}.$
 
$-\ $dans la phase $EH$ : son poids $\overrightarrow{P}$, la réaction normale $\overrightarrow{R}$ du support, les frottements $\overrightarrow{f}$ et la force de freinage $\overrightarrow{F}$
 
2. Si on suppose que le système est soumis à des forces qui ne se compensent pas dans la phase $BO$, alors le système n'est pas pseudo isolé (d'après le principe d'inertie).
 
Si on suppose qu'il évolue à vitesse constante et à trajectoire rectiligne, alors le système est pseudo isolé (d'après le principe d'inertie).
 
Dans la phase $OE$, le système n'est soumis qu'à son poids ; il n'est donc pas pseudo isolé.
 
Dans la phase $EH$, le système freine donc(les forces ne se compensent plus), d'après le principe d'inertie, il n'est pas pseudo isolé.
 
3. Détermination du travail de chaque force de chacune des phases :
 
$-\ $Phase $BO$
 
$\begin{array}{rcl} W_{BO}\left(\overrightarrow{P}\right) &=&-mg\cdot OC\\ &=&-1.00\cdot 10^{3}\times 9.81\times 8.00\\ &=&-78.5\cdot 10^{3}J \end{array}$
 
$W_{BO}\left(\overrightarrow{R}\right)=0\quad\text{car}\quad\overrightarrow{R}\perp\overrightarrow{BO}$
 
$\begin{array}{rcl} W_{BO}\left(\overrightarrow{f}\right) &=&\overrightarrow{f}\cdot BO\\ &=&-\dfrac{500\times 8.00}{\sin 15.5^{\circ}}\\\Rightarrow W_{BO}\left(\overrightarrow{f}\right) &=&-15.5\cdot 10^{3}J \end{array}$
 
$\begin{array}{rcl} W_{BO}\left(\overrightarrow{T}\right) &=& \overrightarrow{T}\cdot\overrightarrow{BO}\\ &=&\dfrac{T\times OC}{\sin\alpha} \end{array}$
 
$-\ $Phase $OE$
 
$\begin{array}{rcl} W_{BO}\left(\overrightarrow{P}\right) &=&-mg(ED-OC)\\ &=&-1.00\cdot 10^{3}\times 9.81\times(10.0-8.00)\\ &=&-19.6\cdot 10^{3}J\end{array}$
 
$-\ $Phase $EH$
 
$W_{EH}\left(\overrightarrow{P}\right)=0J\ (\overrightarrow{P}\perp\overrightarrow{BH})$
 
$W_{EH}\left(\overrightarrow{f}\right)=0J\ (\overrightarrow{R}\perp\overrightarrow{EH})$
 
$\begin{array}{rcl} W_{EH}\left(\overrightarrow{f}\right) &=&-500\times 100\\\Rightarrow\; W_{EH}\left(\overrightarrow{f}\right)&=&-50.0\cdot 10^{3}J \end{array}$
 
4. D'après le théorème de l'énergie cinétique (dans un référentiel galiléen, la variation d'énergie cinétique d'un système en translation entre deux points est égale à la somme des travaux des forces qui s'exercent sur ce système entre ces deux points.) entre $O$ et $E$, on a :
$$\dfrac{1}{2}mv_{1}^{2}-\dfrac{1}{2}mv_{0}^{2} =W_{OE}\left(\overrightarrow{P}\right)$$
$\begin{array}{rcl} \text{ soit }\ \dfrac{1}{2}mv_{1}^{2}-\dfrac{1}{2}mv_{0}^{2} &=&mg(OC-ED)\\\Rightarrow\; v_{0} &=&\sqrt{v_{1}^{2}+2g(DE-OC)}\\\Rightarrow\; v_{0} &=&\sqrt{24^{2}+2\times 9.81(10.0-8.00)}\\\Rightarrow \;v_{0} &=&24.8\,m\cdot s^{-1}  \end{array}$
 
5. D'après le théorème de l'énergie cinétique entre $E$ et $H$, on a :
 
$\dfrac{1}{2}mv_{H}^{2}-\dfrac{1}{2}mv_{1}^{2} =W_{EH}\left(\overrightarrow{F}\right)+W_{EH}\left(\overrightarrow{f}\right).$
 
Or $v_{H}=0\,m\cdot s^{-1}$
 
d'où il vient : $-\dfrac{1}{2}mv_{1}^{2}=-f\times EH-F\times EH.$
 
Donc $F=\dfrac{mv_{1}^{2}}{2EH}-f=\dfrac{1.00\cdot 10^{3}\times 24^{2}}{2\times 10.00}-500=23.8\cdot 10^{3}.$
 
6. La puissance du travail de la force $\overrightarrow{F}$
 
$\begin{array}{rcl} P &=&\dfrac{W_{EH}\left(\overrightarrow{F}\right)}{t}\\ &=&\dfrac{-F\times EH}{t}\\ &=&\dfrac{-23.8\cdot 10^{3}\times 10.00}{8.00}\\ &=& -29.8\cdot 10^{3}W. \end{array}$

Exercice 4

 
1. Calcul des vitesses $V_{B}$ et $V_{C}$ avec lesquelles le skieur passe en $B$ et en $C.$
 
$\bullet\ $Système étudié : le skieur
 
$\bullet\ $Référentiel d'étude : référentiel terrestre supposé galiléen
 
$\bullet\ $Bilan des forces appliquées : $\overrightarrow{P}$ et $\overrightarrow{R}$
 
Le théorème de l'énergie cinétique s'écrit :
 
$-\ $entre $A$ et $B$
$\begin{array}{rcl} E_{c_{B}}-E_{c_{A}}&=&W_{AB}\left(\overrightarrow{P}\right)+W_{AB}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{B^{2}}-0&=&mgr(1-\cos\alpha)+0\\\Rightarrow\dfrac{1}{2}mV_{B^{2}}&=&mgr(1-\cos\alpha)\\ \Rightarrow\;V_{B^{2}}&=&2gr(1-\cos\alpha)\\\Rightarrow\;V_{B}&=&\sqrt{2gr(1-\cos\alpha)}\\&=&\sqrt{2\times 10\times 5\left(1-\cos 60^{\circ}\right)}\\\Rightarrow\;V_{B}&=&7.07m\cdot s^{-1} \end{array}$
 
$-\ $entre $B$ et $C$
 
$\begin{array}{rcl} E_{c_{C}}-E_{c_{B}}&=&W_{BC}\left(\overrightarrow{P}\right)+W_{BC}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{C}^{2}-\dfrac{1}{2}mV_{B}^{2}&=&0+0\\\Rightarrow\;V_{C}^{2}&=&V_{B}^{2}\\\Rightarrow\;V_{C}&=&V_{B}\\\Rightarrow\;V_{C}&=&7.07m\cdot s^{-1} \end{array}$
 
2.1 Expression de $V_{B}$ en fonction de $m$, $r$, $f$, et $g.$
 
Le théorème de l'énergie cinétique s'écrit :
 
$-\ $entre $A$ et $B$
 
$\begin{array}{rcl} E_{c_{B}}-E_{c_{A}}&=&W_{AB}\left(\overrightarrow{P}\right)+W_{AB}\left(\overrightarrow{R}\right)+W_{AB}\left(\overrightarrow{f}\right)\\\Rightarrow\dfrac{1}{2}mV_{B}^{2}-0&=&mgr(1-\cos\alpha)+0-fr\alpha\text{ avec }\left(\alpha=\dfrac{\pi}{3}\right)\\ \Rightarrow\dfrac{1}{2}mV_{B}^{2}&=&mgr(1-\cos\alpha)-f\times\dfrac{\pi}{3}r\\ \Rightarrow\;V_{B}^{2}&=&2gr(1-\cos\alpha)-2f\times\dfrac{\pi}{3}r\\ \Rightarrow\;V_{B}&=&\sqrt{2gr\left(1-\cos\alpha\right)-2f\times\dfrac{\pi}{3}r} \end{array}$
 
2.2 Expression de $V_{c}$ en fonction de $m$, $r$, $f$ et $V_{B}$
 
Le théorème de l'énergie cinétique s'écrit :
 
$-\ $entre $B$ et $C$
 
$\begin{array}{rcl} E_{c_{C}}-E_{c_{B}}&=&W_{BC}\left(\overrightarrow{P}\right)+W_{BC}\left(\overrightarrow{R}\right)+W_{BC}\left(\overrightarrow{f}\right)\\ \Rightarrow\dfrac{1}{2}mV_{C}^{2}-\dfrac{1}{2}mV_{B}^{2}&=&0+0-fr\\ \Rightarrow\;V_{C}^{2}&=&2V_{B}^{2}-\dfrac{2fr}{m}\\\Rightarrow\;V_{C}&=&\sqrt{2\left(V_{B}^{2}-\dfrac{fr}{m}\right)} \end{array}$
 
2.3 Calcul de l'intensité de la force de frottement
 
$\begin{array}{rcl} V_{c}&=&\sqrt{2\left(V_{B}^{2}-\dfrac{fr}{m}\right)}\\&=&0\\ \Rightarrow\;2\left(V_{B}^{2}-\dfrac{fr}{m}\right)&=&0\\ \Rightarrow\dfrac{fr}{m}&=&V_{B}^{2}\\\Rightarrow\;f&=&\dfrac{mV_{B}^{2}}{r}\\&=&\dfrac{80\times 7.07^{2}}{5}\\\Rightarrow\;f&=&8.0\cdot 10^{2}N \end{array}$
 
3.1 Expression de la vitesse $V_{E}$ en fonction de $g$, $r$ et $\theta$
 
Le théorème de l'énergie cinétique s'écrit : 
 
$-\ $entre $C$ et $E$
 
$\begin{array}{rcl} E_{c_{E}}-E_{c_{C}}&=&W_{CE}\left(\overrightarrow{P}\right)+W_{CE}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{E}^{2}-0&=&mgr(1-\sin\theta)\\\Rightarrow\;V_{E}^{2}&=&2gr(1-\sin\theta)\\\Rightarrow\;V_{E}&=&\sqrt{2gr(1-\sin\theta)} \end{array}$
 
3.2 Calcul de la valeur de l'angle $\theta$
 
$\begin{array}{rcl} V_{E}^{2}&=&2gr(1-\sin\theta)\\\Rightarrow(1-\sin\theta)&=&\dfrac{V_{E}^{2}}{2gr}\\ \Rightarrow\sin\theta&=&1-\dfrac{V_{E}^{2}}{2gr}\\\Rightarrow\theta&=&\sin^{-1}\left(1-\dfrac{V_{E}^{2}}{2gr}\right)\\\Rightarrow\theta&=&\sin^{-1}\left(1-\dfrac{5.77^{2}}{2\times 10\times 5}\right)\\ \Rightarrow\theta&=& 60^{\circ} \end{array}$
 
4. vitesse avec laquelle le skireur atterrit sur la piste de réception en un point $G$
 
$\begin{array}{rcl} V_{E}&=&\sqrt{2gr(1-\sin\theta)}\;,\text{ au point }G\;,\ \theta=0\\\Rightarrow\;V_{E}&=&\sqrt{2gr(1-\sin 0)}\\\Rightarrow\;V_{E}&=&\sqrt{2gr}\\&=&\sqrt{2\times10\times5}\\\Rightarrow\;V_{E}&=&10\,m\cdot s^{-1} \end{array}$

 


 

Amplificateur opérationnel - 2nd S

Classe: 
Seconde
 
 
L'amplificateur opérationnel est un assemblage d'éléments actifs et passifs, dont le rôle essentiel est de produire une tension de sortie plus élevée que la tension d'entrée. 
 
Toutefois, les amplificateurs peuvent être utilisés pour remplir d'autres fonctions (mathématique simple addition, soustraction, multiplication) où ils constituent en eux-mêmes des éléments de circuits. 
 
Ils fonctionnent suivant des lois simples.
 
Ce chapitre se consacre au calcul de gain des amplificateurs (inverseur, non inverseur, suiveur...) 

I. Amplificateur opérationnel

1. Description et caractéristiques

1.1. Description 

Le composant se présente sous forme d'un boîtier plastique ou métallique muni de bornes de raccordement.
 
 
C'est un circuit intégré, c'est à dire qu'il est formé d'une multitude de composants électroniques élémentaires (Résistances, transistors, condensateurs, diodes, etc..) formant un circuit complexe et intégrés dans un boîtier.
 
Le composant comporte huit broches :
 
$-\ $les broches $4$ et $7$ servent à l'alimentation,
 
$-\ $les broches $2$ et $3$ sont les entrées
 
$-\ $la broche $6$ correspond à la sortie.
 
$-\ $Les broches $1$ et $5$ sont parfois utilisables pour la correction d'offset
 
La broche $8$ est non utilisée.
 
Lorsque $l'AOP$ est parfait, on fait suivre le triangle du symbole $\infty$, sinon on précise son coefficient d'amplification réel.
 
Le signe $+$ en sortie est souvent omis

1.2. Caractéristiques

1.2.1. Courants d'entrée

En pratique, les courants d'entrée peuvent être négligés :
 
le courant de polarisation sur l'entrée inverseuse
 
$-\ i^{+}$ le courant de polarisation sur l'entrée non inverseuse ; $i^{+}=0$
 
le courant de polarisation sur l’entrée inverseuse
 
$-\ i^{-}$ le courant de polarisation sur l'entrée non, inverseuse $i^{-}=0$
 
 

1.2.2. Tension différentielle d'entrée : $\varepsilon$

La tension différentielle d'entrée est la différence de tension entre l'entrée non inverseuse et l'entrée inverseuse.
 
 
$$\boxed{\varepsilon=U_{e}^{+}-U_{e}^{-}}$$

1.2.3. Caractéristique de transfert : $v_{S}(\varepsilon)$

On distingue trois zones :
 
$\blacktriangleright\ $zone de linéarité : $\varepsilon\approx 0V$ ; $V_{sat^{-}}<v_{S}<V_{sat^{+}}$
 
$\blacktriangleright\ $zone de saturation haute : $\varepsilon>0V$ ; $v_{S}=V_{sat^{+}}$
 
$\blacktriangleright\ $« « basse : $\varepsilon<0V$ ; $v_{S}=V_{sat}$
 
L'amplitude de la tension de sortie est limitée par les sources de polarisation à une valeur légèrement inférieure à $V_{CC.}$
 
Il existe également des $AOP$ dont les tensions de sortie peuvent atteindre les tensions d'alimentation

Remarque : 

si $V_{cc\pm}=±15V$ : $V_{sat\pm}$ est de l'ordre de $\pm14V$

1.2.4. Courant de sortie

Un amplificateur opérationnel ne peut généralement délivrer qu'un courant de sortie assez modeste, de quelques milliampères. 
 
Le courant de court-circuit de la sortie correspond à la valeur maximale de courant que $l'AOP$ peut débiter quand la sortie est reliée à la masse. 
 
Pour certains $AOP$, ce courant de court-circuit est limité en interne, pour d'autres il n'est pas limité et peut être destructeur s'il dure trop.
 
 

1.2.5. Réaction positive et contre-réaction

Afin de contrôler la valeur de la tension de sortie, il est nécessaire de réaliser des montages pour lesquels le coefficient l'amplification n'est pas infinie mais limitée à une valeur déterminée par le concepteur.
 
On réalise donc des montages qui mettent en œuvre des contre réactions négatives : on réinjecte une partie de la tension de sortie sur l'entrée inverseuse.
 
On dit qu'il y a réaction positive quand la sortie est reliée à l'entrée non inverseuse.
 
On dit qu'il y a contre-réaction (ou réaction négative) quand la sortie est reliée à l'entrée inverseuse
 
 

Conséquences importantes :

$\blacktriangleright\ $Une contre-réaction assure un fonctionnement linéaire de $l'A.O.$ : $\varepsilon\approx 0V$
 
$\blacktriangleright\ $Une réaction positive provoque la saturation de $l'A.O.$

2. Fonctionnement d'un amplificateur opérationnel

2.1. Régime linéaire

Le régime linéaire nécessite une boucle de contre-réaction : on ramène du signal de la sortie vers l'entrée inverseuse à l'aide d'un dipôle $D$ qui régule le système.
 
Dans ces conditions, pour $l'AOP$ idéal :  
 
 
$$\boxed{U_{E^{+}}=U_{E^{-}}\Rightarrow\varepsilon=0}$$ 

Remarque 

Ce type de montage ne reste linéaire que si la tension de sortie ne dépasse pas la tension de saturation.

2.2. Régime saturé

Le régime saturé s'obtient lorsque l'amplificateur opérationnel est sans boucle de contre-réaction ; on parle d'amplificateur opérationnel en boucle ouverte ou avec une réaction sur la borne positive.
 
 

II. Amplification d'une tension

1. Gain d'un amplificateur

Le gain en tension est le rapport entre la tension de la sortie et la tension à l'entrée :
$$\boxed{A=\dfrac{U_{S}}{U_{E}}}$$
 
 

2. Montage amplificateur non inverseur

L'amplificateur non inverseur est le deuxième amplificateur de base. 
 
Pour calculer le gain en tension, on va se servir de la loi d'additivité des tensions
 
\begin{eqnarray} U_{E} &=& U_{2}+\varepsilon^{+}\nonumber\\\\\Rightarrow U_{E} &=&R_{2}I_{2}+0\nonumber\\\\\Rightarrow U_{E} &=&R_{2}I_{2} \end{eqnarray}
 
\begin{eqnarray} U_{S} &=& U_{2}+U_{1}\nonumber\\\\\Rightarrow U_{E} &=&R_{2}I_{2}+R_{1}I_{1}\nonumber\\\\\text{or }I_{2} &=&I_{1}\nonumber\\\\\Rightarrow U_{S} &=&\left(R_{1}+R_{2}\right)I_{2} \end{eqnarray} 
 
\begin{eqnarray} A &=& \dfrac{U_{S}}{U_{e}}\nonumber\\\\ &=&\dfrac{\left(R_{1}+R_{2}\right)} I_{2}{R_{2}I_{2}}\nonumber\\\\A &=&\dfrac{R_{1}+R_{2}}{R_{2}}\nonumber\\\\\Rightarrow A &=&l+\dfrac{R_{1}}{R_{2}}  \end{eqnarray}  
 
 
Dans ce cas, le gain en tension est toujours supérieur à $1.$
 
L'amplificateur est dit « non inverseur » car le gain en tension $A$ est positif.
 
La tension de sortie $V_{s}$ est donc bien supérieure ou égale à la tension d'entrée $V_{e}$ $($si $R_{1}/R_{2}<<1)$, et de même signe, d'où son appellation amplificateur non-inverseur.

3. Montage amplificateur inverseur

C'est le montage de base à amplificateur opérationnel. L'entrée non inverseuse est reliée à la masse ; le signal d'entrée est relié à l'entrée inverseuse par une résistance $R_{1}$, et la sortie est reliée à cette entrée par une résistance $R_{2}.$

Déterminons le gain en tension

   
\begin{eqnarray} U_{E} &=& U_{1}+\varepsilon+U_{+}\nonumber\\\\\Rightarrow U_{E} &=&R_{1}I_{1}-0+0\nonumber\\\\\Rightarrow U_{E} &=&R_{1}I_{1} \end{eqnarray}
 
\begin{eqnarray} U_{S} &=& U_{1}-\varepsilon+U_{+}\nonumber\\\\\Rightarrow U_{E} &=&-R_{2}I_{2}-0+0\nonumber\\\\\Rightarrow U_{S} &=&-R_{2}I_{2} \end{eqnarray} 
 
\begin{eqnarray} A &=& \dfrac{U_{S}}{U_{E}}\nonumber\\\\ &=&\dfrac{-R_{2}+I_{2}}{R_{1}I_{1}}\nonumber\\\\\text{or }I_{2}&=&I_{1}\nonumber\\\\\Rightarrow A &=&-\dfrac{R_{2}}{R_{1}}  \end{eqnarray}
 
 
La tension de sortie $U_{s}$ est donc supérieure à la tension d'entrée $U_{e}$ si le rapport $R_{2}/R_{1}>1$, inférieure si $R_{2}/R_{1}<1$, ou égale si $R_{2}/R_{1}=1.$ 
 
Dans tous les cas, son signe est opposé à celui de $U_{e}$ ; d'où son appellation amplificateur inverseur

4. Montage suiveur

Le montage suiveur est un cas particulier du montage non-inverseur. 
 
La tension d'entrée est appliqué directement sur l'entrée non-inverseuse tandis que la rétroaction négative est totale : la tension de sortie est ramené sur l'entrée non-inverseuse.
 
 
La loi d'additivité des tensions s'écrit :
$$\boxed{U_{E}=U_{S}-\varepsilon\Rightarrow U_{E}=U_{S}-0\Rightarrow U_{E}=U_{S}}$$
 
Coefficient d'amplification en tension à vide :
$$\boxed{A=\dfrac{U_{S}}{U_{E}}=\dfrac{U_{E}}{U_{E}}\Rightarrow A=1}$$
  
L'intérêt du circuit réside entièrement dans le fait que le courant d'entrée sur l'entrée non inverseuse est nul (en modèle idéal). 
 
Il transforme un générateur « réel » en générateur « idéal » ; c'est l'adaptation des résistances pour le transfert de tension
 

Auteur: 
Sidy Mouhamed Ndiaye

Dipôles actif - 2nd S

Classe: 
Seconde
 

I. Rappels et compléments

1. Dipôle actif

Les dipôles, encore appelés générateurs, sont des dipôles grâce auxquels un courant électrique peut circuler dans un circuit.
 
Pour qu'un circuit fermé soit parcouru un courant, il faut qu'il comporte au moins un dipôle actif.

2. Convention générateur

II. Dipôles actifs linéaires

1. Caractéristique d'un dipôle actif

1.1. Définition

On appelle graphe caractéristique d'un dipôle actif le graphe de la fonction qui lie la tension $U$ entre ses bornes au courant $I$ qu'il débite dans une charge.

1.2. Étude d'une pile 

1.2.1. Montage

 
Le circuit comporte :
 
$-\ $un générateur qui fournit le courant électrique
 
$-\ $un voltmètre monté en dérivation permettant la tension aux bornes de la pile
 
$-\ $un ampèremètre qui l'intensité du courant
 
$-\ $et rhéostat permettant de régler l'intensité débitée par la pile

1.2. 2. Tracé caractéristique

A l'aide du rhéostat, on choisit une valeur de l'intensité du courant et on lit sur le voltmètre la valeur correspondante de la tension $U_{PN}.$
 
L'ensemble des couples $(I\;,\ U)$ permet de tracer la caractéristique intensité-tension.
 
L'expérience réalisée avec une pile plate a donné les valeurs suivantes
$$\begin{array}{|l|c|c|c|c|c|} \hline I(A)&0.1&0.2&0.3&0.4&0.5\\\hline U_{PN}(V)&4.35&4.2&4.0&3.9&3.85\\\hline \end{array}$$
 
 
Ce graphe est une droite, on dit que le dipôle est linéaire ;
 
La représentation de $U_{PN}=f(I)$ est une droite décroissante de la forme : $U_{PN}=al+b$ où $a$ et $b$ sont la pente et l'ordonnée à l'origine de la droite.
 
$\ast\ $Le coefficient $b$ a la dimension d'une tension : c'est la tension si $I=0\Rightarrow U_{PN}=b=E$
  
Cette tension est appelée force électromotrice (f.é.m.) et elle est notée $E.$
 
Dans l'expérience décrite : $E=4.5V$
 
$\ast\ $Le coefficient $a=\dfrac{\Delta U_{PN}}{I}$ a la dimension d'une résistance : c'est l'opposé de la résistance intérieure $a=-r$ de la pile. 
 
Ce coefficient est appelé résistance interne de la pile
 
$\begin{array}{rcl} -r &=&\dfrac{\Delta U_{PN}}{\Delta I}\\ \\ &=&\dfrac{3.85-4.5}{0.5}\\\\\Rightarrow r &=&1.3\Omega\end{array}$
 
D'où, $U_{PN}=4.5-1.31$

1.4. Loi d'Ohm

L'équation de la demi-droite obtenue est l'expression de la loi d'Ohm pour le générateur.
$$\boxed{U_{PN}=E-rI}$$
 
 
$E$ est la tension aux bornes du générateur lorsqu'il ne débite pas de courant $(I=0).$
 
$E$ est appelée la force électromotrice (f.é.m) du générateur, elle s'exprime en volts $(V).$
 
$r$ est la résistance interne de la pile $($en $\Omega).$

1.5. Intensité de court-circuit

Si par contre, on ferme l'interrupteur $K$, le dipôle actif se trouve branché sur une résistance nulle (on suppose que l'ampèremètre est idéal), on dit qu'il est en court-circuit. 
 
L'intensité qu'il débite est alors maximale, on l'appelle son intensité de court-circuit et on la désigne par la lettre $I_{CC}.$ 
 
Le point de la caractéristique correspondant à ce type de fonctionnement est le point $(U=0$ ; $I=I_{CC}).$

5. Lois d'association en série directe et série inverse

5.1. Loi d'association en série directe

5.1.1. Exemple avec trois dipôles actifs 

 
Soient trois dipôles actifs montés en série.
 
La loi d'additivité des tensions s'écrit :
 
$\begin{array}{rcl} U_{AD}=U_{AB}+U_{BC}+U_{CD}&\Rightarrow&U_{AD}=E_{1}-r_{1}I+E_{2}-r_{2}I+E_{3}-r_{3}I\\\\ &\Rightarrow&U_{AD}=E_{1}+E_{2}+E_{3}+r_{1}I+r_{2}I+r_{3}\\\\&\Rightarrow&U_{AD}=E_{1}+E_{2}+E_{3}+\left(r_{1}+r_{2}+r_{3}\right)I\\\\ &\Rightarrow&U_{AD}=E-rI\\\\ &\Rightarrow& \left\lbrace\begin{array}{rcl} E &=& E_{1}+E_{2}+E_{3}\\ r &=& r_{1}+r_{2}+r_{3} \end{array}\right. \end{array}$

5.1.2. Généralisation

Des générateurs associés en série sont équivalents à un générateur unique, dont la f.é.m. a pour valeur la somme des f.é.m. des générateurs associés, et dont la résistance interne est la somme des résistances internes.
$$\boxed{E=\sum\,E_{i}\quad\text{et}\quad\sum\,r_{i}}$$

III. Générateurs usuels

1. Source de tension idéale

Une source idéale de tension est un générateur de dont la tension aux bornes reste constante et égale à sa force électromotrice notée f.é.m. $E$ quelle que soit l'intensité qu'il débite.
 
La force électromotrice $E$ s'exprime en volt $(V).$
 
 

2. Accumulateur

On appelle « accumulateur » une pile ou une batterie rechargeable.
 
À une plus petite échelle, on se sert de piles rechargeables pour alimenter des jouets ou des baladeurs.
 
Les batteries des automobiles et des voitures électriques sont des accumulateurs.
 
 

3. Redresseurs

Les redresseurs sont des composants électriques qui convertissent un courant alternatif en courant continu. On en trouve dans la plupart des appareils électriques ou électroniques domestiques.
 
 
En effet, la tension fournie par le secteur est une tension alternative de $220\,V$ (valeur efficace), alors que la plupart des appareils domestiques fonctionnent avec du courant continu. 
 
Ceux-ci contiennent donc de quoi convertir la tension du secteur en tension continue. 
 
Par exemple, on en trouve dans l'alimentation d'un ordinateur, dans les box internet, dans les machines à laver, et bien d'autres

4. photopiles

Les photopiles se présentent sous forme de plaques légères et d'épaisseur comparable à celle d'une vitre. Lorsqu'elles sont soumises à la lumière solaire elles fournissent de l'électricité sous forme de courant continu. 
 
Il s'agit de conversion de la lumière en électricité.
 
 

5. Loi de Pouillet

5.1. Étude d'un exemple

Considérons un circuit série, sans dérivations, constitué par trois générateurs en opposition ou non, et de quatre conducteurs ohmiques
 
 
La loi des mailles s'écrit :
 
$U_{AB}+U_{BC}+U_{CD}+U_{DE}+U_{EF}+U_{EG}+U_{AG}=0$
 
$\begin{array}{lll} \Rightarrow&-E_{1}+r_{1}I+R_{1}I+-E_{2}+r_{2}I+R_{3}I+-E_{3}+r_{3}I+R_{4}I&\\\\\Rightarrow&\left(r_{1}+R_{1}+r_{2}+R_{2}+R_{3}+r_{3}+R_{4}\right)I=E_{1}+E_{2}+E_{3}&\\\\\Rightarrow &I=\dfrac{E_{1}+E_{2}+E_{3}}{r_{1}+R_{1}+r_{2}+R_{2}+R_{3}+r_{3}+R_{4}}& \end{array}$

5.2. Généralisation

Loi de Pouillet 

L'intensité du courant électrique qui parcourt un circuit série est égale à la somme algébrique des forces électromotrices des générateurs, l'ensemble étant divisé par la somme de toutes les résistances du circuit.
 
On peut écrire :
$$\boxed{I=\dfrac{\sum\,E}{\sum\,r}}$$
 

Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Travail et puissance mécaniques - 1er s

Classe: 
Première
 

Exercice 1

Un système constitué de deux blocs reliés par un fil $AB$ de masse négligeable est tiré avec une force constante $F$, d'intensité $300\,N$, sur un plan horizontal rugueux.
 
On donne $\alpha=60^{\circ}$
 

 
1. Calcul du travail de la force $\vec{F}$ lorsque le système s'est déplacé de $CD=20\,m.$ On a :
 
$\begin{array}{rcl} W_{CD}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{CD}\\ \\&=&F\times CD\cos\alpha\\ \\&=&300\times 20\cos 60^{\circ}\\ \\&=&3.0\cdot10^{3}\end{array}$
 
Ainsi, $\boxed{W_{CD}\left(\vec{F}\right)=3.0\cdot 10^{3}\;J}$
 
2. La vitesse étant constante, la tension du fil horizontal $AB$ qui relie les deux blocs est alors constante et égale à $120\,N.$
 
Calculons le travail au cours du trajet de la tension du fil appliqué au bloc $S_{2}$ et le travail de la tension du fil appliqué au bloc $S_{1}.$ Soit :
 
$\begin{array}{rcl} W_{CD}\left(\overrightarrow{T_{B}}\right)&=&\overrightarrow{T_{B}}\cdot\overrightarrow{CD}\\ \\&=&-T_{B}\times CD\\ \\&=&-120\times 20\\ \\&=&-2.4\cdot10^{3}\end{array}$
 
Donc, $\boxed{W_{CD}\left(\overrightarrow{T_{B}}\right)=-2.4\cdot 10^{3}\;J}$
 
Par ailleurs, comme $\overrightarrow{T_{B}}+\overrightarrow{T_{A}}=\vec{0}$ alors, $T_{A}=T_{B}$
 
Par suite,
 
$\begin{array}{rcl} W_{CD}\left(\overrightarrow{T_{A}}\right)&=&\overrightarrow{T_{A}}\cdot\overrightarrow{CD}\\ \\&=&T_{A}\times CD\\ \\&=&T_{B}\times CD\\ \\&=&-W_{CD}\left(\overrightarrow{T_{B}}\right)\\ \\&=&2.4\cdot 10^{3}\end{array}$
 
D'où, $\boxed{W_{CD}\left(\overrightarrow{T_{A}}\right)=2.4\cdot 10^{3}\;J}$
 
Calcul du travail total des forces de frottement exercées par le plan sur $S_{1}$ et $S_{2}.$
 
La vitesse est constante, le principe de l'inertie appliqué au système constitué du bloc $S_{1}$ et du bloc $S_{2}$ s'écrit :
 
$\begin{array}{rcl} \vec{F}+\vec{f}=\vec{0}&\Rightarrow&F\cos\alpha-f=0\\\\&\Rightarrow&f=F\cos\alpha \end{array}$
 
Par suite :
 
$\begin{array}{rcl} W_{CD}\left(\vec{f}\right)&=&\vec{f}\cdot\overrightarrow{CD}\\\\&=&-f\times CD\\\\&=&-F\times CD\cos\alpha\\\\&=&-3.0\cdot10^{3}\end{array}$
 
D'où, $\boxed{W_{CD}\left(\vec{f}\right)=-3.0\cdot10^{3}\;J}$
 
3. On envisage maintenant le cas où la vitesse n'est plus constante ; la tension du fil varie au cours du mouvement.
 
Dans ce contexte, les travaux de la tension $\overrightarrow{T_{B}}$ appliquée en $B$ et de la tension $\overrightarrow{T_{A}}$ appliquée en $A$ dépendent du chemin suivi.

Exercice 2

Alpha tire, à vitesse constante, une luge de masse $m=6.00\,kg$ sur un sol horizontal ; la distance parcourue est $d=AB=100\,m.$ 
 
La force $\vec{F}$ exercée sur la luge par l'intermédiaire de la corde est constante sur la distance $d$ ; la corde fait un angle $\alpha=30.0^{\circ}$ avec le sol. 
 
On suppose que la valeur $f$ des forces de frottements vaut le cinquième du poids $P$ de la luge.
 
1. Inventaire des forces qui s'exercent sur le système $\{\text{Alpha+luge}\}.$
 

 
2. Calcul de la valeur de la force de traction qu'exerce Alpha sur sa luge.
 
Système : $\{\text{Alpha} + \text{luge}\}$
 
Bilan des forces appliquées : $\vec{F}\ :\ \vec{P}\ :\ \vec{R}\ :\ \vec{f}$
 
Le système évolue à vitesse constante, le principe de l'inertie s'écrit :
$$\vec{F}+\vec{P}+\vec{R}+\vec{f}=\vec{0}$$
En projetant la relation vectorielle suivant l'axe des $x$, il vient :
 
$\begin{array}{rcl} F\cos\alpha+0+0-f=0&\Rightarrow&F\cos\alpha=f\\ \\&\Rightarrow&F =\dfrac{f}{\cos\alpha}\quad\text{or }f=\dfrac{P}{5}=\dfrac{mg}{5}\\ \\&\Rightarrow&F=\dfrac{mg}{5\cos\alpha}\\ \\&\Rightarrow&F=\dfrac{6.00\times 9.81}{5\cos 30.0^{\circ}}\\ \\&\Rightarrow&F=13.6\;N \end{array}$
 
D'où, $\boxed{F=13.6\;N}$
 
3. Calcul du travail de chacune des forces le long du trajet.
 
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&\overrightarrow{F}\cdot\overrightarrow{AB}\\\\&=&Fd\cos\alpha\\\\&=&13.6\times 100\cos 30.0^{\circ}\\\\&=&11.8\cdot 10^{2}\end{array}$
 
D'où, $\boxed{W_{AB}\left(\vec{F}\right) =11.8\cdot 10^{2}\;J}$
 
$W_{AB}\left(\vec{P}\right)=\vec{P}\cdot\overrightarrow{AB}=0$
 
Or, $\overrightarrow{P}\perp\overrightarrow{AB}$ donc, $\vec{P}\cdot\overrightarrow{AB}=0$
 
D'où, $\boxed{W_{AB}\left(\vec{P}\right)=0\;J}$
 
$\begin{array}{rcl} W_{AB}\left(\vec{f}\right)&=&\vec{f}\cdot\overrightarrow{AB}\\\\&=&-fd\\\\&=&-\dfrac{P}{5}d\\\\&=&-\dfrac{mg}{5}d\\\\&=&-\dfrac{6.00\times 9.81}{5}\times 100\\\\&=&-11.8\cdot 10^{2}J \end{array}$
 
Ainsi, $\boxed{ W_{AB}\left(\vec{f}\right) =-11.8\cdot 10^{2}\;J}$
 
$W_{AB}\left(\vec{R}\right)=\vec{R}\cdot\overrightarrow{AB}=0\;J$ car $\vec{R}\perp\overrightarrow{AB}$
 
Alpha aborde maintenant la piste de luge (de longueur $l=100\,m$) qui forme un plan incliné d'un angle $\beta=15.0^{\circ}$ avec l'horizontale. 
 
Elle tire toujours rectilignement et à vitesse constante ; l'angle entre la corde et la pente est toujours de $30.0^{\circ}.$
 
On suppose que la force de frottements garde la même valeur $f$ que précédemment.

 
 
4. Le travail de la somme des forces est nul.
 
En effet,
 
$\begin{array}{rcl} \vec{v}=\overrightarrow{cte}&\Rightarrow&\vec{F}+\vec{P}+\vec{R}+\vec{f}=\vec{0}\\ \\&\Rightarrow&\vec{F}\cdot\overrightarrow{AB}+\vec{P}\cdot\overrightarrow{AB}+\vec{R}\cdot\overrightarrow{AB}=\vec{0}\cdot\overrightarrow{AB}\\\\&\Rightarrow&W_{AB}\left(\vec{F}\right)+W_{AB}\left(\vec{P}\right)+W_{AB}\left(\vec{R}\right)+W_{AB}\left(\vec{f}\right)=0\end{array}$
 
5. Donnons l'expression du travail de chacune des forces s'exerçant sur la luge.
 
$W_{AB}\left(\vec{F}\right)=\vec{F}\cdot\overrightarrow{AB}=Fl\cos\beta$
 
$W_{AB}\left(\vec{P}\right)=\vec{P}\cdot\overrightarrow{AB}=-Pl\sin\beta$
 
$W_{AB}\left(\vec{R}\right)=\vec{R}\cdot\overrightarrow{AB}=0$ car $\vec{R}\perp\overrightarrow{AB}$
 
$W_{AB}\left(\vec{f}\right)=\vec{f}\cdot\overrightarrow{AB}=-fl$
 
6. Comparons les valeurs de la force de traction sur la partie plane et sur la pente.
 
Sur la partie pente :
 
$\begin{array}{rcl} W_{AB}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{AB}\\\\&=&Fl\cos\beta\\\\&=&13.6\times 100\times\cos 15.0^{\circ}\\\\&=&13.1\cdot 10^{2} \end{array}$
 
Donc, sur la pente : $W_{AB}\left(\vec{F}\right)=13.1\cdot 10^{2}\;J$
 
Sur la partie rectiligne : $W_{AB}\left(\vec{F}\right)=11.8\cdot 10^{2}\;J$
 
Sur la partie pente, Alpha fournit plus d'efforts. 
 
C'est pourquoi $W_{AB}\left(\vec{F}\right)=13.1\cdot 10^{2}\;J>W_{AB}\left(\vec{F}\right)=11.8\cdot 10^{2}\;J$
 
7. Le déplacement est effectué en $2.0\,min.$ 
 
Calculons la puissance moyenne du travail du poids.
 
On a :
 
$\begin{array}{rcl} P_{m}\left(\vec{P}\right)&=&\dfrac{W_{AB}\left(\vec{P}\right)}{\Delta t}\\\\&=&\dfrac{-Pl\sin\beta}{\Delta t}\\\\&=&\dfrac{-6.00\times 9.81\times 100\times\sin 15.0}{2.0\times 60}\\\\&=&-12.7\end{array}$
 
D'où, $\boxed{P_{m}\left(\vec{P}\right)=-12.7\;W}$

Exercice 3

Un chariot de masse $M=20\,Kg$ tiré le long d'une piste horizontale $AB$ de longueur $L=4\,m$ par une force $\vec{F}$ inclinée d'un angle $\alpha=60^{\circ}$ par rapport au déplacement et de valeurs $F=120\,N$ (voir fig). 
 
On néglige tous les frottements.
 
Le long du trajet $AB$, le chariot est tiré avec une vitesse constante $=1\,m\cdot s^{-1}.$
 
1. Expression et calcul du travail effectué par $\vec{F}$ le long du trajet $AB.$
 
On a :
 
$\begin{array}{rcl} W_{AB}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{AB}\\\\&=&Fl\cos\alpha\\\\&=&120\times 4\times\cos 60^{\circ}\\\\&=&240\end{array}$
 
D'où, $\boxed{W_{AB}\left(\vec{F}\right) =240\;J}$
 
2. Expression et calcul de la puissance moyenne développée par cette force
 
On a :
 
$\begin{array}{rcl} P_{m}\left(\vec{F}\right)&=&\vec{F}\vec{v}\\\\&=&Fv\\\\&=& 120\times 1\\\\&=&-120\end{array}$
 
Ainsi, $\boxed{P_{m}\left(\vec{F}\right)=-120\;W}$
 
 
3. En arrivant au point $B$, on supprime la force motrice $\vec{F}$ et le chariot aborde une piste $BC$ de longueur $L'$ incliné par rapport à l'horizontale passant par $C$ d'un angle $\beta=30^{\circ}.$ 
 
Le long du trajet $BC$, le chariot est soumis à des forces de frottement équivalente à une force $\vec{f}$ constamment opposé au déplacement et de valeur $f=30\,N.$ 
 
La différence d'altitude entre les points $B$ et $C$ est $h=2\,m.$
 
a) Expression et calcul du travail du poids $\vec{P}$ du chariot.
 
Soit :
 
$\begin{array}{rcl} W_{BC}\left(\vec{P}\right)&=&\vec{P}\cdot\overrightarrow{BC}\\\\&=&Mgh\\\\&=&20\times 10\times 2\\\\ &=&4\cdot 10^{2}\end{array}$
 
Alors, $\boxed{W_{AB}\left(\vec{P}\right)=4\cdot 10^{2}\;J}$
 
b) Expression et calcul du travail de la force de frottement.
 
On a :
 
$\begin{array}{rcl} W_{BC}\left(\vec{f}\right) &=&\vec{f}\cdot\overrightarrow{BC}\\\\&=&-Fl \\\\&=&-f\dfrac{h}{\sin\beta}\\\\&=&-30\times\dfrac{2}{\sin 30^{\circ}}\\\\ &=&4-120\end{array}$
 
D'où, $\boxed{W_{AB}\left(\vec{f}\right) =4-120\;J}$
 
c) Expression et calcul du travail de la réaction $\vec{R}$ du plan
 
Soit : $W_{AB}\left(\vec{R}\right)=\vec{R}\cdot\overrightarrow{AB}=0$ car $\vec{R}\perp\overrightarrow{AB}$

Exercice 4

Une barre est maintenue horizontale par l'intermédiaire d'un fil métallique et un fil de coton fixés en son milieu. 
 
Les deux fils sont verticaux, le fil métallique est au-dessus de la barre, le fil de coton en dessous. 
 
Le fil métallique a une constante de torsion $C=4.0\cdot10^{-2}N\cdot m\cdot rad^{-1}.$ 
 
Le fil de coton exerce un couple négligeable.
 
1. Schéma du dispositif.
 
 
2. Calcul du travail du couple de torsion dans les situations suivantes :
 
2.1. La barre écartée de $90^{\circ}$ par rapport à sa position d'équilibre. Alors, on a :
 
$\begin{array}{rcl} W_{C}&=&-C\left(\mathcal{g_{f}}-\mathcal{g_{i}}\right)\\\\&=&-4.0\cdot 10^{-2}\left(\dfrac{\pi}{2}-0\right)\\\\&=&-6.28\cdot 10^{-2}\end{array}$
 
Donc, $\boxed{W_{C}=-6.28\cdot 10^{-2}\;J}$
 
2.2 Lorsque la barre passe de la position précédente à la position où elle fait un angle de $45^{\circ}$ par rapport à sa position d'équilibre.
 
Soit alors :
 
$\begin{array}{rcl} W_{C}&=&-C\left(\mathcal{g}_{f}-\mathcal{g}_{i}\right)\\\\&=&-4.0\cdot 10^{-2}\left(\dfrac{\pi}{4}-\dfrac{\pi}{2}\right)\\\\&=& 3.14\cdot 10^{-2}\end{array}$
 
D'où, $\boxed{W_{C}=3.14\cdot 10^{-2}\;J}$
 
2.3 Lorsque la barre passe de cette dernière position à la position où elle est écartée d'un angle de $30^{\circ}$ de l'autre côté de sa position d'équilibre.
 
$\begin{array}{rcl} W_{C} &=&-C\left(\mathcal{g}_{f}-\mathcal{g}_{i}\right)\\\\&=&-4.0\cdot 10^{-2}\left(-\dfrac{\pi}{6}-\dfrac{\pi}{4}\right) \\\\&=&5.24\cdot 10^{-2}\end{array}$
 
Ainsi, $\boxed{W_{C}=5.24\cdot 10^{-2}\;J}$

Exercice 5

Pour hisser, à vitesse constante, un corps sur une plateforme on utilise un treuil entraîné par un moteur (fig 1).
 
La masse du corps $M=1\,000\;kg$, la hauteur $h=2\;m$ et les frottements créent une force $f$ de direction opposée au déplacement. 
 
La force motrice $F=10\,000\;N$ pour un angle $\alpha=30^{\circ}.$
 

 
1. Calculons la force résistante $\left(\vec{F}'\right)$ présentée par le poids : $F'=P\cdot\sin\alpha$ (sens opposé au déplacement) et la force de frottement.
 
Soit :
 
$\begin{array}{rcl}\vec{F'} &=& P\cdot\sin\alpha\\\\&=&Mg\sin\alpha\\\\&=&1\,000\times 10\times\sin 30^{\circ}\\\\&=&5.0\cdot 10^{3}\end{array}$
 
Donc, $\boxed{F'=5.0\cdot 10^{3}\;N}$
 
Le corps se déplace à vitesse constante, le principe de l'inertie s'écrit :
$$\vec{F}+\vec{P}+\vec{R}+\vec{f}=\vec{0}$$
En projetant suivant le sens de la force motrice, il vient :
 
$\begin{array}{rcl} F-F'+0-f=0&\Rightarrow& f=F-F'\\\\&\Rightarrow&f=1\,000-5.0\cdot 10^{5}\\\\&\Rightarrow&f=5.0\cdot 10^{5}\end{array}$
 
D'où, $\boxed{f=5.0\cdot 10^{5}\;N}$
 
2. Calculons le travail de la force $\vec{F}$ et la puissance correspondante si la masse se déplace à $0.2\;m/s.$
 
Soit :
 
$\begin{array}{rcl} W\left(\vec{F}\right) &=&F\dfrac{h}{\sin\alpha}\\\\&=&10\,000\times\dfrac{2}{\sin 30^{\circ}}\\\\&=&4.0\cdot 10^{4}\end{array}$
 
Alors, $\boxed{W\left(\vec{F}\right)= 4.0\cdot 10^{4}\;J}$
 
Pour la puissance, on obtient :
 
$\begin{array}{rcl} P\left(\vec{F}\right)&=&\vec{F}\cdot\vec{v}\\\\&=&Fv\\\\&=&10\,000\times 0.2\\\\&=&2.0\cdot 10^{3}\end{array}$
 
Ainsi, $\boxed{P\left(\vec{F}\right)=2.0\cdot 10^{3}\;W}$
 
Le treuil ayant un diamètre de $20\;cm$ et un rendement de $0.85$
 
3. Calculons :
 
$-\ $ la puissance mécanique du moteur nécessaire
 
On a :
 
$\begin{array}{rcl} \dfrac{P\left(\vec{F}\right)}{P_{M}}=0.85&\Rightarrow&P_{M}=\dfrac{P\left(\vec{F}\right)}{0.85}\\ \\&\Rightarrow&P_{M}=\dfrac{2.0\cdot 10^{3}}{0.85}\\\\&\Rightarrow&P_{M}=2.4\cdot 10^{3}\end{array}$
 
Donc, $\boxed{P_{M}=2.4\cdot 10^{3}\;W}$
 
$-\ $ la vitesse angulaire de rotation,
 
Soit :
 
$\begin{array}{rcl} \omega&=&\dfrac{v}{r}\\\\&=&\dfrac{v}{\dfrac{d}{2}}\\\\&=&\dfrac{2v}{d}\\\\&=&\dfrac{2\times 0.2}{20\cdot 10^{-2}}\\\\&=&20\end{array}$
 
Ainsi, $\boxed{\omega=20\;rad\cdot s^{-1}}$
 
$-\ $ la fréquence de rotation $(tr/min)$
 
On a :
 
$\begin{array}{rcl} \omega=2\pi N&\Rightarrow&N=\dfrac{\omega}{2\pi}\\\\&\Rightarrow&N=\dfrac{20}{2\pi}\\\\&\Rightarrow&N=3\;Hz\end{array}$
 
En convertissant, on obtient :
 
$N=3\;Hz=3\times 60=180\;tr/mn$
 
D'où, $\boxed{N=180\;tr/mn}$
 
$-\ $ le moment du couple moteur
 
Soit :
 
$\begin{array}{rcl} P_{M}=M_{C}\omega&\Rightarrow&M_{C}=\dfrac{P_{M}}{\omega}\\\\&\Rightarrow&M_{C}=\dfrac{2.4\cdot 10^{3}}{20}\\\\&\Rightarrow&M_{C}=1.2\cdot 10^{2}Nm \end{array}$
 
Par suite, $\boxed{M_{C}=1.2\cdot 10^{2}\;Nm }$

Exercice 6

Une tige de cuivre supporte deux boules de fer $(m_{1}=m_{2}=m).$ 
 
L'ensemble est mobile sans frottement autour d'un axe horizontal $\Delta$, qui est perpendiculaire en $O$, au plan de la figure. 
 
Le centre d'inertie de la barre de masse $(M)$ est à la distance $OG=a$ de l'axe.
 
Un aimant attire la boule de fer en $A_{1}$, avec une force horizontale $F_{1}$ ; un deuxième aimant attire la boule de fer $A_{2}$ avec une force $F_{2}.$
 
On pose $OA_{1}=\ell_{1}\ $ et $\ OA_{2}=\ell_{2}$
 
1. La tige fait un angle $\alpha$ avec la verticale.
 
a) Représentons les forces extérieures appliquées sur le système (tige + boules)
 
 
b) Exprimons littéralement les moments de ces forces par rapport à l'axe $\Delta$ en fonction des données.
 
On a :
 
$\begin{array}{rcl} M_{\Delta}\left(\vec{F}_{1}\right)&=&-F_{1}OA_{1}\cos\alpha\\\\&=&-F_{1}l_{1}\cos\alpha \end{array}$
 
Soit : $\boxed{M_{\Delta}\left(\vec{F}_{1}\right)=-F_{1}l_{1}\cos\alpha}$
 
On a :
 
$\begin{array}{rcl} M_{\Delta}\left(\vec{F}_{2}\right)&=&-F_{2}OA_{2}\cos\alpha\\\\&=& -F_{2}l_{2}\cos\alpha\end{array}$
 
Soit alors : $\boxed{M_{\Delta}\left(\vec{F}_{2}\right)=-F_{2}l_{1}\cos\alpha}$
 
On a :
 
$\begin{array}{rcl} M_{\Delta}\left(\vec{P}\right)&=&POG\cos\alpha\\\\&=&Mga\cos\alpha \end{array}$
 
Ainsi, $\boxed{M_{\Delta}\left(\vec{P}\right)=Mga\cos\alpha}$
 
Soit :
 
$\begin{array}{rcl} M_{\Delta}\left(\vec{P}_{1}\right)&=&-P_{1}OA_{1}\sin\alpha\\\\&=& -mgl_{1}\sin\alpha\end{array}$
 
Donc, $\boxed{M_{\Delta}\left(\vec{P}_{1}\right)=-mgl_{1}\sin\alpha}$
 
On a :
 
$\begin{array}{rcl} M_{\Delta}\left(\vec{P}_{2}\right)&=&P_{2}OA_{2}\sin\alpha\\\\&=& mgl_{2}\sin\alpha\end{array}$
 
D'où, $\boxed{M_{\Delta}\left(\vec{P}_{2}\right)=mgl_{2}\sin\alpha}$
 
Enfin, $M_{\Delta}\left(\vec{R}\right)=0$
 
2. Pour la valeur de $=\alpha=20^{\circ}$, l'ensemble est en équilibre. 
 
Déterminons alors l'intensité commune $F$ des forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$
 
Soit :
$$M_{\Delta}\left(\vec{F}_{1}\right)+M_{\Delta}\left(\vec{F}_{2}\right)+M_{\Delta}\left(\vec{P}\right)+M_{\Delta}\left(\vec{P}_{1}\right)+M_{\Delta}\left(\vec{P}_{2}\right)+M_{\Delta}\left(\vec{R}\right)=0$$
Ce qui donne : $F_{1}l_{1}\cos\alpha-F_{2}l_{2}\cos\alpha+Mga\cos\alpha-mgl_{1}\sin\alpha+mgl_{2}\sin\alpha+0=0$
 
Or, $F_{1}=F_{2}=F$ donc, $Fl_{1}\cos\alpha-Fl_{2}\cos\alpha+Mga\cos\alpha+mg\sin\alpha(l_{2}-l_{1})=0$
 
$\Rightarrow\ F\cos\alpha(l_{1}-l_{2})+Mga\cos\alpha+mg\sin\alpha(l_{2}-l_{1})=0$
 
$\Rightarrow\ F=\dfrac{Mga\cos\alpha+mg\sin\alpha\times\left(l_{2}-l_{1}\right)}{\left(l_{2}-l_{1}\right)\cos\alpha}$
 
$\Rightarrow\ F=9.8\dfrac{300\cdot 10^{-3}\times 6.0\cos 20^{\circ}+100\cdot 10^{-3}\times\sin 20^{\circ}\times(24-12)}{(12+24)\cos 20^{\circ}}$
 
$\Rightarrow F=0.61\;N$
 
D'où, $\boxed{F=0.61\;N}$
 
3. Détermination du travail effectué par chaque force pendant deux tours $\theta=2\pi$
 
Soit :
 
$\begin{array}{rcl} W\left(\vec{F}\right)&=&M_{\Delta}\left(\vec{F}\right)\theta\\\\&=&F\left(l_{1}+l_{2}\right)\times 2\pi\\\\&=&0.61(12+24)10^{-2}\times 2\pi\\\\&=&1.38\end{array}$
 
Donc, $\boxed{W\left(\vec{F}\right)= 1.38\;J}$
 
On a :
 
$\begin{array}{rcl} W\left(\vec{P}\right)&=&M_{\Delta}\left(\vec{P}\right)\theta\\\\&=&Mga\cos\alpha \times 2\pi\\\\&=&300\cdot 10^{-2}\times 9.8\times6.0\cdot 10^{-2}\cos 20^{\circ}\times 2\pi\\\\&=& 1.04\end{array}$
 
Donc, $\boxed{W\left(\vec{P}\right)=1.04\;J}$
 
Soit :
 
$\begin{array}{rcl} W\left(\vec{P}_{1}\right)&=&M_{\Delta}\left(\vec{P}_{1}\right)\theta\\\\&=&-100\cdot 10^{-3}\times 9.8\times 12\cdot 10^{-2}\sin 20^{\circ}\times 2\pi\\\\&=&0.25\end{array}$
 
Ainsi, $\boxed{W\left(\vec{P}_{1}\right)=0.25\;J}$
 
On a :
 
$\begin{array}{rcl} W\left(\vec{P}_{2}\right) &=& M_{\Delta}\left(\vec{P}_{2}\right)\theta\\\\&=& 100\cdot 10^{-3}\times 9.8\times 24\cdot 10^{-2}\sin 20^{\circ}\times 2\pi\\\\&=&0.51\end{array}$
 
Donc, $\boxed{W\left(\vec{P}_{2}\right)=0.51\;J}$
 
Soit :
 
$\begin{array}{rcl} W\left(\vec{R}\right) &=&M_{\Delta}\left(\vec{R}\right)\theta\\\\ &=&0\times 2\pi\\\\&=&0\end{array}$
 
D'où, $\boxed{W\left(\vec{R}\right)=0\;J}$

Exercice 7

Un solide ponctuel $S$, de masse $m$, se déplace dans un plan vertical le long d'un trajet $ABCD$ qui comporte deux phases.
 
$-\ $ Une partie horizontale $AB$ rectiligne de longueur $8\;m.$ 
 
Le long de cette partie, le solide est soumis à une force constante $\vec{F}$, faisant un angle $\alpha=60^{\circ}$ avec l'horizontale et développant une puissance $P=6\;W$ en plus d'une force de frottement $\vec{f}$, opposée au déplacement de valeur constante $f=3\;N.$
 
$-\ $ Une demi sphère $BCD$, de centre $O$ et de rayon $R=0.5\;m$ où le solide est soumis uniquement à son poids $\vec{P}.$
 

 
1. Sachant que pendant la partie $AB$ le mouvement est rectiligne uniforme de vitesse $V=2\;m\cdot s^{-1}$,
 
a) Exprimons la puissance moyenne $P$ développée par $\vec{F}$ en fonction de $F\;,\ V\ $ et $\ \alpha.$
 
Soit :
$$P_{m}\left(\vec{F}\right)=\vec{F}\cdot\vec{V}=FV\cos\alpha$$
b) Déduction de la valeur de la force $F.$
 
On a :
 
$\begin{array}{rcl} P_{m}\left(\vec{F}\right)=FV\cos\alpha&\Rightarrow&F=\dfrac{P_{m}\left(\overrightarrow{F}\right)}{V\cos\alpha}\\\\&\Rightarrow&F=\dfrac{6}{2\times\cos 60^{\circ}}\\\\&\Rightarrow&F =6\;N\end{array}$
 
Donc, $\boxed{F=6\;N}$
 
c) Calcul du travail de la force $\vec{F}$ pendant le déplacement $AB.$
 
Soit :
 
$\begin{array}{rcl} W_{AB}\left(\vec{F}\right)&=&\vec{F}\cdot\overrightarrow{AB}\\\\&=&F\cdot AB\cos\alpha\\\\&=& 6\times 8\times\cos 60^{\circ}\\\\&=&24\end{array}$
 
D'où, $\boxed{W_{AB}\left(\vec{F}\right) =24\;J}$
 
2. Détermination du travail de la force de frottement $\vec{f}$ au cours du déplacement de $AB.$
 
On a :
 
$\begin{array}{rcl} W_{AB}\left(\vec{f}\right)&=&\vec{f}\cdot\overrightarrow{AB}\\\\ &=& -f\cdot AB\cos\alpha\\\\ &=& -3\times 8\\\\&=&-24\end{array}$
 
Ainsi, $\boxed{W_{AB}\left(\vec{f}\right) =-24\;J}$
 
3. Arrivant au point $B$, on annule les forces $\vec{F}\ $ et $\ \vec{f}.$
 
Sachant que le travail du poids de $S$ lorsqu'il glisse de $B$ vers $C$ est $W_{B\rightarrow C}\left(\vec{P}\right)=0.5\;J$
 
a) Déterminons la masse du solide $S.$
 
On a :
 
$\begin{array}{rcl} W_{B\rightarrow C}\left(\overrightarrow{P}\right)=mgR&\Rightarrow&m=\dfrac{W_{B\rightarrow C}\left(\overrightarrow{P}\right)}{gR}\\\\&\Rightarrow&m=\dfrac{0.5}{10\times 0.5}\\\\&\Rightarrow&m=0.1\;kg \end{array}$
 
D'où, $\boxed{m=0.1\;kg}$
 
b) Donnons l'expression du travail du poids de $S$ lorsqu'il passe de $B$ vers $E$ en fonction de $m\;,\ g\;,\ R\ $ et $\ \beta.$
 
Soit : $W_{B\rightarrow E}\left(\vec{P}\right)=mgR\sin\beta$
 
Calcul de sa valeur : $W_{B\rightarrow E}\left(\vec{P}\right)= 0.1\times 10\times 0.5\times\sin 30^{\circ}=0.25$
 
Ainsi, $\boxed{W_{B\rightarrow E}\left(\vec{P}\right)=0.25\;J}$
 
c) Déduisons du travail du poids de $S$ lors du déplacement de $E$ vers $C.$
 
Soit :
 
$\begin{array}{rcl} W_{E\rightarrow C}\left(\vec{P}\right)&=&W_{B\rightarrow C}\left(\vec{P}\right)-W_{B\rightarrow E}\left(\vec{P}\right)\\\\&=&mgR-mgR\sin\beta\\\\&=&0.1\times 10\times 0.5(1-\sin 30^{\circ})\\\\&=&0.25\end{array}$
 
Alors, $\boxed{W_{E\rightarrow C}\left(\vec{P}\right)=0.25\;J}$
 
4. Détermination du travail du poids de $S$ lors du déplacement de $C$ vers $D.$
 
Soit : $W_{C\rightarrow D}\left(\vec{P}\right)=-W_{B\rightarrow C}\left(\vec{P}\right)$
 
Donc, $\boxed{W_{C\rightarrow D}\left(\vec{P}\right)=-0.5\;J}$
 

 

Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Les alcanes - 1er s

Classe: 
Première
 

Exercice 1

1. Nommons les alcanes suivants
 
$2-$méthylpropane ou méthylpropane
 
$2\;,\ 2\;,\ 4-$trimétylpentane
 
$4-$éthyl$-3-$méthylnonane
 
$5\;,\ 7-$diéthyl$-2\;,\ 4\;,\ 5-$triméthylnonane
 
$3-$méthylhéptane
 
Pentane
 
$4$éthyl$-3-$méthylhexane
 
$6-$éthyl$-2\;,\ 3-$diméthyldécane
 
$1\;,\ 6-$dibromo$-2-$butyl$-4-$chloro$-8-$éthyl$-3-$iodocyclooctane
 
$1-$bromo$-3-$butyl$-4-$chioro$-6-$propyjhéptane
 
2. Écriture des formules semi développées des hydrocarbures suivants :
 
2.1. $\ 3-$éthyl$-2-$methylhexane :
 
$CH_{3}-CH_{2}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH\left(CH_{3}\right)-CH_{3}$
 
2.2. $\ 2\;,\ 3-$dimethylpentane
 
$CH_{3}-CH_{2}-CH\left(CH_{3}\right)-CH\left(CH_{3}\right)-CH_{3}$
 
2.3. $\ 4-$éthyl$-2\;,\ 5-$méthylheptane
 
$CH_{3}-CH\left(CH_{3}\right)-CH\left(C_{2}H_{5}\right)-CH_{2}-CH\left(CH_{3}\right)-CH_{3}$
 
2.4. $\ 3\;,\ 4-$diéthylhexane
 
$CH_{3}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH\left(C_{2}H_{5}\right)-CH_{2}-CH_{3}$
 
2.5. $\ 3-$éthyl$-2\;,\ 3-$diméthylhexane
 
2.6. $\ 2\;,\ 2-$diméthyl$-5\;,\ 6-$dipropylnonane
 
2.7. $\ 4-$éthyl$-3-$méthyl$-5-$propyloctane
 
2.8. $\ 2\;,\ 2\;,\ 3\;,\ 3-$tétraméthylpentane
 
3. Les formules semi-développées qui correspondent aux noms suivants.
 
a) $4-$propyldécane
 
$CH_{3}-CH_{2}-CH_{2}-CH\left(C_{3}H_{7}\right)-\left(CH_{2}\right)_{5}-CH_{3}$
 
b) $3-$éthyl $4-$méthylnonane
 
$CH_{3}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH\left(CH_{3}\right)-\left(CH_{2}\right)_{4}-CH_{3}$
 
c) $2\;,\ 2-$diméthylbutane
 
$CH_{3}-CH\left(CH_{3}\right)_{2}CH_{2}-CH_{3}$
 
d) $4-$éthylnonane
 
$CH_{3}-CH_{2}-CH_{2}-CH\left(C_{2}H_{5}\right)-\left(CH_{2}\right)_{4}-CH_{3}$
 
e) $4\;,\ 4\;,\ 6\;,\ 6-$tétraméthyloctane
 
$CH_{3}-CH_{2}-CH_{2}-CH\left(CH_{3}\right)_{2}-CH_{2}-CH_{2}-CH\left(CH_{3}\right)_{2}-CH_{3}$
 
Le nom est incorrect ; le nom correct est $2\;,\ 2\;,\ 5\;,\ 5-$tétraméthyloctane
 
f) $1\;,\ 3-$diéthylpropane
 
$CH_{3}\left(C_{2}H_{5}\right)_{2}-CH_{2}-CH_{3}\left(C_{2}H_{5}\right)_{2}$
 
Le nom est incorrect ; le nom correct est $4-$éthyl$-5-$méthyl octane
 
h) $4-$méthyl$-1\;,\ 3-$diéthylpentane
 
$CH_{3}-CH\left(CH_{3}\right)-CH\left(C_{2}H_{5}\right)-CH_{2}-CH_{2}\left(C_{2}H_{5}\right)$
 
Le nom est incorrect ; le nom correct est le $2-$méthyl$-3-$méthylheptane
 
i) $2-$éthyl$-3-$méthyl$-4-$propylnonane
 
$CH_{3}-CH\left(C_{2}H_{5}\right)-CH\left(CH_{3}\right)-CH\left(C_{3}H_{7}\right)-\left(CH_{2}\right)_{4}-CH_{3}$
 
j) $2\;,\ 3\;,\ 4-$triméthylpentane
 
$CH_{3}-CH\left(CH_{3}\right)-CH\left(CH_{3}\right)-CH\left(CH_{3}\right)-CH_{3}$
 
k) $2-$méthylbutane
 
$CH_{3}-CH\left(CH_{3}\right)-CH_{2}-CH_{3}$
 
l) $3\;,\ 5-$diméthylnonane
 
$CH_{3}-CH_{2}-CH\left(CH_{3}\right)-CH_{2}-CH\left(CH_{3}\right)-\left(CH_{2}\right)_{3}-CH_{3}$

Exercice 2

1.1. Des isomères sont des corps de même formule brute mais dont les formules développées sont différentes. 
 
Les molécules ont donc des structures différentes et des propriétés différentes, parfois même très différentes.
 
1.2. Les isomères du pentane sont :
 
$CH_{3}-CH_{2}-CH_{2}-CH_{2}-CH_{3}$
Pentane
 
$2-$méthylbutane
 
$2\;,\ 2-$diméthylpropane ou diméthylpropane
 
2. La molécule proposée :
 
est du $2\;,\ 3-$diméthylpentane.
 
3.
 
3.1. La formule générale d'un alcane à chaîne ouverte et à $n$ atomes de carbone est : $C_{n}H_{2n+2}.$
 
3.2. La masse molaire $M$ de l'alcane peut s'exprimer en fonction de $n$ :
 
$M=n\cdot M_{C}+(2n+2)\cdot M_{H}.$
 
$M=n\times 12+(2n+2)\times 1$
 
$\boxed{M=14n+2}$
 
3.3. Pour l'alcane considéré la masse molaire est $114\,g\cdot mol^{-1}.$
 
On peut donc écrire :
 
$14n+2=114$
 
$\Rightarrow 14n=112$
 
d'où $n=8$ 
 
La formule brute de l'alcane est $C_{8}H_{18}.$
 
3.4. L'alcane de formule $C_{8}H_{18}$ est l'octane

Exercice 3

1. Rappel de la définition d'un hydrocarbure aliphatique.
 
Un hydrocarbure aliphatique est un composé organique constitué d'atomes de carbone et d'hydrogène à chaine ouverte.
 
2. Équation de la réaction.
 
$C_{x}H_{y}+\left(x+\dfrac{y}{4}\right)O_{2}\rightarrow x CO_{2}+\dfrac{y}{2}H_{2}O$
 
3. a) Calcul du nombre de moles de $(A)$ présent dans l'échantillon
 
$n_{A}=\dfrac{m_{A}}{M_{A}}=\dfrac{0.72}{72}\Rightarrow n_{A}=0.01\,mol$
 
b) Montrons que $(A)$ a pour formule brute $C_{5}H_{12}.$
 
Déterminons le nombre de dioxyde de carbone et de l'eau
 
$n_{CO_{2}}=\dfrac{V_{CO_{2}}}{V_{M}}=\dfrac{1.2}{24}\Rightarrow n_{CO_{2}}=0.05\,\text{mol}$
 
$n_{H_{2}O}=\dfrac{m_{H_{2}O}}{M_{H_{2}O}}=\dfrac{1.08}{18}\Rightarrow n_{A}=0.06\,\text{mol}$
D'après le bilan molaire :
 
$\begin{array}{rcl} n_{A}=\dfrac{n_{CO_{2}}}{x}=\dfrac{n_{H_{2}O}}{\dfrac{y}{2}}&\Rightarrow & \left\lbrace\begin{array}{lcl}\dfrac{n_{H_{2}O}}{\dfrac{y}{2}} &=&n_{A}\\\\\dfrac{n_{CO_{2}}}{x} &=&n_{A} \end{array}\right.\\\\&\Rightarrow &\left\lbrace\begin{array}{lcl}\dfrac{2\times 0.06}{0.01} &=&y\\\\\dfrac{0.05}{0.01} &=&x \end{array}\right.\\\\&\Rightarrow &\left\lbrace\begin{array}{lcl}y &=&12\\\\\ x &=&5 \end{array}\right.\\\\ &\Rightarrow & C_{5}H_{12} \end{array}$
 
4. Formules semi - développées des isomères de $(A)$ et leur nom respectif.
 
 
 
 

Exercice 4

1. Équation-bilan de la réaction de combustion en fonction de $x$ et $y.$
 
$C_{x}+H_{y}+\left(x+\dfrac{y}{4}\right)\;O_{2}\ \rightarrow\ xCO_{2}\ +\ \dfrac{y}{2}H_{2}O$
 
2. Le volume de dioxygène en excès
 
$V_{5}=V_{3}-V_{4}+65-40$
 
$\Rightarrow V_{5}=25\,cm^{3}$
 
Déduction du volume de dioxygène réagi.
 
$V_{6}=V_{2}-V_{5}+90-25$
 
$\Rightarrow V_{6}=65\,cm^{3}$
 
3. Montrons que la formule moléculaire brute de l'hydrocarbure $A$ est $C_{4}H_{10}.$
 
D'après le bilan volumique :
 
$\begin{array}{rcl} V_{1} = \dfrac{V_{2}}{x}=\dfrac{V_{6}}{x+\dfrac{y}{4}}&\Rightarrow&\left\lbrace \begin{array}{lcl} V_{1} &=& \dfrac{V_{2}}{x} \\ V_{1} &=&\dfrac{V_{6}}{x+\dfrac{y}{4}} \end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} x&=&\dfrac{V_{2}}{V_{1}}\\ x+\dfrac{y}{4} &=&y\dfrac{V_{6}}{V_{1}} \end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} x &=&\dfrac{40}{10}\\ x+\dfrac{y}{4} &=&\dfrac{65}{10} \end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} x&=&\dfrac{40}{10}\\ y&=&\left(\dfrac{65}{10}-x\right)\end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} y&=& 4\\x&=&10 \end{array}\right.\\\\&\Rightarrow&\boxed{C_{4}H_{10}}\end{array}$
 
4. Formule semi-développée exacte et nom de l'alcane $A$ sachant qu'il contient une chaine carbonée ramifiée.
$$CH_{3}-CH\left(CH_{3}\right)-CH_{3}$$
 
5.1 Rappel des conditions expérimentales : il faut la lumière comme catalyseur et utiliser une solution de sel
 
Équation-bilan de la réaction en utilisant les formules brutes.
 
$C_{4}H_{10}\ +\ Cl_{2}\ \rightarrow\ C_{4}H_{9}Cl\ +\ HCl$
 
5.2. Les formules et les noms des deux dérivés monochlorés qui se forment
 
$CH_{2}Cl-CH\left(CH_{3}\right)-CH_{3}$ : $1-$Chloro$-2-$méthylpropane
 
$CH_{3}-CCl\left(CH_{3}\right)-CH_{3}$ : $2-$Chloro$-2-$méthylpropane

Exercice 5

1. Écriture d'une première relation entre les volumes $V_{1}$ et $V_{2}.$
 
$V_{1}+V_{2}=10L$
 
2. Équations-bilans des réactions de combustions du méthane et du propane avec le dioxygène.
$$CH_{4}\ +\ 2O_{2}\ \rightarrow\ CO_{2}\ +\ 2H_{2}O$$
$$C_{3}H_{8}\ +\ 5O_{2}\ \rightarrow\ 3CO_{2}\ +\ 4H_{2}O$$
 
3.1 Exprimons en fonction de $V_{1}$ et $V_{2}.$
 
les volumes de dioxygène consommés par la combustion complète des volumes $V_{1}$ et $V_{2}.$
 
D'après le bilan volumique :
 
$\left\lbrace\begin{array}{lcl}V_{1}&=&\dfrac{V_{01}}{2}\\\\ V_{2}&=&\dfrac{V_{02}}{5} \end{array}\right.\Rightarrow\left\lbrace\begin{array}{lcl}V_{01}&=&2V_{1}\\V_{02}&=&5V_{2} \end{array}\right.$
 
3.2 Déduction du volume $V_{0}$ de dioxygène nécessaire à la combustion complète du mélange en fonction de $V_{1}$ et $V_{2}.$
 
$V_{0}=V_{01}+V_{02}=2V_{1}+5V_{2}$
 
4. Déduction des valeurs de $V_{1}$ et $V_{2}.$
$\begin{array}{rcl}\left\lbrace\begin{array}{lcl} V_{1}+V_{2} &=& 10L\\ 2V_{1}+5V_{2} &=& 38L \end{array}\right.&\Rightarrow&\left\lbrace\begin{array}{lcl} 2\left(V_{1}+V_{2}\right) &=&10L\\ 2V_{1}+5V_{2} &=&38L\end{array}\right.\\\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 2V_{1}+2V_{2} &=&20L\\ 2V_{1}+5V_{2} &=&38L\end{array}\right.\\\\&\Rightarrow&\left\lbrace\begin{array}{lcl} V_{1}&=&4L\\ V_{2}&=&6L \end{array}\right.\end{array}$
 
5. Détermination de la composition centésimale volumique du mélange étudié.
 
$\begin{array}{rcl} \% CH_{4} &=&\dfrac{V_{1}\times 100}{V_{1}+V_{2}}\\\\ &=& \dfrac{4\times 100}{4+6}\\\\\Rightarrow\% CH_{4} &=&40\ ; \end{array}$
 
$\begin{array}{rcl} \% C_{3}H_{8} &=&\dfrac{V_{2}\times 100}{V_{1}+V_{2}}\\\\ &=& \dfrac{6\times 100}{4+6}\\\\\Rightarrow\% C_{3}H_{8} &=&60 \end{array}$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Éléments, Atomes, classification périodique des éléments - 2nd S

Classe: 
Seconde
 

Exercice 1

Le carbone est le constituant essentiel de la matière vivante.
 
Il est présent dans toutes les molécules organiques.
 
Un atome de carbone, de symbole $C$ a $12$ nucléon.
 
La charge électrique de son nuage électronique est $q=6e.$
 
1. Pourquoi  peut-on dire que le noyau contient $6$ protons ?
 
Justifier.
 
2. Exprimer puis calculer la charge de son noyau.
 
3. Donner le symbole de son noyau.
 
4. Énoncer les règles de remplissage des électrons sur les couches électroniques puis donner la structure électronique de l'atome de carbone.
 
5. Calculer la valeur approchée de la masse de l'atome de carbone.

Données :

$m_{p}=m_{n}=1.7\cdot 10^{-27}kg$ ; 
 
masse de l'électron : $m_{e}=9.1\cdot 10^{-31}kg$ ; 
 
charge élémentaire : $g=1.6\cdot 10^{-19}C$
 
6. Pourquoi peut-on dire que la masse de l'atome est quasiment la même que celle du noyau de l'atome ?
 
Justifier votre réponse par un calcul.
 
7. L'atome de carbone peut être représenté par une sphère de rayon $R=67\,pm.$
 
Calculer le rayon de son noyau $r$ de son noyau.

Exercice 2

La formule électronique d'un atome est : $(K)^{2}(L)^{8}(M)^{7}.$
 
1. Quel est le nom de la couche externe de cet atome ?
 
2. Combien d'électrons externes cet atome possède-t-il ?
 
3. Donner le symbole de son noyau sous la forme $_{Z}^{A}X$, sachant que l'élément correspondant est le chlore et que son noyau comporte $18$ neutrons.
 
4. Donner la composition de cet atome.
 
5. Quel est la masse de cet atome ?

Données :

Masse du proton$=$masse du neutron$=1.67\cdot 10^{-27}kg$ ;
 
masse de l'électron$=9\cdot 10^{-31}kg$
 
6. Quel ion cet atome est-il susceptible de donner et pourquoi ?
 
Énoncer la loi utilisée et donner la structure électronique de cet ion.

Exercice 3

Un atome inconnu possède deux électrons sur sa couche externe $M.$
 
Il est constitué par $20$ neutrons.
 
1. Définir : l'élément chimique - structure lacunaire - isotopes
 
2. Les électrons d'un atome se répartissent sur des couches.
 
Donner symboles de ces couches et le nombre maximal d'électrons qu'elle peut contenir.
 
3. Donner la configuration électronique de cet atome.
 
En déduire le nombre d'électrons 
 
4. Déterminer le numéro atomique $Z$ de cet atome. 
 
Justifier
 
5. Déterminer le nombre de nucléon $A.$
 
En déduire la notation symbolique de l'atome sachant que son symbole chimique est $M_{g}$, donner la composition de cet atome.
 
6. Calculer la masse du noyau en Coulomb.
 
En déduire la charge des électrons 
 
7. Calculer la masse approchée de cet atome.
 
8. Combien d'atome de $M_{g}$ contenant dans un échantillon de $M_{g}$ de masse $m=10g$
 
9. L'ion formé par cet atome résulte de la perte de deux électrons de la couche externe.
 
9.1 Donner la structure électronique de cet atome.
 
Que peut-on dire sur sa couche externe
 
9.2 Définir un cation et un anion.
 
Déterminer la charge électronique porté par cet atome.
 
S'agit - il d'un cation ou d'un anion.
 
9.3 Écrire la formule chimique de cet ion.
 
10. Que peut - on dire de cet atome et des ions suivants dont on donne le couple $(Z\ ;\ A)\ :\ (17\ ;\ 37)\quad\text{et}\quad(17\ ;\ 35)$ ?

Données :

charge élémentaire $e=1.6\cdot 10^{-19}C$ ;
 
la masse d'un proton $m_{p}=1.67\cdot 10^{-27}kg$

Exercice 4

Le bromure de lithium et le chlorure de magnésium sont connus pour leur activité thérapeutique, ce sont des régulateurs de l'humeur.
 
1. L'élément lithium $(Li)$ est dans la première famille et la deuxième période de la classification périodique.
 
1.1 Comment s'appelle la famille chimique à la quelle il appartient ?
 
1.2 Quel est le nombre d'électrons sur sa couche électronique externe ?
 
1.3 Quel ion monoatomique forme facilement un atome de lithium ?
 
Justifier votre réponse en énonçant la règle de stabilité que vous avez utilisée.
 
2. Quel ion monoatomique stable forme l'élément chlore ?
 
Justifier simplement votre réponse.
 
3. Le brome $Br$ appartient à la même famille chimique de chlorure $Cl$ ?
 
3.1 Combien d'électrons possède - t - il sur sa couche électronique externe ?
 
3.2 Quel ion monoatomique forme facilement un atome de brome ?
 
Justifier votre réponse.
 
4. L'élément magnésium $(3^{ième}$ période de la classification$)$ conduit facilement à la formation de l'ion $Mg^{2+}$
 
4.1 Dans quelle colonne se trouve l'élément magnésium.
 
Justifier
 
4.2 Quel est le nom de la colonne où se trouve le magnésium ?
 
5. Quel ion monoatomique stable forme l'élément chlore ?
 
Justifier simplement votre réponse.
 
6. En utilisant les questions précédentes, en déduire la formule du chlorure de magnésium et du bromure de lithium, deux solides électriquement neutres.

Exercice 5

Les atomes de certains éléments ont des noyaux instables qui se décomposent spontanément et se transforment en d'autres éléments : on dit qu'ils sont radioactifs.
 
On les utilise notamment en médecine, mais aussi dans beaucoup de secteurs de l'industrie et en recherche.
 
$\blacktriangleright\ $En médecine, par exemple, on utilise :
 
$-\ $ Le cobalt $60$ $(Z=27)$ pour le traitement de certaines tumeurs cancéreuses $($Cobalt : $Co)$ ;
 
$-\ $ L'iode $131$ et l'iode$123$ $(Z=53)$ comme traceurs et marqueurs pour les images scientifiques $($Iode : $I)$ ;
 
$-\ $ Le sodium $24$ $(Z=11)$ pour la détermination du volume de sang que contient le corps humain $($Sodium : $Na)$
 
$-\ $ Le Plutonium $238$ $(Z=94)$ qui fournit l'énergie aux stimulateurs cardiaques $($plutonium : $Pu).$
 
$\blacktriangleright\ $Dans l'industrie, on utilise :
 
$-\ $ L'uranium $235$ et l'uranium $238$ $(Z=92)$, comme combustibles nucléaires dans des centrales électriques $($Uranium : $U)$ ;
 
$-\ $ Le chlore $36$ $(Z=17)$ et le silicium $32$ $(Z=14)$ pour la datation des eaux dans les nappes phréatiques $($Chlore : $Cl$ ; Silicium : $Si).$
 
$\blacktriangleright\ $En recherche, on utilise :
 
$-\ $ Le carbone $14$ $(Z=6)$, le potassium $40$ $(Z=19)$ et l'argent $40$ $(Z=18)$, en paléontologie, pour la datation des fossiles $($carbone : $C$ ; potassium : $K$ ; argon : $Ar)$

$-\ $ L'oxygène $18$ $(Z=8)$ qui n'est pas radioactif pour déterminer, en climatologie, la température qui régnait à différentes époques (analyse des glaces polaires) $($oxygène : $O).$

1. a) Reprendre chacun des atomes qui apparaissent dans le texte et le symboliser sous forme $_{Z}^{A}X.$

1. b) Combien d'éléments différents apparaissent dans le texte ?

2. Combien de neutrons y a-t-il dans un noyau de cobalt $60$ ?

De plutonium $238$ ?

De chlore $36$ ?

3. Combien de d'électrons se déplacent autour des noyaux de sodium $24$ et de silicium $32$ ?

4. a) Donner les structures électroniques des atomes de carbone $14$ et d'argon $40.$

4. b) Combien d'électrons y a-t-il sur la couche externe de ces deux atomes ?

5. a) Quelle est la formule de l'ion potassium sachant qu'il a $18$ électrons autour de son noyau ?

5. b) L'ion potassium et l'atome de potassium appartiennent-ils au même élément ?

6. a) Quelle est la structure électronique de l'ion chlorure $^{36}Cl^{-}$ ?

6. b) Comparer cette structure à celle de l'atome d'argon $40.$

6. c) Peut-on dire que l'ion $^{36}Cl^{-}$ et l'argon sont des isotopes ?

7. Quels atomes isotopes apparaissent dans le texte.

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Mélanges et corps purs - 2nd S

Classe: 
Seconde
 

Exercice 1

A. Choisir la bonne réponse :
 
$1-\ $ Une eau limpide
 
a) est toujours un corps pur ; 
 
b) peut être un mélange homogène ; 
 
c) est un mélange hétérogène
 
$2-\ $ Les constituants d'un mélange homogène peuvent être séparés par :
 
a) décantation ;     
 
b) distillation ;    
 
c) filtration
 
B. Répondre par $VRAI$ ou $FAUX$ avec justification :
 
$1-\ $ La distillation de l'eau de mer est un phénomène physique.
 
$2-\ $ L'électrolyse de l'eau est un phénomène chimique.
 
$3-\ $ La synthèse de l'eau est un phénomène physique.
 
$4-\ $ L'air est un corps pur composé.
 
$5-\ $ le passage de l'état solide à l'état gazeux est la vaporisation.
 
C. Proposer une ou des méthodes pour séparer les constituants des mélanges suivantes :
 
a) Eau$+$huile ;    
 
b) eau$+$alcool ;   
 
c) fer en poudre$+$sable ;   
 
d) charbon en poudre$+$sel de cuisine ;    
 
e) ciment en poudre$+$cailloux.

Exercice 2

On désire préparer une solution d'eau salée à partir d'eau de robinet et de sel en poudre.
 
$1.1-\ $ Quel type de mélange obtient-on après avoir agité énergiquement si :
 
a) le sel est utilisé en défaut $($mélange $M_{1})$ ;
 
b) le sel est utilisé en excès $($mélange $M_{1}).$
 
Justifier dans chaque cas la réponse.
 
$1.2-\ $ On considère le mélange d'eau salée $M_{1}$ obtenu en utilisant de la poudre de sel en défaut. 
 
Une certaine masse de sel a subi une transformation lors de la préparation du mélange $M_{1}.$ 
 
Cette transformation est-elle un phénomène physique ou un phénomène chimique ? Justifier.
 
On précisera le nom de la transformation en question.
 
$1.3-\ $ On place le mélange $M_{1}$ dans un ballon à pyrex afin de récupérer l'eau seule à l'état pur dans un bécher.
 
a) Sur quel critère de pureté doit-on se baser pour réussir l'opération ? 
 
Justifier.
 
b) Quelle technique doit-on utiliser ? 
 
Expliquer brièvement son principe.
 
$1.4-\ $ Lorsque l'opération est achevée, on constate sur le fond du ballon en pyrex l'apparition d'un dépôt d'un solide sec d'aspect blanc. 
 
Ce dépôt est-il un corps pur, un mélange homogène ou un mélange hétérogène ? 
 
Justifier. 
 
$1.5-\ $ Expliquer alors comment devrait-on procéder pour qu'en fin d'opération, on obtienne dans le ballon un corps pur.

Exercice 3

Lors d'une expérience d'électrolyse de l'eau, on recueille un volume total de $135\,mL$ de gaz au niveau des deux électrodes de l'électrolyse.
 
$1-\ $ Qu'appelle-t-on électrolyse de l'eau ? 
 
Comment identifie-t-on expérimentalement ces deux gaz recueillis ?
 
$2-\ $ Sur quelles électrodes sont recueillis ces gaz ?
 
$3-\ $ Trouver le volume de chacun des gaz recueillis.
 
$4-\ $ Déterminer la masse d'eau décomposée sachant que $1\,L$ de dioxygène pèse $1.428\,g.$
 
$5-\ $ En déduire la masse du dihydrogène recueilli.

Exercice 4

A. Au cours d'une expérience, on introduit dans un eudiomètre du dihydrogène et du dioxygène.
 
Le volume du mélange gazeux est de $52\,cm^{3}.$ 
 
On y provoque une étincelle électrique. 
 
Après réaction et retour aux conditions initiales de température et de pression, il reste $11.5\,cm^{3}$ de dioxygène.
 
$1-\ $ Quel est le nom de cette expérience ?
 
$2-\ $ Déterminer le volume de dihydrogène dans le mélange initial et celui de dioxygène dans le mélange dans le mélange initial.
 
$3-\ $ Calculer la masse initiale de dihydrogène sachant que sa masse volumique est égale à $0.08\,g\cdot L^{-1}.$
 
$4-\ $ Déterminer la masse d'eau formée et celle de dihydrogène disparu.
 
B. Dans un eudiomètre on introduit $50\,cm^{3}$ de dihydrogène et $60\,cm^{3}$ de dioxygène (volumes mesurés dans les mêmes conditions). 
 
Après passage de l'étincelle électrique et retour aux conditions initiales, déterminer la nature et le volume du gaz restant après formation de l'eau.
 
Auteur: 
Sidy Mouhamed Ndiaye

ENSA - Épreuve de Sciences Physiques - 2019

Chimie : (8 points)

Données : $M(H)=1\,g.mol^{-1}\;;\ M(C)=12\,g.mol^{-1}\;;\ M(O)=16\,g.mol^{-1}$
 
Un des composants du vin est l'acide malique $COOH-CH_{2}-CHOH-COOH$ ou acide 2-hydroxybutanedioique.
 
Lors de la fermentation du vin l'acide malique se décompose en donnant du dioxyde de carbone de l'acide lactique ou acide 2-hydroxypropanoïque
 
1) Écrire l'équation de la réaction de fermentation de l'acide malique en entourant les groupes fonctionnels de l'acide obtenu puis les nommer.$\quad(1.5\,\text{pts})$
 
2) Pourquoi la molécule d'acide lactique est chirale ? Donner la représentation de Fischer des deux énantiomères.$\quad(1\,\text{pt})$
 
3) On réalise un suivi cinétique par dosage, l'évolution de la concentration massique $C_{m}(t)$ en fonction du temps de l'acide malique dans un vin de volume constant. Les résultats obtenus ont permis de tracer la courbe $C_{m}=f(t)$ ci-contre.

 
 

 
3.1) Exprimer la concentration molaire $C$ de l'acide malique en fonction de la concentration massique $C_{m}.\quad(0.5\,\text{pt})$
 
3.2) Définir la vitesse volumique de disparition de l'acide malique. L'exprimer en fonction de la concentration massique.$\quad(1\,\text{pt})$
 
3.3) Déterminer la date à laquelle la concentration molaire de l'acide lactique vaut $C'=2.01\cdot 10^{-2}\,mol.L^{-1}\quad(1.5\,\text{pts})$
 
3.4) Déterminer à cette date la vitesse volumique de disparition de l'acide malique. En déduire la vitesse volumique de formation de l'acide lactique.$\quad(0.75\,\text{pt})$
 
4) Déterminer les vitesses volumiques de disparition de l'acide malique aux instants $t_{1}=4\text{ jours}\ $ et $\ t_{2}=20\text{ jours}.$ Comparer les vitesses trouvées puis justifier.$\quad(1.5\,\text{pts})$

Physique

Exercice 2 (6 points)

Données : masse de la terre : $M_{T}=5.98\cdot 10^{24}\,kg$ ; constante de gravitation $K=6.67\cdot 10^{-11}\,\text{SI}$
 
Masses des planètes du système solaire : (la masse de la terre étant prise égale à l'unité).
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text{Terre}&\text{Mercure}&\text{Vénus}&\text{Mars}&\text{Jupiter}&\text{Saturne}&\text{Uranus}&\text{Neptune}&\text{Lune}\\ \hline 1&0.056&0.817&0.11&318&95.2&14.6&17&0.012\\ \hline\end{array}$$
Au cours de son exploration du système solaire, une sonde Voyager, de masse $M=2\,100\;Kg$, s'est approchée d'une planète notée $A.$ On a mesuré à deux altitudes différentes comptée à partir du sol de cette planète la force de gravitation exercée par celle-ci sur la sonde soit :
 
$\centerdot\ $ à l'altitude $z_{1}=8\,499\;Km$ on a trouvé $F_{1}=13\,236.51\;N$
 
$\centerdot\ $ à l'altitude $z_{2}=250\,000\;Km$ on a trouvé $F_{2}=189.25\;N$
 
1) Calculer le diamètre moyen de la planète $A.\quad(1\,\text{pt})$
 
2) Quelle est l'intensité du champ de gravitation au niveau du sol de la planète $A\ ?\quad(1.5\,\text{pts})$
 
3) Quelle est le nom de la planète $A\ ?\quad(1\,\text{pt})$
 
4) Neptune de rayon $R_{N}=24.3\cdot 10^{3}\,Km$, possède un satellite dont la période de révolution autour d'elle (sur une trajectoire supposée circulaire) vaut $T_{S}=5\,j\ 21\,h\ 03\,min.$
 
Calculer la distance séparant le centre du satellite au centre de Neptune.$\quad(1\,\text{pt})$
 
Déterminer le travail de la force de gravitation qui s'applique sur le satellite lorsque celui-ci passe du sol de Neptune à l'altitude $z.$ En déduire l'énergie potentielle de gravitation si l'état de référence est pris sur le sol de Neptune de rayon $R_{N}=24.3\cdot 10^{3}\;Km\quad(1.5\,\text{pts})$

Exercice 3 (6 points)

Données : $\text{électron }\left\lbrace\begin{array}{rcl}\text{masse }m&=&9.109\times 10^{-31}\;Kg\\ \text{charge }-\mathrm{e}&=&-1.602\times 10^{-19}\;C\\k&=&8.988\times 10^{9}\;\text{SI}\end{array}\right.$
 
L'électron n'est pas relativiste.
 
1) Rutherford a décrit l'atome d'hydrogène par un modèle planétaire : l'électron a un mouvement circulaire, de rayon $r$, autour du noyau constitué d'un proton.
 
La force électrostatique subie par l'électron est dirigée selon la droite proton-électron, attractive, de valeur $f=k\dfrac{\mathrm{e}^{2}}{r^{2}}.$ La force gravitationnelle est négligeable devant cette force électrostatique.
 
1.1) Démontrer que le mouvement de l'électron est uniforme.
 
1.2) Établir l'expression de sa vitesse $v$ en fonction de $k\;,\ \mathrm{e}\;,\ r\ $ et $\ m.$
 
1.3) Exprimer son énergie cinétique en fonction des mêmes paramètres.
 
1.4) Exprimer son énergie mécanique $E$ en fonction de $k\;,\ \mathrm{e}\;,\ r$, sachant que son énergie potentielle est $E_{p}=-\dfrac{k\mathrm{e}^{2}}{r}.$ Quelle est sa limite quand $r$ tend vers l'infini ?
 
2) Différents faits expérimentaux, ont conduit Niels Bohr à formuler l'hypothèse suivante : l'électron ne peut se déplacer que sur certains cercles dont les rayons $r_{n}$ obéissent à la loi :
 
$$v_{n}\times r_{n}=n\times\dfrac{h_{r}}{m}$$
 
$h_{r}\ :$ Constante de Dirac : $h_{r}=1.054\times 10^{-34}\;J.s$
 
$n\ :$ nombre entier $\geq 1$
 
$v_{n}\ :$ vitesse de l'électron sur le cercle de rayon $r_{n}.$
 
2.1) Déterminer l'expression de $r_{n}$ en fonction des constantes $k\;,\ h_{r}\;,\ m\;,\ \mathrm{e}$ et de $n.$
 
Exprimer $r_{n}$ en fonction de $r_{1}.$ Calculer $r_{1}.$
 
2.2) Déterminer l'expression de $E_{n}$, énergie mécanique de l'électron sur le cercle de rayon $r_{n}$, en fonction des mêmes paramètres. Exprimer $E_{n}$ en fonction de $E_{1}.$
 
2.3) Calculer $E_{1}\ $ et $\ E_{2}$ en électron-volts. Quelle cause peut faire passer l'énergie de l'électron de $E_{1}\ $ à $\ E_{2}\ ?$
 
$$\text{Durée 2 heures}$$

 

ENSA - Épreuve de Sciences Physiques - 2018

Chimie

Exercice 1 (7 points)

Les esters jouent un rôle important dans la chimie des parfums et dans l'industrie alimentaire car ils possèdent une odeur florale ou fruitée. La transpiration de l'être humain contribue à la disparition de l'odeur du parfum.
 
1) Écrire, à l'aide de formules générales, l'équation-bilan de la réaction d'hydrolyse d'un ester. Justifier alors brièvement l'altération de l'odeur du parfum par la sueur.$\quad(1\,\text{pt})$
 
2) Au laboratoire on étudie l'hydrolyse d'un ester. Une méthode de contrôle de la réaction consiste à mesurer le $\text{pH}$ du milieu réactionnel à intervalles de temps réguliers. Dire comment évolue le $\text{pH}$ du milieu réactionnel en fonction du temps.$\quad(1\,\text{pt})$
 
3) A une date $t$ donnée, la mesure du $\text{pH}$ donne $\text{pH}=2.6$ et à cette date la concentration molaire volumique de l'acide formé est $C_{A}= 6.25\cdot 10^{-3}\,mol.L^{-1}.$
 
L'acide sera noté $AH$ et sa base conjuguée $A^{-}.$
 
Montrer que l'expression du $\text{pK}_{a}$ du couple acide-base associé à cet acide est donnée par la relation :
$$\text{pK}_{a}=2\text{pH}+\log(C_{A}- 10^{-\text{pH}})\qquad(1.5\,\text{pts})$$
En déduire la valeur du $\text{pK}_{a}.\quad(0.5\,\text{pt})$
 
4) L'acide AH est dérivé d'un acide carboxylique $RCOOH$ par remplacement d'un atome d'hydrogène du groupe alkyle $R$ par un atome de chlore.
 
a) Sachant que la masse molaire moléculaire de l'acide vaut : $M=108.5\,g.mol^{-1}$ déterminer sa formule brute.$\quad(1.5\,\text{pts})$
 
Écrire sa formule semi développée.$\quad(0.5\,\text{pt})$
 
b) La molécule de l'acide possède un carbone asymétrique ;
 
Représenter alors les configurations des deux énantiomères de l'acide.$\quad(1\,\text{pt})$
 
On donne :
 
$M(H)=1\,g.mol^{-1}\;;\ M(C)=12\,g.mol^{-1}\;;\ M(O)=16\,g.mol^{-1}\;;\ M(Cl)=35.5\,g.mol^{-1}$

Physique

Exercice 2 (7 points)

Partie A
 
L'isotope 4 de l'Hélium est représenté par le symbole : $_{2}^{4}He.$
 
1) Qu'appelle-t-on nucléides isotopes ?$\quad(0.5\,\text{pt})$
 
2) Donner la composition de l'isotope 4 de l'Hélium.$\quad(0.5\,\text{pt})$
 
3) Quelle est, en MeV/nucléon, l'énergie de liaison par nucléon de ce nucléide ?$\quad(0.5\,\text{pt})$
 
On donne :
 
$-\ $ Célérité de la lumière : $c=3\cdot 10^{8}\,m.s^{-1}$, et
 
$-\ $ Les masses : $m\left(_{2}^{4}He\right)=4.00260\,u\;;\ m_{p}=1.00728\,u\;;\ m_{n}=1.00867\;u\;;\ 1\,u=1.67\cdot 10^{-27}\,kg.$
 
Partie B
 
La fission d'un noyau d'Uranium $235$ produit un isotope du Strontium et un isotope du Xénon selon l'équation :
$$_{0}^{1}n+_{\ 92}^{235}U\ \longrightarrow\ _{\ x}^{94}Sr+_{54}^{\ y}Xe+2_{0}^{1}n$$
1) En utilisant les lois de conservations habituelles, calculer $x\ $ et $\ y.\quad(0.5\,\text{pt})$
 
2) Dans certains réacteurs dits surgénérateurs, il y a possibilité de capture d'un neutron par un noyau $_{\ 92}^{235}U.$
 
Quel est l'isotope de l'uranium obtenu ?$\quad(0.5\,\text{pt})$
 
3) Cet isotope, radioactif, subit une transmutation $\beta^{-1}$ pour donner un isotope du Neptunium $(N_{p})$, lui-même radioactif et qui par une nouvelle désintégration $\beta^{-1}$ donne l'isotope $_{\ 94}^{239}Pu$ du Plutonium.
 
Écrire les deux équations correspondant aux deux transmutations envisagées en utilisant les symboles convenables.$\quad(1\,\text{pt})$
 
Une fission libère d'autres neutrons dits rapides, ayant une vitesse $V_{0}=20\,000\;km.s^{-1}.$ Pour qu'un neutron puisse provoquer une nouvelle fission, il doit avoir une vitesse $V_{1}=2\;km.s^{-1}.$ Le ralentissement des neutrons se fait par chocs successifs avec les noyaux atomiques d'un modérateur. Un neutron de vitesse $V_{0}=20\,000\;km.s^{-1}$ heurte un noyau de deutérium $_{1}^{2}H$ initialement au repos. On suppose que le choc est parfaitement élastique et que les vitesses des particules après le choc ont même direction que la vitesse du neutron incident.
 
4) En appliquant les lois de la mécanique classique, calculer la vitesse du neutron après le choc$\quad(0.5\,\text{pt})$
 
5) Combien de chocs identiques seraient nécessaires pour que la vitesse du neutron soit égale à $2\;km.s^{-1}.\quad(0.5\,\text{pt})$
 
Pour cette question on prendra : Masse du neutron=$1\,u$ ; masse du noyau de $_{1}^{2}H=2\,u.$
 
Partie C
 
Un des déchets radioactifs est le Plutonium $239.$ A un instant pris comme origine des temps, on envisage un échantillon contenant $N_{0}$ noyaux de plutonium.
 
1) Donner, en fonction de $N_{0}\;,\ \lambda\ $ et $\ t$, l'expression du nombre $N(t)$ de noyaux restant dans l'échantillon à la date $t.\quad(0.5\,\text{pt})$
 
2) Quelle est en, années, la demi-vie du Plutonium ?$\quad(0.75\,\text{pt})$
 
3) Quelle est, en fonction de $N_{0}\ $ et $\ \lambda$, l'expression de l'activité initiale $A_{0}$ de l'échantillon ?$\quad(0.5\,\text{pt})$
 
4) Au bout de combien de temps cette activité aura-t-elle diminué de $90\%\ ?\quad(0.5\,\text{pt})$
 
Données :
 
$\lambda$ (constante radioactive du Plutonium) $=0.92\cdot 10^{-12}\, s^{-1}$ ; Une année$=3.1\cdot 10^{7}\,s$

Exercice 3 (6 points)

On réalise une figure d'interférences lumineuses à l'aide d'une source principale $F$ et de fentes fines $F_{1}\ $ et $\ F_{2}.$ La distance $F_{1}F_{2}=a.$ Un écran $E$ est placé parallèlement aux fentes à une distance $D$ de celles-ci.

 

 
A) La source principale $F$ émet une lumière monochromatique de longueur d'onde $\lambda.$
 
1) Les fentes $F_{1}\ $ et $\ F_{2}$ sont-elles des sources cohérentes ? Justifier brièvement la réponse.
 
2) Qu'observe-t-on alors sur l'écran $E\ ?$ Quel caractère de la lumière met-on ainsi en évidence ?
 
3) Exprimer la différence de marche $\delta$ des rayons lumineux se superposant au point $M$ d'abscisse $x$ sur l'écran $E.$ Calculer $\delta$ pour $x= x_{1}.$
 
4) Définir puis calculer l'interfrange $i.$
 
5) Qu'appelle-t-on ordre d'interférence ? A quelle distance du point $O$ on trouve alors la frange noire d'ordre $11\ ?$
 
B) La source $F$ émet maintenant une lumière constituée de radiations de longueurs d'onde $\lambda_{1}\ $ et $\ \lambda_{2}.$
 
1) Calculer les interfranges $i_{1}\ $ et $\ i_{2}$ correspondant respectivement aux radiations de longueurs d'ondes $\lambda_{1}\ $ et $\ \lambda_{2}.$
 
2) Déduire des résultats précédents l'aspect de la frange centrale ainsi que celui de sa voisine immédiate.
 
C) On éclaire cette fois-ci les fentes $F_{1}\ $ et $\ F_{2}$ à l'aide d'une lumière blanche issue de la fente principale $F.$
 
1) Dans quelle région du spectre électromagnétique se situe la lumière blanche ? Cette lumière est-elle monochromatique ? Justifier.
 
2) Quelle est la couleur de la frange centrale ? Quel est l'aspect observé au voisinage immédiat de la frange centrale ?
 
3) Quelles sont les radiations éteintes en un point $M'$ situé à la distance $x_{2}$ du point $O\ ?$ Quel est alors à cet endroit, l'aspect de l'écran ?
 
Données :
 
$D=3.0\,m\;;\ a=1.0\,mm\;;\ x_{1}=2.0\,cm\;;\ x_{2}=3.0\,cm\;;\ \lambda=680\,nm$
 
$\lambda_{1}=700\,nm$ (radiation rouge) ; $\lambda_{2}=500\,nm$ (radiation bleue) ; longueurs d'onde dans la région visible du spectre électromagnétique :
$$400\,nm\leq\lambda\leq 750\,nm$$
 
$$\text{Durée 2 heures}$$

 

Pages