Solution des exercices : Dipôles actifs - 2nd S
Classe:
Seconde
Exercice 9
On réalise le montage suivant :
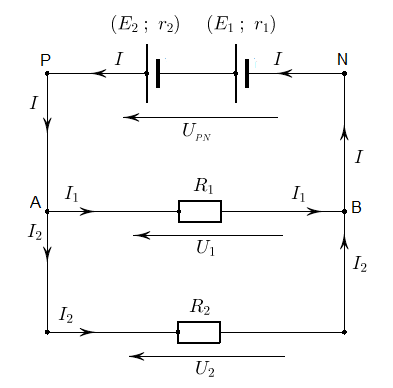
Les deux générateurs sont identiques et ont pour f.é.m $4.5\;V$ et pour résistance interne $1\;\Omega.$ Les conducteurs ohmiques ont pour résistances $R_{1}=500\;\Omega\ $ et $\ R_{2}=200\;\Omega$
1) La f.é.m. $E$ et la résistance interne $r$ du générateur équivalent aux deux générateurs sont données par :
$E=E_{1}+E_{2}\ $ et $\ r=r_{1}+r_{2}$
Les deux générateurs étant identiques alors, $E_{1}=E_{2}\ $ et $\ r_{1}=r_{2}$
Ainsi, $E=4.5+4.5=9\ $ et $\ r=1+1=2$
D'où, $\boxed{E=9\;V\ \text{ et }\ r=2\;\Omega}$
2) Calculons la résistance équivalente $R$ aux deux résistors $R_{1}\ $ et $\ R_{2}$
Comme les résistors sont montés en parallèle alors, leur résistance équivalente $R$ vérifie :
$\begin{array}{rcl}\dfrac{1}{R}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}&\Rightarrow&\dfrac{1}{R}=\dfrac{R_{1}+R_{2}}{R_{1}\times R_{2}}\\\\&\Rightarrow&R=\dfrac{R_{1}\times R_{2}}{R_{1}+R_{2}}\end{array}$
A.N : $R=\dfrac{500\times 200}{500+200}=142.8$
D'où, $\boxed{R=142.8\;\Omega}$
3) Déduisons-en l'intensité du courant débité par les deux piles et la valeur $U_{_{PN}}$
Considérons le circuit équivalent ci-dessous :
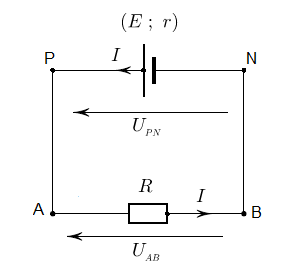
On a : $\left\lbrace\begin{array}{rcl} U_{_{PN}}&=&E-r.I\\\\U_{_{AB}}&=&R.I\end{array}\right.$
Or, $U_{_{PN}}=U_{_{AB}}$
Donc,
$\begin{array}{rcl} E-r.I=R.I&\Rightarrow&R.I+r.I=E\\\\&\Rightarrow&I(R+r)=E\\\\&\Rightarrow&I=\dfrac{E}{R+r}\end{array}$
A.N : $I=\dfrac{9}{142.8+2}=0.062$
Ainsi, $\boxed{I=0.062\;A=62\;mA}$
Par suite,
$\begin{array}{rcl} U_{_{PN}}&=&E-r.I\\\\&=&9-2\times 0.062\\\\&=&8.876\end{array}$
D'où, $\boxed{U_{_{PN}}=8.87\;V}$
4) Déterminons les intensités des courants dans les deux conducteurs ohmiques
On a :
$$U_{_{PN}}=U_{1}=U_{2}$$
Par ailleurs, d'après la loi d'Ohm, on a :
$$U_{1}=R_{1}.I_{1}\ \text{ et }\ U_{2}=R_{2}.I_{2}$$
Par suite,
$\begin{array}{rcl} U_{_{PN}}=R_{1}.I_{1}&\Rightarrow&I_{1}=\dfrac{U_{_{PN}}}{R_{1}}\end{array}$
A.N : $I_{1}=\dfrac{8.87}{500}=0.018$
Ainsi, $\boxed{I_{1}=0.018\;A=18\;mA}$
De la même manière, on :
$\begin{array}{rcl} U_{_{PN}}=R_{2}.I_{2}&\Rightarrow&I_{2}=\dfrac{U_{_{PN}}}{R_{2}}\end{array}$
A.N : $I_{2}=\dfrac{8.87}{200}=0.044$
D'où, $\boxed{I_{2}=0.044\;A=44\;mA}$
On peut aussi utiliser la loi des nœuds pour déterminer le courant $I_{2}.$
En effet, au niveau du nœud $B$, on a :
$$I_{1}+I_{2}=I$$
Ce qui donne,
$\begin{array}{rcl} I_{2}&=&I-I_{1}\\\\&=&0.062-0.018\\\\&=&0.044\end{array}$
D'où, $\boxed{I_{2}=0.044\;A=44\;mA}$

Commentaires
Anonyme (non vérifié)
ven, 02/04/2022 - 17:13
Permalien
Les autres solutions?
Mouad (non vérifié)
mer, 05/11/2022 - 17:45
Permalien
Phizique
Mouad (non vérifié)
sam, 05/14/2022 - 14:44
Permalien
Phizique
Anonyme (non vérifié)
ven, 03/04/2022 - 13:21
Permalien
Nice cool
Sedegnan (non vérifié)
mer, 05/18/2022 - 11:30
Permalien
Eleve
Khlid (non vérifié)
lun, 05/08/2023 - 13:47
Permalien
Hv c
BAH VICTOR (non vérifié)
dim, 04/20/2025 - 06:49
Permalien
Demande de corrigés
Ajouter un commentaire