Triangle rectangle : Théorème de Pythagore - 4e
Classe:
Quatrième
I. Rappel
On appelle triangle rectangle tout triangle possédant un angle de $90^{\circ}$ donc, deux côtés perpendiculaires.
Remarques
$-\ $ Comme $mes\;\hat{A}=90^{\circ}$ alors, $\hat{B}\ $ et $\ \hat{C}$ sont complémentaires.
$-\ $ Le milieu de l'hypoténuse est le centre du cercle circonscrit à $ABC.$
$-\ $ Le sommet de l'angle droit $(A)$ est l'hortocentre de $ABC.$
II. Théorème de Pythagore
II.1. Activité
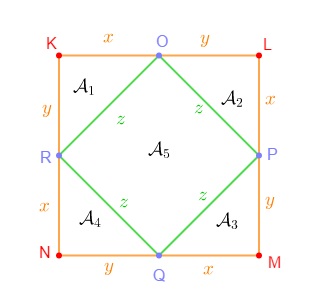
$KLMN$ est un carré dont $O\;,\ P\;,\ Q\ $ et $\ R$ sont respectivement les milieux de $[KL]\;,\ [LM]\;,\ [MN]\ $ et $\ [NK].$
$x\;,\ y\ $ et $\ z$ sont des mesures de longueur.
Calculons de deux manières différentes l'aire $\mathcal{A}$ du carré $KLMN.$
$\centerdot\ $ 1e méthode
$\begin{array}{rcl}\mathcal{A}&=&(x+y)(x+y)\\ \\&=&(x+y)^{2}\end{array}$
Donc, $\boxed{\mathcal{A}=(x+y)^{2}}$
$\centerdot\ $ 2e méthode
$\begin{array}{rcl}\mathcal{A}&=&\mathcal{A}_{1}+\mathcal{A}_{2}+\mathcal{A}_{3}+\mathcal{A}_{4}+\mathcal{A}_{5}\\ \\&=&\dfrac{xy}{2}+\dfrac{xy}{2}+\dfrac{xy}{2}+\dfrac{xy}{2}+z^{2}\\ \\&=&4\times\dfrac{xy}{2}+z^{2}\\ \\&=&2xy+z^{2}\end{array}$
Ainsi, $\boxed{\mathcal{A}=2xy+z^{2}}$
Finalement :
$\begin{array}{rcrcl} 2xy+z^{2}=(x+y)^{2}&\Leftrightarrow&2xy+z^{2}&=&x^{2}+2xy+y^{2}\\ \\&\Leftrightarrow&z^{2}&=&x^{2}+y^{2}\end{array}$
D'où, $\boxed{z^{2}=x^{2}+y^{2}}$
II.2. Énoncé du théorème
Pour tout triangle rectangle le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des côtés perpendiculaires.
Application
$EFG$ est un triangle rectangle en $F$ tel que :
$$FG=3\;cm\quad\text{et}\quad FE=5\;cm$$
Faire la figure et calculer $EG.$
Solution
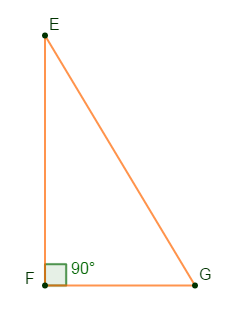
Comme $EFG$ est rectangle en $F$ alors,
$$EG^{2}=EF^{2}+FG^{2}$$
Donc,
$\begin{array}{rcl} EG^{2}&=&3^{2}+4^{2}\\ \\&=&9+16\\ \\&=&25\end{array}$
Par suite, $EG=\sqrt{25}=5$
D'où, $\boxed{EG=5\;cm}$
III. Réciproque du théorème de Pythagore
III.1. Activité
$ABC$ est un triangle tel que :
$$AB=6\;cm\;;\ AC=8\;cm\ \text{et}\ BC=10\;cm$$
1) Calculer $AB^{2}\;;\ AC^{2}\ $ et $\ BC^{2}$
2) Comparer $AB^{2}+AC^{2}\ $ et $\ BC^{2}$
3) Le théorème de Pythagore est-il vérifié ?
En déduire la nature du triangle $ABC.$
Solution
1) Calculons :
$AB^{2}=6^{2}=36$
$AC^{2}=8^{2}=64$
$BC^{2}=10^{2}=100$
2) On a :
$\begin{array}{rcl} AB^{2}+AC^{2}&=&36+64\\ \\&=&100\end{array}$
Donc, $AB^{2}+AC^{2}=BC^{2}$
3) La propriété de Pythagore est donc vérifiée.
D'où, le triangle $ABC$ est rectangle en $A.$
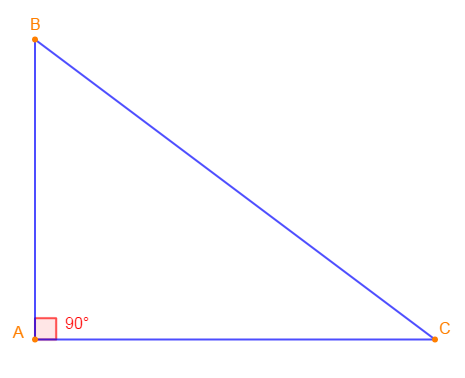
III.2. Énoncé
Si dans un triangle le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés alors, le triangle est rectangle.
IV. Longueur de la hauteur issue du sommet de l'angle droit
IV.1. Activité
Soit $ABC$ un triangle rectangle en $A\ $ et $\ H$ le pied de la hauteur issue de $\hat{A}.$
Donner l'expression de $AH$ en fonction de $AB\;,\ AC\ $ et $\ BC.$
Indication : Calculer de deux manières la surface du triangle $ABC.$
Solution
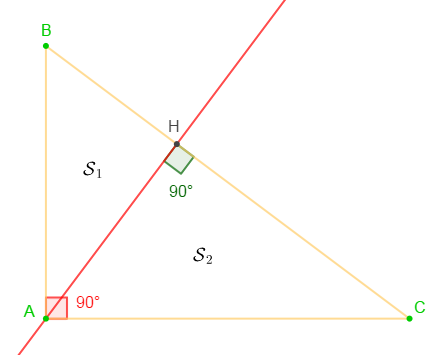
Soit :
$\mathcal{S}$ la surface de $ABC$
$\mathcal{S}_{1}$ la surface de $ABH$
$\mathcal{S}_{2}$ la surface de $ACH$
Calculons $\mathcal{S}$ de deux façons différentes
$\centerdot\ $ 1e méthode
$$\mathcal{S}=\dfrac{AB\times AC}{2}$$
$\centerdot\ $ 2e méthode
$\begin{array}{rcl}\mathcal{S}&=&\mathcal{S}_{1}+\mathcal{S}_{2}\\ \\&=&\dfrac{BH\times AH}{2}+\dfrac{AH\times HC}{2}\\ \\&=&AH\left(\dfrac{BH}{2}+\dfrac{CH}{2}\right)\\ \\&=&AH\left(\dfrac{BH+CH}{2}\right)\\ \\&=&\dfrac{AH\times BC}{2}\end{array}$
Ainsi,
$$\mathcal{S}=\dfrac{AH\times BC}{2}$$
Finalement, on a :
$\begin{array}{rcrcl}\dfrac{AH\times BC}{2}=\dfrac{AB\times AC}{2}&\Rightarrow&AH\times BC&=&AB\times AC\\ \\&\Rightarrow&AH&=&\dfrac{AB\times AC}{BC}\end{array}$
D'où, $\boxed{AH=\dfrac{AB\times AC}{BC}}$
IV.2. Énoncé
Dans un triangle rectangle la longueur de la hauteur issue du sommet de l'angle droit est le produit des longueurs des côtés perpendiculaires divisé par la longueur de l'hypoténuse.
Application
L'unité est le $cm\;;\ 1\;cm$ sur le dessin est égal à $10\;cm$
$FLK$ est un triangle rectangle en $L.$
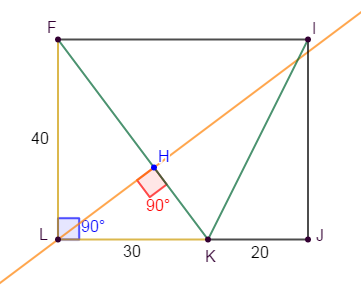
1) Montrer que $FIK$ est un triangle isocèle.
2) Déterminer la longueur du segment $[LH].$
Solution
1) Montrons que $FIK$ est isocèle.
Calculons les longueurs des côtés.
$FLK$ est un triangle rectangle en $L$ donc,
$\begin{array}{rcl} FK^{2}&=&FL^{2}+LK^{2}\\ \\&=&40^{2}+30^{2}\\ \\&=&1600+900\\ \\&=&2500\\ \\&=&50^{2}\end{array}$
Ainsi, $FK=\sqrt{50^{2}}=50$
D'où, $\boxed{FK=50\;cm}$
$IJK$ est un triangle rectangle en $J$ donc,
$\begin{array}{rcl} IK^{2}&=&KJ^{2}+JI^{2}\\ \\&=&20^{2}+40^{2}\\ \\&=&400+1600\\ \\&=&2000\end{array}$
Ainsi, $IK=\sqrt{2000}=20\sqrt{5}$
D'où, $\boxed{IK=20\sqrt{5}\;cm}$
Comme $FI=LJ=50\;cm\ $ et $\ FK=50\;cm$ alors, $FKI$ est isocèle en $F.$
2) Déterminons la longueur du segment $[LH].$
On a : $FLK$ un triangle rectangle en $L\ $ et $\ H$ le pied de la hauteur issue de $L$ donc,
$\begin{array}{rcl} LH&=&\dfrac{FL\times LK}{FK}\\ \\&=&\dfrac{40\times 30}{50}\\ \\&=&24\end{array}$
D'où, $\boxed{LH=24\;cm}$
Auteur:
Mamadou Siradji Dia

Commentaires
hosanna (non vérifié)
mar, 10/27/2020 - 21:36
Permalien
super merci beaucoup
Anonyme (non vérifié)
mar, 10/27/2020 - 21:36
Permalien
super
habib ndiaye (non vérifié)
lun, 07/12/2021 - 20:25
Permalien
super
Anonyme (non vérifié)
lun, 07/12/2021 - 21:38
Permalien
Merci
Anonyme (non vérifié)
jeu, 02/03/2022 - 21:01
Permalien
Excellent j'aimerais
Anonyme (non vérifié)
mer, 06/15/2022 - 22:16
Permalien
Excellent en maths
Ahmadou (non vérifié)
mer, 06/22/2022 - 19:44
Permalien
Merci à vous
Anonyme (non vérifié)
mer, 03/15/2023 - 08:06
Permalien
revoir les erreurs
Anonyme (non vérifié)
lun, 03/10/2025 - 22:54
Permalien
Merc
Anonyme (non vérifié)
ven, 05/16/2025 - 15:03
Permalien
Merci beaucoup c'est très
Ajouter un commentaire