Série d'exercices sur les transformations du plan 1e S
Généralités
Exercice 1
Le plan est rapporté à un repère $(O\;,\ \vec{i}\;,\ \vec{j})$. Au point $M(x\;,\ y)$, on fait correspondre
$M'(x'\;,\ y')$ tel que :
$$\left\lbrace\begin{array}{lcl} x' &=& \alpha x+\beta y \\ \\ y' &=& \gamma x+\delta y \end{array}\right.$$
$\alpha\;,\ \beta\;,\ \gamma\text{ et }\delta$ étant des réels donnés.
1) Cette correspondance est(elle une application de $\mathcal{P}$ vers $\mathcal{P}$ ?
A quelle condition est-ce une transformation de $\mathcal{P}$ ?
Déterminer alors la transformation réciproque.
2) On suppose la condition précédente vérifiée pour l'application $f_{1}$, correspondant aux réels $\alpha_{1}\;,\ \beta_{1}\;,\ \gamma_{1}\text{ et }\delta_{1}$ et pour pour l'application $f_{2}$, correspondant aux réels $\alpha_{2}\;,\ \beta_{2}\;,\ \gamma_{2}\text{ et }\delta_{2}.$
Montrer que $f_{2}\circ f_{1}$ est une transformation de $\mathcal{P}.$
Exercice 2
Dans le plan $\mathcal{P}$ rapporté à un repère $(O\;,\ \vec{i}\;,\ \vec{j})$, on fait correspondre au point $M(x\;,\ y)$ le point $M'(x'\;,\ y')$.
Cette correspondance est-elle une application de $\mathcal{P}\text{ vers }\mathcal{P}$ ?
De $\mathcal{P}$ privé de certains points ?
a) $\left\lbrace\begin{array}{lcl} x' &=& x^{2}+y^{2} \\ \\ y' &=& x^{2}-y^{2}\end{array}\right.$
b) $\left\lbrace\begin{array}{lcl} x' &=& \sqrt{x} \\ \\ y' &=& \sqrt{y}\end{array}\right.$
c) $\left\lbrace\begin{array}{lcl} x' &=& \dfrac{x}{x^{2}+y^{2}} \\ \\ y' &=& \dfrac{y}{x^{2}+y^{2}}\end{array}\right.$
d) $\left\lbrace\begin{array}{lcl} x' &=& \sqrt{x^{2}+y^{2}} \\ \\ y' &=& x-y\end{array}\right.$
Exercice 3
Affinités
Soit deux droites sécantes $\mathcal{D}\text{ et }\Delta$ et un réel $k$ différent de zéro.
Par un point quelconque $M$ du plan, on trace la parallèle à $\Delta$ qui coupe $\mathcal{D}\text{ en }H$ et on construit le point $M'$ tel que $\overrightarrow{HM'}=k\overrightarrow{HM}$.
1) Montrer qu'on a ainsi défini une transformation $f$ du plan.
2) Déterminer les points invariants par $f$ et les droites globalement invariantes par $f.$
3) Déterminer l'image par $f$ d'une droite.
Soit un point $A$ et son image $A'\text{ par }f.$
Utiliser le résultat précédent pour construire simplement l'image $M'$ d'un point $M$ quelconque donné.
4) Déterminer $f^{-1}.$
5) En choisissant un repère $(O\;,\ \vec{i}\;,\ \vec{j})$ convenable, donner une expression analytique de $f.$
Exercice 4
Dans le plan rapporté au repère $(O\;,\ \vec{i}\;,\ \vec{j})$, on considère les droites $\mathcal{D}\text{ et }\mathcal{D'}$ d'équations :
$\mathcal{D}\ :\ 3x+2y-6=0\;;\qquad \mathcal{D'}\ :\ x-4y+4=0$
Soit un point $M(x\;,\ y)$ du plan.
La parallèle à $\mathcal{D}$ menée par $M$ coupe $x'x\text{ en }H$; La parallèle à $\mathcal{D'}$ menée par $M$ coupe $y'y\text{ en }K$.
Soit $M'(x'\;,\ y')$ le point qui se projette en $H\text{ sur }x'x\text{ en }K\text{ sur }y'y.$
1) Montrer que $M'$ est l'image de $M$ dans une application $f\text{ de }\mathcal{P}\text{ dans }\mathcal{P}.$
$f$ est-elle une transformation de $\mathcal{P}$ ?
2) Donner une expression analytique de $f.$
3) Existe-t-il des points invariants par $f$ ?
4) Reprendre les questions précédentes avec $\mathcal{D}\ :\ x+y=0\text{ et }\mathcal{D'}\ :\ x-y=0$
Translations
Exercice 5
Soit $ABC$ un triangle.
Construire l'image de ce triangle par la translation de vecteur :
a) $\overrightarrow{AB}\;;\quad$ b) $\overrightarrow{BC}\;;\quad$ c) $\overrightarrow{CA}\;;\quad$ d) $\vec{V}\text{ quelconque.}$
2) On note $t_{\vec{u}}$ la translation de vecteur $\vec{u}$
Déterminer $t_{\overrightarrow{AB}}\circ t_{\overrightarrow{BC}}\circ t_{\overrightarrow{AC}}$
3) Soit $A'\;,\ B'\text{ et }C'$ les images de $A\;,\ B\text{ et }C$ par la translation $t_{\overrightarrow{AB}}\circ t_{\overrightarrow{AC}}$
Quelle est la nature des quadrilatères $ABA'C\;,\ BCC'B'\;,\ ABB'C$ ?
4) Le quadrilatère $ABA'C$ peut-il être un losange ? un carré ?
Exercice 6
On considère un parallélogramme $ABCD.$
Construire l'image de ce parallélogramme par la translation de vecteur :
a) $\overrightarrow{AB}\;;\qquad$ b) $\overrightarrow{BC}\;;\qquad$ c) $\overrightarrow{CA}\;;\qquad$ d) $\vec{V}\text{ quelconque}$
Exercice 7
1) Soient deux cercles $\mathcal{C}\text{ et }\mathcal{C'}$ de centres $O\text{ et }O '$ et de même rayon.
Montrer que l'un de ces deux cercles est l'image de l'autre dans une translation que l'on précisera.
2) On suppose maintenant que $\mathcal{C}\text{ et }\mathcal{C'}$ sont sécants en $A\text{ et }B.$
$t$ désigne la translation de vecteur $\overrightarrow{OO'}$
Soit $M$ un point de $\mathcal{C}\text{ et }M'$ son image par $t.$
Démontrer que $A$ est l'orthocentre du triangle $MBM'.$
Exercice 8
On considère un parallélogramme $ABCD$, les sommets $A\text{ et }B$ étant fixes.
Quel est l'ensemble des points $D$ lorsque $C$ décrit une droite ou un cercle donné ?
Exercice 9
Soit deux droites sécantes $\mathcal{D}\text{ et }\mathcal{D'}$ et un vecteur $\vec{u}$
Construire un segment $[MM']$ tel que $M$ appartienne à $\mathcal{D}\;,\ M'\text{ appartienne à }\mathcal{D'}$ et que l'on ait $\overrightarrow{MM'}=\vec{u}$
Exercice 10
On donne un cercle $\mathcal{C}$ et deux point $A\text{ et }B.$
Construire, en utilisant une translation deux points $P\text{ et }Q\text{ de }\mathcal{C}$ tels que $ABPQ$ soit un parallélogramme.
Exercice 11
$A\;,\ B\text{ et }C$ sont 3 points non alignés ; $t$ est la translation qui transforme $A\text{ en }B.$
$D$ est l'image de $B\text{ par }t.$ La parallèle à $(BC)$ menée par $\mathcal{D}$ coupe $(AC)\text{ en }E.$
Démontrer que $C$ est le milieu de $[AE].$
Exercice 12
$ABC$ est un triangle.
$M\text{ et }N$ sont les points définis par $\overrightarrow{AM}=\overrightarrow{CA}\text{ et } \overrightarrow{BN}=\overrightarrow{MB}$
1) Construire $M\text{ et }N.$
2) La translation qui transforme $B\text{ en }N$ transforme $A\text{ en }E.$
Montrer que $(EN)\parallel (AB)\text{ et }(CE)\parallel (AB).$
Que peut-on en déduire pour les points $C\;,\ E\text{ et }N$ ?
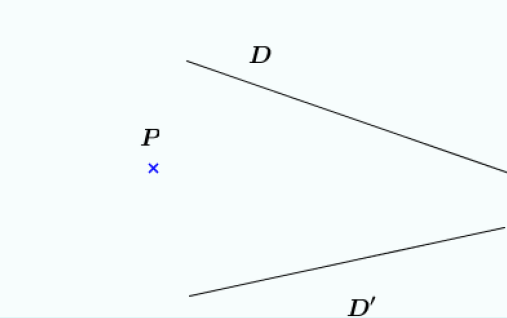
Exercice 13
Construire la droite passant par $P$ et concourante à $D\text{ et }D'.$
Exercice 14
Soit un triangle $ABC$ d'orthocentre $H$ et deux points $D\text{ et }E$ tels que $BCDE$ soit un parallélogramme.
Les perpendiculaires menées de $D\text{ à }(AB)\text{ et de }E\text{ à }(AC)$ se coupent en $K.$
1) Montrer que $K$ est le transformé de $H$ dans la translation de vecteur $\overrightarrow{BE}$
2) En déduire une condition pour que $A\;,\ H\;,\ K$ soient alignés.
Exercice 15
On considère un parallélogramme $ABCD.$
1) Montrer qu'il existe une translation qui transforme la droite $(AB)$ en la droite $(DC)$ et la droite $(AD)$ en la droite $(BC).$
2) Soit $K$ un point du plan.
Une droite $\Delta$ passant par $K\text{ coupe }(AB)\text{ et }(DC)\text{ en }M\text{ et }N$ respectivement, $(AD)\text{ et }(BC)\text{ en }P\text{ et }Q$ respectivement.
Montrer qu'il existe deux droites $\Delta$ telles que les segments $[MN]\text{ et }[PQ]$ aient la même longueur.
Exercice 16
On considère un triangle $ABC$ et une droite $D$ passant par $A.$
On marque sur $D$ deux points $P\text{ et }Q$ tels que $A$ soit le milieu de $[PQ].$
Soit $P'$ l'image de $P$ par la translation de vecteur $\overrightarrow{AB}\text{ et }Q'$ l'image de $Q$ par la translation de vecteur $\overrightarrow{AC}.$
Montrer que les segments $[BC]\text{ et }[PQ]$ ont le même milieu.
Exercice 17
Le plan est muni d'un repère $(O\;,\ \vec{i}\;,\ \vec{j})$
Donner l'expression analytique de la translation de vecteur $\vec{V}$ et une équation cartésienne de la transformée de la droite $\mathcal{D}$ et du cercle $\mathcal{D}$ dans chacun des cas suivants :
1) $\vec{V}(4\;,\ -1)\quad \mathcal{D}\ :\ 5x-y+4=0\quad \mathcal{C}\ :\ x^{2}+y^{2}-9=0.$
2) $\vec{V}(-3\;,\ -5)\quad \mathcal{D}\ :\ x+4y+1=0\quad \mathcal{C}\ :\ x^{2}+y^{2}-2x-2y-7=0$
Exercice 18
Dans le plan muni du repère $(O\;,\ \vec{i}\;,\ \vec{j})$, on considère les points
$A(2\;,\ 0)\;,\ B(1\;,\ -2)\;,\ C(-1\;,\ 2)\text{ et }D(3\;,\ 3).$
Soit $t$ la translation de vecteur $\overrightarrow{AB}\text{ et }B'\;,\ C'\text{ et }D'$ les images respectives de $B\;,\ C\text{ et }D\text{ par }t.$
1) Écrire les formules analytiques de $t$ et en déduire les coordonnées des points $B'\;,\ C'\text{ et }D'.$
2) Soit $G$ le barycentre des points pondérés $(B\;,\ 2)\text{ et }(D\;,\ -3).$
Déterminer les coordonnées de $G.$
3) Soit $G'$ l'image de $G\text{ par }t.$
Déterminer les coordonnées de $G'$ et vérifier que le point $G'$ est le barycentre des points pondérés $(B'\;,\ 2)\text{ et }(D'\;,\ -3).$
4) Soit $K$ l'isobarycentre des points $B\;,\ C\text{ et }D.$ Déterminer les coordonnées de $K.$
5) Montrer que $K'$, image de $K$, est l'isobarycentre des points $B'\;,\ C'\text{ et }D'.$
Exercice 19
$\mathcal{D}\text{ et }\mathcal{D'}$ sont deux droits parallèles ; $A\text{ et }B$ sont deux points fixes situés à l'extérieur de la bande de plan déterminée par $\mathcal{D}\text{ et }\mathcal{D'}$ et de part et d'autre de cette bande.
Déterminer un point $M\text{ sur }\mathcal{D}$ et un point $M'\text{ sur }\mathcal{D'}$ tels que la droite $(MM')$ soit perpendiculaire à $\mathcal{D}\text{ et }\mathcal{D'}$ et que la somme $AM+MM'+M'B$ soit minimale.
Exercice 20
$\mathcal{D}\text{ et }\mathcal{D'}$ sont deux droits parallèles ; $A\text{ et }B$ sont deux points fixes situés de part et d'autre de la bande comprise entre $D\text{ et }\mathcal{D'}.$
Une droite $(\Delta)$ variable, de direction fixée, coupe respectivement $\mathcal{D}\text{ et }\mathcal{D'}\text{ en }M\text{ et }M'.$
Déterminer $(\Delta)$ pour que la longueur de la ligne brisée $AMM'B$ soit minimale.
Homothéties
Exercice 21
Soit un triangle $ABC.$
Construire l'image de ce triangle par l'homothétie de centre $O$ et de rapport $k$ dans les cas suivants :
$a)\ O=A\text{ et }k=-1.\qquad b)\ O=A\text{ et }k=2$
$c)\ O\text{ est le milieu de }[BC]\text{ et }k=2.$
$d)\ O\text{ et }k\text{ sont quelconques.}$
Exercice 22
Montrer que l'image d'un carré par une homothétie est un carré.
Exercice 23
Soit $A\text{ et }B$ deux points du plan, $A'\text{ et }B'$ leurs images par une homothétie $h$ de centre $O$ et de rapport $k$ ; montrer que l'image par $h$ du milieu $I\text{ de }[AB]$ est le milieu $I'\text{ de }[A'B'].$
En déduire que l'image du centre de gravité $G$ d'un triangle $ABC$ par $h$ est le centre de gravité du triangle $A'B'C'$ homothétique du triangle $ABC.$
Exercice 24
Soit $O\;,\ A\;,\ B$ trois points donnés.
Montrer qu'il existe une unique homothétie $h$ de centre $O$ transformant $A\text{ en }B$ dans les cas suivants ; (on déterminera son rapport) :
$a)\ \overrightarrow{OB}=-\dfrac{3}{2}\overrightarrow{OA}\qquad b)\ \overrightarrow{AB}=5\overrightarrow{OA}\qquad c)\ \overrightarrow{OA}+\overrightarrow{OB}=\vec{0}$
Exercice 25
Soit $A\text{ et }B$ deux points donnés.
Montrer qu'il existe une unique homothétie $h$ de rapport $k$ transformant $A\text{ en }B$ dans les cas suivants (on déterminera son centre) :
$a)\ k=2\qquad b)\ k=-\dfrac{1}{2}\qquad c)\ k=-1$
Exercice 26
Soient $A\;,\ B\;,\ A'\;,\ B'$ des points donnés du plan.
On suppose que $A\text{ et }B$ sont distincts, $A'\text{ et }B'$ sont distincts, les droites $(AB)\text{ et }(A'B')$ sont parallèles, et $\overrightarrow{AB}\neq \overrightarrow{A'B'}$
Montrer qu'il existe une unique homothétie $h$ transformant $A\text{ en }A'\text{ et } B\text{ en }B'$
(construire son centre et déterminer son rapport).
Exercice 27
Soit deux triangles $ABC\text{ et }A'B'C'$ dont les cotés $(AB)\text{ et }(A'B')$
$(BC)\text{ et }(B'C')\;,\ (CA)\text{ et }(C'A')$ sont parallèles.
1) On suppose que $AB=A'B'.$
Montrer que l'un de ces triangles est l'image de l'autre dans une translation ou dans une symétrie centrale que l'on précisera.
(On distinguera les deux cas $\overrightarrow{AB}=\overrightarrow{A'B'}\text{ et }\overrightarrow{AB}=-\overrightarrow{A'B'})$
2) On suppose que $AB\neq A'B'.$
Montrer que l'un de ces triangles est l'image de l'autre dans une homothétie que l'on précisera
Exercice 28
Soit un parallélogramme $ABCD.$
Construire l'image de ce parallélogramme par l'homothétie de centre $O$ et de rapport $k$ dans les cas suivants :
$a)\ O=A\text{ et }k=-1\qquad b)\ O=A\text{ et }k=2$
$c)\ O\text{ est le milieu de }[BC]\text{ et }k=2\qquad d)\ O\text{ et }k\text{ sont quelconques.}$
Exercice 29
Montrer que la composée de deux symétries centrales est une translation.
Exercice 30
Soit $ABC$ un triangle.
On note $A'\text{ et }B'$ les milieux des cotés $[BC]\text{ et }[AC]$, $H$ l'orthocentre, $G$ le centre de gravité et $O$ le centre du cercle circonscrit au triangle $ABC.$
On considère l'homothétie $h$ de centre $G$ qui transforme $A\text{ en }A'.$
Quel est son rapport ?
Quelle est l'image de la droite $(AH)$ ? de la droite $(BH)$ ?
En déduire que $H\;,\ G\;,\ O$ sont alignés (la droite contenant ces points est appelée droite d'Euler).
Exercice 31
Le plan est rapporté au repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
On considère le point $I(-2\;,\ 3)$ et la droite $D$ d'équation $2x+y-3=0.$
Définir analytiquement l'homothétie de centre $I$ et de rapport $-\dfrac{2}{3}$, puis donner une équation de l'image de $D\text{ par }h.$
Exercice 32
On considère deux droites $D\text{ et }D'$ sécantes en $O$ et un point $A$ extérieur à ces droites.
Le but de l'exercice est de construire $M\text{ sur }D\text{ et }N\text{ sur }D'$ vérifiant la relation vectorielle :
$\overrightarrow{AN}=-2\overrightarrow{AM}.$
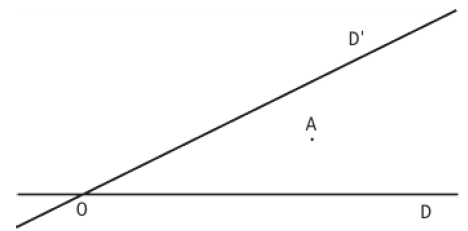
1) Montrer que $N$ est l'image de $M$ par une transformation que l'on précisera.
2) En déduire que $N$ est aussi sur une droite $\Delta$ que l'on précisera.
3) Achever la construction.
Exercice 33
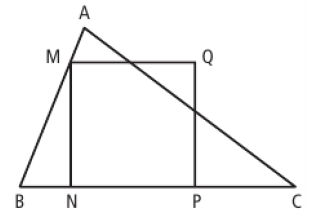
On considère un triangle $ABC$ ayant 3 angles aigus.
$M$ est un point de $[AB].$
$P\text{ et }N$ sont deux points de $[BC].$
$Q$ est tels que $MNPQ$ est un carré.
Construire grâce à une homothétie un carré $IJKL$ dont tous les sommets sont sur les cotés du triangle $ABC.$
Exercice 34
Soit $C$ un cercle et soit $A\text{ et }B$ deux points extérieurs au cercle, $I$ étant le milieu de $[AB].$
1) A tout point $M\text{ de }C$ on associe le point $N$ centre de gravité de $ABM.$
Montrer que $N$ est l'image de $M$ par une homothétie bien choisie.
Déterminer et construire l'ensemble des points $N$ lorsque $M$ décrit $C.$
2) A tout point $M\text{ de }C$ on associe le point $P$ tel que $AMBP$ soit un parallélogramme.
Montrer que $P$ est l'image de $M$ par une transformation que l'on précisera.
Déterminer et construire l'ensemble des points $P$ lorsque $M$ décrit $C.$

Exercice 35
$ABCD$ est un trapèze où les droites $(AB)\text{ et }(CD)$ sont parallèles alors que $(AD)\text{ et }(BC)$ ne le sont pas.
Soient $M\text{ et }N$ les milieux de $[AB]\text{ et }[CD]$, $I$ le point d'intersection de $(AC)\text{ et }(BD)$, $J$ le point d'intersection de $(AD)\text{ et }(BC).$
1) On considère l'homothétie $h$ de centre $I$ qui transforme $A\text{ en }C.$
Quelle est l'image de $B$ ?
2) En déduire que $I\;,\ M\;,\ N$ sont alignés.
3) Montrer de même que $J\;,\ M\;,\ N$ sont alignés.
Exercice 36
Composée de deux homothéties de centres distincts
Soit $h_{1}$ une homothétie de centre $O_{1}$ et de rapport $k_{1}\text{ et }h_{2}$ une homothétie de centre $O_{2}$ et de rapport $k_{2}.$
On pose $f=h_{2}\circ h_{1}.$
1) Soit $M$ un point quelconque du plan, $M_{1}=h_{1}(M)\text{ et }M'=h_{2}(M_{1}).$
On a donc :
$$\overrightarrow{O_{1}M'}=k_{1}\overrightarrow{O_{1}M}\text{ et }\overrightarrow{O_{2}M'}=k_{2}\overrightarrow{O_{2}M_{1}}$$
En déduire que :
$\overrightarrow{O_{1}M'}=k_{1}k_{2}\overrightarrow{O_{1}M}+(1-k_{2})\overrightarrow{O_{1}O_{2}}\quad (1)$
2) On suppose que $k_{1}k_{2}=1.$
Démontrer que l'égalité (1) s'écrit :
$$\overrightarrow{MM'}=(1-k_{2})\overrightarrow{O_{1}O_{2}}$$
En déduire la nature de l'application $f.$
3) On suppose que $k_{1}k_{2}\neq 1.$
a) Démontrer qu'un point $O$ est invariant par $f$ si et seulement si :
$$\overrightarrow{O_{1}O}=k_{1}k_{2}\overrightarrow{O_{1}O}+(1-k_{2})\overrightarrow{O_{1}O_{2}}\quad (2).$$
En déduire l'existence et l'unicité d'un tel point $O$, défini par :
$$\overrightarrow{O_{1}O}=\dfrac{1-k_{2}}{1-k_{1}k_{2}}\overrightarrow{O_{1}O_{2}}$$
b) Déduire de (1) et (2) que $f$ est l'homothétie de centre $O$ et de rapport $k_{1}k_{2}.$
Exercice 37
Centre d'homothétie de deux cercles
A) Deux cercles $\mathcal{C}(O\;,\ R)\text{ et }\mathcal{C'}(O'\;,\ R')$ étant donnés, on se propose de déterminer les homothéties transformant $\mathcal{C}\text{ en }\mathcal{C'}.$
1) Soit $h$ une telle homothétie, si elle existe et $k$ son rapport.
Montrer que l'on a :
$$k=\dfrac{R'}{R}\text{ ou }k=-\dfrac{R'}{R}.$$
2) a) Démontrer que, s'il existe une homothétie de rapport $\dfrac{R'}{R}$ transformant $\mathcal{C}\text{ en }\mathcal{C'}$, son centre $I$ est tel que $R\;\overrightarrow{IO'}+R'\overrightarrow{IO}=\vec{0}.\quad(1)$
Démontrer que si $R\neq R'$, l'égalité (1) définit un point $I$ et un seul.
b) Vérifier que l'homothétie de centre $I$ et de rapport $\dfrac{R'}{R}$ répond alors à la question.
3) a) Démontrer que, s'il existe une homothétie de rapport $-\dfrac{R'}{R}$ transformant $\mathcal{C}\text{ en }\mathcal{C'}$, son centre $J$ est tel que $R\;\overrightarrow{JO'}+R'\overrightarrow{JO}=\vec{0}.\quad(2)$
Démontrer que l'égalité (2) définit un point $J$ et un seul.
b) Vérifier que l'homothétie de centre $J$ et de rapport $\dfrac{R'}{R}$ répond alors à la question.
Ainsi, étant donnés deux cercles $\mathcal{C}\text{ et }\mathcal{C'}$ de centres $O\text{ et }O'$ et de rayons $R\text{ et }R'$ distincts, il existe deux homothéties transformant $\mathcal{C}\text{ en }\mathcal{C'}.$
La première est l'homothétie de centre le point $I$ tel que $\overrightarrow{IO'}=-\dfrac{R'}{R}\overrightarrow{JO}$ et de rapport $-\dfrac{R'}{R}$
La seconde est l'homothétie de centre le point $J$ tel que $\overrightarrow{JO'}=-\dfrac{R'}{R}\overrightarrow{JO}$ et de rapport $-\dfrac{R'}{R}.$
Notons que si $O\text{ et }O'$ sont distincts, alors $I\text{ et }J$ sont alignés avec $O\text{ et }O'$ (droite des centres des deux cercles) et on a :
$\dfrac{\overline{IO'}}{\overline{IO}}=-\dfrac{\overline{JO'}}{\overline{JO}}=\dfrac{R'}{R}.$
$I\text{ et }J$ sont appelés centres d'homothétie des cercles $\mathcal{C}\text{ et }\mathcal{C'}.$
4) Étudier le cas où $O=O'$, puis celui où $R=R'\text{ et }O\neq O'.$
Conclure par un théorème.
B) Soient $\mathcal{C}\text{ et }\mathcal{C'}$ deux cercles de centres $O\text{ et }O'$ distincts et de rayons $R\text{ et }R'$ distincts.
Soient $I\text{ et }J$ leurs centres d'homothétie.
1) Deux demi-droites $Ox\text{ et }O'x'$ parallèles et de même sens, coupent respectivement $\mathcal{C}\text{ en }A\text{ et }\mathcal{C'}\text{ en }A'.$
Démontrer que la droite $(AA')$ passe par $I.$
2) Deux demi-droites $Ox\text{ et }O'x'$ parallèles et de sens contraires, coupent respectivement $\mathcal{C}\text{ en }A\text{ et }\mathcal{C'}\text{ en }A''.$
Démontrer que la droite $(AA'')$ passe par $J.$
3) Déduire des deux questions précédentes une construction des centres d'homothétie $I\text{ et }J.$
B) Soit $\mathcal{D}$ une droite tangente à $\mathcal{C}\text{ en }A$ et tangente à $\mathcal{C'}\text{ en }A'.$
1) Démontrer que la droite $\mathcal{D}$ passe par $I\text{ ou }J.$
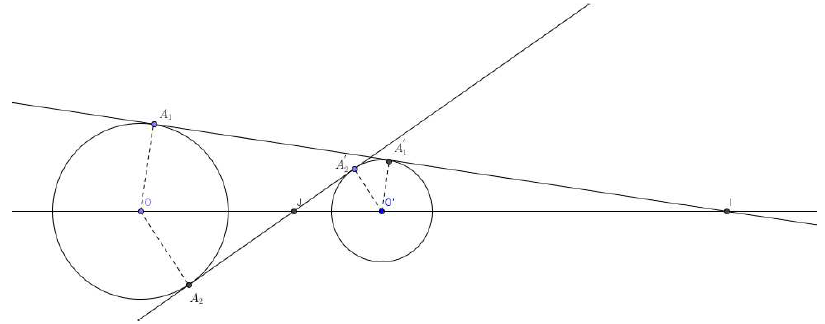
2) En déduire que les éventuelles tangentes communes à $\mathcal{C}\text{ et }\mathcal{C'}$ sont les tangentes à $\mathcal{C}$ passant par $I\text{ et }J$, s'il en existe.
3) Construire $I\text{ et }J$ et les tangentes communes à $\mathcal{C}\text{ et }\mathcal{C'}$ dans les cas suivants :
a) $\mathcal{C}\text{ et }\mathcal{C'}$ sont extérieurs : $OO'>R+R'$ ;
b) $\mathcal{C}\text{ et }\mathcal{C'}$ sont tangents extérieurement : $OO'=R+R'$ ;
c) $\mathcal{C}\text{ et }\mathcal{C'}$ sont sécants : $|R-R'|<OO'<R+R'$ ;
d) $\mathcal{C}\text{ et }\mathcal{C'}$ sont tangents intérieurement : $OO'=|R-R'|$ ;
e) un des deux cercles $\mathcal{C}\text{ et }\mathcal{C'}$ est extérieur à l'autre : $OO'<|R-R'|.$
Exercice 38
La figure ci-après obtenue à partir des quatre droites $(AC)\;,\ (CF)\;,\ (AD)\text{ et }(FB)$
sécantes deux à deux est appelée quadrilatère complet de sommets $A\;,\ B\;,\ C\;,\ D\;,\ E\text{ et }F.$
On se propose de démontrer que les segments $[AF]\;,\ [BD]\text{ et }[EC]$ ont leurs milieux respectifs $I\;,\ J\;,\ K$ alignés.
1) Construire les points $R\text{ et }S$ tels que les quadrilatères $FBRD\text{ et }ESCF$ sont des parallélogrammes.
2) On considère l'homothétie $h_{1}$ de centre $A$ qui transforme $B\text{ en }C$ et l'homothétie $h_{2}$ de centre $A$ qui transforme $D\text{ en }E.$
a) Démontrer que l'image de la droite $(BR)\text{ par }h_{2}\circ h_{1}$ est la droite $(ES).$
b) Déterminer l'image de la droite $(DR)\text{ par }h_{1}\circ h_{2}.$
c) Que dire des transformations $h_{1}\circ h_{2}\text{ et }h_{2}\circ h_{1}$ ?
On pose $h=h_{1}\circ h_{2}.$ Déterminer $h(R).$
En déduire que les points $A\;,\ R\text{ et }S$ sont alignés.
3) On considère l'homothétie $h'$ de centre $F$ et de rapport $\dfrac{1}{2}.$
Déterminer les images des points $A\;,\ R\;,\ S\text{ par }h'.$
En déduire que les points $I\;,\ J\text{ et }K$ sont alignés.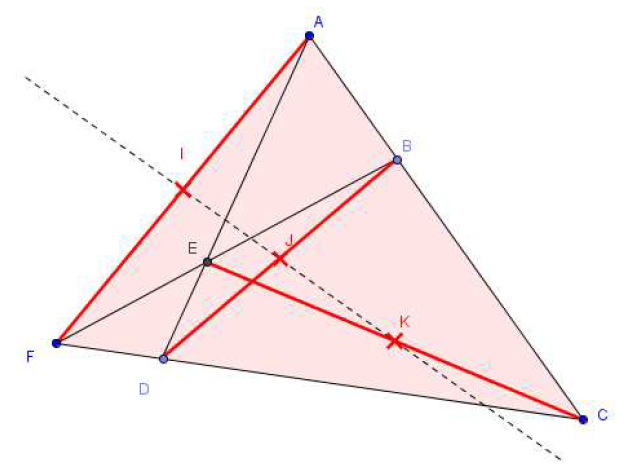
Exercice 39
1) On considère un cercle $C$ de centre $O$, et deux tangentes à $C$ sécantes en $I.$
Montrer que $O$ est sur la bissectrice de l'angle formé par les deux tangentes.
2) Soient deux droites $D\text{ et }D'$ sécantes en $I$, $A$ un point extérieur aux deux droites.
Construire un cercle tangent à $D\text{ et }D'$ :
choisir son centre en tenant compte de la question 1 et construire les points de contact de ce cercle avec $D\text{ et }D'.$
3) Construire en utilisant des homothéties deux cercles tangents à $D\text{ et }D'$ passant par $A.$
Justifier la construction.
Réflexions
Exercice 40
Soit $ABCD$ un parallélogramme et $s$ la réflexion d'axe $(BD).$
On désigne par $A\text{ et }C'$ les images respectives de $A\text{ et }C\text{ par }s.$
1) Déterminer l'image par $s$ de la droite $(AC)$, puis celle du segment $[AC].$
2) Montrer que le milieu $I\text{ de }[AC]$ est invariant par $s.$
3) Déduire des questions précédentes que $AA'CC'$ est un rectangle.
Exercice 41
Soit $ABC$ un triangle rectangle en $A$, $K$ le milieu de $[BC]$, $H$ le projeté orthogonal de $A\text{ sur }[BC]$, $I\text{ et }J$ les projetés orthogonaux de $H\text{ sur }(AB)\text{ et }(AC)$ respectivement.
Le but de l'exercice est de montrer que les droites $(AK)\text{ et }(IJ)$ sont perpendiculaires.
On désigne par $s$ la réflexion d'axe $(AB)$ et on pose $C'=s(C)\;,\ H'=s(H).$
1) a) Construire les points $H'\text{ et }C'.$
Montrer que $B\;,\ H'\text{ et }C'$ sont alignés.
b) Construire le plus simplement possible le point $K'=s(K).$
2) a) Quelle est la nature de $AKK'C'$ ?
b) Montrer que $(IJ)\text{ et }(AH')$ sont parallèles.
3) Montrer que $(AH')\text{ et }(BC')$ sont perpendiculaires.
4) Déduire des questions précédentes que les droites $(AK)\text{ et }(IJ)$ sont perpendiculaires
Exercice 42
$ABC$ est un triangle.
On note $H$ son orthocentre et $O$ le centre de son cercle circonscrit $\mathcal{C}.$
$[AD]$ est un diamètre de $\mathcal{C}.$
La droite $(AH)$ recoupe $\mathcal{C}\text{ en }A''\text{ et }(BC)\text{ en }A'.$
Le point $O'$ est le milieu de $[BC]\text{ et }\Delta$ est la parallèle à $(BC)$ passant par $O.$
On note $s_{1}$ la réflexion d'axe $\Delta$ et $s_{2}$ la réflexion d'axe $(BC).$
1) Montrer que le quadrilatère $BHCD$ est un parallélogramme.
2) Montrer, en utilisant une homothétie, que $\overrightarrow{AH}=2\overrightarrow{OO}.$
3) Identifier la transformation $s_{2}\circ s_{1}.$
Donner l'image de $A\text{ par }s_{2}\circ s_{1}$ et préciser alors $s_{2}\circ s_{1}.$
4) Quelle est l'image de $H\text{ par }s_{2}$ ?
Formuler alors une propriété remarquable de l'orthocentre du triangle et du cercle circonscrit.
5) Application :
Construire un triangle $ABC$ connaissant son cercle circonscrit $\mathcal{C}$ de centre $O$, son orthocentre $H$ et un point $D\text{ du coté }[BC].$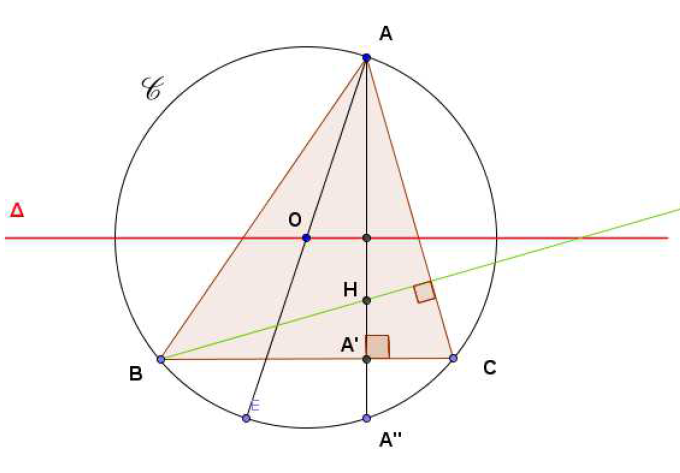
Rotations. Composée D'isométries
Exercice 43
Dans un plan orienté, on considère un triangle $ABC$ tel que $(\overrightarrow{AB}\;,\ \overrightarrow{AC})=\dfrac{\pi}{3}[2\pi]\text{ et }AB<AC$;
On désigne par $\zeta$ le cercle circonscrit à ce triangle et par $O$ son centre
1) Faire un figure
2) Soit $E=\{M\in\;P \setminus(\overrightarrow{AB}\;,\ \overrightarrow{AC})=\dfrac{\pi}{3}[2\pi]\}$
a) Vérifier que $A\in\; E$ puis déterminer et construire $E$
b) Déterminer et construire le point $I$ tel que $IB=IC\text{ et }(\overrightarrow{IB}\;,\ \overrightarrow{IC})=\dfrac{\pi}{3}[\pi]$
3) Soit $P$ le point du segment $[AC]$ tel que $CP=AB$
a) Montrer qu'il existe une unique rotation $R$ telle que $R(A)=P\text{ et }R(B)=C$, quel est son angle
b) Déterminer le centre de la rotation $R$
4) Donner la nature du triangle $IAP$ et en déduire que : $AC=AI+AB$
5) Soit $M$ un point variable de l'ensemble $F\text{ et }G$ le centre de gravité du triangle $MBC.$
Déterminer et construire l'ensemble décrit par le point $G$ lorsque $M$ décrit $E$
Exercice 44
Soit $(O\;,\ \vec{i}\;,\ \vec{j})$ un repère orthonormé du plan
Soit $f$ l'application qui à tout point $M(x\;,\ y)$ du plan associe le point $M'(x'\;,\ y')$ du plan tel que
$$\left\lbrace\begin{array}{lcl} x' &=& \dfrac{1}{2}x-\dfrac{\sqrt{3}}{2}y+\dfrac{\sqrt{3}-2}{2} \\ \\ y' &=& \dfrac{\sqrt{3}}{2}x+\dfrac{1}{2}y+\dfrac{1+2\sqrt{3}}{2}\end{array}\right. $$
1) Montrer que $f$ est une isométrie du plan
2) Montrer que le point $\Omega(-2\;,\ 1)$ est l'unique point invariant par $f$
3) Soit les points $M(x\;,\ y)\text{ et }M'(x'\;,\ y')$ tel que $f(M)=M'$
a) Exprimer en fonction de $x\text{ et }y$ $\overrightarrow{\Omega M}\cdot \overrightarrow{\Omega M'}$ et déterminer $(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}).$
b) En déduire la mesure principale de l'angle $(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}).$
c) Quelle est alors la nature de $f$ ?
Exercice 45
Dans un plan orienté, on considère un parallélogramme $ABCD$ de sens direct
1) Construire le triangle $IAD$ rectangle et isocèle en $I$ tel que
$(\overrightarrow{IA}\;,\ \overrightarrow{ID})=\dfrac{\pi}{2}[2\pi]$
et le triangle $DCE$ rectangle isocèle en $D$ tel que
$(\overrightarrow{DC}\;,\ \overrightarrow{DE})=\dfrac{\pi}{2}[2\pi]$
2) Soit $R$ la rotation de centre $I$ et d'angle $\dfrac{\pi}{2}$
a) Quelle est l'image de $A\text{ par }R$ ?
b) Montrer que $R(B)=E.$
3) Soit $A'$ le symétrique de $A$ par rapport à $I.$
a) Justifier que $A'=R(D)$
b) Montrer que $A'E=BD$ et que les droites $(A'E)\text{ et }(BD)$ sont perpendiculaires
Exercice 46
Dans un plan orienté ; on considère un triangle $ABC$ de sens direct.
$BAB'\text{ et }ACC'$ deux triangles rectangles et isocèles en $A$ et de sens direct
1) En utilisant la rotation $r_{1}$ de centre $A$ et d'angle $\dfrac{\pi}{2}$, montrer que :
$BC'=B'C\text{ et que }(BC')\perp (B'C)$
2) a) Montrer qu'il existe une unique rotation $r_{2}$ qui transforme $B\text{ en }C\text{ et }C'\text{ en }B'$
b) Déterminer son angle $\theta$ et construire son centre $J$
3) Soit $E= B\times C'\text{ et }F=C\times B'$
a) Déterminer $r_{1}(F)\text{ et }r_{2}(E).$
b) En déduire que $AFJE$ est un carré.
Exercice 46
Dans un plan orienté ; on considère un triangle $ABC$ rectangle et isocèle en $A$ tel que
$(\overrightarrow{AB}\;,\ \overrightarrow{AC})=\dfrac{\pi}{2}[2\pi].$
On désigne par $I$ le milieu de $[BC]$ et par $\Delta$ la droite perpendiculaire à $(BC)$ et passant par $C$ et on désigne par $K$ le point d'intersection de $\Delta\text{ et }(AB).$
1) Faire une figure
2) Soit $R$ la rotation de centre $A$ et d'angle $\dfrac{\pi}{2}.$
a) Déterminer $R(B)\;,\ R((AC))et R((BC))$
b) Déduire $R(C)\text{ et }R(I)$
3) On désigne par $\zeta$ le cercle circonscrit au triangle $ABC$
Déterminer l'image $\zeta'$ du cercle $\zeta$ par la rotation $R$ puis déterminer $\zeta\cap\zeta'$
4) Soit $M$ un point du plan tel que $(\overrightarrow{MA}\;,\ \overrightarrow{MB})=\dfrac{5\pi}{4}[2\pi]$
a) Déterminer l'ensemble des points $M$
b) On pose $M'=R(M)$, déterminer l'ensemble des points $M'$ lorsque $M$ varie
c) On pose $R(I)=J$, montrer que $(BM)\perp (CM')\text{ et que }IM=JM'.$
Exercice 47
Dans un plan orienté, on considère un carré $ABCD$ de centre $O$ tel que
$(\overrightarrow{AB}\;,\ \overrightarrow{AD})=\dfrac{\pi}{2}[2\pi].$
Soit $R$ la rotation de centre $O$ et d'angle $\dfrac{\pi}{2}.$
1) a) Montrer que $R(D)=A\text{ et }R(C)=D$
b) Déterminer la nature et les élément caractéristiques de $R\circ R$
c) En déduire que $R(A)=B$
2) Soit $M$ un point du segment $[AD]$ distinct de $A\text{ et }D.$
La perpendiculaire à la droite $(MC)$ passant par $D$ coupe le segment $[AB]$ en un point $N$
a) Déterminer les images du segment $[AD]$ et de la droite $(MC)$ par la rotation $R$
b) En déduire que $R(M)=N$
c) En déduire que $CM=DN\text{ et que }(CM)\perp (DN)$
3) Soit $\zeta$ le cercle de centre $O$ et passant par $A$ ; la demi-droite $[CM)$ recoupe le cercle $\zeta\text{ en }E.$ Soit $F$ le point de la demi-droite $[DN)$ tel que $DF=CE.$
a) Montrer que $R(E)=F.$
b) Déterminer l'image de $\zeta$ par $R.$
c) En déduire l'ensemble des points $F$ lorsque $M$ varie sur le segment $[AD].$
Exercice 48
Dans un plan orienté ; on considère un triangle équilatéral $ABC$ tel que
$(\overrightarrow{AB}\;,\ \overrightarrow{AC})=\dfrac{\pi}{3}[2\pi].$
Soit $I$ le milieu de $[BC].$
Soit le point $J$ tel que $B$ est le milieu de $[JC]$
Soit la rotation $R_{1}$ de centre $A$ et d'angle $\dfrac{\pi}{3}$ et la rotation $R_{2}$ de centre $B$ et d'angle $-\dfrac{2\pi}{3}.$
1) Soit $A'\text{ et }B'$ les images respectifs des points $A\text{ et }B$ par l'application $R_{1}\circ R_{2}$
Montrer que $I$ est le milieu de $[AA']$ et que $B$ est le milieu de $[AB']$
2) On pose $M_{1}=R_{1}(M)\text{ et }M_{2}=R_{2}(M).$
En précisant la nature de $R_{1}\circ R_{2}^{-1}.$
Montrer que pour tout point $M$ du plan, $I$ est le milieu $[M_{1}M_{2}]$
3) Montrer que l'application $R_{1}\circ R_{2}$ est une rotation dont on déterminera le centre et l'angle.

Commentaires
Anonyme (non vérifié)
sam, 01/18/2020 - 22:21
Permalien
Très bon
AMEGNIKOU Yves ... (non vérifié)
sam, 05/23/2020 - 12:15
Permalien
Corrigés des exercices
Abdoul Aziz Ada... (non vérifié)
sam, 06/06/2020 - 01:44
Permalien
Bonsoir, j'ai besoin de
Freddy william (non vérifié)
mer, 02/17/2021 - 20:23
Permalien
Vous avez des très bons
Mamadou SY (non vérifié)
dim, 03/27/2022 - 21:18
Permalien
correction des exercices
bilal el wely (non vérifié)
ven, 05/13/2022 - 22:22
Permalien
svp la correction de exercices
bilal el wely (non vérifié)
ven, 05/13/2022 - 22:29
Permalien
vos exercices sont intéressants
joelle (non vérifié)
dim, 03/19/2023 - 19:44
Permalien
Vos exercices sont très
joelle (non vérifié)
dim, 03/19/2023 - 19:46
Permalien
S'il vous plait puis-je avoir
Victor F (non vérifié)
jeu, 05/11/2023 - 20:07
Permalien
Corrigé svp
j'adore scorpion (non vérifié)
jeu, 11/16/2023 - 03:29
Permalien
Puis je avoir la solution des
Anonyme (non vérifié)
ven, 04/12/2024 - 12:58
Permalien
S'il vous plaît la correction
KITATA NAMURE D... (non vérifié)
jeu, 10/24/2024 - 15:06
Permalien
Réponses aux questions d'exercices sur transformation du plan
Ajouter un commentaire