Les nombres complexes - T S
Classe:
Terminale
I. Définition et notations
On appelle ensemble des nombres complexes l'ensemble noté $\mathbb{C}$ qui :
$-$ contient $\mathbb{R}\;;\quad \mathbb{R}\subset\mathbb{C}$
$-$ muni de l'addition et de la multiplication possède les mêmes propriétés que $\mathbb{R}$ (commutativité, associativité, élément neutre, élément symétrique ou opposé, distributivité, etc...)
$-$ contient un élément noté $\mathrm{i}$ vérifiant $\mathrm{i}^{2}=-1$
$\centerdot\ \ $ tout élément $z\in\mathbb{C}$ s'écrit, de façon algébrique, $z=a+\mathrm{i}b\;,\ a\text{ et }b\in\mathbb{R}$
$a$ est appelé la partie réelle de $z$ notée $\Re e(z)=a$
$b$ est appelé la partie imaginaire de $z$ notée $\Im m(z)=b$
$\centerdot\ \ z=a+\mathrm{i}b$ est réel si, et seulement si, $b=0\quad(\Im m(z)=0)$
$\centerdot\ \ z=a+\mathrm{i}b$ est imaginaire pur si, et seulement si, $a=0\quad(\Re e(z)=0)$
$\centerdot\ \ z=a+\mathrm{i}b=0\ $ si, et seulement si, $$\left\lbrace\begin{array}{rcl} a&=&0 \\ b&=&0\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} \Re e(z)&=&0 \\ \Im m(z)&=&0\end{array}\right.$$
$\centerdot\ \ $ Soient $z$ et $z'$ deux nombres complexes tels que $z=a+\mathrm{i}b$ et $z'=a'+\mathrm{i}b'$ alors $z=z'$ si, et seulement si, $$\left\lbrace\begin{array}{rcl} a&=&a' \\ b&=&b'\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} \Re e(z)&=&\Re e(z') \\ \Im m(z)&=&\Im m(z')\end{array}\right.$$
Remarque
Les identités remarquables de $\mathbb{R}$ restent aussi valables dans $\mathbb{C}$
$(a+\mathrm{i}b)^{2}=a^{2}-b^{2}+2\mathrm{i}ab$
$(a-\mathrm{i}b)^{2}=a^{2}+b^{2}-2\mathrm{i}ab$
II. Conjugué d'un nombre complexe
II.1 Définition
$a\;,\ b\in\mathbb{R}$ , on appelle conjugué du nombre complexe $z=a+\mathrm{i}b$, le nombre complexe noté $\overline{z}=a-\mathrm{i}b$
Exemple
$z_{1}=2-3\mathrm{i}\;,\quad \overline{z}_{1}=2+3\mathrm{i}\;,\quad z_{2}=-4\mathrm{i}\;,\quad \overline{z}_{2}=4\mathrm{i}$
$z_{3}=-7\;,\quad \overline{z}_{3}=-7\;,\quad z_{4}=\mathrm{i}\;,\quad \overline{z}_{4}=-\mathrm{i}$
II.2 Propriétés
$\centerdot\ \ z$ est réel si, et seulement si, $\overline{z}=z$
$\centerdot\ \ z$ est imaginaire pur si, et seulement si, $\overline{z}=-z$
$\centerdot\ \ \Re e(z)=\dfrac{z+\overline{z}}{2}$
$\centerdot\ \ \Im m(z)=\dfrac{z-\overline{z}}{2\mathrm{i}}$
$\centerdot\ \ \overline{z+z'}=\overline{z}+\overline{z}'$
$\centerdot\ \ \overline{zz'}=\overline{z}\times\overline{z}'$
$\centerdot\ \ \overline{\left(\dfrac{1}{z}\right)}=\dfrac{1}{\overline{z}}$
$\centerdot\ \ \overline{\left(\dfrac{z}{z'}\right)}=\dfrac{\overline{z}}{\overline{z'}}$
$\centerdot\ \ p\in\mathbb{Z}\;,\ \overline{z^{p}}=\overline{z}^{p}$
III. Représentation graphique d'un nombre complexe
Soit $(O\;;\ \vec{e}_{1}\;,\ \vec{e}_{2})$ un repère orthonormé direct.
$\centerdot\ \ $ Tout nombre complexe $z=a+\mathrm{i}b\;,\ a\text{ et }b\in\mathbb{R}$ peut être représenté dans le plan par un point $M\begin{pmatrix} a \\ b\end{pmatrix}$ ou par un vecteur $\vec{u}\begin{pmatrix} a \\ b\end{pmatrix}.$
On dira que $M$ est le point image de $z$ et on note $M(z)$ ou que $z$ est l'affixe de $M$ et on note $z_{M}.$
On dit aussi que $\vec{u}$ est le vecteur image de $z$ et on note $\vec{u}(z)$ ou que $z$ est l'affixe de $\vec{u}$ et on note $z_{\vec{u}}.$
$\centerdot\ \ $ Soient $A\begin{pmatrix} a_{1} \\ a_{2}\end{pmatrix}$ et $B\begin{pmatrix} b_{1} \\ b_{2}\end{pmatrix}$ deux points du plan, alors :
$z_{A}=a_{1}+\mathrm{i}a_{2}\;,\ z_{B}=b_{1}+\mathrm{i}b_{2}$ et
$\begin{array}{rcl} z_{\overrightarrow{AB}}&=&b_{1}-a_{1}+\mathrm{i}(b_{2}-a_{2}) \\ \\ &=&(b_{1}+\mathrm{i}b_{2})-(a_{1}+\mathrm{i}a_{2}) \\ \\ &=&z_{B}-z_{A} \end{array}$
Donc $$z_{\overrightarrow{AB}}=z_{B}-z_{A}$$
$\centerdot\ \ $ Soient $A(z_{A})\;,\ B(z_{B})$ et $C(z_{C})$ trois points du plan. Si $G$ est barycentre de $(A\;,\ \alpha)\;;\ (B\;,\ \beta)$ et $(C\;,\ \gamma)$ alors l'affixe de $G$ est $$\dfrac{\alpha z_{A}+\beta z_{B}+\gamma z_{C}}{\alpha+\beta+\gamma}$$
$\centerdot\ \ z$ est réel si, et seulement si, $M(z)\in(x'Ox)$
$\centerdot\ \ z$ est imaginaire pur si, et seulement si, $M(z)\in(y'Oy)$
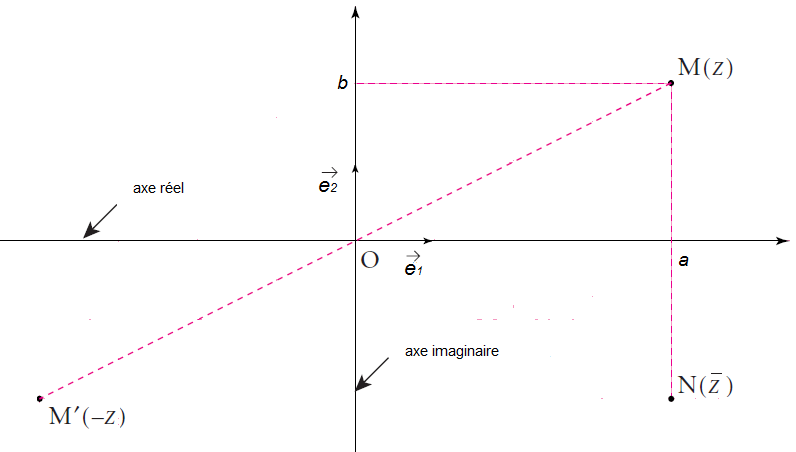
$\centerdot\ \ M(z)\text{ et }N(\overline{z})$ sont symétriques par rapport à $(Ox)$
$\centerdot\ \ M(z)\text{ et }M'(-z)$ sont symétriques par rapport à $O$
Exercice d'application
Le plan est muni d'un repère orthonormé direct $(O\;;\ \vec{u}\;,\ \vec{v})$ et soit $z=x+\mathrm{i}y$ un nombre complexe.
1) Déterminer l'ensemble des points $M(z)$ du plan tels que $z^{2}$ soit :
a) réel
b) imaginaire pur
2) Soient $A\begin{pmatrix} 1\\ -1\end{pmatrix}$ et $B\begin{pmatrix} 0\\ 2\end{pmatrix}$ deux points du plan et $M$ d'affixe $z.$
On pose $Z=\dfrac{z-1+\mathrm{i}}{z-2\mathrm{i}}$
a) Exprimer $\Re e(Z)$ et $\Im m(Z)$ en fonction de $x$ et $y$
b) Déterminer l'ensemble des points $M(Z)$ tels que :
$-\ \ Z$ soit réel
$-\ \ Z$ soit imaginaire pur
Résolution
1) On a $z^{2}=x^{2}-y^{2}+2\mathrm{i}xy$
a)
$\begin{array}{rcl} z^{2}\ \text{ est réel }&\Leftrightarrow&2xy=0 \\ \\ &\Leftrightarrow&x=0\quad\text{ou}\quad y=0\end{array}$
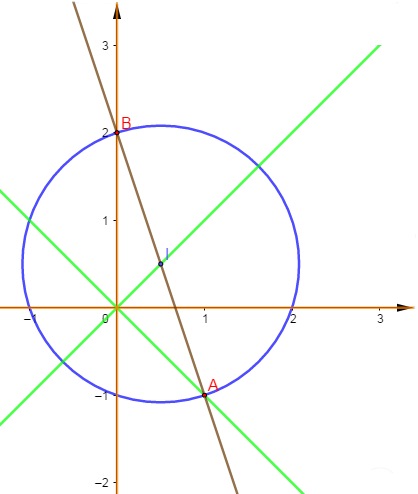
Donc l'ensemble des points $M(z)$ du plan tels que $z^{2}$ soit réel est la réunion des axes du repère.
b)
$\begin{array}{rcl} z^{2}\ \text{ est imaginaire pur }&\Leftrightarrow&x^{2}-y^{2}=0 \\ \\ &\Leftrightarrow&(x-y)(x+y)=0\\ \\ &\Leftrightarrow&x=y\quad\text{ou}\quad x=-y\end{array}$
Donc l'ensemble des points $M(z)$ du plan tels que $z^{2}$ soit imaginaire pur est la réunion des bissectrices du repère.
2)
$\begin{array}{rcl} Z=\dfrac{z-1+\mathrm{i}}{z-2\mathrm{i}}&=&\dfrac{x+\mathrm{i}y-1+\mathrm{i}}{x+\mathrm{i}y-2\mathrm{i}}\\ \\ &=&\dfrac{(x-1)+\mathrm{i}(y+1)}{x+\mathrm{i}(y-2)}\\ \\ &=&\dfrac{[(x-1)+\mathrm{i}(y+1)][x-\mathrm{i}(y-2)]}{[x+\mathrm{i}(y-2)][x-\mathrm{i}(y-2)]}\\ \\ &=&\dfrac{x(x-1)+(y+1)(y-2)+\mathrm{i}[-(x-1)(y-2)+x(y+1)]}{x^{2}+(y-2)^{2}}\\ \\ &=&\dfrac{x^{2}+y^{2}-x-y-2+\mathrm{i}(3x+y-2)}{x^{2}+(y-2)^{2}}\\ \\ &=&\dfrac{x^{2}+y^{2}-x-y-2}{x^{2}+(y-2)^{2}}+\mathrm{i}\dfrac{3x+y-2}{x^{2}+(y-2)^{2}}\end{array}$
Donc $\ \Re e(Z)=\dfrac{x^{2}+y^{2}-x-y-2}{x^{2}+(y-2)^{2}}\ $ et $\ \Im m(Z)=\dfrac{3x+y-2}{x^{2}+(y-2)^{2}}$
b)
$\begin{array}{rcl} Z\ \text{ réel }&\Leftrightarrow&\Im m(Z)=0\\ \\ &\Leftrightarrow&\dfrac{3x+y-2}{x^{2}+(y-2)^{2}}=0\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}3x+y-2&=&0 \\ x^{2}+(y-2)^{2}&\neq&0\ \Rightarrow\ x\neq 0\quad\text{et}\quad y\neq 2 \end{array}\right.\end{array}$
Donc l'ensemble des points $M(Z)$ tels que $Z$ soit réel est la droite $\Delta$ d'équation $3x+y-2=0$ privée du point $B(2\mathrm{i}).$
$\begin{array}{rcl} Z\ \text{ imaginaire pur }&\Leftrightarrow&\Re e(Z)=0\\ \\ &\Leftrightarrow&\dfrac{x^{2}+y^{2}-x-y-2}{x^{2}+(y-2)^{2}}=0\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}x^{2}+y^{2}-x-y-2&=&0 \\ x^{2}+(y-2)^{2}&\neq&0\ \Rightarrow\ x\neq 0\quad\text{et}\quad y\neq 2 \end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\left(x-\dfrac{1}{2}\right)^{2}+\left(y-\dfrac{1}{2}\right)^{2}-\dfrac{1}{4}-\dfrac{1}{4}-2&=&0 \\ \\ x\neq 0&\text{et}&y\neq 2 \end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\left(x-\dfrac{1}{2}\right)^{2}+\left(y-\dfrac{1}{2}\right)^{2}&=&\dfrac{5}{2} \\ \\ x\neq 0&\text{et}&y\neq 2 \end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\left(x-\dfrac{1}{2}\right)^{2}+\left(y-\dfrac{1}{2}\right)^{2}&=&\left(\dfrac{\sqrt{10}}{2}\right)^{2} \\ \\ x\neq 0&\text{et}&y\neq 2 \end{array}\right.\end{array}$
Donc l'ensemble des points $M(Z)$ tels que $Z$ soit imaginaire pur est le cercle $\mathcal{C}\left(I\begin{pmatrix} \dfrac{1}{2} \\ \\ \dfrac{1}{2}\end{pmatrix}\;;\ \dfrac{\sqrt{10}}{2}\right)$ privé du point $B(2\mathrm{i}).$
IV. Module d'un nombre complexe
IV.1 Définition
On appelle module d'un nombre complexe $z=a+\mathrm{i}b$ le réel positif noté $$|z|=\sqrt{z\overline{z}}=\sqrt{a^{2}+b^{2}}$$
$\centerdot\ \ $ Si $M\begin{pmatrix} x\\ y\end{pmatrix}$ est d'affixe $z$ alors, $$||\overrightarrow{OM}||=OM=\sqrt{x^{2}+y^{2}}=|z|$$
$\centerdot\ \ $ Si $A\begin{pmatrix} a_{1} \\ a_{2}\end{pmatrix}$ et $B\begin{pmatrix} b_{1} \\ b_{2}\end{pmatrix}$ deux points du plan alors, $$||\overrightarrow{AB}||=\sqrt{(b_{1}-a_{1})^{2}+(b_{2}-a_{2})^{2}}=|z_{\overrightarrow{AB}}|=|z_{B}-z_{A}|$$
IV.2 Propriétés
$\centerdot\ \ a\in\mathbb{R}\;,\ z=a$, alors $|z|=|a|$
$\centerdot\ \ |\mathrm{i}b|=|b|$
$\centerdot\ \ |z|=|\overline{z}|$
$\centerdot\ \ \lambda\in\mathbb{R}\;,\ |\lambda z|=|\lambda||z|$
$\centerdot\ \ |zz'|=|z|\times|z'|$
$\centerdot\ \ z'\neq 0\;,\ \left|\dfrac{z}{z'}\right|=\dfrac{|z|}{|z'|}$
$\centerdot\ \ p\in\mathbb{Z}\;,\ |z^{p}|=|z|^{p}$
$\centerdot\ \ |z+z'|\leq|z|+|z'|$ (inégalité triangulaire)
$\centerdot\ \ |z_{M}-z_{A}|=AM$
Exercice d'application
Soient $A\begin{pmatrix} 1\\ -1\end{pmatrix}$ et $B\begin{pmatrix} 0\\ 2\end{pmatrix}$ deux points du plan et $M$ d'affixe $z=x+\mathrm{i}y.$
1) Déterminer l'ensemble des points $M(z)$ tels que $|Z|=1$ où $Z=\dfrac{z-1+\mathrm{i}}{z-2\mathrm{i}}$
2) Déterminer l'ensemble des points $M(z)$ tels que $|Z|=2$
3) Déterminer l'ensemble des points $M(z)$ tels que $(z-1+\mathrm{i})(\overline{z}-1-\mathrm{i})=16$
Résolution
1)
$\begin{array}{rcl} |Z|=1&\Rightarrow&\left|\dfrac{z-1+\mathrm{i}}{z-2\mathrm{i}}\right|=1\\ \\ &\Rightarrow&\dfrac{|z-1+\mathrm{i}|}{|z-2\mathrm{i}|}=1\\ \\ &\Rightarrow&|z-1+\mathrm{i}|=|z-2\mathrm{i}|\quad\text{or }M(z)\;,\ A(1-\mathrm{i})\ \text{ et }\ B(2\mathrm{i})\\ \\ &\Rightarrow&|z_{M}-z_{A}|=|z_{M}-z_{B}|\\ \\ &\Rightarrow&AM=BM\end{array}$
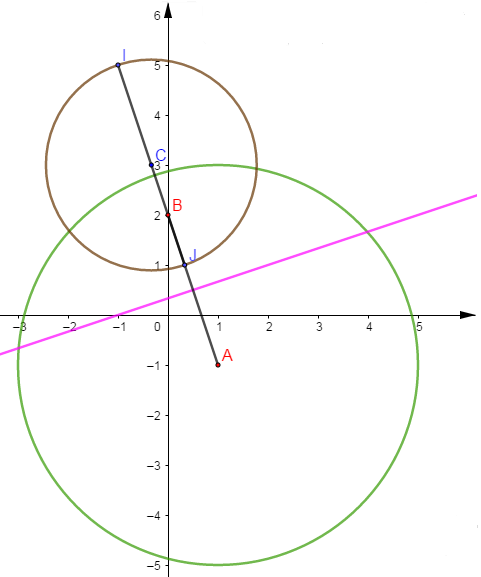
Donc l'ensemble des points $M(z)$ tels que $|Z|=1$ est la médiatrice de $[AB].$
2) Soit $I$ barycentre de $(A\;,\ 1)\;;\ (B\;,\ -2)$ et $J$ barycentre de $(A\;,\ 1)\;;\ (B\;,\ 2)$ alors,
$\begin{array}{rcl} |Z|=2&\Rightarrow&\left|\dfrac{z-1+\mathrm{i}}{z-2\mathrm{i}}\right|=2\\ \\ &\Rightarrow&MA=2MB\\ \\ &\Rightarrow& MA^{2}=4MB^{2}\\ \\ &\Rightarrow&MA^{2}-4MB^{2}=0\\ \\ &\Rightarrow&(\overrightarrow{MA}-2\overrightarrow{MB})\cdot(\overrightarrow{MA}+2\overrightarrow{MB})=0 \\ \\ &\Rightarrow&-\overrightarrow{MI}\cdot(3\overrightarrow{MJ})=0\\ \\ &\Rightarrow& -3\overrightarrow{MI}\cdot\overrightarrow{MJ}=0\\ \\ &\Rightarrow&\overrightarrow{MI}\cdot\overrightarrow{MJ}=0 \end{array}$
Donc l'ensemble des points $M(z)$ tels que $|Z|=2$ est le cercle de diamètre $[IJ].$
3)
$\begin{array}{rcl} (z-1+\mathrm{i})(\overline{z}-1-\mathrm{i})=16&\Leftrightarrow&z\overline{z}-z-\mathrm{i}z-\overline{z}+1+\mathrm{i}+\mathrm{i}\overline{z}-\mathrm{i}+1=16\\ \\ &\Leftrightarrow&z\overline{z}-(z+\overline{z})-\mathrm{i}(z-\overline{z})+2=16\\ \\ &\Leftrightarrow&|z|^{2}-2\Re e(z)-\mathrm{i}2\mathrm{i}\Im m(z)+2=16\\ \\ &\Leftrightarrow&x^{2}+y^{2}-2x+2y+2=16\\ \\ &\Leftrightarrow&(x-1)^{2}+(y+1)^{2}-1-1+2=16\\ \\ &\Leftrightarrow&(x-1)^{2}+(y+1)^{2}=(4)^{2}\end{array}$
Donc l'ensemble des points $M(z)$ tels que $(z-1+\mathrm{i})(\overline{z}-1-\mathrm{i})=16$ est le cercle $\mathcal{C}(A\;,\ 4).$
V. Argument et forme trigonométrique d'un nombre complexe non nul
V.1 Définition
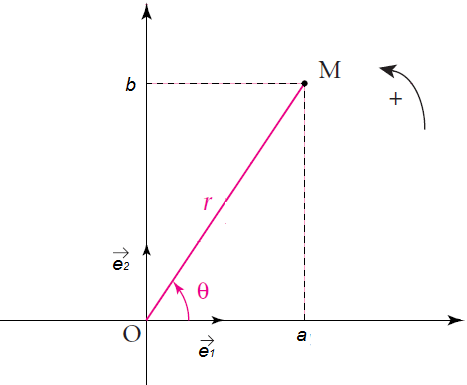
Soit $(O\;;\ \vec{e}_{1}\;,\ \vec{e}_{2})$ un repère orthonormé direct et $(\mathcal{C})$ le cercle de centre $O$ et de rayon 1.
Soit $M\begin{pmatrix} a \\ b\end{pmatrix}$ un point du plan d'affixe $z=a+\mathrm{i}b$
1er cas :
Si $|z|=1$ alors $OM=1\ \Rightarrow\ M\in\mathcal{C}(O\;,\ 1)$.
Donc $\exists\;\theta\in\mathbb{R}\;;\ (\vec{e}_{1}\;,\ \overrightarrow{OM})=\theta\;(2\pi).$
Soit $M\begin{pmatrix} \cos\theta \\ \sin\theta\end{pmatrix}$. Alors, $$z=\cos\theta+\mathrm{i}\sin\theta$$ est appelé forme trigonométrique du complexe $z$ et $$\theta=(\vec{e}_{1}\;,\ \overrightarrow{OM})$$ est l'argument de $z$ noté $arg\;z=\theta\;(2\pi)$
2em cas :
Si $|z|\neq 1$ alors on pose $Z=\dfrac{z}{|z|}\ \Rightarrow\ |Z|=1$.
Alors, d'après le 1er cas
$\begin{array}{rcl} \exists\;\theta\in\mathbb{R}\;;\ Z=\cos\theta+\mathrm{i}\sin\theta&\Rightarrow&\dfrac{z}{|z|}=\cos\theta+\mathrm{i}\sin\theta\\ \\ &\Rightarrow&z=|z|(\cos\theta+\mathrm{i}\sin\theta)\end{array}$
Donc $$z=|z|(\cos\theta+\mathrm{i}\sin\theta)$$ est la forme trigonométrique et $\theta$ est un argument de $z.$
En résumé, si $|z|=r$ et $arg\;z=\theta\;(2\pi)$ alors $$z=r(\cos\theta+\mathrm{i}\sin\theta)$$ est la forme trigonométrique de $z.$
Exercice d'application
Déterminer les formes trigonométriques et arguments de :
$z_{1}=\mathrm{i}\;,\quad z_{2}=-\mathrm{i}\;,\quad z_{3}=-1\;,\quad z_{4}=\dfrac{1}{2}-\mathrm{i}\dfrac{\sqrt{3}}{2}$
$z_{5}=2-2\mathrm{i}\;,\quad z_{6}=\dfrac{\sqrt{6}-\mathrm{i}\sqrt{2}}{2}\;,\quad z_{7}=1+\cos\theta-\mathrm{i}\sin\theta$
Résolution
$z_{1}=\mathrm{i}=\cos\dfrac{\pi}{2}+\mathrm{i}\sin\dfrac{\pi}{2}\ $ donc $\ arg\;z_{1}=\dfrac{\pi}{2}\;(2\pi)$
$z_{2}=-\mathrm{i}=\cos\left(-\dfrac{\pi}{2}\right)+\mathrm{i}\sin\left(-\dfrac{\pi}{2}\right)\ $ donc $\ arg\;z_{2}=-\dfrac{\pi}{2}\;(2\pi)$
$z_{3}=-1=\cos\pi+\mathrm{i}\sin\pi\ $ donc $\ arg\;z_{3}=\pi\;(2\pi)$
$\begin{array}{rcl} z_{4}&=&\dfrac{1}{2}-\mathrm{i}\dfrac{\sqrt{3}}{2}\\ \\ &=&\cos\dfrac{\pi}{3}-\mathrm{i}\sin\dfrac{\pi}{3}\\ \\ &=&\cos\left(-\dfrac{\pi}{3}\right)+\mathrm{i}\sin\left(-\dfrac{\pi}{3}\right)\end{array}$
donc $arg\;z_{4}=-\dfrac{\pi}{3}\;(2\pi)$
$|z_{5}|=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}\ $
donc on a :
$\begin{array}{rcl} z_{5}&=&2-2\mathrm{i}\\ \\ &=&2\sqrt{2}\left(\dfrac{1}{\sqrt{2}}-\mathrm{i}\dfrac{1}{\sqrt{2}}\right)\\ \\ &=&2\sqrt{2}\left(\dfrac{\sqrt{2}}{2}-\mathrm{i}\dfrac{\sqrt{2}}{2}\right)\\ \\ &=&2\sqrt{2}\left(\cos\left(-\dfrac{\pi}{4}\right)+\mathrm{i}\sin\left(-\dfrac{\pi}{4}\right)\right)\end{array}$
donc $arg\;z_{5}=-\dfrac{\pi}{4}\;(2\pi)$
$|z_{6}|=\sqrt{\dfrac{6+2}{4}}=\sqrt{2}$
donc on a :
$\begin{array}{rcl} z_{6}&=&\dfrac{\sqrt{6}-\mathrm{i}\sqrt{2}}{2}\\ \\ &=&\sqrt{2}\left(\dfrac{\sqrt{3}}{2}-\mathrm{i}\dfrac{1}{2}\right)\\ \\ &=&\sqrt{2}\left(\cos\left(-\dfrac{\pi}{6}\right)+\mathrm{i}\sin\left(-\dfrac{\pi}{6}\right)\right) \end{array}$
donc $arg\;z_{6}=-\dfrac{\pi}{6}\;(2\pi)$
$\begin{array}{rcl} z_{7}&=&1+\cos\theta-\mathrm{i}\sin\theta\\ \\ &=&2\cos^{2}\dfrac{\theta}{2}-\mathrm{i}2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}\\ \\ &=&2\cos\dfrac{\theta}{2}\left(\cos\dfrac{\theta}{2}-\mathrm{i}\sin\dfrac{\theta}{2}\right)\end{array}$
On a donc $|z_{7}|=\left|2\cos\dfrac{\theta}{2}\right|$
$-\ $ Si $0\leq\theta\leq\pi\ \Rightarrow\ 0\leq\dfrac{\theta}{2}\leq\dfrac{\pi}{2}\ $ alors $\ \cos\dfrac{\theta}{2}>0$
donc $|z_{7}|=2\cos\dfrac{\theta}{2}\ \Rightarrow\ z_{7}=2\cos\dfrac{\theta}{2}\left(\cos\left(-\dfrac{\theta}{2}\right)+\mathrm{i}\sin\left(-\dfrac{\theta}{2}\right)\right)$ ainsi, $arg\;z_{7}=-\dfrac{\theta}{2}\;(2\pi)$
$-\ $ Si par contre $\pi\leq\theta\leq 2\pi\ \Rightarrow\ \dfrac{\pi}{2}\leq\dfrac{\theta}{2}\leq\pi\ $, alors $\ \cos\dfrac{\theta}{2}<0$
donc,
$\begin{array}{rcl} |z_{7}|=-2\cos\dfrac{\theta}{2}\ \Rightarrow\ z_{7}&=&-2\cos\dfrac{\theta}{2}\left(-\cos\dfrac{\theta}{2}+\mathrm{i}\sin\dfrac{\theta}{2}\right)\\ \\ &=&-2\cos\dfrac{\theta}{2}\left(\cos\left(\pi-\dfrac{\theta}{2}\right)+\mathrm{i}\sin\left(\pi-\dfrac{\theta}{2}\right)\right)\end{array}$
ainsi, $arg\;z_{7}=\left(\pi-\dfrac{\theta}{2}\right)\;(2\pi)$
V.2 Propriétés
Le plan complexe est muni d'un repère orthonormé direct $(O\;;\ \vec{e}_{1}\;,\ \vec{e}_{2}).$ Soient deux nombres complexes $z$ et $z'$ tels que $|z|=r\;,\ |z'|=r'$ et
$arg\;z=\theta\;,\ arg\;z'=\theta'.$ On a :
$\centerdot\ \ z=z'\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} r&=&r' \\ \theta&=&\theta'\;(2\pi)\end{array}\right.$
$\centerdot\ \ arg\;zz'=\theta+\theta'=arg\;z+arg\;z'\;(2\pi)$
$\centerdot\ \ arg\;\dfrac{1}{z}=-\theta=-arg\;z\;(2\pi)$
$\centerdot\ \ arg\left(\dfrac{z}{z'}\right)=\theta-\theta'=arg\;z-arg\;z'\;(2\pi)$
$\centerdot\ \ arg\;(-z)=\theta+\pi=(arg\;z+\pi)\;(2\pi)$
$\centerdot\ \ arg\;\overline{z}=-\theta=-arg\;z\;(2\pi)$
$\centerdot\ \ p\in\mathbb{Z}\;,\ arg\;z^{p}=p\theta=p\;arg\;z\;(2\pi)$
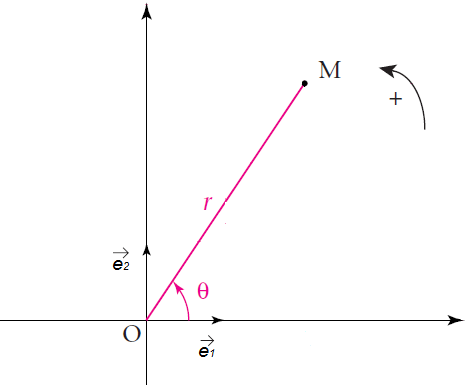
$\centerdot\ \ M(z)\;,\ arg\;z=(\vec{e}_{1}\;,\ \overrightarrow{OM})$
$\centerdot\ \ arg\;(z_{M}-z_{A})=(\vec{e}_{1}\;,\ \overrightarrow{AM})$
$\centerdot\ \ z$ réel si, et seulement si, $arg\;z=0\;(\pi)$
$\centerdot\ \ z$ réel positif si, et seulement si, $arg\;z=0\;(2\pi)$
$\centerdot\ \ z$ réel négatif si, et seulement si, $arg\;z=\pi\;(2\pi)$
$\centerdot\ \ z$ imaginaire pur si, et seulement si, $arg\;z=\dfrac{\pi}{2}\;(\pi)$
$\centerdot\ \ z$ imaginaire pur avec partie imaginaire positive si, et seulement si,
$arg\;z=\dfrac{\pi}{2}\;(2\pi)$
$\centerdot\ \ z$ imaginaire pur avec partie imaginaire négative si, et seulement si,
$arg\;z=-\dfrac{\pi}{2}\;(2\pi)$
$\centerdot\ \ arg\;\left(\dfrac{z_{M}-z_{B}}{z_{M}-z_{A}}\right)=(\overrightarrow{MA}\;,\ \overrightarrow{MB})\;(2\pi)$
Remarque
Soient $A(a)\;,\ B(b)\;,\ C(c)$ et $D(d)$ quatre points du plan complexe alors $A\;,\ B\;,\ C$ et $D$ sont cocycliques si, et seulement si, $\dfrac{(b-d)(a-c)}{(a-d)(b-c)}$ est réel.
Exercice d'application
Soient $A(2-\mathrm{i})$ et $B(1)$ deux points du plan, $M$ d'affixe $z.$
Déterminer l'ensemble des points $M(z)$ tels que $Z=\dfrac{z-2+\mathrm{i}}{z-1}$ soit :
a) réel
b) imaginaire pur
Résolution
On a $Z=\dfrac{z-2+\mathrm{i}}{z-1}=\dfrac{z-z_{A}}{z-z_{B}}$
a)
$\begin{array}{rcl} Z\ \text{ réel }&\Leftrightarrow&arg\;Z=0\;(\pi)\\ \\ &\Leftrightarrow&(\overrightarrow{MA}\;,\ \overrightarrow{MB})=0\;(\pi)\end{array}$
Donc l'ensemble des points $M(z)$ tels que $Z$ soit réel est la droite $(AB)$ privée des points $A$ et $B.$
b)
$\begin{array}{rcl} Z\ \text{ imaginaire pur }&\Leftrightarrow&arg\;Z=\dfrac{\pi}{2}\;(\pi)\\ \\ &\Leftrightarrow&(\overrightarrow{MA}\;,\ \overrightarrow{MB})=\dfrac{\pi}{2}\;(\pi)\end{array}$
Donc l'ensemble des points $M(z)$ tels que $Z$ soit imaginaire pur est le cercle de diamètre $[AB]$ privé des points $A$ et $B.$
$\centerdot\ \ $ Formule de Moivre $$p\in\mathbb{Z}\;,\quad(\cos\theta+\mathrm{i}\sin\theta)^{p}=\cos p\theta+\mathrm{i}\sin p\theta$$
Application : Expression de $\cos nx$ et $\sin nx$ en fonction de $\cos x$ ou $\sin x$
On a $(\cos x+\mathrm{i}\sin x)^{n}=\cos nx+\mathrm{i}\sin nx$ alors, $$\cos nx=\Re e(\cos x+\mathrm{i}\sin x)^{n}\quad\text{et}\quad\sin nx=\Im m(\cos x+\mathrm{i}\sin x)^{n}$$
Exercice d'application
Exprimer $\cos 4x$ et $\sin 4x$ en fonction de $\cos x$ et $\sin x$
On a :
$\begin{array}{rcl} (\cos x+\mathrm{i}\sin x)^{4}&=&\cos^{4}x+4\cos^{3}x\mathrm{i}\sin x-6\cos^{2}x\sin^{2}x-4\cos x\mathrm{i}\sin^{3}x+\sin^{4}x\\ \\ &=&\sin^{4}x+\cos^{4}x-6\cos^{2}x\sin^{2}x+\mathrm{i}(4\cos^{3}x\sin x-4\cos x\sin^{3}x)\end{array}$
or, $(\cos x+\mathrm{i}\sin x)^{4}=\cos 4x+\mathrm{i}\sin 4x$ donc,
$\cos 4x=\sin^{4}x+\cos^{4}x-6\cos^{2}x\sin^{2}x\quad\text{et}\quad\sin 4x=4\cos^{3}x\sin x-4\cos x\sin^{3}x$
VI. Forme exponentielle d'un nombre complexe non nul
VI.1 Définition
Soit $z$ un nombre complexe tel que $|z|=r$ et $arg\;z=\theta.$
On pose $\mathrm{e}^{\mathrm{i}\theta}=\cos\theta+\mathrm{i}\sin\theta.$ On a $z=r(\cos\theta+\mathrm{i}\sin\theta)=r\mathrm{e}^{\mathrm{i}\theta}.$
L'écriture $$z=r\mathrm{e}^{\mathrm{i}\theta}$$ est appelée forme exponentielle du nombre complexe $z.$
Exemple
$1=\mathrm{e}^{\mathrm{i}2k\pi}\;;\ k\in\mathbb{Z}\;,\quad -1=\mathrm{e}^{-\mathrm{i}\pi}\;,\quad \mathrm{i}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}\;,\quad -\mathrm{i}=\mathrm{e}^{-\mathrm{i}\tfrac{\pi}{2}}$
$\mathrm{j}=-\dfrac{1}{2}+\mathrm{i}\dfrac{\sqrt{3}}{2}=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}\;,\quad \overline{\mathrm{j}}=-\dfrac{1}{2}-\mathrm{i}\dfrac{\sqrt{3}}{2}=\mathrm{e}^{\mathrm{i}\tfrac{4\pi}{3}}$
VI.2 Propriétés
$\centerdot\ \ \left(\mathrm{e}^{\mathrm{i}\theta}\right)^{p}=\mathrm{e}^{\mathrm{i}p\theta}\;;\ p\in\mathbb{Z}$
$\centerdot\ \ \mathrm{e}^{\mathrm{i}\theta}\times\mathrm{e}^{\mathrm{i}\theta'}=\mathrm{e}^{\mathrm{i}(\theta+\theta')}$
$\centerdot\ \ \dfrac{\mathrm{e}^{\mathrm{i}\theta}}{\mathrm{e}^{\mathrm{i}\theta'}}=\mathrm{e}^{\mathrm{i}(\theta-\theta')}$
$\centerdot\ \ $ Formule d'Euler
On pose $\mathrm{e}^{\mathrm{i}\theta}=\cos\theta+\mathrm{i}\sin\theta$ et $\mathrm{e}^{-\mathrm{i}\theta}=\cos\theta-\mathrm{i}\sin\theta$, alors on a les formules suivantes appelées formules d'Euler $$\cos\theta=\dfrac{\mathrm{e}^{\mathrm{i}\theta}+\mathrm{e}^{-\mathrm{i}\theta}}{2}\quad\text{et}\quad\sin\theta=\dfrac{\mathrm{e}^{\mathrm{i}\theta}-\mathrm{e}^{-\mathrm{i}\theta}}{2\mathrm{i}}$$
Application : Linéarisation
Expression de $\cos^{n}x$ et $\sin^{n}x$ en fonction de $\cos px$ et $\sin px\;,\ p\in\mathbb{N}^{*}$
Exemple
Linéariser $\cos^{5}x$ et $\sin^{5}x$
Résolution
$\begin{array}{rcl} \cos^{5}x&=&\left(\dfrac{\mathrm{e}^{\mathrm{i}x}+\mathrm{e}^{-\mathrm{i}x}}{2}\right)^{5}\\ \\ &=&\left(\dfrac{1}{2}\right)^{5}\left(\mathrm{e}^{\mathrm{i}5x}+5\mathrm{e}^{\mathrm{i}x}\mathrm{e}^{-\mathrm{i}4x}+10\mathrm{e}^{\mathrm{i}2x}\mathrm{e}^{-\mathrm{i}3x}+10\mathrm{e}^{\mathrm{i}3x}\mathrm{e}^{-\mathrm{i}2x}+5\mathrm{e}^{\mathrm{i}4x}\mathrm{e}^{-\mathrm{i}x}+\mathrm{e}^{-\mathrm{i}5x}\right)\\ \\ &=&\left(\dfrac{1}{2}\right)^{5}\left((\mathrm{e}^{\mathrm{i}5x}+\mathrm{e}^{-\mathrm{i}5x})+5(\mathrm{e}^{\mathrm{i}3x}+\mathrm{e}^{-\mathrm{i}3x})+10(\mathrm{e}^{\mathrm{i}x}+\mathrm{e}^{-\mathrm{i}x})\right)\\ \\ &=&\left(\dfrac{1}{2}\right)^{5}\left(2\cos 5x+10\cos 3x+20\cos x\right)\\ \\ &=&\dfrac{1}{32}\left(2\cos 5x+10\cos 3x+20\cos x\right)\\ \\ &=&\dfrac{1}{16}\left(\cos 5x+5\cos 3x+10\cos x\right)\end{array}$
Donc $\cos^{5}x=\dfrac{1}{16}\left(\cos 5x+5\cos 3x+10\cos x\right)$
$\begin{array}{rcl} \sin^{5}x&=&\left(\dfrac{\mathrm{e}^{\mathrm{i}x}-\mathrm{e}^{-\mathrm{i}x}}{2\mathrm{i}}\right)^{5}\\ \\ &=&\left(\dfrac{1}{2\mathrm{i}}\right)^{5}\left(\mathrm{e}^{\mathrm{i}5x}+5\mathrm{e}^{\mathrm{i}x}\mathrm{e}^{-\mathrm{i}4x}-10\mathrm{e}^{\mathrm{i}2x}\mathrm{e}^{-\mathrm{i}3x}+10\mathrm{e}^{\mathrm{i}3x}\mathrm{e}^{-\mathrm{i}2x}-5\mathrm{e}^{\mathrm{i}4x}\mathrm{e}^{-\mathrm{i}x}-\mathrm{e}^{-\mathrm{i}5x}\right)\\ \\ &=&\left(\dfrac{1}{2\mathrm{i}}\right)^{5}\left((\mathrm{e}^{\mathrm{i}5x}-\mathrm{e}^{-\mathrm{i}5x})-5(\mathrm{e}^{\mathrm{i}3x}-\mathrm{e}^{-\mathrm{i}3x})+10(\mathrm{e}^{\mathrm{i}x}-\mathrm{e}^{-\mathrm{i}x})\right)\\ \\ &=&\dfrac{1}{32\mathrm{i}}\left(2\mathrm{i}\sin 5x-10\mathrm{i}\sin 3x+20\mathrm{i}\sin x\right)\\ \\ &=&\dfrac{1}{16}\left(\sin 5x-5\sin 3x+10\sin x\right)\end{array}$
Donc $\sin^{5}x=\dfrac{1}{16}\left(\sin 5x-5\sin 3x+10\sin x\right)$
VII. Équations dans $\mathbb{C}$
VII.1 Équations de la forme $az^{2}+bz+c=0$ avec $a\neq 0$
Soit l'équation $az^{2}+bz+c=0\;,\ a\neq 0$. On a $\Delta=b^{2}-4ac.$ Alors,
$-\ \ $ Si $\Delta\in\mathbb{R}_{+}^{*}$ l'équation admet deux solutions distinctes $$z_{1}=\dfrac{-b-\sqrt{\Delta}}{2a}\quad\text{et}\quad z_{2}=\dfrac{-b+\sqrt{\Delta}}{2a}$$
$-\ \ $ Si $\Delta=0$ l'équation admet une solution double $$z_{0}=\dfrac{-b-}{2a}$$
$-\ \ $ Si $\Delta\in\mathbb{R}_{-}^{*}$ l'équation admet deux solutions distinctes $$z_{1}=\dfrac{-b-\sqrt{|\Delta|}}{2a}\quad\text{et}\quad z_{2}=\dfrac{-b+\sqrt{|\Delta|}}{2a}$$
Exemple
$\Delta=-4=(2\mathrm{i})^{2}\;,\quad\Delta=-3=(\mathrm{i}\sqrt{3})^{2}$
$-\ \ $ Si $\Delta\in\mathrm{i}\mathbb{R}^{*}$ alors $\Delta$ est de la forme $\mathrm{i}b$
Exemple
$\Delta=6\mathrm{i}=3(2\mathrm{i})=[\sqrt{3}(1+\mathrm{i})]^{2}$
$\Delta=-8\mathrm{i}=4(-2\mathrm{i})=[2(1-\mathrm{i})]^{2}$
$-\ \ $ Si $\Delta\in\mathbb{C}$ l'équation admet deux solutions distinctes $z_{1}$ et $z_{2}.$
$\Delta=x+\mathrm{i}y$, donc il existe deux réels $\alpha$ et $\beta$ tels que $\Delta=(\alpha+\mathrm{i}\beta)^{2}.$ On a :
$\begin{array}{rcl} \Delta=(\alpha+\mathrm{i}\beta)^{2}&\Leftrightarrow&x+\mathrm{i}y=\alpha^{2}-\beta^{2}+2\mathrm{i}\alpha\beta\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} \alpha^{2}-\beta^{2}&=&x \\ 2\alpha\beta&=&y \\ |\Delta|&=&|(\alpha+\mathrm{i}\beta)^{2}|\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} \alpha^{2}-\beta^{2}&=&x\qquad\qquad\quad(1) \\ 2\alpha\beta&=&y\qquad\qquad\quad(2) \\ \alpha^{2}+\beta^{2}&=&\sqrt{x^{2}+y^{2}}\ \quad(3)\end{array}\right.\end{array}$
En additionnant les équations (1) et (3) on obtient $2\alpha^{2}=x+\sqrt{x^{2}+y^{2}}$ et on tire $\alpha.$
En remplaçant $\alpha$ par sa valeur dans l'équation (2) on trouve $\beta.$ Ainsi, on a : $$z_{1}=\dfrac{-b-(\alpha+\mathrm{i}\beta)}{2a}\quad\text{et}\quad z_{2}=\dfrac{-b+(\alpha+\mathrm{i}\beta)}{2a}$$
Exemple
1) On donne $\Delta=-3+4\mathrm{i}$, trouver $\alpha$ et $\beta$ tels que $\Delta=(\alpha+\mathrm{i}\beta)^{2}$
2) Résoudre dans $\mathbb{C}\;,\ z^{2}+(2-\sqrt{3}-\mathrm{i})z+(\sqrt{3}-1)(-1+\mathrm{i})=0$
Résolution
1)
$\begin{array}{rcl} \Delta=-3+4\mathrm{i}=(\alpha+\mathrm{i}\beta)^{2}&\Leftrightarrow&-3+4\mathrm{i}=\alpha^{2}-\beta^{2}+2\mathrm{i}\alpha\beta\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} \alpha^{2}-\beta^{2}&=&-3 \\ 2\alpha\beta&=&4 \\ |\Delta|&=&|(\alpha+\mathrm{i}\beta)^{2}|\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} \alpha^{2}-\beta^{2}&=&-3\quad(1) \\ 2\alpha\beta&=&4\qquad(2) \\ \alpha^{2}+\beta^{2}&=&5\qquad(3)\end{array}\right.\end{array}$
(1)+(3) entraine que $2\alpha^{2}=-3+5=2$ et donc $\alpha^{2}=1$ ; c'est-à-dire $\alpha=1$ ou $\alpha=-1.$
$-\ \ $ Si $\alpha=1$, en remplaçant dans (2) on trouve $\beta=2$, donc $\Delta=(1+2\mathrm{i})^{2}$
$-\ \ $ Si $\alpha=-1$, on trouve $\beta=-2$, donc $\Delta=(-1-2\mathrm{i})^{2}=(1+2\mathrm{i})^{2}$
2) Soit à résoudre l'équation $\mathbb{C}\;,\ z^{2}+(2-\sqrt{3}-\mathrm{i})z+(\sqrt{3}-1)(-1+\mathrm{i})=0.$
On a :
$\begin{array}{rcl} \Delta&=&(2-\sqrt{3}-\mathrm{i})^{2}-4(\sqrt{3}-1)(-1+\mathrm{i})\\ \\ &=&4+3-1-4\sqrt{3}-4\mathrm{i}+2\sqrt{3}\mathrm{i}+4\sqrt{3}-4\sqrt{3}\mathrm{i}-4+4\mathrm{i}\\ \\&=&2-2\sqrt{3}\mathrm{i}\end{array}$
Posons $\Delta=(\alpha+\mathrm{i}\beta)^{2}$ alors $\left\lbrace\begin{array}{rcl} \alpha^{2}-\beta^{2}&=&2 \\ 2\alpha\beta&=&-2\sqrt{3} \\ \alpha^{2}+\beta^{2}&=&4\end{array}\right.$
Ainsi, $2\alpha^{2}=4+2=6$ et donc $\alpha^{2}=3$ ; c'est-à-dire $\alpha=\sqrt{3}$ ou $\alpha=-\sqrt{3}.$
$-\ \ $ Si $\alpha=\sqrt{3}$, on trouve $\beta=-1$, donc
$\begin{array}{rcl} z_{1}&=&\dfrac{-2+\sqrt{3}+\mathrm{i}-(\sqrt{3}-\mathrm{i})}{2} \\ &=&-1+\mathrm{i}\end{array}\quad\text{et}\quad \begin{array}{rcl} z_{2}&=&\dfrac{-2+\sqrt{3}+\mathrm{i}+(\sqrt{3}-\mathrm{i})}{2} \\ &=&-1+\sqrt{3}\end{array}$
$-\ \ $ Si $\alpha=-\sqrt{3}$, on trouve $\beta=1$, donc
$\begin{array}{rcl} z_{1}&=&\dfrac{-2+\sqrt{3}+\mathrm{i}-(-\sqrt{3}+\mathrm{i})}{2} \\ &=&-1+\sqrt{3}\end{array}\quad\text{et}\quad\begin{array}{rcl} z_{2}&=&\dfrac{-2+\sqrt{3}+\mathrm{i}+(-\sqrt{3}+\mathrm{i})}{2} \\ &=&-1+\mathrm{i}\end{array}$
D'où $$S_{\mathbb{C}}=\{-1+\mathrm{i}\;;\ -1+\sqrt{3}\}$$
VII.2 Équations de la forme $az^{3}+bz^{2}+cz+d=0$ avec $a\neq 0$
Exemple
Soit $(E)$ l'équation définie par $(E)\ :\ z^{3}-3z^{2}+(3-\mathrm{i})z-2(1-\mathrm{i})=0.$
1) Montrer que $(E)$ admet une solution réelle à déterminer.
2) Résoudre $(E)$
Résolution
1) Soit $z=a$ la solution réelle de $(E)$
donc,
$\begin{array}{rcl} a^{3}-3a^{2}+(3-\mathrm{i})a-2(1-\mathrm{i})=0&\Rightarrow&a^{3}-3a^{2}+3a-a\mathrm{i}-2+2\mathrm{i}=0\\ \\ &\Rightarrow&a^{3}-3a^{2}+3a-2+\mathrm{i}(2-a)=0\\ \\ &\Rightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+3a-2&=&0 \\ 2-a&=&0\end{array}\right.\\ \\ &\Rightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+3a-2&=&0\quad(1) \\ a&=&2\quad(2)\end{array}\right.\end{array}$
$a=2$ vérifie aussi l'équation (1), donc 2 est la solution réelle cherchée.
2) L'équation $(E)$ devient $(z-2)(az^{2}+bz+c)=0$. En procédant par exemple par la méthode de Hörner, on détermine les coefficients $a\;,\ b$ et $c.$
On a : $(z-2)(z^{2}-z+1-\mathrm{i})=0\ \Leftrightarrow\ z=2\quad\text{ou}\quad z^{2}-z+1-\mathrm{i}=0$
Soit l'équation $z^{2}-z+1-\mathrm{i}=0$ alors,
$\begin{array}{rcl} \Delta&=&1-4+4\mathrm{i}\\ \\ &=&-3+4\mathrm{i}\\ \\ &=&(1+2\mathrm{i})^{2} \end{array}$
Donc $z_{1}=\dfrac{1-1-2\mathrm{i}}{2}=-\mathrm{i}\ \text{ et }\ z_{1}=\dfrac{1+1+2\mathrm{i}}{2}=1+\mathrm{i}$
D'où $$S_{\mathbb{C}}=\{2\;;\ -\mathrm{i}\;;\ 1+\mathrm{i}\}$$
VII.3 Racine $n^{\text{ième}}$ de l'unité
Soit à déterminer $z$ tel que $z^{n}=1$.
On a :
$\begin{array}{rcl} z^{n}=1&\Leftrightarrow&\left\lbrace\begin{array}{rcl} |z|^{n}&=&1 \\ arg\;z^{n}&=&arg\;1\;(2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} |z|&=&1 \\ n\;arg\;z&=&0\;(2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} |z|&=&1 \\ arg\;z&=&\dfrac{2k\pi}{n}\end{array}\right.\end{array}$
Donc les solutions de l'équation $z^{n}=1$ sont de la forme $$z_{k}=\mathrm{e}^{\mathrm{i}\tfrac{2k\pi}{n}}\;,\ k\in\{0\;,\ 1\;,\ \ldots\ldots\;,\ (n-1)\}$$
Exemple
Déterminer les racines cubiques de l'unité
Soit $z^{3}=1$, alors $\left\lbrace\begin{array}{rcl} |z|&=&1 \\ arg\;z&=&\dfrac{2k\pi}{3}\end{array}\right.$
Les solutions de l'équation sont de la forme $z_{k}=\mathrm{e}^{\mathrm{i}\tfrac{2k\pi}{n}}\;,\ k\in\{0\;,\ 1\;,\ 2\}.$
Donc on a $z_{0}=1\;,\ z_{1}=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}$ et $z_{2}=\mathrm{e}^{\mathrm{i}\tfrac{4\pi}{3}}$
On constate que $z_{1}=\mathrm{j}\;,\quad z_{2}=\overline{\mathrm{j}}\;,\quad \mathrm{j}^{2}=\overline{\mathrm{j}}$ et $$1+\mathrm{j}+\mathrm{j}^{2}=0$$
Remarque
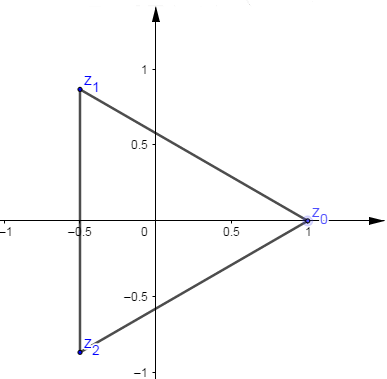
Les points images $M_{0}\;,\ M_{1}\;,\ldots\ldots\;,\ M_{k}$ des solutions $z_{k}$ sont des sommets d'un polygone régulier à $n$ cotés.
En particulier, pour l'exemple, les solutions sont les sommets d'un triangle équilatérale.
VII.4 Racine $n^{\text{ième}}$ d'un nombre complexe non nul et différent de 1
Soit à résoudre l'équation $z^{n}=b\;,\ b\in\mathbb{C}^{*}\setminus\{1\}$
1er cas
Si $a$ est solution particulière alors $a^{n}=b$ donc,
$\begin{array}{rcl} z^{n}=a^{n}&\Rightarrow&\dfrac{z^{n}}{a^{n}}=1\\ \\ &\Rightarrow&\left(\dfrac{z}{a}\right)^{n}=1\end{array}$
On pose $Z=\dfrac{z}{a}$,
On a :
$\begin{array}{rcl} Z^{n}=1&\Leftrightarrow&Z_{k}=\mathrm{e}^{\mathrm{i}\tfrac{2k\pi}{n}}\\ \\ &\Leftrightarrow&\dfrac{z_{k}}{a}=\mathrm{e}^{\mathrm{i}\tfrac{2k\pi}{n}}\\ \\ &\Leftrightarrow&z_{k}=a\mathrm{e}^{\mathrm{i}\tfrac{2k\pi}{n}}\;,\ k\in\{0\;,\ 1\;,\ \ldots\ldots\;,\ (n-1)\}\end{array}$
Donc si $a$ est solution particulière de $z^{n}=b$, alors les solutions de l'équation $z^{n}=b$ s'obtiennent en multipliant $a$ par les racines $n^{\text{ième}}$ de l'unité.
2em cas
cas général :
$z^{n}=b\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} |z|^{n}&=&|b| \\ arg\;z^{n}&=&arg\;b\;(2\pi)\end{array}\right.$
Soit $b=r\mathrm{e}^{\mathrm{i}\theta}$, donc $|b|=r$ et $arg\;b=\theta.$ On a :
$\begin{array}{rcl} \left\lbrace\begin{array}{rcl} |z|^{n}&=&|b| \\ arg\;z^{n}&=&arg\;b\;(2\pi)\end{array}\right.&\Leftrightarrow&\left\lbrace\begin{array}{rcl} |z|^{n}&=&r \\ arg\;z^{n}&=&\theta\;(2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} |z|&=&\sqrt[n]{r} \\ n\;arg\;z&=&\theta\;(2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} |z|&=&\sqrt[n]{r} \\ \\ arg\;z&=&\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\end{array}\right.\end{array}$
Donc les solutions de l'équation $z^{n}=b$ sont de la forme $$z_{k}=\sqrt[n]{r}\mathrm{e}^{\mathrm{i}\left(\tfrac{\theta}{n}+\tfrac{2k\pi}{n}\right)}\;,\ k\in\{0\;,\ 1\;,\ \ldots\ldots\;,\ (n-1)\}$$
Remarque
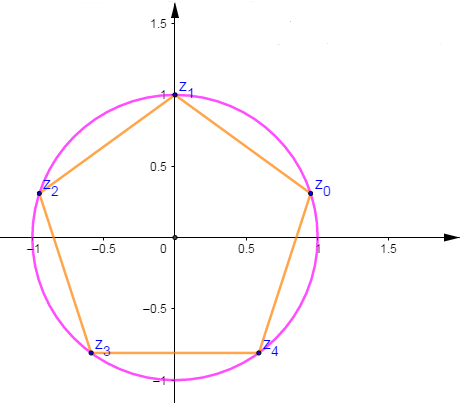
Les points images $M_{0}\;,\ M_{1}\;,\ldots\ldots\;,\ M_{k}$ des solutions $z_{k}$ sont des sommets d'un polygone régulier à $n$ cotés sur le cercle $\mathcal{C}(O\;,\ \sqrt[n]{|b|}).$
Exemple
Résoudre dans $\mathbb{C}$ l'équation $z^{3}=\mathrm{i}$
On a $\mathrm{i}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}$, donc $|\mathrm{i}|=1$ et $arg\;\mathrm{i}=\dfrac{\pi}{2}.$
Ainsi, les solutions de $z^{5}=\mathrm{i}$ sont de la forme $$z_{k}=\mathrm{e}^{\mathrm{i}\left(\tfrac{\pi}{10}+\tfrac{2k\pi}{5}\right)}\;,\ k\in\{0\;,\ 1\;,\ 2\;,\ 3\;,\ 4\}$$
VIII. Transformations du plan et complexes
VIII.1 Définition
Soit $f$ une transformation du plan qui à tout point $M$ d'affixe $z$ associe le point $M'$ d'affixe $z'.$ L'écriture de $z'$ en fonction de $z$ est appelée écriture complexe de la transformation $f.$
VIII.2 Transformations usuelles
Le plan est muni d'un repère orthonormé direct $(O\;;\ \vec{e}_{1}\;,\ \vec{e}_{2})$ et soit $b$ et $\omega$ deux nombres complexes, $k$ et $\theta$ deux réels non nuls.
Translation
La translation de vecteur $\vec{u}(b)$ a pour écriture complexe $$z'=z+b$$
En particulier, $z'=z$ est l'écriture caractéristique de l'identité du plan.
Rotation
La rotation d'angle $\theta$ et de centre $\Omega$ d'affixe $\omega$ a pour expression complexe
$$z'-\omega=\mathrm{e}^{\mathrm{i}\theta}(z-\omega)\quad\text{ou bien}\quad z'=\mathrm{e}^{\mathrm{i}\theta}z+b$$
Homothétie
L'homothétie de rapport $k$ et de centre $\Omega$ d'affixe $\omega$ a pour écriture complexe $$z'-\omega=k(z-\omega)\quad\text{ou bien}\quad z'=kz+b$$
Symétries
La symétrie d'axe réel ou réflexion d'axe $(Ox)$ a pour écriture complexe $$z'=\overline{z}$$
La symétrie d'axe imaginaire ou réflexion d'axe $(Oy)$ a pour écriture complexe $$z'=-\overline{z}$$
La symétrie d'axe $\Delta$ d'équation $y=x$ a pour écriture complexe $$z'=\mathrm{i}\overline{z}$$
La symétrie centrale de centre $O$ a pour écriture complexe $$z'=-z$$
Exemple
Parmi les écritures complexes suivantes, reconnaître les transformations et donner pour chacune d'elles les éléments caractéristiques.
1) $z'=z+3-2\mathrm{i}$
2) $z'=\left(-\dfrac{\sqrt{2}}{2}+\mathrm{i}\dfrac{\sqrt{2}}{2}\right)z$
Résolution
1) Comme le coefficient de $z$ est 1, alors la transformation associée est une translation de vecteur $\vec{u}$ d'affixe $3-2\mathrm{i}.$
2) Le coefficient de $z$ est un complexe de forme exponentielle $\mathrm{e}^{\mathrm{i}\tfrac{3\pi}{4}}$, donc la transformation est une rotation d'angle $\dfrac{3\pi}{4}$ et de centre le point $O$, d'affixe 0.
Auteur:
Diny Faye & Seyni Ndiaye

Commentaires
Kader (non vérifié)
dim, 06/16/2019 - 04:57
Permalien
Félicitations
Anonyme (non vérifié)
sam, 07/27/2019 - 14:25
Permalien
Recevoir des cours en format PDF
Anonyme (non vérifié)
dim, 03/29/2020 - 19:34
Permalien
Vous avez fait un tres bon
Anonyme (non vérifié)
ven, 01/29/2021 - 00:54
Permalien
J'ai vraiment aimé
Sire (non vérifié)
ven, 01/29/2021 - 17:58
Permalien
Je suis contente de ces cours
Anonyme (non vérifié)
ven, 02/05/2021 - 15:37
Permalien
Bien. Le cours est excellent.
Massamba DIOUF (non vérifié)
sam, 02/13/2021 - 21:55
Permalien
Vraiment c'est très gentil
YOUSSOUF Traoré (non vérifié)
mar, 11/09/2021 - 14:43
Permalien
Cette leçon est très
YOUSSOUF Traoré (non vérifié)
mar, 11/09/2021 - 14:45
Permalien
Cette leçon est très
Ajouter un commentaire