Série d'exercices : Droites des milieux 4e
Classe:
Quatrième
Exercice 1
Soit $ABC$ un triangle isocèle en $A$ tel que :
$AB=5\;cm$ et $BC=4\;cm.$
$I$ et $K$ sont les milieux respectifs de $[AB]$ et $[AC].$
1) Faire une figure complète.
2) a) Montrer que $(IK)$ et $(BC)$ sont parallèles.
b) Calculer $IK$ en précisant le théorème utilisé.
3) La parallèle à $(AB)$ passant par $K$ coupe $(BC)$ en $L.$
Montrer que $L$ est le milieu de $[BC].$
Exercice 2
Soit $ABC$ un triangle, $I$ milieu du segment $[AB]\;,\ J$ milieu du segment $[AC]\;,\ K$ milieu du segment $[AI]$ et $L$ milieu du segment $[AJ].$
1) faire une figure.
2) démontrer que : $4KL=BC.$
Exercice 3
On suppose que $AB=7\;cm\;,\ AC=8\;cm$ et $BC=12\;cm$ et on désigne par $I\;,\ J$ et $K$ les milieux respectifs des côtés $[BC]\;,\ [AC]$ et $[AB].$ On désigne par $L$ et $M$ les milieux respectifs de $[KJ]$ et $[KI].$
1) Faire une figure complète.
2) Prouver que la droite $(LM)$ est parallèle à la droite $(AB).$
3) Calculer le périmètre du triangle $KLM.$
Exercice 4
Tracer un cercle $(c)$ de centre $O$ et de diamètre $[AB]$ et $(c')$ un cercle de diamètre $[OA].$ Soit $Q$ un point du cercle $(c).$ La droite $(AQ)$ coupe $(c')$ en $P.$
1) Démontrer que $P$ est le milieu de $[AQ].$
2) Soit $E$ milieu de $[BQ]$, démontrer que : $2PE= AB.$
Exercice 5
Soit $ABC$ un triangle tel que : $AB=6\;cm\;;\ BC=5\;cm$ et $mes\;B=50^{\circ}.$
1) Marquer les points $B'$ et $C'$ milieux respectifs des segments $[AC]$ et $[AB].$
2) Soit $M$ un point du segment $[BC]$ et $(AM)$ coupe $(B'C')$ en $N.$
3) Démontrer que les droites $(BC)$ et $(B'C')$ sont parallèles puis calculer la distance $B'C'.$
4) Démontrer que $N$ est le milieu de $[AM]$
Exercice 6
Soit un triangle $ABC$, le point $I$ est le milieu du segment $[AB]$ et le point $J$ est le celui de $[AC].$
Le point $C'$ est le symétrique de $C$ par rapport à $I$ et le point $B'$ celui de $B$ par rapport à $J.$
1) Faire une figure complète et code-la.
2) a) Démontrer que : $(IJ)//(AB')$ et $IJ=\dfrac{1}{2}AB'.$
b) Démontrer que : $(IJ)//(AC')$ et $IJ=\dfrac{1}{2}AC'.$
3) Démontrer que $A$ est le milieu de $[B'C'].$
Exercice 7
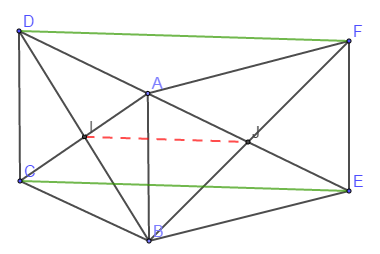
Dans la figure ci-dessus, $ABCD$ et $ABEF$ sont deux parallélogrammes de centres $I$ et $J.$
1) Montrer que les droites $(CE)$ et $(DF)$ sont parallèles (indication : on pourra utiliser $(IJ).$
2) En déduire la nature du quadrilatère $DFEC.$
Exercice 8
$ABC$ est un triangle, $I$ milieu de $[BC]$, $J$ celui de $[AB].$
Démontre que $(IJ)\text{ et }(AC)$ sont parallèles en énonçant la propriété utilisée.
Exercice 9
$ABC$ est un triangle, $I$ le symétrique de $A$ par rapport à $B\text{ et }J$ milieu de $[AC].$
Démontre que les droites $(BJ)\text{ et }(IC)$ sont parallèles en énonçant la propriété utilisée.
Exercice 10
$ABC$ est un triangle, $I$ milieu de $[BC]$, $J$ un point de $[AB]$ tels que ($IJ)$ parallèle à $(CA).$
Démontre que $J$ est le milieu de $[AB]$ en énonçant le théorème utilisé.
Exercice 11
$MNP$ est un triangle rectangle en $M$, $S$ milieu de $[MP]$, la perpendiculaire à $(MP)\text{ en }S$ coupe $[NP]$ en $R.$
Démontre que $R$ est le milieu de $[NP]$
Exercice 12
$OPQ$ est un triangle, $I$ le pied de la hauteur issue de $P.$
$J$ est le milieu de $[OP].$
La perpendiculaire à $(OQ)$ passant par $J$ coupe $[OQ]\text{ en }K.$
Démontre que $K$ est le milieu de $[OI].$
Exercice 13
$ABC$ est un triangle, $I$ milieu de $[AB].$
La parallèle à $(IC)$ passant par $B$ coupe $(AC)$ en $J.$
Montre que $C$ est le milieu de $[AJ]$
Exercice 14
Pour chacun des énoncés ci-dessous, quatre réponses $a\;,\ b\;,\ c\text{ et }d$ sont données dont une seule est juste.
Écris le numéro de l'énoncé et la réponse choisie en justifiant.
1) $ABC$ est un triangle tel que $AB=34\;,\ BC=53\text{ et }AC=29.$
$E$ est milieu de $[AB]$ et $F$ celui de $[BC].$
a) $EF=43.5$ ;
b) $EF=14.5$ ;
c) $EF=17$ ;
d) $EF=27.5$
2) $BAC$ est un triangle tel que $AB=6\;,\ AC=7\;,\ BC=8.$
$O\;,\ P\text{ et }L$ sont les milieux respectifs des segments $[BA]\;,\ [BC]\text{ et }[AC].$
Le périmètre du triangle $POL$ est égal à :
a) $21$ ;
b) $7$ ;
c) $42$ ;
d) $10.5.$
Exercice 15
Trace un cercle de centre $I.$
Soit $A$ un point sur ce cercle et $B$ est un point extérieur à ce cercle tels que $(AB)$ soit tangente au cercle.
Soit $C$ le symétrique de $B$ par rapport à $I$ et soit $D$ le symétrique de $B$ par rapport à $A.$
1) Fais une figure et trace les droites $(DC)\text{ et }(AI).$
2) Démontre que les droites $(DC)\text{ et }(AI)$ sont parallèles.
3) Démontre que $AI=\dfrac{1}{2}DC.$
Exercice 16
$ABC$ est un triangle tel que $BC=3.5\;cm\;;\ AB=3\;cm\text{ et }AC=4\;cm.$
Soit $M$ le point symétrique de $A$ par rapport à $B\text{ et }N$ celui de $A$ par rapport à $C.$
1) Démontre que $(MN)\parallel (BC).$
2) Calcule $MN.$
3) La parallèle à $(AM)$ passant par $C$ coupe $[MN]$ en $O.$
a) Montre que $O$ est le milieu de $[MN].$
b) Calcule $OC.$
Exercice 17
$ABC$ est un triangle ; $M$ milieu de $[AB]$ et $N$ milieu de $[AC].$
1) Démontre que les droites $(MN)\text{ et }(BC)$ sont parallèles.
2) Construis $A'$, symétrique de $A$ par rapport à $0$, milieu du segment $[BC].$
3) La droite $(ON)$ est-elle parallèle à la droite $(AB)$ ?
Justifie.
4) Soit $P$ est le milieu de $[BA']$, quelle est la position relative des droites $(OP)\text{ et }(AB)$ ?
5) La parallèle à $(AC)$ passant par $O$ coupe $(CA')$ en $Q.$
Montre que $Q$ est le milieu de $[CA']$ et que les points $M\;,\ O\text{ et }Q$ sont alignés.
Exercice 18
$ABCD$ est un trapèze tel que $(AB)\parallel(DC).$
Soit $M$ le milieu de $[AD]$ et $P$ celui de $[BD]$
1) Démontre que $(MP)\parallel(AB).$
2) La droite $(MP)$ coupe la droite $(BC)$ en $N.$
Prouve que $N$ est le milieu de $[BC].$
3) Prouve que $MN=\dfrac{AB+DC}{2}.$
Exercice 19
Soit deux droites $(\mathcal{D}_{1})\text{ et }(\mathcal{D}_{2})$ sécantes en un point $I.$
Soit $M$ un point appartenant à $(\mathcal{D}_{1})$ et soit $N$ le symétrique de $I$ par rapport à $M.$
Soit $(\mathcal{D}_{3})$ une droite passant par $M$ qui coupe $(\mathcal{D}_{2})$ en $P.$
Soit $(\mathcal{D}_{4})$ la parallèle à $(\mathcal{D}_{3})$ passant par $N$ qui coupe $(\mathcal{D}_{2})$ en $R.$
1) Fais une figure et trace la droite $(NP)$ puis la parallèle à la droite $(NP)$ passant par $R$ : cette parallèle coupe $(\mathcal{D}_{1})\text{ en }T.$
2) En considérant le triangle $INR$, démontre que $P$ est le milieu de $[IR].$
3) Déduis-en que $N$ est le milieu de $[IT].$
Exercice 20
Soit $ABC$ un triangle, on appelle $I$ le milieu de $[BC]$, $J$ le milieu de $[AB]$ et $K$ le milieu de $[AI].$
Soit $L$ le point d'intersection de $(JK)$ et $(AC).$
1) Fais une figure complète.
2) Démontre que $(JK)\parallel(BC).$
3) Démontre que $L$ est le milieu de $(AC).$
4) On appelle $M$ le milieu de $[IC].$
Montre que $JK=KL=IM.$
Exercice 21
Dans la figure ci-dessous, $ABC$ est un triangle tel que $D$ et $E$ appartiennent à $(AB)$, $G$ et $F$ appartiennent à $(BC)$, $K$ point d'intersection des droites $(GD)$ et $(AF).$
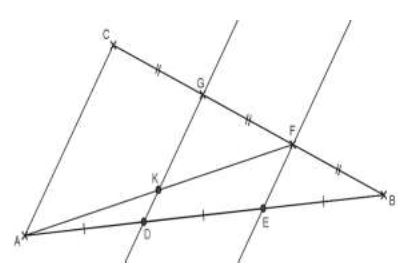
1) Montre que $(EF)$ et $(GD)$ sont parallèles.
2) Montre que $K$ est le milieu de $[AF].$
3) Compare $DK$ et $DG.$
4) Montre que $(DG)$ et $(AC)$ sont parallèles.
Exercice 22
$EFG$ est un triangle rectangle en $F.$
Les points $H\;,\ I\text{ et }J$ sont les milieux respectifs des côtés $[FG]\;,\ [GE]\text{ et }[EF].$
Démontre que le quadrilatère $FHIJ$ est un rectangle.
Exercice 23
$(\mathcal{C})$ et $(\mathcal{C'})$ sont deux cercles de centre $O$ dont les rayons sont respectivement $2.5\;cm$ et $5\;cm.$
Une demi-droite $[Ox)$ coupe $(\mathcal{C})$ au point $A$ et $(\mathcal{C'})$ au point $B.$
Une autre demi-droite $[Oy)$ non opposée à $[Ox)$ coupe $(\mathcal{C})$ au point $E$ et $(\mathcal{C'})$ au point $F.$
1) Démontre que $BF=2AE.$
2) Quelle est la nature du quadrilatère $ABFE$ ?
Justifie ta réponse.

Commentaires
Anonyme (non vérifié)
mer, 02/06/2019 - 22:42
Permalien
pdf
Anonyme (non vérifié)
sam, 10/19/2019 - 15:50
Permalien
Bonjour j'ai besoin de la
Abdou Diop (non vérifié)
jeu, 12/19/2019 - 18:03
Permalien
Correction
Abdou Diop (non vérifié)
jeu, 12/19/2019 - 18:04
Permalien
Correction
Abdou Diop (non vérifié)
jeu, 12/19/2019 - 18:08
Permalien
Correction de exercice droite des millieu
Abdou Diop (non vérifié)
jeu, 12/19/2019 - 18:24
Permalien
Correction de exercice droite des millieu
Abdou Diop (non vérifié)
jeu, 12/19/2019 - 18:27
Permalien
Correction de exercice droite des millieu
Abdou diop (non vérifié)
lun, 12/23/2019 - 10:37
Permalien
Correction exercice 5 et 6
Anonyme (non vérifié)
lun, 12/30/2019 - 21:10
Permalien
Correction
Mohammed_Fig (non vérifié)
jeu, 01/19/2023 - 14:48
Permalien
Besoin de la version pdf de ces exercices
Ajouter un commentaire