Vous êtes ici

Solution des exercices : Géométrie dans l'espace - 3e

Classe:

Troisième

Exercice 1

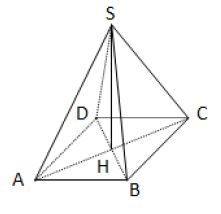
a) Soit

$c$ le côté du carré de base.

D'après la formule donnant le volume d'une pyramide, on a :

$\mathcal{V}=\dfrac{1}{3}c^{2}\times SH$ , soit en remplaçant :

$847=\dfrac{1}{3}c^{2}\times 21.$

On en déduit que :

$3\times 847=c^{2}\times 21$ ,

soit :

$c^{2}=\dfrac{3\times 847}{21}$ , ou encore

$c^{2}=121$ , et par suite :

$\boxed{c=11\;cm}.$

b) Dans le triangle

$ABC$ , rectangle en

$B$ , on a d'après le théorème de Pythagore,

$AB^{2}+BC^{2}=AC^{2}$ ,

d'où :

$AC^{2}=c^{2}+c^{2}=2c^{2}.$

Il s'ensuit que

$\boxed{AC=\sqrt{2}c=11\sqrt{2}}.$

c) Dans le triangle

$SHC$ , rectangle en

$H$ , on a d'après le théorème de Pythagore,

$SH^{2}+HC^{2}=SC^{2}$ ,

d'où :

$SC^{2}=21^{2}+\left(\dfrac{11\sqrt{2}}{2}\right)^{2}=501.5.$

Par suite,

$\boxed{SC=\sqrt{501.5}\cong 22.394\;cm.}$

Comme la pyramide est régulière, il est clair que

$SA$ ,

$SB$ ,

$SD$ ont la même longueur que

$SC.$

Exercice 2

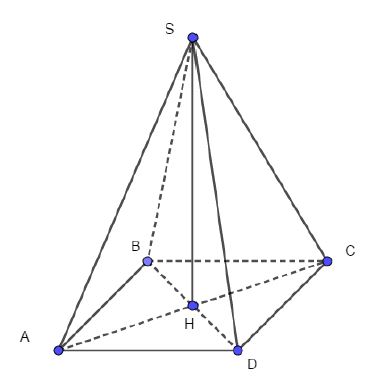
1) L'aire de de base étant celle d'un carré, on

$AB^{2}=50$ , soit

$AB=\sqrt{50}=\sqrt{25\times 2}=\boxed{5\sqrt{2}\;cm.}$

Dans le triangle

$ABC$ , rectangle en

$B$ , on a d'après le théorème de Pythagore,

$AB^{2}+BC^{2}=AC^{2}$ ,

d'où :

$AC^{2}=2AB^{2}=2\times 50=100.$

Il s'ensuit que

$\boxed{AC=\sqrt{100}=10\;cm.}$

2) Dans le triangle

$SHA$ , rectangle en

$H$ , on a d'après le théorème de Pythagore,

$SH^{2}+HA^{2}=SC^{2}$ ,

d'où :

$13^{2}=SH^{2}+5^{2}$ ,

Par suite,

$SH=\sqrt{13^{2}-5^{2}}=\sqrt{144}=\boxed{12\;cm.}$

Le volume de

$SABCD$ est alors :

$\mathcal{V}=\dfrac{1}{3}\times 50\times 12=50\times 4=\boxed{200\;cm^{3}}.$

Exercice 3

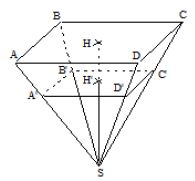
1) Le volume

$\mathcal{V_{1}}$ de la pyramide

$SABCD$ est donné par :

$\mathcal{V_{1}}=\dfrac{1}{3}\times\text{ aire de base}\times\text{ hauteur}$ ,

soit :

$\mathcal{V_{1}}=\dfrac{1}{3}\times(AB\times BC)\times SH=\dfrac{1}{3}\times 6\times 18\times 24=\boxed{864\;cm^{3}}.$

$k=\dfrac{SH'}{SH}=\dfrac{SH-HH'}{SH}=\dfrac{24-8}{24}=\dfrac{16}{24}=\dfrac{2}{3}.$

3) On sait que, dans le cas d'une réduction, le volume obtenu est multiplié par le cube du coefficient de réduction, donc :

$\mathcal{V_{2}}=k^{3}\times\mathcal{V_{1}}=\left(\dfrac{2}{3}\right)^{3}\times 864=\boxed{256\;cm^{3}}.$

$\mathcal{V_{3}}=\mathcal{V_{1}}-\mathcal{V_{2}}=864-256=\boxed{608\;cm^{3}}.$

Exercice 4

1) a) Le coefficient de réduction est :

$k=\dfrac{80}{240}=\dfrac{1}{3}.$

On a par hypothèse (voir figure ci-dessous):

$OO'=30\;cm\text{ et }SO'=\dfrac{1}{3}SO\;,\text{ d'où }OO'=\dfrac{2}{3}SO.$

On en déduit que :

$SO=\dfrac{3}{2}OO'$ ,

soit :

$SO=\dfrac{3}{2}\times 30\dfrac{90}{2}=\boxed{45\;cm}.$

Par suite, la hauteur de la pyramide réduite est :

$SO'=\dfrac{1}{3}\times 45\;cm=\boxed{15\;cm}.$

b) Le volume du récipient est celui du tronc de pyramide.

Or le volume de la pyramide initiale

$SABCD$ est :

$\dfrac{1}{3}\times\text{ Aire }(ABCD)\times\text{ hauteur}=\dfrac{1}{3}\times 240^{2}\times 45=864 000\;cm^{3}$ et celui de la pyramide réduite est égal au volume précédent multiplié par le cube du coefficient de réduction,

soit :

$\left(\dfrac{1}{3}\right)^{3}=\dfrac{1}{27}.$

Le volume du récipient est, par conséquent :

$864 000-\dfrac{1}{27}\times 864 000=\dfrac{26}{27}\times 864 000=\boxed{832 000\;cm^{3}}.$

2) a) Calculons tout d'abord l'apothème de la pyramide initiale

$SABCD.$

Soit

$I$ le milieu de

$[BC].$

Le triangle

$SOI$ est rectangle en

$O$ , d'après une propriété classique (voir figure ci-dessous).

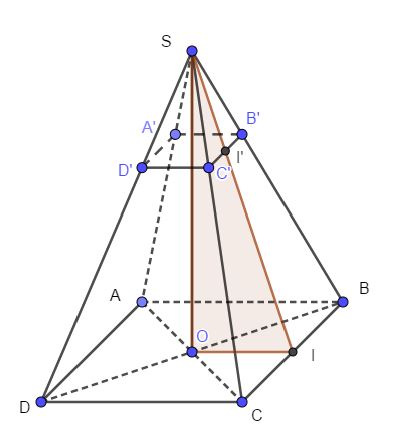
Le théorème de Pythagore appliqué à ce triangle donne :

$SO^{2}+OI^{2}=SI^{2}$ , avec

$SO=45\;cm$

(précédemment calculé) et

$OI=\dfrac{1}{2}AB.$

Or, puisque

$AB=240$ (côté du carré de base), par hypothèse, on a

$OI=120$ et par conséquent :

$SI^{2}=45^{2}+120^{2}=16425\;cm^{2}=25\times 9\times 73\;cm^{2}$ ,

d'où :

$SI=15\sqrt{73}\;cm.$

La hauteur

$[II']$ d'un trapèze tel que

$BB'C'C$ est alors

$II'=\dfrac{2}{3}\times SI=\dfrac{2}{3}\times 15\sqrt{73}=\boxed{10\sqrt{73}\;cm}$

L'aire d'un tel trapèze est alors, d'après la formule :

$\text{Aire du trapèze}=\dfrac{\text{(Grande Base+Petite Base)}\times\text{Hauteur}}{2}$

Aire

$(BB'C'C)=\dfrac{(240+80)\times 10\sqrt{73}}{2}=1600\sqrt{73}\;cm^{2}.$

L'aire latérale de ce récipient est, par conséquent :

$4\times 1600\sqrt{73}\;cm^{2}=\boxed{6400\sqrt{73}\;cm^{2}}.$

Exercice 5

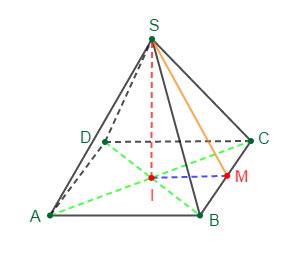
$SABCD$ est une pyramide régulière dont la base est le carré

$ABCD$ de côté

$5\;cm$ et de centre

$I.$ La hauteur

$[SI]$ de la pyramide a pour longueur

$SI=3\;cm.$

1) Calculons le volume de la pyramide.

Soit

$\mathcal{V}$ le volume de ce pyramide alors, on a :

$\mathcal{V}=\dfrac{\mathcal{A}_{B}\times h}{3}$

avec

$\mathcal{A}_{B}$ aire de base et

$h$ hauteur du pyramide.

Or, la base est carrée donc,

$\mathcal{A}_{B}=AB^{2}$

Par suite,

$\begin{array}{rcl}\mathcal{V}&=&\dfrac{\mathcal{A}_{B}\times h}{3}\\ \\&=&\dfrac{AB^{2}\times SI}{3}\\ \\&=&\dfrac{5^{2}\times 3}{3}\\ \\&=&\dfrac{25\times 3}{3}\\ \\&=&25\end{array}$

D'où,

$\boxed{\mathcal{V}=25\;cm^{3}}$

2) Soit

$M$ le milieu de l'arête

$[BC].$

Démontrons que la longueur

$IM=2.5\;cm$

On sait que la base carrée

$ABCD$ a pour centre le point

$I.$ Donc,

$I$ est le milieu des deux diagonales

$[AC]\$ et

$\ [BD].$

De plus

$M$ est milieu de

$[BC].$

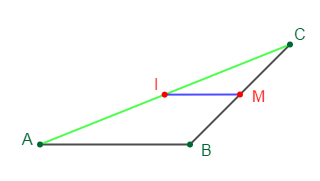
Soit alors, le triangle

$ABC$ ci-dessous

$I$ milieu de

$[AC]\$ et

$\ M$ milieu de

$[BC]$

Or, d'après le théorème de la droite des milieux, dans un triangle le segment qui joint les milieux des deux côtés quelconques a pour longueur la moitié de la longueur du troisième côté.

Donc,

$\begin{array}{rcl} IM&=&\dfrac{AB}{2}\\ \\&=&\dfrac{5}{2}\\ \\&=&2.5\end{array}$

Ainsi,

$\boxed{IM=2.5\;cm}$

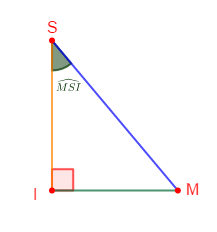
3) On admet que le triangle

$SIM$ est rectangle en

$I.$

Considérons la figure ci-dessous

a) Calculons

$\tan\widehat{MSI}$

On sait que :

$\tan\widehat{MSI}=\dfrac{\text{côté opposé à l'angle }\widehat{MSI}}{\text{côté adjacent à l'angle }\widehat{MSI}}$

Par suite,

$\begin{array}{rcl}\tan\widehat{MSI}&=&\dfrac{IM}{SI}\\ \\&=&\dfrac{2.5}{3}\\ \\&=&0.83\end{array}$

D'où,

$\boxed{\tan\widehat{MSI}=0.83}$

b) En déduisons la mesure de l'angle

$\widehat{MSI}$ à un degré prés

Avec une calculatrice scientifique, on utilise la touche

$\tan^{-1}$ pour trouver la mesure de cet angle.

On obtient alors :

$\tan^{-1}(0.83)=39.69^{\circ}$

On arrondit à

$1^{\circ}$ près.

D'où,

$\boxed{mes\,\widehat{MSI}=40^{\circ}}$

Exercice 6

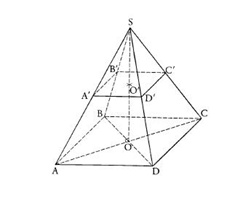
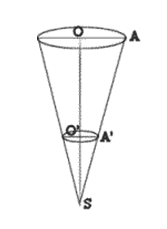
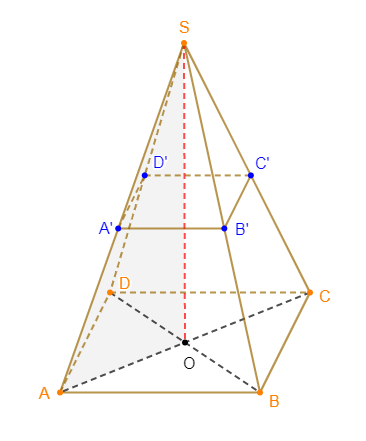
$SABCD$ est une pyramide de hauteur

$[OS].$ Son volume est de

$240\;cm^{3}$ et sa hauteur

$[OS]$ mesure

$15\;cm$

1) A partir de la formule donnant le volume de la pyramide, calculons l'aire de la base

$(ABCD).$

Soit

$V_{(ABCD)}$ le volume de ce pyramide et

$\mathcal{A}_{(ABCD)}$ l'aire de la base

$(ABCD).$

Alors, on a :

$V_{(ABCD)}=\dfrac{\mathcal{A}_{(ABCD)}\times OS}{3}$

Ce qui entraine :

$\mathcal{A}_{(ABCD)}=\dfrac{3\times V_{(ABCD)}}{OS}$

Donc, en remplaçant

$\mathcal{V}\$ et

$\ OS$ par leur valeur, on obtient :

$\begin{array}{rcl} \mathcal{A}_{(ABCD)}&=&\dfrac{3\times V_{(ABCD)}}{OS}\\\\&=&\dfrac{3\times 240}{15}\\\\&=&\dfrac{720}{15}\\\\&=&48\end{array}$

D'où,

$\boxed{\mathcal{A}_{(ABCD)}=48\;cm^{2}}$

Ainsi, l'aire de la base

$(ABCD)$ est égale à

$48\;cm^{2}.$

$O'$ est le point du segment

$[SO]$ tel que

$O'S=\dfrac{1}{2}OS.$

Le plan passant par

$O'$ et parallèle à la base

$(ABCD)$ coupe les droites

$(SA)$ en

$A'\;,\ (SB)$ en

$B'\;,\ (SC)$ en

$C'\$ et

$\ (SD)$ en

$D'.$

Calculons le volume de la pyramide

$(SA'B'C'D').$

En effet, la pyramide

$(SA'B'C'D')$ est une réduction de la pyramide

$(SABCD).$

Comme

$O'S=\dfrac{1}{2}OS$ alors, le coefficient de réduction est égal à

$\dfrac{1}{2}.$

Or, on sait que, dans le cas d'une réduction, le volume de la pyramide

$(SA'B'C'D')$ est obtenu en multipliant le volume de la pyramide

$(SABCD)$ par le cube du coefficient de réduction.

Donc, on a :

$\begin{array}{rcl} V_{(SA'B'C'D')}&=&\left(\dfrac{1}{2}\right)^{3}\times V_{(SABCD)}\\\\&=&\dfrac{1}{8}\times 240\\\\&=&\dfrac{240}{8}\\\\&=&30\end{array}$

Ainsi,

$\boxed{V_{(SA'B'C'D')}=30\;cm^{3}}$

3) On donne

$OA=5\;cm.$ Calculons au degré près la mesure de l'angle

$\widehat{OSA}.$

Pour cela, considérons le triangle

$OSA$ rectangle en

$O.$

Alors, en calculant la tangente de l'angle

$\widehat{OSA}$ , on obtient :

$\begin{array}{rcl}\tan\widehat{OSA}&=&\dfrac{\text{côté opposé à l'angle }\widehat{OSA}}{\text{côté adjacent à l'angle }\widehat{OSA}}\\\\&=&\dfrac{OA}{OS}\\ \\&=&\dfrac{5}{15}\\ \\&=&0.33\end{array}$

D'où,

$\boxed{\tan\widehat{OSA}=0.33}$

Ainsi, avec une calculatrice scientifique, on utilise la touche

$\tan^{-1}$ pour trouver la mesure de l'angle

$\widehat{OSA}.$

On obtient alors :

$\tan^{-1}(0.33)=18.26^{\circ}$

En arrondissant à

$1^{\circ}$ près, on trouve :

$\boxed{mes\,\widehat{OSA}=18^{\circ}}$

Exercice 7

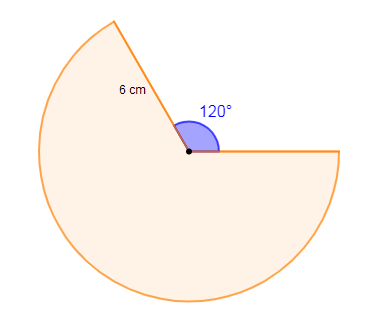
Figure ci-dessous représente le patron de la partie latérale d'un cône de révolution.

1) Montrons que le rayon de sa base est

$4\;cm$ et que sa hauteur

$h$ mesure

$2\sqrt{5}\;cm$

En effet, on sait que la longueur de l'arc de cercle délimitant la partie latérale de ce cône de révolution est égale au périmètre du cercle de base de ce même cône.

Or,

$-\$ la longueur de cet arc est égale à :

$6\times\alpha$

où,

$\alpha$ est l'angle au centre du secteur de disque fournissant le développement de la surface latérale de ce cône.

$-\$ le périmètre du cercle de base de ce même cône est égal à :

$2\pi r$

où,

$r$ est le rayon de la base.

On peut alors écrire :

$2\pi r=6\times\alpha$

avec :

$\alpha=360^{\circ}-120^{\circ}=240^{\circ}\$ et

$\ \pi=180^{\circ}$

Alors, en remplaçant

$\alpha\$ et

$\ \pi$ par leur valeur, on trouve :

$\begin{array}{rcl} 2\pi r=6\times\alpha&\Leftrightarrow&2\times 180^{\circ}\times r=6\times 240^{\circ}\\\\&\Leftrightarrow&360^{\circ}\times r=1\,440^{\circ}\\\\&\Leftrightarrow&r=\dfrac{1\,440^{\circ}}{360^{\circ}}\\\\&\Leftrightarrow&r=4\end{array}$

Ainsi,

$\boxed{r=4\;cm}$

Par ailleurs, on sait que le triangle

$SOA$ est rectangle en

$O$ et on a :

$SO=h$ hauteur de ce cône

$OA=r$ rayon de sa base

$SA$ sa génératrice

Alors, en appliquant le théorème de Pythagore, on obtient :

$SO^{2}+OA^{2}=SA^{2}$

Ce qui donne :

$h^{2}+r^{2}=SA^{2}$

En remplaçant

$r\$ et

$\ SA$ par leur valeur, on trouve :

$\begin{array}{rcl} h^{2}+r^{2}=SA^{2}&\Leftrightarrow&h^{2}+4^{2}=6^{2}\\\\&\Leftrightarrow&h^{2}+16=36\\\\&\Leftrightarrow&h^{2}=36-16\\\\&\Leftrightarrow&h^{2}=20\\\\&\Leftrightarrow&h=\sqrt{20}\\\\&\Leftrightarrow&h=\sqrt{4\times 5}\\\\&\Leftrightarrow&h=2\sqrt{5}\end{array}$

D'où,

$\boxed{h=2\sqrt{5}\;cm}$

2) Calculons le volume de ce cône.

Soit

$V_{\text{cône}}$ le volume de ce cône alors, on a :

$V_{\text{cône}}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

où, l'aire de la base est :

$\pi\times r^{2}=\pi\times 16$

En choisissant

$\pi\simeq 3.14$ , on trouve :

$\begin{array}{rcl} V_{\text{cône}}&=&\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}\\\\&=&\dfrac{\pi\times 16\times 2\sqrt{5}}{3}\\\\&=&\dfrac{3.14\times 16\times 2\sqrt{5}}{3}\\\\&=&74.89\end{array}$

Ainsi,

$\boxed{V_{\text{cône}}=74.89\;cm^{3}}$

3) On coupe ce cône par un plan parallèle à sa base à

$\dfrac{2}{3}$ de la hauteur à partir de la base. Calculons le volume du tronc.

On a :

$V_{\text{tronc}}=V_{\text{cône}}-V_{\text{cône réduit}}$

Déterminons alors le volume du cône réduit.

En effet, comme le cône est coupé par un plan parallèle à sa base à

$\dfrac{2}{3}$ de la hauteur à partir de la base alors, le cône réduit a pour hauteur :

$SO'=SO-\dfrac{2}{3}SO=\dfrac{1}{3}SO$

Par suite, le coefficient de réduction est égal à

$\dfrac{1}{3}.$

Or, on sait que, dans le cas d'une réduction, le volume du cône réduit est obtenu en multipliant le volume du cône initial par le cube du coefficient de réduction.

Ainsi, on a :

$\begin{array}{rcl} V_{\text{cône réduit}}&=&\left(\dfrac{1}{3}\right)^{3}\times V_{\text{cône}}\\\\&=&\dfrac{1}{27}\times 74.89\\\\&=&\dfrac{74.89}{27}\\\\&=&2.77\end{array}$

Donc,

$\boxed{V_{\text{cône réduit}}=2.77\;cm^{3}}$

En remplaçant

$V_{\text{cône}}\$ et

$\ V_{\text{cône réduit}}$ par leur valeur, dans l'expression de

$V_{\text{tronc}}$ , on obtient :

$\begin{array}{rcl} V_{\text{tronc}}&=&V_{\text{cône}}-V_{\text{cône réduit}}\\\\&=&74.89-2.77\\\\&=&72.12\end{array}$

D'où, le volume du tronc est égal à

$72.12\;cm^{3}$

Exercice 8

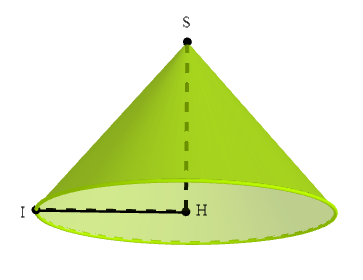
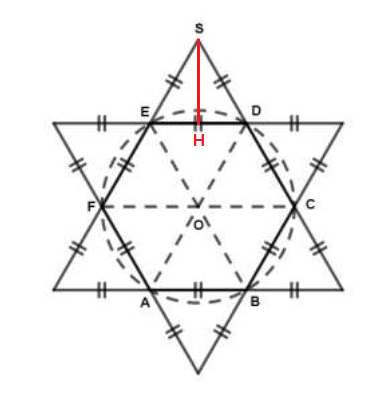
Le chapeau d'un berger a la forme d'un cône de révolution de sommet

$S$ (voir figure ci-dessous) :

$IH=10\;cm\;,\ SH=10\;cm.$

$H$ est le centre du disque de base.

1) Calculons le volume de ce cône.

Soit

$V_{\text{cône}}$ le volume de ce cône alors, on a :

$V_{\text{cône}}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

où, l'aire de la base est donnée par

$\pi\times IH^{2}=\pi\times 100$ et la hauteur est égale à

$SH=10\;cm.$

En choisissant

$\pi\simeq 3.14$ , on trouve :

$\begin{array}{rcl} V_{\text{cône}}&=&\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}\\\\&=&\dfrac{\pi\times 100\times 10}{3}\\\\&=&\dfrac{3.14\times 100\times 10}{3}\\\\&=&\dfrac{3\,140}{3}\\\\&=&1\,046.66\end{array}$

Ainsi,

$\boxed{V_{\text{cône}}=1\,046.66\;cm^{3}}$

2) Le berger recouvre son chapeau extérieurement d'un papier de décoration vendu par feuille carrée de

$10\;cm$ de côté et à

$1\,000\;F$ la feuille. Calculons la dépense minimale.

Pour cela, nous calculons d'abord l'aire latérale de ce cône et la surface d'une feuille.

On a :

$\text{Aire latérale}=\pi\times IH\times SI$

Comme le triangle

$SHI$ est rectangle en

$H$ alors, d'après le théorème de Pythagore, on a :

$SI^{2}=IH^{2}+SH^{2}$

Ce qui donne :

$SI=\sqrt{IH^{2}+SH^{2}}$

En remplaçant

$IH\$ et

$\ SH$ par leur valeur, on trouve :

$\begin{array}{rcl} SI&=&\sqrt{IH^{2}+SH^{2}}\\\\&=&\sqrt{10^{2}+10^{2}}\\\\&=&\sqrt{100+100}\\\\&=&\sqrt{200}\\\\&=&10\sqrt{2}\end{array}$

Donc,

$\boxed{SI=10\sqrt{2}\;cm}$

Par suite, en prenant

$\pi\simeq 3.14$ , on a :

$\begin{array}{rcl} \text{Aire latérale}&=&\pi\times IH\times SI\\\\&=&3.14\times 10\times 10\sqrt{2}\\\\&=&444\end{array}$

Donc,

$\boxed{\text{Aire latérale}=444\;cm^{2}}$

Par ailleurs, comme chaque feuille a une forme carrée de

$10\;cm$ de côté alors, sa surface est donnée par :

$\text{Surface d'une feuille}=10\times 10=100\;cm^{2}$

Ensuite, calculons le nombre minimum de feuilles nécessaires pour recouvrir le chapeau.

On a :

$\begin{array}{rcl} \text{Nombre de feuilles}&=&\dfrac{\text{Aire latérale}}{\text{Surface d'une feuille}}\\\\&=&\dfrac{444}{100}\\\\&=&4.44\end{array}$

Donc, le berger a besoin de

$5$ feuilles de papier de décoration pour recouvrir son chapeau.

Enfin, comme chaque feuille coûte

$1\,000\;F$ alors, la dépense minimale est donnée par :

$\text{Dépense minimale}=5\times 1\,000=5\,000\;F$

Exercice 9

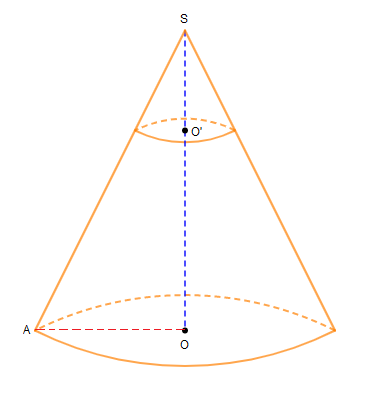
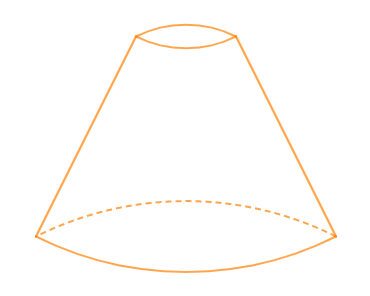
On se propose de calculer le volume d'un seau qui a la forme d'un tronc de cône de révolution.

On donne

$OS=2\sqrt{13}\$ et

$\ OA=2a.$

$a$ étant un nombre réel positif, et

$O'$ milieu de

$[OS].$

1) Calculons

$O'A'$ en fonction de

$a.$

En effet, en observant la figure, on remarque que le plan de la base du cône réduit est parallèle au plan de la base du cône initial.

Par suite,

$(O'A')$ est parallèle à

$(OA).$

D'où, les triangles

$SO'A'\$ et

$\ SOA$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{O'A'}{OA}=\dfrac{O'S}{OS}$

Ce qui entraine :

$O'A'=\dfrac{O'S}{OS}\times OA$

Comme

$O'$ est milieu de

$[OS]$ alors,

$O'S=\dfrac{OS}{2}=\dfrac{2\sqrt{13}}{2}=\sqrt{13}$

Dans l'expression de

$O'A'$ , en remplaçant

$O'S\;,\ OS\$ et

$\ OA$ par leur valeur, on trouve :

$\begin{array}{rcl} O'A'&=&\dfrac{O'S}{OS}\times OA\\\\&=&\dfrac{\sqrt{13}}{2\sqrt{13}}\times 2a\\\\&=&\dfrac{2a}{2}\\\\&=&a\end{array}$

Ainsi,

$\boxed{O'A'=a}$

Autre méthode

En effet, les triangles

$SO'A'\$ et

$\ SOA$ sont en position de Thalès et que le triangle

$SO'A'$ constitue une réduction du triangle

$SOA.$

Or,

$O'$ est milieu de

$[OS]$ donc,

$O'S=\dfrac{1}{2}OS.$

Ce qui signifie que le coefficient de réduction est égal à

$\dfrac{1}{2}.$

Par conséquent, d'après une conséquence du théorème de Thalès, on a :

$O'A'=\dfrac{1}{2}OA$

En remplaçant

$OA$ par sa valeur, on trouve :

$\begin{array}{rcl} O'A'&=&\dfrac{1}{2}OA\\\\&=&\dfrac{1}{2}\times 2a\\\\&=&\dfrac{2a}{2}\\\\&=&a\end{array}$

D'où,

$\boxed{O'A'=a}$

2) On prend

$a=\sqrt{3}$ pour la suite et pour unité le décimètre.

a) Calculons le volume du cône initial.

Soit

$V_{\text{cône initial}}$ le volume de ce cône initial alors, on a :

$V_{\text{cône initial}}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

où, l'aire de la base est donnée par

$\pi\times OA^{2}$ et la hauteur est égale à

$OS.$

Alors, en choisissant

$\pi\simeq 3.14$ , on trouve :

$\begin{array}{rcl} V_{\text{cône initial}}&=&\dfrac{\pi\times OA^{2}\times OS}{3}\\\\&=&\dfrac{3.14\times(\sqrt{3})^{2}\times 2\sqrt{13}}{3}\\\\&=&\dfrac{3.14\times 3\times 2\sqrt{13}}{3}\\\\&=&3.14\times 2\sqrt{13}\\\\&=&22.64\end{array}$

Ainsi,

$\boxed{V_{\text{cône initial}}=22.64\;dm^{3}}$

b) Calculons le volume du cône réduit et en déduisons celui du seau.

En effet, comme

$O'$ est milieu de

$[OS]$ alors,

$O'S=\dfrac{1}{2}OS.$

Ce qui signifie que le coefficient de réduction est égal à

$\dfrac{1}{2}.$

Or, on sait que, dans le cas d'une réduction, le volume du cône réduit est obtenu en multipliant le volume du cône initial par le cube du coefficient de réduction.

Soit

$V_{\text{cône réduit}}$ le volume du cône réduit alors, on a :

$\begin{array}{rcl} V_{\text{cône réduit}}&=&\left(\dfrac{1}{2}\right)^{3}\times V_{\text{cône initial}}\\\\&=&\dfrac{1}{8}\times 22.64\\\\&=&\dfrac{22.64}{8}\\\\&=&2.83\end{array}$

Donc,

$\boxed{V_{\text{cône réduit}}=2.83\;dm^{3}}$

En déduisons le volume seau.

En effet, on sait que le seau est obtenu en enlevant le cône réduit du cône initial.

Ainsi, le volume

$V_{\text{seau}}$ du seau est donné par :

$V_{\text{seau}}=V_{\text{cône initial}}-V_{\text{cône réduit}}$

Alors, en remplaçant

$V_{\text{cône initial}}\$ et

$\ V_{\text{cône réduit}}$ par leur valeur, on obtient :

$\begin{array}{rcl} V_{\text{seau}}&=&V_{\text{cône initial}}-V_{\text{cône réduit}}\\\\&=&22.64-2.83\\\\&=&19.81\end{array}$

D'où,

$\boxed{V_{\text{seau}}=19.81\;dm^{3}}$

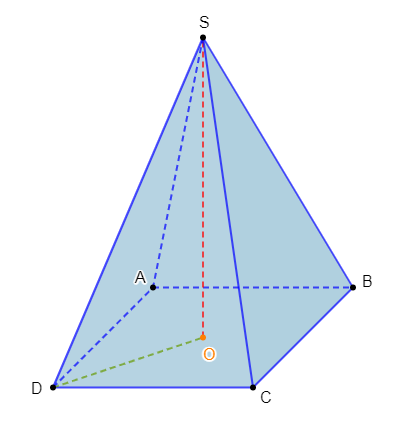
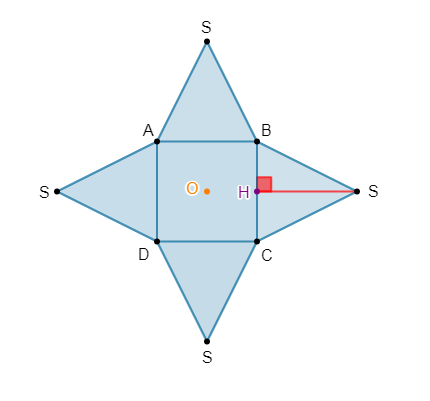
Exercice 10

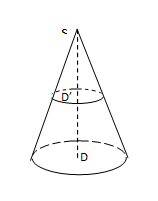
$C$ est un cône de sommet

$S$ et de base un disque

$D$ de rayon

$5\;cm.$ Le volume de ce cône est de

$80\;cm^{3}.$ Le disque

$D'$ de rayon

$3\;cm$ est une section du cône

$C$ par un plan parallèle à la base.

$C'$ est le cône de sommet

$S$ et de base le disque

$D'.$ On se propose de calculer le volume de

$C'.$

$D'$ est une réduction de

$D$ ; à l'aide des rayons de

$D$ et de

$D'$ , calculons l'échelle de cette réduction.

En effet, comme

$D'$ est une réduction de

$D$ alors, l'échelle de réduction

$k$ appelée aussi coefficient de réduction des distances est donnée par :

$k=\dfrac{r'}{r}$

où,

$r$ est le rayon de

$D\$ et

$\ r'$ celui de

$D'.$

En remplaçant

$r\$ et

$\ r'$ par leur valeur, on trouve :

$\begin{array}{rcl} k&=&\dfrac{r'}{r}\\\\&=&\dfrac{3}{5}\\\\&=&0.6\end{array}$

D'où,

$\boxed{k=0.6}$

b) Donnons la formule qui permet de calculer le volume de

$C'$ à partir du volume de

$C.$

En effet, on sait que, dans le cas d'une réduction, le volume du cône réduit est obtenu en multipliant le volume du cône initial par le cube du coefficient de réduction.

Soit

$V_{\text{C}}$ le volume du cône initial et

$V_{\text{C'}}$ le volume du cône réduit alors, on a :

$V_{\text{C'}}=k^{3}\times V_{\text{C}}$

Calculons le volume de

$C'.$

Dans la formule ci-dessus, remplaçons

$k\$ et

$\ V_{\text{C}}$ par leur valeur.

On obtient alors :

$\begin{array}{rcl} V_{\text{C'}}&=&k^{3}\times V_{\text{C}}\\\\&=&(0.6)^{3}\times 80\\\\&=&0.216\times 80\\\\&=&17.28\end{array}$

Donc,

$\boxed{V_{\text{C'}}=17.28\;dm^{3}}$

Exercice 11

Soit

$SABCD$ une pyramide régulière à base carrée. Sa hauteur mesure

$6\;cm$ ; le côté de sa base mesure

$4\;cm.$

$O$ est le centre de la base.

1) Dessinons la pyramide en perspective cavalière

2) Calculons la longueur de ses arêtes latérales.

En effet,

$SABCD$ est pyramide régulière de sommet

$S$ et de hauteur

$[SO]$ avec

$O$ centre de la base.

Donc, ses arêtes latérales ont même longueur :

$SA=SB=SC=SD$

Calculons alors la longueur

$SD.$

En effet, le triangle

$SOD$ est rectangle en

$O$ donc, d'après le théorème de Pythagore, on a :

$SD^{2}=SO^{2}+OD^{2}$

Ce qui donne :

$SD=\sqrt{SO^{2}+OD^{2}}$

Par ailleurs, on sait que

$O$ est milieu de

$[BD]$ donc,

$OD=\dfrac{BD}{2}.$

Or, le triangle

$BCD$ est rectangle en

$C$ donc, en appliquant le théorème de Pythagore, on trouve :

$\begin{array}{rcl} BD^{2}=BC^{2}+CD^{2}&\Rightarrow&BD=\sqrt{BC^{2}+CD^{2}}\\\\&\Rightarrow&BD=\sqrt{4^{2}+4^{2}}\\\\&\Rightarrow&BD=\sqrt{16+16}\\\\&\Rightarrow&BD=\sqrt{32}\\\\&\Rightarrow&BD=4\sqrt{2}\end{array}$

Par suite,

$\boxed{OD=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\;cm}$

Ainsi, en remplaçant,

$SO\$ et

$\ OD$ par leur valeur dans l'expression de

$SD$ , on obtient :

$\begin{array}{rcl} SD&=&\sqrt{SO^{2}+OD^{2}}\\\\&=&\sqrt{6^{2}+(2\sqrt{2})^{2}}\\\\&=&\sqrt{36+8}\\\\&=&\sqrt{44}\\\\&=&\sqrt{4\times 11}\\\\&=&2\sqrt{11}\end{array}$

D'où,

$\boxed{SD=2\sqrt{11}\;cm}$

Donc, chaque arête latérale mesure

$2\sqrt{11}\;cm.$

3) Dessinons le patron de cette pyramide (échelle 1/2)

4) Calculons l'aire latérale et l'aire totale.

$-\$ Calcul de l'aire latérale

En effet, la partie latérale de cette pyramide étant composée de

$4$ triangles identiques alors, l'aire latérale

$\mathcal{A}_{L}$ est donnée par :

$\mathcal{A}_{L}=4\times\mathcal{A}_{(\text{SBC})}$

où,

$\mathcal{A}_{(\text{SBC})}$ est l'aire du triangle

$SBC$

Calculons alors l'aire de

$SBC.$

Soit

$[SH]$ la hauteur issue de

$S$ alors, l'aire du triangle

$SBC$ est donnée par :

$\mathcal{A}_{(\text{SBC})}=\dfrac{BC\times SH}{2}$

Le triangle

$SHB$ étant rectangle en

$H$ alors, d'après le théorème de Pythagore, on a :

$SH^{2}+HB^{2}=SB^{2}$

Par suite,

$SH^{2}=SB^{2}-HB^{2}$

Ce qui entraine :

$SH=\sqrt{SB^{2}-HB^{2}}$

Par ailleurs, on sait que

$SB=SC$ donc, le triangle

$SBC$ est isocèle en

$S.$

Par conséquent,

$H$ est milieu de

$[BC].$

D'où,

$HB=\dfrac{BC}{2}=\dfrac{4}{2}=2\;cm$

Ainsi, en remplaçant

$SB\$ et

$\ HB$ par leur valeur dans l'expression de

$SH$ , on trouve :

$\begin{array}{rcl} SH&=&\sqrt{SB^{2}-HB^{2}}\\\\&=&\sqrt{(2\sqrt{11})^{2}-2^{2}}\\\\&=&\sqrt{44-4}\\\\&=&\sqrt{40}\\\\&=&\sqrt{4\times 10}\\\\&=&2\sqrt{10}\end{array}$

Donc,

$\boxed{SH=2\sqrt{10}\;cm}$

Par suite, en remplaçant

$BC\$ et

$\ SH$ par leur valeur dans l'expression de

$\mathcal{A}_{(\text{SBC})}$ , on trouve :

$\begin{array}{rcl} \mathcal{A}_{(\text{SBC})}&=&\dfrac{BC\times SH}{2}\\\\&=&\dfrac{4\times 2\sqrt{10}}{2}\\\\&=&\dfrac{8\sqrt{10}}{2}\\\\&=&4\sqrt{10}\end{array}$

Ainsi,

$\boxed{\mathcal{A}_{(\text{SBC})}=4\sqrt{10}\;cm^{2}}$

Par conséquent, l'aire latérale

$\mathcal{A}_{L}$ est donnée par :

$\begin{array}{rcl} \mathcal{A}_{L}&=&4\times\mathcal{A}_{(\text{SBC})}\\\\&=&4\times 4\sqrt{10}\\\\&=&16\sqrt{10}\end{array}$

D'où,

$\boxed{\mathcal{A}_{L}=16\sqrt{10}\;cm^{2}}$

$-\$ Calcul de l'aire totale

En effet, l'aire totale

$\mathcal{A}_{T}$ est égale à la somme de l'aire latérale

$\mathcal{A}_{L}$ et de l'aire de la base

$\mathcal{A}_{B}.$

La base étant carrée de côté

$4\;cm$ alors,

$\mathcal{A}_{B}=4^{2}=16\;cm^{2}$

Donc, on a :

$\begin{array}{rcl} \mathcal{A}_{T}&=&\mathcal{A}_{L}+\mathcal{A}_{B}\\\\&=&16\sqrt{10}+16\end{array}$

D'où,

$\boxed{\mathcal{A}_{T}=\left(16+16\sqrt{10}\right)\;cm^{2}}$

5) Calculons le volume de cette pyramide.

En effet, on sait que le volume d'une pyramide est donné par :

$V_{\text{pyramide}}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

Soit

$V_{(\text{SABCD})}$ le volume de la pyramide

$SABCD$ alors, on a :

$\begin{array}{rcl} V_{(\text{SABCD})}&=&\dfrac{\mathcal{A}_{B}\times SO}{3}\\\\&=&\dfrac{16\times 6}{3}\\\\&=&\dfrac{96}{3}\\\\&=&32\end{array}$

D'où,

$\boxed{V_{(\text{SABCD})}=32\;cm^{3}}$

Exercice 12

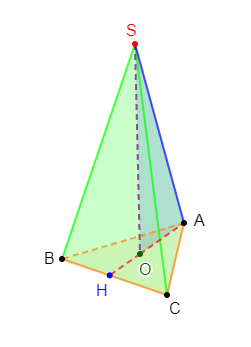
$ABCD$ est un tétraèdre tel que : la base

$ABC$ est rectangle en

$A$ et de hauteur

$[AD].$ On suppose que

$AB=6\;cm\;;\ AC=8\;cm$ et

$AD=8\;cm.$

1) Dessinons ce tétraèdre en perspective cavalière.

2) Montrons que

$BCD$ est un triangle isocèle en

$B.$

Pour cela, il suffit de montrer que

$BC=BD$

On a :

$ABC$ triangle rectangle en

$A$ alors, d'après le théorème de Pythagore :

$BC^{2}=AB^{2}+AC^{2}$

Ainsi,

$\begin{array}{rcl} BC&=&\sqrt{AB^{2}+AC^{2}}\\\\&=&\sqrt{6^{2}+8^{2}}\\\\&=&\sqrt{36+64}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$

Donc,

$\boxed{BC=10\;cm}$

Par ailleurs,

$[AD]$ est la hauteur du tétraèdre donc,

$[AD]$ est perpendiculaire à la base

$ABC.$

Par suite,

$[AD]$ est perpendiculaire à

$[AB]$ d'où :

$ABD$ est triangle rectangle en

$A.$

Ainsi, en appliquant le théorème de Pythagore, on obtient :

$BD^{2}=AB^{2}+AD^{2}$

Donc,

$\begin{array}{rcl} BD&=&\sqrt{AB^{2}+AD^{2}}\\\\&=&\sqrt{6^{2}+8^{2}}\\\\&=&\sqrt{36+64}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$

D'où,

$\boxed{BD=10\;cm}$

On remarque que

$BC=BD$ , ce qui montre que

$BCD$ est un triangle isocèle en

$B.$

3) Calculons le volume de ce tétraèdre.

Soit

$\mathcal{V}$ le volume de ce tétraèdre alors, on a :

$\mathcal{V}=\dfrac{\mathcal{A}_{B}\times h}{3}$

avec

$\mathcal{A}_{B}$ aire de base et

$h$ hauteur de ce tétraèdre.

Par suite,

$\begin{array}{rcl}\mathcal{V}&=&\dfrac{\mathcal{A}_{B}\times h}{3}\\ \\&=&\dfrac{\dfrac{AB\times AC}{2}\times AD}{3}\\ \\&=&\dfrac{AB\times AC\times AD}{3\times 2}\\ \\&=&\dfrac{6\times 8\times 8}{6}\\ \\&=&64\end{array}$

D'où,

$\boxed{\mathcal{V}=64\;cm^{3}}$

4) Calculons l'aire totale de ce tétraèdre.

Soit

$\mathcal{A}$ l'aire totale de ce tétraèdre. On a :

$\mathcal{A}=\mathcal{A}_{B}+\mathcal{A}_{L}$

avec

$\mathcal{A}_{B}$ aire de base et

$\mathcal{A}_{L}$ aire latérale de ce tétraèdre.

Calculons ces différentes aires :

$\ast\ \ \mathcal{A}_{B}=\dfrac{AB\times AC}{2}=\dfrac{6\times 8}{2}=\dfrac{48}{2}=24$

$\ast\ \ \mathcal{A}_{L}=\mathcal{A}_{ABD}+\mathcal{A}_{ACD}+\mathcal{A}_{BCD}$

$-\ \ \mathcal{A}_{ABD}=\dfrac{AB\times AD}{2}=\dfrac{6\times 8}{2}=\dfrac{48}{2}=24$

$-\ \ \mathcal{A}_{ACD}=\dfrac{AC\times AD}{2}=\dfrac{8\times 8}{2}=\dfrac{64}{2}=32$

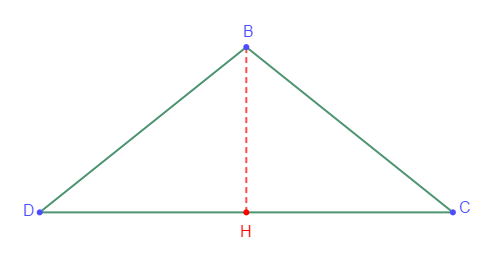
$-\ \ \mathcal{A}_{BCD}=\dfrac{DC\times BH}{2}$

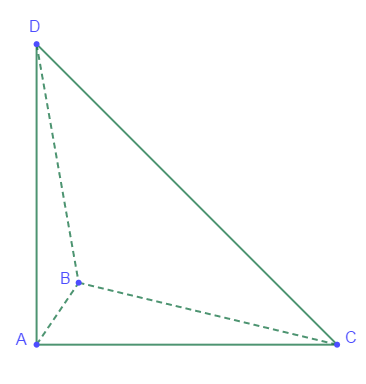
La face latérale

$BCD$ est représentée ci-dessous

Pour calculer la hauteur

$BH$ de ce triangle, on utilise le théorème de Pythagore :

$\begin{array}{rcl} BD^{2}=BH^{2}+DH^{2}&\Rightarrow&BH^{2}=BD^{2}-DH^{2}\\\\&\Rightarrow&BH=\sqrt{BD^{2}-DH^{2}}\end{array}$

Or,

$BCD$ est isocèle donc,

$H$ est milieu de

$[DC].$ Donc,

$DH=\dfrac{DC}{2}$

Ainsi,

$BH=\sqrt{BD^{2}-\left(\dfrac{DC}{2}\right)^{2}}=\sqrt{BD^{2}-\dfrac{DC^{2}}{4}}$

De plus, en appliquant le théorème de Pythagore au triangle

$ADC$ on obtient :

$DC^{2}=AD^{2}+AC^{2}=8^{2}+8^{2}=128$

Donc,

$\boxed{DC=\sqrt{128}=8\sqrt{2}\;cm}$

Par suite,

$\begin{array}{rcl} BH&=&\sqrt{BD^{2}-\dfrac{DC^{2}}{4}}\\ \\&=&\sqrt{10^{2}-\dfrac{(8\sqrt{2})^{2}}{4}}\\ \\&=&\sqrt{100-\dfrac{128}{4}}\\ \\&=&\sqrt{100-32}\\ \\&=&\sqrt{68}\\ \\&=&2\sqrt{17}\end{array}$

Ainsi,

$\mathcal{A}_{BCD}=\dfrac{DC\times BH}{2}=\dfrac{8\sqrt{2}\times 2\sqrt{17}}{2}=8\sqrt{34}$

On obtient alors,

$\begin{array}{rcl}\mathcal{A}&=&\mathcal{A}_{B}+\mathcal{A}_{L}\\\\&=&\mathcal{A}_{B}+\mathcal{A}_{ABD}+\mathcal{A}_{ACD}+\mathcal{A}_{BCD}\\\\&=&24+24+32+8\sqrt{34}\\\\&=&80+8\sqrt{34}\end{array}$

D'où,

$\boxed{\mathcal{A}=80+8\sqrt{34}=126.65\;cm^{2}}$

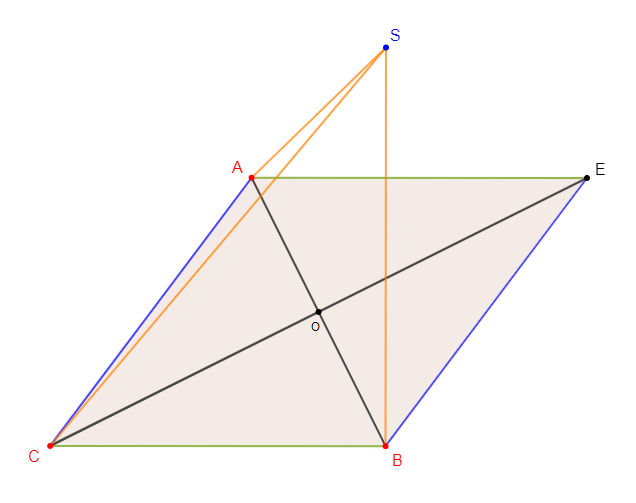
Exercice 13

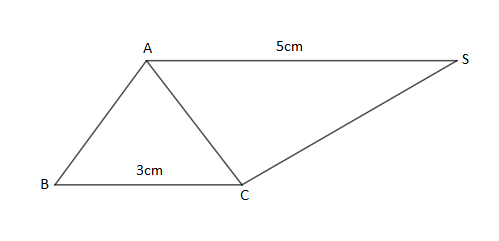
L'unité de longueur est le

$cm.\ ACBE$ est un losange tel que :

$CE=12\$ et

$\ AB=6.$

1) Représentons

$ACBE$ en dimensions réelles.

$S$ est un point n'appartenant pas au plan contenant ce losange tel que :

$SABC$ soit un tétraèdre de hauteur

$[SB]$ avec

$SB=8.$

a) Calculons

$SA\$ et

$\ SC$ (on remarquera que

$(SB)\perp(BA)\$ et

$\ (SB)\perp(BC)).$

$-\$ Calcul de

$SA$

En effet, comme

$(SB)$ est perpendiculaire à

$(BA)$ alors, le triangle

$SBA$ est rectangle en

$B.$

Donc, en appliquant le théorème de Pythagore, on obtient :

$SA^{2}=SB^{2}+AB^{2}$

Ce qui donne :

$SA=\sqrt{SB^{2}+AB^{2}}$

En remplaçant

$SB\$ et

$\ AB$ par leur valeur, on trouve :

$\begin{array}{rcl} SA&=&\sqrt{SB^{2}+AB^{2}}\\\\&=&\sqrt{8^{2}+6^{2}}\\\\&=&\sqrt{64+36}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$

Ainsi,

$\boxed{SA=10\;cm}$

$-\$ Calcul de

$SC$

Comme

$(SB)\$ et

$\ (BC)$ sont perpendiculaires alors, le triangle

$SBC$ est rectangle en

$B.$

Donc, d'après le théorème de Pythagore, on a :

$SC^{2}=SB^{2}+BC^{2}$

Ce qui entraine :

$SC=\sqrt{SB^{2}+BC^{2}}$

Déterminons alors

$BC.$

En effet, on sait que

$ACBE$ est un losange. Donc, ses diagonales

$[AB]\$ et

$\ [CE]$ sont perpendiculaires en leur milieu

$O.$

Par suite, le triangle

$BOC$ est rectangle en

$O.$

Ainsi, d'après le théorème de Pythagore, on a :

$BC^{2}=OB^{2}+CO^{2}$

Or,

$OB=\dfrac{AB}{2}\$ et

$\ CO=\dfrac{CE}{2}$

Donc, en remplaçant

$OB\$ et

$\ CO$ par leur expression, on trouve :

$\begin{array}{rcl} BC^{2}&=&OB^{2}+CO^{2}\\\\&=&\left(\dfrac{AB}{2}\right)^{2}+\left(\dfrac{CE}{2}\right)^{2}\\\\&=&\left(\dfrac{6}{2}\right)^{2}+\left(\dfrac{12}{2}\right)^{2}\\\\&=&3^{2}+6^{2}\\\\&=&9+36\\\\&=&45\end{array}$

Ainsi,

$\boxed{BC=\sqrt{45}=3\sqrt{5}}$

Alors, dans l'expression de

$SC$ , remplaçons

$SB\$ et

$\ BC$ par leur valeur.

On trouve :

$\begin{array}{rcl} SC&=&\sqrt{SB^{2}+BC^{2}}\\\\&=&\sqrt{8^{2}+(\sqrt{45})^{2}}\\\\&=&\sqrt{64+45}\\\\&=&\sqrt{109}\end{array}$

D'où,

$\boxed{SC=\sqrt{109}\;cm}$

b) Calculons l'aire de

$ACBE$ en déduisons l'aire de

$ABC.$

Comme

$ACBE$ est un losange alors, son aire

$\mathcal{A}_{(ACBE)}$ est donnée par :

$\mathcal{A}_{(ACBE)}=\dfrac{\text{grande diagonale}\times\text{petite diagonale}}{2}$

Alors, en calculant, on trouve :

$\begin{array}{rcl} \mathcal{A}_{(ACBE)}&=&\dfrac{CE\times AB}{2}\\\\&=&\dfrac{12\times 6}{2}\\\\&=&\dfrac{72}{2}\\\\&=&36\end{array}$

D'où,

$\boxed{\mathcal{A}_{(ACBE)}=36\;cm^{2}}$

En déduisons l'aire de

$ABC.$

En effet, on sait que l'aire

$\mathcal{A}_{(ABC)}$ du triangle

$ABC$ est donnée par :

$\mathcal{A}_{(ABC)}=\dfrac{\mathcal{A}_{(ACBE)}}{2}$

Ce qui donne :

$\begin{array}{rcl} \mathcal{A}_{(ABC)}&=&\dfrac{36}{2}\\\\&=&18\end{array}$

Ainsi,

$\boxed{\mathcal{A}_{(ABC)}=18\;cm^{2}}$

c) Calculons le volume du tétraèdre

$SABC.$

Soit

$V_{(SABC)}$ le volume du tétraèdre

$SABC$ alors, on a :

$V_{(SABC)}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

Ce qui donne :

$\begin{array}{rcl} V_{(SABC)}&=&\dfrac{\mathcal{A}_{(ABC)}\times SB}{3}\\\\&=&\dfrac{18\times 8}{3}\\\\&=&\dfrac{144}{3}\\\\&=&48\end{array}$

D'où,

$\boxed{V_{(SABC)}=48\;cm^{3}}$

Exercice 14

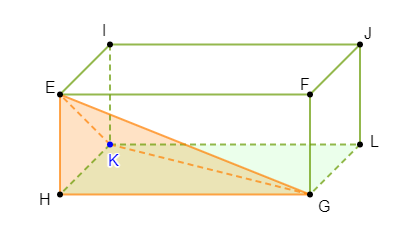
La figure ci-dessous

$EFGHIJLK$ est un parallélépipédique rectangle tel que :

$EF=8\;cm\;;\ EH=6\;cm\ \text{ et }\ HK=4\;cm$

1) Calculons le volume du parallélépipède et l'aire totale.

$-\$ Calcul du volume du parallélépipède

Soit

$V_{(EFGHIJLK)}$ le volume du parallélépipède

$EFGHIJLK$ alors, on a :

$V_{(EFGHIJLK)}=\text{Aire de la base}\times\text{hauteur}$

où, l'aire de la base est égale à l'aire du rectangle

$HKLG$ et la hauteur est égale à

$EH.$

Alors, en remarquant que

$HG=EF$ , on trouve :

$\begin{array}{rcl} V_{(EFGHIJLK)}&=&\text{Aire de la base}\times EH\\\\&=&(HG\times HK)\times EH\\\\&=&EF\times HK\times EH\\\\&=&8\times 4\times 6\\\\&=&192\end{array}$

D'où,

$\boxed{V_{(EFGHIJLK)}=192\;cm^{3}}$

$-\$ Calcul de l'aire totale du parallélépipède

Soit

$\mathcal{A}_{\text{totale}}$ l'aire totale de ce parallélépipède alors, on a :

$\mathcal{A}_{\text{totale}}=\mathcal{A}_{(HKLG)}+\mathcal{A}_{(EFJI)}+\mathcal{A}_{(KLJI)}+\mathcal{A}_{(EFGH)}+\mathcal{A}_{(EIKH)}+\mathcal{A}_{(FJLG)}$

Or, on sait que :

$\mathcal{A}_{(HKLG)}=\mathcal{A}_{(EFJI)}$

$\mathcal{A}_{(KLJI)}=\mathcal{A}_{(EFGH)}$

$\mathcal{A}_{(EIKH)}=\mathcal{A}_{(FJLG)}$

Donc, on obtient :

$\begin{array}{rcl}\mathcal{A}_{\text{totale}}&=&2\times\mathcal{A}_{(HKLG)}+2\times\mathcal{A}_{(EFGH)}+2\times\mathcal{A}_{(EIKH)}\\\\&=&2\times(HG\times HK)+2\times(EF\times EH)+2\times(EH\times HK)\\\\&=&2\times(8\times 4)+2\times(8\times 6)+2\times(6\times 4)\\\\&=&2\times 32+2\times 48+2\times 24\\\\&=&64+96+48\\\\&=&208\end{array}$

Ainsi,

$\boxed{\mathcal{A}_{\text{totale}}=208\;cm^{2}}$

2) Calculons

$EG.$

En effet, comme le triangle

$EGH$ est rectangle en

$H$ alors, d'après le théorème de Pythagore, on a :

$EG^{2}=EH^{2}+HG^{2}$

Ce qui entraine :

$EG=\sqrt{EH^{2}+HG^{2}}$

Or,

$HG=EF$ donc, en remplaçant

$EH\$ et

$\ HG$ par leur valeur, on trouve :

$\begin{array}{rcl} EG&=&\sqrt{EH^{2}+HG^{2}}\\\\&=&\sqrt{6^{2}+8^{2}}\\\\&=&\sqrt{36+64}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$

D'où,

$\boxed{EG=10\;cm}$

3) Calculons l'aire du triangle

$EGH.$

Le triangle

$EGH$ étant rectangle en

$H$ alors, l'aire

$\mathcal{A}_{(EGH)}$ de

$EGH$ est donnée par :

$\mathcal{A}_{(EGH)}=\dfrac{EH\times HG}{2}$

Alors, en remplaçant

$EH\$ et

$\ HG$ par leur valeur, on trouve :

$\begin{array}{rcl} \mathcal{A}_{(EGH)}&=&\dfrac{EH\times HG}{2}\\\\&=&\dfrac{6\times 8}{2}\\\\&=&\dfrac{48}{2}\\\\&=&24\end{array}$

Ainsi,

$\boxed{\mathcal{A}_{(EGH)}=24\;cm^{2}}$

4) Calculons le volume de la pyramide de base

$EGH$ de sommet

$K.$

Soit

$V_{(KEGH)}$ le volume cette pyramide alors, on a :

$V_{(KEGH)}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

où la hauteur est égale à

$HK$

En remplaçant l'aire de la base et la hauteur par leur valeur, on obtient :

$\begin{array}{rcl} V_{(KEGH)}&=&\dfrac{\mathcal{A}_{(EGH)}\times HK}{3}\\\\&=&\dfrac{24\times 4}{3}\\\\&=&\dfrac{96}{3}\\\\&=&32\end{array}$

Donc,

$\boxed{V_{(KEGH)}=32\;cm^{3}}$

Exercice 15

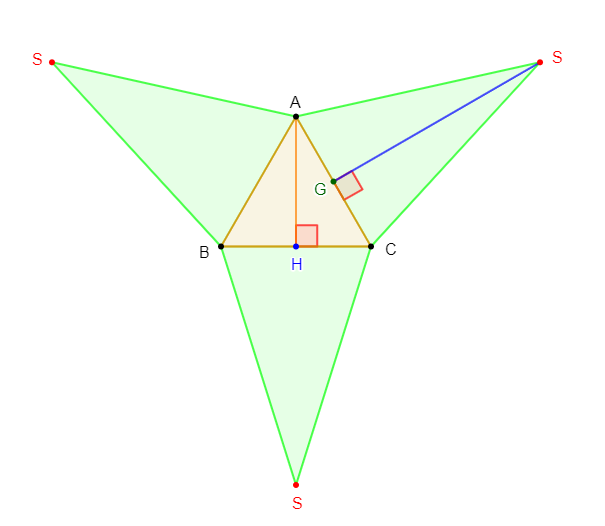
La figure ci-dessous est une partie d'un patron de la pyramide régulière

$SABC.$

1) Terminons ce patron.

2) Calculons l'apothème de cette pyramide.

En effet, l'apothème de cette pyramide est représenté par le segment

$[SG].$

Calculons alors la longueur

$SG.$

Le triangle

$SGC$ étant rectangle en

$G$ alors, en appliquant le théorème de Pythagore, on obtient :

$SG^{2}+GC^{2}=SC^{2}$

Ce qui donne :

$SG^{2}=SC^{2}-GC^{2}$

Ainsi,

$SG=\sqrt{SC^{2}-GC^{2}}$

Déterminons alors la longueur

$GC$

En effet, comme le triangle

$SAC$ est isocèle en

$S$ alors,

$G$ est milieu de

$[AC].$

Par suite,

$GC=\dfrac{AC}{2}=\dfrac{3}{2}$

Ainsi, en remplaçant

$SC\$ et

$\ GC$ par leur valeur, on trouve :

$\begin{array}{rcl} SG&=&\sqrt{SC^{2}-GC^{2}}\\\\&=&\sqrt{5^{2}-\left(\dfrac{3}{2}\right)^{2}}\\\\&=&\sqrt{25-\dfrac{9}{4}}\\\\&=&\sqrt{\dfrac{25\times 4-9}{4}}\\\\&=&\dfrac{\sqrt{100-9}}{\sqrt{4}}\\\\&=&\dfrac{\sqrt{91}}{2}\end{array}$

D'où,

$\boxed{SG=\dfrac{\sqrt{91}}{2}\;cm}$

3) Calculons l'aire latérale et l'aire totale.

$-\$ Calcul de l'aire latérale

Soit

$\mathcal{A}_{L}$ l'aire latérale de cette pyramide.

Comme la partie latérale est constituée de

$3$ triangles identiques alors, l'aire latérale est donnée par :

$\mathcal{A}_{L}=3\times\mathcal{A}_{(SAC)}$

où,

$\mathcal{A}_{(SAC)}$ est l'aire de la face

$SAC$

Ainsi,

$\begin{array}{rcl} \mathcal{A}_{L}&=&3\times\mathcal{A}_{(SAC)}\\\\&=&\mathcal{A}_{L}=3\times\dfrac{SG\times AC}{2}\\\\&=&3\times\dfrac{\dfrac{\sqrt{91}}{2}\times 3}{2}\\\\&=&\dfrac{9\sqrt{91}}{4}\end{array}$

D'où,

$\boxed{\mathcal{A}_{L}=\dfrac{9}{4}\sqrt{91}\;cm^{2}}$

$-\$ Calcul de l'aire totale

Soit

$\mathcal{A}_{T}$ l'aire totale de cette pyramide alors, on a :

$\mathcal{A}_{T}=\text{Aire de la base}+\text{Aire latérale}$

où, l'aire de la base est égale à l'aire de la face

$ABC.$

Soit

$[AH]$ hauteur du triangle

$ABC$ alors,

$\text{Aire de la base}=\dfrac{BC\times AH}{2}$

Déterminons alors la longueur

$AH.$

Le triangle

$AHC$ étant rectangle en

$H$ alors, en appliquant le théorème de Pythagore, on obtient :

$AH^{2}+HC^{2}=AC^{2}$

Ce qui donne :

$AH^{2}=AC^{2}-HC^{2}$

Ainsi,

$AH=\sqrt{AC^{2}-HC^{2}}$

Or, le triangle

$ABC$ est équilatéral donc,

$H$ est milieu de

$[BC].$

Par suite,

$HC=\dfrac{BC}{2}=\dfrac{3}{2}$

Alors, en remplaçant

$AC\$ et

$\ HC$ par leur valeur, on trouve :

$\begin{array}{rcl} AH&=&\sqrt{AC^{2}-HC^{2}}\\\\&=&\sqrt{3^{2}-\left(\dfrac{3}{2}\right)^{2}}\\\\&=&\sqrt{9-\dfrac{9}{4}}\\\\&=&\sqrt{\dfrac{9\times 4-9}{4}}\\\\&=&\dfrac{\sqrt{36-9}}{\sqrt{4}}\\\\&=&\dfrac{\sqrt{27}}{2}\\\\&=&\dfrac{3\sqrt{3}}{2}\end{array}$

Donc,

$\boxed{AH=\dfrac{3\sqrt{3}}{2}\;cm}$

D'où, l'aire

$\mathcal{A}_{(ABC)}$ de la base est :

$\begin{array}{rcl} \mathcal{A}_{(ABC)}&=&\dfrac{BC\times AH}{2}\\\\&=&\dfrac{3\times\dfrac{3\sqrt{3}}{2}}{2}\\\\&=&\dfrac{\dfrac{9\sqrt{3}}{2}}{2}\\\\&=&\dfrac{9\sqrt{3}}{4}\end{array}$

Ainsi,

$\boxed{\mathcal{A}_{(ABC)}=\dfrac{9}{4}\sqrt{3}\;cm^{2}}$

Par conséquent, l'aire totale de cette pyramide est égale à :

$\begin{array}{rcl} \mathcal{A}_{T}&=&\mathcal{A}_{(ABC)}+\mathcal{A}_{L}\\\\&=&\dfrac{9}{4}\sqrt{3}+\dfrac{9}{4}\sqrt{91}\\\\&=&\dfrac{9}{4}(\sqrt{3}+\sqrt{91})\end{array}$

D'où,

$\boxed{\mathcal{A}_{T}=\dfrac{9}{4}(\sqrt{3}+\sqrt{91})\;cm^{2}}$

4) Calculons la hauteur et le volume.

$-\$ Calcul de la hauteur de cette pyramide

Soit

$[SO]$ la hauteur de la pyramide où

$O$ est le centre de gravité du triangle

$ABC.$

Alors, le triangle

$SOA$ est rectangle en

$O.$

Ainsi, en appliquant le théorème de Pythagore, on obtient :

$SO^{2}+AO^{2}=SA^{2}$

Ce qui donne :

$SO^{2}=SA^{2}-AO^{2}$

Par suite,

$SO=\sqrt{SA^{2}-AO^{2}}$

Or,

$O$ est le centre de gravité du triangle

$ABC$ donc,

$AO=\dfrac{2}{3}AH.$

Ainsi, la hauteur

$SO$ est donnée par :

$SO=\sqrt{SA^{2}-\left(\dfrac{2}{3}AH\right)^{2}}$

En remplaçant

$SA\$ et

$\ AH$ par leur valeur, on trouve :

$\begin{array}{rcl} SO&=&\sqrt{SA^{2}-\left(\dfrac{2}{3}AH\right)^{2}}\\\\&=&\sqrt{5^{2}-\left(\dfrac{2}{3}\times\dfrac{3\sqrt{3}}{2}\right)^{2}}\\\\&=&\sqrt{5^{2}-(\sqrt{3})^{2}}\\\\&=&\sqrt{25-3}\\\\&=&\sqrt{22}\end{array}$

D'où,

$\boxed{SO=\sqrt{22}\;cm}$

$-\$ Calcul du volume de cette pyramide

Soit

$V_{(SABC)}$ le volume de cette pyramide alors, on a :

$V_{(SABC)}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

En calculant, on trouve :

$\begin{array}{rcl} V_{(SABC)}&=&\dfrac{\mathcal{A}_{(ABC)}\times SO}{3}\\\\&=&\dfrac{\dfrac{9\sqrt{3}}{4}\times\sqrt{22}}{3}\\\\&=&\dfrac{9\sqrt{66}}{12}\\\\&=&\dfrac{3\sqrt{66}}{4}\end{array}$

D'où,

$\boxed{V_{(SABC)}=\dfrac{3}{4}\sqrt{66}\;cm^{3}}$

Exercice 16

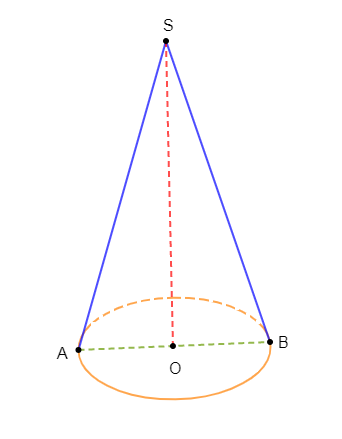
$SAB$ est un cône de révolution de sommet

$S$ de centre

$O$ et du diamètre de base le segment

$[AB]$ tel que :

$AB=4\;cm\$ et

$\ SO=8\;cm.$

1) Dessinons ce cône en perspective cavalière.

2) Calculons la génératrice

$[SA].$

En effet,

$[SO]$ est la hauteur de ce cône donc, le triangle

$SOA$ est rectangle en

$O.$

Ainsi, d'après le théorème de Pythagore, on a :

$SA^{2}=SO^{2}+OA^{2}$

Ce qui entraine :

$SA=\sqrt{SO^{2}+OA^{2}}$

Or,

$O$ est milieu de

$[AB].$

Donc,

$OA=\dfrac{AB}{2}=\dfrac{4}{2}=2\;cm$

Par suite, la longueur de la génératrice

$[SA]$ est donnée par :

$\begin{array}{rcl} SA&=&\sqrt{SO^{2}+OA^{2}}\\\\&=&\sqrt{8^{2}+2^{2}}\\\\&=&\sqrt{64+4}\\\\&=&\sqrt{68}\\\\&=&\sqrt{4\times 17}\\\\&=&2\sqrt{17}\end{array}$

D'où,

$\boxed{SA=2\sqrt{17}\;cm}$

3) Calculons le volume et l'aire totale du cône.

$-\$ Calcul du volume

Soit

$V_{\text{cône}}$ le volume de ce cône alors, on a :

$V=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

où, la hauteur est égale à

$SO$ et l'aire de la base

$\mathcal{A}_{B}$ est donnée par :

$\mathcal{A}_{B}=\pi\times r^{2}=\pi\times OA^{2}$

Alors, en remplaçant la hauteur et l'aire de la base par leur valeur, on trouve :

$\begin{array}{rcl} V_{\text{cône}}&=&\dfrac{\mathcal{A}_{B}\times SO}{3}\\\\&=&\dfrac{\pi\times OA^{2}\times SO}{3}\\\\&=&\dfrac{3.14\times 2^{2}\times 8}{3}\\\\&=&\dfrac{3.14\times 4\times 8}{3}\\\\&=&\dfrac{100.48}{3}\\\\&=&33.49\end{array}$

D'où,

$\boxed{V_{\text{cône}}=33.49\;cm^{3}}$

$-\$ Calcul de l'aire totale

Soit

$\mathcal{A}_{T}$ l'aire totale de ce cône alors, on a :

$\mathcal{A}_{T}=\mathcal{A}_{B}+\mathcal{A}_{L}$

Avec,

$\mathcal{A}_{B}$ aire de la base et

$\mathcal{A}_{L}$ aire latérale.

En effet, l'aire latérale

$\mathcal{A}_{L}$ d'un cône de révolution est donnée par :

$\mathcal{A}_{L}=\pi\times\text{rayon de la base}\times\text{génératrice}$

Donc,

$\mathcal{A}_{L}=\pi\times OA\times SA$

Ainsi, en remplaçant l'aire de la base et l'aire latérale par leur expression, on trouve :

$\begin{array}{rcl} \mathcal{A}_{T}&=&\mathcal{A}_{B}+\mathcal{A}_{L}\\\\&=&\pi\times OA^{2}+\pi\times OA\times SA\\\\&=&3.14\times 2^{2}+3.14\times 2\times 2\sqrt{17}\\\\&=&12.56+51.78\\\\&=&64.34\end{array}$

D'où,

$\boxed{\mathcal{A}_{T}=64.34\;cm^{2}}$

4) Calculons l'angle d'ouverture du développement de ce cône.

Soit

$\alpha^{\circ}$ l'angle d'ouverture du développement de ce cône alors, on a :

$\alpha^{\circ}=\dfrac{\text{rayon de la base}\times 360^{\circ}}{\text{génératrice}}$

Alors, en remplaçant le rayon de la base et la génératrice par leur valeur, on trouve :

$\begin{array}{rcl} \alpha^{\circ}&=&\dfrac{OA\times 360^{\circ}}{SA}\\\\&=&\dfrac{2\times 360^{\circ}}{2\sqrt{17}}\\\\&=&\dfrac{360^{\circ}}{\sqrt{17}}\\\\&=&87.31^{\circ}\end{array}$

Ainsi,

$\boxed{\alpha^{\circ}=87.31^{\circ}}$

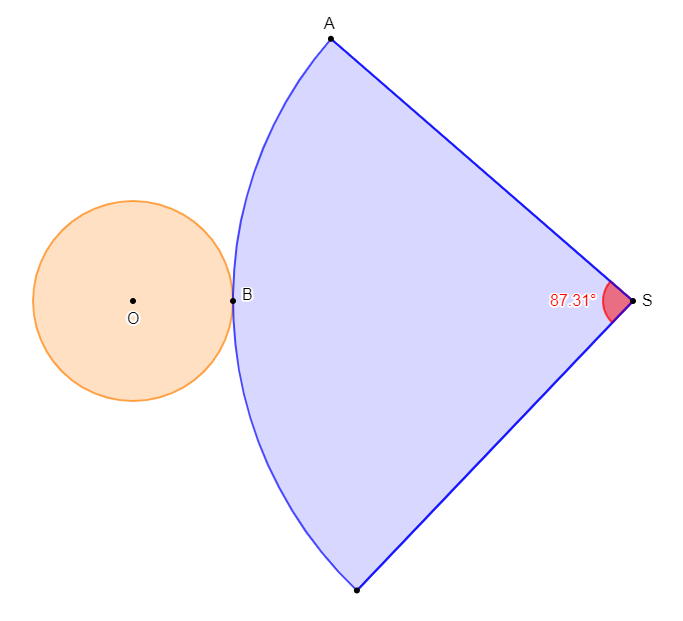
5) Représentons le patron de ce cône

Exercice 17

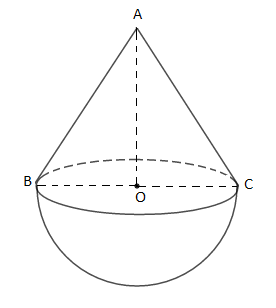
Une balise est formée d'une demi-boule surmontée d'un cône de révolution comme l'indique la figure ci-dessous. On donne

$AB=10\;cm\$ et

$\ BC=12\;cm.$

1) Calculons la distance

$AO.$

En effet,

$[AO]$ est la hauteur du cône donc, le triangle

$AOB$ est rectangle en

$O.$

Ainsi, d'après le théorème de Pythagore, on a :

$AO^{2}+OB^{2}=AB^{2}$

Ce qui entraine :

$AO^{2}=AB^{2}-OB^{2}$

Par suite,

$AO=\sqrt{AB^{2}-OB^{2}}$

Comme

$O$ est milieu de

$[BC]$ alors,

$OB=\dfrac{BC}{2}=\dfrac{12}{2}=6\;cm$

Donc, en remplaçant

$AB\$ et

$\ OB$ par leur valeur, on obtient :

$\begin{array}{rcl} AO&=&\sqrt{AB^{2}-OB^{2}}\\\\&=&\sqrt{10^{2}-6^{2}}\\\\&=&\sqrt{100-36}\\\\&=&\sqrt{64}\\\\&=&8\end{array}$

D'où,

$\boxed{AO=8\;cm}$

2) Calculons le volume

$V$ de la balise.

En effet, pour obtenir le volume

$V$ , nous faisons la somme du volume du cône et de celui de la demi-boule.

Pour cela, nous calculons d'abord le volume

$V_{\text{cône}}$ du cône et le volume

$V_{\text{demi-boule}}$ de la demi-boule.

On a :

$V_{\text{cône}}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

où, la hauteur est égale à

$AO$ et l'aire de la base

$\mathcal{A}_{B}$ est donnée par :

$\mathcal{A}_{B}=\pi\times r^{2}=\pi\times OB^{2}$

Alors, en remplaçant la hauteur et l'aire de la base par leur valeur, on trouve :

$\begin{array}{rcl} V_{\text{cône}}&=&\dfrac{\mathcal{A}_{B}\times AO}{3}\\\\&=&\dfrac{\pi\times OB^{2}\times AO}{3}\\\\&=&\dfrac{3.14\times 6^{2}\times 8}{3}\\\\&=&\dfrac{3.14\times 36\times 8}{3}\\\\&=&\dfrac{904.32}{3}\\\\&=&301.44\end{array}$

D'où,

$\boxed{V_{\text{cône}}=301.44\;cm^{3}}$

On a :

$V_{\text{demi-boule}}=\dfrac{\text{Volume total de la boule}}{2}$

Or, le volume

$V_{\text{boule}}$ d'une boule de rayon

$r$ est donné par :

$V_{\text{boule}}=\dfrac{4\times\pi\times r^{3}}{3}$

Donc, en remplaçant

$r$ par

$OB$ , on trouve :

$\begin{array}{rcl} V_{\text{demi-boule}}&=&\dfrac{V_{\text{boule}}}{2}\\\\&=&\dfrac{\dfrac{4\times\pi\times OB^{3}}{3}}{2}\\\\&=&\dfrac{4\times 3.14\times 6^{3}}{3\times 2}\\\\&=&\dfrac{4\times 3.14\times 216}{6}\\\\&=&\dfrac{2\,712.96}{6}\\\\&=&452.16\end{array}$

D'où,

$\boxed{V_{\text{demi-boule}}=452.16\;cm^{3}}$

Le volume

$V$ de la balise est donc donné par :

$\begin{array}{rcl} V&=&V_{\text{cône}}+V_{\text{demi-boule}}\\\\&=&301.44+452.16\\\\&=&753.6\end{array}$

Ainsi,

$\boxed{V=753.6\;cm^{3}}$

3) Calculons l'aire latérale

$A_{\text{lat}}$ de la balise.

En effet, l'aire latérale

$A_{\text{lat}}$ de la balise est la somme de l'aire latérale du cône et de celle de la demi-boule.

L'aire latérale

$A_{\text{lat cône}}$ du cône est donnée par :

$A_{\text{lat cône}}=\pi\times\text{rayon de la base}\times\text{génératrice}$

En remplaçant le rayon de la base par

$OB$ et la génératrice par

$AB$ , on trouve :

$\begin{array}{rcl} A_{\text{lat cône}}&=&\pi\times OB\times AB\\\\&=&3.14\times 6\times 10\\\\&=&188.4\end{array}$

Donc,

$\boxed{A_{\text{lat cône}}=188.4\;cm^{2}}$

Pour déterminer l'aire latérale

$A_{\text{lat demi-boule}}$ de la demi-boule, on calcule d'abord l'aire totale de la boule.

En effet, on sait l'aire latérale

$A_{\text{lat boule}}$ d'une boule de rayon

$r$ est donnée par :

$A_{\text{lat boule}}=4\times\pi\times r^{2}$

Par suite, l'aire latérale

$A_{\text{lat demi-boule}}$ de la demi-boule est égale à :

$\begin{array}{rcl}A_{\text{lat demi-boule}}&=&\dfrac{A_{\text{lat boule}}}{2}\\\\&=&\dfrac{4\times\pi\times r^{2}}{2}\\\\&=&2\times\pi\times r^{2}\end{array}$

Ainsi, en remplaçant

$r$ par

$OB$ , on trouve :

$\begin{array}{rcl} A_{\text{lat demi-boule}}&=&2\times\pi\times OB^{2}\\\\&=&2\times 3.14\times 6^{2}\\\\&=&2\times 3.14\times 36\\\\&=&226.08\end{array}$

Donc,

$\boxed{A_{\text{lat demi-boule}}=226.08\;cm^{2}}$

Par conséquent, l'aire latérale

$A_{\text{lat}}$ de la balise est donnée par :

$\begin{array}{rcl} A_{\text{lat}}&=&A_{\text{lat cône}}+A_{\text{lat demi-boule}}\\\\&=&188.4+226.08\\\\&=&414.48\end{array}$

D'où,

$\boxed{A_{\text{lat}}=414.48\;cm^{2}}$

Exercice 18

Une pyramide de sommet

$S$ et de base le trapèze

$ABCD$ a pour hauteur

$SA=8\;cm.$ On donne

$AB=6\;cm\;;\ DC=4\;cm\$ et

$\ AD=3\;cm.$ Le trapèze est rectangle de bases

$[AB]\$ et

$\ [DC].$

1) Calculons l'aire de ce trapèze.

On sait que l'aire d'un trapèze est donnée par :

$\text{Aire du trapèze}=\dfrac{(\text{Grande base}+\text{Petite base})\times\text{Hauteur}}{2}$

Soit

$\mathcal{A}_{(ABCD)}$ l'aire du trapèze

$ABCD$ alors, on a :

$\begin{array}{rcl} \mathcal{A}_{(ABCD)}&=&\dfrac{(AB+DC)\times AD}{2}\\\\&=&\dfrac{(6+4)\times 3}{2}\\\\&=&\dfrac{10\times 3}{2}\\\\&=&\dfrac{30}{2}\\\\&=&15\end{array}$

D'où,

$\boxed{\mathcal{A}_{(ABCD)}=15\;cm^{2}}$

2) Faisons une figure de la pyramide.

3) Précisons la nature du triangle

$SAB.$

Comme

$[SA]$ est la hauteur de la pyramide alors, les droites

$(SA)\$ et

$\ (AB)$ sont perpendiculaires.

Par conséquent, le triangle

$SAB$ est rectangle en

$A.$

Calculons

$SB.$

Comme

$SAB$ est un triangle rectangle en

$A$ alors, d'après le théorème de Pythagore, on a :

$SB^{2}=SA^{2}+AB^{2}$

Ce qui entraine :

$SB=\sqrt{SA^{2}+AB^{2}}$

Alors, en remplaçant

$SA\$ et

$\ AB$ par leur valeur, on trouve :

$\begin{array}{rcl} SB&=&\sqrt{SA^{2}+AB^{2}}\\\\&=&\sqrt{8^{2}+6^{2}}\\\\&=&\sqrt{64+36}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$

Ainsi,

$\boxed{SB=10\;cm}$

4) Calculons le sinus de l'angle

$\widehat{ABS}.$

En effet, le sinus de l'angle

$\widehat{ABS}$ est donné par :

$\sin\widehat{ABS}=\dfrac{SA}{SB}$

Alors, en remplaçant

$SA\$ et

$\ SB$ par leur valeur, on trouve :

$\begin{array}{rcl} \sin\widehat{ABS}&=&\dfrac{SA}{SB}\\\\&=&\dfrac{8}{10}\\\\&=&0.8\end{array}$

Donc,

$\boxed{\sin\widehat{ABS}=0.8}$

5) Un plan

$\mathcal{P}$ sectionne la pyramide

$(ABCDS)$ parallèlement à sa base

$(ABCD)$ à

$1/3$ de sa hauteur

$[SA]$ à partir de

$A$ et coupe respectivement les arêtes

$[SA]\;;\ [SB]\;;\ [SC]$ et

$[SD]$ en

$I\;,\ J\;,\ K\$ et

$\ L.$

Complétons la figure et précisons la nature de la section

$(IJKL).$

Comme le plan

$\mathcal{P}$ sectionne la pyramide

$(ABCDS)$ parallèlement à sa base

$(ABCD)$ alors, la section

$(IJKL)$ est de même nature que la base

$ABCD$ de la pyramide.

D'où,

$IJKL$ est un trapèze rectangle de bases

$[IJ]\$ et

$\ [LK]$

6) Montons que

$\dfrac{IJ}{AB}=\dfrac{2}{3}$ et en déduisons

$IJ.$

En effet,

$(IJ)$ étant parallèle à

$(AB)$ alors, les triangles

$SIJ\$ et

$\ SAB$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on obtient :

$\dfrac{IJ}{AB}=\dfrac{SI}{SA}$

Déterminons alors

$SI$

En effet, comme le plan

$\mathcal{P}$ sectionne la pyramide à

$1/3$ de sa hauteur

$[SA]$ à partir de

$A$ alors, cela signifie que :

$IA=\dfrac{1}{3}SA=\dfrac{8}{3}$

Donc,

$\begin{array}{rcl} SI&=&SA-IA\\\\&=&8-\dfrac{8}{3}\\\\&=&\dfrac{3\times 8-8}{3}\\\\&=&\dfrac{24-8}{3}\\\\&=&\dfrac{16}{3}\end{array}$

Ainsi,

$\boxed{SI=\dfrac{16}{3}}$

Alors, dans la relation de Thalès, en remplaçant

$SI\$ et

$\ SA$ par leur valeur, on trouve :

$\begin{array}{rcl} \dfrac{IJ}{AB}&=&\dfrac{SI}{SA}\\\\&=&\dfrac{\dfrac{16}{3}}{8}\\\\&=&\dfrac{16}{3\times 8}\\\\&=&\dfrac{2\times 8}{3\times 8}\\\\&=&\dfrac{2}{3}\end{array}$

D'où,

$\boxed{\dfrac{IJ}{AB}=\dfrac{2}{3}}$

En déduisons la valeur de

$IJ$

On a :

$\dfrac{IJ}{AB}=\dfrac{2}{3}$

Ce qui entraine alors :

$IJ=\dfrac{2}{3}\times AB$

En remplaçant

$AB$ par sa valeur, on trouve :

$\begin{array}{rcl} IJ&=&\dfrac{2}{3}\times AB\\\\&=&\dfrac{2\times 6}{3}\\\\&=&\dfrac{12}{3}\\\\&=&4\end{array}$

Ainsi,

$\boxed{IJ=4\;cm}$

7) Calculons le volume de la pyramide

$(IJKLS)$ et celui du tronc

$(IJKLABCD).$

En effet, la pyramide

$(IJKLS)$ est une réduction de la pyramide

$(ABCDS).$

Comme

$\dfrac{IJ}{AB}=\dfrac{2}{3}$ alors, le coefficient de réduction est égal à

$\dfrac{2}{3}.$

Or, on sait que dans le cas d'une réduction, le volume de la pyramide réduite est obtenu en multipliant le volume de la pyramide initiale par le cube du coefficient de réduction.

Soit

$V_{(ABCDS)}$ le volume de la pyramide

$(ABCDS)\$ et

$\ V_{(IJKLS)}$ le volume de la pyramide

$(IJKLS)$ alors, on a :

$V_{(IJKLS)}=\left(\dfrac{2}{3}\right)^{3}\times V_{(ABCDS)}$

Calculons alors le volume de

$V_{(ABCDS)}$ de la pyramide

$(ABCDS).$

On a :

$V_{(ABCDS)}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

Ce qui donne :

$\begin{array}{rcl} V_{(ABCDS)}&=&\dfrac{\mathcal{A}_{(ABCD)}\times SA}{3}\\\\&=&\dfrac{15\times 8}{3}\\\\&=&\dfrac{120}{3}\\\\&=&40\end{array}$

D'où,

$\boxed{V_{(ABCDS)}=40\;cm^{3}}$

Ainsi, en remplaçant

$V_{(ABCDS)}$ par sa valeur, dans l'expression de

$V_{(IJKLS)}$ , on trouve :

$\begin{array}{rcl} V_{(IJKLS)}&=&\left(\dfrac{2}{3}\right)^{3}\times V_{(ABCDS)}\\\\&=&\dfrac{2^{3}}{3^{3}}\times 40\\\\&=&\dfrac{8\times 40}{27}\\\\&=&\dfrac{320}{27}\\\\&=&11.85\end{array}$

Donc,

$\boxed{V_{(IJKLS)}=11.85\;cm^{3}}$

Calculons le volume du tronc

$(IJKLABCD).$

Soit

$V_{(IJKLABCD)}$ le volume du tronc

$(IJKLABCD)$ alors, on a :

$\begin{array}{rcl} V_{(IJKLABCD)}&=&V_{(ABCDS)}-V_{(IJKLS)}\\\\&=&40-11.85\\\\&=&28.15\end{array}$

D'où,

$\boxed{V_{(IJKLABCD)}=28.15\;cm^{3}}$

Exercice 19

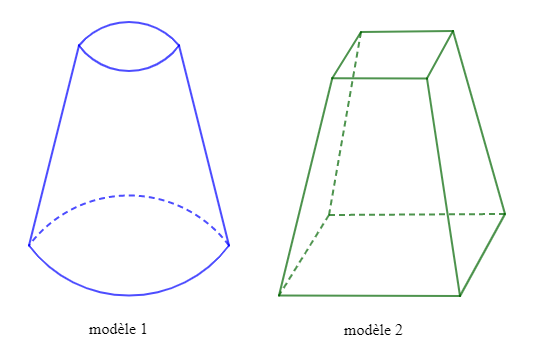
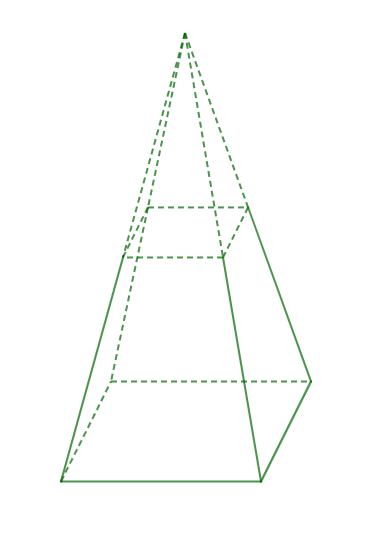
Un entrepreneur des travaux publics doit aménager le long des allées d'une avenue des bancs en béton. Il hésite entre deux modèles :

Le modèle

$1$ a la forme d'un tronc de cône de révolution dont les bases parallèles ont respectivement

$20\;cm\$ et

$\ 10\;cm$ de rayons.

Le modèle

$2$ a la forme d'un tronc de pyramide dont les bases parallèles sont des carrées de cotés respectifs

$40\;cm\$ et

$\ 20\;cm.$

Les deux modèles ont une hauteur de

$50\;cm.$

1) Représentons chaque modèle.

2) Sachant que le modèle le moins volumineux est le plus économique pour l'entrepreneur ; aidons le à faire le bon choix.

Pour cela, nous calculons, pour chaque modèle, le volume.

$-\$ modèle

$1$

En effet, ce modèle se présente comme un cône de révolution coupé à hauteur de

$50\;cm$ à partir de la base.

En calculant le coefficient de réduction

$k$ de ce cône, on trouve :

$k=\dfrac{10}{20}=\dfrac{1}{2}$

Soit

$V_{\text{cône initial}}$ le volume du cône initial,

$V_{\text{cône réduit}}$ le volume du cône réduit et

$V_{\text{tronc de cône}}$ le volume du tronc cône alors, on a :

$V_{\text{tronc de cône}}=V_{\text{cône initial}}-V_{\text{cône réduit}}$

Or, le volume du cône réduit est donné par :

$\begin{array}{rcl} V_{\text{cône réduit}}&=&k^{3}\times V_{\text{cône initial}}\\\\&=&\left(\dfrac{1}{2}\right)^{3}\times V_{\text{cône initial}}\\\\&=&\dfrac{1}{8}\times V_{\text{cône initial}}\end{array}$

Donc,

$\boxed{V_{\text{cône réduit}}=\dfrac{1}{8}\times V_{\text{cône initial}}}$

Calculons alors le volume du cône initial.

On a :

$V_{\text{cône initial}}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

L'aire de la base est égale à :

$\pi\times 20^{2}=\pi\times 400$

Soit

$h$ la hauteur du cône et

$h'$ la hauteur du cône réduit.

Comme la hauteur du tronc de cône est égale à

$50\;cm$ alors, on a :

$h=h'+50$

Or,

$k=\dfrac{1}{2}$ donc,

$h'=\dfrac{1}{2}h$

Ainsi, en remplaçant

$h'$ par

$\dfrac{1}{2}h$ on trouve :

$\begin{array}{rcl} h=h'+50&\Leftrightarrow&h=\dfrac{1}{2}h+50\\\\&\Leftrightarrow&h-\dfrac{1}{2}h=50\\\\&\Leftrightarrow&\dfrac{2}{2}h-\dfrac{1}{2}h=50\\\\&\Leftrightarrow&\dfrac{h}{2}=50\\\\&\Leftrightarrow&h=50\times 2\\\\&\Leftrightarrow&h=100\end{array}$

D'où,

$\boxed{h=100\;cm}$

Alors, en remplaçant l'aire de la base et la hauteur

$h$ par leur valeur, on trouve :

$\begin{array}{rcl}V_{\text{cône initial}}&=&\dfrac{3.14\times 400\times 100}{3}\\\\&=&\dfrac{\pi\times 40\,000}{3}\\\\&=&\dfrac{125\,600}{3}\\\\&=&41\,866.66\end{array}$

Donc,

$\boxed{V_{\text{cône initial}}=41\,866.66\;cm^{3}}$

En remplaçant, on obtient le volume du cône réduit.

$\begin{array}{rcl} V_{\text{cône réduit}}&=&\dfrac{1}{8}\times V_{\text{cône initial}}\\\\&=&\dfrac{41\,866.66}{8}\\\\&=&5\,233.33\end{array}$

Ainsi,

$\boxed{V_{\text{cône réduit}}=5\,233.33\;cm^{3}}$

Le volume du tronc cône est alors égal à :

$\begin{array}{rcl}V_{\text{tronc de cône}}&=&V_{\text{cône initial}}-V_{\text{cône réduit}}\\\\&=&41\,866.66-5\,233.33\\\\&=&36\,633.33\end{array}$

D'où,

$\boxed{V_{\text{tronc de cône}}=36\,633.33\;cm^{3}}$

$-\$ modèle

$2$

Ce modèle se présente comme une pyramide coupée à hauteur de

$50\;cm$ à partir de sa base.

Le coefficient de réduction

$k$ de cette pyramide est donné par :

$k=\dfrac{20}{40}=\dfrac{1}{2}$

Soit

$V_{\text{pyramide initiale}}$ le volume de la pyramide initiale,

$V_{\text{pyramide réduite}}$ le volume de la pyramide réduite et

$V_{\text{tronc de pyramide}}$ le volume du tronc de pyramide alors, on a :

$V_{\text{tronc de pyramide}}=V_{\text{pyramide initiale}}-V_{\text{pyramide réduite}}$

Or, dans le cas d'une réduction, le volume de la pyramide réduite est donné par :

$\begin{array}{rcl} V_{\text{pyramide réduite}}&=&k^{3}\times V_{\text{pyramide initiale}}\\\\&=&\left(\dfrac{1}{2}\right)^{3}\times V_{\text{pyramide initiale}}\\\\&=&\dfrac{1}{8}\times V_{\text{pyramide initiale}}\end{array}$

Donc,

$\boxed{V_{\text{pyramide réduite}}=\dfrac{1}{8}\times V_{\text{pyramide initiale}}}$

Calculons alors le volume de la pyramide initiale.

On a :

$V_{\text{pyramide initiale}}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

Comme la base est carrée de côté

$40\;cm$ alors, l'aire de la base est égale à :

$40^{2}=1\,600.$

Pour la hauteur, en adoptant la même démarche que pour le modèle

$1$ , on trouve :

$\text{Hauteur}=100\;cm.$

Alors, en remplaçant l'aire de la base et la hauteur par leur valeur, on trouve :

$\begin{array}{rcl}V_{\text{pyramide initiale}}&=&\dfrac{1\,600\times 100}{3}\\\\&=&\dfrac{160\,000}{3}\\\\&=&53\,333.33\end{array}$

Donc,

$\boxed{V_{\text{pyramide initiale}}=53\,333.33\;cm^{3}}$

En remplaçant, on obtient le volume de la pyramide réduite.

$\begin{array}{rcl} V_{\text{pyramide réduite}}&=&\dfrac{1}{8}\times V_{\text{pyramide initiale}}\\\\&=&\dfrac{53\,333.33}{8}\\\\&=&6\,666.66\end{array}$

Ainsi,

$\boxed{V_{\text{pyramide réduite}}=6\,666.66\;cm^{3}}$

Le volume du tronc de pyramide est alors égal à :

$\begin{array}{rcl}V_{\text{tronc de pyramide}}&=&V_{\text{pyramide initiale}}-V_{\text{pyramide réduite}}\\\\&=&53\,333.33-6\,666.66\\\\&=&46\,666.67\end{array}$

D'où,

$\boxed{V_{\text{tronc de pyramide}}=46\,666.67\;cm^{3}}$

En comparant le volume du tronc de cône et celui du tronc de pyramide, on constate que :

$V_{\text{tronc de cône}}<V_{\text{tronc de pyramide}}$

Ce qui signifie que le tronc de cône est moins volumineux que le tronc de pyramide.

Par conséquent, le modèle

$1$ est le plus économique pour l'entrepreneur.

Exercice 20

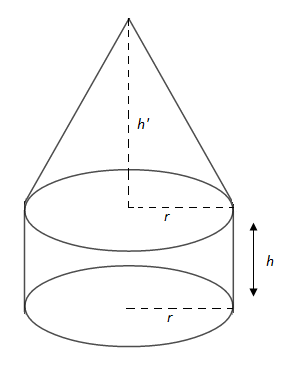
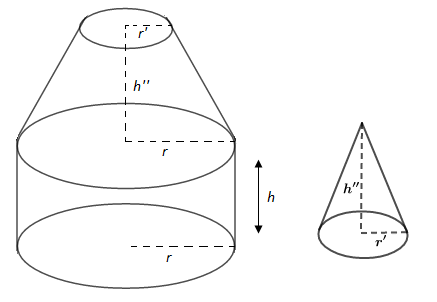
Un réservoir est constitué d'un cylindre de rayon de base

$r$ et de hauteur

$h$ et d'un cône de révolution de même rayon de base et de hauteur

$h'=\dfrac{3h}{2}.$ (Voir la figure ci-dessous)

1) Montrons que le volume de cylindre est le double de celui du cône.

Soit

$\mathcal{V}_{\text{cylindre}}$ le volume du cylindre et

$\mathcal{V}_{\text{cône}}$ celui du cône.

On a :

$\mathcal{V}_{\text{cylindre}}=\mathcal{A}_{B}\times h$

avec

$\mathcal{A}_{B}$ aire de base et

$h$ hauteur du cylindre.

Soit alors :

$\begin{array}{rcl}\mathcal{V}_{\text{cylindre}}&=&r\times r\times\pi\times h\\\\&=&\pi r^{2}h \end{array}$

Donc,

$\boxed{\mathcal{V}_{\text{cylindre}}=\pi r^{2}h}$

On a :

$\mathcal{V}_{\text{cône}}=\dfrac{\mathcal{A}_{B}\times h'}{3}$

avec

$\mathcal{A}_{B}=\pi r^{2}$ aire de base et

$h'=\dfrac{3h}{2}$ hauteur de ce cône.

Par suite,

$\begin{array}{rcl}\mathcal{V}_{\text{cône}}&=&\dfrac{\mathcal{A}_{B}\times h'}{3}\\\\&=&\dfrac{\pi r^{2}\times\dfrac{3h}{2}}{3}\\\\&=&\dfrac{\dfrac{\pi r^{2}\times 3h}{2}}{3}\\\\&=&\dfrac{3\pi r^{2}h}{3\times 2}\\\\&=&\dfrac{\pi r^{2}h}{2}\end{array}$

Ainsi,

$\boxed{\mathcal{V}_{\text{cône}}=\dfrac{\pi r^{2}h}{2}}$

Comme

$\mathcal{V}_{\text{cylindre}}=\pi r^{2}h$ alors, on a :

$\mathcal{V}_{\text{cône}}=\dfrac{\mathcal{V}_{\text{cylindre}}}{2}$

D'où,

$\boxed{\mathcal{V}_{\text{cylindre}}=2\mathcal{V}_{\text{cône}}}$

2) Dans la suite on donne

$r=4\;cm.$ On donne

$\pi\cong\dfrac{22}{7}$

a) Calculons la hauteur

$h'$ du cône pour que le volume du réservoir soit de

$528\;cm^{3}.$

Soit

$\mathcal{V}$ le volume du réservoir alors, on a :

$\begin{array}{rcl}\mathcal{V}&=&\mathcal{V}_{\text{cylindre}}+\mathcal{V}_{\text{cône}}\\\\&=&2\mathcal{V}_{\text{cône}}+\mathcal{V}_{\text{cône}}\\\\&=&3\mathcal{V}_{\text{cône}}\\\\&=&\dfrac{3\pi r^{2}h}{2}\\\\&=&\dfrac{3\times\dfrac{22}{7}\times 16\times h}{2}\\\\&=&\dfrac{3\times 22\times 16\times h}{2\times 7}\\\\&=&\dfrac{528\times h}{7}\end{array}$

Donc,

$\boxed{\mathcal{V}=\dfrac{528\times h}{7}}$

Comme

$\mathcal{V}=528\;cm^{3}$ alors, on a :

$\begin{array}{rcl} \dfrac{528\times h}{7}=528&\Rightarrow&528\times h=7\times 528\\\\&\Rightarrow&h=\dfrac{7\times 528}{528}\\\\&\Rightarrow&h=7\end{array}$

Donc,

$\boxed{h=7\;cm}$

Par suite, en remplaçant dans l'expression de

$h'$ , on trouve :

$\begin{array}{rcl} h'&=&\dfrac{3h}{2}\\\\&=&\dfrac{3\times 7}{2}\\\\&=&\dfrac{21}{2}\\\\&=&10.5\end{array}$

D'où,

$\boxed{h'=10.5\;cm}$

b) Pour créer une ouverture du réservoir on coupe le cône à mi-hauteur parallèlement au plan de sa base. On obtient un réservoir ayant la forme indiquée par la figure ci-dessous :

Calculons le volume restant du réservoir.

On a :

$\mathcal{V}_{\text{restant}}=\mathcal{V}-\mathcal{V}_{\text{enlevé}}$

Soit

$\mathcal{V}_{\text{enlevé}}$ le volume de la partie enlevée ou du couvercle.

Comme le cône a été coupé à mi-hauteur parallèlement au plan de sa base alors, le coefficient de réduction est :

$k=\dfrac{1}{2}$

Or, on sait que, dans le cas d'une réduction, le volume du cône réduit est obtenu en multipliant le volume du cône initial par le cube du coefficient de réduction, donc :

$\begin{array}{rcl}\mathcal{V}_{\text{enlevé}}&=&k^{3}\times\mathcal{V}_{\text{cône}}\\\\&=&\left(\dfrac{1}{2}\right)^{3}\times\dfrac{\pi r^{2}h}{2}\\\\&=&\dfrac{1}{8}\times\dfrac{\dfrac{22}{7}\times4^{2}\times 7}{2}\\\\&=&\dfrac{1}{8}\times\dfrac{\dfrac{22\times 16\times 7}{7}}{2}\\\\&=&\dfrac{1}{8}\times\dfrac{22\times 16}{2}\\\\&=&\dfrac{22\times 16}{8\times 2}\\\\&=&22\end{array}$

Ainsi,

$\boxed{\mathcal{V}_{\text{enlevé}}=22\;cm^{3}}$

Par suite,

$\begin{array}{rcl}\mathcal{V}_{\text{restant}}&=&\mathcal{V}-\mathcal{V}_{\text{enlevé}}\\\\&=&528-22\\\\&=&506\end{array}$

D'où,

$\boxed{\mathcal{V}_{\text{restant}}=506\;cm^{3}}$

Exercice 21

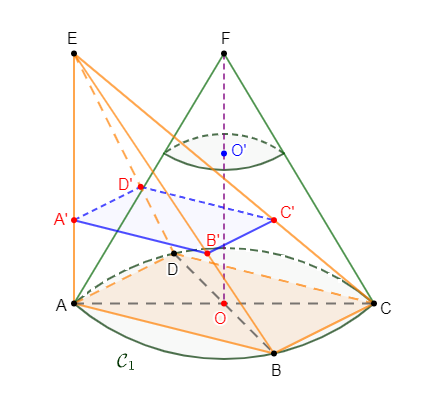
On considère une pyramide de sommet

$E$ et de base un carré

$ABCD$ et de hauteur

$[EA].$

On donne :

$EA=AB=5\;cm.$

1) Calculons la longueur

$AC$ et en déduisons la longueur

$CE.$

Comme

$ABCD$ est un carré alors, le triangle

$ABC$ est rectangle en

$B.$

Donc, en utilisant le théorème de Pythagore, on a :

$AC^{2}=AB^{2}+BC^{2}$

Or,

$BC=AB$ donc,

$AC^{2}=AB^{2}+AB^{2}=2\times AB^{2}$

Ce qui entraine :

$AC=\sqrt{2\times AB^{2}}$

Alors, en remplaçant

$AB$ par sa valeur, on trouve :

$\begin{array}{rcl} AC&=&\sqrt{2\times AB^{2}}\\\\&=&\sqrt{2\times 5^{2}}\\\\&=&5\sqrt{2}\end{array}$

D'où,

$\boxed{AC=5\sqrt{2}\;cm}$

En déduisons la longueur

$CE.$

En effet, comme la pyramide de sommet

$E$ et de base

$ABCD$ a pour hauteur

$[EA]$ alors,

$(EA)\$ et

$\ (AC)$ sont perpendiculaires.

Par suite, le triangle

$ACE$ est rectangle en

$A.$

Donc, d'après le théorème de Pythagore, on a :

$CE^{2}=EA^{2}+AC^{2}$

Ce qui entraine :

$CE=\sqrt{EA^{2}+AC^{2}}$

Alors, en remplaçant

$EA\$ et

$\ AC$ par leur valeur, on trouve :

$\begin{array}{rcl} CE&=&\sqrt{EA^{2}+AC^{2}}\\\\&=&\sqrt{5^{2}+(5\sqrt{2})^{2}}\\\\&=&\sqrt{25+50}\\\\&=&\sqrt{75}\\\\&=&\sqrt{25\times 3}\\\\&=&5\sqrt{3}\end{array}$

Ainsi,

$\boxed{CE=5\sqrt{3}\;cm}$

2) Démontrons que le triangle

$EBC$ est rectangle en

$B.$

Pour cela, calculons d'abord le carré de la longueur de chaque côté du triangle

$EBC.$

On a :

$BC^{2}=5^{2}=25$

$CE^{2}=(5\sqrt{3})^{2}=25\times 3=75$

Par ailleurs,

$ABE$ étant rectangle en

$A$ alors, d'après le théorème de Pythagore, on a :

$\begin{array}{rcl} BE^{2}&=&EA^{2}+AB^{2}\\\\&=&5^{2}+5^{2}\\\\&=&25+25\\\\&=&50\end{array}$

Alors,

$BC^{2}+BE^{2}=25+50=75$

On remarque donc que :

$BC^{2}+BE^{2}=CE^{2}.$

Par conséquent, d'après la réciproque du théorème de Pythagore,

$EBC$ est un triangle rectangle en

$B.$

3) On coupe cette pyramide par un plan

$\mathcal{P}_{1}$ parallèle à sa base à

$\dfrac{1}{3}$ à partir de la base. Calculons le volume du tronc de pyramide obtenu.

Soit

$V_{(EABCD)}$ l volume de la pyramide

$SABCD\$ et

$\ V_{(EABCDA'B'C'D')}$ le volume du tronc de pyramide alors, on a :

$V_{(EABCDA'B'C'D')}=(1-k^{3})\times V_{(EABCD)}$

où,

$k$ est le coefficient de réduction.

Calculons alors

$k$ et le volume

$V_{(EABCD)}$ de la pyramide initiale.

En effet, comme la pyramide a été coupée par un plan

$\mathcal{P}_{1}$ parallèle à sa base à

$\dfrac{1}{3}$ à partir de la base alors, cela signifie que :

$AA'=\dfrac{1}{3}EA$

Par suite, la hauteur

$EA'$ de la pyramide réduite

$EA'B'C'D'$ est donnée par :

$\begin{array}{rcl} EA'&=&EA-AA'\\\\&=&EA-\dfrac{1}{3}EA\\\\&=&\left(1-\dfrac{1}{3}\right)EA\\\\&=&\left(\dfrac{3}{3}-\dfrac{1}{3}\right)EA\\\\&=&\dfrac{2}{3}EA\end{array}$

Donc,

$\boxed{EA'=\dfrac{2}{3}EA}$

Par conséquent, le coefficient de réduction

$k$ est donné par :

$k=\dfrac{EA'}{EA}=\dfrac{2}{3}$

Par ailleurs, le volume

$V_{(EABCD)}$ de la pyramide initiale est donné par :

$\begin{array}{rcl}V_{(EABCD)}&=&\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}\\\\&=&\dfrac{AB^{2}\times EA}{3}\\\\&=&\dfrac{5^{2}\times 5}{3}\\\\&=&\dfrac{125}{3}\\\\&=&41.66\end{array}$

Donc,

$\boxed{V_{(EABCD)}=41.66\;cm^{3}}$

Ainsi, dans l'expression de

$V_{(ABCDA'B'C'D')}$ , en remplaçant

$k\$ et

$\ V_{(EABCD)}$ par leur valeur, on trouve :

$\begin{array}{rcl} V_{(EABCDA'B'C'D')}&=&(1-k^{3})\times V_{(EABCD)}\\\\&=&\left(1-\left(\dfrac{2}{3}\right)^{3}\right)\times 41.66\\\\&=&\left(1-\dfrac{2^{3}}{3^{3}}\right)\times 41.66\\\\&=&\left(1-\dfrac{8}{27}\right)\times 41.66\\\\&=&\left(\dfrac{27}{27}-\dfrac{8}{27}\right)\times 41.66\\\\&=&\dfrac{19}{27}\times 41.66\\\\&=&\dfrac{791.54}{27}\\\\&=&29.31\end{array}$

D'où,

$\boxed{V_{(ABCDA'B'C'D')}=29.31\;cm^{3}}$

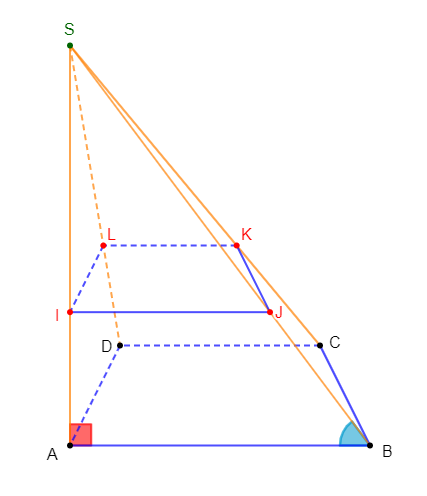
4) Soit

$\mathcal{C}_{1}$ le cercle circonscrit à la base

$ABCD$ de la pyramide

$EABCD.$

Déterminons son centre et son rayon.

Comme

$ABCD$ est un carré alors, le centre de

$\mathcal{C}_{1}$ est le point

$O$ centre de

$ABCD.$

Le rayon

$r$ de

$\mathcal{C}_{1}$ est donné par :

$r=OC$

Or,

$O$ est milieu de

$[AC]$ donc,

$OC=\dfrac{AC}{2}=\dfrac{5\sqrt{2}}{2}$

D'où,

$\boxed{r=\dfrac{5\sqrt{2}}{2}}$

5) On considère le cône de révolution de base

$\mathcal{C}_{1}$ , de sommet

$F$ et de hauteur

$[FO]$ telle que

$FO=5\;cm.$ Calculons l'aire latérale de ce cône.

Soit

$\mathcal{A}_{L}$ l'aire latérale de ce cône alors, on a :

$\mathcal{A}_{L}=\pi\times r\times FA$

Calculons alors la longueur

$FA.$

En effet, le triangle

$FOA$ étant rectangle en

$O$ alors, d'après le théorème de Pythagore, on a :

$FA^{2}=FO^{2}+OA^{2}$

Ce qui entraine :

$FA=\sqrt{FO^{2}+OA^{2}}$

Or,

$OA=OC$ donc, en remplaçant

$FO\$ et

$\ OA$ par leur valeur, on trouve :

$\begin{array}{rcl} FA&=&\sqrt{FO^{2}+OA^{2}}\\\\&=&\sqrt{5^{2}+\left(\dfrac{5\sqrt{2}}{2}\right)^{2}}\\\\&=&\sqrt{25+\dfrac{50}{4}}\\\\&=&\sqrt{\dfrac{4\times 25+50}{4}}\\\\&=&\dfrac{\sqrt{150}}{\sqrt{4}}\\\\&=&\dfrac{5\sqrt{6}}{2}\end{array}$

Donc,

$\boxed{FA=\dfrac{5\sqrt{6}}{2}\;cm}$

Ainsi, dans l'expression de

$\mathcal{A}_{L}$ , en remplaçant

$r\$ et

$\ FA$ par leur valeur, on trouve :

$\begin{array}{rcl} \mathcal{A}_{L}&=&\pi\times r\times FA\\\\&=&3.14\times \dfrac{5\sqrt{2}}{2}\times\dfrac{5\sqrt{6}}{2}\\\\&=&\dfrac{3.14\times 25\sqrt{12}}{4}\\\\&=&\dfrac{3.14\times 25\times 2\sqrt{3}}{4}\\\\&=&\dfrac{157\sqrt{3}}{4}\\\\&=&67.98\end{array}$

D'où,

$\boxed{\mathcal{A}_{L}=67.98\;cm^{2}}$

6) On coupe ce cône par un plan

$\mathcal{P}_{2}$ parallèle à sa base à

$\dfrac{2}{5}$ à partir du sommet. Calculons le volume du tronc de cône obtenu.

Soit

$V_{\text{cône initial}}$ le volume du cône initial et

$V_{\text{tronc de cône}}$ le volume du tronc de cône obtenu alors, on a :

$V_{\text{tronc de cône}}=(1-k^{3})\times V_{\text{cône initial}}$

où,

$k$ est le coefficient de réduction.

Calculons alors

$k$ et le volume

$V_{\text{cône initial}}$ du cône initial.

En effet, le cône a été coupé par un plan

$\mathcal{P}_{2}$ parallèle à sa base à

$\dfrac{2}{5}$ à partir du sommet.

Cela se traduit alors par :

$FO'=\dfrac{2}{5}FO$

Or,

$[FO']$ est la hauteur du cône réduit.

Par conséquent, le coefficient de réduction

$k$ est donné par :

$k=\dfrac{FO'}{FO}=\dfrac{2}{5}=0.4$

Par ailleurs, le volume

$V_{\text{cône initial}}$ du cône initial de hauteur

$[FO]$ est donné par :

$V_{\text{cône initial}}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

où, l'aire de la base est égale à

$\pi\times r^{2}$

Alors, on a :

$\begin{array}{rcl} V_{\text{cône initial}}&=&\dfrac{\pi\times r^{2}\times FO}{3}\\\\&=&\dfrac{3.14\times\left(\dfrac{5\sqrt{2}}{2}\right)^{2}\times 5}{3}\\\\&=&\dfrac{3.14\times\dfrac{50}{4}\times 5}{3}\\\\&=&\dfrac{3.14\times 50\times 5}{4\times 3}\\\\&=&\dfrac{785}{12}\\\\&=&65.41\end{array}$

Donc,

$\boxed{V_{\text{cône initial}}=65.41\;cm^{3}}$

Ainsi, dans l'expression de

$V_{\text{tronc de cône}}$ , en remplaçant

$k\$ et

$\ V_{\text{cône initial}}$ par leur valeur, on obtient :

$\begin{array}{rcl} V_{\text{tronc de cône}}&=&(1-k^{3})\times V_{\text{cône initial}}\\\\&=&\left(1-\left(0.4\right)^{3}\right)\times 65.41\\\\&=&\left(1-0.064\right)\times 65.41\\\\&=&0.936\times 65.41\\\\&=&61.22\end{array}$

D'où,

$\boxed{V_{\text{tronc de cône}}=61.22\;cm^{3}}$

Exercice 22

Répondons par vraie ou fausse en justifiant la réponse

1) Un cône de révolution dont la hauteur mesure

$10\;cm$ et dont le rayon de base mesure

$6\;cm$ a un volume de

$360\pi\;cm^{3}.\quad(\text{Fausse})$

En effet, on sait que le volume

$V_{\text{cône}}$ de ce cône est donné par :

$V_{\text{cône}}=\dfrac{\text{Aire de la base}\times\text{hauteur}}{3}$

où, l'aire de la base est égale à

$\pi\times 6^{2}=\pi\times 36$

Donc, en remplaçant, on trouve :

$\begin{array}{rcl} V_{\text{cône}}&=&\dfrac{\pi\times 36\times 10}{3}\\\\&=&\dfrac{360\pi}{3}\\\\&=&120\pi\end{array}$

D'où,

$\boxed{V_{\text{cône}}=120\pi\;cm^{3}}$

2) Si on double l'arête d'un cube son volume est multiplié par

$2.\quad(\text{Fausse})$

En effet, en doublant l'arête, on agrandit le cube avec un coefficient d'agrandissement égal à

$2.$

Ainsi, le volume agrandi est obtenu en multipliant le volume initial par le cube du coefficient d'agrandissement, c'est-à-dire ; par

$2^{3}=8.$

Donc, si on double l'arête d'un cube son volume est multiplié par

$8.$

Exercice 23

Recopions puis répondons par vrai ou faux :

1) Un tétraèdre est une pyramide qui a quatre faces.

$\quad(\text{vrai})$

2) La hauteur d'une pyramide est la droite qui relie son sommet au centre de sa base.

$\quad(\text{faux})$

3) Une génératrice d'un cône de révolution est un segment qui relie le sommet du cône à un point du cercle de base.

$\quad(\text{vrai})$

4) Si une pyramide a sept faces, alors sa base est un hexagone.

$\quad(\text{vrai})$

5) La hauteur d'une pyramide passe toujours par le centre de la base.

$\quad(\text{faux})$

6) Le patron d'un cône de révolution est constitué de

$2$ disques pleins.

$\quad(\text{faux})$

7) Dans un cône de révolution, la longueur d'une génératrice est le périmètre du disque de base.

$\quad(\text{faux})$

Exercice 24

Reproduisons la figure puis relions chaque phrase de la colonne

$A$ à un nom de figure de la colonne

$B.$

$\begin{array}{|l|l|} \hline \text{Colonne }A&\text{Colonne }B\\ \hline\text{La section d'une pyramide à base carrée}&\text{carré}\\ \text{par un plan parallèle à la base est un}&\\ \hline\text{La section d'un tétraèdre régulier par un}&\text{triangle}\\ \text{plan parallèle à la base est un}&\text{équilatéral}\\ \hline\text{La section d'une pyramide à base}&\\ \text{hexagonale par un plan parallèle à la}&\text{hexagone}\\ \text{base est un}&\\ \hline \end{array}$

Exercice 25

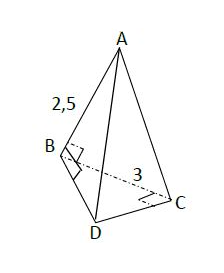
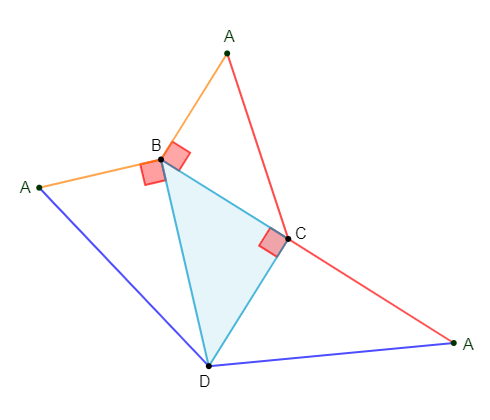
$ABCD$ est une pyramide dont la base est un triangle rectangle et isocèle en

$C$ tel que :

$AB=2.5\;cm\$ et

$\ BC=3\;cm.$

Construisons le patron de cette pyramide.

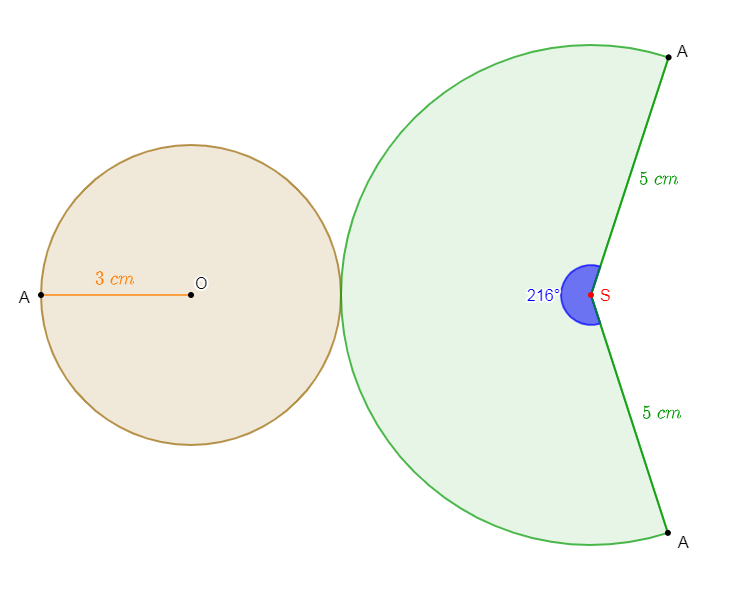
2) Construisons le patron d'un cône de révolution de rayon de base

$3\;cm$ et de génératrice

$5\;cm.$

Pour cela, nous calculons d'abord l'angle d'ouverture du développement de ce cône.

Soit

$\alpha^{\circ}$ l'angle d'ouverture du développement de ce cône alors, on a :

$\alpha^{\circ}=\dfrac{\text{rayon de la base}\times 360^{\circ}}{\text{génératrice}}$

Alors, en remplaçant le rayon de la base et la génératrice par leur valeur, on trouve :

$\begin{array}{rcl} \alpha^{\circ}&=&\dfrac{3\times 360^{\circ}}{5}\\\\&=&\dfrac{1\,080^{\circ}}{5}\\\\&=&216^{\circ}\end{array}$

Ainsi,

$\boxed{\alpha^{\circ}=216^{\circ}}$

Représentons ensuite le patron de ce cône de révolution.

Exercice 27

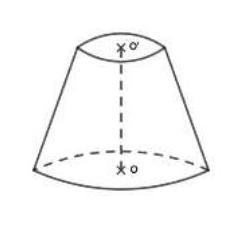
La figure ci-dessous représente un tronc de cône dont les bases ont pour aires

$12\;cm^{2}\$ et

$\ 100\;cm^{2}.$

La distance

$OO'$ des centres de bases est égale à

$6\;cm.$

1) Calculons la hauteur puis le volume du cône.

Pour cela, nous calculons d'abord le coefficient de réduction de ce cône.

En effet, ce tronc de cône est associé à un cône de révolution d'aire de base

$100\;cm^{2}.$

L'aire de la base du cône réduit est égale à

$12\;cm^{2}.$

Soit

$k$ le coefficient de réduction.

On sait que dans le cas d'une réduction, l'aire de la base du cône réduit est obtenue en multipliant l'aire de la base du cône initial par le carré du coefficient de réduction.

Cela se traduit par :

$12=k^{2}\times 100$

Ce qui entraine :

$k^{2}=\dfrac{12}{100}$

Ainsi,

$\begin{array}{rcl} k&=&\sqrt{\dfrac{12}{100}}\\\\&=&\dfrac{\sqrt{12}}{\sqrt{100}}\\\\&=&\dfrac{2\sqrt{3}}{10}\\\\&=&\dfrac{\sqrt{3}}{5}\end{array}$

Donc,

$\boxed{k=\dfrac{\sqrt{3}}{5}}$

$-\$ Calcul de la hauteur de ce cône

Soit

$h$ la hauteur du cône initial et

$h'$ la hauteur du cône réduit.

Comme la hauteur

$OO'$ du tronc de cône est égale à

$6\;cm$ alors, on a :

$h=h'+6$

Or,

$k=\dfrac{\sqrt{3}}{5}$ donc,

$h'=\dfrac{\sqrt{3}}{5}h$

Ainsi, en remplaçant

$h'$ par

$\dfrac{\sqrt{3}}{5}h$ , on trouve :

$\begin{array}{rcl} h=h'+6&\Leftrightarrow&h=\dfrac{\sqrt{3}}{5}h+6\\\\&\Leftrightarrow&h-\dfrac{\sqrt{3}}{5}h=6\\\\&\Leftrightarrow&\dfrac{5}{5}h-\dfrac{\sqrt{3}}{5}h=6\\\\&\Leftrightarrow&\dfrac{5-\sqrt{3}}{5}h=6\\\\&\Leftrightarrow&(5-\sqrt{3})h=6\times 5\\\\&\Leftrightarrow&h=\dfrac{30}{5-\sqrt{3}}\end{array}$

En rendant rationnel le dénominateur, on obtient :

$\begin{array}{rcl} h&=&\dfrac{30}{5-\sqrt{3}}\\\\&=&\dfrac{30(5+\sqrt{3})}{(5-\sqrt{3})(5+\sqrt{3})}\\\\&=&\dfrac{30(5+\sqrt{3})}{5^{2}-(\sqrt{3})^{2}}\\\\&=&\dfrac{30(5+\sqrt{3})}{25-3}\\\\&=&\dfrac{30(5+\sqrt{3})}{22}\\\\&=&\dfrac{75+15\sqrt{3}}{11}\end{array}$

D'où,

$\boxed{h=\dfrac{75+15\sqrt{3}}{11}\simeq 9.18\;cm}$

$-\$ Calcul du volume de ce cône

Soit

$V_{\text{cône initial}}$ le volume du cône initial alors, on a :

$V_{\text{cône initial}}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

Ainsi, en remplaçant l'aire de la base par

$100\;cm^{2}$ et la hauteur par

$9.18\;cm$ , on trouve :

$\begin{array}{rcl}V_{\text{cône initial}}&=&\dfrac{100\times 9.18}{3}\\\\&=&\dfrac{918}{3}\\\\&=&306\end{array}$

Donc,

$\boxed{V_{\text{cône initial}}=306\;cm^{3}}$

2) Calculons le volume du tronc de cône.

Soit

$V_{\text{cône initial}}$ le volume du cône initial et

$V_{\text{tronc de cône}}$ le volume du tronc de cône alors, on a :

$V_{\text{tronc de cône}}=(1-k^{3})\times V_{\text{cône initial}}$

où,

$k$ est le coefficient de réduction.

Ainsi, en remplaçant

$k\$ et

$\ V_{\text{cône initial}}$ par leur valeur, on obtient :

$\begin{array}{rcl} V_{\text{tronc de cône}}&=&\left(1-\left(\dfrac{\sqrt{3}}{5}\right)^{3}\right)\times 306\\\\&=&\left(1-\dfrac{3\sqrt{3}}{125}\right)\times 306\\\\&=&\left(\dfrac{125-3\sqrt{3}}{125}\right)\times 306\\\\&=&0.958\times 306\\\\&=&293.14\end{array}$

D'où,

$\boxed{V_{\text{tronc de cône}}=293.14\;cm^{3}}$

Exercice 28

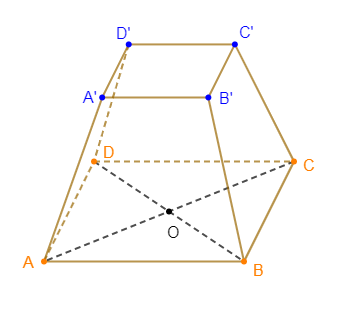
Le solide

$A'B'C'D'ABCD$ est une caisse qui a la forme du tronc d'une pyramide régulière

$SABCD$ à base carrée qui peut contenir

$2\,024\;cm^{3}$ de mil.

On donne :

$SA'=10\;cm\;,\ SO=28\;cm\;,\ AC=20\;cm\$ et

$\ AB=15\;cm.$

$[SA]$ représente une arête latérale pour la pyramide

$SABCD.$

2) Calculons sa longueur.

En effet,

$SABCD$ étant une pyramide régulière et

$O$ centre de la base

$ABCD$ alors,

$[SO]$ est la hauteur de cette pyramide.

Par suite,

$(SO)$ est perpendiculaire à

$(AO).$

D'où, le triangle

$SAO$ est rectangle en

$O.$

Ainsi, en appliquant le théorème de Pythagore, on obtient :

$SA^{2}=SO^{2}+OA^{2}$

Ce qui entraine :

$SA=\sqrt{SO^{2}+OA^{2}}$

Or,

$O$ est milieu de

$[AC]$ donc,

$OA=\dfrac{AC}{2}=\dfrac{20}{2}=10\;cm$

Ainsi, en remplaçant,

$SO\$ et

$\ OA$ par leur valeur, on trouve :

$\begin{array}{rcl} SA&=&\sqrt{SO^{2}+OA^{2}}\\\\&=&\sqrt{28^{2}+10^{2}}\\\\&=&\sqrt{784+100}\\\\&=&\sqrt{884}\\\\&=&29.73\end{array}$

D'où,

$\boxed{SA=29.73\;cm}$

3) Calculons le volume de la pyramide

$SABCD.$

Soit

$V_{(SABCD)}$ le volume de la pyramide

$SABCD$ de hauteur

$[SO]$ alors, on a :

$V_{(SABCD)}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

où, l'aire de la base est égale à

$AB^{2}$

Alors, en remplaçant l'aire de la base et la hauteur par leur valeur, on trouve :

$\begin{array}{rcl}V_{(SABCD)}&=&\dfrac{AB^{2}\times SO}{3}\\\\&=&\dfrac{15^{2}\times 28}{3}\\\\&=&\dfrac{225\times 28}{3}\\\\&=&\dfrac{6\,300}{3}\\\\&=&2\,100\end{array}$

D'où,

$\boxed{V_{(SABCD)}=2\,100\;cm^{3}}$

Autre méthode

Soit

$V_{(SABCD)}$ le volume de la pyramide initiale,

$V_{(SA'B'C'D')}$ le volume de la pyramide réduite et

$V_{(ABCDA'B'C'D')}$ le volume du tronc de pyramide ou de la caisse alors, on a :

$V_{(ABCDA'B'C'D')}=V_{(SABCD)}-V_{(SA'B'C'D')}$

Or, le volume de la pyramide réduite est donné par :

$V_{(SA'B'C'D')}=k^{3}\times V_{(SABCD)}$

où,

$k$ est le coefficient de réduction de la pyramide.

Alors, on a :

$\begin{array}{rcl} V_{(ABCDA'B'C'D')}&=&V_{(SABCD)}-k^{3}\times V_{(SABCD)}\\\\&=&(1-k^{3})\times V_{(SABCD)}\end{array}$

Donc,

$\boxed{V_{(ABCDA'B'C'D')}=(1-k^{3})\times V_{(SABCD)}}$

Ce qui entraine :

$V_{(SABCD)}=\dfrac{V_{(ABCDA'B'C'D')}}{(1-k^{3})}$

Calculons alors le coefficient de réduction

$k.$

On a :

$SA'=10\;cm\$ et

$\ SA=29.73\;cm$ alors, le coefficient

$k$ est donné par :

$k=\dfrac{10}{29.732}=0.33$

Or, le volume de la caisse est égal à

$2\,024\;cm^{3}.$

Donc, en remplaçant le volume du tronc de pyramide par le volume de la caisse et le coefficient

$k$ par sa valeur, on trouve :

$\begin{array}{rcl} V_{(SABCD)}&=&\dfrac{V_{(ABCDA'B'C'D')}}{(1-k^{3})}\\\\&=&\dfrac{2024}{(1-(0.33)^{3})}\\\\&=&\dfrac{2024}{0.964}\\\\&=&2099.58\end{array}$

D'où,

$\boxed{V_{(SABCD)}\simeq 2100\;cm^{3}}$

Exercice 29

Cette médaille ci-dessous est tirée d'un patron d'une pyramide à base hexagonale.

On y voit

$6$ faces qui sont des triangles équilatéraux superposables.

La hauteur de chaque triangle est de

$4\sqrt{3}\;cm.$

1) Calculons l'arête de base de la pyramide.

En effet, les arêtes de base de cette pyramide ont même longueur.

Considérons le triangle

$SEH$ rectangle en

$H.$

Alors, d'après le théorème de Pythagore, on a :

$SE^{2}=SH^{2}+EH^{2}$

Or,

$H$ est milieu de

$[ED]$ donc,

$EH=\dfrac{ED}{2}$

Par suite, en remplaçant

$EH$ par son expression et

$SH$ par

$4\sqrt{3}$ , on obtient :

$SE^{2}=(4\sqrt{3})^{2}+\left(\dfrac{ED}{2}\right)^{2}$

Comme le triangle

$ESD$ est équilatéral alors, on a :

$SE=ED$

Donc,

$ED^{2}=48+\dfrac{ED^{2}}{4}$

$\begin{array}{rcl} ED^{2}=48+\dfrac{ED^{2}}{4}&\Leftrightarrow&ED^{2}-\dfrac{ED^{2}}{4}=48\\\\&\Leftrightarrow&\dfrac{4ED^{2}-ED^{2}}{4}=48\\\\&\Leftrightarrow&\dfrac{3ED^{2}}{4}=48\\\\&\Leftrightarrow&3ED^{2}=48\times 4\\\\&\Leftrightarrow&ED^{2}=\dfrac{192}{3}\\\\&\Leftrightarrow&ED^{2}=64\\\\&\Leftrightarrow&ED=\sqrt{64}\\\\&\Leftrightarrow&ED=8\end{array}$

D'où,

$\boxed{ED=8\;cm}$

Ainsi, chaque arête de base de cette pyramide est de longueur

$8\;cm.$

2) Calculons l'aire de base de la pyramide.

En observant la figure ci-dessus, nous remarquons que la base de cette pyramide est constituée de

$6$ triangles identiques aux faces.

Soit

$\mathcal{A}_{B}$ l'aire de la base de cette pyramide.

Alors, on a :

$\mathcal{A}_{B}=6\times\text{Aire du triangle }ESD$

Or, l'aire

$\mathcal{A}_{(ESD)}$ du triangle

$ESD$ est donnée par :

$\begin{array}{rcl} \mathcal{A}_{(ESD)}&=&\dfrac{ED\times SH}{2}\\\\&=&\dfrac{8\times 4\sqrt{3}}{2}\\\\&=&16\sqrt{3}\end{array}$

Donc,

$\boxed{\mathcal{A}_{(ESD)}=16\sqrt{3}\simeq 27.71\;cm^{2}}$

Ainsi, en remplaçant l'aire du triangle

$ESD$ par sa valeur, on trouve :

$\begin{array}{rcl} \mathcal{A}_{B}&=&6\times\mathcal{A}_{(ESD)}\\\\&=&6\times 16\sqrt{3}\\\\&=&96\sqrt{3}\end{array}$

D'où,

$\boxed{\mathcal{A}_{B}=96\sqrt{3}\simeq 166.27\;cm^{2}}$

3) Sachant que la hauteur

$SO$ de la pyramide vaut

$6\;cm$ , calculons le volume et l'aire latérale de la pyramide.

En effet, le volume

$V$ de cette pyramide est donné par :

$V=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

Alors, en remplaçant l'aire de la base et la hauteur par leur valeur, on trouve :

$\begin{array}{rcl} V&=&\dfrac{\mathcal{A}_{B}\times SO}{3}\\\\&=&\dfrac{96\sqrt{3}\times 6}{3}\\\\&=&\dfrac{576\sqrt{3}}{3}\\\\&=&192\sqrt{3}\end{array}$

D'où,

$\boxed{V=192\sqrt{3}\simeq 332.55\;cm^{3}}$

Comme la partie latérale est formée de

$6$ faces identiques alors, l'aire latérale

$\mathcal{A}_{L}$ est donnée par :

$\mathcal{A}_{L}=6\times\text{Aire du triangle }ESD$

Or, d'après le résultat de la question

$2)$ , l'aire du triangle

$ESD$ est égale à

$16\sqrt{3}.$

Donc, on a :

$\begin{array}{rcl} \mathcal{A}_{L}&=&6\times\mathcal{A}_{(ESD)}\\\\&=&6\times 16\sqrt{3}\\\\&=&96\sqrt{3}\end{array}$

D'où,

$\boxed{\mathcal{A}_{L}=96\sqrt{3}\simeq 166.27\;cm^{2}}$

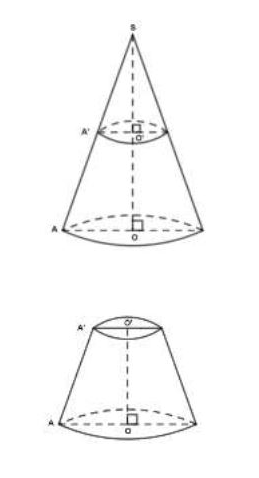
Exercice 30

Fatou mange de la glace ayant la forme d'un cône de révolution.

Au bout d'un moment, la hauteur de sa glace diminue de moitié.

Les figures ci-dessous schématisent la situation.

On donne :

$SA=15\;cm\$ et

$\ OA=2\;cm.$

On admet que les droites

$(OA)\$ et

$\ (O'A')$ sont parallèles.

1) Dessinons le triangle

$SAO$ à l'échelle

$\dfrac{1}{2}$

Calculons

$O'A'.$

En effet, comme les droites

$(OA)\$ et

$\ (O'A')$ sont parallèles alors, les triangles

$SAO\$ et

$\ SA'O'$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{O'A'}{OA}=\dfrac{SO'}{SO}$

Or, on sait que la hauteur de la glace a diminué de moitié.

Ce qui signifie que :

$SO'=\dfrac{SO}{2}$

Ainsi, dans la relation de Thalès, en remplaçant

$SO'$ par

$\dfrac{SO}{2}\$ et

$\ OA$ par sa valeur, on obtient :

$\begin{array}{rcl} \dfrac{O'A'}{OA}=\dfrac{SO'}{SO}&\Leftrightarrow&\dfrac{O'A'}{2}=\dfrac{\dfrac{SO}{2}}{SO}\\\\&\Leftrightarrow&\dfrac{O'A'}{2}=\dfrac{SO}{2\times SO}\\\\&\Leftrightarrow&\dfrac{O'A'}{2}=\dfrac{1}{2}\\\\&\Leftrightarrow&O'A'=\dfrac{2}{2}\\\\&\Leftrightarrow&O'A'=1\end{array}$

D'où,

$\boxed{O'A'=1\;cm}$

2) Calculons le volume de la glace que Fatou a mangé.

En effet, la partie de la glace que Fatou a mangé a la forme d'un cône réduit de hauteur

$SO'$ et de rayon de base

$O'A'.$

Le coefficient de réduction

$k$ de ce cône est donc donné par :

$k=\dfrac{O'A'}{OA}=\dfrac{1}{2}$

Soit

$V_{\text{initial}}$ le volume du cône initial et

$V_{\text{réduit}}$ le volume du cône réduit.

Comme dans le cas d'une réduction, le volume du cône réduit est obtenu en multipliant le volume du cône initial par le cube du coefficient de réduction alors, on a :

$\begin{array}{rcl} V_{\text{réduit}}&=&k^{3}\times V_{\text{initial}}\\\\&=&\left(\dfrac{1}{2}\right)^{3}\times V_{\text{initial}}\\\\&=&\dfrac{1}{8}\times V_{\text{initial}}\end{array}$

Donc,

$\boxed{V_{\text{réduit}}=\dfrac{1}{8}\times V_{\text{initial}}}$

Calculons alors le volume du cône initial.

On a :

$V_{\text{initial}}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

$-\$ Calcul de l'aire de la base

On a :

$\begin{array}{rcl} \text{Aire de la base}&=&\pi\times OA^{2}\\\\&=&3.14\times 2^{2}\\\\&=&3.14\times 4\\\\&=&12.56\end{array}$

Donc,

$\boxed{\text{Aire de la base}=12.56\;cm^{2}}$

$-\$ Calcul de la hauteur

$SO$

En effet, le triangle

$SAO$ étant rectangle en

$O$ alors, d'après le théorème de Pythagore, on a :

$SO^{2}+OA^{2}=SA^{2}$

Ce qui donne :

$SO^{2}=SA^{2}-OA^{2}$

Par suite,

$SO=\sqrt{SA^{2}-OA^{2}}$

En remplaçant

$SA\$ et

$\ OA$ par leur valeur, on trouve :

$\begin{array}{rcl} SO&=&\sqrt{SA^{2}-OA^{2}}\\\\&=&\sqrt{15^{2}-2^{2}}\\\\&=&\sqrt{225-4}\\\\&=&\sqrt{221}\end{array}$

Donc,

$\boxed{SO=\sqrt{221}\simeq 14.86\;cm}$

Le volume du cône initial est alors donné par :

$\begin{array}{rcl} V_{\text{initial}}&=&\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}\\\\&=&\dfrac{12.56\times 14.86}{3}\\\\&=&\dfrac{186.6416}{3}\\\\&=&62.21\end{array}$

D'où,

$\boxed{V_{\text{initial}}=62.21\;cm^{3}}$

Par conséquent, le volume réduit est égal à :

$\begin{array}{rcl} V_{\text{réduit}}&=&\dfrac{1}{8}\times V_{\text{initial}}\\\\&=&\dfrac{1}{8}\times 62.21\\\\&=&\dfrac{62.21}{8}\\\\&=&7.77\end{array}$

Ainsi,

$\boxed{V_{\text{réduit}}=7.77\;cm^{3}}$

Fatou a donc mangé

$7.77\;cm^{3}$ de cette glace.

Déterminons la fraction du volume initial qui lui reste à manger.

Soit

$V_{\text{reste}}$ le volume qui lui reste à manger.

Comme la partie restante a la forme d'un tronc de cône alors, on a :

$V_{\text{reste}}=(1-k^{3})\times V_{\text{initial}}$

où,

$k$ est le coefficient de réduction du cône.

En remplaçant

$k$ par sa valeur ;

$\dfrac{1}{2}$ , on trouve :

$\begin{array}{rcl} V_{\text{reste}}&=&(1-k^{3})\times V_{\text{initial}}\\\\&=&\left(1-\left(\dfrac{1}{2}\right)^{3}\right)\times V_{\text{initial}}\\\\&=&\left(1-\dfrac{1}{8}\right)\times V_{\text{initial}}\\\\&=&\left(\dfrac{8}{8}-\dfrac{1}{8}\right)\times V_{\text{initial}}\\\\&=&\dfrac{7}{8}\times V_{\text{initial}}\end{array}$

D'où,

$\boxed{V_{\text{reste}}=\dfrac{7}{8}\times V_{\text{initial}}}$

Par conséquent, il lui reste

$\dfrac{7}{8}$ du volume initial à manger.

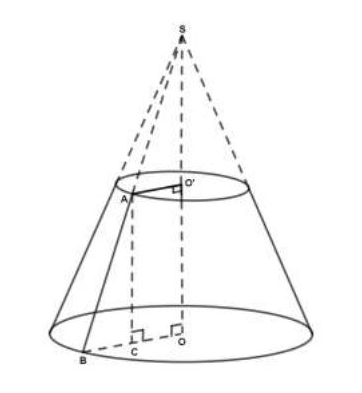
Exercice 31

On considère le tronc de cône ci-dessous associé à un cône de révolution de sommet

$S$ et de rayon

$OB=6\;cm.$

1) Sachant que

$OO'=4\;cm\;;\ OB=6\;cm\$ et

$\ O'A=3\;cm$ , montrons que :

$AB=5\;cm.$

En effet, le triangle

$ABC$ étant rectangle en

$C$ alors, d'après le théorème de Pythagore, on a :

$AB^{2}=AC^{2}+BC^{2}$

Ce qui donne :

$AB=\sqrt{AC^{2}+BC^{2}}$

Déterminons alors les longueurs

$AC\$ et

$\ BC$

En observant la figure nous remarquons que le quadrilatère

$ACOO'$ est un rectangle.

Par conséquent,

$OC=O'A=3\;cm\$ et

$\ AC=OO'=4\;cm$

Par suite,

$\begin{array}{rcl} BC&=&OB-OC\\\\&=&6-3\\\\&=&3\end{array}$

Donc,

$\boxed{BC=3\;cm}$

Ainsi, dans l'expression de

$AB$ , en remplaçant

$AC\$ et

$\ BC$ par leur valeur, on trouve :

$\begin{array}{rcl} AB&=&\sqrt{AC^{2}+BC^{2}}\\\\&=&\sqrt{4^{2}+3^{2}}\\\\&=&\sqrt{16+9}\\\\&=&\sqrt{25}\\\\&=&5\end{array}$

D'où,

$\boxed{AB=5\;cm}$

2) Montrons que la hauteur

$SO$ de ce cône est égale à

$8\;cm.$

En effet, les droites

$(AC)\$ et

$\ (SO)$ étant parallèles alors, les triangles

$ABC\$ et

$\ SBO$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{SO}{AC}=\dfrac{OB}{BC}$

Ainsi, en remplaçant

$AC\;,\ OB\$ et

$\ BC$ par leur valeur, on obtient :

$\begin{array}{rcl} \dfrac{SO}{AC}=\dfrac{OB}{BC}&\Leftrightarrow&\dfrac{SO}{4}=\dfrac{6}{3}\\\\&\Leftrightarrow&\dfrac{SO}{4}=2\\\\&\Leftrightarrow&SO=2\times 4\\\\&\Leftrightarrow&SO=8\end{array}$

D'où,

$\boxed{SO=8\;cm}$

3) La génératrice

$SB$ de ce cône est égale à

$10\;cm$ ; calculons l'aire latérale

$A_{L}$ du cône.

En effet, l'aire latérale

$A_{L}$ du cône est donnée par :

$A_{L}=\pi\times\text{rayon de la base}\times\text{génératrice}$

Ainsi, en remplaçant le rayon de la base et la génératrice par leur valeur, on trouve :

$\begin{array}{rcl} A_{L}&=&\pi\times OB\times SB\\\\&=&3.14\times 6\times 10\\\\&=&188.4\end{array}$

D'où,

$\boxed{A_{L}=188.4\;cm^{2}}$

4) Ce cône de révolution est obtenu d'un secteur circulaire d'angle

$\alpha.$

Calculons en degré la mesure de l'angle

$\alpha$ du développement de ce cône.

Soit

$\alpha$ l'angle d'ouverture du développement de ce cône alors, on a :

$\alpha=\dfrac{\text{rayon de la base}\times 360^{\circ}}{\text{génératrice}}$

Alors, en remplaçant le rayon de la base et la génératrice par leur valeur, on trouve :

$\begin{array}{rcl} \alpha&=&\dfrac{6\times 360^{\circ}}{10}\\\\&=&\dfrac{2\,160^{\circ}}{10}\\\\&=&216^{\circ}\end{array}$

Ainsi,

$\boxed{\alpha=216^{\circ}}$

5) Calculons le volume

$V_{c}$ du cône initial.

Le volume

$V_{c}$ du cône initial est donné par :

$V_{c}=\dfrac{\pi\times OB^{2}\times SO}{3}$

Alors, en remplaçant

$OB\$ et

$\ SO$ par leur valeur, on trouve :

$\begin{array}{rcl} V_{c}&=&\dfrac{\pi\times OB^{2}\times SO}{3}\\\\&=&\dfrac{3.14\times 6^{2}\times 8}{3}\\\\&=&\dfrac{3.14\times 36\times 8}{3}\\\\&=&\dfrac{904.32}{3}\\\\&=&301.44\end{array}$

D'où,

$\boxed{V_{c}=301.44\;cm^{3}}$

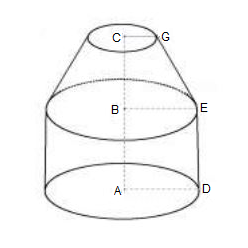
Exercice 32

Le dessin ci-dessous représente un réservoir formé d'un tronc de cône de hauteur

$6\;dm$ et de rayon de base (petite base)

$4\;dm$ ; d'un cylindre de hauteur

$8.5\;dm$ et de rayon

$7\;dm.$

a) Calculons le volume

$V_{1}$ du tronc de cône.

Soit

$V_{\text{cône initial}}$ le volume du cône initial et

$V_{1}$ le volume du tronc de cône alors, on a :

$V_{1}=(1-k^{3})\times V_{\text{cône initial}}$

où,

$k$ est le coefficient de réduction.

$-\$ Calcul de

$k$

Comme

$CG$ est le rayon de la base du cône réduit et

$BE$ le rayon de la base du cône initial alors, le coefficient de réduction

$k$ est donné par :

$k=\dfrac{CG}{BE}=\dfrac{4}{7}$

$-\$ Calcul de

$V_{\text{cône initial}}$

On a :

$V_{\text{cône initial}}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

L'aire de la base est donnée par :

$\begin{array}{rcl}\text{Aire de la base}&=&\pi\times BE^{2}\\\\&=&3.14\times 7^{2}\\\\&=&3.14\times 49\\\\&=&153.86\end{array}$

Donc,

$\boxed{\text{Aire de la base}=153.86\;dm^{2}}$

Déterminons la hauteur de ce cône.

Soit

$h$ la hauteur du cône initial et

$h'$ la hauteur du cône réduit.

Comme la hauteur

$BC$ du tronc de cône est égale à

$6\;dm$ alors, on a :

$h=h'+6$

Or,

$k=\dfrac{4}{7}$ donc,

$h'=\dfrac{4}{7}h$

Ainsi, en remplaçant

$h'$ par

$\dfrac{4}{7}h$ , on trouve :

$\begin{array}{rcl} h=h'+6&\Leftrightarrow&h=\dfrac{4}{7}h+6\\\\&\Leftrightarrow&h-\dfrac{4h}{7}=6\\\\&\Leftrightarrow&\dfrac{7h}{7}-\dfrac{4h}{7}=6\\\\&\Leftrightarrow&\dfrac{7h-4h}{7}=6\\\\&\Leftrightarrow&\dfrac{3h}{7}=6\\\\&\Leftrightarrow&3h=6\times 7\\\\&\Leftrightarrow&h=\dfrac{42}{3}\\\\&\Leftrightarrow&h=14\end{array}$

Donc,

$\boxed{h=14\;dm}$

Ainsi, en remplaçant l'aire de la base et la hauteur par leur valeur, on trouve :

$\begin{array}{rcl}V_{\text{cône initial}}&=&\dfrac{153.86\times 14}{3}\\\\&=&\dfrac{2\,154.04}{3}\\\\&=&718\end{array}$

Donc,

$\boxed{V_{\text{cône initial}}=718\;dm^{3}}$

Enfin, en remplaçant

$k\$ et

$\ V_{\text{cône initial}}$ par leur valeur, on obtient :

$\begin{array}{rcl} V_{1}&=&\left(1-\left(\dfrac{4}{7}\right)^{3}\right)\times 718\\\\&=&\left(1-\dfrac{4^{3}}{7^{3}}\right)\times 718\\\\&=&\left(1-\dfrac{64}{343}\right)\times 718\\\\&=&\left(\dfrac{343-64}{343}\right)\times 718\\\\&=&\dfrac{279}{343}\times 718\\\\&=&584\end{array}$

D'où,

$\boxed{V_{1}=584\;dm^{3}}$

b) Calculons le volume

$V_{2}$ du cylindre et le volume total

$V_{t}$ du réservoir.

En effet, le volume

$V_{2}$ du cylindre est donné par :

$V_{2}=\text{Aire de la base}\times\text{Hauteur}$

Or, l'aire de la base est égale à

$\pi\times 7^{2}$ et la hauteur

$8.5\;dm$

On obtient alors :

$\begin{array}{rcl} V_{2}&=&\pi\times 7^{2}\times 8.5\\\\&=&3.14\times 49\times 8.5\\\\&=&1\,307.81 \end{array}$

Ainsi,

$\boxed{V_{2}=1\,307.81\;dm^{3}}$

Enfin, le volume total

$V_{t}$ du réservoir est donné par :

$V_{t}=V_{1}+V_{2}$

Alors, en remplaçant

$V_{1}\$ et

$\ V_{2}$ par leur valeur, on trouve :

$\begin{array}{rcl} V_{t}&=&V_{1}+V_{2}\\\\&=&584+1\,307.81\\\\&=&1\,891.81 \end{array}$

D'où,

$\boxed{V_{t}=1\,891.81\;dm^{3}}$

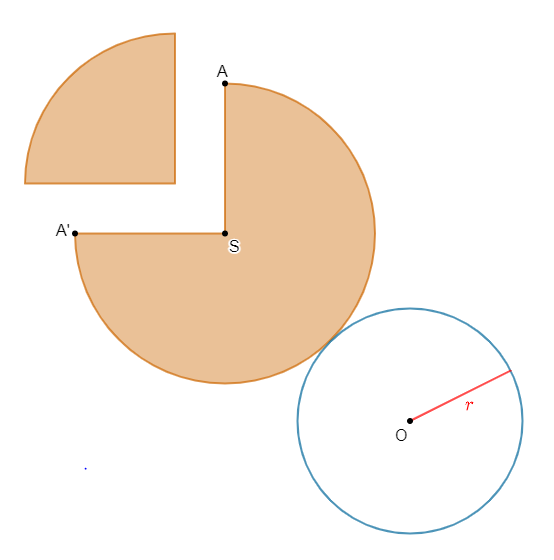
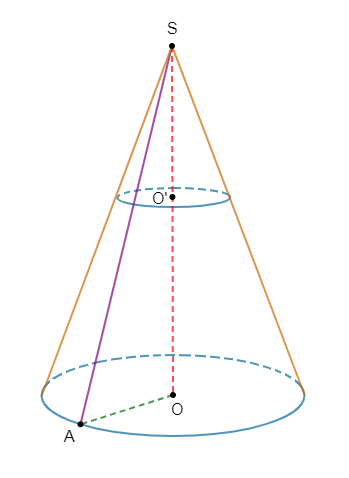
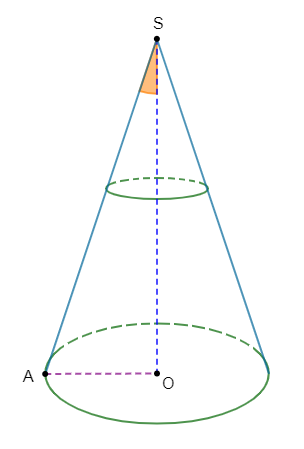
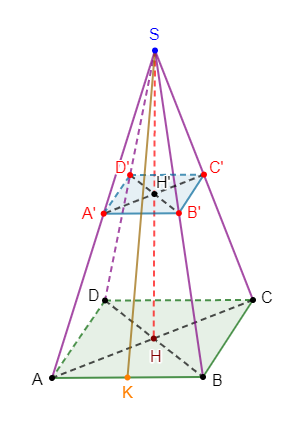
Exercice de Synthèse

I. Le schéma ci-dessous représente le patron d'un cône de révolution de sommet

$S$ , de rayon de base

$r.$

La génératrice

$[SA]$ a pour longueur

$36\;cm.$

1) Justifions que la circonférence de sa base mesure

$54\pi\;cm.$

En effet, on sait que la circonférence de la base de ce cône est égale à la longueur de l'arc

$\overset{\displaystyle\frown}{AA'}$

Or, si

$\alpha$ est l'angle du développement de ce cône alors, la longueur de l'arc

$\overset{\displaystyle\frown}{AA'}$ est donnée par :

$\text{Longueur de l'arc }\overset{\displaystyle\frown}{AA'}=\text{Génératrice}\times\alpha$

Déterminons alors la mesure en radian de l'angle

$\alpha$

En observant le schéma ci-dessus, nous constatons que l'angle

$\alpha$ du développement de ce cône de révolution est donné par :

$\alpha=360^{\circ}-90^{\circ}$

Or,

$360^{\circ}=2\pi\$ et

$\ 90^{\circ}=\dfrac{\pi}{2}$

Donc, en remplaçant

$360^{\circ}$ par

$2\pi\$ et

$\ 90^{\circ}$ par

$\dfrac{\pi}{2}$ , on trouve :

$\begin{array}{rcl}\alpha&=&360^{\circ}-90^{\circ}\\\\&=&2\pi-\dfrac{\pi}{2}\\\\&=&\dfrac{4\pi}{2}-\dfrac{\pi}{2}\\\\&=&\dfrac{3\pi}{2}\end{array}$

D'où,

$\boxed{\alpha=\dfrac{3\pi}{2}}$

Ainsi,

$\begin{array}{rcl}\text{Longueur de l'arc }\overset{\displaystyle\frown}{AA'}&=&SA\times\alpha\\\\&=&36\times\dfrac{3\pi}{2}\\\\&=&\dfrac{36\times 3\pi}{2}\\\\&=&\dfrac{108\pi}{2}\\\\&=&54\pi\end{array}$

D'où,

$\boxed{\text{Longueur de l'arc }\overset{\displaystyle\frown}{AA'}=54\pi\;cm}$

Par conséquent, la circonférence de la base de ce cône de révolution mesure

$54\pi\;cm.$

2) Montrons que son rayon de base

$r$ vaut

$27\;cm.$

En effet, la circonférence de la base est égale à :

$2\pi\times r$

Or, d'après le résultat de la question

$1)$ , cette circonférence mesure

$54\pi\;cm.$

Donc, en comparant, on a :

$2\pi\times r=54\pi$

Ce qui entraine :

$r=\dfrac{54\pi}{2\pi}=27$

D'où,

$\boxed{r=27\;cm}$

3) Justifions que la hauteur de ce cône est égale à

$9\sqrt{7}\;cm$

Considérons la figure ci-dessous.

Soit

$[SO]$ la hauteur de ce cône.

Le triangle

$SAO$ étant rectangle en

$O$ alors, en appliquant le théorème de Pythagore, on obtient :

$SO^{2}+OA^{2}=SA^{2}$

Donc,

$SO^{2}=SA^{2}-OA^{2}$

Ce qui entraine :

$SO=\sqrt{SA^{2}-OA^{2}}$

Or, d'après le résultat de la question

$3)$ , on a :

$r=OA=27\;cm$

Donc, en remplaçant

$SA\$ et

$\ OA$ par leur valeur, on trouve :

$\begin{array}{rcl}SO&=&\sqrt{SA^{2}-OA^{2}}\\\\&=&\sqrt{36^{2}-27^{2}}\\\\&=&\sqrt{1\,296-729}\\\\&=&\sqrt{567}\\\\&=&\sqrt{81\times 7}\\\\&=&9\sqrt{7}\end{array}$

D'où,

$\boxed{SO=9\sqrt{7}\;cm}$

4) Calculons l'aire totale de ce cône.

On prendra

$\pi=3.14$

En effet, l'aire totale de ce cône est donnée par :

$\text{Aire totale}=\text{Aire latérale}+\text{Aire de la base}$

avec,

$\text{Aire latérale}=\pi\times r\times SA$

$\text{Aire de la base}=\pi\times r^{2}$

Par suite,

$\begin{array}{rcl}\text{Aire totale}&=&\text{Aire latérale}+\text{Aire de la base}\\\\&=&\pi\times r\times SA+\pi\times r^{2}\\\\&=&3.14\times 27\times 36+3.14\times 27^{2}\\\\&=&3\,052.08+2\,289.06\\\\&=&5\,341.14\end{array}$

D'où,

$\boxed{\text{Aire totale}=5\,341.14\;cm^{2}}$

5) On sectionne ce cône et le rayon du cône réduit est égal à

$15\;cm.$

Déterminons le coefficient de réduction ainsi que le volume du cône réduit

Soit

$k$ le coefficient de réduction de ce cône alors, on a :

$k=\dfrac{\text{rayon cône réduit}}{\text{rayon cône initial}}=\dfrac{15}{27}$

D'où, en simplifiant par

$3\ :\ \boxed{k=\dfrac{5}{9}}$

Calculons le volume du cône réduit.

Soit

$V_{\text{réduit}}$ le volume du cône réduit et

$V_{\text{initial}}$ le volume du cône initial.

Comme dans le cas d'une réduction, le volume du cône réduit est obtenu en multipliant le volume du cône initial par le cube du coefficient de réduction alors, on a :

$V_{\text{réduit}}=k^{3}\times V_{\text{initial}}$

Déterminons alors le volume du cône initial.

On a :

$\begin{array}{rcl} V_{\text{initial}}&=&\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}\\\\&=&\dfrac{\pi\times r^{2}\times SO}{3}\\\\&=&\dfrac{3.14\times 27^{2}\times 9\sqrt{7}}{3}\\\\&=&3.14\times 729\times 3\sqrt{7}\\\\&=&18\,168.85\end{array}$

D'où,

$\boxed{V_{\text{initial}}=18\,168.85\;cm^{3}}$

Ainsi, le volume du cône réduit est égal à :

$\begin{array}{rcl} V_{\text{réduit}}&=&k^{3}\times V_{\text{initial}}\\\\&=&\left(\dfrac{5}{9}\right)^{3}\times 18\,168.85\\\\&=&\dfrac{5^{3}}{9^{3}}\times 18\,168.85\\\\&=&\dfrac{125\times 18\,168.85}{729}\\\\&=&3\,115.37\end{array}$

Donc,

$\boxed{V_{\text{réduit}}=3\,115.37\;cm^{3}}$

II. Soit un cône de révolution de sommet

$S$ et dont la base est un disque de centre

$O$ et de rayon

$OA$ égal à

$3\;cm$

1) Sachant que l'angle

$\widehat{OSA}=30^{\circ}$ ; calculons la génératrice

$SA$ de ce cône et montrons que

$SO=3\sqrt{3}$

En effet, comme le triangle

$SOA$ est rectangle en

$O$ alors, on peut utiliser le sinus de l'angle

$\widehat{OSA}$ pour calculer la génératrice

$SA.$

On a :

$\sin\widehat{OSA}=\dfrac{OA}{SA}$

Donc,

$SA\times\sin\widehat{OSA}=OA$

Par suite,

$SA=\dfrac{OA}{\sin\widehat{OSA}}$

Ainsi, en remplaçant

$OA\$ et

$\ \sin\widehat{OSA}$ par leur valeur, on trouve :

$\begin{array}{rcl} SA&=&\dfrac{3}{\dfrac{1}{2}}\\\\&=&3\times 2\\\\&=&6\end{array}$

D'où,

$\boxed{SA=6\;cm}$

Montrons que

$SO=3\sqrt{3}$

En utilisant le cosinus de l'angle

$\widehat{OSA}$ , on a :

$\cos\widehat{OSA}=\dfrac{SO}{SA}$

Ce qui donne :

$SO=SA\times\cos\widehat{OSA}$

Alors, en remplaçant

$SA\$ et

$\ \cos\widehat{OSA}$ par leur valeur, on trouve :

$\begin{array}{rcl} SO&=&6\times\dfrac{\sqrt{3}}{2}\\\\&=&\dfrac{6\sqrt{3}}{2}\\\\&=&3\sqrt{3}\end{array}$

Ainsi,

$\boxed{SO=3\sqrt{3}\;cm}$

Remarque :

On peut aussi utiliser le théorème de Pythagore pour montrer que

$SO=3\sqrt{3}.$

2) Montrons que le volume de ce cône de révolution est

$9\pi\sqrt{3}\;cm^{3}$

Soit

$V$ le volume du cône initial alors, on a :

$\begin{array}{rcl} V&=&\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}\\\\&=&\dfrac{\pi\times OA^{2}\times SO}{3}\\\\&=&\dfrac{\pi\times 3^{2}\times 3\sqrt{3}}{3}\\\\&=&\dfrac{\pi\times 9\times 3\sqrt{3}}{3}\\\\&=&\pi\times9\sqrt{3}\\\\&=&9\times\pi\times\sqrt{3}\end{array}$

D'où,

$\boxed{V=9\pi\sqrt{3}\;cm^{3}}$

3) On coupe ce cône par un plan parallèle à sa base de telle sorte que la base du cône réduit qui en résulte ait une aire de

$\dfrac{9}{4}\pi\;cm^{2}.$

Calculons le coefficient de réduction

$k$ et en déduisons le volume

$V'$ du cône réduit.

En effet, on sait que dans le cas d'une réduction, l'aire de la base du cône réduit est obtenue en multipliant l'aire de la base du cône initial par le carré du coefficient de réduction.

Cela se traduit par :

$\dfrac{9}{4}\pi=k^{2}\times 9\pi$

Ce qui entraine :

$k^{2}=\dfrac{\dfrac{9}{4}\pi}{9\pi}=\dfrac{9\pi}{4\times 9\pi}=\dfrac{1}{4}$

Ainsi,

$\begin{array}{rcl} k&=&\sqrt{\dfrac{1}{4}}\\\\&=&\dfrac{\sqrt{1}}{\sqrt{4}}\\\\&=&\dfrac{1}{2}\end{array}$

D'où,

$\boxed{k=\dfrac{1}{2}}$

En déduisons le volume

$V'$ du cône réduit.

On a :

$\begin{array}{rcl} V'&=&k^{3}\times V\\\\&=&\left(\dfrac{1}{2}\right)^{3}\times 9\pi\sqrt{3}\\\\&=&\dfrac{1}{8}\times 9\pi\sqrt{3}\\\\&=&\dfrac{9\pi\sqrt{3}}{8}\end{array}$

Donc,

$\boxed{V'=\dfrac{9\pi\sqrt{3}}{8}\;cm^{3}}$

III.

$SABCD$ est une pyramide à base carrée

$ABCD$ de centre

$H.$

On donne :

$AB=20\;cm\;,\ SA=40\;cm\;,\ SH$ est la hauteur et

$A'$ est le milieu de

$[SA].$

On coupe la pyramide par un plan parallèle à sa base passant par

$A'.$

1) Calculons

$AC\;,\ AH\$ et

$\ SH$

$-\$ Calcul de

$AC$

En effet, comme la base

$ABCD$ est carrée alors, le triangle

$ABC$ est rectangle en

$B.$

Donc, d'après le théorème de Pythagore, on a :

$AC^{2}=AB^{2}+BC^{2}$

Or,

$AB=BC$

Par suite, en remplaçant

$BC$ par

$AB$ , on obtient :

$AC^{2}=AB^{2}+AB^{2}=2AB^{2}$

Ce qui entraine :

$\begin{array}{rcl} AC&=&\sqrt{2AB^{2}}\\\\&=&\sqrt{2\times AB^{2}}\\\\&=&AB\sqrt{2}\\\\&=&20\sqrt{2}\end{array}$

D'où,

$\boxed{AC=20\sqrt{2}\;cm}$

$-\$ Calcul de

$AH$

En effet, comme

$H$ est le centre du carré

$ABCD$ alors,

$H$ est milieu de la diagonale

$[AC].$

Par conséquent,

$AH=\dfrac{AC}{2}$

Alors, en remplaçant

$AC$ par sa valeur, on trouve :

$\begin{array}{rcl} AH&=&\dfrac{20\sqrt{2}}{2}\\\\&=&10\sqrt{2}\end{array}$

Donc,

$\boxed{AH=10\sqrt{2}\;cm}$

$-\$ Calcul de

$SH$

En effet, comme

$[SH]$ est la hauteur de cette pyramide alors,

$(SH)$ est perpendiculaire à

$(AH).$

Par conséquent, le triangle

$SAH$ est rectangle en

$H.$

Ainsi, en appliquant le théorème de Pythagore, on obtient :

$SH^{2}+AH^{2}=SA^{2}$

Par suite,

$SH^{2}=SA^{2}-AH^{2}$

Ce qui entraine :

$SH=\sqrt{SA^{2}-AH^{2}}$

Donc, en remplaçant

$SA\$ et

$AH$ par leur valeur, on trouve :

$\begin{array}{rcl} SH&=&\sqrt{40^{2}-(10\sqrt{2})^{2}}\\\\&=&\sqrt{1\,600-100\times 2}\\\\&=&\sqrt{1\,600-200}\\\\&=&\sqrt{1\,400}\\\\&=&\sqrt{100\times 14}\\\\&=&10\sqrt{14}\end{array}$

D'où,

$\boxed{SH=10\sqrt{14}\;cm}$

2) Soit

$K$ milieu de

$[AB]$ , calculons

$SK$

En effet, comme

$[SK]$ est un apothème de cette pyramide.

Donc,

$(SK)$ est perpendiculaire à

$(AB).$

Par conséquent, le triangle

$SAK$ est rectangle en

$K.$

Ainsi, en utilisant le théorème de Pythagore, on obtient :

$SK^{2}+AK^{2}=SA^{2}$

Par suite,

$SK^{2}=SA^{2}-AK^{2}$

Ce qui entraine :

$SK=\sqrt{SA^{2}-AK^{2}}$

Ce qui entraine :

$SK=\sqrt{SA^{2}-AK^{2}}$

Or,

$K$ est milieu de

$[AB]$ donc,

$AK=\dfrac{AB}{2}=\dfrac{20}{2}=10\;cm$

Donc, en remplaçant

$SA\$ et

$AK$ par leur valeur, on trouve :

$\begin{array}{rcl} SK&=&\sqrt{40^{2}-10^{2}}\\\\&=&\sqrt{1\,600-100}\\\\&=&\sqrt{1\,500}\\\\&=&\sqrt{100\times 15}\\\\&=&10\sqrt{15}\end{array}$

D'où,

$\boxed{SK=10\sqrt{15}\;cm}$

3) Calculons l'aire de base

Comme

$ABCD$ est carré alors, l'aire de la base est donnée par :

$\text{Aire de la base}=AB^{2}$

Alors, en remplaçant

$AB$ par sa valeur, on trouve :

$\begin{array}{rcl} \text{Aire de la base}&=&AB^{2}\\\\&=&20^{2}\\\\&=&400\end{array}$

D'où,

$\boxed{\text{Aire de la base}=400\;cm^{2}}$

4) Calculons le volume de la pyramide

$SABCD.$

Le volume

$V_{_{(SABCD)}}$ de cette pyramide est donné par :

$V_{_{(SABCD)}}=\dfrac{\text{Aire de la base}\times\text{Hauteur}}{3}$

Ce qui donne :

$\begin{array}{rcl} V_{_{(SABCD)}}&=&\dfrac{400\times SH}{3}\\\\&=&\dfrac{400\times 10\sqrt{14}}{3}\\\\&=&\dfrac{4\,000\sqrt{14}}{3}\\\\&=&4\,988.87\end{array}$

D'où,

$\boxed{V_{_{(SABCD)}}=4\,988.87\;cm^{3}}$

Déduisons-en le volume

$V'$ de la pyramide réduite.

En effet, on sait que dans le cas d'une réduction, le volume de la pyramide réduite est obtenu en multipliant le volume de la pyramide initiale par le cube du coefficient de réduction.

Soit

$\ell$ le coefficient de réduction de cette pyramide alors, on a :

$V'=\ell^{3}\times V_{_{(SABCD)}}$

Calculons alors le coefficient

$\ell.$

Comme

$A'$ est milieu de

$[SA]$ alors,

$SA'=\dfrac{1}{2}SA$

Donc, le coefficient

$\ell$ est égal à :

$\ell=\dfrac{SA'}{SA}=\dfrac{1}{2}$

Ainsi, le volume

$V'$ de la pyramide réduite est donné par :

$\begin{array}{rcl} V'&=&\ell^{3}\times V_{_{(SABCD)}}\\\\&=&\left(\dfrac{1}{2}\right)^{3}\times 4\,988.87\\\\&=&\dfrac{1}{8}\times 4\,988.87\\\\&=&\dfrac{4\,988.87}{8}\\\\&=&623.60\end{array}$

D'où,

$\boxed{V'=623.60\;cm^{3}}$

VI. Dans cet exercice, les longueurs sont exprimées en

$cm$

La relation entre la longueur

$c$ du côté d'un carré et la longueur

$d$ de sa diagonale est donnée par la formule

$d=c\sqrt{2}.$

On donne

$c=\sqrt{8}$

1) a) Montrons que la longueur de sa diagonale est un nombre entier.

On a :

$d=c\sqrt{2}$

Alors, en remplaçant

$c$ par

$\sqrt{8}$ , on trouve :

$\begin{array}{rcl} d&=&c\sqrt{2}\\\\&=&\sqrt{8}\times\sqrt{2}\\\\&=&\sqrt{8\times 2}\\\\&=&\sqrt{16}\\\\&=&4\end{array}$

D'où,

$\boxed{d=4\text{ qui est bien un nombre entier}}$

Ce qui montre que la longueur de sa diagonale est un nombre entier.

b) Montrons que l'aire en

$cm^{2}$ de ce carré est un nombre entier

Soit

$A$ l'aire de ce carré alors, on a :

$A=c^{2}$

Donc, remplaçons

$c$ par

$\sqrt{8}.$

On obtient :

$\begin{array}{rcl} A&=&c^{2}\\\\&=&(\sqrt{8})^{2}\\\\&=&8\end{array}$

Ainsi,

$\boxed{A=8\text{ qui est bien un nombre entier}}$

Ce qui signifie que l'aire en

$cm^{2}$ de ce carré est un nombre entier

2) La longueur de la diagonale d'un autre carré est

$\sqrt{40}$

Calculons la longueur de son côté et exprimons cette longueur sous la forme

$a\sqrt{5}$ où

$a$ est un nombre entier naturel

Soit

$d'$ la longueur de la diagonale de ce carré et

$c'$ la longueur de son côté.

D'après le théorème de Pythagore, on a :

$c'^{2}+c'^{2}=d'^{2}$

C'est-à-dire ;

$2c'^{2}=d'^{2}$

Ce qui donne :

$c'^{2}=\dfrac{d'^{2}}{2}$

Ce qui entraine :

$c'=\sqrt{\dfrac{d'^{2}}{2}}$

Alors, en remplaçant

$d'$ par

$\sqrt{40}$ , on trouve :

$\begin{array}{rcl} c'&=&\sqrt{\dfrac{d'^{2}}{2}}\\\\&=&\sqrt{\dfrac{(\sqrt{40})^{2}}{2}}\\\\&=&\sqrt{\dfrac{40}{2}}\\\\&=&\sqrt{20}\\\\&=&\sqrt{4\times 5}\\\\&=&2\sqrt{5}\end{array}$

D'où,

$\boxed{c'=2\sqrt{5}}$

V. Le volume d'un parallélépipède est égal :

$L\times l\times h$

Auteur:

Diny Faye & Mouhamadou Ka