Solution des exercices : Les parallélogrammes - 5e
Classe:
Cinquième
Exercice 1
1) Construisons un triangle $ABC$ tel que :
$$AB=3\;cm\;;\ AC=4\;cm\quad\text{et}\quad BC=5.5\;cm$$
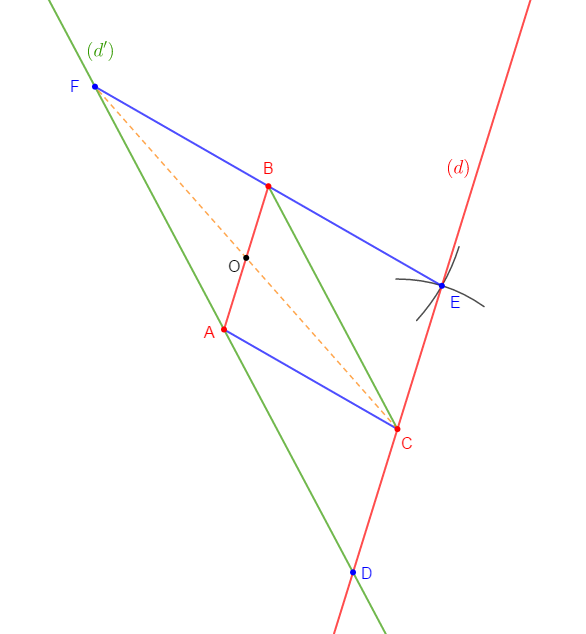
2) a) Construisons le point $D$ pour que le quadrilatère $ABCD$ soit un parallélogramme.
Pour cela, on commence par tracer la droite $(d)$ parallèle à la droite $(AB)$ et passant par le point $C.$
Ensuite, on trace la droite $(d')$ parallèle à la droite $(BC)$ et passant par le point $A.$
Enfin, on place le point $D$ qui est le point de rencontre des deux droites $(d)\ $ et $\ (d').$
b) Construisons le point $E$ pour que le quadrilatère $ABEC$ soit un parallélogramme.
Pour construire le point $E$, on peut utiliser le compas. On mesure l'écartement du segment $[AB]$ ensuite, en se plaçant sur $C$ avec le même écartement, on trace un arc de cercle.
De la même manière, on mesure l'écartement du segment $[AC]$ ensuite, en se plaçant sur $B$ avec le même écartement, on trace un arc de cercle.
Enfin, les deux arcs de cercle se coupent au point $E.$
c) Construisons le point $F$ pour que le quadrilatère $AFBC$ soit un parallélogramme.
Pour cela, on place le point $O$ milieu de la diagonale $[AB].$ Ensuite, on place le point $F$ qui est le symétrique de $C$ par rapport à $O.$
Exercice 2
1) Construisons un triangle $ABC$ tel que :
$$AB=5\;cm\;;\ mes\;\widehat{A}=30^{\circ}\quad\text{et}\quad mes\;\widehat{B}=50^{\circ}$$
2) a) Plaçons le point $I$ milieu du segment $[BC].$
b) Plaçons le point $K$ symétrique de $A$ par rapport au point $I.$
3) $ABKC$ est un parallélogramme.
Justification
On a : $K$ symétrique de $A$ par rapport au point $I$, cela signifie que le point $I$ est milieu du segment $[AK].$
Ainsi, les diagonales $[BC]\ $ et $\ [AK]$ du quadrilatère $ABKC$ ont même milieu $I.$
Or, si un quadrilatère a ses diagonales de même milieu, alors c'est un parallélogramme.
Par suite, $ABKC$ est un parallélogramme.
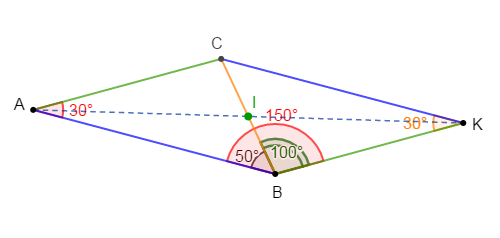
4) Calculons : $mes\;\widehat{BKC}\;;\ mes\;\widehat{ABK}\ $ et $\ mes\;\widehat{CBK}.$
$-\ $ Calcul de $mes\;\widehat{BKC}$
On a : dans le parallélogramme $ABKC$, les angles $\widehat{BKC}\ $ et $\ \widehat{CAB}$ sont opposés.
Or, dans un parallélogramme, deux angles opposés ont même mesure.
Donc, $mes\;\widehat{BKC}=mes\;\widehat{CAB}=30^{\circ}$
D'où, $\boxed{mes\;\widehat{BKC}=30^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{ABK}$
On a : dans le parallélogramme $ABKC$, les angles $\widehat{CAB}\ $ et $\ \widehat{ABK}$ sont consécutifs.
Comme dans un parallélogramme, deux angles consécutifs sont supplémentaires alors,
$mes\;\widehat{CAB}+mes\;\widehat{ABK}=180^{\circ}$
Par suite, $mes\;\widehat{ABK}=180^{\circ}-mes\;\widehat{CAB}$
Or, $mes\;\widehat{CAB}=30^{\circ}$
Donc, en remplaçant, on obtient :
$mes\;\widehat{ABK}=180^{\circ}-30^{\circ}=150^{\circ}$
D'où, $\boxed{mes\;\widehat{ABK}=150^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{CBK}$
On a : les angles $\widehat{ABC}\ $ et $\ \widehat{CBK}$ sont adjacents.
Donc, $mes\;\widehat{ABC}+mes\;\widehat{CBK}=mes\;\widehat{ABK}$
Par suite, $mes\;\widehat{CBK}=mes\;\widehat{ABK}-mes\;\widehat{ABC}$
Or, $mes\;\widehat{ABK}=150^{\circ}\ $ et $\ mes\;\widehat{ABC}=50^{\circ}$
Donc en remplaçant, on obtient :
$mes\;\widehat{CBK}=150^{\circ}-50^{\circ}=100^{\circ}$
Ainsi, $\boxed{mes\;\widehat{CBK}=100^{\circ}}$
Exercice 3
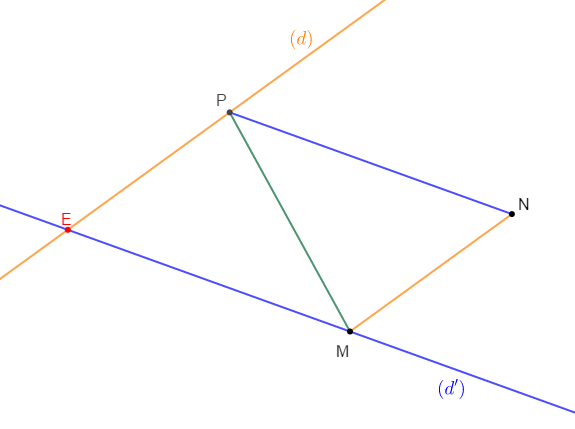
1) Soit $MNP$ un triangle tel que :
$$MN=4\;cm\;;\ NP=6\;cm\ \text{ et }\ MP=5\;cm$$
2) Traçons la droite $(d)$ passant par $P$ et parallèle à $(MN).$
3) Traçons la droite $(d')$ passant par $M$ et parallèle à $(PN).$
4) a) Soit $E$ le point d'intersection de $(d)\ $ et $\ (d').$
b) $MNPE$ est un parallélogramme.
Justifions
En effet, la droite $(d)$ passant par $P\ $ et $\ E$ est parallèle à $(MN).$
Donc, $(PE)$ est parallèle à $(MN)$
De la même manière, on a : $(d')$ passant par $M\ $ et $\ E$ est parallèle à $(PN).$
Ce qui signifie que $(ME)$ parallèle à $(PN)$
Alors, on obtient :
$$(PE)\parallel(MN)\ \text{ et }\ (ME)\parallel(PN)$$
Ainsi, le quadrilatère $MNPQ$ a ses côtés parallèles deux à deux.
Par conséquent, c'est un parallélogramme
5) Déterminons la longueur des segments $[ME]\ $ et $\ [PE]$
Comme $MNPE$ est un parallélogramme alors, deux côtés opposés ont même longueur. Donc,
$$ME=NP\ \text{ et }\ PE=MN$$
Or, $NP=6\;cm\ $ et $\ MN=4\;cm$
Par conséquent, la longueur des segments $[ME]\ $ et $\ [PE]$ est :
$$ME=6\;cm\ \text{ et }\ PE=4\;cm$$
Exercice 4
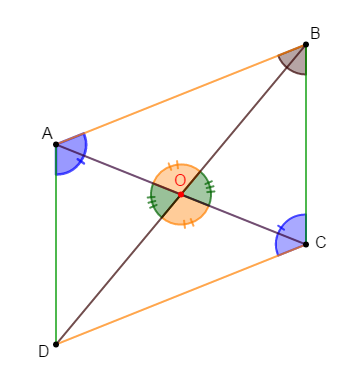
$ABCD$ est un parallélogramme de centre $O.$
1) Comparons les angles de sommet $O.$
$\widehat{AOD}\ $ et $\ \widehat{BOC}$ sont deux angles opposés par le sommet $O$ donc, ils ont la même mesure.
Ainsi,
$$mes\;\widehat{AOD}=mes\;\widehat{BOC}$$
$\widehat{AOB}\ $ et $\ \widehat{COD}$ sont deux angles opposés par le sommet $O$ donc, ils sont de même mesure.
Donc,
$$mes\;\widehat{AOB}=mes\;\widehat{COD}$$
2) Comparons les angles de sommets $A\ $ et $\ C.$
On sait que : dans un parallélogramme, deux angles opposés ont même mesure.
Donc, comme $ABCD$ est un parallélogramme alors, les angles de sommets $A\ $ et $\ C$ ont même mesure.
D'où,
$$mes\;\widehat{BAD}=mes\;\widehat{BCD}$$
3) Les angles de sommets $A\ $ et $\ B$ sont supplémentaires.
En effet, les angles de sommets $A\ $ et $\ B$ sont consécutifs.
Or, on sait que : dans un parallélogramme, deux angles consécutifs sont supplémentaires
D'où, les angles de sommets $A\ $ et $\ B$ sont supplémentaires.
$$mes\;\widehat{BAD}+mes\;\widehat{ABC}=180^{\circ}$$
Exercice 5
1) Soit $ABC$ un triangle tel que :
$$AB=4\;cm\;;\ AC=5\;cm\ \text{ et }\ BC=5.5\;cm$$
2) Plaçons les points $I\ $ et $\ J$ milieux respectifs des segments $[AB]\ $ et $\ [AC].$
3) Construisons les points $D\ $ et $\ E$ tel que :
Le point $D$ est le symétrique de $B$ par rapport à $J.$
Le point $E$ est le symétrique de $C$ par rapport à $I.$
4) Les quadrilatères $ABCD\ $ et $\ ACBE$ sont des parallélogrammes.
Justifions les réponses.
On a :
$J$ milieu $[AC]\ $ et $\ D$ symétrique de $B$ par rapport à $J$ alors, $J$ est aussi milieu de $[DB].$
Or, on sait que : si un quadrilatère a ses diagonales de même milieu, alors c'est un parallélogramme.
Par conséquent, le quadrilatère $ABCD$ est un parallélogramme.
De la même manière, on a :
$I$ milieu $[AB]\ $ et $\ E$ symétrique de $C$ par rapport à $I$ donc, $I$ est aussi milieu de $[CE].$
Ainsi, le quadrilatère $ACBE$ a ses diagonales $[AB]\ $ et $\ [CE]$ de même milieu $I.$
Par conséquent, c'est un parallélogramme.
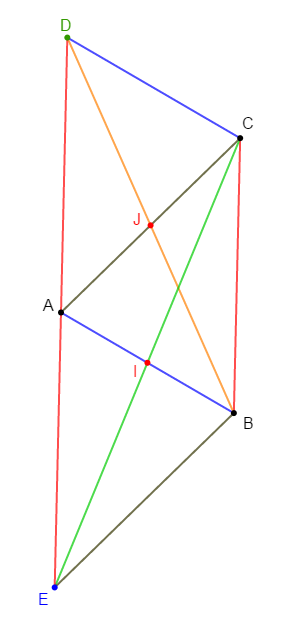
Exercice 6
1) Traçons un triangle $ABC.$
2) Traçons les hauteurs issues des sommets $B$ et $C$ ; ces hauteurs se coupent au point $I.$
3) Construisons la droite perpendiculaire à $(AC)$ passant par $C$ et la droite perpendiculaire à $(AB)$ passant par $B$ ; ces perpendiculaires se coupent au point $O.$
4) $CIBO$ est un parallélogramme.
Justifions.
On a : $(IC)$ hauteur issue de $C$ donc, $(IC)$ est perpendiculaire à $(AB).$
On a aussi : $(OB)$ perpendiculaire à $(AB).$
Or, on sait que : si deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.
Donc, $(IC)\ $ et $\ (OB)$ sont parallèles.
De la même manière, on a : $(IB)$ hauteur issue de $B$ donc, $(IB)$ est perpendiculaire à $(AC).$
On a aussi : $(OC)$ perpendiculaire à $(AC).$
Or, deux droites perpendiculaires à une même droite sont parallèles.
Donc, $(IB)\ $ et $\ (OC)$ sont parallèles.
On constate alors que le quadrilatère $CIBO$ a ses côtés parallèles deux à deux.
Par conséquent, c'est un parallélogramme.
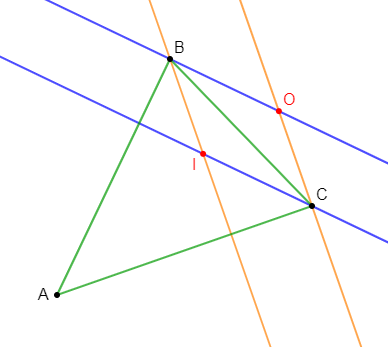
Exercice 7
Soit $ABC$ un triangle ; $M$ est le milieu de $[BC].$
1) Construisons le point $D$ symétrique de $B$ par rapport au point $A.$
2) Construisons le point $N$ symétrique de $M$ par rapport au point $A.$
3) Montrons que le quadrilatère $BMDN$ est un parallélogramme.
On a :
$D$ symétrique de $B$ par rapport au point $A$ alors, $A$ est le milieu de $[BD]$
$N$ symétrique de $M$ par rapport au point $A$ alors, $A$ est le milieu de $[MN]$
Ainsi, le quadrilatère $BMDN$ a ses diagonales $[BD]\ $ et $\ [MN]$ de même milieu $A.$
Par conséquent, c'est un parallélogramme.
4) a) Montrons que : $ND=MC$ puis $(ND)//(MC).$
On a : $BMDN$ un parallélogramme.
Or, on sait que : dans un parallélogramme, deux côtés opposés ont même longueur.
Donc, $ND=BM$
Comme $M$ est milieu de $[BC]$ alors, $BM=MC$
Ainsi, on a : $ND=BM\ $ et $\ BM=MC$
Ce qui entraine alors : $ND=MC$
Par ailleurs, dans le parallélogramme $BMDN$, on a : $(ND)$ parallèle à $(MB).$
Comme, $B\;;\ M\ $ et $\ C$ sont alignés alors, $(MB)\ $ et $\ (MC)$ sont confondues.
D'où, $(ND)$ parallèle à $(MC).$
b) En déduisons que le quadrilatère $CDNM$ est un parallélogramme.
En effet, on sait que : si un quadrilatère a deux côtés parallèles de même longueur alors, c'est un parallélogramme.
Or, d'après le résultat de $4)\,a)$, on a : $ND=MC\ $ et $\ (ND)$ parallèle à $(MC).$
Ce qui signifie que le quadrilatère $CDNM$ a deux côtés parallèles de même longueur.
Par conséquent, c'est un parallélogramme.
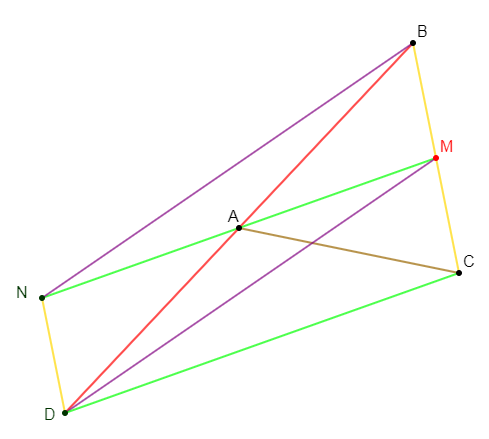
Exercice 8
$ABC$ est un triangle ; $I\ $ et $\ J$ sont des milieux respectifs des segments $[BC]\ $ et $\ [AC].$
1) Construisons le point $A'$ symétrique de $A$ par rapport au point $I.$
2) Construisons le point $B'$ symétrique de $B$ par rapport au point $J.$
3) Montrons que les quadrilatères $ABA'C\ $ et $\ ABCB'$ sont des parallélogrammes.
On a : $A'$ symétrique de $A$ par rapport au point $I.$ Ce qui signifie que $I$ est le milieu de $[AA'].$
Or, $I$ est aussi milieu de $[BC].$
Ainsi, le quadrilatère $ABA'C$ a ses diagonales $[AA']\ $ et $\ [BC]$ de même milieu $I.$
Par conséquent, c'est un parallélogramme.
De la même manière, on a : $B'$ symétrique de $B$ par rapport au point $J$ alors, $J$ est le milieu de $[BB'].$
On a aussi : $J$ milieu de $[AC].$
Ainsi, on remarque que le quadrilatère $ABA'C$ a ses diagonales $[BB']\ $ et $\ [AC]$ de même milieu $J.$
Par conséquent, c'est un parallélogramme.
4) En déduisons que $C$ est le milieu du segment $[A'B'].$
En effet, $ABA'C\ $ et $\ ABCB'$ sont des parallélogrammes.
Or, on sait que : dans un parallélogramme, deux côtés opposés ont même longueur.
Donc :
dans le parallélogramme $ABA'C$, on a : $AB=A'C$
dans le parallélogramme $ABCB'$, on a :$AB=CB'$
On peut alors écrire : $AB=A'C\ $ et $\ AB=CB'$
Ce qui entraine : $A'C=CB'$
Ce qui signifie que $C$ est le milieu de $[A'B'].$
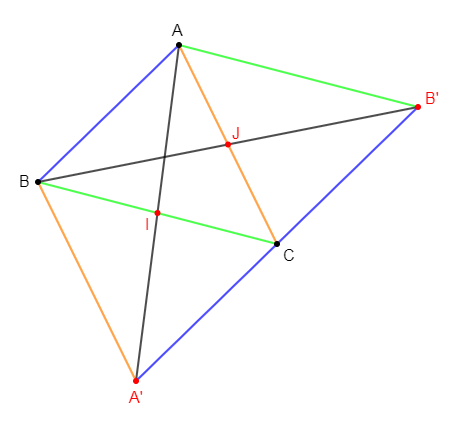
Exercice 12
Dans chacun des cas ci-dessous, construisons le parallélogramme $ABCD$ tel que :
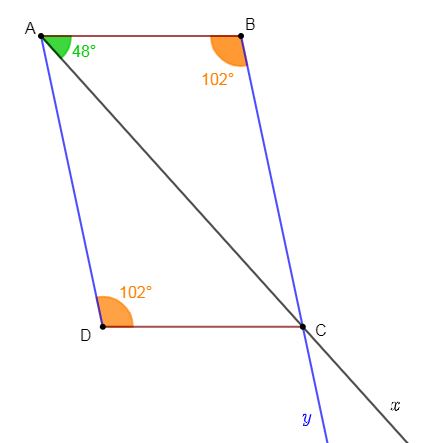
1) $AB=4\;cm\;;\ \widehat{BAC}=48^{\circ}\ $ et $\ \widehat{ADC}=102^{\circ}.$
Pour cela, on trace d'abord le segment $AB]$ de longueur $4\;cm$ puis, on construit l'angle $\widehat{BAx}$ de mesure $48^{\circ}.$
Comme dans un parallélogramme deux angles opposés ont même mesure alors, on a : $\widehat{ABC}=\widehat{ADC}=102^{\circ}$
On construit alors, l'angle $\widehat{ABy}$ de mesure $102^{\circ}$
Le côté $[Ax)$ de l'angle $\widehat{BAx}$ et le côté $[By)$ de l'angle $\widehat{ABy}$ se coupent au point $C.$
Comme dans un parallélogramme, deux côtés parallèles ont même longueur alors, on trace le segment $[CD]$ parallèlement à $(AB)$, dans le sens $[BA)$ et de longueur $4\;cm.$
Pour finir, on trace le segment $[AD]$ joignant les points $A\ $ et $\ D.$
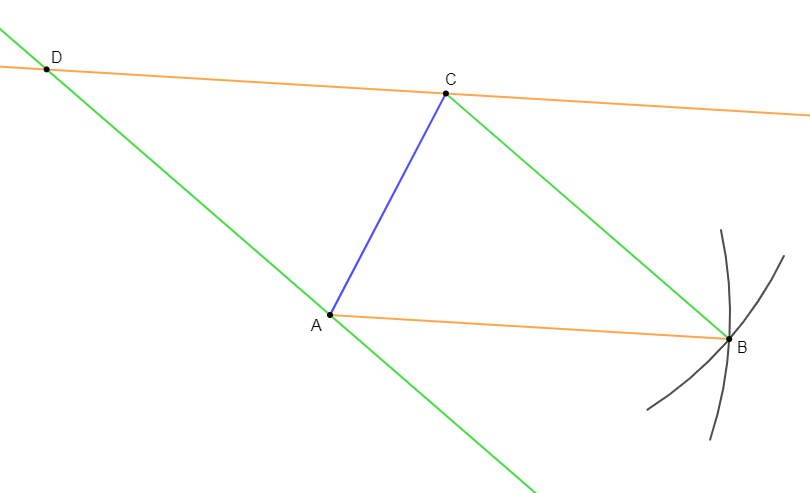
2) $AC=5\;cm\;;\ CD=8\;cm\ $ et $\ BC=7.5\;cm$
Pour cela, on trace d'abord la diagonale $[AC]$ de longueur $5\;cm.$
Comme dans un parallélogramme, deux côtés opposés ont même longueur alors, on a : $AB=CD=8\;cm.$
Donc, avec le compas on se place sur $A$ et on trace un arc de cercle de rayon $8\;cm$ puis, on se place sur $C$ et on trace un arc de cercle de rayon $7.5\;cm$
Les deux arcs de cercle se coupent alors au point $B.$
On trace ensuite, la parallèle à $(AB)$ passant par $C$ et la parallèle à $(CD)$ passant par $A.$
Ces deux parallèles se coupent au point $D.$
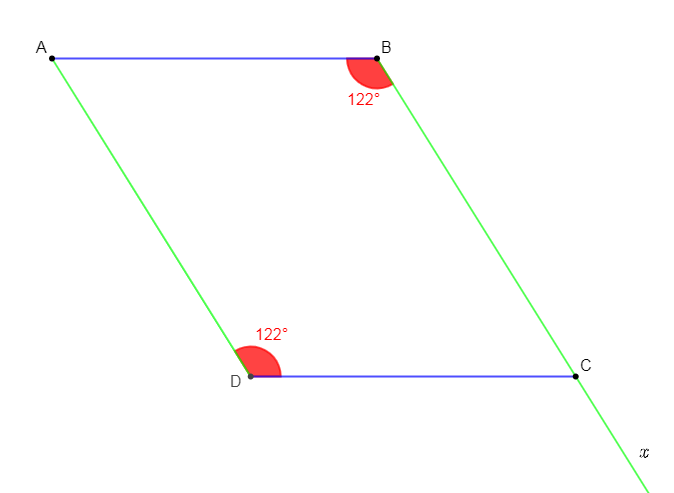
3) $AB=6.5\;cm\;;\ BC=7.5\;cm\ $ et $\ \widehat{ADC}=122^{\circ}.$
Pour cela, on trace d'abord le côté $[AB]$ de longueur $6.5\;cm$
Comme dans un parallélogramme deux angles opposés ont même mesure alors, on a : $\widehat{ABC}=\widehat{ADC}=122^{\circ}$
On construit alors, l'angle $\widehat{ABx}$ de mesure $122^{\circ}$
Sur le côté $[Bx)$ on place le point $C$ tel que $BC=7.5\;cm$
Comme dans un parallélogramme, deux côtés parallèles sont de même longueur alors, on trace le segment $[CD]$ parallèlement à $(AB)$, dans le sens $[BA)$ et de longueur $6.5\;cm$
Pour finir, on trace le côté $[AD]$ en joignant les points $A\ $ et $\ D.$
Exercice 13
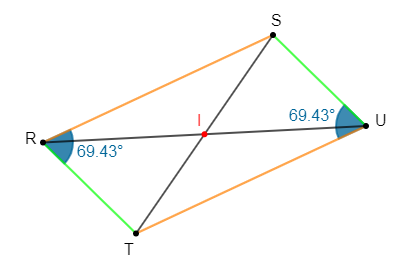
$RSUT$ est un parallélogramme.
Justifions que :
1) $TU=RS$,
On a : $RSUT$ est un parallélogramme.
Or, on sait que : dans un parallélogramme deux côtés opposés ont même longueur.
Donc, $TU=RS$
2) $2\times RI=RU$ où $I$ est le point d'intersection de $[RU]\ $ et $\ [ST].$
Comme $RSUT$ est un parallélogramme alors, ses diagonales $[RU]\ $ et $\ [ST]$ ont même milieu $I.$
Donc, $I$ est milieu de $[RU].$
Ce qui signifie que : $RI=\dfrac{RU}{2}$
D'où, $2\times RI=RU$
3) $\widehat{TUS}=\widehat{TRS}.$
On a : $RSUT$ un parallélogramme.
Or, dans un parallélogramme deux angles opposés ont même mesure.
Par conséquent, $\widehat{TUS}=\widehat{TRS}$
Dans notre exemple, on trouve : $\widehat{TUS}=\widehat{TRS}=69.43^{\circ}$
Exercice 15
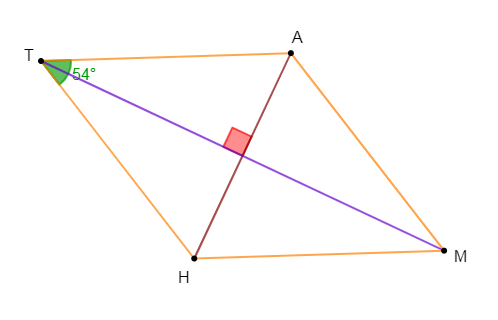
Construisons un losange $MATH$ tel que $MA=5\;cm\ $ et $\ \widehat{ATH}=54^{\circ}.$
En effet, on sait que : dans un losange, les côtés ont même longueur et les diagonales sont perpendiculaires.
Donc, pour construire le losange $MATH$, on trace d'abord le triangle $TAH$ isocèle en $T$ tel que : $TA=TH=5\;cm\ $ et $\ \widehat{ATH}=54^{\circ}.$
Puis, on place le point $M$ symétrique de $T$ par rapport à $(AH).$
On trace ensuite les côtés $[AM]\ $ et $\ [MH].$
Exercice 16
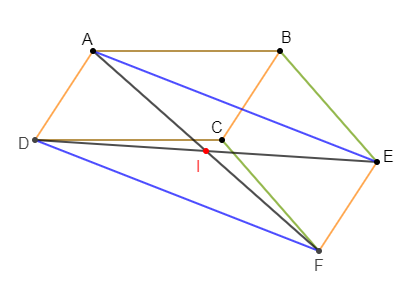
On considère la figure ci-dessous où $ABCD\ $ et $\ BEFC$ sont des parallélogrammes.
1) Donnons, en justifiant, deux droites parallèles à la droite $(BC).$
$(AD)\ $ et $\ (EF)$ sont deux droites parallèles à la droite $(BC).$
On a : $ABCD$ est parallélogramme donc, $(AD)$ est parallèle à $(BC).$
On a aussi : $BEFC$ est parallélogramme alors, $(EF)$ est parallèle à $(BC).$
D'où, $(AD)\ $ et $\ (EF)$ sont deux droites parallèles à la droite $(BC).$
2) Démontrons que $AEFD$ est un parallélogramme.
En effet, on sait que : si un quadrilatère a deux côtés parallèles de même longueur alors, c'est un parallélogramme.
Donc, pour cette question, on va juste montrer que $(AD)\ $ et $\ (EF)$ sont parallèles et $AD=EF.$
D'après le résultat de $1)$, on a : $(AD)\ $ et $\ (EF)$ parallèles à $(BC).$
Or, on sait que : si deux droites sont parallèles à une même droite alors, ces deux droites sont parallèles.
Donc, $(AD)\ $ et $\ (EF)$ sont parallèles.
Aussi, on a : $ABCD\ $ et $\ AEFD$ sont des parallélogrammes.
Or, on sait que : dans un parallélogramme, deux côtés opposés ont même longueur.
Donc :
dans le parallélogramme $ABCD$, on a : $AD=BC$
dans le parallélogramme $AEFD$, on a :$BC=EF$
On peut alors écrire : $AD=BC\ $ et $\ BC=EF$
Ce qui entraine : $AD=EF$
Nous obtenons alors : $AD=EF\ $ et $\ (AD)\ $ et $\ (EF)$ sont parallèles.
Par conséquent, $AEFD$ est un parallélogramme.
3) Démontrons que les segments $[AF]\ $ et $\ [ED]$ se coupent en leur milieu.
En effet, $[AF]\ $ et $\ [ED]$ sont les diagonales du parallélogramme $AEFD.$
Or, on sait que : dans un parallélogramme, les diagonales se coupent en leur milieu.
Par conséquent, les segments $[AF]\ $ et $\ [ED]$ se coupent en leur milieu $I.$
Exercice 17
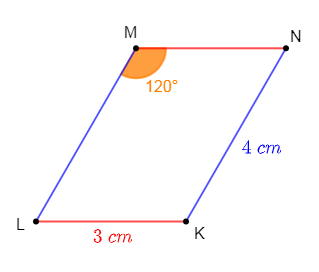
Dans la figure ci-dessous, le quadrilatère dessiné est un parallélogramme.
Donnons les longueurs ou les angles demandés. Justifions en citant les propriétés utilisées.
On a :
$$LM=4\;cm\;;\ MN=3\;cm\;;\ \widehat{LKN}=120^{\circ}\;;\ \widehat{KLM}=60^{\circ}\;;\ \widehat{KNM}=60^{\circ}$$
$-\ $ Dans un parallélogramme, deux côtés opposés ont même longueur.
Donc, $[LM]\ $ et $\ [KN]$ ont même longueur.
D'où, $\boxed{LM=4\;cm}$
On a : $MN=3\;cm$
De la même manière, $[MN]\ $ et $\ [KL]$ ont même longueur.
Ce qui signifie que $\boxed{MN=3\;cm}$
$-\ $ Dans un parallélogramme, deux angles opposés ont même mesure.
Donc, $\widehat{LKN}\ $ et $\ \widehat{LMN}$ ont même mesure.
D'où, $\boxed{\widehat{LKN}=120^{\circ}}$
$-\ $ Dans un parallélogramme, deux angles consécutifs sont supplémentaires.
Donc, $\widehat{LMN}\ $ et $\ \widehat{KLM}$ sont supplémentaires.
Ce qui signifie que : $\widehat{KLM}+\widehat{LMN}=180^{\circ}$
Ce qui entraine alors : $\widehat{KLM}=180^{\circ}-\widehat{LMN}$
En remplaçant $\widehat{LMN}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{KLM}&=&180^{\circ}-\widehat{LMN}\\\\&=&\widehat{KLM}=180^{\circ}-120^{\circ}\\\\&=&60^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{KLM}=60^{\circ}}$
$-\ $ Dans un parallélogramme, deux angles opposés ont même mesure.
Donc, $\widehat{KNM}\ $ et $\ \widehat{KLM}$ ont même mesure.
D'où, $\boxed{\widehat{KNM}=60^{\circ}}$
Exercice 19
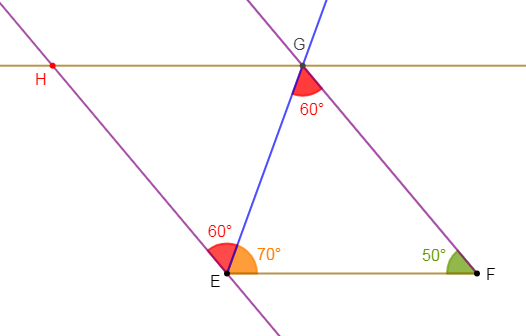
1) Traçons le triangle $EFG$ tel que :
$$EF=5\;cm\;;\ \widehat{GEF}=70^{\circ}\ \text{ et }\ \widehat{EFG}=50^{\circ}$$
La mesure de l'angle $\widehat{EGF}$ est égale à $60^{\circ}.$
En effet, on sait que : dans un triangle, la somme des angles est égale à $180^{\circ}.$
Donc, en considérant le triangle $EFG$, on a :
$$\widehat{EGF}+\widehat{GEF}+\widehat{EFG}=180^{\circ}$$
Ce qui entraine alors : $\widehat{EGF}=180^{\circ}-(\widehat{GEF}+\widehat{EFG})$
En remplaçant $\widehat{GEF}\ $ et $\ \widehat{EFG}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{EGF}&=&180^{\circ}-(\widehat{GEF}+\widehat{EFG})\\\\&=&=180^{\circ}-(70^{\circ}+50^{\circ})\\\\&=&180^{\circ}-120^{\circ}\\\\&=&60^{\circ}\end{array}$
D'où, $\boxed{\widehat{EGF}=60^{\circ}}$
2) Construisons le point $H$ tel que $EHGF$ soit un parallélogramme.
La mesure de $\widehat{GEH}$ est égale à $60^{\circ}.$
Justifions.
Comme $EHGF$ soit un parallélogramme alors, $(EH)\ $ et $\ (FG)$ sont parallèles.
Par conséquent, $\widehat{GEH}\ $ et $\ \widehat{EGF}$ sont deux angles alternes-internes de même mesure.
Ce qui signifie que : $\widehat{GEH}=\widehat{EGF}$
D'où, $\boxed{\widehat{GEH}=60^{\circ}}$
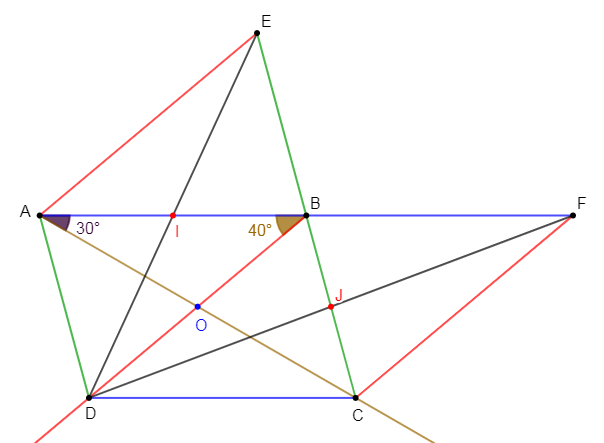
Exercice 20
1) Construisons le parallélogramme $ABCD$ de centre $O$ tel que :
$$AB=8\;cm\;,\ \widehat{BAC}=40^{\circ}\ \text{ et }\ \widehat{ABD}=30^{\circ}$$
2) Plaçons le point $I$ milieu de $[AB]$ et le point $J$ milieu de $[BC].$
3) Construisons $E$ symétrique de $D$ par rapport à $I$ et le point $F$ symétrique de $D$ par rapport à $J.$
4) Les quadrilatères $AEBD\ $ et $\ DBFC$ sont des parallélogrammes.
Justifions notre réponse.
On a : $E$ symétrique de $D$ par rapport au point $I.$ Ce qui signifie que $I$ est le milieu de $[DE].$
Or, $I$ est aussi milieu de $[AB].$
Ainsi, le quadrilatère $AEBD$ a ses diagonales $[AB]\ $ et $\ [DE]$ de même milieu $I.$
Par conséquent, c'est un parallélogramme.
De la même manière, on a : $F$ symétrique de $D$ par rapport au point $J$ alors, $J$ est le milieu de $[DF].$
On a aussi : $J$ milieu de $[BC].$
Ainsi, on remarque que le quadrilatère $DBFC$ a ses diagonales $[BC]\ $ et $\ [DF]$ de même milieu $J.$
Par conséquent, c'est un parallélogramme.
5) Les points $A\;,\ B\ $ et $\ F$ sont alignés.
Justifions notre réponse.
Comme $AEBD$ est un parallélogramme alors, $(AB)$ est parallèle à $(DC).$
Comme $DBFC$ est un parallélogramme alors, $(BF)$ est parallèle à $(DC).$
Ainsi, on a : $(AB)\ $ et $\ (BF)$ parallèles à $(DC).$
Or, on sait que : si deux droites sont parallèles à une même droite alors, ces deux droites sont parallèles.
Donc, $(AB)\ $ et $\ (BF)$ sont parallèles.
Ce qui signifie que les $(AB)\ $ et $\ (BF)$ sont confondues.
D'où, les points $A\;,\ B\ $ et $\ F$ appartiennent à une même droite.
Par conséquent, ces points sont alignés.
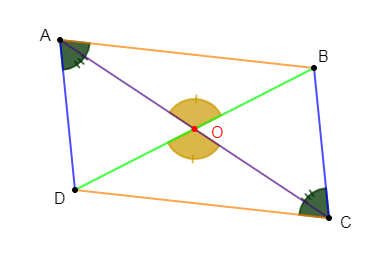
Exercice 21
Soit $ABCD$ est un parallélogramme de centre $O.$
1) Les angles $\widehat{AOB}\ $ et $\ \widehat{DOC}$ ont la même mesure.
En effet, $\widehat{AOB}\ $ et $\ \widehat{DOC}$ sont deux angles opposés par le sommet $O.$
Par conséquent, ils ont la même mesure.
D'où, $\boxed{\widehat{AOB}=\widehat{DOC}}$
2) Les angles $\widehat{BAD}\ $ et $\ \widehat{DCB}$ sont de même mesure.
En effet, dans un parallélogramme, deux angles opposés ont même mesure.
Or, dans le parallélogramme $ABCD\;,\ \widehat{BAD}\ $ et $\ \widehat{DCB}$ sont deux angles opposés.
Par conséquent, ils sont de même mesure.
D'où, $\boxed{\widehat{BAD}=\widehat{DCB}}$
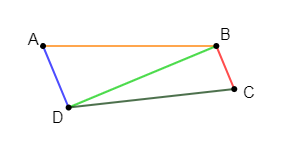
Exercice 22
$ABCD$ est un quadrilatère tel que :
$AD=2\;cm\;,\ AB=5.2\;cm\;,\ DB=4.8\;cm\;,\ BC=1.4\;cm\ $ et $\ DC=5\;cm.$
Alors, $ABCD$ n'est pas un parallélogramme.
Justifions notre réponse.
En effet, on sait que : dans un parallélogramme, deux côtés opposés ont même longueur.
Or, nous constatons que dans le quadrilatère $ABCD$, les côtés opposés $[AB]\ $ et $\ [DC]$ ont des longueurs différentes.
De même, les côtés opposés $[AD]\ $ et $\ [BC]$ ont des longueurs différentes.
Par conséquent, le quadrilatère $ABCD$ n'est pas un parallélogramme.
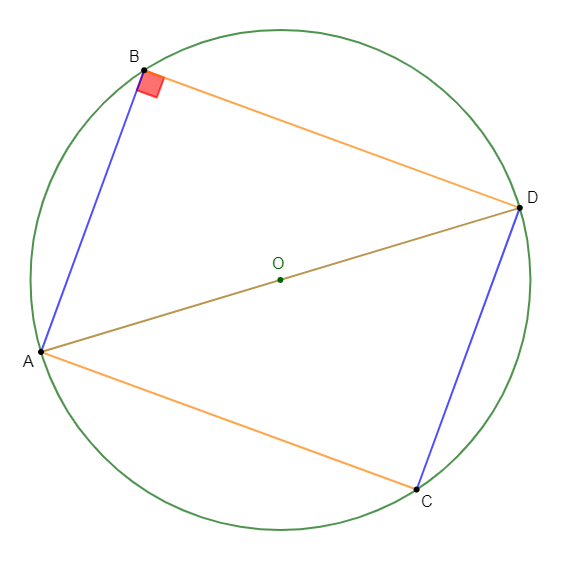
Exercice 23
1) Soit $ABDC$ un parallélogramme tel que $AB=6\;cm\;,\ BD=8\;cm\ $ et $\ (AB)$ perpendiculaire à $(BD).$ Le cercle circonscrit au triangle $ABD$ a pour rayon $5\;cm.$
Calculons $BC.$
Dans le parallélogramme $ABDC$, on a : $(AB)$ perpendiculaire à $(BD).$
Donc, $\widehat{ABD}$ est un angle droit.
Or, on sait que : si un parallélogramme a un angle droit alors, c'est un rectangle.
Donc, $ABDC$ est un rectangle.
Par conséquent, ses diagonales $[AD]\ $ et $\ [BC]$ ont la même longueur.
Ce qui signifie que :
$$BC=AD$$
Calculons alors la longueur $AD.$
Comme le triangle $ABD$ est rectangle en $B$ alors, $[AD]$ représente son hypoténuse.
Ainsi, le centre $O$ du cercle circonscrit à ce triangle est le milieu de $[AD].$
Par conséquent, $[AD]$ est un diamètre de ce cercle.
Comme le rayon de ce cercle est égal à $5\;cm$ alors, $AD=2\times 5=10\;cm$
D'où, $\boxed{BC=10\;cm}$
2) Calculons le périmètre et l'aire de $ABDC.$
$-\ $ Calcul du périmètre
Comme $ABDC$ est un rectangle de longueur $L=8\;cm$ et de largeur $\ell=6\;cm$ alors, son périmètre $\mathcal{P}$ est donné par :
$\begin{array}{rcl}\mathcal{P}&=&2\times(L+\ell)\\\\&=&2\times(8+6)\\\\&=&2\times 14\\\\&=&28\end{array}$
D'où, $\boxed{\mathcal{P}=28\;cm}$
$-\ $ Calcul de l'aire
Comme $ABDC$ est un rectangle de longueur $L=8\;cm$ et de largeur $\ell=6\;cm$ alors, son aire $\mathcal{A}$ est donnée par :
$\begin{array}{rcl}\mathcal{A}&=&L\times\ell\\\\&=&8\times 6\\\\&=&48\end{array}$
D'où, $\boxed{\mathcal{A}=48\;cm^{2}}$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
jeu, 04/22/2021 - 00:56
Permalien
construis un quadrilatere
Anonyme (non vérifié)
jeu, 04/22/2021 - 00:56
Permalien
construis un quadrilatere
Anonyme (non vérifié)
jeu, 04/22/2021 - 00:56
Permalien
construis un quadrilatere
Anonyme (non vérifié)
jeu, 04/22/2021 - 00:56
Permalien
construis un quadrilatere
Anonyme (non vérifié)
jeu, 04/22/2021 - 00:56
Permalien
construis un quadrilatere
Anonyme (non vérifié)
jeu, 04/22/2021 - 00:56
Permalien
construis un quadrilatere
mariama gaye (non vérifié)
jeu, 04/22/2021 - 00:57
Permalien
construis un quadrilatere
Koumé (non vérifié)
jeu, 03/17/2022 - 04:19
Permalien
La correction de exercice
Koumé (non vérifié)
jeu, 03/17/2022 - 04:19
Permalien
La correction de exercice
JRF (non vérifié)
lun, 05/29/2023 - 09:33
Permalien
Exercice 20 point N°5
Fatou Kiné Thiam (non vérifié)
lun, 03/10/2025 - 22:23
Permalien
Élève
Samate (non vérifié)
dim, 02/16/2025 - 22:23
Permalien
Travail
Samate (non vérifié)
dim, 02/16/2025 - 22:24
Permalien
Travaux
Ajouter un commentaire