Série d'exercices : Vecteurs et translations 4e
Classe:
Quatrième
Exercice 1
Soit $ABCD$ un parallélogramme de centre $O.$
Parmi les vecteurs :
$\overrightarrow{AB}\;;\ \overrightarrow{BC}\;;\ \overrightarrow{CD}\;;\ \overrightarrow{DA}\;;\ \overrightarrow{AC}\;;\ \overrightarrow{BD}\;;\ \overrightarrow{AO}\;;\ \overrightarrow{OC}\;;\ \overrightarrow{DO}$ et $\overrightarrow{OB}$
indique :
a) Ceux de même direction.
b) Ceux de même sens.
c) Ceux de même longueur.
d) Ceux qui sont égaux.
Exercice 2
$DEFG$ est un rectangle.
Les égalités suivantes : $$\overrightarrow{GD}=\overrightarrow{EG}\;;\ \overrightarrow{DF}=\overrightarrow{EG}\;;\ \overrightarrow{DE}=\overrightarrow{FG}$$
sont-elles vraies ? Justifier la réponse.
Exercice 3 Image d'un segment
Soit $\vec{U}$ un vecteur du plan
1) Construire un segment $[AB]$ tel que $AB=4\;cm.$
2) Construire les points $A'$ et $B'$ image respectif de $A$ et $B$ par la translation de vecteur $\vec{U}.$
3) a) Quelle est la longueur de $A'B'$ ?
b) Quelle est la position relative de $(AB)$ et $(A'B')\ ?$
4) Énoncer la propriété.
Exercice 4
On donne trois points non alignés $A\;;\ B\;;\ C.$
1) Construire les points $M$ et $N$ tels que :
$\overrightarrow{BC}=\overrightarrow{AM}\quad$ et $\quad\overrightarrow{BN}=\overrightarrow{AC}.$
2) Démontrer que $C$ est le milieu du segment $[MN].$
Exercice 5
$ABCD$ est un parallélogramme
1) Construire le point $E$ image de $C$ par la translation de vecteur $\overrightarrow{DC}.$
2) a) Expliquer pourquoi $\overrightarrow{AB}=\overrightarrow{DC}\ ?\quad \overrightarrow{CE}=\overrightarrow{DC}\ ?$
b) En déduire que $\overrightarrow{AB}=\overrightarrow{CE}.$
Exercice 6
Soit $MNP$ un triangle isocèle en $M.$ on désigne par $M'$ le milieu de $[NP].$
Soit $Q$ le point tel que : $\overrightarrow{M'Q}=\overrightarrow{MM}'.$
1) Démontrer que $(MM')$ est la médiatrice de $[NP].$
2) Démontrer que le quadrilatère $MNQP$ est un losange.
3) Construire l'image de $MNPQ$ par la translation de vecteur $\overrightarrow{NP}.$
Exercice 7
Soit $(c)$ un cercle de centre $O$ de diamètre $[AB]$ et $M$ un point de ce cercle.
1) Quelle est la nature du triangle $AMB$ ? Justifier
2) a) Construire les points $A'\;,\ B'\;,\ M'$ images respectives de $A\;,\ B\;,\ M$ par la translation de vecteur $\overrightarrow{OM}.$
b) Quel est l'image de $O$ par la translation de vecteur $\overrightarrow{OM}.$
3) Quelle est la nature du quadrilatère $ABB'A'$ ?
4) a) Démontrer que $A'B'M'$ est un triangle rectangle.
b) On donne : $OB=5\;cm$ et $MB=6\;cm.$ Calculer $AM$ puis en déduire l'aire du triangle $A'B'M'.$
Exercice 8
Soit $ABC$ un triangle rectangle en $A$ tel que :
$AB=3\;cm$ et $AC=4\;cm.$
1) Calculer la distance $BC$
2) Soit $I$ milieu du segment $[AC].$
a) Construisons le point $B'$ tel que : $\overrightarrow{BI}=\overrightarrow{IB'}$
b) Démontrer que $ABCB'$ est un parallélogramme.
3) Construire :
$-\ C'$ image de $C$ par la translation de vecteur $\overrightarrow{BB}'$
$-\ A'$ image de $A$ par la translation de vecteur $\overrightarrow{BB}'.$
4) a) Quel est le vecteur de translation qui envoie $ABC$ en $A'B'C'$ ?
b) Quelle est la nature du triangle $A'B'C'$ ? Puis calculer son aire ?
5) Démontrer que $B'$ est le milieu de $[A'C].$
Exercice 9
Soit un segment $[AB]$ et $I$ son milieu.
1) Comment sont disposés les points $A$, $I$ et $B.$
2) Compare les longueurs $AI$ et $IB.$
3) Quelle est l'image de $I$ par la translation qui transforme $A$ en $I$ ?
Exercice 10
1) Trace deux droites $(\mathcal{D})$ et $(\mathcal{D'})$ parallèles puis marque deux points $A$ et $B$ sur $(\mathcal{D})$ et un point $C$ sur $(\mathcal{D'}).$
2) Construis le point $C'$ tel que $ABC'C$ soit un parallélogramme.
3) Quelle translation transforme $C$ en $C'$ ?
Exercice 11
Répond par vrai ou faux à chacune des affirmations ci-dessous :
Soit un vecteur $\overrightarrow{EF}$ et $O$ un point du plan.
1) Si $\overrightarrow{OE}=\overrightarrow{FE}$ alors $O$ est le milieu du segment $[EF].$
2) Si $\overrightarrow{EO}=\overrightarrow{OF}$ alors $O$ est le milieu du segment $[EF].$
3) Si $\overrightarrow{EO}=\overrightarrow{FO}$ alors $O$ est le milieu du segment $[EF].$
4) Si $\overrightarrow{OE}=\overrightarrow{OF}$ alors $O$ est le milieu du segment $[EF].$
Exercice 12
Recopie puis complète les phrases ci-dessous.
1) Si trois points sont alignés alors leurs images par une translation $\ldots\ldots\ldots$
2) L'image d'un segment par une translation est un segment $\ldots\ldots\ldots$
3) L'image d'une droite par une translation est une droite $\ldots\ldots\ldots$
4) L'image d'un cercle par une translation est un cercle de $\ldots\ldots\ldots$ et $\ldots\ldots\ldots$
5) L'image d'un angle par une translation est un $\ldots\ldots\ldots$
Exercice 13
$ABC$ est un triangle rectangle en $A$ tel que $AB=5\;cm$ et $AC=4\;cm.$
Soit $I$ le milieu de $[BC]$
1) Construis les points $B'\;,\ C'\text{ et }I'$ images respectives des points $B\;,\ C\text{ et }I$ par la translation qui transforme $A$ en $C.$
2) Quelle est la longueur du segment $[B'C']$ ? Justifie.
3) Quelle est la position des trois points $B'\;,\ I'\text{ et }C'$ ? Justifie.
4) Quelle est la mesure de l'angle $\widehat{B'CC'}$ ? Justifie.
Exercice 14
Soit le cercle $\mathcal{C}(O.3\;cm).$
1) Marque un point $M$ sur le cercle et un point $N$ à l'extérieur du cercle.
2) Construis les points $O'$ et $M'$ images respectives des points $O$ et $M$ par la translation qui transforme $M$ en $N.$
3) Construis le cercle $(\mathcal{C'})$ de centre $O'$ et de rayon $O'M'.$
4) Montre que $(\mathcal{C'})$ est l'image de $(\mathcal{C})$ par la translation qui transforme $M$ en $N.$
Exercice 15
Répond par vrai ou faux à chacune des affirmations ci-dessous.
1) Si $ABCD$ est un parallélogramme alors $\overrightarrow{AB}=\overrightarrow{CD}.$
2) Si $ABCD$ est un parallélogramme alors $\overrightarrow{AD}=\overrightarrow{BC}.$
3) Si $ABCD$ est un parallélogramme alors $\overrightarrow{AC}=\overrightarrow{BD}.$
4) Si $ABCD$ est un parallélogramme alors $\overrightarrow{DA}=\overrightarrow{BC}.$
5) Si $ABCD$ est un parallélogramme alors $\overrightarrow{CD}=\overrightarrow{BA}.$
Exercice 16
1) Construis un triangle $EFG$, puis les points $H$, $A$, $B$ tels que :
$H$ pied de la hauteur issue de $E$ ;
$A$ l'image de $E$ par la translation de vecteur $\overrightarrow{HF}$ ;
$B$ l'image de $E$ par la translation de vecteur $\overrightarrow{HG}$ ;
2) Donne la nature des quadrilatères $BEHG$ et $HFAE.$
Justifie.
Exercice 17
1) Construis un cercle $\mathcal{C}(O\;;\ 3\;cm).$
2) Marque les points $I$, $J$ et $K$ sur $(\mathcal{C})$ tels que les points $I$ et $J$ soient diamétralement opposés.
3) Construis le point $A$ l'image de $K$ par la translation de vecteur $\overrightarrow{JI}.$
4) Quelle est la nature du quadrilatère $AIJK$ ? Justifie.
Exercice 18
Reproduis la figure ci-dessous puis construis :
$-\ $ Le point $B'$ image de $B$ par la translation qui transforme $A$ en $C$ ;
$-\ $ Le point $C'$ image de $C$ par la translation qui transforme $E$ en $A$
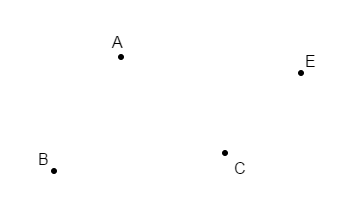
Exercice 19
Reproduis la figure ci-dessous puis construis l'image du segment $[IF]$ par la translation qui transforme $E$ en $B.$
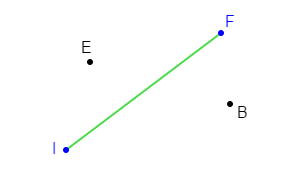
Exercice 20
Reproduis la figure ci-dessous puis construis l'image du cercle $(\mathcal{C})$ de centre $O$ et de rayon $3\;cm$ par la translation qui transforme $B$ en $A.$
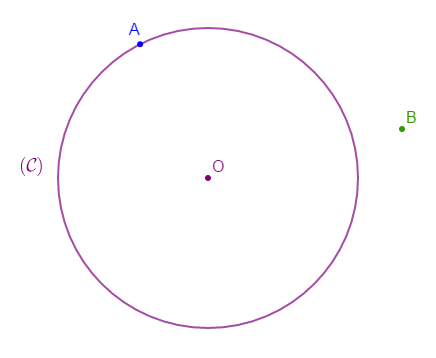
Exercice 21
Reproduis la figure ci-dessous puis construis l'image $(\mathcal{D'})$ de la droite $(\mathcal{D})$ par la translation qui transforme $A$ en $B.$
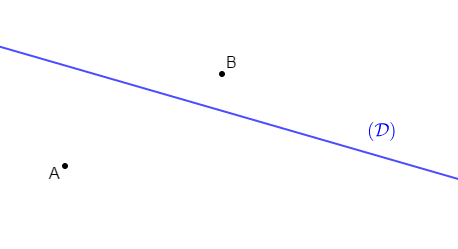
Exercice 22
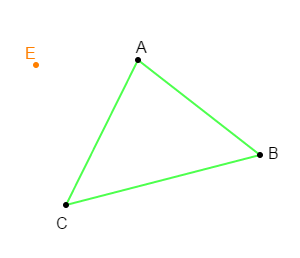
Reproduis la figure ci-dessous puis construis l'image $A'B'C'$ du triangle $ABC$ par la translation qui transforme $A$ en $E.$
Exercice 23
Dans la figure $(F)$ ci-dessous, $ABC$ est un triangle équilatéral et $O$ est le centre du demi-cercle de diamètre $[BC].$
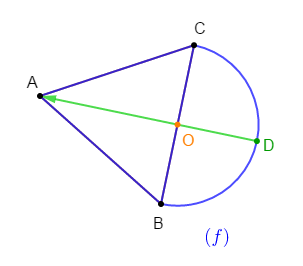
1) Reproduis la figure $(f)$
2) Construis l'image $(f')$ de $(f)$ par la translation de vecteur $\overrightarrow{DA}.$
3) Justifie que $A'$, $O'$ et $D'$ images respectives de $A$, $O$ et $D$ par cette translation de vecteur $\overrightarrow{DA}.$ sont alignés.
Exercice 24
Pour chacun des énoncés ci-dessous, trois réponses $a\;,\ b\ $ et $\ c$ sont données dont une seule est juste.
Écris le numéro de l'énoncé et la réponse choisie.
$$\begin{array}{|c|c|c|c|c|} \hline N^{\circ}&\text{Enoncé}&a&b&c\\ \hline 1&\text{Si }ABCD\text{ est un}&\overrightarrow{AB}=\overrightarrow{CD}&\overrightarrow{BC}= \overrightarrow{AD}&\overrightarrow{AC}=\overrightarrow{BD}\\ &\text{parallélogramme}& & &\\ &\text{alors}& & &\\ \hline 2&\text{Si le point }M\text{ est}&A\text{ est milieu}&M\text{ est milieu}&B\text{ est milieu}\\ &\text{l'image de }B\text{ par la}&\text{de }[BM]&\text{de }[AB]&\text{de }[AM]\\ &\text{translation de vecteur}& & & \\ &\overrightarrow{AB}\text{ alors}& & &\\ \hline 3&\text{Si }F\text{ est milieu de}&\overrightarrow{EF}=\overrightarrow{GF}&\overrightarrow{EF}=\overrightarrow{FG}& \overrightarrow{EG}=\overrightarrow{GF}\\ &[EG]\text{ alors}& & &\\ \hline \end{array}$$
Exercice 25
Soit $ABCD$ un parallélogramme et $E$ un point du plan.
1) Construis le point $F$ tel que $\overrightarrow{EF}=\overrightarrow{AB}$
2) Démontre que $EFCD$ est un parallélogramme.
Exercice 26
1) Trace un triangle $ABC.$
2) Construis le point $F$ tel que $BCFA$ soit un parallélogramme.
3) Construis le point $H$ de façon que $A$ soit le milieu de $[HB].$
4) Démontre que $AHFC$ est un parallélogramme.
Exercice 27
Soit un carré $ABCD$ de centre $O$ et de côté $4\;cm.$
Soit $t$ la translation de vecteur $\overrightarrow{BO}.$
1) Fais la figure et construis les points $E\;,\ F\;,\ G\ $ et $\ H$ images respectives des points $A\;,\ B\;,\ C\ $ et $\ D$ par $t.$
2) Démontre que $EFGH$ est carré.
Exercice 28
Soit $A$, $F$, $G$ trois points d'une droite $(\mathcal{D})$ et $E$ un point n'appartenant pas à $(\mathcal{D}).$
1) Construis les points $M\ $ et $\ N$ images respectives des points $F$ et $G$ par la translation de vecteur $\overrightarrow{AE}.$
2) Démontre que les points $E$, $M$ et $N$ sont alignés.
Exercice 29
Soit $ABC$ est un triangle rectangle en $A.\ E$ et $F$ deux points distincts.
1) Construis l'image $A'B'C'$ du triangle $ABC$ par la translation de vecteur $\overrightarrow{EF}$
2) Quelle est la nature du triangle $A'B'C'$ ? Justifie.

Commentaires
Roussel (non vérifié)
sam, 01/05/2019 - 15:04
Permalien
erreur
fdini
sam, 01/05/2019 - 15:13
Permalien
Bonjour Roussel, nous vous
Bonjour Roussel, nous vous remercions bcp, et c'est cela qui fera avancer les choses. Encore merci !
Cordialement
Anonyme (non vérifié)
jeu, 06/03/2021 - 23:39
Permalien
IL Y A UNE ERREUR AU NIVEAU
Anonyme (non vérifié)
ven, 06/04/2021 - 00:05
Permalien
OUI IL Y A AUSSI UNE ERREUR
randrianarisoa (non vérifié)
lun, 03/15/2021 - 13:35
Permalien
Remerciement
Ajouter un commentaire