Vous êtes ici

Série d'exercices : Les angles 6e

Classe:

Sixième

Exercice 1

On considère la figure ci-dessous.

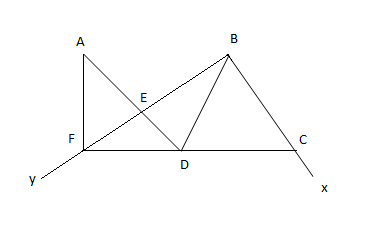
1) Colorier en rouge l'angle $\widehat{DBx}$

2) Colorier en vert l'angle $\widehat{DEB}$

3) Colorier en Jaune l'angle $\widehat{AFE}$

4) Colorier en noir l'angle $\widehat{AEF}$

Exercice 2

On considère la figure ci-dessous.

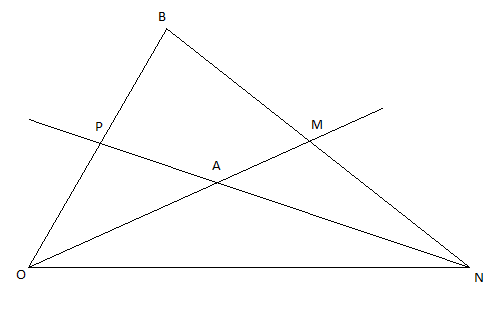
1) Donner quatre autres façons de noter l'angle $\widehat{AOP}.$

2) Colorier en vert l'angle $\widehat{ANM}.$

3) Donner cinq autres façons de noter l'angle $\widehat{ANM}.$

Exercice 3

1) Construire un angle $\widehat{ABC}$ tel que : $mes\;\widehat{ABC}=50^{\circ}.$

2) Donner la nature de l'angle $\widehat{ABC}.$

Exercice 4

1) Construire un angle $\widehat{MNP}$ tel que : $mes\;\widehat{MNP}=120^{\circ}.$

2) Donner la nature de l'angle $\widehat{MNP}.$

Exercice 5

1) Construire un angle droit $\widehat{IJK}.$

2) Construire un angle plat $\widehat{LMN}.$

Exercice 6

1) a) Tracer une demi-droite $[SU).$

b) Construire une demi-droite $[SV)$ telle que $mes\;\widehat{USV}=40^{\circ}.$

2) Combien y a-t-il de possibilités ?

Exercice 7

1) Trace un angle $\widehat{ABC}$ de $50^{\circ}.$ Trace une demi-droite $[BI)$ opposée à la demi-droite $[BA).$

2) Calculer $mes\;\widehat{CBI}$ en degré puis en grade.

Exercice 8

1) Construire deux angles adjacents complémentaires $\widehat{xOy}$ et $\widehat{xOt}$ tels que : $mes\;\widehat{xOy}=30^{\circ}.$

2) Calculer $mes\;\widehat{xOt}$ en degré puis en grade.

Exercice 9

1) Construire un angle $\widehat{ABC}$ tel que : $mes\;\widehat{ABC}=30^{\circ}.$

2) Construire la demi-droite $[BJ)$ bissectrice de l'angle $\widehat{ABC}.$ Calculer $mes\;\widehat{JBA}.$

Exercice 10

1) Donner la définition de deux angles superposables.

2) Construire deux angles adjacents et superposables dont chacun mesure $30^{\circ}.$

3) Construire le symétrique de ces deux angles par rapport à une droite $(d).$

Exercice 11

1) Construire deux angles adjacents supplémentaires $\widehat{ABC}$ et $\widehat{CBN}$ tels que : $mes\;\widehat{ABC}=30^{\circ}.$

2) Calculer $mes\;\widehat{CBN}.$

Exercice 12

On considère la figure ci-dessous.

On donne $mes\;\widehat{CAB}=59^{\circ}$ et $mes\;\widehat{HAD}=30^{\circ}.$

1) Reproduire la figure ci-dessous.

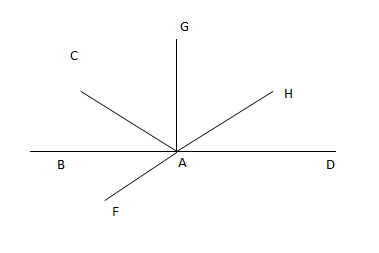
2) Calculer la mesure des angles : $mes\;\widehat{DAC}\;;\ mes\;\widehat{GAH}\;;\ mes\;\widehat{GAC}\;;\ mes\;\widehat{FAD}$ et $mes\;\widehat{FAB}$

Exercice 13

1) Construire deux angles adjacents $\widehat{xOy}$ et $\widehat{yOz}$ de côté commun $[Oy)$ tels que : $mes\;\widehat{xOy}=40^{\circ}$ et $mes\;\widehat{yOz}=140^{\circ}$

2) Calculer $mes\;\widehat{xOz}$ puis donner sa nature.

3) a) Construire les demi-droites $[OM)$ et $[ON)$ bissectrices respectives des angles $\widehat{xOy}$ et $\widehat{yOz}$

b) Calculer $mes\;\widehat{MON}$ puis donner sa nature.

Exercice 14

1) a) Construire deux angles $\widehat{AOB}$ et $\widehat{BOC}$ de côté commun $[OB)$ tels que : $mes\;\widehat{AOB}=40^{\circ}$ et $mes\;\widehat{BOC}=50^{\circ}$

b) Comment sont les angles $\widehat{AOB}$ et $\widehat{BOC}$ ? Justifier la réponse.

c) Calculer la mesure de l'angle $\widehat{AOC}$ en degré $(^{\circ})$ puis en grade $(gr).$

2) a) Construire un angle droit $\widehat{EOG}$ puis marque le point $H$ tel que $\widehat{EOH}$ soit un angle plat.

b) Que peut-on dire des angles $\widehat{EOG}$ et $\widehat{GOH}$ ?

c) Que représente la droite $(GO)$ pour l'angle $\widehat{EOH}.$ Calculer $mes\;\widehat{EOH}.$

Exercice 15

On donne les angles de la figure ci-dessous :

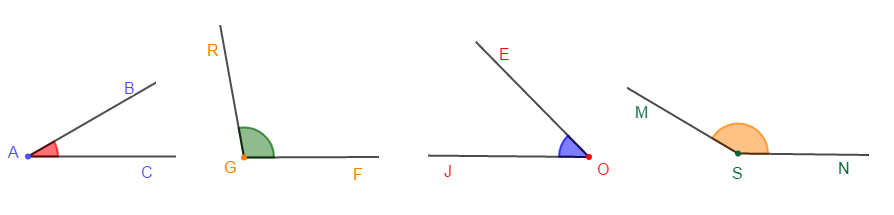
1) Nomme chacun des angles de la figure.

2) Pour chaque angle précise son sommet et ses côtés.

3) Mesure chaque angle puis donne la mesure en grade.

4) Indique parmi ces angles ceux qui sont aigus, plats, obtus ou droits.

Exercice 16

$TMF$ est un triangle tel que $\widehat{TMF}=65^{\circ}.$

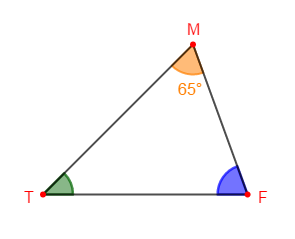
1) Mesure les angles $\widehat{MTF}\ $ et $\widehat{TFM}.$

2) Calcule la somme des trois angles du triangle.

Exercice 17

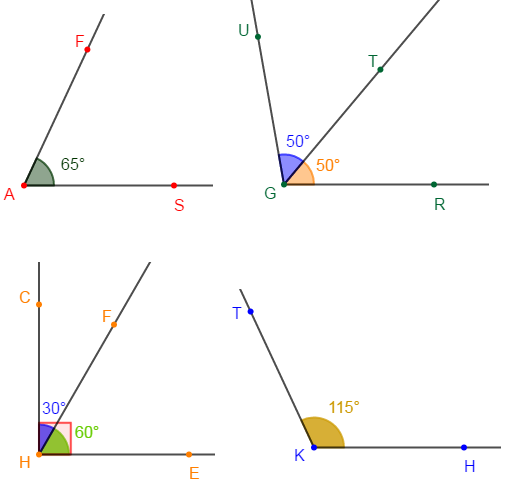
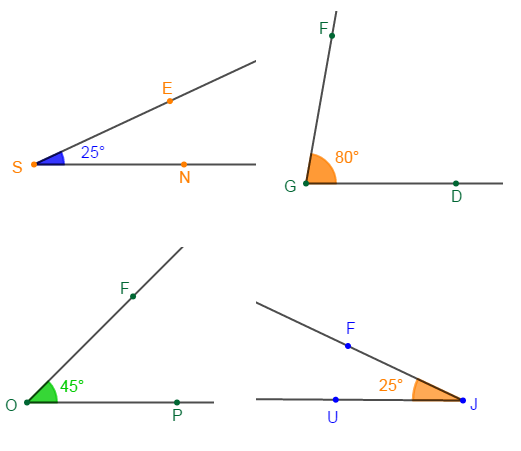
1) Complète les phrases par les mots ou groupe de mots ci-dessous et justifie ta réponse.

complémentaires ; supplémentaires ; correspondants ; bissectrice ; superposables ; adjacents ; angle droit ; angle obtus ; angle aigu ; angle plat.

a) Les angles $\widehat{CHF}\ $ et $\ \widehat{FHE}$ sont $\ldots\ldots\ldots\ldots$

b. Les angles $\widehat{SAF}\ $ et $\ \widehat{TKH}$ sont $\ldots\ldots\ldots\ldots$

c) Les angles $\widehat{SAF}\ $ et $\ \widehat{FJU}$ sont $\ldots\ldots\ldots\ldots$

d) Les angles $\widehat{ESN}\ $ et $\ \widehat{FJU}$ sont $\ldots\ldots\ldots\ldots$

e) $\widehat{TKH}$ est un angle $\ldots\ldots\ldots\ldots$

f) $\widehat{FOP}$ est un angle $\ldots\ldots\ldots\ldots$

g) Les angles $\widehat{UGR}\ $ et $\ \widehat{FGD}$ sont $\ldots\ldots\ldots\ldots$

h) Les angles $\widehat{UGT}\ $ et $\ \widehat{TGR}$ sont $\ldots\ldots\ldots\ldots$ et $\ldots\ldots\ldots\ldots$

2) Réponds par vrai ou faux aux affirmations ci-dessous :

a) $[FH)$ est la bissectrice de l'angle $\widehat{CHE}.$

b) $[TG)$ est la bissectrice de l'angle $\widehat{UGR}.$

c) Les angles $\widehat{FJU}\ $ et $\ \widehat{FOP}$ sont superposables.

d) Les angles $\widehat{TKH}\ $ et $\ \widehat{FGD}$ sont supplémentaires.

Exercice 18

Les questions sont indépendantes.

1) Construis les angles suivants.

a) $\widehat{ACF}$ est un angle tel que $\widehat{ACF}=40^{\circ}.$

b) $\widehat{STM}$ est un angle tel que $\widehat{STM}=70^{\circ}.$

c) $\widehat{DCV}$ est un angle tel que $\widehat{DCV}=100^{\circ}.$

d) $\widehat{RGB}$ est un angle tel que $\widehat{RGB}=120^{\circ}.$

e) $\widehat{PJS}$ est un angle tel que $\widehat{PJS}=80^{\circ}.$

2) Construis un angle $\widehat{MAN}$ tel que $\widehat{MAN}=55^{\circ}.$ Construis l'angle $\widehat{GEF}$ pour que les angles $\widehat{MAN}\ $ et $\ \widehat{GEF}$ soient complémentaires.

3) Construis un angle $\widehat{BAC}$ tel que $\widehat{BAC}=120^{\circ}.$ Construis l'angle $\widehat{GEF}$ pour que les angles $\widehat{FEG}\ $ et $\ \widehat{BAC}$ soient supplémentaires.

4) Construis deux angles adjacents $\widehat{TSC}\ $ et $\ \widehat{CSR}$ tels que $\widehat{TSC}=50^{\circ}\ $ et $\ \widehat{CSR}=70^{\circ}.$

Exercice 19

1) Construis deux angles adjacents $\widehat{MNP}\ $ et $\ \widehat{PNA}$ tels que $\widehat{MNP}=50^{\circ}\ $ et $\ \widehat{PNA}=40^{\circ}.$

2) Justifie que les angles $\widehat{MNP}\ $ et $\ \widehat{PNA}$ sont complémentaires.

3) Place le point $B$ sur la demi-droite $[PN)$ tel que le point $N$ soit le milieu $[PB].$

4) Détermine la mesure des angles $\widehat{MNB}\ $ et $\ \widehat{ANB}$ sachant que $\widehat{PNB}$ est un angle plat.

Exercice 20

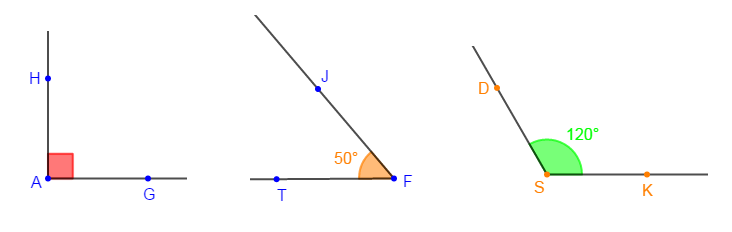
1) Reproduis les angles ci-dessus en utilisant uniquement la règle et le compas.

2) Convertis la mesure de chaque angle de la figure en grade.

Exercice 21

Construis la bissectrice de chacun des angles ci-dessous avec la règle et le rapporteur :

1) $\widehat{RDF}$ est un angle tel que mes $\widehat{RDF}=50^{\circ}$

2) $\widehat{FHM}$ est un angle tel que mes $\widehat{FHM}=80^{\circ}$

3) $\widehat{CEV}$ est un angle tel que mes $\widehat{CEV}=130^{\circ}$

4) $\widehat{ADB}$ est un angle tel que mes $\widehat{ADB}=120^{\circ}$

5) $\widehat{PJS}$ est un angle tel que mes $\widehat{PJS}=70^{\circ}$

Exercice 22

Construis la bissectrice de chacun des angles ci-dessous avec la règle et le compas :

1) $\widehat{ABC}$ est un angle qui a pour mesure $65^{\circ}$

2) $\widehat{MNF}$ est un angle qui a pour mesure $87^{\circ}$

3) $\widehat{CZS}$ est un angle qui a pour mesure $122^{\circ}$

4) $\widehat{JUB}$ est un angle qui a pour mesure $110^{\circ}$

5) $\widehat{PFD}$ est un angle qui a pour mesure $90^{\circ}$

Exercice 23

1) Construis deux angles complémentaires $\widehat{RDF}\ $ et $\ \widehat{FDH}$ tels que $\widehat{RDF}=50^{\circ}.$

2) Les angles $\widehat{RDF}\ $ et $\ \widehat{FDH}$ sont-ils adjacents ? Justifie ta réponse.

3) Construis la bissectrice $[DA)$ de l'angle $\widehat{RDF}.$

4) Place le point $B$ sur la demi-droite $[HD)$ tel que $HB>DH.$ Détermine la mesure de l'angle $\widehat{BDA}$ sachant que $\widehat{BDH}$ est un angle plat.

Exercice 24

1) Construis deux angles supplémentaires $\widehat{TMP}\ $ et $\ \widehat{TMA}$ tel que $\widehat{TMP}=80^{\circ}.$

2) Les angles $\widehat{TMP}\ $ et $\ \widehat{TMA}$ sont-ils adjacents ? Justifie ta réponse.

3) Trace la droite $(D)$ perpendiculaire à $(AP)$ et passant par le point $M.$ Place les points $C\ $ et $\ S$ sur $(D)$ tels que $M$ soit le milieu de $[CS].$

4) Détermine la mesure de l'angle $\widehat{TMA}.$

Exercice 25

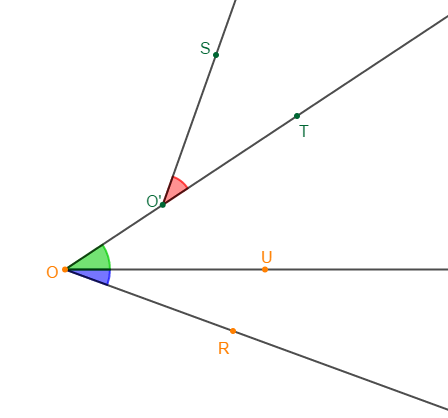
1) Les angles $\widehat{SO'T}\ $ et $\ \widehat{TOU}$ sont-ils adjacents ? Justifie ta réponse.

2) Les angles $\widehat{TOU}\ $ et $\ \widehat{UOR}$ sont-ils adjacents ? Justifie ta réponse.

3) $\widehat{SO'T}\ $ et $\ \widehat{UOR}$ sont-ils adjacents ? Justifie.

Exercice 26

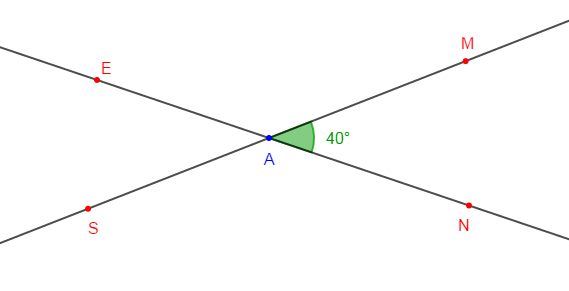
Sur la figure l'angle $\widehat{NAM}$ mesure $40^{\circ}\ $ et $\ (D)$ une droite du plan.

1) Comment sont les angles $\widehat{MAN}\ $ et $\ \widehat{EAS}\ ?$ Déduis-en la mesure de l'angle $\widehat{EAS}.$

2) Reproduis la figure en vrai grandeur en respectant l'angle $40^{\circ}.$

3) Construis le symétrique de la figure par rapport à la droite $(D)$ ; les points points $A\;,\ M\;,\ N\;,\ E\ $ et $\ S$ ont symétriques respectifs $A'\;,\ M'\;,\ N'\;,\ E'\ $ et $\ S'$

4) Compare les angles $\widehat{M'A'N'}\ $ et $\ \widehat{MAN}.$

Exercice 27

1) Trace deux droites $(L)\ $ et $\ (D)$ sécantes au point M formant un angle de $50^{\circ}.$

2) Place les points $A\ $ et $\ B$ sur la droite $(L)$ tels que $AB=8\;cm\ $ et $\ M$ soit le milieu de $[AB].$

3) Trace la droite $(L_{1})$ perpendiculaire à $(L)$ passant par le point $A$ ; elle coupe la droite $(D)$ au point $C.$

4) Détermine la mesure de chacun des angles du triangle $AMC.$

Exercice 28

1) Trace un angle $\widehat{MNE}$ tel que $\widehat{MNE}=40^{\circ}\ $ et $\ NE=NM=3\;cm.$

2) Trace le cercle $(C_{1})$ de centre $N$ et de rayon $NM.$

3) Place le point $A$ sur le cercle $(C_{1})$ tel que $\widehat{MNA}=40^{\circ}.$

Que représente la droite $(NM)$ pour l'angle $\widehat{ANE}\ ?$

4) Place le point $F$ sur le cercle $(C_{1})$ tel que les points $E\;,\ N\ $ et $\ F$ soient alignés.

a) Quelle est la mesure de l'angle $\widehat{FNE}\ ?$ justifie ta réponse.

b) Calcule la mesure de l'angle $\widehat{FNA}.$

Exercice 29

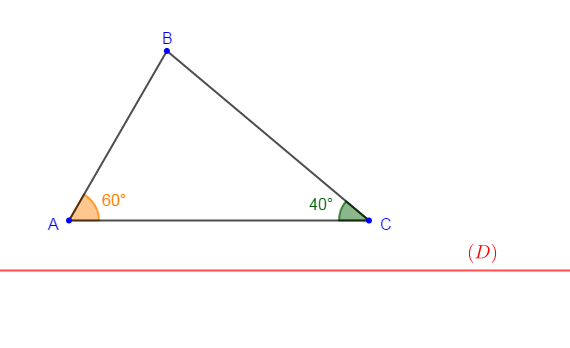
Reproduis la figure ci-dessous puis construis le symétrique du triangle $ABC$ par rapport à la droite $(D).$

Exercice 30

Sur la figure codée ci-dessous :

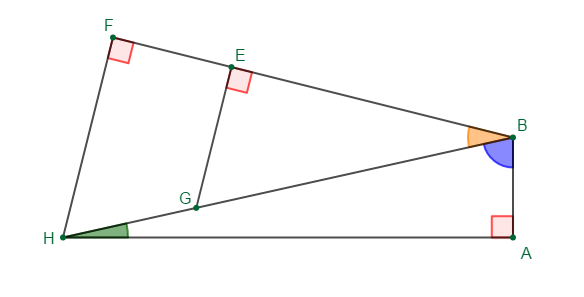
1) Cite deux angles aigus.

2) Cite un angle obtus.

3) Cite deux angles complémentaires.

4) Cite deux angles supplémentaires.

Exercice 31

1) Construis un angle droit $\widehat{ABE}$ puis trace la demi-droite $[BC)$ telle que $\widehat{EBC}=20^{\circ}\ $ et $\ \widehat{EBC}$ adjacent à $\widehat{CBA}.$

2) Construis la demi-droite $[BD)$ bissectrice de l'angle $\widehat{CBA}.$

3) Calcule la mesure l'angle $\widehat{CBA}.$

4) Détermine la mesure des angles $\widehat{DBA}\ $ et $\ \widehat{DBC}$ en justifiant ta réponse.