Série d'exercices : Le cercle 6e

Classe: 
Sixième

Exercice 1

Soit $(\zeta)$ un cercle de centre de centre $O$ et de rayon $3.5\;cm.$

1) Marquer quatre points $A\;;\ B\;;\ E\ $ et $\ F$ sur ce cercle.

2) Combien y a t-il de cordes reliant deux à deux les quatre points marqués ?

Exercice 2

1) Marque un point $O.$ Trace le cercle $(\zeta_{1})$ de centre $O$ et de rayon $2\;cm.$

2) a) Tracer un diamètre $[AB]$ de ce  cercle ; tracer le cercle $(\zeta_{2})$ de centre $A$ et dont un des rayons est le segment $[AB].$

b) Quelle est la position relative de $(\zeta_{1})$ et $(\zeta_{2})\ ?$

3) a) Marque un point $E$ sur le cercle $(\zeta_{1}).$ Trace le cercle $(\zeta_{3})$ de centre $E$ et passant par $B.$

b) Quelle est la position relative de $(\zeta_{1})$ et $(\zeta_{3})\ ?$

Exercice 3

1) Construire une demi-droite oblique $[Ox).$

2) Marque les points  $A\;;\ B\ $ et $\ C$ dans cet ordre tel que : $OA=3\;cm\;;\ AB=3\;cm\ $ et $\ BC=2\;cm.$

3) a) Calculer les distances $OB\ $ et $\ AC.$

b) Que représente le point $A$ pour le segment $[OB]\ ?$

4) Construire les cercles : $(\zeta_{2})\;;\ (\zeta_{2})\ $ et $\ (\zeta_{3})$ tels que :  $\zeta_{1}(O\;;\ 3\;cm)\;,\ \zeta_{2}(B\;;\ 3\;cm)\ $ et $\ \zeta_{2}(C\;;\ 3\;cm).$

5) Déterminer les positions relatives des cercles : $(\zeta_{1})\ $ et $\ (\zeta_{2})\ ?$ $(\zeta_{2})\ $ et $\ (\zeta_{3})\ ?$ $(\zeta_{1})\ $ et $\ (\zeta_{3})\ $

Exercice 4

Soit $A\;,\ B\ $ et $\ C$ trois points alignés tels que : $AB=5\;cm\ $ et $\ BC=3\;cm.$

1) Combien de points $C$ peut-on marquer ?

2) Dans chaque cas, tracer les cercles de diamètre $[AC].$

Exercice 5

1) a) Construire deux cercles $\zeta\ $ et $\ \zeta'$ tels que : $\zeta(O\;;\ 3\;cm)\ $ et $\ \zeta'(O\;;\ 4\;cm).$

b) Quelle est la position relative de $\zeta\ $ et $\ \zeta'$

2) Calculer la valeur exacte des périmètres de $\zeta$ et $\zeta'.$

3) a) Calculer l'aire de $\zeta\ $ et $\ \zeta'$ ($\pi=3.2)$   

b) En déduire l'aire de la couronne formés par les cercles $\zeta\ $ et $\ \zeta'.$

Exercice 6

1) Placer les points $I\;,\ E\ $ et $\ O$ dans cet ordre sur une droite $(d)$ oblique tels que : $IE=5\;cm\ $ et $\ EO=4\;cm$

2) Construire  $\zeta_{1}(I\;;\ 5.5\;cm)\;;\  \zeta_{2}(E\;;\ 1.5\;cm)\;;\ \zeta_{3}(O\;;\ 2.5\;cm).$

3) Quelle est  la position relative de $(\zeta_{1})\ $ et $\ (\zeta_{2})\ ?$ Justifier.

4) Quelle est la position relative de  $(\zeta_{2})\ $ et $\ (\zeta_{3})\ ?$ Justifier.

5) Quelle est la position relative de  $(\zeta_{1})\ $ et $\ (\zeta_{3})\ ?$ Justifier.

Exercice 7

1) Un cercle a un périmètre de $15\;cm.$

Calculer le rayon et le diamètre de ce cercle si $\pi=3.$

2) Un disque a une aire de $75\;cm^{2}.$ 

Calculer le rayon et le diamètre  correspondant à ce disque si $\pi=3.$

Exercice 8

1) Tracer $[AB]$ tel que : $AB=3\;cm.$

2) a) Tracer le cercle $\zeta$ dont $[AB]$ est un diamètre.

b) Tracer le cercle $\zeta'$ dont $[AB]$ est un rayon.

c) Quelle est la position relative de $\zeta\ $ et $\zeta'\ ?$

3) a) Calculer le périmètre de $\zeta\;\ (\pi=3.2)$

b) Calculer le périmètre de $\zeta'\;\ (\pi=3.1).$

4) Colorier en bleu puis déterminer  l'aire formée par le disque intérieur de  $\zeta'$ et extérieur de $\zeta\;\ (\pi=3).$

Exercice 9

1) Tracer un cercle $\mathcal{C}_{1}$ de centre $O$ et diamètre $7\;cm.$

2) Marquer un point $I$ intérieur à $\mathcal{C}_{1}$ tel que $OI=1.5\;cm$

3) Construire le cercle $\mathcal{C}_{2}(I\;;\ 2\;cm).$

4) Quelle est la position relative de ces deux cercles ?

5) a) Donner la valeur exacte du périmètre de $\mathcal{C}_{1}.$

b) Donner une valeur approchée du périmètre du cercle $\mathcal{C}_{1}\;\ (\pi=3.1).$

Exercice 10

1) Trace un cercle $(C)$ de centre $O$ et de rayon $2\;cm.$
 
2) Place les points $A\;,\ B\;,\ E\;,\ M\ $ et $\ D$ sur ce cercle.
 
3. Indique trois rayons et trace deux cordes.

Exercice 11

1) Trace un segment $[AB]$ de longueur $5\;cm.$
 
2) Construis un cercle de rayon $3\;cm$ passant par les points $A\ $ et $\ B.$
 
3) Explique ta méthode.

Exercice 12

On donne la figure ci-contre :

 

 
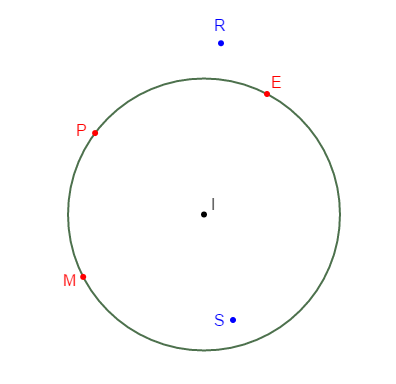
1) Cite deux points n'appartenant pas au cercle.
 
2) Cite deux points du cercle.
 
3) Le point $S$ appartient-il au cercle ? 
 
Justifie ta réponse.
 
4) Comment placer le point $H$ tel que $[PH]$ soit un diamètre.
 
5) Le point $I$ est-il un point du cercle ? Justifie ta réponse.
 
6) Justifie que $[SP]$ n'est pas une corde.

Exercice 13

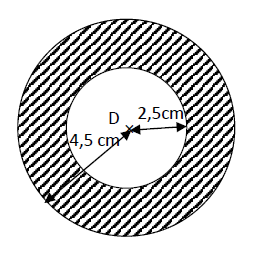
La figure ci-dessous est une couronne délimitée par deux cercles concentriques.
 
Calcule l'aire de la partie hachurée.

 

 

Exercice 14

A l'aide d'une poulie de $15\;cm$ de diamètre, Astou doit puiser de l'eau dans un puits de $9.42\;m$ de profondeur. 
 
Combien de tours doit faire la poulie pour sortir le seau du puits ?

Exercice 15

Un berger a un enclos circulaire de $12\;m$ de diamètre qu'il veut entourer d'un grillage qui coûte $450\;F$ le mètre et doit y laisser une porte de $3.5\;m.$
 
Calcule le prix du grillage.

Auteur: 
Diny Faye & adem

Commentaires

Anonyme (non vérifié)

ven, 12/13/2019 - 19:13

Bonne initiative

Mahamat Azarack... (non vérifié)

sam, 03/02/2024 - 14:35

Correction des exercices

Ajouter un commentaire