Exercices : Les triangles - 5e
Classe:
Cinquième
Exercice 1
$ABC$ est triangle, compléter le tableau.
$$\begin{array}{|c|c|c|c|c|c|}\hline mes\;\widehat{A} & 30^{\circ} & 63.5^{\circ} & 45^{\circ} & & 20^{\circ} \\ \hline mes\;\widehat{B} & 60^{\circ} & & & 13^{\circ} & 90^{\circ} \\ \hline mes\;\widehat{C} & & 13.5^{\circ} & 45^{\circ} & 29^{\circ} & \\ \hline\text{Nature de }ABC & & & & & \\ \hline\end{array}$$
Exercice 2
1) Construire un triangle $ABC$ tel que : $AB=5\;cm\;;\ AC=4\;cm$ et $BC=6\;cm.$
2) Tracer les droites $(d)$ et $(d')$ médiatrices respectifs des segments $[AB]$ et $[BC].$
3) Construire le cercle $(\mathcal{C})$ circonscrit à $ABC.$
Exercice 3
1) Construire un triangle $MNP$ tel que :
$MN=6\;cm\;;\ mes\;\widehat{M}=50^{\circ}$ et $mes\;\widehat{N}=70^{\circ}.$
2) Calculer la mesure de l'angle $P.$
3) Construire les droites $(b)$ et $(b')$ bissectrices des angles $\widehat{M}$ et $\widehat{P}.$
4) Construire le cercle $(\mathcal{C})$ inscrit à $MNP.$
Exercice 4
1) Construire un triangle $IJK$ tel que :
$IJ=6\;cm\;;\ IK=5\;cm\;;\ mes\;\widehat{I}=50^{\circ}.$
2) Construire les droites $(h)$ et $(h')$ hauteurs issues de $I$ et de $K.$
3) Placer le point $H$ orthocentre du triangle $IJK.$
4) Expliquer pourquoi $(JH)$ est une hauteur.
Exercice 5
1) Construire un triangle $FBM$ tel que :
$FB=6\;cm\;;\ FM=5\;cm$ et $BM=4\;cm.$
2) Construire les droites $(m)$ et $(m')$ médianes issues de $F$ et de $B.$
3) Placer le point $G$ centre de gravité du triangle $FBM.$
4) Expliquer pourquoi $(MG)$ est une médiane.
Exercice 6
1) Tracer un triangle $ABC$ tel que : $AB=5\;cm\;;\ mes\;\widehat{B}=100^{\circ}$ et $mes\;\widehat{C}=40^{\circ}.$
2) Tracer les bissectrices des angles $\widehat{B}$ et $\widehat{C}$ ; on appelle $I$ leur point d'intersection.
3) Tracer par $I$ la parallèle à la droite $(BC)$ ; elle coupe $(AB)$ en $M$ et $(AC)$ en $N.$
4) Calculer la mesure des angles du triangle $MIB.$
5) En déduire que $MIB$ est triangle isocèle en $I.$
Exercice 7
1) Construire un triangle $ABC$ tel que :
$AB=6\;cm\;;\ mes\;\widehat{A}=40^{\circ}$ et $mes\;\widehat{B}=40^{\circ}.$
2) Quelle est la nature du triangle $ABC$ ? Justifier puis calculer $mes\;\widehat{C}.$
3) Soit $H$ le pied de la hauteur issue de $A.$
4) Calculer la mesure de l'angle $\widehat{BAH}.$
Exercice 8
1) Construire un triangle isocèle $ABC$ de sommet principal $A$ tel que : $mes\;\widehat{BAC}=50^{\circ}.$
2) a) Construire le cercle $(\mathcal{C})$ circonscrit au triangle à $ABC.$
b) Marque le point $O$ centre de ce cercle.
3) a) Calculer $mes\;\widehat{ABC}$ et $mes\;\widehat{BCA}.$
b) Calculer la mesure de l'angle $\widehat{AOB}.$
Exercice 9
1) Construire un triangle $ABC$ rectangle en $A$ tel que : $AB=6\;cm$ et $mes\;\widehat{B}=60^{\circ}.$
2) Calculer la mesure de l'angle $\widehat{C}.$
3) Construire les bissectrices des angles $\widehat{B}$ et $\widehat{C}$ qui se coupent en $I.$ Calculer $mes\;\widehat{BIC}.$mes BIC.
4) a) Construire le cercle $(\mathcal{C}_{1})$ circonscrit à $ABC.$
b) Construire le cercle $(\mathcal{C}_{2})$ inscrit à $ABC.$
Exercice 10
1) a) Construire un triangle $ABC$ tel que : $AB=AC=5\;cm$ et $mes\;\widehat{ABC}=70^{\circ}.$
b) Quelle est la nature de $ABC$ ? Justifier
2) a) Construire le point $D$ symétrique de $B$ par rapport à $A.$
b) Quelle est la nature du triangle $ADC$ ?
3) Calculer : $mes\;\widehat{BAC}\;;\ mes\;\widehat{CAD}$ et $mes\;\widehat{ADC}.$
4) En déduire $mes\;\widehat{BCD}$ et la nature de $BCD.$
5) Construire le cercle $(\mathcal{C})$ circonscrit à $BDC.$
Exercice 11
Parmi les affirmations données ci-dessous certaines sont vraies d'autres sont fausses.
Recopie celles qui sont fausses et corrige-les.
1) Dans un triangle $ABC$ isocèle en $A$, la hauteur issue de $A$ est aussi une médiatrice du triangle.
2) Un triangle isocèle qui a un angle de mesure $60^{\circ}$ est un triangle équilatéral.
3) Les deux hauteurs d'un triangle rectangle sont les cotés de l'angle droit.
4) Une des hauteurs d'un triangle isocèle est un axe de symétrie de ce triangle.
5) L'orthocentre d'un triangle rectangle est l'un des sommets de ce triangle.
6) Le centre du cercle circonscrit à un triangle se trouve sur l'un de ses cotés.
7) Si un triangle est inscrit dans un cercle et l'un de ses cotés est diamètre du cercle, alors ce triangle est rectangle.
8) Un triangle rectangle dont l'un des angles mesure $60^{\circ}$ est rectangle et isocèle.
9) Un triangle ayant deux angles complémentaires est rectangle.
10) Un triangle qui a deux axes de symétrie est un triangle équilatéral.
11) La somme des angles d'un triangle est égale à $180^{\circ}.$
Exercice 12
1) Construis le triangle $ABC$ tel que $AB=7\;cm\;,\ AC=5\;cm\ \text{ et }\ BC=3\;cm$
2) Construis le triangle $KLM$ tel que $KL=5\;cm\;,\ LM=4\;cm$ et l'angle $\widehat{L}=45^{\circ}.$
3) Construis le triangle $XYZ$ tel que $XY=4.7\;cm\;,\ \widehat{X}=50^{\circ}\ $ et $\ \widehat{Y}=40^{\circ}.$
Exercice 13
On considère les trois triangles ci-dessous.
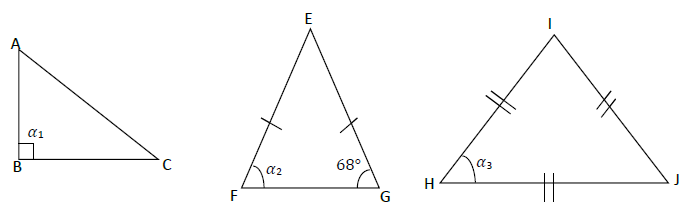
1) Donne la nature de chacun de ces triangles en justifiant.
2) Donne la mesure de chacun des angles $\alpha_{1}\;,\ \alpha_{2}\ $ et $\ \alpha_{3}$
Exercice 14
1) Dans chacun des cas ci-dessous construis le triangle indiqué en laissant les traits de construction :
a) $EDF$ tel que : $ED=6\;cm\;;\ \widehat{FED}=60^{\circ}\;;\ \widehat{FDE}=30^{\circ}.$
b) $CDE$ tel que : $CD=8\;cm\;;\ CE=5\;cm\ $ et $\ DE=4\;cm.$
2) Place l'orthocentre du triangle $EDF.$
3) Construis le cercle circonscrit au triangle $CDE.$
Exercice 15
On considère un triangle $IJK$ isocèle en $J.$
Les bissectrices des angles $\widehat{I}\ $ et $\ \widehat{K}$ se coupent en un point $L.$
1) Montre que $\widehat{LIK}=\widehat{IKL}.$
2) Déduis- en la nature du triangle $IKL.$ Justifie ta réponse.
Exercice 16
On considère le triangle $ABC$ ci-dessous.
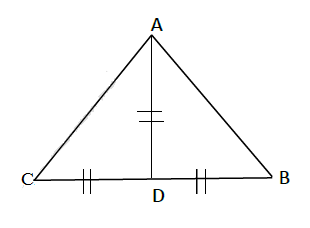
1) Quelle est la nature du triangle $ABC.$ Justifie ta réponse
2) Que représente le point D pour le triangle. Justifie ta réponse
3) Calcule $\widehat{B}+\widehat{C}$
Exercice 17
1) Construis un cercle $(\gamma)$ de centre $O$ et de rayon $3\;cm$ puis marque sur $(\gamma)$ deux points $A\ $ et $\ B$ diamétralement opposés.
2) La médiatrice de [AB] coupe le cercle en $C\ $ et $\ D.$
Place les points $C\ $ et $\ D$ puis précise la nature exacte des triangles $ABC\ $ et $\ ABD.$
3) $M$ est un point de $(\gamma)$ tel que $\widehat{ABM}=35^{\circ}.$
Calcule les mesures des angles du triangle $MAB$ en justifiant.
Exercice 18
1) Trace le demi-cercle $(C)$ de diamètre $[AB]$ tel que $AB=6\;cm.$
2) Place le point $I$ milieu de $[AB]\ $ et $\ M$ un point de $(C)$ tel que $\widehat{MIB}=60^{\circ}.$
Précise la nature du triangle $MIB$ et déduis-en la mesure de ses angles.
3) La parallèle à $(MB)$ passant par $I$ coupe $(AM)$ en $K.$
Calcule en justifiant les angles des triangles $MIK\ $ et $\ AKI.$
Exercice 19
1) Construis un triangle $ABC$ et place son orthocentre $H.$
2) Quels sont les orthocentres des triangles $AHB\ $ et $\ AHC.$
Exercice 20
1) Trace deux droites $(D_{1})\ $ et $\ (D_{2})$ sécantes en un point $O$ et place un point $A$ n'appartenant pas à ces droites.
2) Construis le point $B$ symétrique de $A$ par rapport à $(D_{1})$ et le point $C$ symétrique de $A$ par rapport à $(D_{2}).$
3) Que représente le point $O$ pour le triangle $ABC ?$ justifie ta réponse.
Exercice 21
Reproduis et complète le tableau ci- dessous.
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Angles}&&&&&&\\\text{d'un}&\text{Triangle 1}&\text{Triangle 2}&\text{Triangle 3}&\text{Triangle 4}&\text{Triangle 5}&\text{Triangle 6}\\\text{triangle}&&&&&&\\\hline \widehat{a}&36^{\circ}&&&&&45^{\circ}\\\hline\widehat{b}&&36^{\circ}&60^{\circ}&72^{\circ}&63^{\circ}& \\\hline\widehat{c}&&&&36^{\circ}&27^{\circ}& \\\hline\widehat{a}+\widehat{b}&144^{\circ}&90^{\circ}&120^{\circ}&&&90^{\circ}\\\hline\text{Nature}&&&&&&\\\text{du}&&&&&&\\\text{triangle}&&&&&&\\\hline\end{array}$$
Exercice 22
1) Quelle relation existe-t-il entre les angles aigus d'un triangle rectangle ?
2) Construis un triangle $ABC$ tel que $\widehat{ABC}=56^{\circ}\ $ et $\ \widehat{BAC}=34^{\circ}.$
3) Trace $(D)$ la bissectrice de l'angle $\widehat{ACB}.\ (D)$ coupe $[AB]$ en $E.$
4) Calcule la mesure de chacun des angles $\widehat{ACE}\ $ et $\ \widehat{BCE}$
Exercice 23
1) Trace le triangle $ABC$ tel que :
$$AB=5\;cm\;,\ \widehat{CAB}=50^{\circ}\ \text{ et }\ \widehat{ABC}=60^{\circ}$$
Construis le cercle $(C)$ de centre $O$ circonscrit au triangle $ABC.$
2) Place le point $M$ diamétralement opposé à $A.$
Quelle est la nature du triangle $AMC ?$
justifie ta réponse.
3) a) Construis le point $H$ symétrique de $B$ par rapport au point $I$ milieu de $[AC].$
b) Quelle est la nature du quadrilatère $ABCH\ ?$ Justifie ta réponse.
c) Détermine la mesure de chacun des angles $\widehat{ACH}\ $ et $\ \widehat{AHC}.$
Exercice 24
1) Construis un triangle $ABC$ rectangle en $A$ tel que : $AB=5\;cm\ $ et $\ \widehat{ACB}=35^{\circ}.$
2) Construis un triangle $EFG$ isocèle en $E$ avec $FG=5\;cm\ $ et $\ \widehat{FEG}=100^{\circ}.$
3) a) Trace un segment $[IJ]$ de $5\;cm$ de longueur et place $H$ un point n'appartenant pas à $[IJ]$ tel que $HI=HJ=4\;cm.$
b) Construis le triangle $IJK$ dont le cercle circonscrit a pour centre le point $H.$
Exercice 25
$POT$ est le triangle tel que :
$$PT=5\;cm\;,\ \widehat{OPT}=32^{\circ}\ \text{ et }\ \widehat{OTP}=58^{\circ}$$
1) Quelle est la nature du triangle $OPT\ ?$ Justifie ta réponse.
Marque le point $E$ milieu de $[PT].$
Quelle est la nature du triangle $EOP\ ?$
Justifie ta réponse.
2) La hauteur issue de $E$ dans le triangle $OET$ coupe le segment $[OT]$ en $I.$
a) Montre que l'angle $\widehat{OEI}=32^{\circ}.$
b) Justifie que la droite $(EI)$ est la bissectrice de l'angle $\widehat{OET}.$
3) La parallèle à la droite $(OE)$ passant par $P$ et la parallèle à la droite $(PE)$ passant par $O$ se coupent en $A.$
a) Justifie que le quadrilatère $AOEP$ est un parallélogramme.
b) Justifie que l'angle $\widehat{PAO}= 116^{\circ}.$
Exercice 26
1) Trace le triangle $EFG$ tel que
$$EF=5\;cm\;,\ EG=5\;cm\ \text{ et }\ \widehat{FEG}=60^{\circ}$$
2) Quelle est la nature du triangle $EFG ?$ Justifie ta réponse.
3) Soit $I$ le milieu de $[EF].$
a) Justifie que la droite $(GI)$ est la médiatrice du segment $[EF].$
b) Déduis-en la nature du triangle $EIG.$
4) Marque le point $J$ milieu de $[EG].$
a) Montre que les droites $(IJ)\ $ et $\ (GF)$ sont parallèles.
b) Justifie que le triangle $EIJ$ est équilatéral.
Exercice 27
Pass, Véréane et Darou sont des villages du Sénégal situés sur des axes différents.
Ces villages sont désignés respectivement par les lettres $P\;,\ V\ $ et $\ D.$
Les distances entre ces villages sont les suivantes :
$$PV=600\;m\;,\ PD=500\;m\ \text{ et }\ VD=700 \;m$$
1) Représente ces villages sur un plan à l'échelle $\dfrac{1}{10\,000}$
2) Une $O.N.G$ décide de leur construire un forage situé à égale distance des villages.
Tu es désigné pour choisir l'emplacement du forage.
Établis sur le plan l'emplacement du forage en justifiant ta réponse.
Exercice 28
Votre école organise une kermesse durant laquelle un des jeux consiste à ramasser un mouchoir posé à terre.
Le premier à ramasser le mouchoir remporte le gain.
1) Deux filles Astou et Fama prennent position sur la même ligne.
On les désignera respectivement par les lettres $A\ $ et $\ F.$
Quelle doit être la position $M$ du mouchoir pour que le jeu soit équitable ?
Fais un schéma.
2) Bineta veut participer au jeu sans être sur la même ligne de départ que les $2$ autres filles.
Elle est désignée par la lettre $B.$
Place $B$ sur le schéma précédent pour que le jeu soit équitable pour les $3$ candidates.
3) Tu es chargé par tes camarades de donner toutes les positions possibles de tout concurrent afin que le jeu soit équitable.
Indique ces positions sur le schéma en justifiant votre réponse.
Exercice 29
Pour financer ses activités, le foyer de votre école a aménagé un jardin ayant la forme d'un triangle $ABC$ dont les distances sont
$$AB=40\;m\;,\ AC=20\;m\ \text{ et }\ BC=30\;m$$
1) Représente le jardin sur le plan à l'échelle $\dfrac{1}{1\,000}.$
2) Calcule le périmètre réel du jardin.
3) On clôture le jardin avec du grillage vendu à $700\;F$ le mètre en laissant une porte de $4\;m$ de large et une autre de $3.5\;m$ de large.
Calcule le prix du grillage et le prix de revient de la clôture sachant qu'il faut $7$ piquets vendus à $500\;F$ pièce et qu'il faut payer $45\,000\;F$ pour la main d'œuvre.
Exercice 30
1) Trace un triangle $ABC$ puis marque un point $E$ sur $[AB].$
Trace la parallèle à $(BC)$ passant par $E$; elle coupe $[AC]$ en $F.$ Place $F.$
2) a) Trace la hauteur issue de $A$ dans le triangle $AEF.$
Elle coupe $(EF)$ en $H.$ Peut-on affirmer que $(AH)$ est aussi une hauteur du triangle $ABC\ ?$
b) Trace la hauteur $(L)$ issue de $C$ dans le triangle $ABC.$
3) a) Trace un triangle $ABD\;,\ D\ $ et $\ C$ n'appartenant pas au demi plan de frontière $(AB).$
b) Trace $(L')$ la hauteur issue de $D$ dans le triangle $ABD.$ Justifie que les droites $(L)\ $ et $\ (L')$ sont parallèles.
Exercice 31
1) Construis un triangle $ABC$ isocèle en $A.$
2) A l'extérieur de ce triangle, place les points $E\ $ et $\ F$ de sorte que les triangles $AEB\ $ et $\ AFC $soient équilatéraux.
Justifie que le triangle $AEF$ est isocèle.
Exercice 32
1) Trace un triangle $ABC$ isocèle en $A.$
Place le point $D$ tel que $A\ $ et $\ D$ soient situés de part et d'autre de la droite $(BC)$ et que le triangle $BDC$ soit isocèle.
2) Justifie que $\widehat{ABD}=\widehat{ACD}.$
Exercice 33
1) Construis un triangle $ABC$ rectangle en $A$ tel que $AB=4\;cm\ $ et $\ AC=3\;cm.$
2) Dans le demi-plan de frontière $(BC)$ ne contenant pas le point $A,$ place le point $D$ de sorte que $BCD$ soit équilatéral.
3) Le cercle de diamètre $[BC]$ coupe $(CD)\ $ et $\ (DB)$ respectivement en $H\ $ et $\ J.$
Démontre que les droites $(JC)\ $ et $\ (BD)$ sont perpendiculaires.
4) Que représente $(JC)$ pour le triangle $CBD\ ?$ Justifie ta réponse.
5) $(JC)\ $ et $\ (BH)$ se coupent en $F.$
Place $F$ puis montre que $BF=CF=DF.$
6) Calcule la mesure de chacun des angles du triangle $BCJ.$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Auteur:
Diny Faye & adem

Commentaires
Elbacky Thioub2.0 (non vérifié)
lun, 11/23/2020 - 00:19
Permalien
Je trouve ce site vraiment
Anonyme (non vérifié)
mar, 03/22/2022 - 23:27
Permalien
C'est leçons sont vraiment
Elbacky Thioub2.0 (non vérifié)
lun, 11/23/2020 - 00:20
Permalien
Interessant vraiment
Elbacky Thioub2.0 (non vérifié)
lun, 11/23/2020 - 00:21
Permalien
Telechargement de fichier
Heiba (non vérifié)
lun, 04/11/2022 - 23:35
Permalien
Travail tres excellence
Anonyme (non vérifié)
mer, 12/21/2022 - 21:13
Permalien
Très bons exercices
Anonyme (non vérifié)
mer, 09/06/2023 - 19:48
Permalien
trés bon exo
Mbaye FAYE (non vérifié)
sam, 05/03/2025 - 15:13
Permalien
Seulement les publicités qui
Ajouter un commentaire