Limites et Continuité - 1er S
Classe:
Première
I Limites
I.1 Limites à l'infinie
I.1.1 Limites infinies à l'infinie
Considérons la fonction $f$ définie par $f(x)=x^{2}$ ; son ensemble de définition est $D_{f}=\mathbb{R}.$
Examinons le tableau suivant : $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline x&-10^{18}&-10^{9}&-10^{4}&-100&-10&-1&0&1&10&10^{2}&10^{4}&10^{6} \\ \hline f(x)&10^{36}&10^{18}&10^{8}&10^{4}&10^{2}&1&0&1&10^{2}&10^{4}&10^{8}&10^{12} \\ \hline\end{array}$$
Nous constatons que lorsque $x$ prend des valeurs de plus en plus grandes, les valeurs de $f(x)$ deviennent de plus en plus grandes. On dira que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $+\infty.$
De même lorsque $x$ prend des valeurs de plus en plus grandes en valeurs absolues mais en étant négatives, $f(x)$ prend des valeurs de plus en plus grandes. On dira que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $-\infty.$
Définitions intuitives
Soit $f$ une fonction définie sur un domaine $D_{f}$.
$\centerdot\ \ $Lorsque $x$ tend vers $+\infty$, si les $f(x)$ tendent vers $+\infty$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $+\infty$ est égale à $+\infty$ et on note : $$\lim_{x\rightarrow +\infty}f(x)=+\infty$$
$\centerdot\ \ $Lorsque $x$ tend vers $-\infty$, si les $f(x)$ tendent vers $+\infty$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $-\infty$ est égale à $+\infty$ et on note : $$\lim_{x\rightarrow -\infty}f(x)=+\infty$$
$\centerdot\ \ $Lorsque $x$ tend vers $+\infty$, si les $f(x)$ tendent vers $-\infty$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $+\infty$ est égale à $-\infty$ et on note : $$\lim_{x\rightarrow +\infty}f(x)=-\infty$$
$\centerdot\ \ $Lorsque $x$ tend vers $-\infty$, si les $f(x)$ tendent vers $-\infty$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $-\infty$ est égale à $-\infty$ et on note : $$\lim_{x\rightarrow -\infty}f(x)=-\infty$$
I.1.2 Limites finies à l'infinie
Considérons la fonction $f$ définie sur $D_{f}=\mathbb{R}^{*}$ par $f(x)=\dfrac{1}{x^{3}}.$
Soit le tableau de valeurs suivant : $$\begin{array}{|c|c|c|c|c|c|c|c|}\hline x&-10^{4}&-10^{2}&-10&10&10^{2}&10^{4}&10^{6} \\ \hline f(x)&-10^{-12}&-0.000001&-0.001&0.001&0.000001&10^{-12}&10^{-18} \\ \hline\end{array}$$ En examinant ce tableau, nous constatons que lorsque $x$ prend des valeurs de plus en plus grandes, les valeurs de $f(x)$ restent très proches de 0. On dira que $f(x)$ tend vers 0 quand $x$ tend vers $+\infty.$
De même, lorsque $x$ prend des valeurs de plus en plus grandes en valeurs absolues, tout en étant négatives, les valeurs de $f(x)$ deviennent de plus en plus proches de la valeur 0. On dira que $f(x)$ tend vers 0 quand $x$ tend vers $-\infty.$
Définitions intuitives
Soit $f$ une fonction définie sur un domaine $D_{f}$ et $\ell\in\mathbb{R}.$
$\centerdot\ \ $Lorsque $x$ tend vers $+\infty$, si les $f(x)$ tendent vers un réel $\ell$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $+\infty$ est égale à $\ell$ et on note : $$\lim_{x\rightarrow +\infty}f(x)=\ell$$
$\centerdot\ \ $Lorsque $x$ tend vers $-\infty$, si les $f(x)$ tendent vers un réel $\ell$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $-\infty$ est égale à $\ell$ et on note : $$\lim_{x\rightarrow -\infty}f(x)=\ell$$
Remarque
La limite lorsqu'elle existe, elle est unique.
I.2 Limites en un point $x_{0}$
Activité
Soit $f$ une fonction dont la courbe représentative $C_{f}$ est illustrée sur la figure ci-dessous.
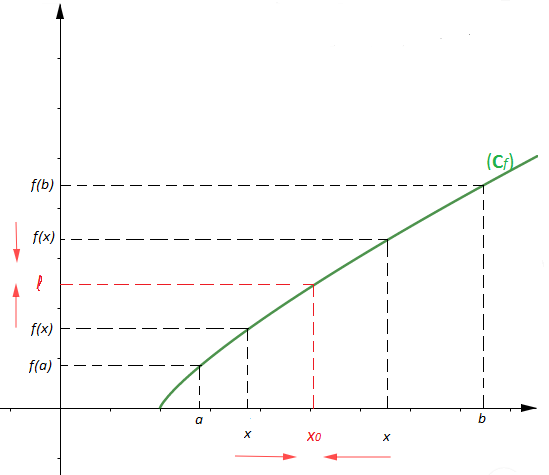
En examinant ce graphique nous pouvons constater que les valeurs de $f(x)$ tendent vers $L$ lorsque $x$ tend vers $x_{0}$ de part et d'autre.
Cet fait peut être exprimer en disant que $f(x)$ a pour limite $\ell$ lorsque $x$ tend vers $x_{0}$ et on note : $$\lim_{x\rightarrow x_{0}}f(x)=\ell$$
I.2.1 Limite à gauche - limite à droite de $x_{0}$
Définitions
Soit $f$ une fonction d'ensemble de définition $D_{f}$ et $x_{0}$ un réel.
$\centerdot\ \ $La limite éventuelle de la restriction de $f$ à $D_{f}\cap]-\infty\;;\ x_{0}[$ est appelée limite de $f$ à gauche au point $x_{0}$ ou encore la limite de $f$ lorsque $x$ tend vers $x_{0}$ en étant inférieur à $x_{0}$, et on note : $$\lim_{\substack{x \to x_{0} \\ x<x_{0}}}f(x)\quad\text{ou plus simplement}\quad\lim_{x\rightarrow x_{0}^{-}}f(x)$$
$\centerdot\ \ $La limite éventuelle de la restriction de $f$ à $D_{f}\cap]x_{0}\;;\ +\infty[$ est appelée limite de $f$ à droite au point $x_{0}$ ou encore la limite de $f$ lorsque $x$ tend vers $x_{0}$ en étant supérieur à $x_{0}$, et on note : $$\lim_{\substack{x \to x_{0} \\ x>x_{0}}}f(x)\quad\text{ou plus simplement}\quad\lim_{x\rightarrow x_{0}^{+}}f(x)$$
Théorème
On dit que $f$ admet une limite fini $\ell$ en $x_{0}$ si et seulement si $$\lim_{x\rightarrow x_{0}^{-}}f(x)=\lim_{x\rightarrow x_{0}^{+}}f(x)=\ell$$
I.2.2 Limites infinies en $x_{0}$
Soit la fonction $f$ définie par $f(x)=\dfrac{1}{x}\;;\quad D_{f}=\mathbb{R}^{*}.$
Examinons le tableau suivant : $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline x&-0.1&-0.01&-10^{-4}&-10^{-8}&\cdots&0&\cdots&10^{-6}&10^{-3}&0.01&0.1 \\ \hline f(x)&-10&-100&-10^{4}&-10^{8}&\cdots&\times&\cdots&10^{6}&10^{3}&100&10 \\ \hline\end{array}$$
Nous constatons que lorsque $x$ prend des valeurs de plus en plus proches de 0 en étant supérieures à 0, les valeurs de $f(x)$ deviennent de plus en plus grandes. On dira que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $0^{+}.$ On note : $\lim_{x\rightarrow 0^{+}}f(x)=+\infty$
De même lorsque $x$ prend des valeurs de plus en plus proches de $0$ en étant inférieures à $0\;,\ f(x)$ prend des valeurs de plus en plus grandes en valeurs absolues mais en étant négatives. On dira que $f(x)$ tend vers $-\infty$ quand $x$ tend vers $0^{-}.$ On note : $\lim\limits_{x\rightarrow 0^{-}}f(x)=-\infty$
Définitions intuitives
Soit $f$ une fonction définie sur un domaine $D_{f}$ et $x_{0}$ appartenant à l'intérieur de ce domaine :
$\centerdot\ \ $ Lorsque $x$ tend vers $x_{0}$, si les $f(x)$ tendent vers $+\infty$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $x_{0}$ est égale à $+\infty$ et on note : $$\lim_{x\rightarrow x_{0}}f(x)=+\infty$$
$\centerdot\ \ $ Lorsque $x$ tend vers $x_{0}$, si les $f(x)$ tendent vers $-\infty$ alors on dira que la limite de $f(x)$ quand $x$ tend vers $x_{0}$ est égale à $-\infty$ et on note : $$\lim_{x\rightarrow x_{0}}f(x)=-\infty$$
I.2.3 Limites finies en $x_{0}$
Soit $f$ la fonction définie par $f(x)=\dfrac{x^{2}-4}{x-2}$. On a $D_{f}=\mathbb{R}\setminus\{2\}.$
Considérons le tableau suivant : $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline x&1.8&1.9&1.99&1.999&2.00001&2.0001&2.001&2.01&2.1 \\ \hline f(x)&3.8&3.9&3.99&3.999&4.00001&4.0001&4.001&4.01&4.1 \\ \hline\end{array}$$
Nous constatons que lorsque $x$ prend des valeurs de plus en plus proches de 2 en restant dans $D_{f}$, les valeurs de $f(x)$ semblent s'approcher de la valeur 4. On exprime ce fait en disant que $f(x)$ tend vers $4$ quand $x$ tend vers $2.$ On note : $\lim\limits_{x\rightarrow 2}f(x)=4$
Définition
Soit $f$ une fonction définie sur un domaine $D\;,\ x_{0}$ appartenant à l'intérieur de ce domaine et $\ell$ un réel. Lorsque $x$ prend des valeurs proches de $x_{0}$, si les valeurs de $f(x)$ deviennent de plus en plus proches du réel $\ell$ alors on dira que $f(x)$ a pour limite $\ell$ lorsque $x$ tend vers $x_{0}$ et on note : $$\lim_{x\rightarrow x_{0}}f(x)=\ell$$
Travaux pratiques
Déterminer la limite des fonctions suivantes au point $x_{0}=1$
a) $f(x)=\left\lbrace\begin{array}{rcl} 2x+1&\text{si}&x<1 \\ 3x^{2}-x-1&\text{si}&x>1\end{array}\right.$
b) $g(x)=\left\lbrace\begin{array}{rcl} x^{2}-1&\text{si}&x<1 \\ \\ \dfrac{3x}{x^{2}+1}&\text{si}&x>1\end{array}\right.$
c) $h(x)=\left\lbrace\begin{array}{rcl} \dfrac{2x}{x-1}&\text{si}&x>1 \\ \\ \dfrac{-x^{2}}{(x-1)^{2}}&\text{si}&x<1\end{array}\right.$
Résolution
a) $\lim\limits_{x\rightarrow 1^{-}}f(x)=\lim\limits_{x\rightarrow 1^{-}}2x+1=2\times 1+1=3$
$\lim\limits_{x\rightarrow 1^{+}}f(x)=\lim\limits_{x\rightarrow 1^{+}}3x^{2}-x-1=3\times(1)^{2}-1-1=1$
b) $\lim\limits_{x\rightarrow 1^{-}}g(x)=\lim\limits_{x\rightarrow 1^{-}}x^{2}-1=1-1=0$
$\lim\limits_{x\rightarrow 1^{+}}g(x)=\lim\limits_{x\rightarrow 1^{+}}\dfrac{3x}{x^{2}+1}=\dfrac{3\times 1}{1^{2}+1}=\dfrac{3}{2}$
c) $\lim\limits_{x\rightarrow 1^{+}}h(x)=\lim\limits_{x\rightarrow 1^{+}}\dfrac{2x}{x-1}$ or lorsque $x$ tend vers $1^{+}\;,\ (x-1)$ tend vers $0^{+}.$
Donc, $\lim\limits_{x\rightarrow 1^{+}}\dfrac{2x}{x-1}=\dfrac{2}{(x-1)\rightarrow 0^{+}}=+\infty.$
D'où, $\lim\limits_{x\rightarrow 1^{+}}h(x)=+\infty$
$\lim\limits_{x\rightarrow 1^{-}}h(x)=\lim\limits_{x\rightarrow 1^{-}}\dfrac{-x^{2}}{(x-1)^{2}}$ or lorsque $x$ tend vers $1^{-}\;,\ (x-1)$ tend vers $0^{-}$ et donc $(x-1)^{2}$ va tendre vers $0^{+}.$
Ainsi, $\lim\limits_{x\rightarrow 1^{-}}\dfrac{-x^{2}}{(x-1)^{2}}=\dfrac{-1}{(x-1)^{2}\rightarrow 0^{+}}=-\infty.$
D'où, $\lim\limits_{x\rightarrow 1^{-}}h(x)=-\infty$
I.3 Opération sur les limites
Soient $f$ et $g$ deux fonctions de limites finies ou non. Les limites de $f+g\;,\ f\times g$ et de $\dfrac{f}{g}$ sont récapitulées dans les tableaux ci-dessous.
N.B : Dans les cas où on ne peut conclure, on dira qu'on est en face d'une indétermination ou simplement une "forme indéterminée" notée $(F.I)$
I.3.1 Limites d'une somme de deux fonctions
$$\begin{array}{|c|c|c|c|c|c|c|}\hline \lim f&\ell&\ell&\ell&+\infty&-\infty&+\infty \\ \hline \lim g&\ell'&+\infty&-\infty&+\infty&-\infty&-\infty \\ \hline \lim (f+g)&\ell+\ell'&+\infty&-\infty&+\infty&-\infty&F.I \\ \hline\end{array}$$
Exemple
a) $\lim\limits_{x\rightarrow +\infty}\left(x+1-\dfrac{1}{x^{3}}\right)=+\infty$ car en posant $f(x)=x+1\ $ et $\ g(x)=-\dfrac{1}{x^{3}}$ on a $\lim\limits_{x\rightarrow +\infty}f(x)=+\infty\ $ et $\ \lim\limits_{x\rightarrow +\infty}g(x)=0.$
Donc, $\lim\limits_{x\rightarrow +\infty}(f(x)+g(x))=+\infty$
b) $\lim\limits_{x\rightarrow 0^{-}}\left(x+1-\dfrac{1}{x^{3}}\right)=+\infty$ car $\ \lim\limits_{x\rightarrow 0^{-}}(x+1)=1\ $ et $\ \lim\limits_{x\rightarrow 0^{-}}-\dfrac{1}{x^{3}}=+\infty$
c) $\lim\limits_{x\rightarrow +\infty}(x^{3}-x^{2})\;,\ (F.I)$ car $\ \lim\limits_{x\rightarrow +\infty}x^{3}=+\infty\ $ et $\ \lim\limits_{x\rightarrow +\infty}-x^{2}=-\infty$
I.3.2 Limites d'un produit
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline \lim f&\ell&\ell>0&\ell<0&\ell>0&\ell<0&+\infty&-\infty&+\infty&0 \\ \hline \lim g&\ell'&+\infty&+\infty&-\infty&-\infty&+\infty&-\infty&-\infty&\infty \\ \hline \lim (f\times g)&\ell\times\ell'&+\infty&-\infty&-\infty&+\infty&+\infty&+\infty&-\infty&F.I \\ \hline\end{array}$$
Exemple
a) $\lim\limits_{x\rightarrow +\infty}(x^{2}+2x-3)=\lim\limits_{x\rightarrow +\infty}x^{2}\left(1+\dfrac{2}{x}-\dfrac{3}{x^{2}}\right)=+\infty$
car $\ \lim\limits_{x\rightarrow +\infty}x^{2}=+\infty\ $ et $\ \lim\limits_{x\rightarrow +\infty}\left(1+\dfrac{2}{x}-\dfrac{1}{x^{2}}\right)=1$ du fait que $\lim\limits_{x\rightarrow +\infty}\left(\dfrac{2}{x}-\dfrac{1}{x^{2}}\right)=0$
b) $\lim\limits_{x\rightarrow 0}(x^{2}+1)(x^{3}+2x+1)=1$ car $\ \lim\limits_{x\rightarrow 0}(x^{2}+1)=1\ $ et $\ \lim\limits_{x\rightarrow 0}(x^{3}+2x+1)=1$
c) $\lim\limits_{x\rightarrow 1^{+}}(x^{2}-1)\sqrt{\dfrac{1}{x-1}}\;,\ (F.I)$ car $\ \lim\limits_{x\rightarrow 1^{+}}(x^{2}-1)=0\ $ et $\ \lim\limits_{x\rightarrow 1^{+}}\sqrt{\dfrac{1}{x-1}}=+\infty$
I.3.3 Limites d'un quotient
$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline \lim f&\infty&\ell&\ell&+\infty&+\infty&-\infty&-\infty \\ \hline \lim g&\infty&\ell'\neq 0&\infty&\ell'<0&\ell'>0&\ell'<0&\ell'>0 \\ \hline \lim\left(\dfrac{f}{g}\right)&F.I&\dfrac{\ell}{\ell'}&0&-\infty&+\infty&+\infty&-\infty \\ \hline\end{array}$$
$$\begin{array}{|c|c|c|c|c|c|}\hline \lim f&\ell>0&\ell>0&\ell<0&\ell<0&0 \\ \hline \lim g&0^{+}&0^{-}&0^{+}&0^{-}&0 \\ \hline \lim\left(\dfrac{f}{g}\right)&+\infty&-\infty&-\infty&+\infty& F.I \\ \hline\end{array}$$
Exemple
a) $\lim\limits_{x\rightarrow +\infty}\dfrac{3}{x-2}=0^{+}$ car $\ \lim\limits_{x\rightarrow +\infty}3=3\ $ et $\ \lim\limits_{x\rightarrow +\infty}(x-2)=+\infty$
b) $\lim\limits_{x\rightarrow 0^{-}}\dfrac{x-1}{x^{3}}=+\infty$ car $\ \lim\limits_{x\rightarrow 0^{-}}(x-1)=-1\ $ et $\ \lim\limits_{x\rightarrow 0^{-}}x^{3}=0^{-}$
c) $\lim\limits_{x\rightarrow +\infty}\dfrac{x-1}{x}\;,\ (F.I)$ car $\ \lim\limits_{x\rightarrow +\infty}(x-1)=+\infty\ $ et $\ \lim\limits_{x\rightarrow +\infty}x=+\infty$
I.4 Méthodes de calcul des limites - levée d'une forme indéterminée
Pour calculer des limites ou pour lever une indétermination on peut procéder selon les méthodes suivantes :
Méthode 1 : utiliser l'un des théorème suivants
Théorème 1
La limite en $\pm\infty$ d'un polynôme est la limite en $\pm\infty$ de son monôme de plus haut degré.
Théorème 2
La limite en $\pm\infty$ d'une fraction rationnelle est la limite en $\pm\infty$ du quotient de monôme de plus haut degré.
Exemple
a) $\lim\limits_{x\rightarrow +\infty}x^{2}-2x+1=\lim\limits_{x\rightarrow +\infty}x^{2}\left(1-\dfrac{2}{x}+\dfrac{1}{x^{2}}\right)=\lim\limits_{x\rightarrow +\infty}x^{2}$ car $\ \lim\limits_{x\rightarrow +\infty}\left(1-\dfrac{2}{x}+\dfrac{1}{x^{2}}\right)=1$
donc $\lim\limits_{x\rightarrow +\infty}x^{2}-2x+1=\lim\limits_{x\rightarrow +\infty}x^{2}=+\infty$
b) $\lim\limits_{x\rightarrow +\infty}\dfrac{x^{3}-2x^{2}+1}{x^{2}-4x+3}=\lim\limits_{x\rightarrow +\infty}\dfrac{x^{3}}{x^{2}}=\lim\limits_{x\rightarrow +\infty}x=+\infty$
Méthode 2 : factoriser par $(x-x_{0})$
Si, pour une fonction rationnelle, $x_{0}$ annule aussi bien le numérateur que le dénominateur, alors pour chercher la limite de cette fonction en $x_{0}$ on factorise par $(x-x_{0})$ au numérateur comme au dénominateur et on simplifie.
Exemple
$\begin{array}{rcl} \lim\limits_{x\rightarrow 2}\dfrac{x^{2}-4}{x^{2}-6x+8}&=&\lim\limits_{x\rightarrow 2}\dfrac{(x-2)(x+2)}{(x-2)(x-4)}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{(x+2)}{(x-4)}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{4}{-2}\\ \\&=&-2\end{array}$
donc $$\lim_{x\rightarrow 2}\dfrac{x^{2}-4}{x^{2}-6x+8}=-2$$
Méthode 3 : multiplier par l'expression conjuguée
Pour calculer la limite d'une fraction irrationnelle en un point $x_{0}$ annulant le numérateur et le dénominateur, on multiplie par l'expression conjuguée et on simplifie.
Exemple
$\begin{array}{rcl} \lim\limits_{x\rightarrow 2}\dfrac{\sqrt{2x+5}-3}{x-2}&=&\lim\limits_{x\rightarrow 2}\dfrac{(\sqrt{2x+5}-3)(\sqrt{2x+5}+3)}{(x-2)(\sqrt{2x+5}+3)}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{2x+5-9}{(x-2)(\sqrt{2x+5}+3)}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{2x-4}{(x-2)(\sqrt{2x+5}+3)}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{2(x-2)}{(x-2)(\sqrt{2x+5}+3)}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{2}{\sqrt{2x+5}+3}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{2}{\sqrt{4+5}+3}\\ \\ &=&\lim\limits_{x\rightarrow 2}\dfrac{2}{6}\\ \\&=&\dfrac{1}{3} \end{array}$
donc $$\lim_{x\rightarrow 2}\dfrac{\sqrt{2x+5}-3}{x-2}=\dfrac{1}{3}$$
Méthode 4 : utiliser les théorèmes de comparaison
Soit $f\;,\ g\ :\ I\longrightarrow \mathbb{R}$ et soit $x_{0}\in I$ ou $x_{0}=\pm\infty$
Théorème 1
Si au voisinage de $x_{0}$ on a $f(x)\leq g(x)$ alors on a :
$$\begin{array}{rcl} \text{si }\lim f(x)=+\infty&\text{alors}&\lim g(x)=+\infty\\ \\ \text{si }\lim g(x)=-\infty&\text{alors}&\lim f(x)=-\infty\end{array}$$
Exemple
Soit la fonction $f$ définie sur $\mathbb{R}^{+}$ par $f(x)=x-\sqrt{x}+4$
1) Montrer que $\forall\;x\in\;[0\;;\ +\infty[\;,\ f(x)\geq 3\sqrt{x}$
2) en déduire $\lim_{x\rightarrow +\infty}f(x)$
Résolution
1)
$\begin{array}{rcl} f(x)-3\sqrt{x}&=&x-\sqrt{x}+4-3\sqrt{x}\\ \\ &=&x-4\sqrt{x}+4\\ \\ &=&(\sqrt{x}-2)^{2}\geq 0\end{array}$
Donc, $f(x)-3\sqrt{x}\geq 0\ \Rightarrow\ f(x)\geq 3\sqrt{x}$
2) On a : $\lim\limits_{x\rightarrow +\infty}3\sqrt{x}=+\infty\ $ et $\ f(x)\geq 3\sqrt{x}$ donc, $\ \lim\limits_{x\rightarrow +\infty}f(x)=+\infty$
Théorème 2 : (Théorème des gendarmes)
Si au voisinage de $x_{0}$ on a $g(x)\leq f(x)\leq h(x)$ et que $\lim\limits_{x\rightarrow x_{0}}g(x)=\lim\limits_{x\rightarrow x_{0}}h(x)=\ell$ (finie ou infinie) alors $\lim\limits_{x\rightarrow x_{0}}f(x)=\ell$
Exemple
Calculer $\lim\limits_{x\rightarrow 0^{+}}x^{2}\cos\dfrac{1}{x}$
Nous avons ; $-1\leq\cos\dfrac{1}{x}\leq 1\;,\ \forall\;x\ \Rightarrow\ -x^{2}\leq x^{2}\cos\dfrac{1}{x}\leq x^{2}$
Or, $\ \left.\begin{array}{lcl}\lim\limits_{x\rightarrow 0^{+}}-x^{2}&=&0 \\ \lim\limits_{x\rightarrow 0^{+}}x^{2}&=&0\end{array}\right\rbrace$ donc, $\ \lim\limits_{x\rightarrow 0^{+}}x^{2}\cos\dfrac{1}{x}=0$
Corollaire du théorème des gendarmes
Si au voisinage de $x_{0}$ on a : $|f(x)-\ell|\leq g(x)$ et que $\lim\limits_{x\rightarrow x_{0}}g(x)=0$ alors, $\ \lim\limits_{x\rightarrow x_{0}}f(x)=\ell$
Méthode 5 : utiliser le théorème de composée de fonctions
Théorème
Soit deux fonctions $f\ $ et $\ g$ telles que : $f\ :\ I\longrightarrow\mathbb{R}\;,\ g\ :\ J\longrightarrow\mathbb{R}$
$I\ $ et $\ J$ sont deux intervalles de $\mathbb{R}$ tels que $f(I)\subset J$ et soit $x_{0}\;,\ \ell\;,\ \ell'$ finis ou infinis, on a :
Si $\lim\limits_{x\rightarrow x_{0}}f(x)=\ell$ et si $\lim\limits_{x\rightarrow \ell}g(x)=\ell'$ alors, $\ \lim\limits_{x\rightarrow x_{0}}g\circ f(x)=\ell'$
Exemple
a) Soit $h(x)=\sqrt{\dfrac{4x+5}{x-2}}$, calculer $\lim\limits_{x\rightarrow +\infty}h(x)$
Posons $f(x)=\dfrac{4x+5}{x-2}\;,\ g(x)=\sqrt{x}$ et $h(x)=g\circ f(x)$
alors, $g\circ f(x)=g[f(x)]=\sqrt{f(x)}=\sqrt{\dfrac{4x+5}{x-2}}$
On a : $\lim\limits_{x\rightarrow +\infty}\dfrac{4x+5}{x-2}=\lim\limits_{x\rightarrow +\infty}\dfrac{4x}{4}=4$
donc,
$\begin{array}{rcl} \lim\limits_{x\rightarrow +\infty}\sqrt{\dfrac{4x+5}{x-2}}&=&\lim\limits_{x\rightarrow 4}g(x)\\\\&=&\lim\limits_{x\rightarrow 4}\sqrt{x}\\ \\&=&\lim\limits_{x\rightarrow 4}\sqrt{4}\\ \\&=&2\end{array}$
donc, $$\lim_{x\rightarrow +\infty}\sqrt{\dfrac{4x+5}{x-2}}=2$$
b) On donne $h(x)=\sqrt{\dfrac{x+9}{x-2}}$, calculer $\lim\limits_{x\rightarrow 2^{+}}h(x)$
Soit $f(x)=\dfrac{x+9}{x-2}\;,\ g(x)=\sqrt{x}$ et $h(x)=g\circ f(x)$
On a : $\lim\limits_{x\rightarrow 2^{+}}\dfrac{x+9}{x-2}=\lim\limits_{x\rightarrow 2^{+}}\dfrac{11}{0^{+}}=+\infty$
donc,
$\begin{array}{rcl} \lim\limits_{x\rightarrow 2^{+}}\sqrt{\dfrac{x+9}{x-2}}&=&\lim\limits_{x\rightarrow +\infty}g(x)\\ \\ &=&\lim\limits_{x\rightarrow +\infty}\sqrt{x}\\ \\ &=&+\infty\end{array}$
D'où, $$\lim_{x\rightarrow 2^{+}}\sqrt{\dfrac{x+9}{x-2}}=+\infty$$
I.5 Notion d'asymptotes
Soit $f$ une fonction de courbe représentative $(C_{f})$.
I.5.1 Asymptote horizontale
Si $\lim\limits_{x\rightarrow -\infty}f(x)=\ell$ ou $\ \lim\limits_{x\rightarrow +\infty}f(x)=\ell$ alors on dira que $(C_{f})$ admet une asymptote horizontale $\Delta$ d'équation $y=\ell$

$(C_{f})$ s'approche de plus en plus de la droite $\Delta$ d'équation $y=\ell$ lorsque $x$ devient infini.
I.5.2 Asymptote verticale
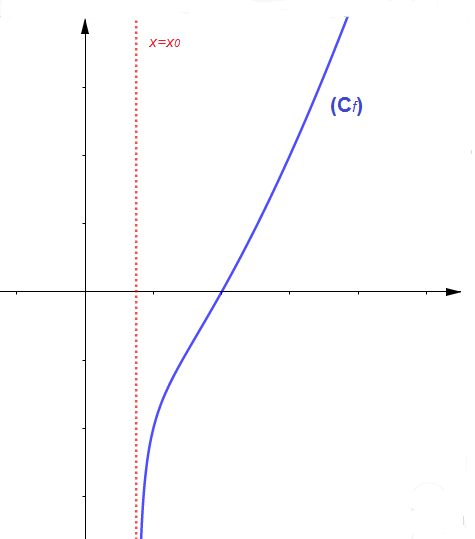
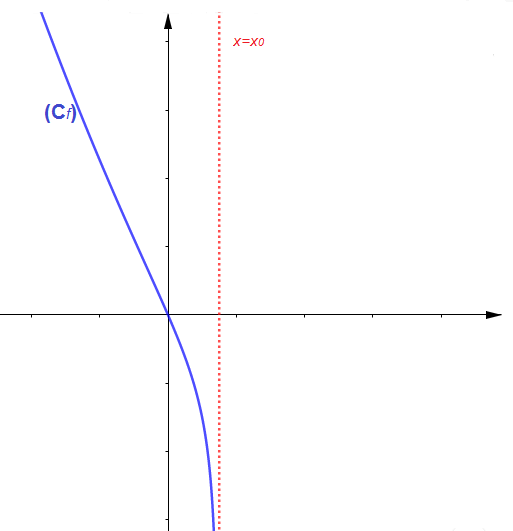
Si $\lim\limits_{x\rightarrow x_{0}^{-}}f(x)=-\infty\text{ ou }(+\infty)$ ou $\ \lim\limits_{x\rightarrow x_{0}^{+}}f(x)=-\infty\text{ ou }(+\infty)$ alors on dit que $(C_{f})$ admet une asymptote verticale $\Delta'$ d'équation $x=x_{0}$
$\centerdot\ \ \lim\limits_{x\rightarrow x_{0}^{+}}f(x)=-\infty$
$\centerdot\ \ \lim\limits_{x\rightarrow x_{0}^{-}}f(x)=-\infty$
Exemple
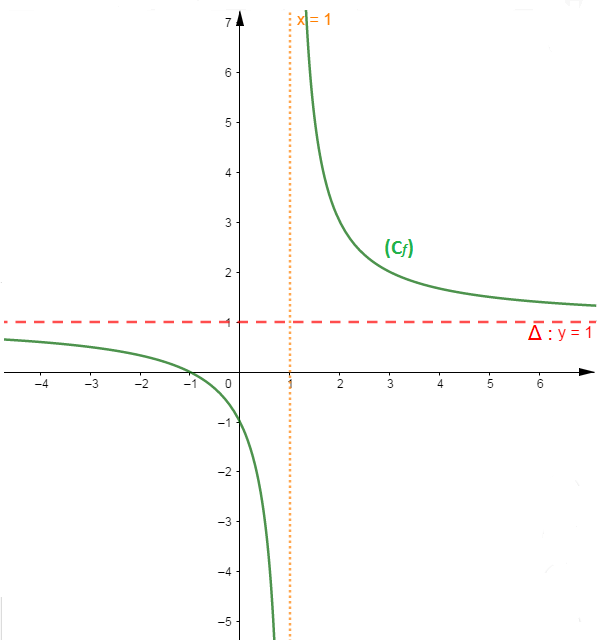
Soit $f(x)=\dfrac{x+1}{x-1}$, on a $D_{f}=\mathbb{R}\setminus\{1\}=]-\infty\;;\ 1[\cup]1\;;\ +\infty[$
$\lim\limits_{x\rightarrow -\infty}f(x)=\lim\limits_{x\rightarrow +\infty}f(x)=1$, donc la droite $\Delta$ d'équation $y=1$ est asymptote horizontale à $(C_{f})$
$\lim\limits_{x\rightarrow 1^{-}}f(x)=\lim\limits_{x\rightarrow 1^{-}}\dfrac{x+1}{x-1}=\lim\limits_{x\rightarrow 1^{-}}\dfrac{2}{0^{-}}=-\infty$
$\lim\limits_{x\rightarrow 1^{+}}f(x)=\lim\limits_{x\rightarrow 1^{+}}\dfrac{x+1}{x-1}=\lim\limits_{x\rightarrow 1^{+}}\dfrac{2}{0^{+}}=+\infty$ donc la droite $\Delta'$ d'équation $x=1$ est asymptote verticale à $(C_{f})$
illustration graphique
I.5.3 Asymptote oblique
S'il existe une fonction affine $x\mapsto ax+b\;;\ (a\neq 0)$ telle que $\lim\limits_{x\rightarrow \infty}[f(x)-(ax+b)]=0$, on dit que $(C_{f})$ admet une asymptote oblique d'équation $y=ax+b$
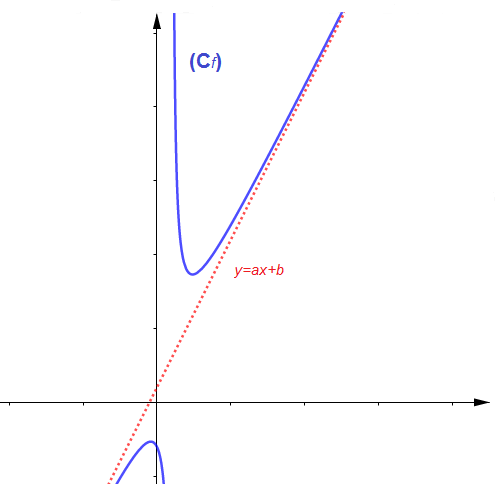
Exemple
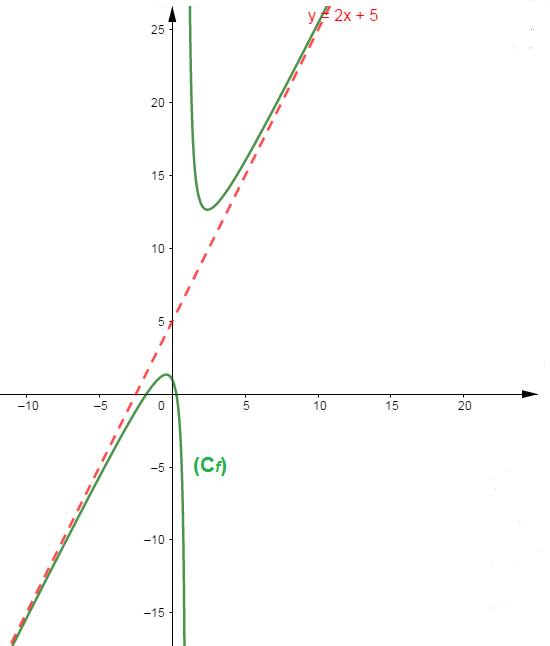
Soit $f$ la fonction définie par $f(x)=\dfrac{2x^{2}+3x-1}{x-1}$
$D_{f}=\mathbb{R}\setminus\{1\}=]-\infty\;;\ 1[\cup]1\;;\ +\infty[\ $ et $\ \forall\;x\in D_{f}\;,\ f(x)=2x+5+\dfrac{4}{x-1}$
Montrons que la droite d'équation $y=2x+5$ est asymptote oblique à $(C_{f})$.
On a : $f(x)-y=2x+5+\dfrac{4}{x-1}-(2x+5)=\dfrac{4}{x-1}$
$\lim\limits_{x\rightarrow -\infty}[f(x)-y]=\lim\limits_{x\rightarrow -\infty}\dfrac{4}{x-1}=0^{-}$ et
$\lim\limits_{x\rightarrow +\infty}[f(x)-y]=\lim\limits_{x\rightarrow +\infty}\dfrac{4}{x-1}=0^{+}$ donc la droite d'équation $y=2x+5$ est asymptote oblique à $(C_{f})$ au voisinage de $-\infty$ et de $+\infty.$
illustration graphique
Détermination pratique de $a$ et $b$
Dans l'équation $y=ax+b$, pour déterminer les coefficients $a\ $ et $\ b$ on procède comme suit :
calculer : $\lim\limits_{x\rightarrow \infty}\dfrac{f(x)}{x}=a\ $ et $\ \lim\limits_{x\rightarrow \infty}f(x)-ax=b$
Exemple
$f(x)=\dfrac{2x^{2}+3x-1}{x-1}$
$\begin{array}{rcl} \lim_{x\rightarrow \infty}\dfrac{f(x)}{x}&=&\lim\limits_{x\rightarrow \infty}\dfrac{\dfrac{2x^{2}+3x-1}{x-1}}{x}\\ \\&=&\lim\limits_{x\rightarrow \infty}\dfrac{2x^{2}+3x-1}{(x-1)}\times\dfrac{1}{x}\\ \\&=&\lim\limits_{x\rightarrow \infty}\dfrac{2x^{2}+3x-1}{x^{2}-x}\\ \\&=&\lim\limits_{x\rightarrow \infty}\dfrac{2x^{2}}{x^{2}}\\ \\ &=&2\end{array}$
Donc, $\lim\limits_{x\rightarrow \infty}\dfrac{f(x)}{x}=2\ \Rightarrow\ a=2$
Ainsi,
$\begin{array}{rcl} \lim\limits_{x\rightarrow \infty}f(x)-2x&=&\lim\limits_{x\rightarrow \infty}\dfrac{2x^{2}+3x-1}{x-1}-2x\\ \\ &=&\lim\limits_{x\rightarrow \infty}\dfrac{2x^{2}+3x-1-2x^{2}+2x}{x-1}\\ \\ &=&\lim\limits_{x\rightarrow \infty}\dfrac{5x-1}{x-1}\\ \\ &=&\lim\limits_{x\rightarrow \infty}\dfrac{5x}{x}\\ \\ &=&5\end{array}$
Donc $\lim\limits_{x\rightarrow \infty}f(x)-2x=5\ \Rightarrow\ b=5$, d'où la droite d'équation $y=2x+5$ est asymptote oblique à $(C_{f})$ au voisinage de $\pm\infty.$
II Continuité
II.1 Définition
Soit $f\ :\ I\longrightarrow\mathbb{R}$ et $x_{0}\in I$
$\centerdot\ \ $On dit que $f$ est continue en $x_{0}$ si, et seulement si, $$\lim_{x\rightarrow x_{0}}f(x)=f(x_{0})$$
$\centerdot\ \ $On dit que $f$ est continue à gauche de $x_{0}$ si, et seulement si, $$\lim_{x\rightarrow x_{0}^{-}}f(x)=f(x_{0})$$
$\centerdot\ \ $On dit que $f$ est continue à droite de $x_{0}$ si, et seulement si, $$\lim_{x\rightarrow x_{0}^{+}}f(x)=f(x_{0})$$
Théorème 1
Soit $f\ :\ I\longrightarrow\mathbb{R}\ $ et $\ x_{0}\in I$
On dit que $f$ est continue en $x_{0}$ si, et seulement si, $f$ est continue à gauche et à droite de $x_{0}$, c'est-à-dire $$\left\lbrace\begin{array}{lcl}\lim\limits_{x\rightarrow x_{0}^{-}}f(x)&=&f(x_{0}) \\ \lim\limits_{x\rightarrow x_{0}^{+}}f(x)&=&f(x_{0})\end{array}\right.$$
Exemple
Soit $f$ la fonction définie par $f(x)=\left\lbrace\begin{array}{lcl}\dfrac{\sqrt{1+x^{2}}-1}{2x}&\text{si}&x>0 \\ \\ 2x-1&\text{si}&x\leq 0\end{array}\right.$
Étudier la continuité de $f$ en $0.$
Résolution
$\begin{array}{rcl} \lim\limits_{x\rightarrow 0^{+}}f(x)&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{\sqrt{1+x^{2}}-1}{2x}\\ \\ &=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{(\sqrt{1+x^{2}}-1)(\sqrt{1+x^{2}}+1)}{2x(\sqrt{1+x^{2}}+1)}\\ \\ &=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{1+x^{2}-1}{2x(\sqrt{1+x^{2}}+1)}\\ \\ &=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{x^{2}}{2x(\sqrt{1+x^{2}}+1)}\nonumber \\ &=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{x}{2(\sqrt{1+x^{2}}+1)}\\ \\ &=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{0}{4}=0\end{array}$
Or, $\ f(0)=-1=\lim\limits_{x\rightarrow 0^{-}}f(x)$ donc, $\ \lim\limits_{x\rightarrow 0^{-}}f(x)\neq\lim\limits_{x\rightarrow 0^{+}}f(x)$
ainsi, $f$ n'est pas continue en $0.$
Théorème 2
Soient $f\ $ et $\ g$ deux fonctions continues en un point $x_{0}\ $ et $\ \alpha$ un réel ; alors les fonctions $\alpha f\;,\ (f+g)$ et $(f\times g)$ sont continues en $x_{0}.$
Si de plus $g(x_{0}\neq 0$ alors les fonctions $\dfrac{1}{g}\ $ et $\ \dfrac{f}{g}$ sont aussi continues en $x_{0}.$
II.2 Fonction continue sur un intervalle
Définition
Une fonction $f$ est continue sur un intervalle $I$ de $\mathbb{R}$ si elle est continue en tout point de $I.$
Théorème 1
Toute fonction polynôme est continue sur $\mathbb{R}$
Toute fonction rationnelle est continue sur son domaine de définition.
La fonction $\sqrt{U}$ est continue sur son domaine de définition.
La fonction $|U|$ est continue sur son domaine de définition.
Théorème 2
Soient $f\ $ et $\ g$ deux fonctions telles que $f$ soit continue sur un intervalle $I\ $ et $\ g$ continue sur un intervalle $J$ contenant $f(I)$ alors $g\circ f$ est continue sur $I.$
Prolongement par continuité d'une fonction
Soit \begin{eqnarray} f\ :\ \mathbb{R}&\longrightarrow&\mathbb{R}\nonumber \\ x&\longrightarrow&\dfrac{x^{2}-1}{x-1}\nonumber \end{eqnarray}
$D_{f}=\mathbb{R}\setminus\{1\}\;,\ 1\notin D_{f}$ ;
$f$ n'est pas continue au point 1. $\lim\limits_{x\rightarrow 1}f(x)=F.I$
On a : $\forall\;x\in\mathbb{R}\setminus\{1\}\;,\ f(x)=\dfrac{(x-1)(x+1)}{x-1}=x+1$
donc, $\lim\limits_{x\rightarrow 1}f(x)=\lim\limits_{x\rightarrow 1}x+1=2$
Soit alors $g$ la fonction définie par $\left\lbrace\begin{array}{rcl} g(x)&=&x+1\quad\text{si }x\neq 1 \\ g(1)&=&2 \end{array}\right.$
$\lim\limits_{x\rightarrow 1}g(x)=\lim\limits_{x\rightarrow 1}x+1=2$ donc, $\ \lim\limits_{x\rightarrow 1}g(x)=g(1)$
ainsi, $g$ est continue au point 1. D'où $g$ est appelé le prolongement par continuité de $f$ au point $1.$
Auteur:
Diny Faye & Seyni Ndiaye

Commentaires
M Pouye (non vérifié)
lun, 01/11/2021 - 07:13
Permalien
C'est vraiment un très bon
Anonyme (non vérifié)
ven, 02/05/2021 - 13:24
Permalien
Cours très intéressants.
Anonyme (non vérifié)
ven, 02/05/2021 - 13:24
Permalien
Cours très intéressants.
Nafiu (non vérifié)
ven, 05/07/2021 - 01:28
Permalien
Les cours ne se terminent pas
Anonyme (non vérifié)
jeu, 07/22/2021 - 13:34
Permalien
Cours tres complet
Baye Kebe (non vérifié)
lun, 05/23/2022 - 01:08
Permalien
Besoin d'aide sur svt,pc et maths
Aly thimbo (non vérifié)
dim, 07/06/2025 - 01:21
Permalien
Très bien
Ajouter un commentaire