Série d'exercices : Division des nombres décimaux arithmétiques - 6e
Classe:
Sixième
Exercice 1
1) Poser puis effectuer les opérations suivantes :
a) $6110\div 235\quad$ b) $734.32\div 26.3$ (à $0.01$ près).
2) Calculer mentalement les quotients suivants.
c) $2\,009\div 100\quad$ d) $45.37\div 0.1$
3) Donner un ordre de grandeur de chacun des quotients.
e) $305\div 19.5\quad$ f) $69\div 6.9$
Exercice 2
1) Donner le quotient entier approché par Défaut de $\dfrac{27}{7}$
2) Donner le quotient entier approché de la division de $213$ par $13$ à l'unité près par excès.
Exercice 3
1) a) Calculer le quotient au dixième près de $96.4$ par $34$ par défaut.
b) En déduire le reste de la division à $\dfrac{1}{10}$ près.
2.a) Calculer le quotient à $\dfrac{1}{100}$ près de $\dfrac{117}{17}$ par excès.
b) En déduire le reste de la division.
Exercice 4
1) Donner l'écriture décimale de : $\dfrac{13.5}{6}\ $ et $\ \dfrac{70.2}{26}$
2) $\dfrac{117}{11}$ admet-il une écriture décimale ? Pourquoi ?
3) Donne une écriture fractionnaire de $7.25$
Exercice 5
1) Donner l'écriture décimale de $\dfrac{23}{8}$
2) a) Encadrer $\dfrac{23}{8}$ entre deux entiers naturels consécutifs.
b) Encadrer $\dfrac{23}{8}$ entre deux décimaux consécutifs à $0.01$ près.
Exercice 6
1) Donner le quotient approché par excès à l'unité près de la division de $200.87$ par $49.$
2) Donner le quotient approché par défaut au centième près de la division de $347.3$ par $17.$
3) Donner le reste de la division de $75.1$ par $6.3$ aux dixièmes près.
Exercice 7
Écris les nombres décimaux suivants sous la forme $\dfrac{a}{b}$ avec $b$ non nul
$$3.5\;;\ 27.04\;;\ 100.001\;;\ 4\;;\ 58.273\;;\ 0.4\;;\ 0.045\;;\ 0.0102\;;\ 0.54321$$
Exercice 8
a) Exprime ces écritures fractionnaires sous forme de nombres décimaux.
$$\dfrac{14.7}{7}\;;\quad \dfrac{123}{8}\;;\quad \dfrac{154}{11}\;;\quad \dfrac{18.75}{7.5}$$
b) Range les écritures fractionnaires dans l'ordre décroissant.
Exercice 9
Effectue les divisions suivantes
a) $48.7\div 7.8\;;\quad 40.1\div 0.09$ à l'unité près
b) $30.75\div 4.7\;;\quad 7\,454.28\div 12\ $ à $\ 0.1$ près
c) $0.956\div 0.5\ $ à $\ 0.01$ près
Exercice 10
1) Relève dans cette liste les nombres divisibles : par $2$ ; par $3$ ; par $2$ et $3$
$$12\;;\ 31\;;\ 45\;;\ 810\;;\ 27\;;\ 34\;;\ 312\;;\ 431$$
2) Relève dans cette liste les nombres divisibles : par $5$ ; par $9$ ; par $5$ et $9$
$$27\;;\ 90\;;\ 45\;;\ 35\;;\ 54\;;\ 792\;;\ 838\;;\ 5$$
Exercice 11
Reproduis puis complète le tableau ci-dessous
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline a&b&\text{Ecriture fractionnaire }a\text{ sur }b&\text{Ecriture décimale}\\\hline 3&4&&\\\hline 1&8&&\\\hline 5&2&&\\\hline 0&19&&\\\hline&&&\\ &&\dfrac{1}{4}&\\&&&\\\hline&&&\\ &&\dfrac{2}{200}&\\&&&\\\hline&&&1\\\hline\end{array}$$
Exercice 12
Calcule: $6\times\dfrac{5}{3}\;;\quad\dfrac{7}{4}\times 12$
Exercice 13
Un journaliste dispose de $1\;h\;51\;min$ pour son émission "Wakh sa halate". Il veut accorder à chacun des ses $27$ auditeurs un temps de parole équivalent.
De combien de temps disposera chacun des auditeurs.
Exercice 14
Peut-on enregistrer sur un $CD$ où il ne reste que $19$ minutes d'enregistrement $2$ chansons dont les durées sont : $11\;min\;53\;s\ $ et $\ 6\;min\;58\;s.$
Exercice 15
Quatre personnes règlent une facture qui s'élève à $4\,200\;F.$ Les trois premières versent respectivement $\dfrac{1}{3}\;;\ \dfrac{1}{4}\ $ et $\ \dfrac{2}{7}$ de cette somme. La quatrième paye le reste.
Quelle est la somme versée par chacune ?
Quelle fraction de la dépense totale a versé la quatrième personne ?
Exercice 16
a) Parmi les écritures fractionnaires suivantes, écris celles dont le numérateur est multiple du dénominateur :
$$\dfrac{10}{2.5}\;;\quad \dfrac{22}{4}\::\quad \dfrac{105}{21}\;;\quad \dfrac{210}{10}$$
b) Exprime ces écritures fractionnaires sous forme de nombres décimaux.
Exercice 17
Reproduis la figure ci-dessous en utilisant le quadrillage du cahier

a) Recopie et complète les égalités ci-dessous :
$$AC=\dfrac{\ldots}{\ldots}\times AB\;;\quad AD=\dfrac{\ldots}{\ldots}\times AB\;;\quad AE=\dfrac{\ldots}{\ldots}\times AB$$
b) Place $F\ $ et $\ G$ tels que $AF=\dfrac{3}{10}\times AB\ $ et $\ AG=\dfrac{11}{10}\times AB$
Exercice 18
a) Combien de minutes y-a-t-il dans une heure ?
b) Complète
$$\dfrac{1}{4}\,h=\ldots min\;;\quad\dfrac{1}{2}\,h=\ldots min\;;\quad\dfrac{3}{4}\,h=\ldots min$$
Exercice 19
Le parcours d'un rallye automobile a une longueur totale de $4\,620\;km.$
Combien de postes distants de $140\;km$ les uns des autres peut on installer ?
Exercice 20
On considère les nombres de la forme $2\spadesuit 93\spadesuit$, où les $\spadesuit$ remplacent des chiffres. Trouve tous les nombres de cette forme qui sont divisibles à la fois par $3$ et par $5.$
Exercice 21
Une piste d'athlétisme a une longueur de $400\;m.$
Combien de tours doivent effectuer les coureurs de :
a) $5\,000\;m\ ?\quad$ b) $10\,000\;m\ ?$
Exercice 22
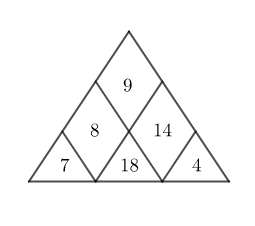
Le triangle ci-dessous est dit magique, car les produits des trois nombres écrits sur les côtés sont égaux.
Son produit magique est :
$$504=7\times 8\times 9=7\times 18\times 4=9\times 14\times 4$$
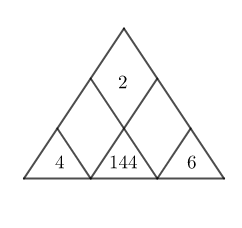
Complète le triangle ci-dessous pour qu'il soit magique :
Exercice 23
Recopie et complète les divisions à trous suivantes :
$$\begin{array}{r} 7\cdot 7\\7\cdot\\ \\\end{array}\begin{array}{|l} \cdot 7\\\hline 7\\ \\\end{array}\qquad\begin{array}{r} 123\cdot\\37\\\cdot\cdot\\ \\\end{array}\begin{array}{|l} \cdot\cdot\\\hline 51\\ \\ \\\end{array}$$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Auteur:
Diny Faye & adem

Commentaires
Anonyme (non vérifié)
dim, 02/06/2022 - 02:02
Permalien
C important
Ajouter un commentaire