Exercices : Trigonométrie 3e
Classe:
Troisième
Exercice 1
Soit $RSU$ un triangle rectangle en $U$ tel que $RS=3$ et $SU=2$
1) Calculer $RU$
2) Calculer $\cos\widehat{R}\;,\ \sin\widehat{R}\;,\ \cos\widehat{S}\;,\ \sin\widehat{S}$ et $\tan\widehat{S}$
Exercice 2
1) $ABC$ est un triangle rectangle en $A$ tel que $\widehat{ABC}=56^{o}$ et $BC=4.2\;cm$. Calculer $AB$ et $AC$
2) Construire un triangle $OIE$ rectangle en $O$ tel que $\widehat{OEI}=72^{o}$ et $OE=2\;cm.$ Calculer l'arrondi au dixième près de $OI$ et vérifier sur la figure.
Exercice 3
Les questions sont indépendantes. On demande de faire la figure à main levée
1) $ABC$ est un triangle rectangle en $C$ tel que : $CB=4\;cm$ et $AC=3\;cm.$
Calculer : $\sin\widehat{B}\;,\ \cos\widehat{B}$ et $\tan\widehat{B}$. En déduire $mes\widehat{B}$ à 0.1 près.
2) Dans le triangle $HBC$ rectangle en $H$, $mes\widehat{B}=60^{o}$ et $HB=4\;cm$. Calculer les distances $BC$ et $HC.$
3) $ABC$ est un triangle rectangle en $B$ tel que : $mes\widehat{A}=30^{o}$ et $CB=5\;cm$. Calculer $AC$ et $AB.$
4) $STV$ est un triangle rectangle en $T$ tel que : $\tan\widehat{S}=\dfrac{4}{3}$ et $TV=\sqrt{6}\;cm$. Calculer $ST$ et $SV.$
5) Dans le triangle $ABC$ rectangle en $B$, on a : $\sin\widehat{A}=\dfrac{\sqrt{5}}{3}$. Calculer $\cos\widehat{A}$ et $\tan\widehat{A}.$
6) Soit $\widehat{A}$ et $\widehat{B}$ deux angles aigus tels que : $\cos\widehat{A}=\dfrac{\sqrt{3}-1}{6}$ et $\sin\widehat{B}=\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{72}}$. Montrer que $\widehat{A}$ et $\widehat{B}$ sont deux angles complémentaires.
Exercice 4
$ABC$ est un triangle rectangle en $B$ tel que $AC=10\;cm$ et $BC=5\;cm$. $\ I$ est un point de $[AB]$ tel que $AI=5\;cm$. La perpendiculaire à $(AB)$ passant par $I$ coupe $[AC]$ en $J.$
1) En utilisant le sinus de $\widehat{BAC}$, montrer que $\dfrac{IJ}{AJ}=\dfrac{BC}{AC}$, puis calculer $IJ.$
2) Calculer $\sin\widehat{BAC}$ et en déduire sa mesure en degrés.
Exercice 5
$(C)$ est un cercle de centre $O$ et de rayon $r$. $\ [BC]$ est un diamètre du cercle et $A$ un point de $(C)$ tel que $AB=r.$
1) Montrer que le triangle $ABC$ est rectangle en $A.$
2) Calculer $AC$ en fonction de $r.$
3) Calculer $\sin$ de $\widehat{ABC}.$
Exercice 6
Soit un cercle $(C)$ de centre $O$ et de rayon $r$. $\ [AB]$ est un diamètre de ce cercle et $I$ milieu de $[OA]$. La perpendiculaire à la droite $(AB)$ passant par $I$ coupe le cercle en deux points $D$ et $E.$
1) Démontrer que $ABD$ est un triangle rectangle puis montrer que $AD=r.$
2) Calculer $\cos\widehat{DAB}$. En déduire $\sin\widehat{DBO}.$
3) Démontrer que $\dfrac{AI^{2}}{AD^{2}}+\dfrac{DB^{2}}{AB^{2}}=1$
Exercice 7
Soit $ABC$ un triangle isocèle de sommet $A$ tel que $\widehat{B}= 30^{o}$ et $BC=6\;cm$. On appelle $I$ milieu de $[BC]$
1) Calculer $AB$ et $AI$
2) Calculer l'aire $S$ du triangle $ABC$ puis donner son encadrement à $0.1\;cm^{2}$ près sachant que $1.732<\sqrt{3}<1.733$
Exercice 8
$KLM$ est un triangle $KL=4\;cm\;;\ LM=4\sqrt{3}\;;\ KM=8\;cm.$
1) Montrer que $KLM$ est un triangle rectangle.
2) Faire une figure.
3) Calculer $LH$ et $KH$ , $\ H$ étant le projeté orthogonal de $L$ sur $(KM).$
4) Soit $I$ le projeté orthogonal de $H$ sur $(ML)$. Calculer $IH.$
Exercice 9
1) On donne une valeur trigonométrique déduis-en les autres : $\cos x=\dfrac{1}{4}\;,\ \sin x=\ldots\;,\ \tan x=\ldots$
2) Construire un triangle $COS$ tel que $\widehat{OCS}=75^{o}$ et $\widehat{CSO}=55^{o}$
Placer deux points $E$ et $F$ sur la droite $(CO)$ tels que $S$ soit le projeté orthogonal de $F$ sur $(OS)$ et $EF=8\;cm$
Placer le point $R$ projeté orthogonal de $E$ sur $(OS)$
On appelle $I$ et $J$ les projetés orthogonaux respectifs de $E$ et $F$ sur $(CS)$
Calculer les arrondis au dixième de $IJ$ et $RS$. Vérifier sur le dessin les résultats trouvés.
Exercice 10
1) $OAB$ est un triangle, $OA=\sqrt{10}\;;\ OB=3\sqrt{10}$ et $AB=10\;cm$. Quelle est la nature de $OAB$ ?
2) Calculer le cosinus de l'angle $\widehat{OBA}$. En déduire $\sin\widehat{OBA}$ ?
3) Sachant que $3.162<\sqrt{10}<3.163$ donner la valeur approchée par défaut à l'ordre 4 de $\cos\widehat{OBA}$. En déduire la valeur approchée à 1 degré près de $\widehat{OBA}.$
On donne : $\cos 17^{o}\approx 0.9543\;,\ \cos 18^{o}\approx 0.9511\;,\ \cos 19^{o}\approx 0.9455$ et $\cos 20^{o}\approx 0.9397$
Exercice 11
Soit un demi-cercle de centre $O$ et de diamètre $[AB]$ tel que $AB=6\;cm$. Tracer la droite $(D)$ perpendiculaire à $(AB)$ passant par $B$. Marquer un point $C$ sur le demi-cercle tel que l'angle $\widehat{CAB}=30^{o}$. La demi droite $[AC)$ coupe la droite $(D)$ en $E.$
1) Quelle est la nature des triangles $ABC$ et $AEB$ ? Justifier les réponses.
2) Calculer $AC\;,\ BC\;,\ AE$ et $EB.$
3) Sur l'arc $\overset{\displaystyle\frown}{BC}$ , marquer le point $M$ tel que les points $O\;,\ M$ et $E$ soit alignés.
a) Calculer le cosinus de l'angle $\widehat{MOB}$.
b) Donner sa valeur approchée par défaut à $10^{-3}$ près sachant que $4.582\leq \sqrt{21}\leq 4.583$
c) Déduire la mesure de l'angle $\widehat{EOB}$ à un degré près par défaut.
Exercice 12
1) Tracer un demi-cercle $(C)$ de centre $O$ et de diamètre $[AB]$ tel que $AB=2r$. Soit $M$ un point du demi-cercle $(C)$ plus proche de $B$ que de $A$. Quelle est la nature du triangle $AMB$ ? Justifier.
2) Soit $a$ et $b$ les mesures respectives en degrés des angles $\widehat{BAM}$ et $\widehat{BOM}$ et $C$ le pied de la hauteur du triangle $AMB$ issue de $M.$
a) Donner deux expressions différentes de $\cos a$.
b) En déduire que : $AC=AM\cos a\;,\ AM^{2}=AB\times AC$
c) On sait que $AC=AO+OC$ : Exprimer $OC$ en fonction de $\cos b$. En déduire que $AC=r(1+\cos b)$
d) Déduire des questions précédentes que $\cos^{2}a=\dfrac{1+\cos b}{2}.$
Exercice 13
$x$ et $a$ sont des angles aigus
1) Sachant que $\cos x=\dfrac{\sqrt{5}}{3}$, calculer $\sin x$ et $\tan x.$
2) Soit l'expression $F(a)=(1-\cos a)(1+\cos a)(1+\tan^{2}a)$
a) Démontrer que $F(a)=\tan^{2}a$
b) Calculer $F(30^{o})$
3) Soit un triangle quelconque $ABC$ ; $\ H$ le pied de la hauteur issue de $A.$
Démontrer que : $\dfrac{\sin\widehat{B}}{AC}=\dfrac{\sin\widehat{C}}{AB}.$
Exercice 14
1) Sachant que $\sin 15^{\circ}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$, vérifier que $\cos 15^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4}$ puis, donner la valeur exacte de $\ tan 15^{\circ}.$
2) $x\in\;]0^{\circ}\;;\ 90^{\circ}[$
a) Établir les égalités suivantes :
$1+\tan^{2}x=\dfrac{1}{\cos^{2}x}$
$1-2\sin^{2}x=2\cos^{2}x-1$
$(\cos x+\sin x)(\cos x-\sin x)=2\cos^{2}x-1$
$1+\dfrac{1}{\tan^{2}x}=\dfrac{1}{\sin^{2}x}$
b) Simplifier $\sqrt{1-\cos x}\times\sqrt{1+\cos x}\ $ et $\ \sqrt{1+\tan^{2}x}$ (Utiliser les résultats de la question a))
Exercice 15
1) a) Construire un cercle $(\mathcal{C})$ de centre $I$ et de rayon $4\;cm.\ A$ et $B$ sont diamétralement opposés.
Placer un point $M$ sur $(\mathcal{C})$ tel que : $AM=4\;cm.$
b) Quelle est la nature du triangle $AMI$ ?
c) En déduire la mesure de l'angle $\widehat{BIM}.$
2) $K$ est le point d'intersection de la perpendiculaire à $(AB)$ passant par $I$ et la droite $(AM).$
a) Justifier que $AMB$ est un triangle rectangle.
b) En remarquant que $\cos\widehat{BAM}=\cos\widehat{KAI}.$
Calculer $AK$ et $KI.$
3) Le point $H$ est le projeté de $M$ sur $(AB).$
a) Calculer $\cos\widehat{B}$ de 2 manières différentes.
b) Exprimer $BH$ en fonction de $\cos\widehat{B}$ puis démontrer que : $BH=\dfrac{BM^{2}}{AB}$
4) Placer le point $E$ sur le segment $[AM]$ tel que : $AE=3\;cm.$ La parallèle à $(IM)$ passant par $E$ coupe $[AI]$ en $F.$
Quelle est la nature du triangle $AEF$ ?
Exercice 16
On considère un cercle $(\mathcal{C})$ de centre $O$ et de rayon $r.$ Soit $[AB]$ un diamètre de ce cercle ; $(\Delta)$ la tangente en $B$ à $(\mathcal{C}).$ Une droite $(L)$ passant par $A$ recoupe $(\mathcal{C})$ en $C$ et recoupe $(\Delta)$ en $E.$ On désigne par $\alpha$ la mesure de $\widehat{BAC}.$
1) Exprimer en fonction de $r$ et $\alpha$ : $CA\;;\ CB\;;\ EA\;;\ EB.$
2) Calculer : $CA\;;\ CB\;;\ EA\;;\ EB$ pour $r=2\;cm$ et $\alpha=30^{\circ}.$
Exercice 17
Soit un segment $[OA]$, $OA=4\;cm.$
$M$ est un point appartenant au cercle $\mathcal{C}(O\;,\ 3\;cm)$ tel que :
$\widehat{AOM}=30^{\circ}$, $R$ un point du plan tel que $OARM$ est un parallélogramme.
Calcule l'aire de $OARM.$
(Tu peux projeter orthogonalement $M$ sur $[AO]).$
Exercice 18
$(\mathcal{C})$ est un cercle de diamètre $[AB]$, de rayon $r$, $(BX)$ est tangente à $(\mathcal{C})$ en $B.$
Une droite passant par $A$ coupe $(\mathcal{C})$ en $M$ et la tangente $(BX)$ en $T$, avec $\widehat{BAT}=a^{\circ}.$
Exprime $AM$, $MB$, $BT$, $AT$ à l'aide de $a$ et $r.$
Exercice 19
Construis le triangle $ABC$ rectangle en $A$ tel que $AB=8\;cm$ et $AC=6\;cm.$
1) Calcule $BC$, $\cos\widehat{ABC}$, $\sin\widehat{ABC}$ puis $\tan\widehat{ABC}.$
2) Place le point $M$ sur le segment $[AB]$ tel que :
$AM=\dfrac{1}{3}AB.$
3) La parallèle à $(BC)$ passant par $M$ coupe $(AC)$ en $N.$
Calcule $AN.$
4) Soient $O$ et $P$ les symétriques respectifs des points $M$ et $N$, par rapport à $A.$
Montre que $(MN)$ est parallèle à $(OP).$
Exercice 20
$ABC$ est un triangle rectangle en $B.$
$H$ est le pied de la hauteur issue de $B.$
On note $\alpha$ la mesure de $B̂CA.$
On donne :
$\sin(\alpha)=\dfrac{\sqrt{5}}{3}\;;\ BH=\dfrac{\sqrt{5}}{2}$ et $AC=\sqrt{5}.$
1) a) Sachant que $\cos^{2}(\alpha)+\sin^{2}(\alpha)=1$, calcule $\cos(\alpha).$
b) Déduis-en $HC$ et $AB.$
2) Une droite $(\Delta)$ parallèle à $(BC)$ et passant par $H$ coupe $[AB]$ en $E.$
a) Compare les mesures des angles $\widehat{EHA}$ et $\widehat{BCA}.$
b) Déduis-en que $$\dfrac{AB}{BC}=\dfrac{EA}{EH}$$
Exercice 21
1) Soit un triangle $ABC$ rectangle en $A$ tel que $AB=8\;cm$ et $AC=4\;cm.$
Calcule $BC.$
2) Soit $H$ le projeté orthogonal de $A$ sur $[BC].$
On donne $AB^{2}=BH\times BC$ et $AC^{2}=CH\times BC$
a) Calcule $BH$, $CH$ puis $AH.$
b) La parallèle à $(AH)$ passant par $C$ coupe $(AB)$ en $E.$
Calcule $AE$ puis déduis-en $EC.$
c) Calcule $\sin\widehat{E}.$
Exercice 22
On donne la figure ci-dessous où $HG=6\;cm$, $\widehat{EGH}=45^{\circ}$, $\sin\widehat{HFG}=\dfrac{3}{5}$, $(GH)$ est la hauteur du triangle $EFG$ issue de $G\ $ et $\ (HG)$ parallèle à $(ER).$
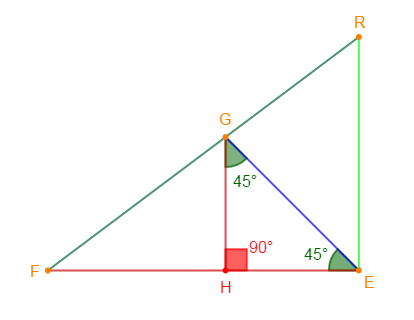
1) Détermine $\cos\widehat{HGF}.$
2) En utilisant les relations trigonométriques dans le triangle rectangle, calcule les longueurs $FG$ et $FH.$
3) Justifie que le triangle $EGH$ est rectangle et isocèle en $H$ puis déduis-en $EH.$
4) Calcule la longueur $RE.$
Exercice de Synthèse
Soit $ABC$ un triangle rectangle en $B$ et $AC$ l'hypoténuse, $\sin\widehat{A}$ est égal :
a) $\dfrac{AC}{BC}$ b) $\dfrac{AB}{AC}$ c) $\dfrac{BC}{AC}$

Commentaires
WADE (non vérifié)
sam, 11/10/2018 - 20:14
Permalien
intéressant
CHERIF BA (non vérifié)
lun, 12/02/2019 - 18:02
Permalien
SALUT
CHERIF BA (non vérifié)
lun, 12/02/2019 - 18:02
Permalien
SALUT
CHERIF BA (non vérifié)
lun, 12/02/2019 - 18:02
Permalien
SALUT
CHERIF BA (non vérifié)
lun, 12/02/2019 - 18:02
Permalien
SALUT
CHERIF BA (non vérifié)
lun, 12/02/2019 - 18:02
Permalien
SALUT
Anonyme (non vérifié)
lun, 12/02/2019 - 18:13
Permalien
Merci vous l'aurez bientôt
Anonyme (non vérifié)
sam, 07/11/2020 - 22:40
Permalien
Is good
Ajouter un commentaire