Série d'exercices : Amplificateur opérationnel : montages dérivateur et intégrateur - 1er s
Classe:
Première
Exercice 1
1) Représenter symboliquement un amplificateur opérationnel idéal.
2) Identifier ces montages suivant :
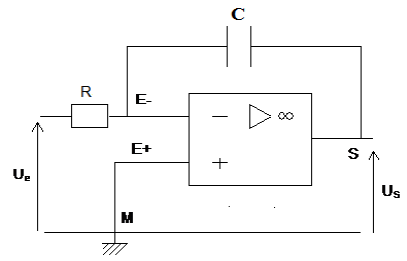
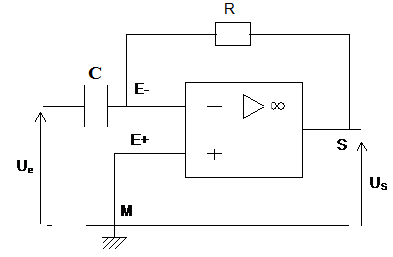
Exercice 2
Dans le montage ci-dessous, on donne $C=0.1\mu F$ ; $R=10\,K\Omega.$
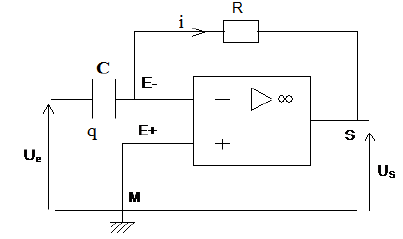
La tension appliquée à l'entrée $U_{e}$ est triangulaire de fréquence $N=50\,Hz$ et d'amplitude $U=1\,V$
1) Représenter sur de papier millimétrique les variations de la tension $U_{e}$ et de la tension $U_{s}$ à la sortie.
2) On branche à la sortie entre $S$ et la masse un résistor de résistance $R_{s}=10\Omega$
Représenter les variations de l'intensité du courant dans ce résistor
Exercice 3
On réalise un montage comportant un amplificateur opérationnel.
L'amplification opérationnel est supposé parfait et fonctionne en régime linéaire.
A l'entrée du dispositif, on applique la tension $U_{e}(t)$ en créneau de période $10\,ms$ et d'amplitude $0.1\,V$ (voir figure)
Représenter la tension de sorti $U_{s}$
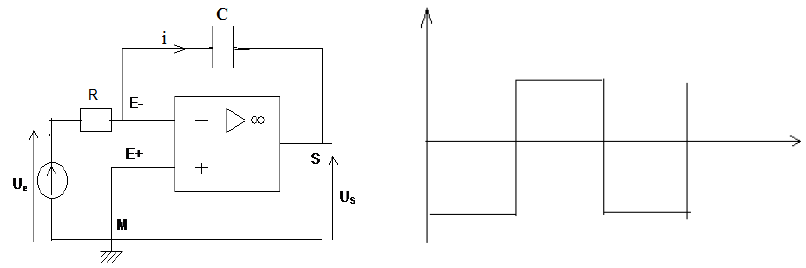
Exercice 4
1) Faire le schéma d'un montage intégrateur comportant :
$-\ $ Un amplificateur opérationnel
$-\ $ Un résistor de résistance $R=20\,k\Omega$
$-\ $ Un condensateur de capacité $C+10\,Nf$
2) On applique à l'entrée du montage la tension en créneau périodique de période $4\,ms$ et d'amplitude $6\,V$ représenter graphiquement les variations de $U_{s}(t).$
Exercice 5
On réalise le montage de la figure 1.
$L'A.O$ est considéré comme idéal
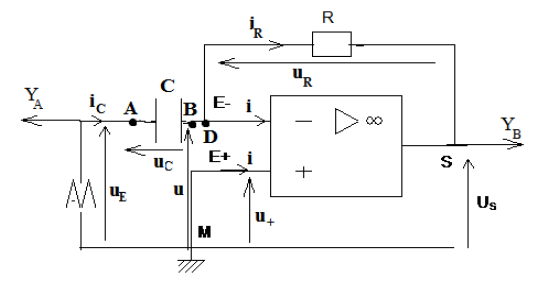
1. Pour établir l'expression liant $u_{s}$ à $\dfrac{\mathrm{d}u_{C}}{\mathrm{d}t}$ :
1.1 En appliquant la loi des nœuds en $D$, monter $i_{R}=i_{C}$
1.2 si $q$ désigne la charge du condenseur à un instant de date $t$ quelconque, exprimer $i_{R}$ en fonction $\dfrac{\mathrm{d}q}{\mathrm{d}t}$
En déduire l'expression liant $i_{R}$ à $u_{c}$ et à $C$
1.3 En appliquant la loi des tensions, établir que $u_{C}=-u_{R}$ et que $u_{E}=u_{C}$
1.4 A partir de la relation établie à la question 1.2 et des deux relations précédentes, et en appliquant la loi d'Ohm au conducteur ohmique, exprimer $u_{s}$ en fonction de $R$, $C$ et $\dfrac{\mathrm{d}u_{C}}{\mathrm{d}t}$
2. Un oscillographe mesure en voie $A$ la tension d'entrée $u_{E}$, et en voie $B$, la tension de sortie $u_{S}$
L'oscillogramme obtenu en voie $A$ est représenté sur la figure 2.
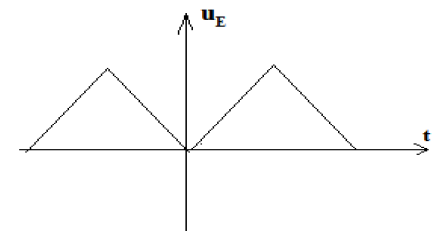
Dessiner l'oscillogramme obtenu en voie $B$
Données numériques $R=10\cdot10^{3}\Omega$, $C=1.0\mu F$
Sensibilité en voie $A$ : $2\,V\ div^{-1}$
Sensibilité en vois $B$ : $5\,V\ div^{-1}$
Durée par division du balayage : $2\,ms\ div^{-1}$
3. La tension d'entrée est maintenant une tension sinusoïdale de la forme : $u_{E}=u_{Em}\cos(2\pi\,Nt)$
$u_{E}$ désigne la valeur de la tension d'entrée à un instant de date $t$ quelconque
$u_{Em}$, sa valeur maximale : $50_{HZ}$
Donner les caractéristiques de la tension de sortie $u_{s}$
L'oscillographe étant branché et utilisé dans les mêmes conditions que précédemment, dessiner les oscillogrammes obtenus en vois $A$ et en voie $B.$
A l'origine des dates, le spot est à gauche de l'écran
Exercice 6
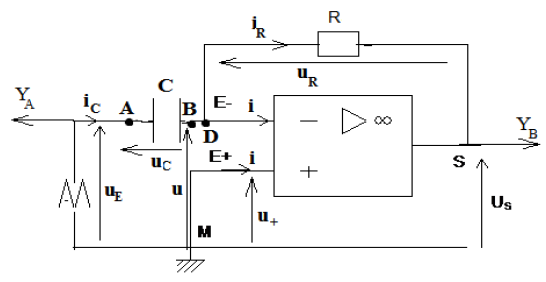
Soit le montage de la figure 1
$L'A.O$ est considéré comme idéal.
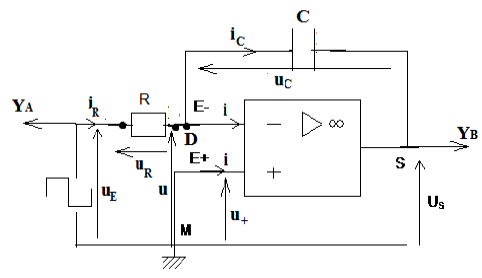
1. Afin d'établir une relation entre $\dfrac{\mathrm{d}u_{S}}{\mathrm{d}t}$ et $u_{E}.$
1.1 Appliquer la loi des nœuds en $D$ et montre que $i_{C}=i_{R}$
1.2 Si $q$ désigne la charge du condensateur à un instant de date $t$ quelconque, exprimer $i_{R}$ en fonction $\dfrac{\mathrm{d}q}{\mathrm{d}t}$
En déduire une relation entre $i_{R}$, $\dfrac{\mathrm{d}u_{C}}{\mathrm{d}t}$ et $C$
1.3 En appliquant la loi des tensions, établir que $u_{S}=-u_{C}$ et que $u_{R}=u_{E}$
1.4 A partir de la relation établie 1.2 et des relations précédentes, en appliquant la loi d'Ohm au conducteur ohmique, exprimer $\dfrac{\mathrm{d}u_{S}}{\mathrm{d}t}$ en fonction de $R$, $C$ et $u_{E}$
2. L'oscillographe électronique mesure en voie $A$ la tension d'entrée $u_{E}$ et en voie $B$, la tension de sortie $u_{S}$ ci-dessous.
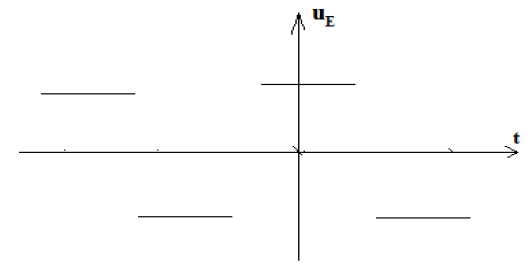
Données numériques $R=10\cdot10^{3}\Omega$ ; $C=1.0\mu F$
Sensibilité en vois $A$ : $2\,V\ div^{-1}$
Sensibilité en vois $B$ : $2\,V\ div^{-1}$
Durée par division du balayage : $5\,ms\ div^{-1}$
Note :
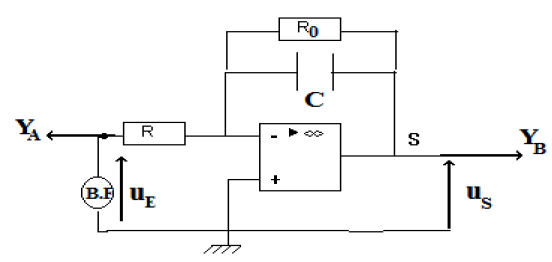
En fait pour pouvoir observer $u_{E}$ et $u_{S}$ à l'oscillographe, il est nécessaire réaliser le montage suivant :
2.1 Montrer que sur l'intervalle de temps $t\in\left[0\;,\ \dfrac{T}{2}\right]$, $u_{S}$ peut se mettre sous la forme : $u_{S}=-\dfrac{1}{RC}u_{Em}t+b$ où $u_{Em}$ est la valeur maximale de $u_{E}$ et $b$ une constante
2.2 Montrer que sur l'intervalle de temps $t\in\left[0\;,\ \dfrac{T}{2}\right]$, $u_{S}$ peut se mettre sous la forme : $u_{S}=-\dfrac{1}{RC}u_{Em}t+c$ où $u_{Em}$ est la valeur maximale de $u_{E}$ et $c$ une constante
2.3 Les segments de droite d'équations précédentes se raccordant en $\dfrac{T}{2}$, trouver une relation entre $b$ et $c$
Poser $b=0$, en déduire $c$
2.4 Déduire de l'étude précédente, l'oscillogramme obtenu en voie $B$
3. La tension $u_{E}$ est maintenant une tension sinusoïdale de la forme : $u_{E}=-U_{Em}\cos(2\pi\,Nt)$
$u_{E}$ est la valeur de la tension d'entrée à un instant de date quelconque
$u_{Em}$ est sa valeur maximale : $6.0\,V$
$N$, la fréquence : $50\,Hz$
3.1 Montrer que la valeur instantanée de la tension de sortie $u_{S}$ peut se mettre sous la forme : $u_{S}=-U_{Sm}\sin(2\pi\,Nt)+d$
$U_{Sm}$ est la valeur maximale de la tension de sortie, $d$ est une constante
Calculer $U_{Sm}.$
En supposant qu'à $t=0$, $u_{S}=0$, calculer $d$
3.2 Dessiner les oscillogrammes obtenus en voie $A$ et en voie $B$
A l'origine des dates $t=0$, le spot est à gauche de l'écran
Exercice 7
On utilise le montage ci-dessous.
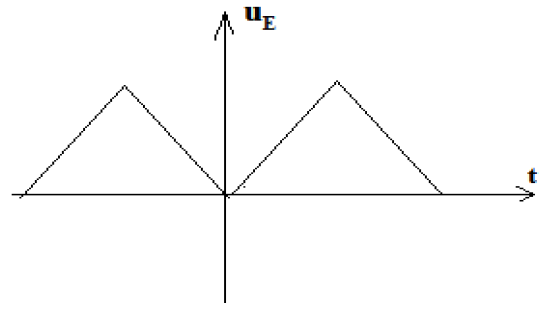
La tension $U_{E}$ est observé en voie $A$ d'un oscillographe électronique.
L'oscillogramme obtenu est représenté ci-dessous
La sensibilité utilisée en voie $A$ est $2\,V\ div^{-1}$
La durée par division de balayage est $\tau=10\,ms\ div^{-1}$
1) Rappeler l'expression qui lie $\dfrac{\mathrm{d}u_{E}}{\mathrm{d}t}$, $R$, $C$ et $u_{S}$
2) La tension de sortie $u_{S}$ étant observé en voie $B$ de l'oscillographe électronique, dessiner l'oscillogramme obtenu
Sensibilité en voie $B$ : $2\,V\ div^{-1}$

Commentaires
ADECHINAN TANGUY (non vérifié)
mar, 05/04/2021 - 20:30
Permalien
Je veux avoir la main en pct
Ajouter un commentaire