Vous êtes ici

Solution des exercices : La cinétique chimique - Ts

Classe:

Terminale

Exercice 1

Montrons que la concentration molaire restante de l'eau oxygénée est par :

$\left[H_{2}O_{2}\right]=C=C_{0}-\dfrac{2V_{0}}{V_{M}}$

Équation de la réaction s'écrit :

$2H_{2}O_{2}\ \rightarrow\ O_{2}+2H_{2}O$

D'après l'équation de la réaction :

$\begin{array}{lcl} \dfrac{n_{H_{2}O_{2}}}{2}&=&\dfrac{n_{O_{2}}}{1}\\&\Rightarrow&n_{H_{2}O_{2}}=2n_{O_{2}}\\&=&2\dfrac{V_{O_{2}}}{V_{M}} \end{array}$

Or $\begin{array}{lcl} n_{H_{2}O_{2}}\text{restant}&=&n_{H_{2}O_{2}}\text{initial}-n_{H_{2}O_{2}}\text{dissocié}\\&\Rightarrow&\left[H_{2}O_{2}\right]V=C_{0}V-\dfrac{2V_{O_{2}}}{V_{M}} \end{array}$

2 Tableau

$$\begin{array}{|c|c|c|c|c|c|c|} \hline t(min)&0&5&10&15&20&30\\ \hline V_{O_{2}}\left(10^{-3}L\right)&0&1.56&2.76&3.65&4.44&5.26\\ \hline C=\left[H_{2}O_{2} \right]&6&4.7&3.7&3.0&2.3&1.6\\ \left(10^{-2}mol/L\right)& & & & & &\\ \hline \end{array}$$

3) Tracé de la courbe $C=f(t)$

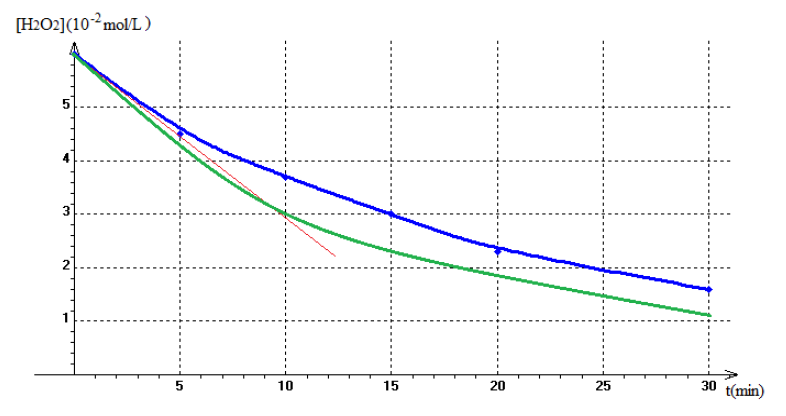
4) La vitesse instantanée de $H_{2}O_{2}$ est égale à l'opposé du coefficient directeur de la tangente à la courbe au temps considéré.

5) Tracé de la courbe pour une température supérieure à celle de la première expérience

Exercice 2

Exercice 3

1) Équation de la réaction d'oxydoréduction

Demi-équation : $2I^{-}\ \rightarrow\ I_{2}\ +\ 2e$

électronique : $S_{2}O_{8}^{2-}\ +\ 2e\ \rightarrow\ 2SO_{4}^{2-}$

Bilan : $2I^{-}\ +\ S_{2}O_{8}^{2-}\ \rightarrow\ I_{2}\ +\ 2SO_{4}^{2-}$

2) a) la vitesse de la réaction à date $t$ est égale à l'opposé du coefficient directeur de la tangente à la courbe à cette date.

b) Montrons que l'expression de la vitesse s'écrit sous la forme :

$v=-\dfrac{V}{2}\dfrac{d[I^{-}]}{dt}$

D'après l'équation-bilan de la réaction :

$\begin{array}{lcl} \dfrac{n_{I^{-}}}{2}&=&\dfrac{n_{S_{2}O_{8}^{2-}}}{1}-\dfrac{dn_{I^{-}}}{2dt}\\&=&-\dfrac{dn_{S_{2}O_{8}^{2-}}}{dt}\\&=&v\\&\Rightarrow&v=-\dfrac{dn_{I^{-}}}{2dt} \end{array}$

Or $\begin{array}{lcl} n_{I^{-}}&=&\left[I^{-}\right]V\\&\Rightarrow&v=-\dfrac{d\left[I^{-}\right]V}{2dt} \end{array}$

comme $V$ est constant $\Rightarrow v=-\dfrac{V}{2}\dfrac{d\left[I^{-}\right]}{dt}$

c) Cette vitesse diminue au cours du temps car la concentration des ions iodures diminue.

d) Détermination de la valeur maximale de la vitesse

$\begin{array}{lcl} v&=&-\dfrac{\left[I^{-}\right]_{6}-\left[I^{-}\right]_{0}}{t_{6}-t_{0}}\\&=&-\dfrac{(0-10\cdot 10^{-3})}{6-0}\\&\Rightarrow& v=1.67\cdot 10^{-3}mol\cdot L^{-1}min^{-1} \end{array}$

3) a) La vitesse moyenne d'une réaction correspond à la variation de la quantité de matière (nombre de môles ou concentration) pendant de temps donnée

Expression de la vitesse moyenne :

$v_{moy}=-\dfrac{\Delta\left[I^{-}\right]}{\Delta t}$

b) Calcul de la valeur de la vitesse moyenne entre les instants $t_{1}$ et $t_{2}$

$\begin{array}{lcl} v_{moy}&=&-\dfrac{\left(10\cdot 10^{-3}-16\cdot 10^{-3}\right)}{4-0}\\&\Rightarrow&v_{moy}=1.5\cdot 10^{-3}mol\cdot L^{-1}min^{-1} \end{array}$

4) Tableau descriptif d'évolution du système chimique

$$\begin{array}{|c|c|lccccr|} \hline \text{Système}&\text{Avancement}& &2I^{-}& &\ +\ S_{2}O_{8}^{2-}&\ \rightarrow\ I_{2}&\ +\ &2SO_{4}^{2-}&\\ \hline \text{initial}&x=0& &C_{1}V_{1}&|&C_{2}V_{2}&|&0&|&0\\ \hline \text{intermédiaire}&x& &C_{1}V_{1}-2x&|&C_{2}V_{2}-x&|&x&|&2x\\ \hline \text{final}&x_{max}& &C_{1}V_{1}-2x_{max}&|&C_{2}V_{2}-x_{max}&|&x_{max}&|&2x_{max}\\ \hline \end{array}$$

b) Détermination de la quantité de matière initiale $n_{0}(I^{-})$

$n_{0}(I^{-})=16\cdot 10^{-3}mol$

Valeur de $C_{1}$

$\begin{array}{lcl} n_{0}(I^{-})&=&C_{1}V_{1}\\&\Rightarrow&C_{1}=\dfrac{n_{0}\left(I^{-}\right)}{V_{1}}\\&=&\dfrac{16\cdot 10^{-3}}{200\cdot 10^{-3}}\\&\Rightarrow& C_{1}=8\cdot 10^{-3}mol\cdot L^{-1} \end{array}$

c)Le temps de demi-réaction est le temps au bout duquel la moitié de réactif limitant est consommée par la réaction.

Détermination de l'avancement final (maximale) de la réaction

$\begin{array}{lcl} \text{A }t_{1/2}&=&4\,min[I^{-}]\\&=&10\cdot 10^{-3}mol\cdot L^{-1}\\&\Rightarrow&x_{max}=2[I^{-}]V\\&=&2\times 10\cdot 10^{-3}\times(200+300)10^{-3} \end{array}$

d'où $\boxed{x_{max}=10^{-2}mol}$

d) Détermination du réactif limitant

Soient $x_{1}$ et $x_{2}$ les avancements maximums respectifs des réactifs

$I^{-}$ et $S_{2}O_{8}^{2-}$

$\begin{array}{lcl} C_{1}V_{1}-2x_{1}&=&0\\&\Rightarrow&x_{1}=\dfrac{C_{1}V}{2}\\&\Rightarrow&x_{1}=\dfrac{8\cdot 10^{-2}\times 200\cdot 10^{-3}}{2}\\&\Rightarrow&\boxed{x_{1}=8\cdot 10^{-3}mol} \end{array}$

$\begin{array}{lcl} C_{2}V_{2}-x_{2}&=&0\\&\Rightarrow&x_{2}=C_{2}V_{2}\\&\Rightarrow&x_{2}=10^{-2}\times 300\cdot 10^{-3}\\&\Rightarrow&\boxed{x_{2}=3\cdot 10^{-3}mol} \end{array}$

$x_{2}<x_{1}$ le peroxodisulfate de potassium est le réactif limitant

Exercice 4

1) Expression de la quantité de matière de dioxygène à l'instant $t$ en fonction de $V\left(O_{2}\right)_{t}$ et de $V_{m}$

$$n_{\left(O_{2}\right)_{t}}=\dfrac{V\left(O_{2}\right)_{t}}{V_{m}}$$

2) Tableau d'avancement de la réaction

$$\begin{array}{|c|c|ccccc|} \hline \text{Système}&\text{Avancement} &2H_{2}O_{2}(l) &\ \rightarrow\ &2H_{2}O(g)&\ +&\ O_{2}(g)\\ \hline \text{initial}&x=0&8\cdot 10^{-2}&|&0&|&0\\ \hline \text{intermédiaire}&x&8\cdot 10^{-2}-2x &|&2x&|&x\\ \hline \text{final}&x_{max} &8\cdot 10^{-2}-x_{max} &|&2x_{max}&|&x_{max} \\ \hline \end{array}$$

Valeur de l'avancement maximale

L'avancement est maximal lorsque $8\cdot 10^{-2}-2x_{max}=0$

$\Rightarrow\boxed{x_{max}=4\cdot 10^{-2}mol}$

3) Complétons le tableau de mesure

$x=\dfrac{V\left(O_{2}\right)_{t}}{V_{m}}$

$\begin{array}{lcl} \text{Pour }V\left(O_{2}\right)_{t}&=&0.2\,L\\&\Rightarrow&x=\dfrac{0.2}{24}\\&\Rightarrow&x=0.83\cdot 10^{-3}mol \end{array}$

d'où le tableau

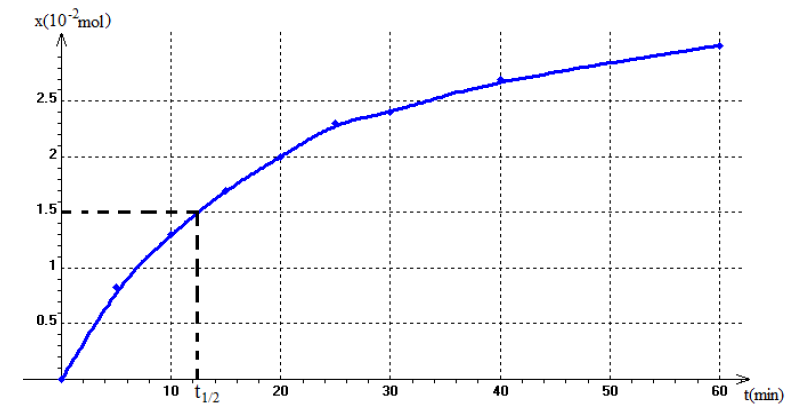
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline t(min)&0&5&10&15&20&25&30&40&60\\ V\left(O_{2}\right)_{t}&0&0.2&0.31&0.40&0.48&0.54&0.58&0.65&0.72\\ \hline x\left(10^{-2}mol\right)&0&0.83&1.3&1.7&2&2.3&2.4&2.7&3\\ \hline \end{array}$$

4) Tracé de la courbe $x=f(t)$

5) Vitesse moyenne de la réaction entre les $t_{1}$ et $t_{2}$

6) La vitesse instantanée de la réaction est égale ou coefficient directeur de la tangente à la courbe au temps considéré.

Cette vitesse de formation diminue au cours du temps (car la concentration du réactif diminue).

7) Temps de demi-réaction

$t_{1/2}=12.4\,min$

Taux d'avancement à cette date

$\begin{array}{lcl} \tau&=&\dfrac{x\left(t_{1/2}\right)}{x_{max}}\\&=&\dfrac{1.5\cdot 10^{-2}}{4\cdot 10^{-2}}\\&\Rightarrow&\tau=0.375\\&\Rightarrow&\boxed{\tau=37.5\%} \end{array}$

Exercice 5

1) a) calcule de la concentration initiale du mélange en ions peroxodisulfate

$\begin{array}{lcl} \left[S_{2}O_{8}^{2-}\right]&=&\dfrac{C_{1}V_{1}}{V_{1}+V_{2}}\\&=&\dfrac{0.05\times 30}{30+30}\\&\Rightarrow&\left[S_{2}O_{8}^{2-}\right]=2.5\cdot 10^{-2}mol\cdot L^{-1} \end{array}$

b) Tableau d'avancement

$$\begin{array}{|c|c|ccccccc|} \hline \text{Système}&\text{Avancement}&2I^{-}& &\ +S_{2}O_{8}^{2-}\ &\rightarrow\ I_{2}&\ &+\ &2SO_{4}^{2-}\\ \hline \text{initial}&x=0&C_{1}V_{1}&|&C_{2}V_{2}&|&0&|&0 \\ \hline \text{intermédiaire}&x &C_{1}V_{1}-2x&|&C_{2}V_{2}-x&|&x&|&2x\\ \hline \text{final}&x_{max} &C_{1}V_{1}-2x_{max}&|&C_{2}V_{2}-x_{max}&|&x_{max}&|&2x_{max} \\ \hline \end{array}$$

Montrons que $I^{-}$ est le réactif limitant

D'après l'équation de la réactif :

$n_{I^{-}}=2n_{I_{2}}=2\left[I_{2}\right]V$

avec $V=V_{1}+V_{2}$

$\begin{array}{lcl} \dfrac{n_{I^{-}}}{2}&=&\left[I_{2}\right]V\\&=&15\cdot 10^{-3}\times(30+30)10^{-3}\\&=&0.9\cdot 10^{-3}mol \end{array}$

$\begin{array}{lcl} \dfrac{n_{S_{2}O_{8}^{2-}}}{1}&=&C_{2}V_{2}\\&=&0.05\times 30\cdot10^{-3}\\&=&1.5\cdot 10^{-3}mol \end{array}$

$\dfrac{n_{I^{-}}}{2}<\dfrac{n_{S_{2}O_{2}^{2-}}}{1}$ $I^{-}$ est donc le réactif limitant

c) Détermination de la concentration initiale de

$\begin{array}{lcl} n_{I^{-}}&=&2n_{I_{2}}\\&=&2\left[I_{2}\right]V\\&\Rightarrow&\left[I^{-}\right]_{0}=\dfrac{n_{I^{-}}}{V}\\&=&2\left[I_{2}\right]\\&=&2\times 15\cdot 10^{-3}\\&\Rightarrow&\left[I^{-}\right]_{0}\\&=&3\cdot 10^{-2}mol\cdot L^{-1} \end{array}$

d) Détermination de la concentration $C_{1}$

$\begin{array}{lcl} C_{1}&=&\dfrac{n_{I^{-}}}{V_{1}}\\&=&\dfrac{1.8\cdot 10^{-3}}{30\cdot 10^{-3}}\\&\Rightarrow& C_{1}=6\cdot 10^{-3}mol\cdot L^{-1} \end{array}$

2) Détermination en $mole\cdot L^{-1}$, de la composition du mélange à l'instant $t_{1}=1000\,s$

$\begin{array}{lcl} \left[I^{-}\right]&=&\dfrac{C_{1}V_{1}-2x}{V}\\&=&\dfrac{C_{1}V_{1}-2\left[I_{2}\right]V}{V}\\&=&\dfrac{6\cdot 10^{-2}\times 30-2\times 2\cdot 10\cdot10^{-3}\times 60}{60}\\&\Rightarrow&\left[I^{-}\right]=10^{-2}mol\cdot L^{-1} \end{array}$

$\begin{array}{lcl} \left[S_{2}O_{8}^{2-}\right]&=&\dfrac{C_{2}V_{2}-x}{V}\\&=&\dfrac{C_{2}V_{2}-\left[I_{2}\right]V}{V}\\&=&\dfrac{0.5\times 30-10\cdot 10^{-3}\times 60}{60}\\&\Rightarrow&\left[S_{2}O_{8}^{2-}\right]=1.5\cdot10^{-2}mol\cdot L^{-1} \end{array}$

$\left[I_{2}\right]=10\cdot 10^{-3}mol\cdot L^{-1}$

$\left[SO_{4}^{2-}\right]=2\cdot 10\cdot 10^{-3}mol\cdot L^{-1}$

3) a Détermination de la vitesse moyenne de la réaction

$\begin{array}{lcl} V_{moy}&=&\dfrac{\Delta\left[I_{2}\right]}{\Delta t}\\&=&\dfrac{\left[I_{2}\right]_{t1}-\left[I_{2}\right]_{t2}}{t_{2}-t_{1}}&=&\dfrac{10\cdot 10^{-3}-0}{1000-0}&\Rightarrow&V_{moy}=10^{-5}mol\cdot L^{-1}\cdot s^{-1} \end{array}$

4) a) La vitesse instantanée de la réaction est égale au coefficient directeur de la tangente à la courbe au temps considéré.

b) La vitesse instantanée diminue au cours du temps car la concentration ne varie pas.

c) Détermination de la concentration initiale de $I^{-}$

$\begin{array}{lcl} v&=&\left(\dfrac{\mathrm{d}\left[I_{2}\right]}{\mathrm{d}t}\right)_{t1}\\&=&\dfrac{\left[I_{2}\right]_{t1}-\left[I_{2}\right]_{t2}}{t_{2}-t_{1}}\\&=&\dfrac{10\cdot 10^{-3}-5\cdot 10^{-3}}{1000-0}&\Rightarrow&v=5\cdot 10^{-6}mol\cdot L^{-1}\cdot s^{-1} \end{array}$

5) a) Équation de la réaction :

Demi-équations : $2S_{2}O_{3}^{2-}\ \rightarrow\ S_{4}O_{6}^{2-}\ +\ 2e$

électronique : $I_{2}\ +\ 2e\ \rightarrow\ 2I^{-}$

bilan : $2S_{2}O_{3}^{2-}\ +\ I_{2}\ \rightarrow\ S_{4}O_{6}^{2-}\ +\ 2I^{-}$

b) calcul de la concentration $C$

D'après l'équation de la réaction ;

$\begin{array}{lcl} n_{S_{2}O_{3}^{2-}}&=&2n_{I_{2}}\\&\Rightarrow&CV=2\left[I_{2}\right]V_{I_{2}}\\&\Rightarrow&C=\dfrac{2\left[I_{2}\right]V_{I_{2}}}{V}\\&=&\dfrac{2\times 10\cdot10^{-3}\times 5}{2}\\&\Rightarrow&C=5\cdot 10^{-2}mol\cdot L^{-1} \end{array}$

Exercice 6

1) Tableau d'avancement

$$\begin{array}{|c|c|ccccccccc|} \hline \text{Système}&\text{avancement}&5H_{2}O_{2}&+&2MnO_{4}^{-}&+&6H^{+}&\rightarrow\ 5O_{2}&+2Mn^{2+}&+&8H_{2}O\\ \hline \text{initiale}&x=0&4\cdot 10^{-2}&|&CV&||&0&|&0&|&\text{excès}\\ \hline \text{Intermédiaire}&x&4\cdot 10^{-2}-5x&|&CV-2x&||&5x&|&2x&|&\text{excès}\\ \hline \text{final}&x_{max}&4\cdot 10^{-2}-5x_{max}&|&CV-2x_{max}&||&5x_{max}&|&2x_{max}&|&\text{excès}\\ \hline \end{array}$$

L'avancement maximale correspond à $4\cdot 10^{-2}-5x_{max}=0$

$\Rightarrow\;x_{max}=\dfrac{4\cdot 10^{-2}}{5}$

$\Rightarrow\;x_{max}=8\cdot 10^{-3}$

2) a) la vitesse instantanée de disparition est à l'opposé du coefficient directeur de la tangente à la courbe à l'instant considéré

b) Détermination de la vitesse instantanée à la date $t=20\,min$

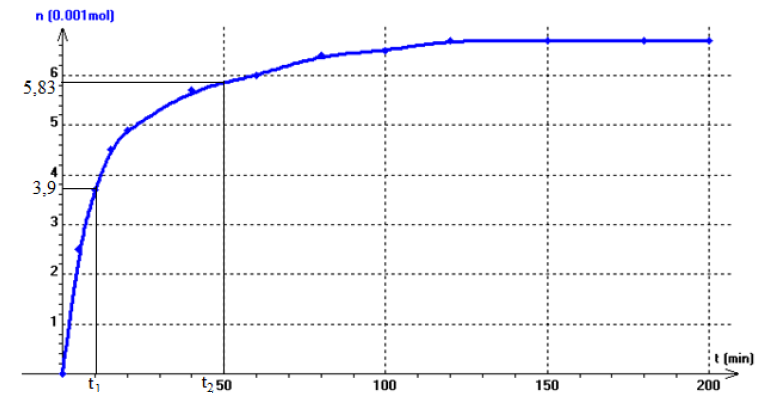
$\begin{array}{lcl} v&=&-\dfrac{\mathrm{d}n_{H_{2}O_{2}}}{\mathrm{d}t}\\&=&\dfrac{\left(0-3.35\cdot 10^{-2}\right)}{49-0}\\&\Rightarrow&v=6.8\cdot 10^{-4}mol\cdot L^{-1}\cdot min^{-1} \end{array}$

c) La vitesse diminue au cours du temps, car la quantité de matière de l'eau oxygénée diminue

3) La vitesse moyenne est égale à la variation du nombre de moles ou de la concentration par la variation de temps

$\begin{array}{lcl} V_{moy}&=&\dfrac{\Delta n_{H_{2}O_{2}}}{\Delta t}\\&=&\dfrac{2\cdot 10^{-2}-0}{20-0}\\&\Rightarrow&V_{moy}=10^{-3}mol\cdot L^{-1}\cdot min^{-1} \end{array}$

4) a) Le volume nécessaire pour le dosage

A la date $t=20\,min$, $n_{H_{2}O_{2}}=2\cdot 10^{-2}mol$

D'après l'équation bilan :

$\begin{array}{lcl} \dfrac{n_{MnO_{4}^{-}}}{2}&=&\dfrac{n_{H_{2}O_{2}}}{5}\\&\Rightarrow&\dfrac{CV}{2}\\&=&\dfrac{n_{H_{2}O_{2}}}{5}\\&\Rightarrow& V=\dfrac{2n_{H_{2}O_{2}}}{5C}\\&=&\dfrac{2\times 2\cdot 10^{-2}}{5\times 0.5}\\&\Rightarrow& V=16\,mL \end{array}$

b) Date à laquelle disparait $75\%$ de la quantité initiale de $H_{2}O_{2}$

$\begin{array}{lcl} H_{2}O_{2}n_{H_{2}O_{2}}&=&75\% n_{H_{2}O_{2}}\\&=&\dfrac{75\times 4\cdot 10^{-2}}{100}\\&=&3\cdot 10^{-2}mol \end{array}$

Cette date correspond l'abscisse d'ordonnée $n_{H_{2}O_{2}}=2\cdot 10^{-2}mol$

$\Rightarrow\;t=10\,min$

Exercice 7

1) Équation-bilan de la réaction

Demi-équations : $S_{2}O_{8}^{2-}\ +\ 2e\ \rightarrow\ 2SO_{4}^{2-}$

Électroniques : $2I^{-}\ \rightarrow\ I_{2}\ +\ 2e$

Bilan : $S_{2}O_{8}^{2-}\ +\ 2I^{-}\ \rightarrow\ 2SO_{4}^{2-}\ +\ I_{2}$

2) a) Description de l'expérience (à faire)

On peut reconnaitre expérimentalement le point d'équivalence par la disparition de couleur bleue due à l'action de l'amidon sur le diode

b) Calcule de la concentration molaire initiale des ions iodures $\left[I^{-}\right]_{0}$ et des ions peroxodisulfate $\left[S_{2}O_{8}^{2-}\right]_{0}$ dans le mélange réactionnel.

$\begin{array}{lcl} \left[I^{-}\right]_{0}&=&\dfrac{C_{1}V_{1}}{V_{1}+V_{2}}\\&=&\dfrac{16\cdot 10^{-2}\times 50}{50+50}\\&\Rightarrow&\left[I^{-}\right]_{0}=8\cdot 10^{-2}mol\cdot L^{-1} \end{array}$

$\begin{array}{lcl} \left[S_{2}O_{8}^{2-}\right]_{0}&=&\dfrac{C_{2}V_{2}}{V_{1}+V_{2}}\\&=&\dfrac{5\cdot 10^{-2}\times 50}{50+50}\\&\Rightarrow&\left[S_{2}O_{8}^{2-}\right]_{0}=2.5\cdot 10^{-2}mol\cdot L^{-1} \end{array}$

c) Tableau d'avancement

$$\begin{array}{|c|c|ccccccc|} \hline \text{Système}&\text{Avancement}&2I^{-}&+&S_{2}O_{8}^{2-}&\rightarrow\ &I_{2}\ &+&\ 2SO_{4}^{2-}\\ \hline \text{initiale}&x=0&C_{2}V_{2}&|&C_{1}V_{1}&|&0&|&0\\ \hline \text{Intermédiaire}&x&C_{2}V_{2}-2x&|&C_{1}V_{1}-x&|&x&|&2x\\ \hline \text{final}&x_{max}&C_{2}V_{2}-2x_{max}&|&C_{1}V_{1}-x_{max}&|&x_{max}&|&2x_{max}\\ \hline \end{array}$$

3) Montrons qu'à la date $t\left[I^{-}\right]_{t}=\left[I^{-}\right]_{0}-2y$

D'après le tableau d'avancement,

$\begin{array}{lcl} n_{1}&=&C_{2}V_{2}-2x\\&\Rightarrow&\left[I^{-}\right]_{t}\left(V_{1}+V_{2}\right)=C_{2}V_{2}-2x\\&\Rightarrow&\left[I^{-}\right]_{t}=\dfrac{C_{2}V_{2}}{\left(V_{1}+V_{2}\right)}-\dfrac{2x}{\left(V_{1}+V_{2}\right)} \end{array}$

Or $\left[I^{-}\right]_{0}=\dfrac{C_{2}V_{2}}{\left(V_{1}+V_{2}\right)}$

et $y=\dfrac{x}{\left(V_{1}+V_{2}\right)}$

d'où $\left[I^{-}\right]_{t}=\left[I^{-}\right]_{0}-2y$

4) a) Précisons le réactif limitant

Soient $x_{1}$ et $x_{2}$ respectivement les avancements finaux des réactif $S_{2}O_{8}^{2-}$ et $I^{-}$

$\begin{array}{lcl} C_{1}V_{1}-x_{1}=0\\&\Rightarrow& x_{1}=C_{1}V_{1}=5\cdot 10^{-2}\times 50\cdot 5\cdot 10^{-3}\\&\Rightarrow& x_{1}=2.5\cdot10^{-3}mol \end{array}$

$\begin{array}{lcl} C_{2}V_{2}-2x_{2}=0\\&\Rightarrow& x_{2}=\dfrac{C_{2}V_{2}}{2}\\&=&\dfrac{16\cdot 10^{-2}\times 50\cdot10^{-3}}{2} \\&\Rightarrow& x_{2}=4\cdot10^{-3}mol \end{array}$

$x_{2}>x_{1}.$

L'ion peroxodisulfate est le réactif limitant.

b) Déterminations de la concentration finale en ions iodures $x_{max}=x_{1}$

$\begin{array}{lcl} \left[I^{-}\right]_{f}&=&\dfrac{C_{2}V_{2}-2x_{1}}{V_{1}+V_{2}}\\&=&\dfrac{C_{2}V_{2}-2C_{1}V_{1}}{V_{1}+V_{2}} \end{array}$

$\begin{array}{lcl}\text{Or }V_{1}=V_{2}&\Rightarrow&\left[I^{-}\right]_{f}=\dfrac{C_{2}2C_{1}}{2}\\&=&\dfrac{16\cdot 10^{-2}-2\times 5\cdot 10^{-2}}{2}\\&\Rightarrow&\left[I^{-}\right]_{f}=3\cdot 10^{-2}mol\cdot L^{-1} \end{array}$

c) La vitesse d'une réaction chimique est à l'opposé du coefficient directeur de la tangente à la courbe au temps considéré

Montrons que s'écrit sous la forme $V_{vol}=-\dfrac{1}{2}\dfrac{\mathrm{d}\left[I^{-}\right]}{\mathrm{d}t}$

D'après l'équation de la réaction : $\dfrac{n_{S_{2}O_{8}^{4-}}}{1}=\dfrac{n_{I^{-}}}{2}.$

En passant aux petites variation, on obtient

$\dfrac{\mathrm{d}n_{S_{2}O_{8}^{4-}}}{\mathrm{d}t}=-\dfrac{\mathrm{d}n_{I^{-}}}{2\mathrm{d}t}$ ; puis en disant par $V$, il vient : $\dfrac{\mathrm{d}n_{S_{2}O_{8}^{4-}}}{V\mathrm{d}t}=-\dfrac{\mathrm{d}n_{I^{-}}}{2V\mathrm{d}t}=v_{vol}$

Or $n_{I^{-}}=\left[I^{-}\right]V\Rightarrow\;v_{vol}=-\dfrac{\mathrm{d}\left[I^{-}\right]V}{2V\mathrm{d}t}$ comme $V=\text{constant}\Rightarrow\;v_{vol}=\dfrac{V\mathrm{d}\left[I^{-}\right]}{2V\mathrm{d}t}$

$\Rightarrow\;v_{vol}=-\dfrac{1}{2}\dfrac{\mathrm{d}\left[I^{-}\right]}{\mathrm{d}t}$

La vitesse instantanée à la date $t=20\;min$

A $t=30\,min$ $\left[I^{-}\right]=\left[I^{-}\right]_{f}=3\cdot 10^{-2}mol\cdot L^{-1}$

et à $t_{0}=0\,min\left[I^{-}\right]=5.5\cdot 10^{-2}mol\cdot L^{-1}$

$\begin{array}{lcl} v&=&\dfrac{\left[I^{-}\right]_{f}-\left[I^{-}\right]}{t-t_{0}}\\&=&-\dfrac{3\cdot 10^{-2}-5.5\cdot10^{-2}}{30-0}\end{array}$

$\Rightarrow\;v=8.3\cdot 10^{-4}mol\cdot L^{-1}\cdot s^{-1}$

Exercice 8

1) Équation de la réaction d'estérification

$CH_{3}-COOH+CH_{3}-\left(CH_{2}\right)_{2}-CH_{2}OH$

$CH_{3}-COO-\left(CH_{2}\right)_{3}-CH_{3}+H_{2}O$

2) Tableau d'avancement

$$\begin{array}{|c|c|ccccccc|} \hline \text{Système}&\text{Avancement}&CH_{3}COOH&+&\ C_{4}H_{9}OH&\rightarrow&CH_{3}COOC_{4}H_{9}&+&H_{2}O\\ \hline \text{Initial}&x=0&a&|&a&|&0&|&0\\\hline \text{Intermédiaire}&x&a-x&|&a-x&|&x&|&x\\ \hline \text{Final}&x_{f}&a-x_{f}&|&a-x_{f}&|&x_{f}&|&x_{f}\\ \hline \end{array}$$

3) a) Expression de l'avancement $x$ en fonction de $a$, $C_{B}$ et $V_{BE}$

$-\ $ Équation de la réaction de dosage

$CH_{3}COH\ +\ OH^{-}\ \rightarrow\ CH_{3}COO^{-}\ +\ H_{2}O$

A l'équivalence :

$\begin{array}{lcl} n_{A}&=&n_{B}\\&\Rightarrow& x-a=C_{B}V_{BE}\\&\Rightarrow& x=a-C_{B}V_{BE} \end{array}$

b) Le taux d'avancement final

$\begin{array}{lcl}\tau_{f}&=&\dfrac{x}{a}&=&\dfrac{a-C_{B}V_{BE}}{a}\\&\Rightarrow&\tau_{f}=1-\dfrac{C_{B}V_{BE}}{a} \end{array}$

4) a) L'état d'équilibre du système est atteint à partir de la date $t=30\,min$

b) La réaction est :

$-\ $ limitée

$-\ $ réalisée entre au acide carboxylique et un alcool primaire (pourcentage $67\%$)

c) Expression de la constant d'équilibre $K$ en fonction de $\tau_{f}$

$\begin{array}{lcl} k&=&\dfrac{[ester][eau]}{[acide][alcool]}\\&=&\dfrac{x\times x}{(a-x)(a-x)} \end{array}$

Or $\tau_{f}=\dfrac{x}{a}\Rightarrow\;x=a\tau_{f}\Rightarrow$

$\begin{array}{lcl} k&=&\dfrac{a\tau_{f}\times a\tau_{f}}{\left(a-a\tau_{f}\right)\left(a-a\tau_{f}\right)}\\&\Rightarrow&k=\dfrac{a^{2}\tau_{f}^{2}}{a^{2}\left(1-\tau_{f}\right)\left(1 \tau_{f}\right)}\\&\Rightarrow&k=\dfrac{\tau_{f}^{2}}{\left(1-\tau_{f}\right)^{2}} \end{array}$

d) Détermination, en nombre de moles, de la composition du mélange à la date $t=30\,min$

$\begin{array}{lcl} R&=&\dfrac{x}{a}\\&\Rightarrow& x=Ra\\&\Rightarrow&n_{C_{4}H_{9}OH}=a-Ra\\&=&a(1-R)\\&=&1.33\cdot 10^{-3}(1-0.67) \end{array}$

$n_{C_{4}H_{9}OH}=4.4\cdot 10^{-3}mol$ ;

$n_{CH_{3}COOH}=n_{C_{4}H_{9}OH}=4.4\cdot 10^{-3}mol$

$\begin{array}{lcl} n_{CH_{3}COOC_{4}H_{9}}&=&n_{H_{2}O}\\&=&x\\&=&Ra\\&=&0.67\times 1.33\cdot 10^{-3}&\Rightarrow& n_{CH_{3}COOC_{4}H_{9}}\\&=&n_{H_{2}O}\\&=&8.9\cdot 10^{-3}mol \end{array}$

Le volume $V_{BE}$ versé à la date

$\begin{array}{lcl} \tau_{f}&=&\dfrac{a-C_{B}V_{BE}}{a}\\&\Rightarrow&a-C_{B}V_{BE}\\&=&a\tau_{f}\\&\Rightarrow& C_{B}V_{BE}=a-a\tau_{f}\\&=&a\left(1-\tau_{f}\right)\\&\Rightarrow& V_{BE}=\dfrac{a\left(1-\tau_{f}\right)}{C_{B}}\\&=&\dfrac{1.33\cdot 10^{-3}(1-067)}{1}&\Rightarrow& V_{BE}=4.4\,mL \end{array}$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye