Physique

Aspect corpusculaire de la lumière ; dualité onde-corpuscule - TL

 
Le modèle ondulatoire de la lumière explique bien les phénomènes de la diffraction et d'interférences lumineuses.
 
Mais d'autres découvertes, comme le spectre lumineux et l'effet photoélectrique ont montré l'insuffisance de la théorie ondulatoire de la lumière. 
 
On est amené à faire appel au modèle corpusculaire de la lumière
 
I. Effet photoélectrique
 
1. Mise en évidence expérimentale : Expérience de Hertz
 
fig183
 
fig184
 
Une lame de zinc fraichement décapée est placée sur un électroscope.
 
On éclaire cette plaque à l'aide d'une lampe à vapeur de mercure dont la caractéristique est d'émettre un rayonnement riche en radiations ultra-violettes.
 
L'électroscope chargé négativement se décharge progressivement (1).
 
En introduisant une plaque de verre, absorbant les radiations ultra-violettes $UV$ mais transparente aux radiations visibles, l'électroscope reste chargé même après une illumination prolongée (2).
                                                                  
2. Conclusion
 
Les électrons en excès sur la lame de $Zn$ sont arrachés au métal : c'est l'effet photoélectrique.
 
Cet effet ne se produit pas pour des rayonnements peu énergétiques comme la lumière visible (grandes longueurs d'onde) mais qu'avec les $UV$ (longueurs d'onde plus petites)
 
Une illumination prolongée de lumière visible ne permet pas d'« accumuler de l'énergie » pour extraire les électrons (contrairement à une succession de vagues qui pourraient finir par « casser une digue »). 
 
Ce phénomène, appelé photoélectrique, peut être observé avec d'autres métaux soumis à d'autres rayonnements.
 
De manière générale, on appelle effet photoélectrique, l'émission d'électrons par des métaux convenablement éclairés
 
II. La théorie d'Einstein
 
1. Hypothèse d'Einstein
 
En $1905$, Albert Einstein, pour expliquer l'effet photoélectrique, attribua une structure corpusculaire au rayonnement lumineux lui-même. 
 
Selon lui, tout rayonnement répartit son énergie sur un ensemble de particules élémentaires appelées photons (grains de photons ou grains de lumière)transportant chacun un quantum d'énergie, dont la valeur est proportionnelle à la fréquence qui lui est associée. 
 
Un photon est une particule qui possède une masse nulle, qui n'a pas de charge électrique se déplaçant en permanence à la vitesse de la lumière.
 
Une lumière de fréquence ν est constituée de grains d'énergie : constante
$$\boxed{E=hv\quad\text{ou}\quad E=\dfrac{hc}{\lambda}}$$
 
$E$ en joules $(J)$
 
fig185
 
Selon Einstein, l'absorption d'un photon, permettait d'expliquer parfaitement l'effet photoélectrique. 
 
Les photons de la source lumineuse possèdent une énergie caractéristique déterminée par la fréquence de la lumière. 
 
Lorsqu'un électron du matériau absorbe un photon et que l'énergie de celui-ci est suffisante, l'électron est éjecté; sinon l'électron ne peut s'échapper du matériau.
 
2. Le phénomène seuil
 
Une masse métallique est formée d'ions positifs disposés de façon régulière entre circulent les électrons. 
 
Ces électrons restent dans la masse métallique liés aux réseaux d'ions. 
 
Un électron ne peut sortir de la masse métallique que s'il acquiert une énergie minimale $E_{0}$ dite énergie d'extraction $$\2boxed{E_{0}=hv_{0}=\dfrac{hc}{\lambda_{0}}}$$
 
$v_{0}$ est la fréquence seuil caractéristique du métal ;
 
 
$\lambda_{0}$ Est la longueur d'onde seuil caractéristique du métal.
 
Si le photon incident a une énergie supérieure à l'énergie d'extraction (ou travail d'extraction), le surplus d'énergie se trouve sous forme d'énergie cinétique pour l'électron
 
$\begin{array}{rcl} E_{c}=E-E_{0}\\&\Rightarrow&\boxed{E_{c}=h\left(v-v_{0}\right)}\\&\text{ou}&\boxed{E_{c}=hc\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda_{0}}} \end{array}$
 
3. Application de l'effet photoélectrique
 
Le soleil est une source d'énergie inépuisable, l'exploitation de son rayonnement pour produire de l'électricité a été possible par la compréhension de l'effet photoélectrique : un panneau photovoltaïque convertit une partie de l'énergie lumineuse du soleil en énergie électrique
 
4. Dualité onde-corpuscule 
 
La lumière se présente sous aspects :
 
$-\ $un aspect corpusculaire où la lumière est formée de corpuscules appelés photons animés de la célérité de la lumière et transportant un quantum d'énergie
 
$-\ $un aspect ondulatoire où la lumière est considérée comme un phénomène vibratoire se propageant par onde
 
(La lumière a un comportement double : selon les circonstances, elle se comporte comme une onde ou comme un faisceau de particules .On parle de dualité onde-corpuscule)

Généralités sur les signaux et ondes mécaniques - TL

Classe: 
Terminale
 

I. Signal  

1. Exemple d'un signal mécanique non entretenu

Une corde élastique $AB$ est tendue. 
 
On veut envoyer un message de $A$ vers $B.$
 
Pour cela, on soulève et descend rapidement l'extrémité $A$, puis on la ramène à sa position initiale. 
 
Après un certain intervalle de temps, la personne en $B$ ressent la secousse produite en $A$ (schéma ci-dessous)
 

 
On dit qu'un signal s'est propagé le long de la corde

2. Définitions

Un signal est une déformation ou ébranlement de courte durée émise par une source et reçue par un récepteur.
 
$\bullet\ $La corde qui permet de transmettre le signal constitue le milieu de propagation 
 
$\bullet\ $La personne en $A$ qui crée le signal s'appelle l' émetteur ou la source
 
$\bullet\ $La personne en $B$ est le récepteur du signal.
 
$\bullet\ $La direction et le sens dans lesquels le signal se déplace constituent la direction et le sens de propagation

II. Ondes mécaniques progressives 

1. Observations 

Lorsque l'on jette un caillou sur la surface parfaitement calme et plane de l'eau d'un lac, on crée une perturbation : une ou plusieurs petites vagues circulaires se forment, dont le diamètre grandit. 
 
Cette perturbation se propage dans le milieu aquatique. 
 
Au bout de quelques instants le calme revient, la perturbation est passée
 
Une perturbation qui se propage dans un milieu matériel s'appelle une onde mécanique
 
Cette perturbation peut modifier la position d'un objet lors de son passage : elle possède donc de l'énergie. 
 
Ensuite, l'objet déplacé retourne à sa place initiale : l'onde ne le transporte pas avec elle.
 

Exemple

Le bateau bouge localement verticalement mais revient à sa position initiale après passage de l'onde
 

2. Définition 

On appelle onde mécanique progressive le phénomène de propagation d'une perturbation (ou d'une déformation) dans un milieu élastique, sans transport de matière, mais avec transport d'énergie.

Exemples d'ondes progressives

Onde le long d'une corde
 
Ondes rectiligne, 
 
Onde circulaire à la surface d'un liquide
 
Onde sonore

Remarque

Une onde est une série de signaux qui se suivent à des intervalles de temps réguliers 

4. Propriétés des ondes mécaniques 

4.1. Vitesse de propagation 

4.1.1. Définition

La célérité ou vitesse de propagation d'une onde mécanique correspond à la vitesse à laquelle se propage une onde mécanique dans un milieu matériel donné.

4.1.2. Expression de la vitesse de propagation 

Une perturbation, créée en un point source $S$, atteint le point $A$ de l'espace à la date $t_{A}$ et le point $B$ à la date $t_{B}$
 
 
Le décalage temporel entre ces instants est appelé retard et noté $\Delta t.$ 
 
Il s'exprime en seconde dans le système international.
 
Le retard $\Delta t$ est la durée nécessaire à l'onde progressive pour parcourir la distance $d$ entre $2$ points $A$ et $B$ du milieu de propagation : $\Delta t=t_{B}-t_{A}$
 
Pendant cette durée $\tau$, la perturbation a parcouru la distance $d.$
 
L'onde se propage alors à la célérité (vitesse de propagation) :$$\boxed{V=\dfrac{d}{\Delta t}}$$
 
$d$ en mètres $(m)$ ;
 
$\Delta t$ en secondes $(s)$ et  
 
$V$ en mètres par secondes $\left(m\cdot s^{-1}\right)$

4.2.3. Propriétés

$\bullet\ $Dans un milieu homogène, la célérité est la même en tout point 
 
$\bullet\ $Dans un milieu isotrope la célérité est la même dans toutes les directions.
 
La célérité d'une onde dépend du type d'onde et également du milieu de propagation.
 
Plus le milieu est rigide (difficile à déformer) plus la célérité est grande. 
 
Dans un gaz, plus les particules du milieu sont légères, plus la célérité est grande.

 

Auteur: 
Sidy Mouhamed Ndiaye

Énergie nucléaire : réactions spontanées, fusion et fission - TL

Classe: 
Terminale
 

I. Le noyau 

1. Constituants du noyau 

Le noyau d'un atome est formé de particules appelés nucléons qui sont de deux sortes : les protons et les neutrons.
 
Le proton est une particule de masse $m_{p}=1.672\cdot 10^{-27}kg$ et de charge $q_{p}=1.6\cdot 10^{-19}C$
 
Le neutron est une particule de masse $m_{n}=1.674\cdot 10^{-27}Kg$ sensiblement et de charge nulle.

2. Nucléide

On appelle nucléide la famille de noyaux caractérisés par un nombre donné de protons et un nombre donné de neutrons. 
 
 
Les noyaux d'un nucléide ont :
 
$-\ $le même nombre de masse $A$
 
$-\ $le même de charge $Z$
 
On le représente par : $_{Z}^{A}X$ où $X$ est le symbole de l'élément   

Exemples : 

$_{1}^{1}H$, $_{2}^{4}He$, $_{6}^{12}C$, $_{8}^{16}O$, $_{1}^{2}H$, $_{1}^{3}H$, $_{7}^{14}N$, $_{26}^{56}Fe$, $_{9}^{19}F$,

3. Isotopie

Des atomes possédant le même numéro atomique, (même nombre de protons) mais de masse atomique différente (nombre différent de neutrons) sont appelés isotopes.

4. Énergie de masse

4.1. Formule d'Einstein 

Elle s'exprime l'équivalence entre la masse et l'énergie :$$\boxed{E=mc^{2}}$$
 
$E$ en joules $(J)$
 
$m$ en mètres $(m)$
 
$c$ en mètres par seconde $\left(m\cdot s^{-1}\right)$

4.2. Défaut de masse

La masse du noyau $m_{X}$ est toujours inférieure à la masse des nucléons qui le constituent $$\boxed{\Delta m=Zm_{p}+(A-Z)m_{n}-m_{X}}$$ 
 
La différence de masse est appelée défaut de masse.
 
On appelle défaut de masse d'un noyau, la différence entre la masse des nucléons séparés au repos et la masse du noyau du noyau au repos.

4.3. Unité de masse atomique

Le kilogramme $(kg)$ n'est pas pratique d'utilisation à l'échelle microscopique. 
 
On utilise alors une unité plus appropriée : l'unité de masse atomique.
 
L'unité de masse atomique $($symbole : $u)$ est le douzième de la masse d'un atome de carbone 
 
$\begin{array}{rcl} 1u&=&\dfrac{1}{12}\dfrac{12\cdot 10^{-3}}{N_{A}}\\&=&\dfrac{10^{-3}}{N_{A}}\dfrac{10^{-3}}{6.02\cdot 10^{23}}\\\Rightarrow\boxed{1u\approx 1.66\cdot 10^{-27}kg} \end{array}$
 
En première approximation, les masses des noyaux sont voisines de multiple entier de la masse atomique 

Exemple :  

$M\left(_{17}^{35}Cl\right)=34.958u\approx35u$

5. Stabilité du noyau

5.1. Énergie de liaison : relation d'Einstein

On appelle énergie de liaison d'un noyau, l'énergie qu'il faut fournir à un noyau au repos pour le dissocier en nucléons séparés au repos 
 
Pour un noyau $_{Z}^{A}X$ $$\boxed{E_{l}=\left(Zm_{p}+(A-Z)m_{n}-m_{X}\right)c^{2}}$$   
 
On exprime également l'énergie de liaison du noyau en mégaélectronvolt $(MeV)$

Remarque

On peut alors exprimer les masses en leur équivalent énergétique d'après la relation précédente $1u=931.MeV/c^{2}$
$$\begin{array}{|l|c|c|c|} \hline\text{particules}&p^{+}&n^{0}&e^{-}\\ \hline \text{charge}&+e&0&-e\\ \hline m(u)&1.0073u&1.0087u&0.55^{\ast}10^{-3}u\\ \hline m\left(MeV/c^{2}\right)&938.280&939.573&0.511003\\ \hline \end{array}$$
 
De manière générale, à toute variation de masse d'un système correspond une variation d'énergie :$$\boxed{\Delta E=\Delta mc^{2}}$$
 
Cette relation constitue la relation d'Einstein 

5.2. Énergie de liaison par nucléon

Pour comparer les différents noyaux entre, on définit l'énergie de liaison par nucléon. 
 
C'est l'énergie à fournir à un noyau pour lui arracher un nucléon $$\boxed{E_{A}=\dfrac{E_{1}}{A}}$$

5.3. Stabilité du noyau : courbe d'Aston

 
Ce graphe donne les valeurs moyennes de l'énergie de liaison par nucléon $E_{1}$ en fonction du nombre de masse $A$ : cette est appelée courbe d'Aston
 
$\bullet\ $Pour les noyaux dont le nombre de masse est compris entre $50$ et $80$, la courbe présente un minimum aplati qui correspond aux noyaux les plus stables $\left(E_{A}=-8.7eV\right).$
 
$\bullet\ $Les extrémités de la courbe correspondent aux   noyaux instables :
 
$-\ $un noyau lourd $(A\succ 100)$ peut se casser en des noyaux stables pour gagner en stabilité
 
$-\ $des noyaux légers, pour gagner en stabilité, peuvent s'unir pour donner des noyaux stables.
 
Il existe, d'après la courbe d'Aston, deux façons possibles d'extraire de l'énergie : ou bien fusionner des noyaux légers ou fissionner des noyaux lourds pour avoir des noyaux stables

II. La radioactivité 

Les noyaux contiennent des protons chargés positivement, qui devraient se repousser d'après l'interaction électromagnétique. 
 
Pour expliquer la cohésion des noyaux, on admet l'existence d'une interaction attractive qui unit l'ensemble des nucléons et qui prédomine (aux courtes distances) devant l'interaction électromagnétique : c'est l'interaction forte
 
Cependant, dans certains cas, la cohésion est insuffisante : les noyaux sont instables et se désintègrent spontanément : ils sont radioactifs 

1. Définition

La radioactivité est la désintégration spontanée d'un noyau en un autre noyau, accompagnée de l'émission de particules subatomiques et(ou) de rayonnement électromagnétique

2. Caractéristiques de transformations radioactives

Les transformations radioactives sont :
 
$\surd\ $Indépendantes de la nature des liaisons entre les atomes (combinaisonchimique) dont le noyau radioactif fait partie 

Exemples : 

$\left(UO_{2}\;,\ UF_{6}\ \longrightarrow\ U\text{ radioactif}\right)$
 
$\surd\ $indépendantes de paramètres usuels(pression, température, état physique : solide, liquide ou gazeux
 
$\surd\ $spontanées (elles se réalisent seules, sans intervention extérieure pour les déclencher)
 
$\surd\ $inéluctables (un noyau radioactif se désintègrera tôt ou tard, rien ne peut empêcher sa désintégration)
 
$\surd\ $aléatoires (si on « sélectionne » un noyau radioactif, il est impossible de prévoir l'instant de sa désintégration)

3. Évolution temporelle d'une substance radioactive 

3.1. Loi de désintégration radioactive

Si on étudie un seul noyau, on ne sait pas quand il va se désintégrer
 
Le noyau ne « vieillit » pas : la probabilité de désintégration ne dépend pas du temps.
 
On peut étudier un ensemble de noyaux afin de réaliser des statistiques.
 
La probabilité qu'un noyau radioactif se désintègre pendant un intervalle de temps est donnée par la relation $$\boxed{N=\dfrac{N_{0}}{2^{n}}}$$
 
Courbe de décroissance radioactive $$n\,T\ \longrightarrow\ N=\dfrac{N_{0}}{2^{n}}$$
 

4.2. La période radioactive

La période radioactive ou demi-vie est la durée nécessaire à la désintégration de la moitié des noyaux présents initialement dans l'échantillon $$\boxed{T=\dfrac{\ln 2}{\gamma}}$$

Remarque :

Le période a une signification complètement différente de celle que nous attribuons habituellement. 
 
Il ne s'agit pas d'un phénomène période 

4.3. Activité d'un échantillon radioactif 

L'activité d'une source est le nombre d'atomes désintégrés pendant l'unité de temps 
 
$$\boxed{A=\dfrac{A_{0}}{2^{n}}}\text{ avec }A_{0}=\gamma N_{0}$$
 
 
L'unité internationale de l'activité est le becquerel $\left(B_{q}\right).$
 
Le becquerel correspond à une désintégration par seconde. 
 
On utilise également une ancienne unité le curie $(Ci)$ $1Ci=3.7\cdot 10^{10}Bq$

3. Analyse du rayonnement radioactif

 
Un mélange de substances radioactives est placé dans une ceinte en plomb (le rayonnement traverse difficilement le plomb).
 
Une plaque photographique placée à la sortie du champ permet de détecter les impacts des rayonnements.
 
En présence d'un champ magnétique ou électrique, la plaque montre quatre impacts : $A$, $B$, $C$ et $D$
 
Les champs électrique et magnétique séparent donc les rayonnements en parties : trois déviés par les champs appelés $\alpha$, $\beta^{+}$, $\beta^{-}$ et un non dévié appelée $\lambda$

4. Les différents types radioactivités

4.1. Les lois de conservation

Lors des radioactivités $\alpha$ et $\beta$, un noyau père $X$ se transforme en un noyau fils $Y$ avec production de particules chargées $\left(\alpha\;,\ \beta^{+}\text{ ou }\beta\right)$
$$\begin{array}{ccc} _{Z}^{A}X\ \longrightarrow\ &_{Z}^{A'}Y&+\ _{z}^{a}Q\\ \text{Père}&\text{fils}&\text{particule} \end{array}$$
 
Les équations bilan doivent respecter (lois de Soddy) :
 
$\bullet\ $la conservation du nombre de masse (ou de nucléons) : $A=A'+a$
  
$\bullet\ $la conservation de la charge (c'est-à-dire du nombre de protons) : $Z=Z'+z$  
 
$\bullet\ $la conservation de l'énergie : $E_{\text{total}}\left(_{Z}^{A}X\right)=E_{\text{total}}\left(_{Z}^{A'}Y\right)+E_{\text{total}}\left(_{z}^{a}Q\right)$

Définitions

Caractéristiques

lois, période.

III. Rayonnement $\alpha$, $\beta$, $\gamma$

1. Radioactivité $\alpha$

1.1. Principe

La radioactivité $\alpha$ est la transformation spontanée d'un noyau en autre noyau accompagnée d'un noyau d'hélium
 
Le rayonnement $\alpha$ très dangereux mais peu pénétrant : arrêté par quelques $cm$ d'air ou une feuille de papier

1.2. Équation de la réaction désintégration 

$$\begin{array}{ccc}_{Z}^{A}X\ \longrightarrow\ &_{Z}^{A'}Y^{\ast}&+\ _{2}^{4}He\\ \text{Père}&\text{fils}&\text{particule }\alpha \end{array}$$ 
 
Comme toute réaction nucléaire, la désintégration $\alpha$ vérifie :
 
$-\ $la conservation du nombre de masse : $A=A'+4\ \Rightarrow\ A'=A-4$
  
$-\ $la conservation du nombre de charge :  $Z=Z'+2\ \Rightarrow\ Z'=Z-2$
 
Généralement le noyau fils, dans un état excité, se désexcite en émettant un rayonnement $\lambda$
 
L'équation-bilan de désintégration s'écrit finalement : $$_{Z}^{A}X\ \longrightarrow\ _{Z-2}^{A-4}Y\ +\ _{2}^{4}He\ +\ \lambda$$

Exemple :

$$_{92}^{238}U\ \longrightarrow\ _{90}^{234}Th\ +\ _{2}^{4}He$$

Remarque : 

le noyau fils se situe toujours « deux cases avant » le noyau père dans la classification périodique des éléments 

1.3. Bilan énergétique

La réaction se fait avec libération d'énergie (réaction exo énergétique). 
 
Cette énergie provient de la perte de masse $$\boxed{\Delta E=\left(m_{\lambda}+m_{\alpha}-m_{x}\right)c^{2}}$$

2. Radioactivité $\beta^{-}$

2.1. Principe

La radioactivité $\beta^{-}$ est la transformation d'un noyau en autre noyau accompagné de l'émission d'un électron et un antineutrino
 
L'antineutrino est une particule non chargée de masse nulle se déplaçant à la célérité de la lumière. 
 
Cette particule intervient dans le bilan de la réaction nucléaire de façon à assurer la conservation de l'énergie et de la quantité de mouvement.
 
L'antineutrino possède un pouvoir de pénétration extraordinaire $($arrêtés par $35$ années lumières de plomb $!)\ldots$ ce qui rend la détection très difficile.
 
Le rayonnement $\beta^{-}$ pénétrant (mais moins dangereux que le rayonnement $\alpha)$, arrêtées par plusieurs mètres d'air ou quelques $mm$ d'aluminium (plexiglas)

2.2. Équation de la réaction désintégration 

$\begin{array}{ccc} _{A}^{Z}X&\longrightarrow_{Z'}^{A'}Y^{\ast}&+_{-1}^{0}e\\ \text{Père}&\text{fils}&\text{particule }\beta^{-}\left(_{-1}^{0}e\right) \end{array}$
 
Le plus souvent dans un état excité, le noyau fils, se désexcite en émettant un rayonnement $\gamma$
 
L'équation-bilan de désintégration s'écrit finalement :
 
$_{Z}^{A}X\ \longrightarrow\ _{Z+1}^{A}Y\ + _{-1}^{0}e+\gamma+\overline{v}$

Exemple :

$_{15}^{32}P\ \longrightarrow\ _{16}^{32}S\ +\ _{-1}^{0}e\ +\ \overline{v}$
 
La désintégration $\beta^{-}$ se produit pour des nucléides instables trop riches en neutrons. 
 
Elle résulte de la désintégration, dans le noyau, d'un neutron qui se transforme en un proton avec émission d'un électron et d'un antineutrino :
 
$_{0}^{1}n\ \longrightarrow\ _{1}^{1}p\ +\ _{-1}^{0}e\ +\ \overline{v}$

Remarque : 

Le noyau fils se situe toujours « une case après » le noyau père dans la classification périodique des éléments

2.3. Bilan énergétique 

La réaction se fait avec libération d'énergie (réaction exo énergétique). 
 
Cette énergie provient de la perte de masse $$\boxed{\Delta E=\left(m_{y}+m_{\beta^{-}}-m_{x}\right)c^{2}}$$

3. Radioactivité $\beta^{+}$

3.1. Principe

La radioactivité $\beta^{+}$ est la transformation d'un noyau en autre noyau accompagné de l'émission d'un positron (ou positon) et un neutrino (antiparticule de l'antineutrino)
 
Le rayonnement possède $\beta^{+}$ le même pouvoir de pénétration que le rayonnement $\beta^{-}$

3.2. Équation de la réaction désintégration 

$\begin{array}{ccc} _{Z}^{A}X&\longrightarrow_{Z'}^{A'}Y^{\ast}&+_{1}^{0}e\\ \text{Père}&\text{fils}&\text{particule }\beta^{+}\left(_{1}^{0}e\right) \end{array}$
 
La désexcitation du noyau fils s'accompagne de l'émission du rayonnement $\gamma$
  
L'équation bilan de la désintégration s'écrit :$$\boxed{_{Z}^{A}X\ \longrightarrow\ _{Z'}^{A'}Y^{\ast}\ +\ _{1}^{0}e+v+\gamma}$$

Exemple : 

$_{15}^{30}P\ \longrightarrow\ _{14}^{30}Si\ +\ _{1}^{0}e+_{0}^{0}v+\gamma$
 
La radioactivité $\beta^{+}$ se produit pour des nucléides obtenus artificiellement au laboratoire. 
 
C'est pourquoi on la qualifie de radioactivité artificielle, elle est caractéristique des noyaux trop riches en protons. 
 
Elle résulte de la désintégration, dans le noyau, d'un proton qui se transforme en un neutron avec émission d'un positron et d'un neutrino :
 
$_{1}^{1}p\ \longrightarrow\ _{1}^{0}n\ +\ _{1}^{0}e+v$

3.3. Bilan énergétique 

L'énergie libérée lors de la désintégration $\beta^{+}$ s'écrit :$$\boxed{\Delta E=\left(m_{y}+m_{\beta^{+}}-m_{x}\right)c^{2}}$$

4. Radioactivité 

Le rayonnement $\gamma$ est l'émission d'un photon par un noyau lors du retour d'un état excité à l'état stable.
 
La radioactivité $\gamma$ accompagne souvent les radioactivités $\alpha$ et $\beta$

IV. Réactions nucléaires provoquées : fission et fusion

Les réactions nucléaires sont :
 
$\bullet\ $spontanées : elles relèvent de la radioactivité naturelle 
 
$\bullet\ $ou provoquées : elles sont dues aux bombardements des noyaux par des projectiles

1. Réaction de transmutation

1.1. Définition 

La transmutation est une réaction nucléaire provoquée au cours de laquelle un élément se transforme en un autre 
 
Les projectiles utilisés pour réaliser les transmutations sont divers :
 
$-\ $neutron : particule électriquement neutre
 
$-\ $proton ; particule $\alpha$ : particules électriquement chargés
 
Certains nucléides, crées par transmutation provoquée, sont instables ; leur désintégration en noyaux fils stables définit la radioactivité artificielle

Exemples

$_{7}^{14}N\ +\ _{2}^{4}He\ \longrightarrow\ _{8}^{17}O\ +\ _{1}^{1}H$
 
$_{3}^{7}Li\ +\ _{1}^{1}H\ \longrightarrow\ _{2}^{4}He\ +\ _{2}^{4}He$
 
$_{92}^{238}U\ +\ _{0}^{1}n\ \longrightarrow\ _{92}^{239}U\ +\ \gamma$

2. Fission nucléaire 

2.1. Définition

La fission est une réaction nucléaire provoquée au cours de laquelle un noyau lourd se scinde pour donner naissance à des noyaux plus légers
 

2.1. Bilan énergétique 

Les réactions de fission sont exo énergétiques, car elles s'accompagnent d'une diminution de l'énergie de masse des noyaux réagissant 
 
$\boxed{\Delta E=\Delta mc^{2}\quad\text{ou}\quad\Delta E=\Delta m\varepsilon_{u}\quad\text{avec}\quad\varepsilon_{u}=931.5MeV}$

Exemple

$_{92}^{235}U\ +\ _{0}^{1}n\ \longrightarrow\ _{42}^{95}Mo\ +\ _{57}^{139}La\ +\ 2_{0}^{1}n\ +\ 7_{-1}^{0}e$
 
$\boxed{\Delta m=m_{\text{produits}}-m_{\text{réactifs}}\ \Rightarrow\ \Delta E=\Delta m\varepsilon_{u}}$
 
$\boxed{\Delta E=\left(\left(m_{La}+m_{Mo}+2m_{n}+7m_{e}\right)-\left(m_{U}+m_{n}\right)\right)\varepsilon_{u}}$
 
$\begin{array}{rcl} \Delta E&=&\left(\left(94.8828+138.875+2\times 1.0087+7\times 0.0638\right)-\left(234.9935+1.0087\right)\right)\times931.5\\\Rightarrow\Delta E&=&-208MeV \end{array}$

2.2. Réaction en chaine

Une fission émet en moyenne $2.47$ neutrons. 
 
Ces neutrons sont susceptibles à leur tour d'engendrer d'autres fissions. 
 
Il en résulte une réaction en chaine. 
 
L'énergie dégagée devient très vite considérable, sans précaution la réaction en chaine conduirait à une explosion : on obtient l'effet d'une bombe $A$
 
Convenablement maitrisé dans un réacteur nucléaire : cette réaction en chaine peut constituer la source d'énergie nécessaire au fonctionnement des centrales nucléaires

2. Fusion 

2.1. Principe 

La fusion est une réaction provoquée au cours de laquelle des noyaux légers s'unissent pour donner un noyau plus lourd
 

2.2. Bilan énergétique 

Lors de ces réactions, le bilan de masse montre qu'il y a perte de masse, donc libération d'énergie.
 
L'énergie libérée par la fusion appelée aussi l'énergie thermonucléaire est à l'origine du rayonnement des étoiles et du Soleil. 
 
Lors de l'explosion des bombes thermonucléaires $($Bombe $H)$, l'énergie libérée est produite par une réaction de fusion non contrôlée 
 
Malheureusement aujourd'hui, on ne sait ni contrôler la réaction de fusion, ni construire des réacteurs qui produiraient cette énergie de manière régulée et continue
 
$\boxed{\Delta E=\Delta mc^{2}\quad\text{ou}\quad\Delta E=\Delta m\varepsilon_{u}\quad\text{avec}\quad\varepsilon_{u}=931.5MeV}$

Exercice d'application

On considère la réaction nucléaire suivante :
$_{1}^{2}H\ +\ _{1}^{1}\ \longrightarrow\ _{2}^{4}He\ +\ _{0}^{1}n$
 
Quelle énergie $($en $MeV)$ est libérée lors de la formation du noyau de l'hélium.
 
On donne les énergies de liaison par nucléon :
 
$-\ $pour le deutérium : $E\left(_{1}^{2}H\right)=1.10\,MeV$
 
$-\ $pour le tritium : $E\left(_{1}^{3}H\right)=2.83\,MeV$
 
$-\ $pour l'hélium : $E\left(_{1}^{4}He\right)=7.07\,MeV$

Solution

L'énergie libérée lors de la formation de l'hélium
 
$\begin{array}{rcl}\Delta E&=&\left(\left(m_{\alpha}+m_{n}\right)-\left(m_{D}+m_{T}\right)\right)c^{2}\\&=&m_{\alpha}c^{2}+m_{n}c^{2}-m_{D}c^{2}-m_{T}c^{2}\end{array}$
 
$\begin{array}{rcl} \text{Or}\;,\quad E_{1}&=&\left(Zm_{p}+\left(A-Z\right)m_{n}-m_{x}\right)c^{2}\\\Rightarrow\;m_{x}c^{2}&=&Zm_{p}c^{2}+\left(A-Z\right)m_{n}c^{2}-E_{1x} \end{array}$
 
$\begin{array}{rcl} \Delta E&=&2m_{p}c^{2}+2m_{n}c^{2}-E_{1\alpha}+m_{n}c^{2}-m_{p}c^{2}-2m_{n}c^{2}+E_{1T}-m_{p}c^{2}-m_{n}c^{2}+E_{1D}\\\Rightarrow\Delta E&=&E_{1\alpha}+E_{1T}+E_{1D}\\&=&4\times 7.07+3\times 2.83+2\times 1.01\\\Rightarrow\Delta E&=&-17.6MeV \end{array}$

L'énergie stellaire

V. Les applications

1. Centrales nucléaires

Le combustible d'une centrale nucléaire contient des atomes fissiles c'est-à-dire des atomes dont le noyau a la capacité de se casser sous l'action d'un neutron, et, ce faisant, de libérer une quantité considérable d'énergie. 
 
D'où le nom de « combustible » par analogie avec la matière fossile brûlée dans une centrale thermique classique. 
 
Les principaux atomes fissiles sont l'uranium $233$, l'uranium $235$, le plutonium $239$ et le plutonium $241.$
 
Seul l'uranium $235$ se trouve à l'état naturel.
 
C'est donc le plus souvent lui qui est utilisé comme combustible dans les centrales nucléaires. 
 

2. Datation

La datation par le carbone $14$ dans le temps, mais pas plus de $30.000\text{ ans.}$ 
 
D'autres nucléides tels que le potassium $_{19}^{40}K$ sont utilisés pour la datation

3. Traceur

Les isotopes de même élément ayant des propriétés chimiques identiques ; on ne modifie pas le comportement chimique d'un isotope stable en le remplaçant par un isotope radioactif. 
 
C'est le principe des traceurs et marqueurs radioactifs dont on connait de nombreuses applications.
 
$\bullet\ $En chimie, l'étude cinétique de certaines réactions s'appuie sur la mesure des rayonnements émis par des noyaux radioactifs.
 
Le marquage des molécules organiques par introduction par un atome de carbone $14$ en position connue est utilisé pour analyser les mécanismes réactionnels de la chimie organique
 
$\bullet\ $En biologie,certains phénomènes métaboliques sont étudiés par des types de marquage des mécanismes de biosynthèse
 
$\bullet\ $En médecine,les traceurs radioactifs sont utilisés à des fins diagnostics : étude du fonctionnement de la glande thyroïde à l'iode $131$, détermination de certaines anémies
 

Auteur: 
Sidy Mouhamed Ndiaye

Aspect ondulatoire de la lumière - TL

Classe: 
Terminale
 

I. Émission - Réception - Propagation de la lumière

1. Sources et récepteurs de lumière

1.1. Sources lumineuses

On appelle source de lumière tout corps ou dispositif qui émet de la lumière.
 
Il existe deux types de sources de lumière :
 
$-\ $les sources lumineuses réelles ou primaires sont celles qui produisent la lumière qu'elles émettent.

Exemple :

Les sources primaires naturelles : le Soleil, les étoiles, les lucioles.
 
Les sources primaires artificielles : la bougie et les lampes allumées.
 
$-\ $les sources lumineuses apparentes ou secondaires celles qui renvoient la lumière qu'elles reçoivent d'autres sources lumineuses.

Exemples : 

La lune, le miroir etc.

1.2. Récepteur de lumière

Un récepteur de lumière est un corps sensible à la lumière ou qui réagit à la lumière.

Exemples : 

l'œil, la photorésistance, la peau, la chlorophylle$\ldots$
 
Il existe deux types de récepteurs de lumière :
 
$-\ $les récepteurs naturels.

Exemples : 

l'œil, la chlorophylle, la peau$\ldots$
 
$-\ $les récepteurs artificiels.

Exemples : 

la pellicule photographique, la photorésistance ou $LDR$, les photopiles ou pilessolaires, le chlorure d'argent$\ldots$

2. Propagation rectiligne de la lumière : notion de faisceau et rayon lumineux

2.1. Propagation rectiligne de la lumière 

2.1.1. Expérience

Dans une salle obscure contenant de l'air, on place trois plaques en bois percé, entre une source de lumière

Exemple : 

une lampe et l'œil d'un observateur.
 
 

2.1.2. Observation

La lumière de la bougie n'atteint l'œil d'un observateur que si les trous sont alignés, ce qui indique que la lumière se propage selon une ligne droite.

2.1.3. Conclusion 

Dans un milieu de propagation transparent et homogène, la lumière se propage en ligne droite.
 
On parle de propagation rectiligne.

2.2. Rayon et faisceau lumineux

2.2.1. Rayon lumineux

On représente un rayon lumineux par une droite munie d'une flèche indiquant le sens de propagation.
 

2.2.2. Faisceau lumineux

On appelle faisceaux lumineux l'ensemble des rayons lumineux émis par une source primaire ou diffusés par une source secondaire
 
On distingue trois types de faisceaux lumineux :
 
$\bullet\ $Les faisceaux cylindriques : tous les rayons sont parallèles.
 
$\bullet\ $Les faisceaux convergents : tous les rayons arrivent au même point.
 
$\bullet\ $Les faisceaux divergents : tous les rayons partent d'un même point
 
 

3. Vitesse de propagation de la lumière 

3.1. Notion de la vitesse 

On définit la vitesse comme étant le quotient de la distance parcourue par la durée :$$V=\dfrac{d}{t}$$
 
La vitesse de la lumière dans le vide, notée $c$, appelée célérité de la lumière est une constante universelle.
 
Sa valeur est : $c=299792458\,m\cdot s^{-1}$
 
C'est une vitesse limite.
 
On utilise généralement pour la vitesse de la lumière dans le vide et dans l'air la valeur voisine : $C=3\cdot 10^{8}m\cdot s^{-1}$ 

Remarque :

La distance $(d)$ parcourue par un faisceau de lumière, dans un intervalle de temps $(t)$ est donnée par la formule suivante :$$d=c\times t$$

3.2. Année lumière 

Une année-lumière est une unité utilisée en astronomie pour exprimer les distances. 
 
Elle correspond à la distance parcourue par la lumière dans le vide pendant une année : $1\text{al}=9.46\times 10^{12}km.$
 
C'est une unité de longueur notée : $\text{al}.$

II. Réflexion, réfraction, diffraction de la lumière

1. Réflexion et réfraction

1.1. La réflexion de la lumière 

1.1.1. Observation

Lorsqu'une lumière provenant d'une source lumineuse tombe sur une surface plane et polie métallisée (miroir), une partie de cette lumière est renvoyée par la surface : c'est le phénomène de réflexion.
 

1.1.2. Définition 

La réflexion de la lumière est le changement de direction de la lumière lorsqu'elle atteint la limite entre deux milieux et retourne dans le milieu d'origine.

Remarque :

L'écho est le phénomène de réflexion d'une onde sonore sur une surface ou sur des inhomogénéités existant dans le milieu de propagation ; l'onde ainsi réfléchie.

1.2. La réfraction de la lumière 

 
Lorsqu'on envoie des rayons lumineux monochromatiques (Lasers) sur la surface libre de l'eau colorée avec de la fluorescéine, on constate que : 
 
$-\ $Une petite partie de la lumière est réfléchie. 
 
$-\ $Une majeure partie du faisceau pénètre dans l'eau avec un changement de direction : le faisceau semble brisé 
 
Le premier phénomène est celui de la réflexion partielle.
 
Le phénomène pour lequel la lumière change de direction lorsqu'elle passe d'un milieu transparent à un autre, s'appelle la réfraction.
 
 
Quand un rayon lumineux incident arrive au niveau du point d'incidence $I$ avec un angle d'incidence $i_{1}$ le rayon traverse la surface de séparation entre les deux milieux et le rayon réfracté repart avec un angle de réfraction $i_{2}.$

1.3. Les lois de la réflexion et de réfraction de la lumière 

Les phénomènes de réflexion et de réfraction sont régis par les lois de Snell-Descartes. 
 
$1^{ère}$ loi : 
 
Les rayons réfléchi et réfracté appartiennent au plan défini par le rayon incident et la normale à la surface de séparation (dioptre). 
 
$2^{ème}$ loi : 
 
Les angles d'incidence $i_{1}$ et de réflexion $r$ ont des valeurs identiques : $i_{1}=r$ 
 
$3^{ème}$ loi : 
 
Les angles d'incidence $i_{1}$ et de réfraction $i_{2}$ sont liés par la relation : $n_{1}\cdot\sin\,i_{1}=n_{2}\cdot\sin\,i_{2}$ Où $n_{1}$ et $n_{2}$ sont des nombres sans unité appelés indices de réfraction, qui caractérisent les milieux d'incidence et de réfraction.

III. Interférences lumineuses

Deux ondes de même de  fréquence se propageant dans le même milieu peuvent se superposer pour donner naissance aux phénomènes d'interférences.
 
Si la lumière est une onde, elle doit permettre d'obtenir un tel phénomène

1. Expérience des fentes de Young

1.1. Dispositif expérimental

Une source monochromatique intense éclaire un écran percé d'une fente $S.$ 
 
Cette fente donne naissance à un faisceau divergeant qui éclaire un second écran percé de deux fentes très fines et parallèles, $S_{1}$ et $S_{2}$, appelées fentes de Young.
 
Par le phénomène de diffraction, les deux fentes $S_{1}$ et $S_{2}$ se comportent comme des sources identiques divergentes. 
 
Un écran, placé parallèlement au plan des fentes, recueille la lumière issue de $S_{1}$ et $S_{2}$
 
 

1.2. Observations

On observe sur l'écran des zones alternativement sombres et claires appelées franges d'interférence.
 
Ces franges au voisinage du point de projection $S$ sur l'écran sont pratiquement rectilignes, parallèles, équidistantes et perpendiculaires au plan de la figure. 
 
Ces franges sont observées dans un champ d'interférence quelque soit la position de l'écran : on dit que ces franges sont délocalisées  
 
 

1.3. Interprétation 

L'existence des franges montre que sous certaines conditions la superposition de deux faisceaux lumineux peut :
 
$-\ $en certains points, accentuer le phénomène lumineux en donnant des franges brillantes
 
$-\ $en d'autres points, détruire le phénomène lumineux en donnant des franges sombres.
 
Le phénomène d'interférence peut s'interpréter si on suppose que les sources secondaires se comportent comme des sources de vibrations de même longueur d'onde.
 
En point $M$ de l'écran appartenant au champ d'interférence, les vibrations issues de $S_{1}$ et $S_{2}$ arrivent l'une par rapport l'autre avec un certain retard.
 
Il y a interférences constructives en un point de la zone d'interférences si la différence de marche en ce point est un multiple entier de la longueur d'onde : $\boxed{\delta=k\lambda\quad\left(k\in\mathbb{R}\right)}$
 
Le point $M$ est alors le milieu d'une frange brillante.
 
Il y a interférences destructives en un point de la zone d'interférences si la différence de marche en ce point est un multiple entier impair de la demi-longueur d'onde : $\boxed{\delta=\left(2k+1\right)\dfrac{\lambda}{2}\left(k\in\mathbb{R}\right)}$  
 
Le point $M$ est alors le milieu d'une frange sombre

2. Conditions d'interférences 

On ne peut obtenir d'interférences lumineuses avec des sources distinctes où on essaie de superposer les faisceaux.
 
Pour obtenir des franges d'interférences, il faut deux sources cohérentes
 
Deux sources sont cohérentes si :
 
$-\ $elles émettent des vibrations de même fréquence (même période).
 
On dit qu'elles sont synchrones 
 
$-\ $elles présentent une différence de phase constante 
 
$-\ $le rapport d'amplitude constant 

3. Interfrange

3.1. Différence de marche  

La différence de marche $(\text{notée }\delta)$ est la différence de distance parcourue par les deux ondes avant d'arriver au point $M$ $$\boxed{\delta=\dfrac{ax}{D}}$$

3.2. Position des franges

3.2.1. Position des milieux des franges brillantes

Les abscisses des milieux des franges brillantes sont tels que :$$\boxed{X_{k}=k\lambda\dfrac{D}{a}}$$

3.2.2. Position des milieux des franges sombres

Les abscisses des milieux des franges sombres sont tels que :$$\boxed{X_{k}=\left(2k+1\right)\dfrac{\lambda}{2}\dfrac{D}{a}}$$

3.3. Expression de l'interfrange

 
L'interfrange est la distance qui sépare deux franges consécutives de même nature $$\boxed{i=\lambda\dfrac{D}{a}}$$

Remarque :

L'ordre d'interférence en un point $M$ de l'écran où la différence de marche est $\delta$, est : $\boxed{p=\dfrac{\delta}{\lambda}}$ $\lambda$ étant la longueur d'onde de la radiation.
 
Si le point $M$ est le milieu d'une frange brillante, on a alors : $\boxed{p=\dfrac{\delta}{\lambda}=k}$
  
Les franges brillantes ont un ordre d'interférence entier.
 
Si le point $M$ est le milieu d'une frange sombre, on a alors : $\boxed{p=\dfrac{\delta}{\lambda}=k+\dfrac{1}{2}}$
 
Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Étude expérimentale des lentilles - 1er s

Classe: 
Première
 

Exercice 1 : Obtention de l'image d'un objet $AB$  par une lentille mince.

Construction de l'image de l'objet AB par la lentille mince
 
Cas $n^{\circ}1$ :
 
 
 
L'image est réelle, inversée(ou renversée) et réduite
 
Cas $n^{\circ}2$ :
 
 
 
L'image est virtuelle, droite et agrandie
 
Cas $n^{\circ}3$ :
 
 
 
L'image est virtuelle, droite et réduite
 
Cas $n^{\circ}4$ :
 
 
 
L'image est virtuelle, droite et réduite

Exercice 2

1. Plaçons les points $F$, $F^{\prime}$, $A$ et $B$
 
 
 
$NB$ : $1$ carreau pour $2\,cm$
 
2. Calcul de $\overline{OF}$, $\overline{OF}^{\prime}$ et $\overline{OA}$
 
$\overline{OF}=4.0\,cm$ ; 
 
$\overline{OF}^{\prime}=4.0\,cm$ et
 
$\overline{OA}=-10.0\,cm$
 
3. Détermination graphique l'image $A'B'$ de $AB$
 
$A'B'=1.4\,cm$
 
Caractérisation de l'image obtenue.
 
L'image obtenue est réelle, renversée, plus petite que l'objet et à droite du plan focal image
 
4. Déduction graphique $\overline{OA^{\prime}}$ et $\overline{A'B'}$
 
$\overline{OA^{\prime}}=6.8\,cm\quad\text{et}\quad\overline{A'B'}=-1.4\,cm$
 
5.  Retrouvons $\overline{OA^{\prime}}$  et  $\overline{A'B'}$ en utilisant la formule de conjugaison
 
$\begin{array}{rcl} \dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}&=&\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{OA'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{\overline{OA}}\\\Rightarrow\overline{OA'}&=&\dfrac{\overline{OA}f'}{OA+f'}\\&=&\dfrac{-10\times4}{-10+4}\\\Rightarrow\boxed{\overline{OA'}=6.7\,cm} \end{array}$
 
$\begin{array}{rcl} \dfrac{\overline{A'B'}}{\overline{AB}}&=&\dfrac{\overline{OA'}}{OA}\\\Rightarrow\overline{A'B'}&=&\dfrac{OA'}{\overline{OA}}\overline{AB}\\&=&\dfrac{6.7}{-10}\times2\\\Rightarrow\boxed{\overline{A'B'}=-1.34\,cm} \end{array}$
 
6. Calculons le grandissement de l'image
 
$\begin{array}{rcl} G&=&\dfrac{\overline{A'B'}}{AB}\\&=&\dfrac{-1.4}{2}\\\Rightarrow\boxed{G=-0.7} \end{array}$

Exercice 3

Un objet de grandeur $2.0\,cm$ est placé à $4.0\,cm$ cm d'une loupe, dans un plan perpendiculaire à l'axe principal de celle-ci ; la vergence de cette loupe est $C=20$ dioptries.
 
1. Calcul de la distance focale de cette loupe
 
$\begin{array}{rcl} C&=&\dfrac{1}{f}\\\Rightarrow\;f&=&\dfrac{1}{C}\\&=&\dfrac{1}{20}\\\Rightarrow\;f&=&0.05\,m\\\Rightarrow\boxed{f=5\,cm}\end{array}$
 
2. Construisons l'image de cet objet à travers la loupe à l'échelle $1/2.$
 
 
$NB$ : $1\,cm$ pour un carreau
 
a. Précisons sa nature, réelle ou virtuelle.
 
L'image est virtuelle 
 
b. Précisons son sens.
 
L'image est droite, c'est-à-dire même que l'objet
 
c. Mesurons sa position par rapport à la loupe.
 
$\begin{array}{rcl} \overline{A'B'}&=&4.8\times 2\\\Rightarrow\boxed{\overline{A'B'}=9.6\,cm} \end{array}$
 
d. Mesurons sa grandeur
 
$\overline{A'B'}=4.8\,cm$
 
Déduisons le rapport de la grandeur de l'image à celle de l'objet
 
$\begin{array}{rcl} G&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\&=&\dfrac{4.8}{2}\\\Rightarrow\boxed{G=2.4} \end{array}$

Exercice 4

1. Calcul de la vergence de la lentille et donnons son unité.
 
$\begin{array}{rcl} C&=&\dfrac{1}{f'}\\&=&\dfrac{1}{10\cdot10^{-2}}\\\Rightarrow\boxed{C=10\delta} \end{array}$
 
L'unité de la vergence est la dioptrie
 
2. a. Expérience simple pouvant permettre vérifier la distance focale de la lentille.
 
Pour vérifier la distance focale d'une lentille, il suffit construire l'image nette d'un objet à l'infini.
 
b. Critère de reconnaissance d'une lentille convergente.
 
Une lentille convergente est une lentille aux bords plus minces qu'au centre
 
3.a. Donnons la relation algébrique de Descartes (relation entre les positions de l'objet et de l'image)
 
La relation entre les positions de l'objet et de l'image est :
 
$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{f^{\prime}}$
 
b. Précisons les orientations sur un schéma.
 
 
 
c. Calcul numérique de $\overline{OA}$ et de $\overline{OA^{\prime}}$

$\overline{OA}=16\,cm$

 
$\begin{array}{rcl} \dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}&=&\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{OA'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{\overline{OA}}\\\Rightarrow\overline{OA'}&=&\dfrac{\overline{OA}\cdot f'}{\overline{OA}+f'}\\&=&\dfrac{-16\times10}{-16+10}\\\Rightarrow\boxed{\overline{OA'}=26.7\,cm} \end{array}$
 
4. L'objet est une petite flèche de hauteur $2.0\,cm$
 
Donnons la formule de Descartes du grandissement $\gamma$
 
$\gamma=\dfrac{\overline{OA'}}{\overline{OA}}$
 
Calcul de $\gamma$
 
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{OA'}}{\overline{OA}}\\&=&\dfrac{26.7}{16}\\\Rightarrow\boxed{\gamma=-1.7} \end{array}$
 
Déduisons la taille de l'image $\overline{A'B'}$
 
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\\Rightarrow\overline{A'B'}&=&\gamma\overline{AB}\\&=&-1.7\times2\\\Rightarrow\boxed{\overline{A'B'}=-3.4\,cm} \end{array}$

Exercice 5

1. Calcul :
 
De la position de l'image $A'B'$ de $AB$ à travers la lentille $L_{1}$
 
$\begin{array}{rcl} \dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}&=&\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{OA'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{OA}\\\Rightarrow\overline{OA'}&=&\dfrac{\overline{OA}\cdot}{\overline{OA}+f}\\&=&\dfrac{-20\times16}{-20+16}\\\Rightarrow\boxed{\overline{OA'}=80\,mm}\end{array}$
 
$\bullet\ $du grandissement de la lentille $L_{1}$ dans ces conditions.
 
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{OA'}}{\overline{OA}}\\&=&\dfrac{80}{-20}\\\Rightarrow\boxed{\gamma=-4} \end{array}$
 
$\bullet\ $la dimension (algébrique) de l'image $A'B'$
 
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\\Rightarrow\overline{A'B'}&=&\gamma\overline{AB}\\&=&-4\times5\\\Rightarrow\boxed{\overline{A'B'}=-20\,mm} \end{array}$
 
2. L'image $A'B'$ est réelle, renversée par rapport à $AB$
 
L'image est réelle car l'objet est placé derrière la lentille convergente (Cette image peut être recueillie sur un écran)
 
L'image est renversée car une lentille convergente donne d'un objet réel, placée derrière le foyer objet, une image renversée
 
3. Confirmons la position de l'image par une construction.
 
 

Exercice 6

Détermination, par le calcul, la position, la nature, le sens et la grandeur de l'image
 
a) L'objet est réel à $2\,m$ de la lentille
 
$\begin{array}{rcl} \overline{OA'}&=&\dfrac{\overline{OA}\cdot f}{\overline{OA}+f}\\&=&\dfrac{-2\cdot10^{2}\times25}{-2\cdot10^{2}+25}\\\Rightarrow\boxed{\overline{OA'}=28.6\,cm} \end{array}$
 
L'image est réelle et renversée par rapport à l'objet

Grandeur de l'image
 
$\begin{array}{rcl} \dfrac{\overline{A'B'}}{\overline{AB}}&=&\dfrac{\overline{OA'}}{\overline{OA}}\overline{AB}\\&=&\dfrac{-100}{-20}\times5\\\Rightarrow\boxed{\overline{A'B'}=25\,cm} \end{array}$
 
b. L'objet est virtuel et à $15\,cm$ de la lentille
 
$\begin{array}{rcl} \overline{OA'}&=&\dfrac{\overline{OA'}\cdot f}{OA+f}\\&=&\dfrac{15\times25}{15+25}\\\Rightarrow\boxed{\overline{OA'}=9.4\,cm} \end{array}$
 
L'image est virtuelle et droite par rapport à l'objet Grandeur de l'image
 
$\begin{array}{rcl} \overline{A'B'}&=&\dfrac{OA'}{OA}\overline{AB}\\&=&\dfrac{-37.5}{-15}\times5\\\Rightarrow\boxed{\overline{A'B'}=12.5\,cm} \end{array}$
 
 
e) L'objet est virtuel et à $1\,cm$ de la lentille
 
 
$\begin{array}{rcl} \overline{OA'}&=&\dfrac{\overline{OA}\cdot f}{\overline{OA}+f}\\&=&\dfrac{1\times25}{1+25}\\\Rightarrow\boxed{\overline{OA'}=0.96\,cm} \end{array}$
 
L'image est virtuelle et droite par rapport à l'objet
Grandeur de l'image
 
$\begin{array}{rcl} \overline{A'B'}&=&\dfrac{\overline{OA'}}{\overline{OA}}\overline{AB}\\&=&\dfrac{-1.04}{-1}\times5\\\Rightarrow\boxed{\overline{A'B'}=5.2\,cm} \end{array}$
 
C'est le dans cas $(c)$ on a un fonctionnement en loupe

Exercice 7

1. La distance focale de l'objectif standard
 
$\begin{array}{rcl} f&=&L\\&=&\sqrt{36^{2}+24^{2}}\\\Rightarrow\boxed{f=43.3\,mm} \end{array}$
 
Déduisons l'objectif qui convient
 
La lentille dont la distance focale $f_{2}=50\,cm$ est celui convient
 
2. Donnons la vergence de cet objectif
 
$\begin{array}{rcl} C&=&\dfrac{1}{f_{2}}\\&=&\dfrac{1}{50\cdot10^{-3}}\\\Rightarrow\boxed{C=20\delta} \end{array}$
 
3. Construisons graphiquement l'image $A'B'$ de $AB$

 
4. Indiquons :
 
a. La distance de l'image au centre optique
 
La relation de conjugaison s'écrit :
 
$\begin{array}{rcl} \dfrac{1}{\overline{O_{1}A^{'}}}-\dfrac{1}{\overline{O_{1}A}}1+1\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{O_{1}A'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{\overline{O_{1}A}}\\\Rightarrow\overline{O_{1}A'}&=&\dfrac{\overline{O_{1}A}\cdot f}{O_{1}A+f}\\&=&\dfrac{-7.5\times50\cdot10^{-3}}{-7.5+50\cdot10^{-3}}\\\Rightarrow\boxed{\overline{O_{1}A'}=5.0\,cm} \end{array}$
 
b. Le grandissement et la taille de l'image,
 
$\begin{array}{rcl} G&=&\dfrac{\overline{O_{1}A'}}{\overline{O_{1}A}}\\&=&\dfrac{-5.0}{7.5\cdot10^{2}}\\\Rightarrow\boxed{G=-0.067} \end{array}$
 
$\begin{array}{rcl} \dfrac{\overline{A'B'}}{\overline{AB}}&=&G\\\Rightarrow\overline{A'B'}&=&G\times\overline{AB}\\&=&-0.067\times1.70\\\Rightarrow\boxed{\overline{A'B'}=-11.6\,cm} \end{array}$
 
c. Le sens de l'image.
 
L'image est renversée

Exercice 8

A. Étude graphique

1. Plaçons sur un schéma : la lentille $L$ ; le centre optique O: le foyer objet $F$ ; le foyer image $F'$ et l'objet $AB$
 
 
$NB$ : $1\,cm$ pour carreau
 
2. Construction de l'image $A'B'$ de l'objet $AB$ donnée par la lentille (Voir figure)
 
3. Détermination graphique :
 
a. De la hauteur de l'image $\overline{A'B'}$
 
$\overline{A'B'}=2\,cm$
 
b. De la position de l'image $\overline{OA'}$
 
$\overline{OA'}=-14\,cm$
 
4. Déduisons le grandissement $y$
 
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\&=&\dfrac{2}{1}\\\Rightarrow\boxed{\gamma=2} \end{array}$

B. Étude théorique 

On se propose de vérifier par les calculs les résultats précédents
 
On rappelle les formules suivantes :
 
$\dfrac{1}{\overline{O_{1}A'}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{\overline{OF'}}$
 
$\gamma=\dfrac{\overline{OA'}}{\overline{OA}}=\dfrac{\overline{A'B'}}{\overline{AB}}$
 
1. Calculer $\overline{OA'}$
 
$\begin{array}{rcl} \overline{O_{1}A'}&=&\dfrac{\overline{O_{1}A}\cdot f}{O_{1}A+f}\\&=&\dfrac{-8\times 10} {-8+10}\\\Rightarrow\boxed{\overline{O_{1}A'}=-40\,cm} \end{array}$
 
 
2. Calcul du grandissement $\gamma$
 
$\begin{array}{rcl}\gamma &=&\dfrac{\overline{OA'}}{OA}\\&=&\dfrac{-40}{-8}\\\Rightarrow\boxed{\gamma =5} \end{array}$
 
Interpréter le résultat
 
3. Calculer $\overline{A'B'}$
 
4. Calcul de la vergence c de la lentille.
 
$\begin{array}{rcl} C&=&\dfrac{1}{f}\\&=&\dfrac{1}{10\cdot10^{-2}}\\\Rightarrow\boxed{C=10\delta} \end{array}$

Exercice 9

1. Distinction expérimentale puis théorique d'une lentille divergente d'une lentille convergente
 
Expérimentalement, pour une lentille divergente on peut placer une lentille sur un texte, la soulever et observer :
 
$\bullet $si les lettres paraissent plus grosses, la lentille est convergente;
 
$\bullet $si les lettres paraissent plus petites, la lentille est divergente
 
Théoriquement, si les bords de la lentille sont plus minces que le centre de la lentille, alors c'est une lentille
convergente.
2. Établissons l'expression de la vergence $C$ de la lentille en fonction $\gamma$ de et $x.$
 
$\begin{array}{rcl} \dfrac{1}{\overline{O_{1}A'}}-\dfrac{1}{\overline{O_{1}A}}&=&\dfrac{1}{\overline{f'}}\\&=&C\ ;\ \\\text{ or }\gamma&=&\dfrac{\overline{O_{1}A'}}{O_{1}A}\\\Rightarrow\overline{O_{1}A'}&=&\gamma\overline{O_{1}A}\\&=&\gamma x\\\Rightarrow\dfrac{1}{yx}-\dfrac{1}{x}&=&C\\\Rightarrow\boxed{C=\dfrac{1}{x}\left(\dfrac{1}{\gamma}-1\right)} \end{array}$
 
3. Calcul de $C$
 
$\begin{array}{rcl} C&=&\dfrac{1}{x}(\dfrac{1}{\gamma}-1)\\&=&\dfrac{1}{1.2}(\dfrac{1}{-2}-1)\\\Rightarrow\boxed{C=-1.25\delta} \end{array}$
 
Déduisons la nature de la lentille.
 
La vergence est négative, la lentille est une lentille divergente
 
4. Détermination de la position de l'image $A'B'$ de l'objet $AB$ donnée par la lentille
 
$\begin{array}{rcl} \overline{O_{1}A'}&=&\gamma\overline{O_{1}A}\\&=&-2\times1.2\\\Rightarrow\boxed{\overline{O_{1}A'}=-2.4\,m} \end{array}$
 
5. Schéma et construction de l'image $A'B'$ de $AB$
 
 

Solution des exercices : Amplificateur opérationnel : montages dérivateur et intégrateur 1er S

Classe: 
Première

Exercice 1. 

1. Représentation symbolique d'un amplificateur opérationnel idéal
 
 
 
2. Identification de ces montages
 
 
 
 
 
La loi d'additivité des tensions s'écrit :
 
$-\ $Pour le premier montages (fig 1) :
 
$\begin{array}{rcl} U_{e}&=&U_{c}-U_{d}\\\Rightarrow\;U_{e}&=&\dfrac{q}{C}-0\\\Rightarrow\;q&=&CU_{e}\\\Rightarrow\dfrac{dq}{dt}&=&\dfrac{d}{dt}\left(CU_{e}\right)\\\Rightarrow\;i&=&C\dfrac{dU_{e}}{dt}\quad(1) \end{array}$
 
$\begin{array}{rcl} U_{S}&=&-U_{R}-U_{d}\\\Rightarrow\;U_{S}&=&-Ri-0\\\Rightarrow\;U_{S}&=&-Ri\quad(2)\ ;\\(1)\text{ et }\quad(2)\Rightarrow\;U_{S}&=&-RC\dfrac{dU_{e}}{dt} \end{array}$
 
La tension de sortie est proportionnelle à l'opposée de la dérivée par rapport au temps de la tension d'entrée.
 
Le montage est donc un montage dérivateur
 
$-\ $Pour le deuxième montage (fig2) :
 
$\begin{array}{rcl} U_{e}&=&U_{R}-U_{d}\\\Rightarrow\;U_{d}\\\Rightarrow\;U_{e}&=&Ri\\\Rightarrow\;i&=&\dfrac{U_{e}}{R}\quad(1) \end{array}$
 
$$\begin{array}{rcl} U_{S}&=&-U_{c}-U_{d}\\\Rightarrow\;U_{S}&=&-\dfrac{q}{C}-\dfrac{q}{C}-0\\\Rightarrow\;U_{S}&=&-\dfrac{q}{C}\quad(2)\\\text{ or }q&=&\int\,idt\text{ et }i\\&=&\dfrac{U_{e}}{R}\quad(1)\\\Rightarrow\;q&=&\int\dfrac{U_{e}}{R}dt\text{ dans }\quad\\\Rightarrow\;U_{S}&=&-\dfrac{1}{RC}\int\,U_{e}dt \end{array}$$
 
La tension de sortie est proportionnelle à l'opposé de l'intégral par rapport au temps de la tension d'entrée.
 
Le montage est donc un montage intégrateur

Exercice 2

1. Représentation, sur de papier millimétrique, des variations de la tension $U_{e}$ en et de la tension $U_{s}$ à la sortie
 
Le montage est un montage dérivateur qui transforme la tension triangulaire de la forme $U_{e}=at+b$ en tension carrée de la forme $U_{S}=a$
 
 
2. Représentation des variations de l'intensité du courant dans le résistor (Voir figure)
 
$\begin{array}{rcl} U_{S}&=&R_{S}i\\\Rightarrow\;i&=&\dfrac{U_{S}}{R_{S}} \end{array}$
 
Les variations de l'intensité du courant i correspondent aux variations de la tension de sortie $U_{S}$ à une constante prés

Exercice 3

Représentation de la tension de sortie US(voir figure)
 
Ce montage est un montage intégrateur qui transforme une tension d'entrée $U_{e}$ carrée en tension de sortie $U_{S}$ triangulaire
 
$\begin{array}{rcl} \Rightarrow\;U_{S}&=&\dfrac{1}{RC}\int\,U_{e}dt \end{array}$
 
 
 
 
 

Exercice 4

1. Schéma d'un montage intégrateur
 
 
 
2. Représentation graphique des variations de $U_{S}(t)$
 

 
Exercice 5
 
 
1.1 En appliquant la loi des nœuds en $D$, montons $i_{R}=i_{C}$
 
La loi des nœuds en $D$ s'écrit : 
 
$\begin{array}{rcl} i_{C}&=&i_{R}+i_{-}\\\text{ or }i_{-}&=&0\\\Rightarrow\;i_{C}{R}&=&i_{C} \end{array}$
 
1.2. Exprimons $i_{R}$ en fonction de 
 
$\begin{array}{rcl} i_{R}&=&i_{C}\\\text{ or }i_{C}&=&\dfrac{dq}{dt}\\\Rightarrow\;i_{R}&=&\dfrac{dq}{dt} \end{array}$
 
Déduction de l'expression liant $i_{R}$ à $u_{C}$ et à $C$
 
$\begin{array}{rcl} i_{R}&=&i_{C}\\\text{ or }\,q&=&Cu_{c}\\\Rightarrow\;i_{R}&=&\dfrac{d\left(Cu_{c}\right)}{dt}\\\Rightarrow\;i_{R}&=&C\dfrac{du_{c}}{dt} \end{array}$
 
1.3. En appliquant la loi des tensions, établissons que $u_{c}=-u_{R}$ et que $u_{E}=u_{c}$
 
La loi d'additivité des tensions :
 
$\begin{array}{rcl} u_{S}+u_{R}+u_{E^{+}E^{-}}+u_{+}&=&0\\\text{ or }u_{E^{+}E^{-}}&=&0\\\Rightarrow\;u_{S}&=&-u_{R} \end{array}$
 
$\begin{array}{rcl} u_{E}&=&u_{c}+u_{-}\\\text{ or }u_{-}&=&0\\\Rightarrow\;u_{E}&=&u_{C} \end{array}$
 
1.4 Expression de $u_{s}$ en fonction de $R$, $C$ et $\dfrac{du_{c}}{dt}$
 
$\begin{array}{rcl} u_{S}&=&-u_{R}\\&=&-Ri_{R}\\\text{ or }i_{R}&=&C\dfrac{du_{c}}{dt}\\\Rightarrow\;u_{s}&=&-RC\dfrac{du_{c}}{dt} \end{array}$
 
2. Oscillogramme obtenu en voie $B$
 
$\begin{array}{rcl} u_{s}&=&-RC\dfrac{du_{c}}{dt}\\\text{ or }u_{E}&=&u_{c}\\\Rightarrow\;u_{s}&=&-RC\dfrac{du_{E}}{dt} \end{array}$
 
Le montage est un montage dérivateur qui transforme la tension triangulaire de la forme $U_{e}=at+b$ en tension carrée de la forme $U_{s}=a$
 
 
3 Les caractéristiques de la tension de sortie $u_{s}$
 
$\begin{array}{rcl} u_{s}&=&-RC\dfrac{du_{E}}{dt}\\\text{ or }u_{E}&=&u_{Em}\cos\left(2\pi Nt\right)\\\Rightarrow\;u_{s}&=&2\pi NRCu_{Em}\sin\left(2\pi Nt\right) \end{array}$
 
La tension de sortie $u_{s}$ est une fonction sinusoidale du temps d'amplitude : $u_{sm}=2\pi NRCu_{Em}$ : de pulsation :
 
$\alpha=2\pi N$ et de fréquence $N$
 
Oscillogrammes obtenus en voie $A$ et en voie $B\cdot A$ l'origine des dates , le spot est à gauche de l'écran

Exercice 6

Soit le montage de la figure $1$
 
$L'A\cdot O$ est considéré comme idéal
 
 
1. Afin d'établir une relation entre $\dfrac{du_{s}}{dt}$ et $u_{E}$
 
1.1. Appliquons la loi des nœuds en $D$ et montrons que $i_{c}=i_{R}$
 
La loi des nœuds en $D$ s'écrit : 
 
$\begin{array}{rcl}i_{c}&=&i_{R}+i_{-}\\\text{ or }i_{-}&=&0\\\Rightarrow\;i_{R}&=&i_{c}\end{array}$
 
1.2. Expression de $i_{R}$ en fonction de $\dfrac{dq}{dt}$
 
 
$i_{R}=\dfrac{dq}{dt}$
 
Déduction d'une relation entre $i_{R}$, $\dfrac{du_{c}}{dt}$ et $C$
 
$\begin{array}{rcl} i_{R}&=&\dfrac{dq}{dt}\\\text{ or }q&=&Cu_{c}\\\Rightarrow\,i_{R}&=&\dfrac{d\left(Cu_{c}\right)}{dt}\\\Rightarrow\;i_{R}&=&C\dfrac{du_{c}}{dt} \end{array}$
 
1.3. En appliquant la loi des tensions, établissons que
 
 
$\begin{array}{rcl} u_{s}&=&-u_{c}\text{ et que }u_{R}=u_{E} \end{array}$
 
 
$\begin{array}{rcl} u_{S}+u_{C}+u_{E^{+}E^{-}} +u_{+}&=&0\\\text{ or }u_{E^{+}E^{-}}&=&u_{+}\\&=&0\\\Rightarrow\;u_{S}&=&-u_{C} \end{array}$
 
 
$\begin{array}{rcl} u_{E}&=&u_{R}+u_{-}\\\text{ or }u_{-}&=&0\\\Rightarrow\;u_{R}&=&u_{E} \end{array}$
 
1.4. A partir de la relation établie $1\cdot 2\cdot$ et des relations précédentes, en appliquant la loi d’Ohm au conducteur
ohmique, exprimer $\dfrac{du_{s}}{dt}$ en fonction de $R$, $C$ et $u_{E}$
 
$\begin{array}{rcl} u_{s}&=&-u_{c}\\\Rightarrow\dfrac{du_{s}}{dt}&=&\dfrac{du_{c}}{dt}\\\text{ or }i_{R}&=&C\dfrac{du_{c}}{dt}\\\text{ et }u_{R}&=&Ri_{R}=u_{E}\\\Rightarrow\;i_{R}&=&\dfrac{u_{E}}{R}\\\Rightarrow\;C\dfrac{du_{c}}{dt}&=&\dfrac{u_{E}}{R}\\\Rightarrow\dfrac{du_{c}}{dt}&=&\dfrac{u_{E}}{RC}\\\Rightarrow\dfrac{du_{s}}{dt}&=&-\dfrac{u_{E}}{RC} \end{array}$
 
2. L'oscillographe électronique mesure en voie A la tension d'entrée $u_{E}$ et en voie $B$, la tension de sortie $u_{S}$
ci-dessous
 
 
 
2.1. Montrons que sur l'intervalle de temps $t\in\left[0\,; \dfrac{T}{2}\right]$, $u_{s}$ peut se mettre sous la forme : $u_{s}=-\dfrac{1}{RC}u_{Em}t+b$ où $u_{Em}$ est la valeur maximale de $u_{E}$ et $b$ une constante
 
$\begin{array}{rcl} t\in\left[0\;,\dfrac{T}{2}\right]\;,u_{E}&=&u_{Em}\\\Rightarrow\dfrac{du_{s}}{dt}&=&-\dfrac{u_{Em}}{RC}\\\Rightarrow\;u_{S}&=&-\dfrac{1}{RC}u_{Em}t+b \end{array}$
 
2.2. Montrons que sur l'intervalle de temps : $t\in[0\;,\dfrac{T}{2}]$, $u_{s}$ peut se mettre sous la forme : $u_{s}=\dfrac{1}{RC}u_{Em}t+c$ où $c$ est une constante
 
$\begin{array}{rcl} t\in(\dfrac{T}{2})&=&\dfrac{1}{RC}u_{Em}\dfrac{T}{2}+c\\&=&-\dfrac{1}{RC}u_{Em}\dfrac{T}{2}+b\cdot\\\text{ Pour } b&=&0\\\Rightarrow\;C&=&-\dfrac{2}{RC}u_{Em}\dfrac{T}{2}\\\Rightarrow\;u_{s}(t)&=&-\dfrac{1}{RC}u_{Em}(t+T) \end{array}$
 
2.4. Déduction de l'étude précédente, l'oscillogramme obtenu en voie $B;$ (Voir figure)
 
3.1. Montrons que la valeur instantanée de la tension de sortie uS peut se mettre sous la forme :
 
 
$u_{s}=U_{Sm}\sin(2\pi Nt)+d$
 
$$\begin{array}{rcl} U_{s}&=&-\dfrac{1}{RC}\int u_{E}dt\\\text{ or }u_{E}&=&-u_{Em}\cos(2\pi Nt)\\\Rightarrow\;U_{S}&=&\dfrac{1}{RC}\int u_{Em}\cos(2\pi Nt)dt
  \\\Rightarrow\;U_{S}&=&-\dfrac{1}{2\pi NRC}u_{Em}\cos(2\pi Nt)+d\\\Rightarrow\;U_{s}1+1 U_{Sm}\cos(2\pi  Nt)+d\\\Rightarrow\;U_{Sm}&=&\dfrac{1}{2\pi NRC}U_{Em} \end{array}$$
 
$U_{Sm}$ est la valeur maximale de la tension de sortie, d est une constante
 
Calcul de $U_{Sm}.$
 
En supposant qu'à $t=0$, $u_{s}=0$,
 
$\begin{array}{rcl} U_{Sm}&=&\dfrac{1}{2\pi \times 50\times 10\cdot10^{3}1.0\cdot10^{-6}}\times6.0\\\Rightarrow\;U_{Sm}&=&1.9\,V \end{array}$
 
Calcul de $d$
 
$\begin{array}{rcl} U_{x}(0)&=&-\dfrac{1}{2\pi NCR}u_{Em}\cos(2\pi N\times 0)+d\\&=&0\\\Rightarrow-\dfrac{1}{2\pi NRC}U_{Em}+d&=&0\\\Rightarrow\;d&=&\dfrac{1}{2\pi NRC}U_{Em}\\\Rightarrow\;d&=&1.9\,V \end{array}$
 
2.2. Oscillogrammes obtenus en voie $A$ et en voie $B$

Exercice 7

 
 
 
 
1. Rappel de l'expression qui lie $\dfrac{du_{E}}{dt}$, $R$, $C$, et $u_{S}$
 
$\begin{array}{rcl} u_{S}+u_{R}+u_{E^{+}E^{-}}+u^{+}&=&0\\\Rightarrow\;u_{S}+u_{R}+0+0&=&0\\\Rightarrow\;u_{S}&=&-u_{R}\\\Rightarrow\;u_{S}&=&-Ri_{R}\quad(1) \end{array}$
 
$\begin{array}{rcl} u_{E}+u_{C}+U^{-}&=&0\\\Rightarrow\;u_{E}&=&+u_{C}+0\\&=&0\\\Rightarrow\;u_{C}&=&-u_{E}\\\text{ or }i_{R}&=&\dfrac{dq}{dt}\\&=&\dfrac{dCu_{c}}{dt}\\&=&C\dfrac{du_{c}}{dt}\\&=&C\dfrac{du_{c}}{dt}\\\Rightarrow\;i_{R}&=&-C\dfrac{du_{E}}{dt}\quad (2) \end{array}$
 
$\begin{array}{rcl} (1)\text{ et }(2)&\Rightarrow&\;u_{s}\\&=&-RC\dfrac{du_{E}}{dt} \end{array}$
 
2. Oscillogramme obtenu (Voir figure)
 
Un montage à amplificateur opérationnel est en mode linéaire s'il est rebouclé sur l'entrée inverseuse de l'amplificateur opérationnel (montage en contre réaction)

Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Condensateurs : capacité, énergie emmagasinée - 1er s

Classe: 
Première

Exercice 1

1. Tracé du graphique $U=f(t)$
 
 
Le graphe $U=f(t)$ est une fonction linéaire du temps
 
2. Détermination de la variation de $U$ en fonction du temps.
 
$\begin{array}{rcl} U&=&kt\\\text{ avec }k&=&\dfrac{\Delta U}{\Delta t}\\&=&\dfrac{4.5-3.5}{(90-70)\cdot10^{-3}}\\\Rightarrow\;K&=&50\,V_{s}^{-1}\\\Rightarrow\;U&=&50\,t \end{array}$
 
Déduction de la capacité du condensateur
 
$\begin{array}{rcl} q&=&It\\&=&Cu\\\text{ or }u&=&50t\\\Rightarrow\;q&=&It\\&=&50Ct\\\Rightarrow\;C&=&\dfrac{I}{50}\\&=&\dfrac{0.5\cdot10^{-3}}{50}\\\Rightarrow\;C&=&1.0\cdot10^{-5}F \end{array}$

Exercice 2

1. Calcul la capacité équivalente pour chaque schéma
$\begin{array}{rcl} \text{a. }\quad\dfrac{1}{C_{\text{éq}}}&=&\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dfrac{1}{C_{3}}\\\Rightarrow\dfrac{1}{C_{\text{éq}}}&=&\dfrac{C_{2}C_{3}}{C_{1}C_{2}C_{3}}+\dfrac{C_{1}C_{2}}{C_{1}C_{2}C_{3}}+\dfrac{C_{1}C_{2}}{C_{1}C_{2}C_{3}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{C_{1}C_{2}C_{3}}{C_{1}C_{2}+C_{1}C_{3}+C_{2}C_{3}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{10\cdot10^{-6}\times2\cdot10^{-6}\times1000\cdot10^{-9}}{10\cdot10^{-6}\times2\cdot10^{-6}+10\cdot10^{-6}\times1000\cdot10^{-9}+2\cdot10^{-6}\times1000\cdot10^{-9}}\\\Rightarrow\;C_{\text{éq}}&=&0.625\cdot10^{-6}F \end{array}$
 
 
$\begin{array}{rcl}\text{b.   } \quad C_{\text{éq}}&=&C_{1}+C_{2}+C_{3}\\&=&10\cdot10^{-6}+2\cdot10^{-6}+1000\cdot10^{-9}\\\Rightarrow\;C_{\text{éq}}&=&2.7\cdot10^{-6}F \end{array}$
 
 
$\begin{array}{rcl}\text{c. }\quad C_{\text{éq}}&=&\dfrac{C_{2}C_{1}}{C_{2}+C_{1}}+C_{3}\\&=&\dfrac{2\cdot10^{-6}\times10\cdot10^{-6}} {2\cdot10^{-6}+10\cdot10^{-6}}+1000\cdot10^{-9}\\\Rightarrow\;C_{\text{éq}}&=&2.7\cdot10^{-6}F \end{array}$
 
 
2. Déterminer la valeur de $C_{AB}$
 
 
$\begin{array}{rcl} \dfrac{1}{C_{\text{éq}}}&=&\dfrac{1}{C_{1}+C_{3}}+\dfrac{1}{C_{2}}+\dfrac{1}{C_{3}}+\dfrac{1}{C_{6}+\dfrac{C_{4}C_{7}}{C_{4}+C_{7}}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{1}{\dfrac{1}{C_{1}+C_{5}+\dfrac{1}{C_{2}+\dfrac{1}{C_{3}+\dfrac{1}{C_{6}+\dfrac{C_{4}C_{7}}{C_{4}+C_{7}}}}}}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{1}{\dfrac{1}{4.36+5000}+\dfrac{1}{2000}+\dfrac{1}{200}+\dfrac{1}{10\dfrac{5000\times27}{5000+27}}} \\\Rightarrow\;C_{\text{éq}}&=&9.96\cdot10^{-11}F \end{array}$
 
Calcul de la capacité $C_{3}$
 
 
$\begin{array}{rcl} \dfrac{1}{C_{\text{éq}}}&=&\dfrac{1}{C_{1}+C_{2}}+\dfrac{1}{C_{3}+C_{4}}+\dfrac{1}{C_{5}}\\\Rightarrow\dfrac{1}{C_{3}+C_{4}}&=&\dfrac{1}{C_{\text{éq}}}-\dfrac{1}{C_{1}+C_{2}}-\dfrac{1}{C_{5}}\\\Rightarrow\;C_{3}+C_{4}&=&\dfrac{\left(C_{1}+C_{2}\right)C_{5}C_{\text{éq}}}{\left(C_{1}+C_{2}\right)C_{5}-C_{\text{éq}}C_{5}-C_{\text{éq}}\left(C_{1}+C_{2}\right)}\\\Rightarrow\;C_{3}&=&\dfrac{\left(C_{1}+C_{2}+C_{5}\right)C_{\text{éq}}}{\left(C_{1}+C_{2}\right)C_{5}-C_{\text{éq}\left(C_{1}+C_{2}\right)}}-C_{4}\\\Rightarrow\;C_{3}&=&\dfrac{(100+100+1000)\times155}{(100+100)\times1000-155\times1000-155(100+100)}-470\\\Rightarrow\;C_{3}&=&2.21\mu\cdot F \end{array}$

Exercice 3

I. Calcul de :
 
1. La surface des armatures.
 
$\begin{array}{rcl} \Rightarrow\;C&=&\dfrac{\varepsilon S}{e}\\&=&\dfrac{\varepsilon_{r}\varepsilon_{0}S}{e}\\\Rightarrow\;S&=&\dfrac{Ce}{\varepsilon_{r}\varepsilon_{0}}\\&=&\dfrac{0.12\cdot10^{-6}\times0.2\cdot10^{-3}}{5\times8.84\cdot 10^{-12}}\\\Rightarrow\;S&=&0.54\,m^{2} \end{array}$
 
2. La charge du condensateur soumis à la tension de service.
 
$\begin{array}{rcl} Q&=&CU_{S}\\&=&0.12\cdot10^{-6}\times100\\\Rightarrow\;Q&=&12\cdot10^{-6}C \end{array}$
 
3. L'énergie emmagasinée.
 
$\begin{array}{rcl} E&=&\dfrac{1}{2}\dfrac{Q^{2}}{C}\\&=&\dfrac{1}{2}\dfrac{\left(12\cdot10^{-6}\right)^{2}}{0.12\cdot10^{-6}}\\\Rightarrow\;E&=&5.0\cdot10^{-4}J \end{array}$
 
II. Calcul de :
 
1. La charge total de l'ensemble formé par les deux condensateurs.
 
$Q=12\cdot10^{-6}C$
 
2. La tension commune aux deux condensateurs en régime permanent.
 
$U=100\,V$
 
3. L'énergie emmagasinée par le montage
 
$E=5.0\cdot10^{-4}J$

Exercice 4

1. Schéma du montage permettant de suivre l'évolution de $U_{c}$ au cours du temps
 
 
2. Détermination graphique de la capacité $C$ du condensateur.
 
$\begin{array}{rcl} E&=&\dfrac{1}{2}\dfrac{q^{2}}{C}\\\text{ or }q&=&It\\\Rightarrow\;E&=&\dfrac{1}{2}\dfrac{I^{2}}{C}t^{2}\dfrac{1}{2}\dfrac{I^{2}}{C}\\&=&\dfrac{\Delta E}{\Delta t^{2}}\\\Rightarrow\;C&=&\dfrac{I^{2}\Delta t^{2}}{2\Delta E}\\&=&\dfrac{\left(50\cdot10^{-6}\right)^{2}\times(100-0)}{2\times\left(1.25\cdot10^{-2}-0\right)}\\\Rightarrow\;C&=&10^{-5}F \end{array}$
 
3. Calcul de la permittivité relative du condensateur.
 
$\begin{array}{rcl} C&=&\dfrac{\varepsilon S}{e}\\&=&\dfrac{\varepsilon_{r}\varepsilon_{0}S}{e}\\\Rightarrow\varepsilon_{r}&=&\dfrac{Ce}{S\varepsilon_{0}}\\&=&\dfrac{10^{-5}\times0.1\cdot10^{-3}}{1\times8.85\cdot10^{-12}}\\\Rightarrow\varepsilon_{r}&=&113 \end{array}$

Exercice 5

1.La capacité C du condensateur en $\mu F$
 
$\begin{array}{rcl} C&=&\dfrac{Q}{U}\\\text{ or }Q&=&I_{0}t\\\Rightarrow\;C&=&\dfrac{I_{0}t}{U}\\&=&\dfrac{0.30\cdot10^{-3}\times8}{12}\\&=&2\cdot10^{-4}F\\\Rightarrow\;C&=&200\mu F \end{array}$
 
2. Valeur de la charge $q$ portée par son armature positive
 
$\begin{array}{rcl} q&=&CU\\&=&150\cdot10^{-3}\times500\\\Rightarrow\;q&=&75.0\,C \end{array}$
 
L'énergie $E$ stockée par ce condensateur
 
$\begin{array}{rcl} E&=&\dfrac{1}{2}CU^{2}\\&=&\dfrac{1}{2}\times150\cdot10^{-3}\times500^{2}\\\Rightarrow\;E&=&18.8\cdot10^{3}J \end{array}$

Exercice 6

1. Calcul de la valeur de l'énergie $W_{1}$ emmagasinée par $C_{1}$
 
$\begin{array}{rcl} W_{1}&=&\dfrac{1}{2}C_{1}U_{1}^{2}\\&=&\dfrac{1}{2}\times470\cdot10^{-6}\times24^{2}\\\Rightarrow\;W_{1}&=&0.14J \end{array}$
 
2. La valeur de l'énergie $W_{2}$ emmagasinée par $C_{2}.$
 
$\begin{array}{rcl} W_{2}&=&\dfrac{1}{2}C_{1}U_{2}^{2}\\&=&\dfrac{1}{2}\times1000\cdot10^{-6}\times0^{2}\\\Rightarrow\;W_{2}&=&0\cdot J \end{array}$
 
3. Détermination de la valeur de la tension $U$ aux bornes des deux condensateurs
 
$U=24\,V$
 
4. Calcul de la valeur de l'énergie $W_{12}$ emmagasinée
 
$\begin{array}{rcl} W_{12}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}U^{2}\\&=&\dfrac{470\cdot10^{-6}\times1000\cdot10^{-6}}{470\cdot10^{-6}+1000\cdot10^{6}}\times24^{2}\\\Rightarrow\;W_{12}&=&0.18\,J \end{array}$
 
5. Comparons $W_{12}$ avec $W_{1}+W_{2}$ et donnons une explication au résultat.
 
$W_{12}=.18\,J$  
 
 
$W_{1}=0.14\,J$ 
 
 
$\begin{array}{rcl} W_{1}+W_{2}&=&0.14+0\\\Rightarrow\;W_{1}+W_{2}&=&0.14 \end{array}$
 
 
$W_{12}\succ W_{1}+W_{2}$
 
Le condensateur $C_{2}$ n'était pas totalement déchargé

Exercice 7 : Charge d'un condensateur à courant constant

1. Rappel de l'expression de la charge $Q(i\;,\ t)$ et les unités utilisées.
 
$Q=it$ avec $i$ en ampères, $t$ en secondes et $Q$ en coulombs
 
2. Rappel de l'expression de la tension $Q(C\;,\ U)$ et les unités utilisées.
 
$Q=CU$ avec $C$ en farads, $U$ en vols et $Q$ en coulombs
 
3. Détermination de la charge $Q$ portée par une armature du condensateur à l'instant $t=t_{1}$
 
$\begin{array}{rcl} Q&=&It_{1}\\&=&250\cdot10^{-6}\times7\times60\\\Rightarrow\;Q&=&0.105\,C \end{array}$
 
4.Tracé de la courbe $U(Q)$
 
 
5. Déduction de la capacité $C$ du condensateur.
 
$\begin{array}{rcl}C&=&\dfrac{\Delta Q}{\Delta U}\\&=&\dfrac{(105-0)\cdot10^{-3}}{31.8-0}\\\Rightarrow\;C&=&3.30\cdot10^{-3}F \end{array}$
 
6. Calcul de l'énergie $W$ emmagasinée par le condensateur à la l'instant $t_{1}$
 
$\begin{array}{rcl} W&=&\dfrac{1}{2}QU\\&=&\dfrac{1}{2}\times0.105\times31.8\\\Rightarrow\;W&=&1.67\,J \end{array}$

Exercice 8: Association de condensateurs

1. Expression de la capacité équivalente $C_{S}$
 
$\begin{array}{rcl} C_{S}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}\\&=&\dfrac{2.2\times3.3}{2.2+3.3}\\\Rightarrow\;C_{S}&=&1.32\;m\cdot F \end{array}$
 
2. Expression de la capacité équivalente $C_{p}$
 
$\begin{array}{rcl} C_{p}&=&C_{1}+C_{2}\\&=&2.2+3.3\\\Rightarrow\;C_{p}&=&5.5\,m\cdot F \end{array}$
 
3. Détermination de la charge $Q_{1}$ portée par une armature de ce condensateur.
 
$\begin{array}{rcl} Q_{1}&=&C_{1}U\\&=&2200\cdot10^{-6}\times30\\\Rightarrow\;Q_{1}&=&66\cdot10^{-3}C \end{array}$
 
4. Détermination de la charge portée par l'ensemble.
 
$\begin{array}{rcl} Q&=&Q_{1}\\\Rightarrow\;Q&=&66\cdot10^{-3}C \end{array}$
 
5. Déduction de la tension U' aux bornes de l'ensemble.
 
$\begin{array}{rcl} U'&=&\dfrac{Q}{C_{p}}\\&=&\dfrac{66\cdot10^{-3}}{5.5\cdot10^{-3}}\\\Rightarrow\;U^{'}&=&12\,V \end{array}$

Exercice 9 : Association de condensateurs en parallèle

1.1. La capacité équivalente du groupe de deux condensateurs
 
$\begin{array}{rcl} C_{EQ}&=&C_{1}+C_{2}\\&=&6\cdot10^{-6}+10\cdot10^{-3}\\\Rightarrow\;C_{EQ}&=&10^{-2}F \end{array}$
 
1.2. La $d\cdot d\cdot p\cdot$ aux bornes des condensateurs en parallèle 
 
$\begin{array}{rcl} U&=&\dfrac{Q}{C}\\&=&\dfrac{200\cdot10^{-3}}{10^{-2}}\\\Rightarrow\;U&=&20\,V \end{array}$
 
1.3 Charge accumulée sur les armatures du condensateur de $6\,m\cdot F$
 
$\begin{array}{rcl} Q&=&CU\\&=&6\cdot10^{-3}\times 20\\\Rightarrow\;Q&=&12\cdot10^{-2}C \end{array}$
 
1.4. Charge accumulée sur les armatures du condensateur de $10\,m\cdot F$
 
$\begin{array}{rcl} Q&=&CU\\&=&10\cdot10^{-3}\times20\\\Rightarrow\;Q&=&2.0\cdot10^{-1}C \end{array}$
 
2.1 Détermination des charges $Q_{1}$ et $Q_{2}$ 
 
$\begin{array}{rcl} Q_{1}&=&C_{1}U\\&=&3.3\cdot10^{-3}\times20\\\Rightarrow\;Q_{1}&=&6.6\cdot10^{-2}C \end{array}$
 
$\begin{array}{rcl} Q_{2}&=&C_{2}U'\\&=&2200\cdot10^{-6}\times10\\\Rightarrow\;Q_{2}&=&22\cdot10^{-3}C \end{array}$
 
2.2 La charge $Q$ portée par l'ensemble
 
$\begin{array}{rcl} Q&=&Q_{1}+Q_{2}\\&=&6.6\cdot10^{-2}+2.2\cdot10^{-2}\\\Rightarrow\;Q&=&8.8\cdot10^{-2}C\end{array}$
 
2.3. Déduction de la tension $U"$ aux bornes de l'ensemble
 
$\begin{array}{rcl} U"&=&\dfrac{Q}{C_{1}+C_{2}}\\&=&\dfrac{8.8\cdot10^{-2}}{3.3\cdot10^{-2}+2200\cdot10^{-6}}\\\Rightarrow\;U"&=&1.6\,V \end{array}$

Exercice 10 : Association de condensateurs en série.

1. Détermination de la capacité équivalente $C_{EQ}.$
 
$\begin{array}{rcl} C_{EQ}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}\\&=&\dfrac{20\times33}{20+33}\\\Rightarrow\;C_{EQ}&=&12\,n\cdot F \end{array}$
 
2. Calcul de la charge $Q$ portée par la capacité équivalente.
 
$\begin{array}{rcl} Q&=&C_{EQ}U\\&=&12\cdot10^{-9}\times20\\\Rightarrow\;Q&=&24\cdot10^{-8}C \end{array}$
 
3. La charge $q$ portée par un condensateur.
 
$\begin{array}{rcl} q&=&Q\\\Rightarrow\;q&=&24\cdot10^{-8}C \end{array}$
 
4. Déduction de la tension $U_{1}$ aux bornes de $C_{1}$ et de la tension $U_{2}$ aux bornes de $C_{2}.$
 
$\begin{array}{rcl} U_{1}&=&\dfrac{q}{C_{1}}\\&=&\dfrac{24\cdot10^{-8}}{20\cdot10^{-9}}\\\Rightarrow\;U_{1}&=&12\,V \end{array}$
 
$\begin{array}{rcl} U_{2}&=&\dfrac{q}{C_{2}}\\&=&\dfrac{24\cdot10^{-8}}{33\cdot10^{-9}}\\\Rightarrow\;U_{2}&=&7.3\,V \end{array}$
 
5. Calcul de l'énergie $W$ emmagasinée par l'ensemble.
 
$\begin{array}{rcl} W&=&\dfrac{1}{2}QU\dfrac{1}{2}\times24\cdot10^{-8}\times20\\\Rightarrow\;W&=&24\cdot10^{-7}J \end{array}$

Exercice 11

 
1. Les caractéristiques de la force électrique $\overrightarrow{F}$ qui s'exerce sur chaque ion entre les deux plaques $A$ et $B$
Direction et sens (voir figure)
 
Intensité :

$\begin{array}{rcl} F&=&2eE\\&=&2e\dfrac{U_{AB}}{d}\\&=&2\times1.6\cdot10^{-19}\times\dfrac{4\cdot10^{4}}{0.10}\\\Rightarrow\;F&=&12.8\cdot10^{-14}N\end{array}$
 
2. Evaluons le rapport $\dfrac{P}{f'}$
 
$\begin{array}{rcl} \dfrac{F}{P}&=&\dfrac{F}{mg}\\&=&\dfrac{12.8\cdot10^{-14}}{1.16\cdot10^{-25}\times10}\\\Rightarrow\dfrac{F}{P}&=&11\cdot10^{10}\\\Rightarrow\;F&\succ& P \end{array}$
 
Le poids $P$ est négligeable devant la force $F$
 
3. Calcul de l'énergie cinétique de chaque ion arrivant en $B'$, en Joules et en électronvolts :
 
3.1. Par utilisation du théorème de l'énergie cinétique.
 
$\begin{array}{rcl} E_{C_{B}}-E_{C_{A}}&=&W\left(\overrightarrow{F}\right)\\\Rightarrow\;E_{C_{B}}&=&W\left(\overrightarrow{F}\right)+E_{C_{A}}\\&=&2eU_{AB}+\dfrac{1}{2}mV_{A}^{2}\\&=&2\times1.6\cdot10^{-19}\times4\cdot10^{4}+\dfrac{1}{2}\times1.16\cdot10^{-25}\times\left(10^{5}\right)^{2}\\\Rightarrow\;E_{C_{B}}&=&1.34\cdot10^{-14}J\\\Rightarrow\;E_{C_{B}}&=&84\,e\cdot V \end{array}$
 
3.2 Par utilisation de la conversation de l'énergie total $\left(E_{c}+E_{p}\right)$ de l'ion,
 
$\begin{array}{rcl} E_{m_{B}}&=&E_{m_{B}}\\\Rightarrow\;E_{C_{B}}+E_{P_{B}}&=&E_{C_{A}}+E_{P_{A}}\\\Rightarrow\;E_{C_{B}}+2eV_{B}&=&\dfrac{1}{2}mV_{A}^{2}+2eV_{A}\\\Rightarrow\;E_{C_{B}}&=&2e\left(V_{A}-V_{B}\right)+\dfrac{1}{2}mV_{A}^{2}\\\Rightarrow\;E_{C_{B}}&=&2eU_{AB}+\dfrac{1}{2}mV_{A}^{2}\\&=&2\times1.6\cdot10^{-19}\times4\cdot10^{4}+\dfrac{1}{2}\times1.16\cdot10^{-25}\times\left(10^{5}\right)^{2}\\\Rightarrow\;E_{C_{B}}&=&1.34\cdot10^{-14}\\\Rightarrow\;E_{C_{B}}&=&84\;e\,V \end{array}$
 
3.3 Déduction de la vitesse d'un ion en $B'$
 
$\begin{array}{rcl} E_{C_{B}}&=&\dfrac{1}{2}mV_{B}^{2}\\\Rightarrow\;V_{B}&=&\sqrt{\dfrac{2E_{C_{B}}}{m}}\\&=&\dfrac{2\times1.34\cdot10^{5}m\cdot s^{-1}}{1.16\cdot10^{-25}}\\\Rightarrow\;V_{B}&=&4.8\cdot10^{5}m\cdot s \end{array}$

Exercice 12

a. La tension entre ses bomes à la fin de la charge
 
$\begin{array}{rlc} U_{C}&=&E\\\Rightarrow\;U_{C}&=&6\;V \end{array}$
 
b. L'énergie emmagasinée par ce condensateur
 
$\begin{array}{rcl} W&=&\dfrac{1}{2}C_{1}U_{c}^{2}\\&=&\dfrac{1}{2}\times2\cdot10^{-6}\times6^{2}\\\Rightarrow\;W&=&36\cdot10^{-6}J \end{array}$
 
2. a. Le courant s'annule dans le circuit formé par $C_{1}$ et $C_{2}$ lorsque la tension du condensateur $C_{2}$ est égale à la
tension du condensateur $C_{1}$
 
b. Calcul des charges électriques finales de chacun de deux condensateurs.
 
$\begin{array}{rcl} Q_{1}&=&C_{1}U_{c}\\&=&2\cdot10^{-6}\times6\\\Rightarrow\;Q_{1}&=&12\cdot10^{-6}C \end{array}$
 
$\begin{array}{rcl} Q_{2}&=&C_{2}U_{C}\\&=&1\cdot10^{-6}\times6\\\Rightarrow\;Q_{2}&=&6\cdot10^{-6}C\end{array}$
 
3. La capacité du condensateur équivalent à l'association de condensateurs $C_{1}$ et $C_{2}$ dans chacun des cas
 
a. Les condensateurs $C_{1}$ et $C_{2}$ sont branchés en série
 
$\begin{array}{rcl} C_{EQ}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}\\&=&\dfrac{2\times1}{2+1}\\\Rightarrow\;C_{EQ}&=&0.7\mu\,F \end{array}$
 
b. Les condensateurs $C_{1}$ et $C_{2}$ sont branchés en parallèle
 
$\begin{array}{rcl} C_{EQ}&=&C_{1}+C_{2}\\&=&2+1\\\Rightarrow\;C_{EQ}&=&3\mu\,F \end{array}$
 

Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Énergie électrique mise en jeu dans un circuit électrique 1er s

Classe: 
Première

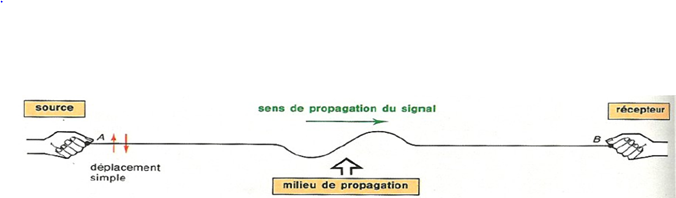
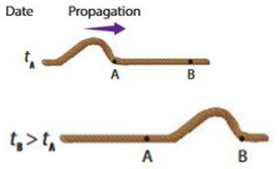
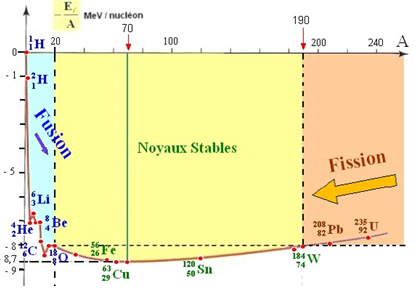
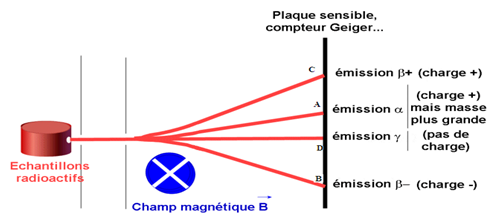
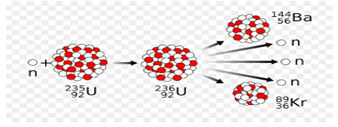
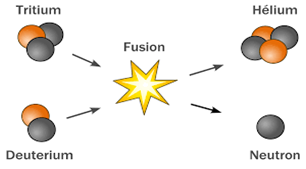
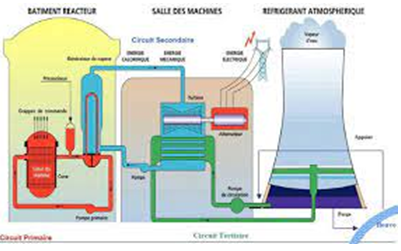
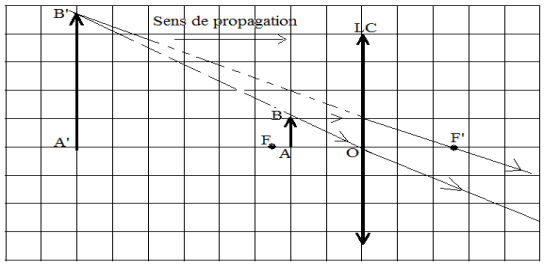
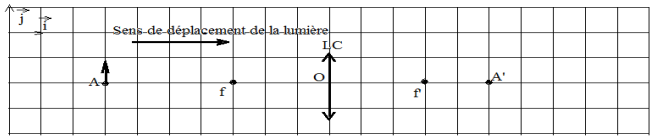
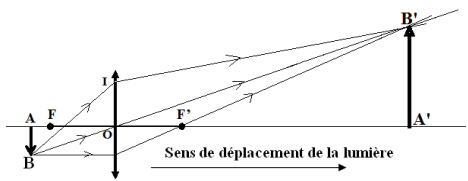
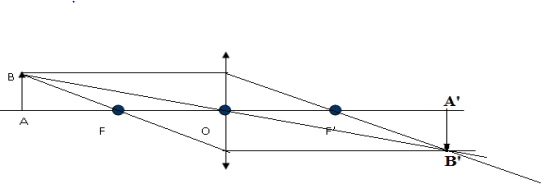
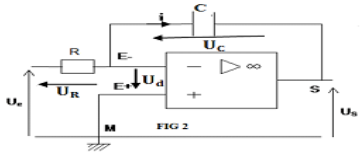
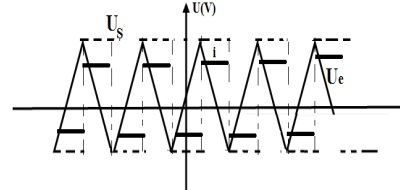
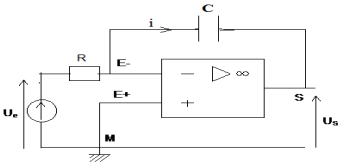
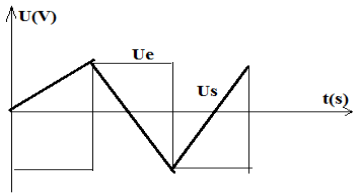
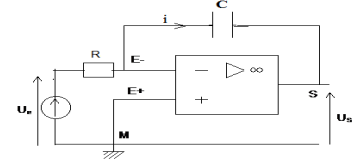
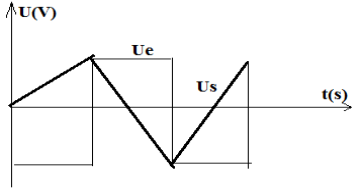
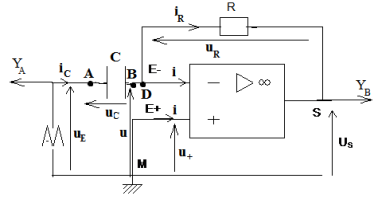
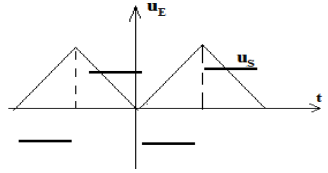
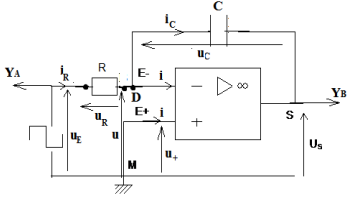
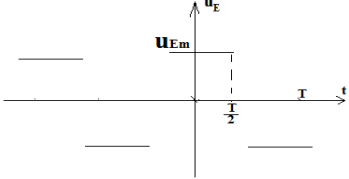
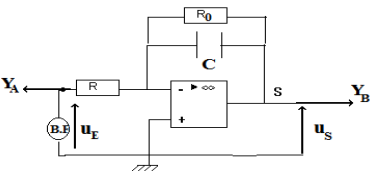
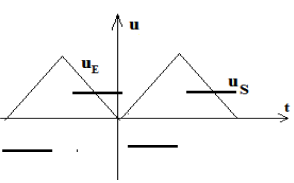
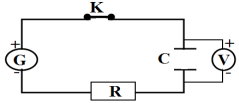
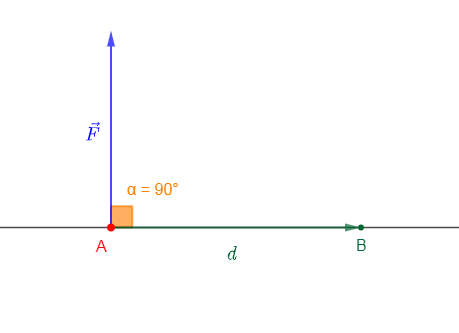
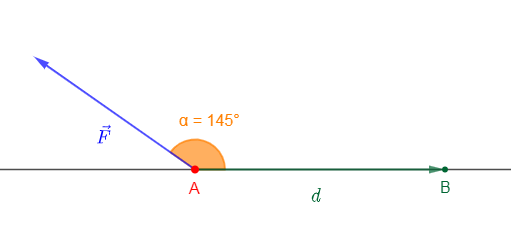
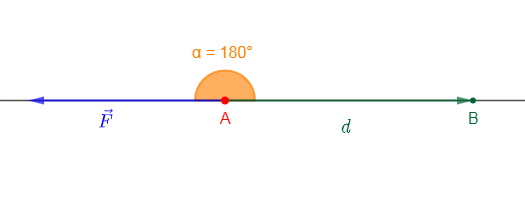
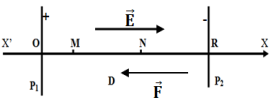
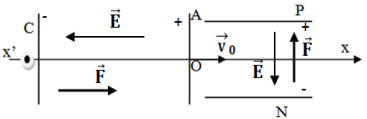
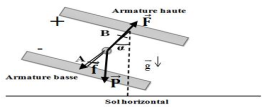
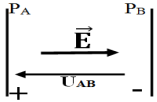
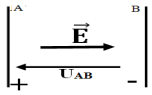
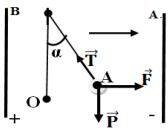
Exercice 1

1. Définitions
 
Générateur : Un générateur est un dipôle assurant la conversion de l'énergie chimique, mécanique ou d'une autre forme d'énergie en énergie électrique fournie à un circuit récepteur.
 
Un récepteur est un dipôle électrique qui reçoit de l'énergie électrique pour la convertir en d'autres formes d'énergie.
 
2. L'alternateur est un des dispositifs permettant de transformer l'énergie mécanique en énergie électrique.
 
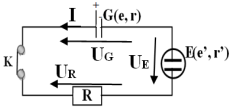
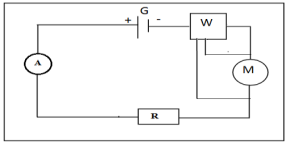
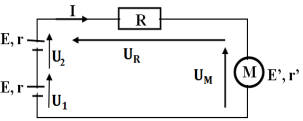
3.1. Schéma du montage
 
 
Expression de l'intensité $I$ en fonction de $e'$, $e$, $r'$, $r$ et $R$
 
La loi d'additivité de tension s'écrit :
 
$\begin{array}{rcl} U_{G}+U_{E}+U_{R}&=&0\\\text{ or }U_{G}&=&rI-e\;,\\U_{E}&=&e'+r'I\\\text{ et }U_{R}&=&RI\\\Rightarrow\;rI -e+e'+r'I+RI&=&0\\\Rightarrow\left(R+r+r'\right)I&=&e-e'\\\Rightarrow\;I&=&\dfrac{e-e'}{R+r+r'} \end{array}$
 
3.2. Valeur de $R$
 
$\begin{array}{rcl} I&=&\dfrac{e-e'}{R+r+r'}\\\Rightarrow\;R+r+r'&=&\dfrac{e-e'}{I}\\\Rightarrow\;R&=&\dfrac{e-e'}{I}-\left(r-r'\right)\\\Rightarrow\;R&=&\dfrac{15-1.8}{2}-(0.8+4.8)\\\Rightarrow\;R&=&1.5\Omega \end{array}$
 
Calcul du rendement du générateur et le rendement de l'électrolyseur.
 
Pour le générateur :

$\begin{array}{rcl} r'&=&\dfrac{P_{u}}{P_{e}}\\&=&\dfrac{U_{G}I}{eI}\\&=&\dfrac{U_{G}}{e}\\&=&\dfrac{e-r'I}{e}\\&=&\dfrac{15-0.8\times 2}{15}\\ \Rightarrow\;r'&=&0.89\\\Rightarrow\;r&=&89\% \end{array}$
 
3.4. Calcul de la puissance chimique (puissance utile) de l'électrolyseur et de la puissance totale du générateur.
 
$\begin{array}{rcl} P_{u}&=&e'I\\&=&1.8\times 2\\\Rightarrow\;P_{u}&=&3.6\,W \end{array}$
 
$\begin{array}{rcl} P_{G}&=&(e-rI)I\\&=&(15-0.8\times 2)\times\\\Rightarrow\;P_{G}&=&26.8\,W \end{array}$
 
3.5. En $5$ minutes, quelle est Énergie dissipée par effet Joule dans le circuit ?
 
$\begin{array}{rcl} W_{J}&=&\left(R+r+r'\right)I^{2}t\\&=&(1.5+0.8+4.3)\times2^{2}\times5\times60\\\Rightarrow\;J&=&7.9\cdot^{3}J \end{array}$
 

Exercice 2

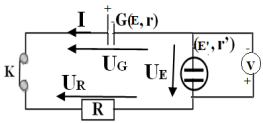
Schématisation du circuit
 
 
Justification théorique du résultat expérimental en donnant l'expression de la puissance mécanique développée par le moteur en fonction de l'intensité $I$ et la $f\cdot c\cdot é\cdot m\cdot E';$
 
$P_{m}=E'I$
 
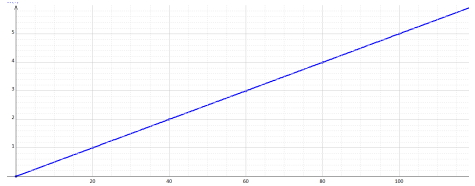
Le graphe représentant puissance mécanique développée par le moteur en fonction de l'intensité I est une droite linéaire, ce qui confirme le résultat expérimental
 
Calcul de la $f\cdot c\cdot é\cdot m\cdot E'$ du moteur.
 
$\begin{array}{rcl} P_{m}&=&E'I\\\Rightarrow\;E'&=&\dfrac{\Delta P_{m}}{\Delta I}\\&=&\dfrac{3-0}{0.5-0}\\\Rightarrow\;E'&=&6\,V \end{array}$
 
Calcul pour $I=0.5\,A$ et pendant $30\text{min}$
 
1. L'énergie mécanique développée par le moteur.
 
$\begin{array}{rcl} W_{m}&=&E'It\\&=&6\times0.5\times30\times60\\\Rightarrow\;W_{m}&=&4.5\cdot10^{2}J \end{array}$
 
2. L'énergie électrique consommée par le resistor résistance $R$
 
$\begin{array}{rcl} W_{R}&=&RI^{2}t\\&=&10\times0.5^{2}\times30\times60\\\Rightarrow\;W_{R}&=&4.5\cdot10^{2}J \end{array}$
 
3.3. L'énergie électrique totale fournie par le générateur au circuit extérieur.
 
$\begin{array}{rcl} W_{G}&=&U_{G}It\\&=&(E-rI)It\\&=&(12-1\times0.5)\times0.5\times30\times60\\\Rightarrow\;W_{G}&=&10.4\cdot10^{3}J \end{array}$
 
4. L'énergie électrique totale consommée par le moteur.
 
$\begin{array}{rcl} E_{m}&=&W_{G}-W_{R}\\&=&10.4\cdot10^{3}-4.5\cdot10^{2}\\\Rightarrow\;E_{m}&=&99.5\cdot10^{2} \end{array}$
 
Déduction du rendement du moteur.
 
$\begin{array}{rcl} \eta&=&\dfrac{W_{m}}{E_{m}}\\&=&\dfrac{5.4\cdot10^{3}}{9.95\cdot10^{3}}\\\Rightarrow\eta&=&0.54\\\Rightarrow\eta&=&54\% \end{array}$
 
5. Calculer $r'$ la résistance interne de moteur.
 
$\begin{array}{rcl} W_{r}&=&rI^{2}t\\&=&E_{m}-W_{m}\\\Rightarrow\;r&=&\dfrac{E_{m}-W_{m}}{I^{2}t}\\&=&\dfrac{9.95\cdot10^{3}-5.4\cdot10^{3}}{0.5^{2}\times30\times60}\\\Rightarrow\;r&=&1.0\Omega \end{array}$

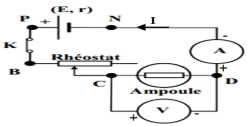
Exercice 3

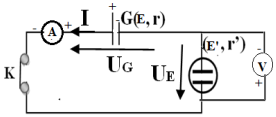
1. Schéma du circuit
 
 
2.1 Montrons que l'ampèremètre indique un curant d'intensité $I=lA$
 
$\begin{array}{rcl}W_{E}&=&U_{E}ITt\\\Rightarrow\;I&=&\dfrac{W_{E}}{U_{E}t}\\&=&\dfrac{5100}{17\times5\times60}\\\Rightarrow\;I&=&lA\end{array}$
 
2.2 Déduction de la résistance intense $r'$ du moteur.
 
$\begin{array}{rcl} U_{E}&=&E'+r'I\\\Rightarrow\;r'&=&\dfrac{U_{E}-E'}{I}\\&=&\dfrac{17-12}{l}\\\Rightarrow\;r'&=&5\Omega \end{array}$
 
2.3 Détermination de $R$
 
$\begin{array}{rcl} U_{G}&=&U_{E}+U_{R}\\\Rightarrow\;E-rI&=&U_{E}+RI\\\Rightarrow\;R&=&\dfrac{E-rI-U_{E}}{I}\\&=&\dfrac{24-2\times 1-17}{l}\\\Rightarrow\;R&=&5\Omega \end{array}$
 
3. Détermination de, pour une durée de $5\;min$ :
 
3.1 L'énergie électrique totale fournie par le générateur au circuit extérieur.
 
$\begin{array}{rcl} W_{G}&=&U_{G}It\\&=&(E-rI)It\\&=&(24-2\times1)\times1\times5\times60\\\Rightarrow\;W_{G}&=&6.6\cdot10^{3}J \end{array}$
 
3.2 L'énergie thermique dissipée dans tout le circuit.
 
$\begin{array}{rcl} W_{j}&=&\left(R+r+r'\right)I^{2}t\\&=&(5+2+5)\times1^{2}\times5\times60\\\Rightarrow\;W_{j}&=&3.6\cdot10^{3}J \end{array}$
 
3.3. L'énergie mécanique et l'énergie électrique reçue par le moteur.
 
$\begin{array}{rcl} W_{m}&=&E'It\\&=&12\times1\times5\times60\\\Rightarrow\;W_{m}&=&3.6\cdot10^{3}J \end{array}$
 
$\begin{array}{rcl} W_{é}&=&W_{m}+W_{j}^{'}\\&=&E'It+r'It^{2}\\&=&3.6\cdot10^{3}+5\times1(5\times60)^{2}\\\Rightarrow\;W_{é}&=&45.4\cdot10^{4}J \end{array}$

Exercice 4

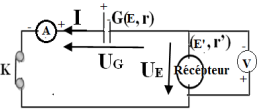
11. Schéma du circuit électrique comprenant le moteur et le générateur.
 
 
2. Expression de l'intensité du courant $I$ en fonction de $E$, $r$, $E'$ et $r'.$
 
La loi d'additivité des tensions s'écrit :
 
$\begin{array}{rcl} U_{G}+U_{E}&=&0\\\text{ or }U_{G}&=&rI\\\text{ et }U_{E}&=&E'+r'I\\\Rightarrow\;rI-E+E'+r'I&=&0\\\Rightarrow\left(r+r'\right)I&=&E-E'\\\Rightarrow\;I&=&\dfrac{E-E'}{r+r'} \end{array}$
 
4. Calcul de :
 
$-\ $La puissance électrique $P_{e}$ reçue par le moteur ;
 
$\begin{array}{rcl} P_{E}&=&U_{E}I\\&=&\left(E'+r'I\right)I\\&=&(7.2+11\times0.72)\times0.72\\\Rightarrow\;P_{E}&=&10.9\,W \end{array}$
 
$-\ $La puissance mécanique $P_{m}$ développée par le moteur ;
 
$\begin{array}{rcl} P_{m}&=&E'I\\&=&7.2\times0.72\\\Rightarrow\;P_{m}&=&5.2W \end{array}$
 
$-\ $La puissance $P_{j}$ dissipée par effet Joule dans l'ensemble du circuit.
 
$\begin{array}{rcl} P_{j}&=&\left(r+r'\right)I^{2}\\&=&(1.2+11)\times0.72^{2}\\\Rightarrow\;P_{j}&=&6.3\,W \end{array}$
 
5. Calcul de :
 
$-\ $Le rendement du générateur ; $\rho_{G}$
 
$\begin{array}{rcl} \rho_{G}&=&\dfrac{U_{G}I}{EI}\\&=&\dfrac{E-rI}{E}\\&=&\dfrac{16.0-1.2\times0.72}{16}\\\Rightarrow\rho_{G}&=&0.95\\\Rightarrow\rho_{G}&=&95\% \end{array}$
 
$-\ $du rendement du moteur ; $\rho_{M}$
 
$\begin{array}{rcl} \rho_{M}&=&\dfrac{E'I}{\left(E'+r'I\right)I}\\&=&\dfrac{E'}{\left(E'+r'I\right)}\\&=&\dfrac{7.2}{7.2+11\times0.72}\\\Rightarrow\rho_{M}&=&0.48\\\Rightarrow\rho_{G}&=&48\% \end{array}$
 
$-\ $du rendement du circuit ; $\rho=\rho_{M}\times\rho_{G}$
 
$\begin{array}{rcl} \rho&=&\rho_{M}\rho_{G}\\&=&0.48\times0.95\\\Rightarrow\rho&=&0.46\\\Rightarrow\rho&=&46\% \end{array}$
 

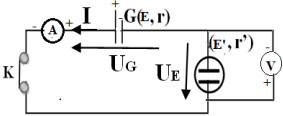
Exercice 5 : Transferts de puissance

1.1.1 Schéma du circuit électrique
 
 
1.2. Définitions de la $f\cdot é\cdot m.$ d'un générateur de tension et de la $f\cdot c\cdot é\cdot m.$ d'un récepteur
 
1.3. Expression de la tension aux bornes du générateur de tension en fonction de $E$, $r$ et $I.$
 
$U_{G}=E-rI$
 
1.4. Expression de la tension aux bornes du récepteur en fonction de $E'$, $r'$ et $I.$
 
$U_{E}=E'+r'I$
 
1.5 Déduction de l'expression de $I$ en fonction de $E$, $E'$, $r$ et $r'.$
 
La loi des tensions s'écrit : 
 
$\begin{array}{rcl} U_{E}&=&U_{G}\\\Rightarrow\;E'+r'I&=&E-rI\\\Rightarrow\left(r+r'\right)I&=&E-E'\\\Rightarrow\;I&=&\dfrac{E-E'}{r+r'} \end{array}$
 
2. On se place dans le cas où $E'=0.$
 
2.1. Le récepteur se comporte alors comme un conducteur ohmique (ou un résistor)
 
2.2. Expression de la puissance $P_{j}$  dissipée par effet Joule dans le récepteur en fonction de $E$, $r$ et $r'.$
 
$\begin{array}{rcl} P_{j}&=&r'I^{2}\\\text{ or }I&=&\dfrac{E}{r+r'}\\\Rightarrow\;P_{j}&=&r'r'\left(\dfrac{E}{r+r'}\right)^{2}\\\Rightarrow\;P_{j}&=&\dfrac{r'E^{2}}{\left(r+r'\right)^{2}} \end{array}$
 
2.3. Expression de la puissance $P_{\text{géné}}$ générée par le générateur de tension.
 
$\begin{array}{rcl} P_{\text{géné}}&=&EI\\\text{ or }I&=&\dfrac{E}{r+r'}\\\Rightarrow\;P_{\text{géné}}&=&\dfrac{E^{2}}{r+r'} \end{array}$
 
2.4. Déduction de la définition du rendement global η du circuit
 
C'est le rapport entre la puissance $P_{j}$ dissipée par effet joule par le récepteur et la puissance $P_{\text{géné}}$ générée
par le générateur de tension
 
Expression, rendement global $\eta$ du circuit du, appelé encore rendement du transfert de puissance.
 
$\begin{array}{rcl} \eta&=&\dfrac{P_{u}}{P_{\text{géné}}}\\&=&\dfrac{\dfrac{r'E^{2}}{r+r'}}{\dfrac{E^{2}}{r+r'}}\\\Rightarrow\eta&=&\dfrac{r'}{r+r'} \end{array}$
 
2.5. Relation entre $r$ et $r'$ pour que le rendement $\eta$ proche de $1.00$
 
$\begin{array}{rcl} \\\Rightarrow\eta&=&1.00\\\Rightarrow\dfrac{r'}{r+r'}&=&1.00\\\Rightarrow\;r'&=&r+r'\\\Rightarrow\;r&=&r'-r'\\\Rightarrow\;r&=&0\Omega \end{array}$
 
2.6 Expression de $P_{j}$ et de $P_{\text{géné}}$ lorsque $r=r'$
 
$\begin{array}{rcl} P_{j}&=&\dfrac{r'E^{2}}{\left(r+r'\right)^{2}}\;,r\\&=&r'\\\Rightarrow\;P_{j}&=&\dfrac{rE^{2}}{(2r)^{2}}\\\Rightarrow\;P_{j}&=&\dfrac{rE^{2}}{(2r)^{2}}\\\Rightarrow\;P_{j}&=&\dfrac{E^{2}}{4r} \end{array}$
 
$\begin{array}{rcl} P_{\text{géné}}&=&\dfrac{E^{2}}{r+r'}\;,r'&=&r'\\\Rightarrow\;P_{\text{géné}}&=&\dfrac{E^{2}}{2r}\\\Rightarrow\;P_{\text{géné}}&=&\dfrac{rE2} {(2r)^{2}}\\\Rightarrow\;P_{\text{géné}}&=&\dfrac{E^{2}}{4r} \end{array}$
 
Valeur numérique du rendement $\eta$ du transfert de puissance.
 
$\begin{array}{rcl} \eta&=&\dfrac{P_{j}}{P_{\text{géné}}}\\&=&1 \end{array}$
 
3.1 Expression de $P_{\text{géné}}$ en fonction de $E$, $E'$, $r$ et $r'.$
 
$\begin{array}{rcl} P_{\text{géné}}&=&EI\\\text{ or }I&=&I\\&=&\dfrac{E-E^{'}}{r+r'}\\\Rightarrow\;P\text_{{géné}}&=&\dfrac{E(E-E')}{r+r'} \end{array}$
 
3.2 Expression  de la puissance utile $P_{u}$ convertie par le récepteur.
 
$\begin{array}{rcl} P_{u}&=&E'I\\\text{ or }I&=&\dfrac{E-E'}{r+r'}\\\Rightarrow\;P_{u}&=&\dfrac{\left(E-E'\right)E'}{r+r'} \end{array}$
 
3.3. Déduction de l'expression du rendement  $\eta$ du transfert de puissance du circuit.
 
$\begin{array}{rcl} \eta&=&\dfrac{P_{u}}{P_{\text{géné}}}\\&=&\dfrac{\dfrac{\left(E-E'\right)E'}{r+r'}}{\dfrac{E\left(E-E'\right)}{r+r'}}\\\Rightarrow\eta&=&\dfrac{E'}{E} \end{array}$
 
Si $E'>E$, le récepteur ne fonctionne pas
 
3.4 Condition entre $E$ et $E'$ pour laquelle le rendement $\eta'$  est proche de $1.00$ 
 
$\begin{array}{rcl} \eta'&=&\\\Rightarrow\eta&=&\dfrac{E'}{E}\\&=&1.00\\\Rightarrow\;E'&=&E \end{array}$
 
3.5 Valeur numérique du rendement $\eta$
 
$\begin{array}{rcl} \eta&=&\dfrac{E'}{E}\\\Rightarrow\;E'&=&0.500E\\\Rightarrow\eta&=&\dfrac{0.500E}{E}\\\Rightarrow\eta&=&0.500\\\Rightarrow\eta&=&500\% \end{array}$

Exercice 6

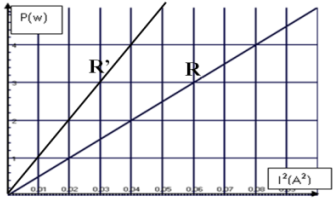
1. Justifions théoriquement la courbe obtenue
 
$P=RI^{2}$
 
La courbe représentant $P=f\left(I^{2}\right)$ est une droite qui passe par l'origine.
 
Ce qui est confirmé par la courbe expérimentale
 
2. Déduction de la valeur de $R$
 
$\begin{array}{rcl} R&=&\dfrac{\Delta P}{\Delta I^{2}}\dfrac{4-0}{0.08-0}\\\Rightarrow\;R&=&50\Omega \end{array}$
 
3. Calcul de $I$ lorsque la puissance consommée par le resistor
 
$\begin{array}{rcl} P&=&RI^{2}\\\Rightarrow\;I&=&\sqrt{\dfrac{P}{R}}\\&=&\sqrt{\dfrac{2.25}{50}}\\\Rightarrow\;I&=&0.21\,A \end{array}$
 
4. Calcul de :
 
a. La puissance électrique totale fournie par le générateur au circuit extérieur.
 
$\begin{array}{rcl} P&=&(E-rI)I\\&=&(24-2\times 0.2)\times 0.2\\\Rightarrow\;P_{G}&=&4.72\,W \end{array}$
 
b. La puissance consommée par le résistor. 
 
$\begin{array}{rcl} P&=&RI^{2}\\&=&50\times0.2^{2}\\\Rightarrow\;P&=&2\,W \end{array}$
 
c. La puissance électrique totale consommée par le moteur.
 
$\begin{array}{rcl} P_{G}&=&P+P_{m}\\\Rightarrow\;P_{m}&=&P_{G}-P\\&=&4.72-2\\\Rightarrow\;P_{m}&=&2.72\,W \end{array}$
 
Calcul de :
 
$-\ $La puissance mécanique développée par le moteur.

$\begin{array}{rcl} \rho&=&\dfrac{P_{\text{MECANIQ}}}{P_{m}}\\\Rightarrow\;P_{\text{MECANIQ}}&=&\rho P_{m}\\&=&0.92\times2.72\\\Rightarrow\;P_{\text{MECANIQ}}&=&2.5\,W \end{array}$
$-\ $La $f\cdot c\cdot é\cdot m\cdot E'$ et la résistance interne $r'$ du moteur.
 
$\begin{array}{rcl} P_{\text{MECANIQ}}&=&EI\\\Rightarrow\;E&=&\dfrac{P_{\text{MECANIQ}}}{I}\\&=&\dfrac{2.5}{0.2}\\\Rightarrow\;E&=&12.5\,V \end{array}$
 
$\begin{array}{rcl} \Rightarrow\;P_{m}&=&\left(E'+r'\right)I\\\Rightarrow\;E'+r'I&=&\dfrac{P_{m}}{I}\\\Rightarrow\;r'&=&\dfrac{P_{m}}{I^{2}}-\dfrac{E'}{I}\\&=&\dfrac{2.72}{0.2^{2}}-\dfrac{12.5}{0.2}\\ \Rightarrow\;r'&=&5.5\Omega \end{array}$
 
5. Tracé sur la même feuille l'allure de la courbe représentative de la variation de la puissance électrique
 
consommée par le résistor de résistance $R'$ et celle consommée par R en fonction de $I^{2}$
 

Exercice 7

 
1.a. Détermination de l'intensité du courant dans le circuit.
 
$\begin{array}{rcl} W_{M}&=&W_{u}+W_{j}\\\Rightarrow\;W_{u}&=&W_{M}-W_{j}\\\Rightarrow\;W_{u}&=&E'It\\&=&W_{M}-W_{j}\\\Rightarrow 12I\times5\times 60&=&17I\times5\times 60 -1500\\\Rightarrow 36I&=&51I-15\\\Rightarrow 15I&=&15\\\Rightarrow\;I&=&1.0\,A \end{array}$
 
b. Déduction de la résistance interne $r'$ du moteur.
 
$\begin{array}{rcl} W_{j}&=&r'I^{2}t\\\Rightarrow\;r'&=&\dfrac{W_{j}}{I^{2}t}\\&=&\dfrac{1500}{1.0^{2}\times 5\times 60}\\\Rightarrow\;r'&=&5.0\Omega \end{array}$
 
2. Détermination de 
 
a. L'énergie électrique totale fournie par les deux piles.
 
$\begin{array}{rcl} W_{p}&=&U_{1}It+U_{2}It\\\text{ or }U_{1}&=&U_{2}\\\Rightarrow\;W_{p}&=&2U_{1}It\\&=&2(E-rI)It\\&=&2(12-1\times1.0)\times1.0\times5\times60\\\Rightarrow\;W_{p}&=&6.6\cdot10^{3}J \end{array}$
 
b. L'énergie thermique dissipée dans tout le circuit.
 
$\begin{array}{rcl} W_{j}&=&\left(R+r+r'\right)I^{2}t\\&=&(5+1+5)\times1.0^{2}\times5\times60\\\Rightarrow\;W_{j}&=&3.3\cdot10^{3}J \end{array}$
 
c. L'énergie mécanique et l'énergie électrique reçue par le moteur.
 
$\begin{array}{rcl} W_{M}&=&W_{p}-W_{j}\\&=&6.6\cdot10^{3}-3.3\cdot10^{3}\\\Rightarrow\;W_{M}&=&3.3\cdot10^{3}J \end{array}$
 
$\begin{array}{rcl} W_{E}&=&W_{M}+r'It^{2}\\&=&3.3\cdot10^{3}+5\times1.0\times(5\times 60)^{2}\\\Rightarrow\;W_{E}&=&4.8\cdot10^{3}J \end{array}$
 
Déduction du rendement du moteur.
 
$\begin{array}{rcl} \eta&=&\dfrac{W_{M}}{W_{E}}\\&=&\dfrac{3.3\cdot10^{3}}{4.8\cdot10^{3}}\\\Rightarrow\eta&=&0.69\\\Rightarrow\eta&=&69\% \end{array}$

Exercice 8

1.1 Expression de la tension $U_{PN}$ aux bornes de la pile lorsqu'elle débite un courant d'intensité $I.$
 
$U_{PN}=E-rI$
 
1.2 Déduction de la valeur de $E$ et de $r$
 
$\begin{array}{rcl} U_{PN}&=&E-rI\\&\Rightarrow&\left\lbrace\begin{array}{rcl} 3.9&=&E-0.3\,r\quad(1)\\ 3.5&=&E-0.5\,r\quad(2) \end{array}\right.\\(1)-(2)&\Rightarrow&0.4=0.2\,r\\\Rightarrow\; r&=&2\,0\Omega\ ;\ (1)3.9\\&=&E-0.3\times2\\\Rightarrow\;E&=&4.5\,V \end{array}$
 
2. Calculer l'intensité $I$ du courant lorsque la tension aux bornes de la pile est $U_{PN}=2.5\,V.$
 
$\begin{array}{rcl} U_{PN}&=&E-rI\\\Rightarrow\;I&=&\dfrac{E-U_{PN}}{r}\\&=&\dfrac{4.5-2.5}{2.0}\\\Rightarrow\;I&=&1.0\,A. \end{array}$
 
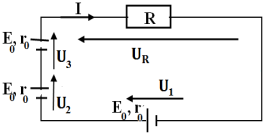
3.1 Calcul du nombre $N$ des piles associées en série.
 
$\begin{array}{rcl} E&=&N\cdot E_{0}\\\Rightarrow\;N&=&\dfrac{E}{E_{0}}\\&=&\dfrac{13.5}{4.5}\\\Rightarrow\;N&=&3\text{piles} \end{array}$
 
3.2 Calculer la résistance $r$ du générateur équivalent.
 
$\begin{array}{rcl} r&=&Nr_{0}\\&=& 3\times 2\\\Rightarrow\;r&=&6\Omega \end{array}$
 
3.3 Ces $N$ piles montées en série sont branchées aux bornes d'un résitor de résistance $R=50\Omega$
 
$\bullet $Schéma du montage 
 
 
$\bullet $Calcul de l'intensité $I$ du courant dans le circuit.
Appliquons la loi de Pouillet :
 
$\begin{array}{rcl} I&=&\dfrac{\sum E_{i}}{\sum r_{i}}\\&=&\dfrac{E_{0}+E_{0}+E_{0}}{r+r+r+R}\\&=&\dfrac{3E_{0}}{3r+R}\\&=&\dfrac{3\times4.5}{3\times 2+50}\\\Rightarrow\;I&=&0.24\,A \end{array}$

Exercice 9

Calcul de :
 
1. La puissance électrique transformée en puissance thermique dans le moteur.
 
$\begin{array}{rcl} P_{Th}&=&\dfrac{W_{Th}}{t}\\&=&\dfrac{12\cdot10^{3}}{60}\\\Rightarrow\;P_{Th}&=&2.0\cdot10^{2}W \end{array}$
 
2. La puissance électrique totale consommée par le moteur.
 
$\begin{array}{rcl} P&=&P_{Th}+P_{M}\\&=&2.0\cdot10^{2}+1000\\\Rightarrow\;P&=&1.2\cdot10^{2}W \end{array}$
 
3. L'énergie électrique consommée par le moteur en $lh.$
 
$\begin{array}{rcl} W&=&Pt\\&=&1.2\cdot10^{2}\times 1\times60\times60\\\Rightarrow\;W&=&47\cdot10^{4}J \end{array}$
 
4. Le rendement du moteur 
 
$\begin{array}{rcl} r&=&\dfrac{P_{M}}{P}\\&=&\dfrac{1000}{1.2\cdot10^{2}}\\\Rightarrow\;r&=&0.83\\\Rightarrow\;r&=&83\%\end{array}$

Exercice 10

1. L'association les deux piles en parallèles ne permet pas d'alimenter le moteur car la tension d'alimentation du circuit $(E=4.5\,V)$ nécessaire pour faire fonctionner le moteur.
 
IL faut une source d'alimentation plus élevée, et l'association en série convient
 
2. Schéma du circuit qui permet au moteur de tourner
 
3. Expression de l'intensité du courant qui traverse le circuit.
 
La loi des mailles s'écrit :
 
$\begin{array}{rcl} U_{1}+U_{2}+U_{M}&=&0\\\Rightarrow\;r_{1}I-E_{1}+r_{2}I-E_{2}+E'+r'I&=&0\\\Rightarrow\left(r_{1}+r_{2}+r'\right)I&=&E_{1}+E_{2}-E'\\\Rightarrow\;I&=&\dfrac{E_{1}+E_{2}-E'}{r_{1}+r_{2}+r'} \end{array}$
 
Calcul de l'intensité :
 
$\begin{array}{rcl} \\\Rightarrow\;I&=&\dfrac{4.5+4.5-5}{1.5+1.5+2}\\\Rightarrow\;I&=&0.8\,A \end{array}$
 
4. Bilan énergétique et calcul de ces énergies électriques après une heure de fonctionnement
 
\begin{eqnarray} W_{1}&=&U_{1}It\nonumber\\&=&\left(E_{1}-r_{1}I\right)It\nonumber\\&=&(4.5-1.5\times 0.8)\times 0.8\times 1\times 60\times 60\nonumber\\\Rightarrow\;W&=&9.5\cdot 10^{3}J \end{eqnarray}
 
$\begin{array}{rcl} W_{2}&=&W_{1}\\\Rightarrow\;W_{2}&=&9.5\cdot10^{3}J \end{array}$
 
$\begin{array}{rcl} W_{M}&=&U_{M}It\\&=&\left(E_{M}+r'I\right)It\\&=&(5+2\times0.8)\times 0.8\times 1\times60\times60\\\Rightarrow\;W_{M}&=&19\cdot10^{3}J \end{array}$
 
 
5. Rappel de l'expression de la puissance électrique consommée par un dipôle et signification physique de chaque terme.
 
$\begin{array}{rcl} P&=&E'I+rI^{2}\\&=&P_{u}+P_{j}\text{ avec }P_{u}&=&E'I\ ;\ \\P_{u}&=&rI^{2} \end{array}$
 
$P_{u}=E'I$ : est la puissance utile
 
$P_{u}=rI^{2}$ : est la puissance dissipée,par effet Joule
 
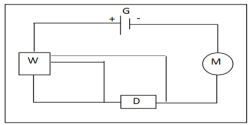
6.1 Nature du dipôle $D$
 
Le dipôle D transforme entièrement l'énergie électrique qu'il reçoit en énergie thermique. 
 
$D$ est un résistor (ou conducteur ohmique)
 
6.2 Déduction de sa grandeur électrique caractéristique
 
$\begin{array}{rcl} P_{u}&=&rI^{2}\\ \Rightarrow\;r&=&\dfrac{P_{u}}{I^{2}}\\&=&\dfrac{200}{2^{2}}\\\Rightarrow\;r&=&50\Omega \end{array}$
 
7.1 Détermination de l'énergie électrique $W_{1}$ consommée par le moteur
 
$\begin{array}{rcl} W_{1}&=&\left(E'+r'I\right)It\\&=&(6+2\times2)\times2\times10\times60\\\Rightarrow\;W_{1}&=&12\cdot10^{3}J \end{array}$
 
7.2 $W_{1}$ est transformée en énergie mécanique et en énergie thermique
 
Détermination de la valeur de chacune de ces énergies.
 
$\begin{array}{rcl} W_{\text{méc}}&=&E'It\\&=&6\times2\times10\times60\\\Rightarrow\;W_{\text{méc}}&=&7.2\cdot10^{3}J \end{array}$
 
$\begin{array}{rcl} W_{j}&=&r'I^{2}t\\&=&2\times2^{2}\times10\times60\\\Rightarrow\;W_{j}&=&4.8\cdot10^{3}J \end{array}$
 
8.1.Détermination, pendant la même durée, de l'énergie électrique produite par le générateur $G.$
 
L'énergie électrique produite par le générateur $G$ est transférée au moteur et au conducteur ohmique
 
$\begin{array}{rcl} W_{G}&=&W_{1}+rI^{2}t\\\Rightarrow\;W_{G}&=&12\cdot10^{3}+50\times2^{2}\times10\times60\\\Rightarrow\;W_{G}&=&13.2\cdot10^{4}J \end{array}$
 
8.3 Retrouvons,  la valeur de $E$ par application de la loi de Pouillet.
 
$\begin{array}{rcl} I&=&\dfrac{\sum E_{i}}{\sum r_{i}}\\&=&\dfrac{E-E^{'}}{r+r'}\\\Rightarrow\;E E'&=&\left(r+r'\right)I\\ \Rightarrow\;E&=&\left(r+r'\right) I+E'\\\Rightarrow\;E&=&(50+2)\times2+6\\\Rightarrow\;E&=&110\,V \end{array}$

Exercice 11

1. Rappel des lois d'ohm relatives à chaque dipôle. 
 
Pour le générateur : $U_{PN}=E_{1}-r_{1}I$
 
Pour le resistor : $U_{R}=RI$
 
Pour le moteur : $U_{m}=E'+r'I$
 
2. L'ampèremètre indique $I_{1=}0A$
 
On peut dire que la $f\cdot c\cdot é\cdot m E'$ du moteur est supérieure à la tension générateur $U_{PN}=E_{1}-r_{1}I$ 
 
3. Déduction des valeurs de $E'$ et $r'$
 
$\begin{array}{rcl} U_{PN}=U_{R}+U_{M}\Rightarrow;E_{1}-r_{1}=RI+E'+r'&\Rightarrow&\left\lbrace\begin{array}{lcl} E_{2}-1.5I_{2}&=&RI_{2}+E'+r'I_{2}\\ E_{2}-1.5I_{3}&=&RI_{3}+E'+r'I_{3} \end{array}\right. \\&\Rightarrow&\left\lbrace\begin{array}{lcl} 16-1.5\times0.6&=&5\times0.6+E'+0.6r'\\ 16-1.5\times1.8&=&E'+1.8r' \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{rcl} E'+0.6r'&=&12.1\quad(1)\\ E'+1.8r'&=&13.3\quad(2) \end{array}\right.\\(2)-(1)&\Rightarrow&1.2r'=1.2\\&\Rightarrow&\;r'=1.0\Omega\\&\Rightarrow&\;E'+0.6\times1.0=12.1\\&\Rightarrow&\;E'=11.5\,V \end{array}$
 
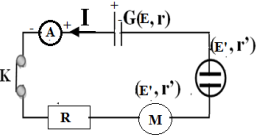
4.1. Détermination du dipôle équivalent de l'association étudiée 
 
Déterminations le générateur équivalent
$\left.\begin{array}{lllll}G_{1}(E_{1}&=&12V\quad ;\quad r_{1}&=&1\Omega)\\G_{1}(E_{2}&=&16V\quad;\quad r_{2}&=&1.5\Omega) \end{array}\right\rbrace$
 
$\begin{array}{rcl} &\Rightarrow&\;G\left(E=E_{1}+E_{2}=12V\quad ;\quad r=r_{1}+r_{2}=1\Omega+1.5\Omega\right)\\&\Rightarrow&\;G\left(E=28V\quad ;\quad r=2.5\Omega\right) \end{array}$
 
Détermination la résistance équivalente
 
$\begin{array}{rcl} R&=&R_{1}+R_{2}+R_{3}\\&=&5\Omega+5\Omega+5\Omega\\&\Rightarrow&\,R=15\Omega \end{array}$
 
 
4.2.Détermination de l'intensité du courant qui circule dans le circuit
Par application de la loi de Pouillet, on a :
 
$\begin{array}{rcl} I&=&\dfrac{\sum E_{i}}{\sum r_{i}}\\&=&\dfrac{E-\left(E'+E'\right)}{r+r'+r'+R}\\&=&\dfrac{28-(11.5+10}{2.5+1+2+15}\\\Rightarrow\,I&=&0.32\,A \end{array}$

Exercice 12

1. Écriture de la loi d'Ohm aux bornes de chaque dipôle.
 
$\begin{array}{rcl} U_{G}&=&E-rI_{1}\\&=&R_{1}I_{1}\\\Rightarrow\;E-2r&=&4\times 2\\\Rightarrow\;E-2r&=&8 \end{array}$
 
$\begin{array}{rcl} U_{G}&=&E-rI_{2}\\&=&R_{2}I_{1}\\\Rightarrow\;E-4r&=&1\times 4\\\Rightarrow\;E-4r&=&4 \end{array}$
 
2. Détermination des grandeurs caractéristiques $(E\ ;\ r)$ du générateur.
 
$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} E-2r&=&2\quad(1)\\E-4r&=&4\quad(2) \end{array}\right.\ ;\ \\(1)-(2)\Rightarrow& 2r&=&4\\\Rightarrow&\;r&=&2\Omega\\\Rightarrow&\;E-2\times2&=&8\\\Rightarrow&\;E&=&12V \end{array}$
 
3. 
 
 
3.1. Schéma du circuit.
 
 
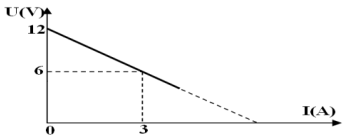
3.2 Retrouvons, à partir du graphe, les valeurs des grandeurs caractéristiques du générateur.
 
$E=12\,V$
 
$\begin{array}{rcl} r&=&-\dfrac{\Delta U}{\Delta I}\\&=&-\dfrac{6-12}{3-0}\\\Rightarrow\,r&=&2\Omega \end{array}$
 
3.3 . Détermination graphique et par calcul de la valeur de l'intensité du courant électrique de court-circuit
 
Par méthode graphique : $I_{cc}=6\,A$
 
Par calcul :
 
$\begin{array}{rcl} U&=&E-rI\\&=&0\\\Rightarrow12-2I&=&0\\\Rightarrow2I&=&12\\\Rightarrow\;I&=&6A \end{array}$
 
4.1. Détermination de l'intensité du courant électrique qui circule dans le circuit par application de la loi de Pouillet
 
$\begin{array}{rcl} U_{G}&=&U_{E}\\\Rightarrow\;E-rI&=&E'+r'I\\\Rightarrow12-2I&=&8+2I\\\Rightarrow4I&=&4\\\Rightarrow\,I&=&1\,A  \end{array}$
 
4.2. Déduction des coordonnées du point de fonctionnement $P.$
 
$\begin{array}{rcl} P\left\lbrace\begin{array}{lcl} I_{p}&=&1\,A\\ U_{p}&=&12-2\times1 \end{array}\right.\\\Rightarrow\;P\left\lbrace\begin{array}{lcl} I_{p}&=&1\,A\\ U_{p}&=&10\,V \end{array}\right. \end{array}$
 
Les deux dipôles sont adaptés
 

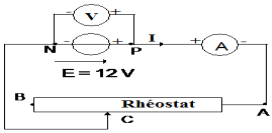
Exercice 13 : Fonctionnement d'une lampe de poche

 
1. On peut faire varier l'intensité I du courant électrique dans le circuit en déplaçant le curseur du rhéostat
 
2. Schéma, sens conventionnel du courant électrique et bornes des appareils de mesure
 
 
3. Calcul de $U_{PN}$
 
$\begin{array}{rcl} U_{PN}1&=&E-rI\\&=&4.5-1.5\times0.2\\\Rightarrow\,U_{PN}&=&4.2\,V \end{array}$
 
 
$-\ $Valeur de la résistance $R$du rhéostat
 
$\begin{array}{rcl} U_{BC}&=&U_{PN}-U_{CD}\\\Rightarrow\,RI&=&U_{PN}-U_{CD}\\\Rightarrow\;R&=&\dfrac{U_{PN}-U_{CD}}{I}\\\Rightarrow\;R&=&\dfrac{4.2-2.0}{0.20}\\\Rightarrow\,R&=&11\Omega \end{array}$
 
$-\ $Valeur $P_{1}$ de la puissance fournie par le générateur au circuit extérieur
 
$\begin{array}{rcl} P_{1}&=&U_{PN}I\\&=&4.2\times0.20\\\Rightarrow\;P_{1}&=&0.84\,W \end{array}$
 
$-\ $Puissance $P_{2}$ dissipée par effet joule dans le générateur
 
$\begin{array}{rcl} P_{2}&=&rI^{2}\\&=&1.5\times(0.20)^{2}\\\Rightarrow\;P_{2}&=&0.06\,W \end{array}$
 
4. Rappel de la relation donnant la puissance électrique $P_{3}$ consommée dans l'ampoule.
 
$P_{3}=U_{CD}I$
 
5. Détermination de la tension U aux bornes de l'ampoule.
 
$\begin{array}{rcl} P&=&1.0\,W\\\Rightarrow\,U_{CD}&=&3.6\,V \end{array}$
 
Déduction de la valeur de l'intensité I du courant électrique qui la traverse
 
$\begin{array}{rcl} P&=&U_{CD}I\\\Rightarrow\;I&=&\dfrac{P}{U_{CD}}\\&=&\dfrac{1.0}{3.6}\\\Rightarrow\;I&=&0.28\,A \end{array}$
 
L'indication portée par l'ampoule : $1\,W\ ;\ 0.3\,A$ est cohérente avec les résultats

Exercice 14:  Caractéristique d'un électrolyseur

1. Schéma du montage
 
 
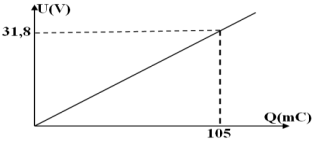
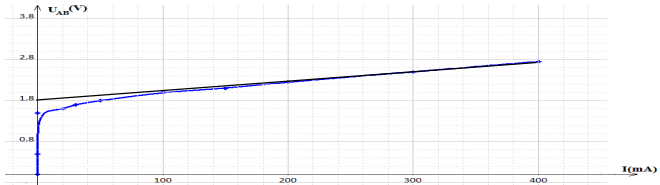
2 Représentation graphique de la tension $U_{AB}$ en fonction de l'intensité $I$ du courant électrique
 
 
3. Pour la partie linéaire de la courbe de la forme : $U=a+bI$ :
 
$-\ a$ représente la force contre électromotrice $(f\cdot c\cdot é\cdot m) $ $E’$ de lélectrolyseur
 
$-\  b$ représente la résistance interne  $r'$ de l'électrolyseur
 
Détermination graphique a et b en détaillant soigneusement les calculs.
 
$a=1.8\,V$
 
$\begin{array}{rcl} b&=&\dfrac{\Delta U_{AB}}{\Delta I}\\&=&\dfrac{2.75-2.25}{(400-200)\cdot10^{-3}}\\\Rightarrow\;b&=&2.5\Omega \end{array}$
 
Équation numérique $U=f(I)$
 
$U=1.8+2.5I$
 
4. Expression de la puissance électrique reçue par l'électrolyseur
 
$\begin{array}{rcl} P&=&UI\\&=&(1.8+2.5I)I \end{array}$
 
Calcul de sa valeur
 
$\begin{array}{rcl} P&=&\left(1.8+2.5\times200\cdot10^{-3}\right)\times200\cdot10^{-3}\\\Rightarrow\;P&=&0.46\,W \end{array}$
 
$=200\,m\cdot A$
 
5.5. Énergie, exprimée en $kWh$, reçue par l'électrolyseur
 
$\begin{array}{rcl} W&=&Pt\\&=&0.46\times 5\times 60\times 60\\\Rightarrow\;W&=&8.28\cdot10^{3}J\\\Rightarrow\;W&=&\dfrac{8.28}{3600}\\\Rightarrow\;W&=&2.3\cdot10^{-3}kW \end{array}$

 

Solution des exercices : le Travail et la Puissance mécaniques - 3e

Classe: 
Troisième

Exercice 1

En effet, soit $\vec{F}$ une force constante dont le déplacement rectiligne de son point d'application $A$ vers un point $B$ est $d=AB$ et soit $\alpha$ l'angle entre la force et le déplacement.
 
 
Alors, le travail $W(\vec{F})$ de cette force $\vec{F}$ est donné par :
$$W(\vec{F})=F\times d\times\cos\alpha$$
Par suite, calculons le travail d'une force de $12.0\;N$ dont le point d'application se déplace de $7.00\;m$, si l'angle $\alpha$ entre la force et le déplacement vaut : 
 
a) $\alpha=0.00^{\circ}$
 
 
 
Dans l'expression de $W(\vec{F})$, en remplaçant $F\;,\ d\ $ et $\ \alpha$ par leur valeur, on trouve :
 
$\begin{array}{rcl} W(\vec{F})&=&12.0\times 7.00\times\cos 0^{\circ}\\\\&=&84\times 1\\\\&=&84\end{array}$
 
D'où, $\boxed{W(\vec{F})=84\;J}$
 
b) $\alpha=60.0^{\circ}$
 
 
 
Dans l'expression de $W(\vec{F})$, remplaçons $F\;,\ d\ $ et $\ \alpha$ par leur valeur.
 
On obtient alors :
 
$\begin{array}{rcl} W(\vec{F})&=&12.0\times 7.00\times\cos 60^{\circ}\\\\&=&84\times 0.5\\\\&=&42\end{array}$
 
Donc, $\boxed{W(\vec{F})=42\;J}$
 
c) $\alpha=90.0^{\circ}$
 
 
 
Dans l'expression de $W(\vec{F})$, en remplaçant $F\;,\ d\ $ et $\ \alpha$ par leur valeur, on trouve :
 
$\begin{array}{rcl} W(\vec{F})&=&12.0\times 7.00\times\cos 90^{\circ}\\\\&=&84\times 0\\\\&=&0\end{array}$
 
Ainsi, $\boxed{W(\vec{F})=0\;J}$
 
d) $\alpha=145^{\circ}$
 
 
 
Dans l'expression de $W(\vec{F})$, en remplaçant $F\;,\ d\ $ et $\ \alpha$ par leur valeur, on obtient :
 
$\begin{array}{rcl} W(\vec{F})&=&12.0\times 7.00\times\cos 145^{\circ}\\\\&=&84\times(-0.82)\\\\&=&-68.88\end{array}$
 
D'où, $\boxed{W(\vec{F})=-68.88\;J}$
 
e) $\alpha=180^{\circ}$
 
 
 
Dans l'expression de $W(\vec{F})$, en remplaçant $F\;,\ d\ $ et $\ \alpha$ par leur valeur, on trouve :
 
$\begin{array}{rcl} W(\vec{F})&=&12.0\times 7.00\times\cos 180^{\circ}\\\\&=&84\times(-1)\\\\&=&-84\end{array}$
 
Ainsi, $\boxed{W(\vec{F})=-84\;J}$

Solution des exercices : Travail de la force électrostatique - Énergie potentielle électrostatique - 1er s

Classe: 
Première

Exercice 1
 

 
 
1. Direction et sens (voir figure)
 
Intensité du champ électrique $\overrightarrow{E}$ qui règne dans le domaine situé $D$ entre les deux plaques
 
$\begin{array}{rcl} E&=&\dfrac{U}{d}\\&=&\dfrac{500}{10\cdot10^{-2}}\\\Rightarrow\;E&=&50\cdot10^{2}Vm^{-1} \end{array}$
 
2. Calcul des $d\cdot d\cdot p V_{O}-V_{M}$ ;
 
$V_{O}-V_{N}$ et $V_{M}-V_{N}$
 
$\begin{array}{rcl} V_{0}-V_{M}&=&\overrightarrow{E}\cdot\overrightarrow{OM}\\&=&E\times OM\\&=&50\cdot10^{2}\times2\cdot10^{-2}\\\Rightarrow\;V_{0}-V_{M}&=&100V \end{array}$
 
$\begin{array}{rcl} V_{0}-V_{N}&=&\overrightarrow{E}\cdot\overrightarrow{ON}\\&=&E\times ON\\&=&E\times ON\\&=&50\cdot10^{2}\times7\cdot10^{-2}\\\Rightarrow\;V_{0}-V_{M}&=&3.5\cdot10^{2}V \end{array}$
 
$\begin{array}{rcl} V_{M}-V_{N}&=&\overrightarrow{E}\cdot\overrightarrow{MN}\\&=&E\times MN\\&=&50\cdot10^{2}\times\left|7\cdot10^{-2}-2\cdot10^{-2}\right|\\\Rightarrow\;V_{M}-V_{N}&=&2.5\cdot10^{2}V \end{array}$
 
3.1 Caractéristiques de la force électrostatique $\overrightarrow{F}$ qui s'exerce sur l'électron
 
Direction et sens (voir figure)
 
Intensité : 
 
$\begin{array}{rcl} F&=&qE\\&=&1.6\cdot 1.6\cdot10^{-19}\times50\cdot10^{2}\\\Rightarrow\;F&=&80\cdot10^{-17}N \end{array}$
 
3.2 Vitesse de l'électron à son passage en $N$, $M$, puis en $O$
 
Appliquons le théorème de l'énergie cinétique : 
Entre $R$ et $N$ :
 
$\begin{array}{rcl} E_{C_{N}}-E_{C_{R}}&=&W_{NR}\left(\overrightarrow{F}\right)+W_{NR}\left(\overrightarrow{P}\right)\\\Rightarrow\dfrac{1}{2}m_{e}V_{N}^{2}-0&=&-eU_{RN}+0\\\Rightarrow\dfrac{1}{2}m_{e}V_{N}^{2}-0&=&-e\times-\left(U-U_{ON}\right) \end{array}$
 
$\begin{array}{rcl} V_{N}&=&\sqrt{\dfrac{2e\left(U-U_{ON}\right)}{me}}\\&=&\sqrt{\dfrac{2\times1.6\cdot10^{-19}\times\left(500-3.5\cdot10^{2}\right)}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{N}&=&7.3\cdot10^{6}m\cdot s^{-1} \end{array}$
 
$\begin{array}{rcl} V_{M}&=&\sqrt{\dfrac{2e\left(U-U_{OM}\right)}{m_{e}}}\\&=&\sqrt{\dfrac{2\times1.6\cdot10^{-19}\times(500-100)}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{N}&=&11\cdot10^{6}m\cdot s^{-1} \end{array}$
 
$\begin{array}{rcl} V_{O}&=&\sqrt{\dfrac{2e\left(U-U_{OO}\right)}{m_{e}}}\\&=&\sqrt{\dfrac{2\times1.6\cdot10^{-19}\times(500-0)}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{o}&=&13\cdot10^{6}m\cdot s^{-1} \end{array}$
 
4. Calculer le travail $W\left(\overrightarrow{F}\right)$ de la force lorsque l'électron déplace de $N$ à $M$
 
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&-e\left(V_{N}-V_{M}\right)\\&=&-e\times-\left(V_{M}-V_{N}\right)\\&=&e\times\left(V_{M}-V_{N}\right)\\&=&1.6\cdot10^{-19}\times2.5\cdot10^{2}\\\Rightarrow\;W \left(\overrightarrow{F}\right)&=&4.0\cdot10^{-17}J \end{array}$
 

Exercice 2

 
1.1 Détermination des caractéristiques du vecteur champ électrostatique entre  $C$ et $A$
 
Direction et sens (voir figure)
 
Intensité du champ électronique $\overrightarrow{E}$
 
$\begin{array}{rcl} E&=&\dfrac{U_{AC}}{CA}\\&=&\dfrac{640}{5\cdot10^{-2}}\\\Rightarrow\;E&=&12.8\cdot10^{3}V\cdot m^{-1} \end{array}$ 
 
1.2 Calcul du travail de la force électrostatique appliquée à un électron pour aller de $C$ à $A$
 
$\begin{array}{rcl} W_{CA}\left(\overrightarrow{F}\right)&=&-eU_{CA}\\&=&-e\times-U_{AC}\\&=&eU_{AC}\\&=&1.6\cdot10^{-19}\times640\\\Rightarrow\;w_{CA}\left(\overrightarrow{F}\right)&=&1.0\cdot10^{-16}J \end{array}$
 
2. Calcul de la tension $U_{OM}$
 
$\begin{array}{rcl} U_{OM}&=&\overrightarrow{E}\cdot\overrightarrow{OM}\\&=&-E\times OM\text{ or }E\\&=&\dfrac{U_{PN}}{d}\\\Rightarrow\;U_{OM}&=&-\dfrac{U_{PN}}{d}\times d'\\&=&-\dfrac{1000}{5}\times 2\\\Rightarrow\;U_{OM}&=&-400V \end{array}$ 
 
3. Calcul de l'énergie potentielle électrostatique d'un électron en $O$ et en $M.$
 
$E_{p}=qV+\text{cte}$ ; 
 
$\begin{array}{rcl} Q_{1}+Q_{2}&=&0\\\Rightarrow\left(\rho_{\text{eau}}V_{0}C_{\text{eau}}+\mu\right)\left(\theta_{4}-\theta_{0}\right)-m'L_{v}+m'C_{\text{eau}}\left(\theta_{4}-\theta_{3}\right)&=&0\\\Rightarrow\;-m'L_{v} &=&\left(\rho_{\text{eau}}V_{0}C_{\text{eau}}+\mu\right)\left(\theta_{0}-\theta_{4}\right)+m'C_{\text{eau}}\left(\theta_{3}-\theta_{4}\right)\\\Rightarrow\;L_{v}&=&-\dfrac{\left(\rho_{\text{eau}}V_{0}C_{\text{eau}}+\mu\right)\left(\theta_{0}-\theta_{4}\right)+m'C_{\text{eau}}\left(\theta_{3}-\theta_{4}\right)}{m'}\\\Rightarrow\;L_{v}&=&-\dfrac{\left(1\times450\cdot10^{-3}\times4185+100\right)(20.0-45.2)+20.0\cdot10^{-3}\times4185(100-45.2)}{20.0\cdot10^{-3}}\\\Rightarrow\;L_{v}&=&2.27\cdot10^{6}J\cdot kg^{-1} \end{array}$
 
4. Détermination du travail de la force électrostatique s'exerçant sur un électron pour aller de $O$ à 
 
$\begin{array}{rcl} W_{OM}\left(\overrightarrow{F}\right)&=&-\Delta E_{p}\\&=&-\left(E_{P_{M}}-E_{P_{o}}\right)\\&=& \left(-14.4\cdot10^{-17}-8.0\cdot10^{-17}\right)\\\Rightarrow\;W_{OM}\left(\overrightarrow{F}\right)&=&6.4\cdot10^{-17} \end{array}$
 
5. Calcul de :
 
5.1. L'énergie cinétique de sortie $E_{CM}$ de l'électron en $M.$
 
Appliquons le théorème de l'énergie cinétique

$\begin{array}{rcl} W_{OM}\left(\overrightarrow{F}\right)&=&\Delta E_{C}\\&=&E_{C_{M}}-E_{C_{o}}\\&=&W_{OM}\left(\overrightarrow{F}\right)\\\Rightarrow\;E_{C_{M}}&=&W_{OM}\left(\overrightarrow{F}\right)+E_{C_{o}}\\\text{or }E_{C_{o}}=E_{C_{A}}=-eU_{CA}=-e\times -U_{AC}\\\Rightarrow\;E_{C_{M}}&=&W_{OM}\left(\overrightarrow{F}\right)+eU_{AC}\\\Rightarrow\;E_{C_{M}}&=&6.4\cdot10^{-17}+1.6\cdot 10^{-19}\times 640\\\Rightarrow\;E_{C_{M}}&=&7.4\cdot10^{-17}J \end{array}$
 
5.2 La vitesse de l'élection $V_{M}$ au point $M.$
 
$\begin{array}{rcl} E_{C_{M}}&=&\dfrac{1}{2}mV_{M}^{2}\\\Rightarrow\;V_{M}^{2}&=&\dfrac{2E_{C_{M}}}{m}\\\Rightarrow\;V_{M}&=&\sqrt{\dfrac{2E_{C_{M}}}{M}}\\&=&\sqrt{\dfrac{2\times7.4\cdot10^{-17}}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{M}&=&13\cdot10^{6}m\cdot s^{-1} \end{array}$
 

Exercice 3

 
1. Inventaire des forces que subit la particule au cours de son déplacement de $A$ vers $B.$
 
La particule est soumise à : son poids $\overrightarrow{P}$ , la force électrostatique $\overrightarrow{F}$ et aux forces de frottement $\overrightarrow{F}$
 
2. Le poids $\overrightarrow{P}$ et la force électrostatique $\overrightarrow{F}$ sont des forces conservatives (le travail d'une force conservative ne dépend pas du chemin suivi)
 
3. Expression du travail de la force de frottement de l'air $f$ en fonction de $AB$ et $f.$
 
$W_{AB}\left(\overrightarrow{f}\right)=-f\times AB$
 
4. Le signe de la charge électrique de l'armature haute est positif car les électrons chargés négativement se déplacent vers l'armature chargée positivement
 
5. Représentation du champ électrique $E$ et du champ de pesanteur $g$ sur la figure.  
 
(Voir figure
 
6. Expression du travail de la force électrique $Fe$ et du poids $P$, en fonction de $m$, $q$ $V_{A}$, $V_{B}$, $g$, $\alpha$ et $AB.$
 
$W_{AB}\left(\overrightarrow{F_{e}}\right)=q\left(V_{A}-V_{B}\right)$
 
$W_{AB}\left(\overrightarrow{P}\right)=-mgAB\cos\alpha$
 
7. Précisons pour chacune de ces forces si leur travail est moteur ou résistant.
 
$-\ $Le travail de la force électronique $\overrightarrow{F_{e}}$ est moteur car il favorise le déplacement.
 
$-\ $Le travail de la force électrostatique $\overrightarrow{P}$ est résistance car il s'oppose au déplacement.
 
8. Calcul du travail de ces forces sur le trajet $AB=1.8\,m$
 
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F_{e}}\right)&=&q\left(V_{A}-V_{B}\right)\\&=&-2e\left(V_{A}-V_{B}\right)\\&=&-2\times1.6\cdot10^{-19}(-3-5)\\\Rightarrow\;W_{AB}\left(\overrightarrow{F_{e}}\right)&=&16\cdot10^{-19}J \end{array}$
 
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{P}\right)&=&-mgAB\cos\alpha\\&=&-3.210^{-27}\times 10\times 1.8\cos 30^{\circ}\\\Rightarrow\;W_{AB}\left(\overrightarrow{P}\right)&=&5.0\cdot10^{26}J \end{array}$
 
$W_{AB}\left(\overrightarrow{F_{e}}\right)\succ W_{AB}\left(\overrightarrow{P}\right)$, on peut négliger l'énergie potentielle de pesanteur de la particule.
 
Alors, on ne prend en compte que l'énergie potentielle électrique.
 
9. Déduction de l'expression de l'énergie mécanique de la particule au point $A$ en fonction de sa vitesse $v_{A}$
et des grandeurs $V_{A}$, $q$ et $m$
 
$\begin{array}{rcl} E_{m_{A}}&=&E_{P_{A}}+E_{C_{A}}\\\Rightarrow\;E_{m_{A}}&=&qV_{A}+\dfrac{1}{2}mv_{A}^{2} \end{array}$
 
10 Déduction de l'expression de l'énergie mécanique de la particule au point $B$ en fonction de la vitesse $v_{B}$
et des grandeurs $V_{B}$, $q$, et $m.$
 
$\begin{array}{rcl} E_{m_{B}}&=&E_{P_{B}}+E_{C_{B}}\\\Rightarrow\;E_{m_{B}}&=&qV_{B}+\dfrac{1}{2}mv_{B}^{2} \end{array}$
 
11 L'énergie mécanique se conserve car il y a un vide parfait ; les forces de frottement sont négligeables
 
12. Déduction de la vitesse $v_{B}$ de la particule
 
La conservation de l'énergie mécanique s'écrit :
 
$\begin{array}{rcl} E_{m_{B}}&=&E_{m_{A}}\\\Rightarrow\;qV_{B}+\dfrac{1}{2}mv_{B}^{2}&=&qV_{A}+\dfrac{1}{2}mv_{A}^{2}\\\Rightarrow\dfrac{1}{2}mv_{B}^{2}&=&q\left(V_{A}-V_{B}\right)+\dfrac{1}{2}mv_{A}^{2}\\\Rightarrow\;V_{B}&=&\sqrt{\dfrac{2q\left(V_{A}-V_{B}\right)}{m}+v_{A}^{2}}\\\Rightarrow\;V_{B} &=&\sqrt{\dfrac{-2\times1.6\cdot10^{-19}(-3-5)}{3.2\cdot10^{-27}}+(0.53)^{2}}\\\Rightarrow\;V_{B}&=&28\cdot10^{3}m\cdot s^{-1} \end{array}$

Exercice 4 

1. Expression du travail de la force électrostatique $\overrightarrow{F}$
 
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&q\overrightarrow{E}\cdot\overrightarrow{AB}\\&=&qE\times AB \end{array}$
 
2. Montrons que le travail de cette force s'écrit :
 
$\begin{array}{rcl}W_{AB}\left(\overrightarrow{F}\right)&=&qU_{AB}  W_{AB}\left(\overrightarrow{F}\right)\\&=&q\overrightarrow{E}\cdot\overrightarrow{AB}\text{ or  }\overrightarrow{E}\cdot\overrightarrow{AB}=U_{AB}\\\Rightarrow\;W_{AB}\left(\overrightarrow{F}\right)&=&qU_{AB} \end{array}$
 
3. Calcul de sa valeur dans le cas d'un noyau d'hélium $He^{2+}$ se déplaçant de $A$ à $B$
 
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&qU_{AB}\\&=&2e\times U_{AB}\\&=&2\times 1.60\cdot10^{-19}\times400\\\Rightarrow\;W_{AB}\left(\overrightarrow{F}\right)&=&12.8\cdot10^{-19}J \end{array}$

Exercice 5

 
1. Charge $q_{\alpha}$ de la particule $\alpha$
 
$\begin{array}{rcl} q_{\alpha}&=&2e\\&=&2\times1.60\cdot10^{-19}\\\Rightarrow\;q_{\alpha}&=&3.20\cdot10^{-19}C \end{array}$
 
2. Établissement de l'expression du travail de la force électrostatique et expression du travail en fonction $q_{\alpha}$, $V_{A}$  et $V_{B}$
 
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&q\alpha\overrightarrow{E}\cdot\overrightarrow{AB}\\\text{or }\overrightarrow{E}\cdot\overrightarrow{AB}&=&V_{A}-V_{B}\\\Rightarrow\;W_{AB}\left(\overrightarrow{F}\right)&=&q\alpha\left(V_{A}-V_{B}\right) \end{array}$
 
3. Déduction de l'expression de la variation d'énergie potentielle électrique entre $A$ et $B$
 
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&q_{\alpha}\overrightarrow{E}\cdot\overrightarrow{AB}\\\text{ or }\overrightarrow{E}\cdot\overrightarrow{AB}&=&q_{\alpha}\left(V_{A}-V_{B}\right)\\\Rightarrow\Delta E_{p}&=&-q_{\alpha}\left(V_{A}-V_{B}\right) \end{array}$
 
4. L'énergie mécanique se conserve car les frottements sont négligeables lors de ce mouvement
 
5.1. Expression de la différence de potentiel $V_{A}-V_{B}$ en fonction de $v_{B}$, $m_{\alpha}$ et $q_{\alpha}$
 
La conservation de l'énergie mécanique s'écrit :
 
$\begin{array}{rcl} -\Delta E_{p}&=&\Delta E_{c}\\\Rightarrow\;q\alpha\left(V_{A}-V_{B}\right)&=&\dfrac{1}{2}m_{\alpha }v_{B}^{2}-0\\\Rightarrow\;V_{A}-V_{B}&=&\dfrac{m_{\alpha} v_{B}^{2}}{2q_{\alpha}} \end{array}$
 
5.2 Calcul de la valeur de la différence de potentiel $V_{A}-V_{B}$
 
$\begin{array}{rcl} V_{A}-V_{B}&=&\dfrac{m_{\alpha}v_{B}^{2}}{2q_{\alpha}}\\&=&\dfrac{6.70\cdot10^{-27}\times\left(1.00\cdot10^{6}\right)^{2}}{2\times2\times1.60\cdot10^{-19}}\\\Rightarrow\;V_{A}-V_{B}&=&1.05\cdot10^{4}V \end{array}$

Exercice 6

1. Détermination des constantes $a$ et $b.$
 
$E=a+bz$
 
$\begin{array}{rcl} z=0\;,E&=&100V\cdot m^{-1}\\\Rightarrow\;E&=&a+b\times 0\\&=&100V\cdot m^{-1}\\\Rightarrow\alpha&=&100V\cdot m^{-1} \end{array}$
 
$\begin{array}{rcl} z=140m\;,E&=&20V\cdot m^{-1}\\\Rightarrow\;E&=&100+1400b\\&=&20V\cdot m^{-1}\\\Rightarrow\;b&=&\dfrac{20-100}{1400}\\\Rightarrow\;b&=&-5.7\cdot10^{-2}V\cdot m^{-2}\\\Rightarrow\;E&=&100-5.7\cdot10^{-2}z \end{array}$
 
Les constantes $a$ et $b$ sont respectivement $V\cdot m^{-1}$ et $V\cdot m^{-2}$
 
Représentation graphique $E$ en fonction de $z$
 
 
2. Détermination du travail des forces électriques s'exerçant sur la charge par une méthode graphique.
 
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&\dfrac{1}{2}qEz\\\text{or }E&=&a+bz\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&\dfrac{1}{2}q(a+bz)z\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&\dfrac{1}{2}\times10^{-10}\left(100-5.7\cdot10^{-2}z\right)z \end{array}$
 
Déduction du potentiel électrostatique d'un point situé à l'altitude $h$
 
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&qU\\&=&\dfrac{1}{2}q(a+bz)z\\\Rightarrow\;U&=&\dfrac{1}{2}(a+bz)\ ;\ z\\&=&h\\\Rightarrow\;U&=&\dfrac{1}{2}(a+bh)h\\\Rightarrow\;U&=&\dfrac{1}{2}(a+bh)h\\\Rightarrow\;U&=&\dfrac{1}{2}\left(100-5.7\cdot10^{-2}h\right)h \end{array}$
 
3. Calcul de l'énergie potentielle de pesanteur et de l'énergie potentielle électrostatique de cet ion.
 
$\begin{array}{rcl} E_{pp}&=&mgz\\&=&\dfrac{1.0\cdot10^{-3}}{6.02\cdot10^{23}}\times10\times1400\\\Rightarrow\;E_{pp}&=&2.3\cdot10^{-23}J  \end{array}$
 

$\begin{array}{rcl} E_{PE}&=&\dfrac{1}{2}q(a+bz)z\\&=&\dfrac{1}{2}\times1.6\cdot10^{-19}\left(100-5.7\cdot10^{-2}\times1400\right)\times1400\\ \Rightarrow\;E_{PE}&=&16.2\cdot10^{-19}J \end{array}$
 
L'énergie potentielle électrostatique est grande devant l'énergie potentielle de pesanteur. 
 
Cette dernière peut être négligée
 
Vitesse de l'ion à l'arrivée sur le sol
 
Appliquons la conservation de l'énergie mécanique
 
$\begin{array}{rcl} E_{C_{f}}+E_{P_{f}}&=&E_{C_{I}}+E_{P_{I}}\\\Rightarrow\;E_{C_{f}}+0&=&0+E_{P_{I}}\\\Rightarrow\dfrac{1}{2}mv^{2}&=&E_{P_{I}}\\\Rightarrow\;v&=&\sqrt{\dfrac{2E_{P_{I}}}{m}}\\&=&\sqrt{\dfrac{2\times16.2\cdot10^{-19}\times6.02\cdot10^{23}}{1.0\cdot10^{-3}}}\\\Rightarrow\;v&=&44\cdot10^{3}m\cdot s^{-1} \end{array}$

Exercice 7 

 
1. Calcul de la charge $q$ du pendule si, à l'équilibre
 
La condition d'équilibre, appliquée à la sphère, s'écrit :
 
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F} \overrightarrow{T}&=&\overrightarrow{0}\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+F-T\sin\alpha&=&0\\ mg+0-T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&F\quad(1)\\ T\cos\alpha&=&mg\quad(2) \end{array}\right.\\\Rightarrow\tan\alpha&=&\dfrac{qE}{mg}\\\Rightarrow\;q&=&\dfrac{m\times g\times\tan\alpha}{E}\\\text{ or }E&=&\dfrac{U_{PN}}{d}\\\Rightarrow\;q&=&\dfrac{mgd\tan\alpha}{U_{PN}}\\&=&\dfrac{0.5\cdot10^{-3}\times10\times15\cdot10^{-2}\times\tan 30^{\circ}}{1500V}\\ \Rightarrow\;q&=&2.9\cdot10^{-7}C \end{array}$
 
2. Expression en fonction de $\alpha$ l'énergie potentielle de pesanteur $\varepsilon pg$ et l'énergie potentielle électrostatique
 
$\varepsilon pe.$
 
$\varepsilon pg=mgz+\text{cte}$
 
$\begin{array}{rcl} \varepsilon pg(z=0)&=&mg\times 0+\text{cte}\\&=&0\\\Rightarrow\text{cte}&=&0\\\Rightarrow\varepsilon&=&mgz \end{array}$
 
$\begin{array}{rcl} Z_{A}&=&1-1\cos\alpha\\&=&1(1-\cos\alpha)\\\Rightarrow\varepsilon_{pg}&=&mgl(1-\cos\alpha) \end{array}$
 
$\begin{array}{rcl} \Delta\varepsilon pe&=&-W\left(\overrightarrow{F}\right)\\\Rightarrow\varepsilon pe-0&=&-Fl\sin\alpha\\\text{ or }F&=&qE\\&=&q\dfrac{U_{PN}}{d}\\\Rightarrow\varepsilon pe&=&-q\dfrac{U_{PN}}{d}l\sin\alpha \end{array}$
 
Valeur de $\alpha$ pour laquelle la somme $\varepsilon P$ de ces énergies potentielles est minimale
 
$\begin{array}{rcl} \varepsilon_{p}&=&\varepsilon_{pg}+\varepsilon_{pe}\\&=&mgl(l-\cos\alpha)-q\dfrac{U_{PN}}{d}l\sin\alpha\\\Rightarrow\varepsilon'_{p}&=&mgl\sin\alpha-q\dfrac{U_{PN}}{d}l\cos\alpha\\&=&0\\\Rightarrow\;mgl\sin\alpha&=&q\dfrac{U_{PN}}{d}l\cos\alpha\\\Rightarrow\dfrac{\sin\alpha}{\cos\alpha}&=&\dfrac{qU_{PN}}{mgd}\\ \Rightarrow\tan\alpha&=&\dfrac{qU_{PN}}{mgd}\\\Rightarrow\alpha&=&\tan^{-1}\left(\dfrac{qU_{PN}}{mgd}\right)\\ \Rightarrow\alpha&=&\tan^{-1}\left(\dfrac{2.9\cdot 10^{-7}\times 1500}{0.5\cdot10^{-3}\times 10\times 15\cdot10^{-2}}\right)\\\Rightarrow\alpha&=&30^{\circ} \end{array}$
 
Conclure. 
 
Données : masse de la sphère : $m=0.5\;g$ ; longueur du fil : $1=20\;m$ ; $g=10\;m\cdot s^{2}$

Exercice 8

 
1. Calcul du travail de la force électrostatique qui s'exerce sur cet élection
 
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&-eU\\&=&-1.60\cdot10^{-19}\times200\\ \Rightarrow\;W\left(\overrightarrow{F}\right)&=&-3.20\cdot10^{-17}J \end{array}$
 
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&\dfrac{-3.20\cdot10^{-17}}{1.60\cdot10^{-19}}\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&-200eV \end{array}$
 
2/ Caractérisation du champ électrostatique en tout point de l'espace compris entre les plaques.
 
Le champ électrostatique en tout point de l'espace a même direction, même sens et même intensité
 
$\begin{array}{rcl} E&=&\dfrac{U}{d}\\&=&\dfrac{200}{2\cdot10^{-2}}\\\Rightarrow\;E&=&10\cdot10^{3}V \end{array}$
 
3. Calcul du travail de la force et caractérisation du champ électrostatique
 
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&-eU\\&=&-1.60\cdot10^{-19}\times\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&-3.20\cdot 10^{-17}J \end{array}$
 
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&\dfrac{-3.20\cdot10^{-17}}{1.60\cdot10^{-19}}\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&-200eV \end{array}$
 
Le champ électrostatique en tout point de l'espace a même direction, même sens et même intensité
 
$\begin{array}{rcl} E'&=&\dfrac{U}{d'}\\&=&\dfrac{200}{4\cdot10^{-2}}\\\Rightarrow\;E'&=&5\cdot10^{3}V \end{array}$
 
Le travail de la force électrostatique ne dépend que de la charge et de la différence de potentiel (d.d.p)
 
4.  On peut toujours calculer simplement le travail de la force électrostatique qui s'exerce sur l'électron allant
de la plaque positive à la plaque négative. 
 
Il suffit de connaitre la différence de potentiel ou la tension entre deux les plaques

Exercice 9


 
1. Vitesse $V_{1}$ minimale des électrons qui parviennent à traverser la grille $G_{2}$
 
La conservation de l'énergie mécanique entre les grilles $G_{1}$ et $G_{2}$ s'écrit :
 
$\begin{array}{rcl} E_{m_{1}}&=&E_{m_{2}}\\\Rightarrow\;-eV_{1}+\dfrac{1}{2}mv_{1}^{2}&=&-eV_{2}+0\\\Rightarrow\dfrac{1}{2}mv_{1}^{2}&=&-e\left(V_{2}-V_{1}\right)+\dfrac{1} {2}mv_{1}^{2}\\\Rightarrow\;v_{1}&=&\sqrt{\dfrac{-2e\left(V_{2}-V_{1}\right)}{m}}\\\Rightarrow\;v_{1} &=&\sqrt{\dfrac{-2\times1.6\cdot10^{-19}\times-100}{9.1\cdot10^{-31}}}\\\Rightarrow\;v_{1}&=&5.9\cdot10^{6}m\cdot s^{-1} \end{array}$
 
2. Vitesse $V_{2}$ d'un électron traversant $G_{2}$
 
La conservation de l'énergie mécanique entre les grilles $G_{1}$ et $G_{2}$ s'écrit :
 
$\begin{array}{rcl} E_{m_{2}}&=&E_{m_{1}}\\\Rightarrow\;-eV_{2}+\dfrac{1}{2}mv_{2}^{2}&=&-eV_{1}+\dfrac{1}{2}mv_{1}^{2}\\\Rightarrow\dfrac{1}{2}mv_{2}^{2}&=&-e\left(V_{A}-V_{B}\right)+\dfrac{1}{2}mv_{1}^{2}\\\Rightarrow\;v_{2}&=&\sqrt{\dfrac{-2e\left(V_{1}-V_{2}\right)}{m}+v_{1}^{2}}\\\Rightarrow\;v_{2}&=&\sqrt{\dfrac{-2\times1.6\cdot^{-19}\times 100}{9.1\cdot10^{-31}}+\left(9\cdot10^{6}\right)^{2}}\\\Rightarrow\;v_{2}&=&1.8\cdot10^{6}m\cdot s^{-1} \end{array}$
 
3.Vitesse avec laquelle l'élection retraverse $G_{1}$ 
 
Au cours d'un choc élastique il y a conservation de l'énergie cinétique et conservation de la quantité de mouvement du système (électrons, neutron).
 
$\begin{array}{rcl} \overrightarrow{m_{e}v_{e}}+\overrightarrow{0}&=&\overrightarrow{m_{e}v_{e}^{'}}+\overrightarrow{m_{n}v_{n}}\\\Rightarrow\;m_{e}v_{e}&=&-m_{e}v^{'}+m_{n}v_{n}\\\Rightarrow\;m_{e}\left(v_{e}+v_{e}^{'}\right)&=&m_{n}v_{n}\\\Rightarrow\;m_{e}\left(v_{e}+v_{e}^{'}\right)&=&1840\,m_{e}v_{n}\\\Rightarrow\;v_{e}+v_{e}^{'}&=&1840\,v_{n}\quad(1) \end{array}$
 
$\begin{array}{rcl} \dfrac{1}{2}m_{e}v_{e}^{2}+0&=&\dfrac{1}{2}m_{e}v_{2}^{'2}+\dfrac{1}{2}m_{n}v_{n}^{2}\\\Rightarrow\;m_{e}\left(v_{e}^{2}-v_{e}^{'2}\right)&=&m_{n}v_{n}^{2}\\\Rightarrow\;m_{e}\left(v_{e}^{2}-v_{e}^{'2}\right)&=&1840m_{e}v_{n}^{2}\quad(2)\\\Rightarrow\;v_{e}^{2}-v_{e}^{'2}&=&1840\,v_{n}^{2}\quad(2) \end{array}$
 
$\begin{array}{rcl} &\Rightarrow&\dfrac{(2)}{(1)}\\&\Rightarrow&\;v_{e}-v_{e}^{'}=1840\,v_{n}\\&\Rightarrow&\left\lbrace\begin{array}{lcl} v_{e}+v_{e}^{'}&=&1840\,v_{n}\\ v_{e}-v_{e}^{'}&=&1840\,v_{n} \end{array}\right.\\\Rightarrow\;v_{e}+v_{e}^{'}&=&v_{e}-v_{e}^{'}\\\Rightarrow\;2v_{e}^{'}&=&v_{e}-v_{e}\\\Rightarrow\;v_{e}^{'}&=&0m\cdot s^{-1} \end{array}$

Exercice 10

 
2.2. Calcul de l'intensité du champ électrique
 
La condition d'équilibre, appliquée à la boule, s'écrit :
 
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}&=&0\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+F-T\sin\alpha&=&0\\  mg+0-T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&F\quad(1)\\T\cos\alpha&=& mg\quad(2) \end{array}\right.\\\text{ or }F&=&|q|E\\\Rightarrow\tan\alpha&=&\dfrac{|q|E}{mg}\\\Rightarrow\;E&=&\dfrac{mg\tan\alpha}{|q|}\\\Rightarrow\;E&=&\dfrac{2.5\cdot10^{-3}\times10\times\tan30^{\circ}}{|-0.50|\cdot10^{-6}}\\\Rightarrow\;E&=&2.9\cdot10^{4}Vm^{-1} \end{array}$
 
2.3 Angle d'inclinaison du fil par rapport à la verticale
 
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}&=&0\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+F-T\sin\alpha&=&0\\ mg+0-T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&F\quad(1)\\ T\cos\alpha&=&mg\quad(2) \end{array}\right.\\\Rightarrow\tan\alpha&=&\dfrac{|q|E}{mg}\\\Rightarrow\alpha&=&\tan^{-1}(\dfrac{|q|E}{mg})\\&=&\tan^{-1}\left(\dfrac{|0.50|\cdot10^{-6}\times1.0\cdot10^{4}}{2.5\cdot10^{-3}\times10}\right)\\\Rightarrow\alpha&=&11^{\circ} \end{array}$
 

Auteur: 
Sidy Mouhamed Ndiaye

Pages