Solution des exercices : Interférences lumineuses - Ts
Classe:
Terminale
Exercice 1
1) Établissement de l'expression de la différence de marche au pots $M$ de l'écran
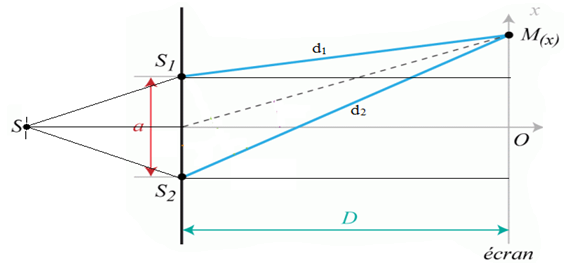
\begin{eqnarray} \delta &=&\left(SS_{2}+S_{2}M\right)-\left(SS_{1}+S_{1}M\right)\nonumber\\\\&=&S_{2}M-S_{1}M\ ;\ \left(SS_{2}=SS_{1}\right) \end{eqnarray}
\begin{eqnarray} S_{2}M^{2}&=&d_{2}^{2}\nonumber\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}\ ; \end{eqnarray}
\begin{eqnarray} S_{1}M^{2}&=&d_{1}^{2}\nonumber\\\\&=&D^{2}+\left(x-\dfrac{a}{2}\right)^{2} \end{eqnarray}
\begin{eqnarray} d_{2}^{2}-d_{1}^{2}&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-\left(D^{2}+\left(x-\dfrac{a}{2}\right)^{2}\right)\nonumber\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-D^{2}-\left(x-\dfrac{a}{2}\right)^{2}\nonumber\\\\\left(d_{2}-d_{1}\right)\left(d_{2}+d_{1}\right)&=&\left(\left(x+\dfrac{a}{2}\right)+\left(x-\dfrac{a}{2}\right)\right)\left(\left(x+\dfrac{a}{2}\right)-\left(x-\dfrac{a}{2}\right)\right)\nonumber\\\\&=&2ax \end{eqnarray}
Les grandeurs $x$ et $a$ sont petites devant la grandeur $D.$ Dans ces conditions,
\begin{eqnarray} d_{2}+d_{1}&=&2D\nonumber\\\\\Rightarrow\delta &=& d_{2}-d_{1}\nonumber\\\\ &=&\dfrac{ax}{D} \end{eqnarray}
2) Détermination de la distance entre les deux sources
$x_{n}=\dfrac{n\lambda D}{a}$
\begin{eqnarray} x_{9}-x_{6}&=&\dfrac{9\lambda D}{a}-\left(-\dfrac{6\lambda D}{a}\right)\nonumber\\\\&=&\dfrac{15\lambda D}{a}\nonumber\\\\&=&d\nonumber\\\\\Rightarrow a&=&\dfrac{15\lambda D}{d}\nonumber\\\\&=&\dfrac{15\times 0.6\cdot10^{-6}\times 2.5}{1.5\cdot 10^{-2}}\nonumber\\\\\Rightarrow a&=&1.5\cdot 10^{-3}m\nonumber\\\\&=&1.5mm \end{eqnarray}
3) Détermination de la nature de la frange en point $P$ de $E$ distant de $2.5mm$ de la frange centrale
\begin{eqnarray} x_{n}-0&=&\dfrac{n\lambda D}{a}-0\nonumber\\\\&=&d\nonumber\\\\\Rightarrow n&=&\dfrac{ad}{\lambda D}\nonumber\\\\&=&\dfrac{1.5\cdot10^{-3}\times2.5\cdot10^{-3}}{2.5\times0.6\cdot10^{-6}}\nonumber\\\\\Rightarrow n=\dfrac{5}{2} \end{eqnarray}
l'ordre d'interférence est un demi-entier ; la frange au point $P$ est une frange sombre
Exercice 2
1) Les vibration lumineuses issues des fentes $f_{1}$ et $f_{2}$ sont cohérentes et en phase puisqu'elle sont d'une même sources
2) Expression du retard en fonction de $d_{1}$ et de la vitesse $c$de la lumière dans l'air
$t_{1}=\dfrac{d_{1}}{c}$
3) Expression du retard en fonction de $d_{2}$ de la vitesse $c$ de la lumière dans l'air
$t_{2}=\dfrac{d_{2}}{c}$
4) Conditions le point $M$ sera :
Sur frange brillante :
$d_{2}-d_{1}=k\lambda$
Sur une frange sombre : $d_{2}-d_{1}=\left(k+\dfrac{1}{2}\right)\lambda$
5) Que peut-on dire des points $M$ suivants :
$d_{2}-d_{1}=0$ ; $M$ est le milieu d'une frange centrale.
$-\ d_{2}-d_{1}=3.20\mu m$ :
$\begin{array}{lll} k&=&\dfrac{d_{2}-d_{2}}{\lambda}\\\\&=&\dfrac{3.20}{0.64\cdot 10}\\\\\Rightarrow\,k&=&5 \end{array}$
$M$ est le milieu d'une frange brillante.
$-\ d_{2}-d_{1}=2.24\mu m$ :
\begin{eqnarray} k&=&\dfrac{d_{2}-d_{2}}{\lambda}\nonumber\\\\ &=&\dfrac{2.24}{0.64\cdot 10}\nonumber\\\\\Rightarrow k &=&\dfrac{7}{2}\nonumber\\\\ &=&\left(3+\dfrac{1}{2}\right) \end{eqnarray}
$M$ est le milieu d'une frange sombre.
Exercice 3
1) a) Le phénomène qui se produit à la sortie de chaque fente est le phénomène de diffraction
L'aspect ondulatoire de la lumière est mis en évidence.
b) Pour obtenir des interférences lumineuses, il est nécessaire d'utiliser un dispositif fournissant deux images d'une même source et les faisceaux issus de ces sources secondaires produisent des interférences lumineuses
c) Schéma et représentation de la marche des faisceaux lumineux issus des fentes $F_{1}$ et $F_{2}.$

2) a) On observe sur l'écran des zones alternativement sombres et claires appelées franges d'interférences. Ces franges, sur l'écran, sont pratiquement rectilignes, parallèles, équidistantes et au plan de figure.
La frange centrale qui se forme en $O$ est une frange brillante claire.
b) Valeur de $\lambda.$
$\begin{array}{lll} l&=&\dfrac{5\lambda D}{a}\\\\\Rightarrow\lambda&=&\dfrac{al}{5D}\\\\&=&\dfrac{1.5\cdot 10^{-3}\times 8\cdot 10^{-3}}{5\times 2}\\\\\Rightarrow\lambda&=&1.2\cdot 10^{-6}m\\\\&=&1.2\mu m \end{array}$
3) Distance $x$ où se produit la première coïncidence de franges brillantes
$x_{1}=\dfrac{k_{1}\lambda_{1}D}{a}$ ;
$x_{2}=\dfrac{k_{2}\lambda_{2}D}{a}$
$\begin{array}{lll} x_{1}&=&x_{2}\\\\\Rightarrow\dfrac{k_{1}\lambda_{1}D}{a}\\\\&=&\dfrac{k_{2}\lambda_{2}D}{a}\\\\\Rightarrow\dfrac{k_{1}}{k_{2}} &=&\dfrac{\lambda_{2}}{\lambda_{1}}\\\\&=&\dfrac{0.54}{0.60}\\\\&=&\dfrac{9}{10}\\\\\Rightarrow\,k_{1}&=&9\ ;\\\\k_{2}&=&10\\\\k_{2}=10\Rightarrow\,x_{2}&=&\dfrac{10\lambda_{2}D}{a}\\\\&=&\dfrac{10\times 0.54\cdot 10^{-6}\times 2}{1.5\cdot 10^{-3}}\\\\\Rightarrow\,x_{2}&=&7.2mm \end{array}$
Exercice 4
Dispositif expérimental

1) Interprétation de la formation des franges brillantes et obscures.
Les franges brillantes (ou interférences constructives) résultent de la superposition de deux vibrations lumineuses qui arrivent en phase. C'est-à-dire la différence de marche en un point est un multiple entier de la longueur d'onde
Les franges obscures (ou interférences destructives) résultent de la superposition de deux vibrations lumineuses qui arrivent en opposition de phase. C'est-à-dire la différence de marche en un point est un multiple demi- entier de la longueur d'onde
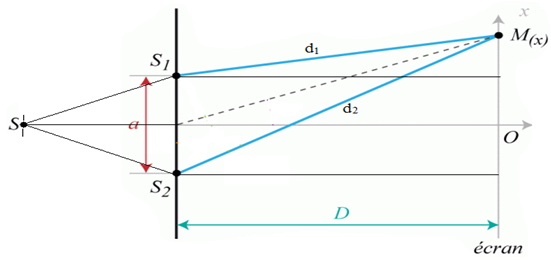
2) Différence de marche aux 2 fentes d'un point $M$ de l'écran
$\begin{array}{lll} \delta &=&\left(SS_{2}+S_{2}M\right)-\left(SS_{1}+S_{1}M\right)\\\\&=&S_{2}M-S_{1}M\\\\SS_{2}&=&SS_{1} \end{array}$
$\begin{array}{lll} S_{2}M^{2}&=&d_{2}^{2}\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}\ ; \end{array}$
$\begin{array}{lll} S_{1}M^{2}&=&d_{1}^{2}\\\\&=&D^{2}+\left(x-\dfrac{a}{2}\right)^{2} \end{array}$
\begin{eqnarray} d_{2}^{2}-d_{1}^{2}&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-\left(D^{2}+\left(x-\dfrac{a}{2}\right)^{2}\right)\nonumber\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-D^{2}-\left(x-\dfrac{a}{2}\right)^{2}\nonumber\\\\\left(d_{2}-d_{1}\right)\left(d_{2}+d_{1}\right)&=&\left(\left(x+\dfrac{a}{2}\right)+\left(x-\dfrac{a}{2}\right)\right)\left(\left(x+\dfrac{a}{2}\right)-\left(x-\dfrac{a}{2}\right)\right)\nonumber\\\\&=&2ax \end{eqnarray}
Les grandeurs $x$ et $a$ sont petites devant la grandeur $D.$ Dans ces conditions,
$\begin{array}{lll} d_{2}+d_{1}&=&2D\\\\\Rightarrow\delta &=&d_{2}-d_{1}\\\\&=&\dfrac{ax}{D} \end{array}$
La position des franges brillantes correspond à :
\begin{eqnarray} \dfrac{ax}{D}&=&k\lambda\nonumber\\\\\Rightarrow\,x_{k}&=&\dfrac{k\lambda D}{a} \end{eqnarray}
La position des franges obscures correspond à :
\begin{eqnarray} \dfrac{ax}{D}&=&\left(k+\dfrac{1}{2}\right)\lambda\nonumber\\\\\Rightarrow\,x_{k}&=&\left(k+\dfrac{1}{2}\right)\dfrac{\lambda D}{a} \end{eqnarray}
5) Calcul de la longueur d'onde et de la fréquence de la lumière émise par le laser,
$\begin{array}{lll} x_{6}&=&\dfrac{6\lambda D}{a}\\\\\Rightarrow\lambda &=&\dfrac{ax_{n}}{6D}\\\\&=&\dfrac{0.5\cdot 10^{-3}\times 12.7\cdot 10^{-3}}{6\times 2}\\\\\Rightarrow\lambda&=&5.29\cdot 10^{-7}m \end{array}$
$\begin{array}{lll} v&=&\dfrac{c}{\lambda}\\\\&=&\dfrac{3\cdot 10^{8}}{5.29\cdot 10^{-7}}\\\\\Rightarrow\,v&=&5.67\cdot 10^{14}Hz \end{array}$
6) La longueur d'onde est une caractéristique du milieu de propagation, elle change donc avec le milieu.
La fréquence est une caractéristique de l’onde ; elle ne change donc pas le milieu de propagation.
Calcul de la nouvelle valeur de la longueur d'onde
$\begin{array}{lll} \lambda &=&\dfrac{c}{v}\\\\&=&\dfrac{200000\cdot 10^{3}}{5.67\cdot 10^{14}}\\\\\Rightarrow\lambda &=&3.47\cdot 10^{-7}m \end{array}$
Exercice 5
1) On observe sur l'écran $K$ une figure des franges d'interférences, c'est-à-dire des bandes étroites alternativement colorées (franges brillantes) et noires (franges sombres) équidistantes, parallèles et parallèles aux fentes
2) Établissement de la formule donnant $a$ en fonction de $\lambda$, $N$, $d$ et $L$
$\begin{array}{lll} L&=&\dfrac{N\lambda d}{a}\\\\\Rightarrow\,a&=&\dfrac{N\lambda d}{L} \end{array}$
Calcul de $a$
$\begin{array}{lll} a&=&\dfrac{N\lambda d}{L}\\\\&=&\dfrac{7\times 0.55\cdot 10^{-6}\times 1.20}{7.2\cdot 10^{-3}}\\\\\Rightarrow\,a&=&0.64mm \end{array}$
3) En augmentant l'intervalle $a=F_{1}F_{2}$, l'intervalle $L$ séparant $N$ franges brillantes consécutives augmente et on observe sur l'écran un étalement du phénomène d'interférence (à revoir)
Valeur limite $a'$ de la distance $F_{1}F_{2}$ séparant les deux fentes
$\begin{array}{lll} i&=&\dfrac{\lambda d}{a'}\\\\\Rightarrow\,a'&=&\dfrac{\lambda d}{i}\\\\&=&\dfrac{0.55\cdot 10^{-6}\times 1.20}{0.2\cdot 10^{-3}}\\\\\Rightarrow\,a'&=&0.33mm \end{array}$
4) Nombre de franges brillantes observées sur l'intervalle $L$
$\begin{array}{lll} L&=&\dfrac{N\lambda d}{a}\\\\\Rightarrow\,N&=&\dfrac{aL}{\lambda d}\\\\&=&\dfrac{7.2\cdot 10^{-3}\times 0.33\cdot 10^{-3}}{0.55\cdot 10^{-6}\times 1.20}\\\\\Rightarrow\,N&=&4\text{franges brillantes} \end{array}$
Exercice 6
1) 1) Relation donnant $\lambda$ en fonction de $a$, $d$, $l$ et $N$
$\begin{array}{lll} l&=&\dfrac{N\lambda d}{a}\\\\\Rightarrow\lambda&=&\dfrac{al}{Nd}\\\\&=&\dfrac{2.00\cdot 10^{-3}\times 4.00\cdot 10^{-3}}{12\times 1.00}\\\\\Rightarrow\lambda &=&6.67\cdot 10^{-7}m \end{array}$
1) 2) Nouvelle longueur $l.$
$\begin{array}{lll} n_{0}&=&\dfrac{\lambda}{\lambda'}\\\\\Rightarrow\lambda'&=&\dfrac{\lambda}{n_{0}} \end{array}$
$\begin{array}{lll} l&=&\dfrac{N\lambda' d}{a}\\\\&=&\dfrac{N\lambda d}{an_{0}}\\\\&=&\dfrac{12\times 6.67\cdot 10^{-7}\times 1.00}{2.00\cdot 10^{-3}\times 1.30}\\\\\Rightarrow\,l&=&3.1mm \end{array}$
Exercice 7
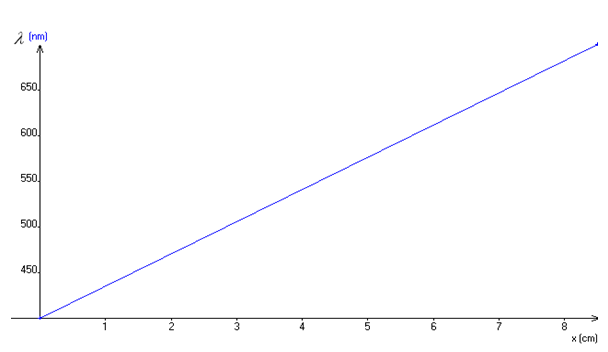
1) Pour plus de précision on mesure la distance correspondant à $6$ interfranges plutôt que celle mesurant $1$ interfrange
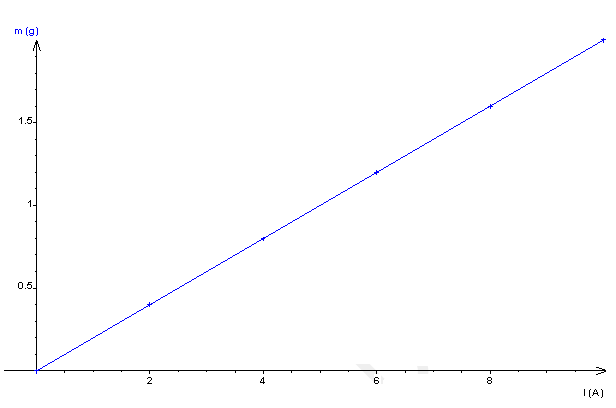
$$\begin{array}{|l|c|c|c|c|c|} \hline \text{Couleur}&\text{Bleu}&\text{Vert}&\text{Jaune}&\text{Orange}&\text{Rouge}\\\hline 6i&14.1&15.6&17.4&18.3&19.5\\\hline\lambda(\mu m)&0.47&0.52&0.58&0.61&0.65\\\hline \end{array}$$
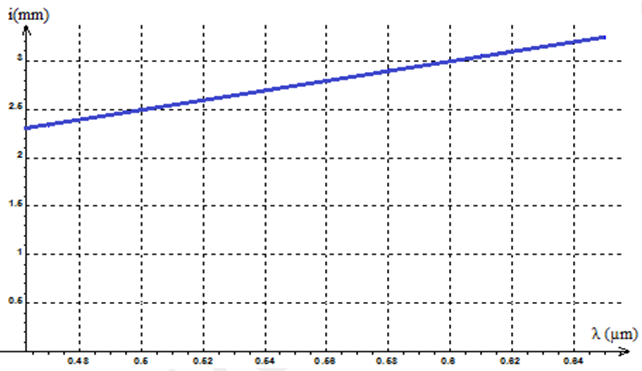
3) Tracé de la courbe représentative de la fonction $i=f(\lambda).$
$$\begin{array}{|l|c|c|c|c|c|} \hline \text{Couleur}&\text{Bleu}&\text{Vert}&\text{Jaune}&\text{Orange}&\text{Rouge}\\\hline 6i&14.1&15.6&17.4&18.3&19.5\\\hline\lambda(\mu m)&0.47&0.52&0.58&0.61&0.65\\\hline i&2.35&2.6&2.9&3.05&3.25\\\hline \end{array}$$

4) La courbe $i=f(\lambda)$ représentant est une droite. La relation $i=\lambda\dfrac{D}{a}$ est en accord avec la courbe obtenue précédemment.
5) Il faudrait réduire la largeur des fentes $F_{1}$ et $F_{2}$ ; augmenter la distance fentes-écran du dispositif expérimental pour obtenir des mesures avec une plus grande précision
6) Valeur de l'interfrange obtenu avec une radiation de longueur d'onde $0.50\mu m$
$\begin{array}{lll} i&=&a\lambda\\\\\Rightarrow\,a&=&\dfrac{\Delta i}{\Delta\lambda}\\\\&=&\dfrac{3.25-2.35}{0.65-0.47}\\\\\Rightarrow\,a&=&5\\\\\Rightarrow\,i&=&5\lambda \end{array}$
$\begin{array}{lll} \lambda &=&0.50\mu m\\\\\Rightarrow\,i&=&5\times 0.50\\\\&=&2.5mm \end{array}$
7) Pour la déterminer expérimentalement la longueur d'onde inconnue, il suffit de déterminer expérimentalement l'interfrange correspondant à deux franges brillantes ou à deux franges sombres de cette source monochromatique et déduire à partir de la relation $i=5\lambda$ la valeur de la longueur de la source monochromatique
Exercice 8
1) a) Description et explication du phénomène observé sur l'écran $(E).$