Corrigé devoir n° 1 maths - 4e
Classe:
Quatrième
Exercice 1
Soit deux cercle $\mathcal{C}(A\;,\ 2.5)\ $ et $\mathcal{C}'(O\;,\ 2)$ tangents en $F.$
Soit $[ED]$ un diamètre de $(\mathcal{C})$ et soit $B$ le milieu de $[DO].$
La parallèle à $(ED)$ passant par $B$ coupe $(OE)$ en $I.$
1) Complétons la figure
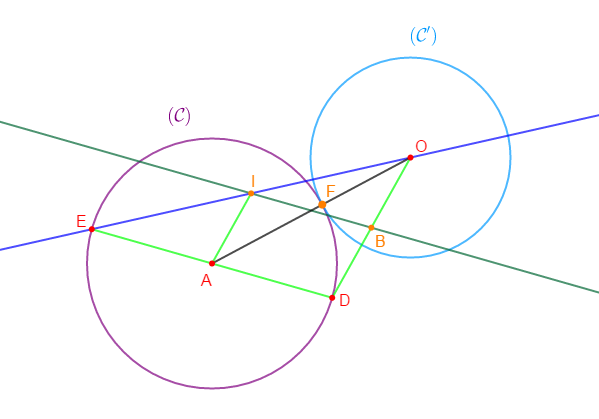
2) Démontrons que $AIBD$ est un parallélogramme
On a : la parallèle à $(ED)$ passant par $B$ coupe $(OE)$ en $I.$ Donc, $(BI)$ est parallèle à $(ED).$
Par suite, $(BI)$ est parallèle à $(AD)$ car les points $E\;,\ A\;,\ D$ sont alignés.
Par ailleurs, en considérant le triangle $OED$, on a : $B$ milieu de $[DO]$ et la parallèle à $(ED)$ passant par $B$ coupe $(OE)$ en $I.$
Donc, d'après le théorème de la droite des milieux, $I$ est le milieu de $[OE].$
De plus, comme $[ED]$ est un diamètre de $(\mathcal{C})$ alors, $A$ est milieu de $[ED].$
Ainsi, d'après la réciproque du théorème de la droite des milieux, $(AI)$ est parallèle à $(DB).$
Par conséquent, $AIBD$ est un parallélogramme
Résumé :
$$\left.\begin{array}{r} (BI)//(AD)\\\\(AI)//(DB)\end{array}\right\rbrace\ \Rightarrow\ AIBD\ \text{parallélogramme}$$
3) Démontrons que $OJ<3.5\;cm$
Pour cela, on considère le triangle $OEA.$
$OEA$ étant un triangle alors, en appliquant l'inégalité triangulaire, on a :
$$OE<EA+OA$$
Or, $I$ milieu de $[OE]$ donc, $OE=2\times OI$
Aussi, $OA=OF+FA$
Ainsi, en remplaçant, on obtient :
$\begin{array}{rcl} OE<EA+OA&\Rightarrow&2\times OI<EA+OF+FA\\\\&\Rightarrow&2\times OI<2.5+2+2.5\\\\&\Rightarrow&2\times OI<7\\\\&\Rightarrow&OI<\dfrac{7}{2}\\\\&\Rightarrow&OI<3.5\end{array}$
D'où, $\boxed{OI<3.5\;cm}$
Exercice 2
Calculons puis rendons irréductible.
$\begin{array}{rcl} A&=&\dfrac{\dfrac{1}{3}+\dfrac{5}{2}}{\dfrac{2}{5}\times\dfrac{1}{3}\times\dfrac{1}{4}}+\dfrac{\dfrac{\dfrac{2}{4}}{3}\times\dfrac{1}{7}-\dfrac{2}{3}}{\dfrac{1}{2}\div\dfrac{3}{\dfrac{1}{5}\times\dfrac{1}{3}}}\\\\&=&\dfrac{\dfrac{2}{6}+\dfrac{15}{6}}{\dfrac{2}{60}}+\dfrac{\dfrac{2}{4}\times\dfrac{1}{3}\times\dfrac{1}{7}-\dfrac{2}{3}}{\dfrac{1}{2}\div\dfrac{3}{\dfrac{1}{15}}}\\\\&=&\dfrac{\dfrac{17}{6}}{\dfrac{2}{60}}+\dfrac{\dfrac{2}{84}-\dfrac{2}{3}}{\dfrac{1}{2}\div 45}\\\\&=&\dfrac{17}{6}\times\dfrac{60}{2}+\dfrac{\dfrac{2}{84}-\dfrac{56}{84}}{\dfrac{1}{2}\times\dfrac{1}{45}}\\\\&=&\dfrac{1\,020}{12}+\dfrac{-\dfrac{54}{84}}{\dfrac{1}{90}}\\\\&=&\dfrac{1\,020}{12}-\dfrac{54}{84}\times\dfrac{90}{1}\\\\&=&\dfrac{1\,020}{12}-\dfrac{4\,860}{84}\\\\&=&\dfrac{7\times 1\,020}{7\times 12}-\dfrac{4\,860}{84}\\\\&=&\dfrac{7\,140}{84}-\dfrac{4\,860}{84}\\\\&=&\dfrac{2\,280}{84}\end{array}$
Ainsi, $A=\dfrac{2\,280}{84}$
Pour rendre irréductible $A$ on divise le numérateur et le dénominateur par leur $PGDC.$
On a : $PGDC(2280\;;\ 84)=12$
Donc,
$\begin{array}{rcl} A&=&\dfrac{2280}{84}\\\\&=&\dfrac{2280\div 12}{84\div 12}\\\\&=&\dfrac{190}{7}\end{array}$
D'où, $\boxed{A=\dfrac{190}{7}}$
$\begin{array}{rcl} B&=&\dfrac{\left(-\dfrac{2}{3}\right)^{2}\times\dfrac{1}{3}\times(-3)^{2}}{\dfrac{2}{3}-\dfrac{1}{2}}\div\dfrac{(-1)^{7}-\dfrac{1}{3}\times\dfrac{5}{2}}{\dfrac{5}{4}-\dfrac{1}{7}}\\\\&=&\dfrac{\dfrac{4}{9}\times\dfrac{1}{3}\times 9}{\dfrac{4}{6}-\dfrac{3}{6}}\div\dfrac{-1-\dfrac{5}{6}}{\dfrac{35}{28}-\dfrac{4}{28}}\\\\&=&\dfrac{\dfrac{36}{27}}{\dfrac{1}{6}}\div\dfrac{-\dfrac{6}{6}-\dfrac{5}{6}}{\dfrac{31}{28}}\\\\&=&\dfrac{36}{27}\times\dfrac{6}{1}\div\dfrac{-\dfrac{11}{6}}{\dfrac{31}{28}}\\\\&=&\dfrac{216}{27}\div -\dfrac{11}{6}\times\dfrac{28}{31}\\\\&=&\dfrac{216}{27}\div -\dfrac{308}{186}\\\\&=&\dfrac{216}{27}\times\left(-\dfrac{186}{308}\right)\\\\&=&-\dfrac{216\times 186}{27\times 308}\\\\&=&-\dfrac{40\,176}{8\,316}\end{array}$
Donc, $B=-\dfrac{40\,176}{8\,316}$
Rendons alors $B$ irréductible.
Soit : $PGDC(40\,176\;;\ 8\,316)=108$
Alors,
$\begin{array}{rcl} B&=&-\dfrac{40\,176}{8\,316}\\\\&=&-\dfrac{40\,176\div 108}{8\,316\div 108}\\\\&=&-\dfrac{372}{77}\end{array}$
Ainsi, $\boxed{B=-\dfrac{372}{77}}$
Exercice 3
1) Développons, réduisons puis ordonnons les expressions suivantes.
Soit :
$\begin{array}{rcl} A&=&3x-2+5x^{2}-(-2x^{2}+5x)+(-8x^{3}-9+x)\\\\&=&3x-2+5x^{2}+2x^{2}-5x-8x^{3}-9+x\\\\&=&-8x^{3}+5x^{2}+2x^{2}+3x-5x+x-2-9\\\\&=&-8x^{3}+7x^{2}-x-11\end{array}$
Donc, $\boxed{A=-8x^{3}+7x^{2}-x-11}$
On a :
$\begin{array}{rcl} B&=&(mn-2)+(3m^{4}-nm+12)-2m^{2}\\\\&=&mn-2+3m^{4}-nm+12-2m^{2}\\\\&=&3m^{4}-2m^{2}+nm-mn-2+12\\\\&=&3m^{4}-2m^{2}+10\end{array}$
Ainsi, $\boxed{B=3m^{4}-2m^{2}+10}$
Soit :
$\begin{array}{rcl} C&=&7y^{2}+(3y-2)-(-(2y)^{2}-(-5y^{3})+(-(-7y)))\\\\&=&7y^{2}+3y-2-(-4y^{2}+5y^{3}+7y)\\\\&=&7y^{2}+3y-2+4y^{2}-5y^{3}-7y\\\\&=&-5y^{3}+7y^{2}+4y^{2}+3y-7y-2\\\\&=&-5y^{3}+11y^{2}-4y-2\end{array}$
D'où, $\boxed{C=-5y^{3}+11y^{2}-4y-2}$
Soit :
$\begin{array}{rcl} D&=&x^{2}(x^{3}-3x)-6x^{2}(x^{2}-2x-1)\\\\&=&x^{2}\times x^{3}-x^{2}\times(3x)-6x^{2}\times x^{2}+(6x^{2})\times(2x)+6x^{2}\\\\&=&x^{5}-3x^{3}-6x^{4}+12x^{3}+6x^{2}\\\\&=&x^{5}-6x^{4}-3x^{3}+12x^{3}+6x^{2}\\\\&=&x^{5}-6x^{4}+9x^{3}+6x^{2}\end{array}$
D'où, $\boxed{D=x^{5}-6x^{4}+9x^{3}+6x^{2}}$
On a :
$\begin{array}{rcl} E&=&\dfrac{1}{4}x(x^{2}-3)+\dfrac{1}{4}\left(x-\dfrac{4}{3}\right)\\\\&=&\dfrac{1}{4}x\times x^{2}-\dfrac{1}{4}x\times 3+\dfrac{1}{4}\times x-\dfrac{1}{4}\times\dfrac{4}{3}\\\\&=&\dfrac{1}{4}x^{3}-\dfrac{3}{4}x+\dfrac{1}{4}x-\dfrac{1}{3}\\\\&=&\dfrac{1}{4}x^{3}-\dfrac{2}{4}x-\dfrac{1}{3}\\\\&=&\dfrac{1}{4}x^{3}-\dfrac{1}{2}x-\dfrac{1}{3}\end{array}$
Donc, $\boxed{E=\dfrac{1}{4}x^{3}-\dfrac{1}{2}x-\dfrac{1}{3}}$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
jeu, 12/29/2022 - 16:09
Permalien
Comment factoriser et
Anonyme (non vérifié)
sam, 11/09/2024 - 17:21
Permalien
Meilleure
Fatima (non vérifié)
jeu, 11/16/2023 - 18:20
Permalien
C'est vraiment un très bon
Dado sy (non vérifié)
jeu, 11/16/2023 - 23:51
Permalien
Reuissire
Mame diarra (non vérifié)
dim, 09/15/2024 - 21:09
Permalien
Sa était vraiment très bonne
Dado sy (non vérifié)
jeu, 11/16/2023 - 23:51
Permalien
Reuissire
Adama Dieng (non vérifié)
mer, 12/13/2023 - 20:20
Permalien
Je n'ai pas compris l
Adama Dieng (non vérifié)
mer, 12/13/2023 - 20:24
Permalien
Je n'ai pas compris
Adama Dieng (non vérifié)
mer, 12/13/2023 - 20:24
Permalien
Je n'ai pas compris
Adama Dieng (non vérifié)
mer, 12/13/2023 - 20:24
Permalien
Je n'ai pas compris
Adama Dieng (non vérifié)
mer, 12/13/2023 - 20:24
Permalien
Je n'ai pas compris
Mbéya barry (non vérifié)
mar, 11/12/2024 - 16:23
Permalien
Passé en classe 3em
Mbéya barry (non vérifié)
mar, 11/12/2024 - 16:24
Permalien
Passé la classe 4em
Anonyme (non vérifié)
mer, 01/31/2024 - 09:11
Permalien
Il ya pas à traduire en
Miya Mendy (non vérifié)
mer, 02/21/2024 - 23:12
Permalien
Je n'ai pas compris
Marie Ndiaye (non vérifié)
mer, 11/13/2024 - 21:25
Permalien
Je veux apprendre
Miya Mendy (non vérifié)
mer, 02/21/2024 - 23:12
Permalien
Je n'ai pas compris
Habibatou penda sow (non vérifié)
mar, 06/18/2024 - 02:17
Permalien
Savoir
Anonyme (non vérifié)
jeu, 12/05/2024 - 22:43
Permalien
jai compris
Ajouter un commentaire