Activité
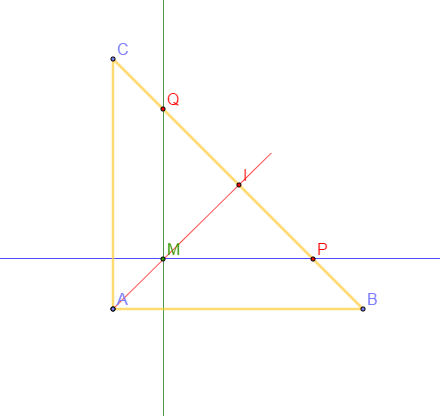
Soit $ABC$ un triangle, $I$ milieu de $[BC]$ et $M$ un point défini par : $\overrightarrow{AM}=\dfrac{2}{5}\overrightarrow{AI}$. La parallèle à $(AB)$ passant par $M$ coupe $(BC)$ en $P$ et la parallèle à $(AC)$ passant par $M$ coupe $(BC)$ en $Q$. On veut montrer que $I$ est le milieu de $[PQ]$. Soit le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AC}).$
1) Déterminer les coordonnées de $A\;,\ B\;,\ C\ $ et $\ M.$
2) Vérifier que l'ordonnée de $P$ est $\dfrac{1}{5}.$
3) Soit $x$ l'abscisse de $P$, donner les coordonnées de $\overrightarrow{BP}$ en fonction de $x$. Calculer $x.$
Déterminer les coordonnées de $Q$ puis montrer que $I$ est milieu de $[PQ].$
Résolution
1) Soit le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AC})$ donc, $A\begin{pmatrix} 0 \\ 0\end{pmatrix}\;,\quad B\begin{pmatrix} 1 \\ 0\end{pmatrix}$ et $C\begin{pmatrix} 0 \\ 1\end{pmatrix}$
$\begin{array}{rcl}\overrightarrow{AM}&=&\dfrac{2}{5}\overrightarrow{AI}=\dfrac{2}{5}(\overrightarrow{AB}+\overrightarrow{BI}) \\ \\ &=&\dfrac{2}{5}\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right)\\ \\ &=&\dfrac{2}{5}\left(\overrightarrow{AB}+\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\right)\\ \\ &=&\dfrac{2}{5}\left(\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\\ \\ &=&\dfrac{2}{5}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\\ \\ &=&\dfrac{1}{5}\overrightarrow{AB}+\dfrac{1}{5}\overrightarrow{AC}\end{array}$
D'où, $M\begin{pmatrix}\dfrac{1}{5} \\ \\ \dfrac{1}{5}\end{pmatrix}$
2) $(MP)$ parallèle à $(AB)$ qui est l'axe des abscisses donc $M$ et $P$ ont la même ordonnée. D'où : $y_{P}=\dfrac{1}{5}.$
3) $x_{P}=x$ donc, $P\begin{pmatrix} x \\ \dfrac{1}{5}\end{pmatrix}$ et $\overrightarrow{BP}\begin{pmatrix} x-1 \\ \dfrac{1}{5}\end{pmatrix}$
$\overrightarrow{BP}$ est colinéaire à $\overrightarrow{BC}$, donc $B\;,\ P$ et $C$ sont alignés.
Soit $\overrightarrow{BC}\begin{pmatrix} -1 \\ 1\end{pmatrix}$ alors on a : $$\begin{array}{rcl} (x-1)(1)-\left(\dfrac{1}{5}\right)(-1)=0&\Leftrightarrow&x-1+\dfrac{1}{5}=0\\\\&\Leftrightarrow&x=1-\dfrac{1}{5}\\ \\&\Leftrightarrow&x=\dfrac{4}{5}\end{array}$$
D'où : $P\begin{pmatrix}\dfrac{4}{5} \\ \\ \dfrac{1}{5}\end{pmatrix}$
$(MQ)$ parallèle à $(AC)$ qui est l'axe des ordonnées donc $Q$ a même abscisse que $M.$ D'où : $x_{Q}=\dfrac{1}{5}.$
Soit $Q\begin{pmatrix}\dfrac{1}{5} \\ y_{Q}\end{pmatrix}$ et $\overrightarrow{CQ}\begin{pmatrix}\dfrac{1}{5} \\ y_{Q}-1\end{pmatrix}$
\begin{eqnarray}\overrightarrow{CQ}\text{ colinéaire à }\overrightarrow{BC}&\Leftrightarrow&\left(\dfrac{1}{5}\right)(1)-(y_{Q}-1)(-1)=0\nonumber\\ \\ &\Leftrightarrow&\dfrac{1}{5}+y_{Q}-1=0\nonumber\\ \\ &\Leftrightarrow&y_{Q}=1-\dfrac{1}{5}=\dfrac{4}{5}\nonumber \end{eqnarray}
D'où : $Q\begin{pmatrix}\dfrac{1}{5} \\ \\ \dfrac{4}{5}\end{pmatrix}$
$I$ est milieu de $[BC]$ alors $I\begin{pmatrix}\dfrac{1}{2} \\ \\ \dfrac{1}{2}\end{pmatrix}$
Calculons les coordonnées du milieu de $[PQ]$
Soit $$\begin{array}{ccc}\dfrac{x_{P}+x_{Q}}{2}&=&\dfrac{\left(\dfrac{4}{5}+\dfrac{1}{5}\right)}{2} \\ \\ &=&\dfrac{1}{2}\ =\ x_{I} \end{array}\quad\text{et}\quad\begin{array}{ccc}\dfrac{y_{P}+y_{Q}}{2}&=&\dfrac{\left(\dfrac{1}{5}+\dfrac{4}{5}\right)}{2} \\ \\ &=&\dfrac{1}{2}\ =\ y_{I} \end{array}$$
Donc $I$ est aussi milieu de $[PQ]$
I. Définitions
Soient deux vecteurs non nuls $\vec{u}$ et $\vec{v}$ et non colinéaires, $A$ un point du plan. Le triplet $(A;\ \vec{u},\ \vec{v})$ est un repère du plan où $A$ est l'origine et $\vec{u}$ et $\vec{v}$ sont les vecteurs de base du plan.
$\centerdot$ $\forall\;$ $M\in\mathcal{P}$ $\exists\;$ $x$ et $y$ tels que $\overrightarrow{AM}=x\vec{u}+y\vec{v}$
$x$ et $y$ sont les coordonnées de $M$. $\ x$ est l'abscisse de $M\;$; $\ x_{M}=x$, $\ y$ est l'ordonnée de $M\;$; $y_{M}=y$
$\centerdot\ \ $ Si $\vec{u}$ est orthogonal à $\vec{v}\ $ ($\vec{u}\perp\vec{v}$) on dira que le repère $(A;\ \vec{u},\ \vec{v})$ est un repère orthogonal.
$\centerdot\ \ $ Si de plus $||\vec{u}||=||\vec{v}||=1$ on dira qu'on a un repère orthonormé.
$\centerdot\ \ (A;\ \vec{u})$ est l'axe des abscisses, $(A;\ \vec{v})$ est l'axe des ordonnées.
II. Équations cartésiennes et paramétriques de droite
II.1 Colinéarité de vecteurs
$\centerdot\ \ $ Deux vecteurs $\vec{u}\begin{pmatrix}
x\\
y
\end{pmatrix}$ et $\vec{v}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ sont colinéaires si, et seulement si, le déterminant de $\vec{u}$ et $\vec{v}$ noté $$det(\vec{u},\ \vec{v})=\begin{vmatrix}
x & x'\\
y & y'
\end{vmatrix}=xy'-x'y=0$$
$\centerdot\ \ $ Deux vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires si, et seulement si, il existe $k\in\mathbb{R}$ tel que $\vec{u}=k.\vec{v}$
$\vec{u}$ et $\vec{v}$ ont même direction.
II.2 Vecteurs orthogonaux
$\centerdot\ \ $ Deux vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si, et seulement si, ils ont des directions orthogonales. On note $\vec{u}\perp\vec{v}$.
$\centerdot\ \ $ Deux vecteurs $\vec{u}\begin{pmatrix}
x\\
y
\end{pmatrix}$ et $\vec{v}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ sont orthogonaux si, et seulement si, $$xx'+yy'=0$$
II.3 Équation cartésienne de droite
II.3.1 Définitions
Soient $\vec{u}$ un vecteur non nul, $A$ un point du plan. L'ensemble des points $M$ du plan tels que $\overrightarrow{AM}$ colinéaire à $\vec{u}$ est la droite passant par $A$ de direction $\vec{u}$ noté $(D)=(A,\ \vec{u}).$
$\vec{u}$ est un vecteur directeur de $(D)$ et tout vecteur $\vec{v}$ colinéaire à $\vec{u}$ est aussi un vecteur directeur de $(D).$
II.3.2 Équation cartésienne et réduite d'une droite
L'équation cartésienne d'une droite $(D)$ est de la forme $$ax+by+c=0$$ avec $(a,\ b)\neq(0,\ 0)\;$; $\ a$ et $b$ ne sont pas nuls en même temps.
$\centerdot\ \ $ Le vecteur $\vec{u}\begin{pmatrix}
-b\\
a
\end{pmatrix}$ est un vecteur directeur de $(D)$.
$\centerdot\ \ $ Le vecteur $\vec{n}\begin{pmatrix}
a\\
b
\end{pmatrix}$ est appelé un vecteur normal à $(D)$. C'est un vecteur orthogonal à la direction de $(D)$.
$\centerdot\ \ $ Si $a=0$ alors, la droite $(D)$ a pour équation $y=\dfrac{-c}{b}$ et est parallèle à l'axe des abscisses.
$\centerdot\ \ $ Si $b=0$ alors, la droite $(D)$ a pour équation $y=\dfrac{-c}{a}$ et est parallèle à l'axe des ordonnées.
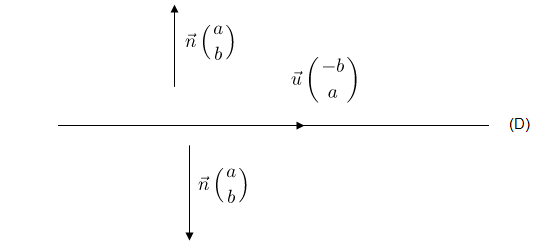
Exercice d'application
Soit $A\begin{pmatrix} 2 \\ 5\end{pmatrix}\;,\quad B\begin{pmatrix} 3 \\ -4\end{pmatrix}\;,\quad C\begin{pmatrix} 1 \\ 7\end{pmatrix}$
Déterminer les équations cartésiennes de :
1) $(AB)$
2) la droite $(D)$ passant par $C$ et parallèle à $(AB)$
3) la médiatrice de $[AC]$
Résolution
1) Équation cartésienne de $(AB)$ :
Nous avons : $A\begin{pmatrix} 3-2 \\ -4-5\end{pmatrix}=\begin{pmatrix} 1 \\ -9\end{pmatrix}$
Soit $M\begin{pmatrix} x \\ y\end{pmatrix}\in(AB)\;;\quad \overrightarrow{AM}\begin{pmatrix} x-2 \\ y-5\end{pmatrix}$
$$\begin{array}{rcl} M\begin{pmatrix} x \\ y\end{pmatrix}\in(AB)&\Leftrightarrow&\overrightarrow{AB}\ \text{ colinéaire à }\ \overrightarrow{AM} \\ \\ &\Leftrightarrow&det(\overrightarrow{AM}\;,\ \overrightarrow{AB})=0\\ \\ &\Leftrightarrow&\begin{vmatrix} x-2&1 \\ y-5&-9\end{vmatrix}=(x-2)(-9)-(y-5)=0\\ \\ &\Leftrightarrow&-9x-y+23=0\end{array}$$
Donc, $(AB)\ :\ -9x-y+23=0$
2) Soit $M\begin{pmatrix} x \\ y\end{pmatrix}\in(D)\;;\quad \overrightarrow{CM}\begin{pmatrix} x-1 \\ y-7\end{pmatrix}$
$$\begin{array}{rcl} (D)\ \text{ parallèle à }\ (AB)&\Leftrightarrow&\overrightarrow{AB}\ \text{ colinéaire à }\ \overrightarrow{CM} \\ \\ &\Leftrightarrow&det(\overrightarrow{AB}\;,\ \overrightarrow{CM})=0\\ \\ &\Leftrightarrow&\begin{vmatrix} 1&x-1 \\ -9&y-7\end{vmatrix}=(y-7)-(-9)(x-1)=0\\ \\ &\Leftrightarrow&y+9x-7-9=0 \end{array}$$
D'où, $(D)\ :\ y+9x-16=0$
3) Soit $(\Delta)$ la médiatrice de $[AC]$ donc $\overrightarrow{AC}\begin{pmatrix} -1 \\ 2\end{pmatrix}$ est un vecteur normal à $(\Delta).$
Soit $I$ milieu de $[AC]\;;\quad I\begin{pmatrix}\dfrac{3}{2} \\ \\ 6\end{pmatrix}$ et soit $M\begin{pmatrix} x \\ y\end{pmatrix}\in(\Delta)\;;\quad \overrightarrow{IM}\begin{pmatrix} x-\dfrac{3}{2} \\ \\ y-6\end{pmatrix}$
$$\begin{array}{rcl} (\Delta)\ \text{ perpendiculaire à }\ (AC)&\Leftrightarrow&(-1)\left(x-\dfrac{3}{2}\right)+2(y-6)=0 \\ \\ &\Leftrightarrow&-x+\dfrac{3}{2}+2y-12=0\\ \\ &\Leftrightarrow&-x+2y-\dfrac{21}{2}=0\end{array}$$
Donc, $\Delta\ :\ -x+2y-\dfrac{21}{2}=0$
Remarques
L'équation réduite d'une droite $(D)$ est de la forme $y=\alpha x+\beta$ où $\alpha$ est le coefficient directeur de la droite $(D)$. Donc si $(D) \: : y=\alpha x+\beta \: \Longrightarrow \: \alpha x-y+\beta=0$ et $\vec{u}\begin{pmatrix} 1\\ \alpha \end{pmatrix}$ est un vecteur directeur de $(D).$
Soit $(D) \: : ax+by+c=0$, si $b\neq 0 \: \Rightarrow \: y=\dfrac{-a}{b}x-\dfrac{c}{b}$ et $\dfrac{-a}{b}$ est le coefficient directeur de la droite $(D).$
II.3.3 Conditions de parallélisme et d'orthogonalité de droites
$\centerdot\ \ $ Deux droites $(D) \: : ax+by+c=0$ de vecteur directeur $\vec{u}\begin{pmatrix} -b\\ a \end{pmatrix}$ et $(D') \: : a'x+b'y+c'=0$ de vecteur directeur $\vec{u}'\begin{pmatrix} -b'\\ a' \end{pmatrix}$ sont parallèles si, et seulement si, les vecteurs directeurs $\vec{u}$ et $\vec{u}'$ sont colinéaires ($det(\vec{u},\ \vec{u}')=0$)
$\centerdot\ \ (D)$ et $(D')$ sont orthogonales si, et seulement si, les vecteurs directeurs $\vec{u}$ et $\vec{u}'$ sont orthogonaux ($x_{\vec{u}}x'_{\vec{u}'}+y_{\vec{u}}y'_{\vec{u}'}=0$)
$\centerdot$ Deux droites $(D) \: : y=\alpha x+\beta$ et $(D') \: : y=\alpha' x+\beta'$ sont parallèles si, et seulement si, $$\alpha=\alpha'$$
$\centerdot\ \ (D)$ et $(D')$ sont perpendiculaires si, et seulement si, $$\alpha.\alpha'=-1$$
Exercice d'application
Soit $(D_{1})\ :\ 2x-3y+5=0$ et $A\begin{pmatrix} 3 \\ 4\end{pmatrix}\;,\quad B\begin{pmatrix} 2 \\ 3\end{pmatrix}$ deux points du plan.
1) $A$ et $B$ appartiennent-ils à $(D_{1})$ ?
2) Déterminer l'équation de la droite $(D_{2})$ passant par $A$ et parallèle à $(D_{1}).$
3) Soit $(D_{3})\ :\ y=3x-1$
$(D_{3})$ et $(D_{1})$ sont-elles parallèles ? perpendiculaires ?
Résolution
1) $M\begin{pmatrix} x \\ y\end{pmatrix}\in(D_{1})$ si, et seulement si, ses coordonnées vérifient l'équation de $(D_{1})$
$$\begin{array}{rcl} A\begin{pmatrix} 3 \\ 4\end{pmatrix}\ :\quad 2\times 3-3\times 4+5&=&6-12+5\\ \\ &=&-1\ \neq 0\end{array}$$
Donc, $A\notin(D_{1})$
$$\begin{array}{rcl} B\begin{pmatrix} 2 \\ 3\end{pmatrix}\ :\quad 2\times 2-3\times 3+5&=&4-9+5\\ \\ &=&0\end{array}$$
Donc, $B\in(D_{1})$
2) Soit $M\begin{pmatrix} x \\ y\end{pmatrix}\in(D_{2})\;;\quad \overrightarrow{AM}\begin{pmatrix} x-3 \\ y-4\end{pmatrix}$ et soit $\vec{u}\begin{pmatrix} 3 \\ 2\end{pmatrix}$ vecteur directeur de $(D_{1})$ alors
$$\begin{array}{rcl} (D_{2})\ \text{ parallèle à }\ (D_{1})&\Leftrightarrow&\overrightarrow{AM}\ \text{ colinéaire à }\ \vec{u} \\ \\ &\Leftrightarrow&det(\overrightarrow{AM}\;,\ \vec{u})=0\\ \\ &\Leftrightarrow&\begin{vmatrix} x-3&3 \\ y-4&2\end{vmatrix}=(x-3)(2)-(3)(y-4)=0\\ \\ &\Leftrightarrow&2x-3y+6=0\end{array}$$
D'où, $(D_{2})\ :\ 2x-3y+6=0$
3) $(D_{1})\ :\ 2x-3y+5=0$ donc $y=\dfrac{2}{3}x+\dfrac{5}{3}$ est une équation réduite pour $(D_{1}).$
Soient $u_{1}\begin{pmatrix} 1 \\ \\ \dfrac{2}{3}\end{pmatrix}$ et $u_{3}\begin{pmatrix} 1 \\ 3\end{pmatrix}$ vecteurs directeurs respectifs de $(D_{1})$ et $(D_{3}).$
$3\neq\dfrac{2}{3}\;,\ $ donc, $(D_{1})$ et $(D_{3})$ ne sont pas parallèles.
$3\times\dfrac{2}{3}=1\neq -1\;,\ $ alors, $(D_{1})$ et $(D_{3})$ ne sont pas perpendiculaires.
II.3.4 Équations paramétriques
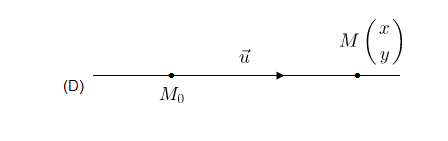
Soient $\vec{u}\begin{pmatrix} \alpha\\ \beta \end{pmatrix}$ et $M_{0}\begin{pmatrix} x_{0}\\ y_{0} \end{pmatrix}$, $\ (D)$ est une droite passant par $M_{0}$ de vecteur directeur $\vec{u}\;$; $\ (D)=(M_{0},\ \vec{u}).$
$M\begin{pmatrix}
x\\
y
\end{pmatrix}\in(D)$ si, et seulement si, $\overrightarrow{M_{0}M}$ est colinéaire à $\vec{u}.$
Donc, $\exists\;$ $k\in\mathbb{R}$ tel que $\overrightarrow{M_{0}M}=k.\vec{u}.$
Ainsi, $\left\lbrace\begin{array}{lcl}
x-x_{0} &=& k\alpha\\
y-y_{0} &=& k\beta
\end{array}
\right. \Longrightarrow \left\lbrace\begin{array}{lcl}
x &=& x_{0}+k\alpha\\
y &=& y_{0}+k\beta
\end{array}
\right.$ qui est un système d'équations paramétriques de $(D)$
$M_{k}\begin{pmatrix}
x_{0}+\alpha k\\
y_{0}+\beta k
\end{pmatrix}$ est le point de paramètre $k$.
Exercice d'application
Soit $A\begin{pmatrix} 1 \\ 2\end{pmatrix}\;,\quad B\begin{pmatrix} 3 \\ 4\end{pmatrix}$ deux points du plan et $(D_{1})\ :\ 2x-3y+5=0.$
1) Déterminer un système d'équations paramétriques des droites $(AB)$ et $(D_{1}).$
2) Soit $(D_{2})\ :\ \left\lbrace\begin{array}{rcl} x&=&2-t \\ y&=&3+4t\end{array}\right.$
a) $A\begin{pmatrix} 1 \\ 2\end{pmatrix}$ et $D\begin{pmatrix} 0 \\ 11\end{pmatrix}$ appartiennent-ils à $(D_{2})\;\ ?$
b) Déterminer l'équation cartésienne de $(D_{2})$
3) Déterminer les coordonnées des points d'intersection de $(D_{1})$ et $(D_{2})$
Résolution
Soit $M\begin{pmatrix} x \\ y\end{pmatrix}\in(AB)$ alors $\overrightarrow{AB}$ et $\overrightarrow{AM}$ sont colinéaires.
$$\begin{array}{rcl} \overrightarrow{AB}\ \text{ colinéaire à }\ \overrightarrow{AM}&\Leftrightarrow&\overrightarrow{AM}=t\overrightarrow{AB}\;,\quad t\in\mathbb{R}\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x-1&=&2t \\ y-2&=&2t \end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&2t+1 \\ y&=&2t+2\end{array}\right.\quad\text{équation paramétrique de }(AB)\end{array}$$
Soit $\vec{u}\begin{pmatrix} 3 \\ 2\end{pmatrix}$ vecteur directeur de $(D_{1})$ et $A\begin{pmatrix} -1 \\ 1\end{pmatrix}$ un point de $(D_{1})$
$M\begin{pmatrix} x \\ y\end{pmatrix}\in(D_{1})$ alors $\overrightarrow{AM}$ et $\vec{u}$ sont colinéaires.
$$\begin{array}{rcl} \overrightarrow{AM}\ \text{ colinéaire à }\ \vec{u}&\Leftrightarrow&\overrightarrow{AM}=t\vec{u}\;,\quad t\in\mathbb{R}\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x+1&=&3t \\ y-1&=&2t \end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&3t-1 \\ y&=&2t+1\end{array}\right.\quad\text{équation paramétrique de }(D_{1})\end{array}$$
2) a) $\left\lbrace\begin{array}{rcl} 1&=&2-t \\ 2&=&3+4t\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} t&=&1 \\ \\ t&=&-\dfrac{1}{4}\end{array}\right.\quad\text{impossible}$
D'où, $A\notin(D_{2})$
$\left\lbrace\begin{array}{rcl} 0&=&2-t \\ 11&=&3+4t\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} t&=&2 \\ t&=&2\end{array}\right.\quad\text{donc }D\in(D_{2})$
b) $\left\lbrace\begin{array}{rcl} x&=&2-t \\ y&=&3+4t\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} t&=&2-x \\ y&=&3+4(2-x)\ =\ -4x+11\end{array}\right.$
D'où, $y+4x-11=0$ est une équation cartésienne de $(D_{2})$
3) Dans $(D_{1})$, remplaçons $x$ et $y$ par leur valeur dans $(D_{2})$
$$\begin{array}{rcl} 2(2-t)-3(3+4t)+5=0&\Leftrightarrow&-14t=0\\\\&\Leftrightarrow&t=0\end{array}$$
Donc, $\left\lbrace\begin{array}{rcl} x&=&2 \\ y&=&3\end{array}\right.$ ; d'où $(D_{1})\cap(D_{2})=I\begin{pmatrix} 2 \\ 3\end{pmatrix}$
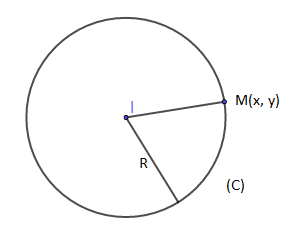
II.3.5 Équations de cercle
Soit $\mathcal{C}$ le cercle de centre $I\begin{pmatrix}
\alpha\\
\beta
\end{pmatrix}$ et de rayon $R$ noté $\mathcal{C}(I,\ R).$
$M\begin{pmatrix}
x\\
y
\end{pmatrix}\in\mathcal{C}(I,\ R) \: \Rightarrow IM=R.$
Donc, $IM^{2}=R^{2} \: \Longrightarrow (x_{M}-x_{I})^{2}+(y_{M}-y_{I})^{2}=R^{2}.$
D'où : $\ (x_{M}-\alpha)^{2}+(y_{M}-\beta)^{2}=R^{2}$ qui est l'équation réduite du cercle $\mathcal{C}\left(I\begin{pmatrix}
\alpha\\
\beta
\end{pmatrix}, R\right).$
$$x^{2}+y^{2}-2\alpha x-2\beta y+\alpha^{2}+\beta^{2}-R^{2}=0$$ est l'équation cartésienne du cercle $(\mathcal{C}).$
Exemple
Les équations suivantes sont-elles des équations de cercle. Si oui, donner le centre et le rayon.
a) $x^{2}+y^{2}-6x+8y-5=0$
b) $x^{2}+y^{2}+2x+4y-1=0$
c) $x^{2}+y^{2}+3x+4y+20=0$
Résolution
a) $$\begin{array}{rcl} x^{2}+y^{2}-6x+8y-5=0&\Leftrightarrow&(x-3)^{2}-9+(y+4)^{2}-16-5=0\\ \\ &\Leftrightarrow&(x-3)^{2}+(y+4)^{2}=30\end{array}$$
Donc, cette équation définie bien un cercle $\mathcal{C}\left(I\begin{pmatrix} 3 \\ -4\end{pmatrix}\;;\ \sqrt{30}\right)$
b) $$\begin{array}{rcl} x^{2}+y^{2}+2x+4y-1=0&\Leftrightarrow&(x+1)^{2}-1+(y+2)^{2}-4-1=0\\ \\ &\Leftrightarrow&(x+1)^{2}+(y+2)^{2}=6\end{array}$$
On obtient bien un cercle $\mathcal{C}\left(I\begin{pmatrix} -1 \\ -2\end{pmatrix}\;;\ \sqrt{6}\right)$
c) $$\begin{array}{rcl} x^{2}+y^{2}+3x+4y+20=0&\Leftrightarrow&\left(x+\dfrac{3}{2}\right)^{2}-\dfrac{9}{4}+(y+2)^{2}-4+20=0\\ \\ &\Leftrightarrow&\left(x+\dfrac{3}{2}\right)^{2}+(y+2)^{2}=-\dfrac{55}{4}\end{array}$$
$-\dfrac{55}{4}<0$ donc cette équation ne définie pas un cercle.
III. Formule de changement de repère
Soient $(O;\ \vec{i},\ \vec{j})$ un repère du plan, $S$ un point de coordonnées $(a,\ b)$ , dans $(O;\ \vec{i},\ \vec{j}).$
Considérons un nouveau repère $(S;\ \vec{i},\ \vec{j}).$
Donc, $M\begin{pmatrix}
x\\
y
\end{pmatrix}$ dans $(O;\ \vec{i},\ \vec{j})$ et $M\begin{pmatrix}
X\\
Y
\end{pmatrix}$ dans $(S;\ \vec{i},\ \vec{j})$
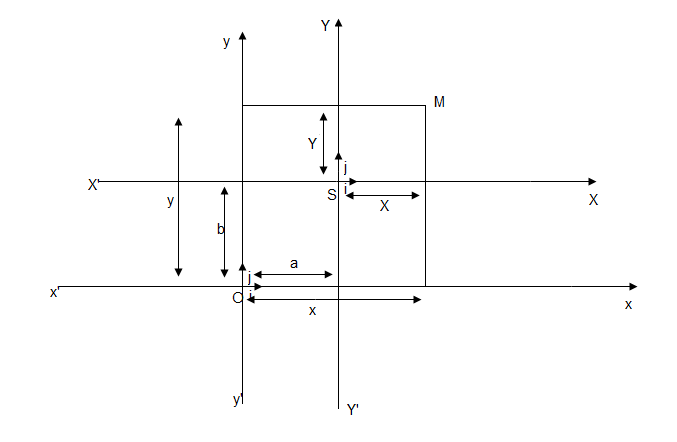
Nous obtenons $\left\lbrace\begin{array}{lcl}
x &=& X+a\\
y &=& Y+b
\end{array}
\right.$ qui constitue la formule de changement de repère.
Exemple
Soit $(O\;;\ \vec{i}\;,\ \vec{j})$ un repère du plan, $A\begin{pmatrix} 2 \\ 1\end{pmatrix}\;,\ B\begin{pmatrix} 3 \\ 4\end{pmatrix}$ et $\Omega(3\;;\ 2)$ dans $(O\;;\ \vec{i}\;,\ \vec{j}).$
Trouver les coordonnées de $A$ et $B$ dans $(\Omega\;;\ \vec{i}\;,\ \vec{j}).$
Résolution
D'après la formule de changement de repère on a : $$\left\lbrace\begin{array}{rcl} x&=&X+3 \\ y&=&Y+2\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{rcl} X&=&x-3 \\ Y&=&y-2\end{array}\right.$$
Les coordonnées de $A$ dans $(\Omega\;;\ \vec{i}\;,\ \vec{j})$ sont donc données par : $$A\begin{pmatrix} X=2-3 \\ Y=1-2\end{pmatrix}=\begin{pmatrix} -1 \\ -1\end{pmatrix}$$
$$\begin{array}{rcl}\overrightarrow{OB}=\overrightarrow{O\Omega}+\overrightarrow{\Omega B}&\Rightarrow&\overrightarrow{\Omega B}=\overrightarrow{OB}-\overrightarrow{O\Omega}\\ \\ &\Rightarrow&\overrightarrow{\Omega B}=3\vec{i}+4\vec{j}-3\vec{i}-2\vec{j}\\ \\ &\Rightarrow&\overrightarrow{\Omega B}=2\vec{j}\end{array}$$
D'où : $B\begin{pmatrix} 0 \\ 2\end{pmatrix}$ dans $(\Omega\;;\ \vec{i}\;,\ \vec{j}).$


Commentaires
Anonyme (non vérifié)
dim, 01/27/2019 - 16:55
Permalien
des bien conçu et c'est
Anonyme (non vérifié)
dim, 07/04/2021 - 02:10
Permalien
Très bien
Anonyme (non vérifié)
dim, 07/04/2021 - 02:58
Permalien
De très bonnes éxo
Ndeye Fatou Ndiaye (non vérifié)
lun, 10/18/2021 - 14:19
Permalien
merci beaucoup
Lelouch Lamperouge (non vérifié)
lun, 02/21/2022 - 20:17
Permalien
Super cours à mon avis. Sinon
Anonyme (non vérifié)
mer, 06/12/2024 - 09:01
Permalien
Merci
Ajouter un commentaire