Corrigé Exercice 8 : Les solutions 3e
Classe:
Troisième
Exercice 8
1) La masse d'hydroxyde de sodium a-t-on utilisée
On a : $c=\dfrac{n}{V}$ or, $\ n=\dfrac{m}{M}$
Par conséquent, $c=\dfrac{m}{V\times M}$
D'où, $m=c\times V\times M$ avec, $M_{NaOH}=23+16+1=40$
A.N : $m=0.01\times 200\;10^{-3}\times 40=0.08$
Donc, $\boxed{m=0.08\;g}$
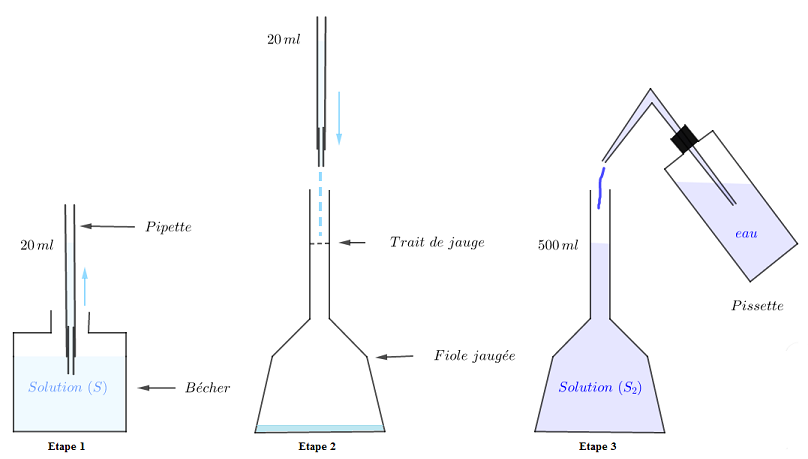
2) Trouvons la molarité de la solution diluée obtenue.
Soit $c'$ la concentration de la solution diluée
On a : $c'=\dfrac{n'}{V'}\ $ or, $n'=n$ et $V'=V+450$
Donc, $c'=\dfrac{n}{V+450}\ $ avec, $n=c\times V$
Ainsi, $c'=\dfrac{cV}{V+450}$
A.N : $c'=\dfrac{0.01\times 50}{50+450}=0.001$
Donc, $\boxed{c'=0.001\;mol\cdot l^{-1}}$