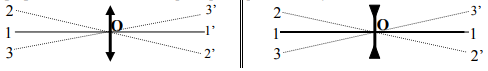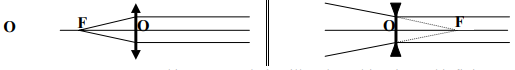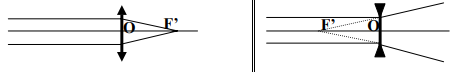Situation - problème
Pour attirer davantage de clients et donner l'immensité de ses pouvoirs à résoudre tous les problèmes qu'on lui présente, un charlatan présente quelques phénomènes spectaculaires à partir d'objets transparents :
$-\ $ A quelques mal - voyants, il rend une vision à peu près correcte.
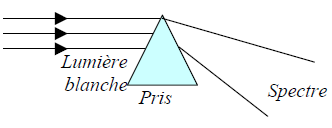
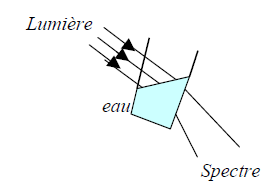
$-\ $ Il brûle des objets à partir de la seule lumière du soleil
$-\ $ Il arrive à donner de certains objets des images petites et renversées...
Ces phénomènes sont-ils surnaturels ?
Et quels sont ces objets ?
Qu'est-ce qui fait leurs particularités ?
1 - Définition.
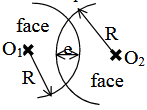
Une lentille mince est un milieu transparent limité par deux faces sphériques
$R_1$ et $R_2$ sont les rayons de courbures respectifs des faces $1$ et $2$
$e$ est l'épaisseur de la lentille
N.B :
Une lentille est dite mince si son épaisseur au centre e est infiniment petite devant ses rayons de courbures
2-1 Distinction géométrique:
On distingue deux sortes de lentilles minces :
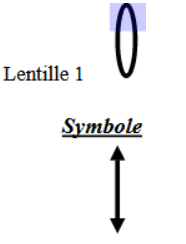
➭ Des lentilles à bords minces $(1)$ bords minces
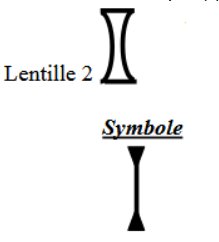
➭ Des lentilles à bords épais $(2)$ bords épais
2-2 Distinction physique:
Envoyons des faisceaux cylindriques sur chacune des deux sortes de lentilles.
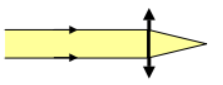
La lentille à bords minces transforme le faisceau cylindrique en faisceau convergent : c'est une lentille convergente
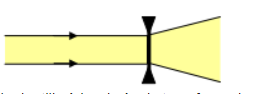
La lentille à bords épais transforme le faisceau cylindrique en faisceau divergent : c'est une lentille divergente
III- Caractéristiques d'une lentille mince.
III-1 Le centre optique :
Le centre optique $O$ d'une lentille est le point par lequel aucun rayon incident n'est dévié.
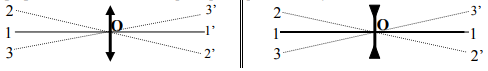
III-2 Les axes optiques
On appelle axe optique d'une lentille la trajectoire du rayon lumineux passant par son centre optique.
Exemples :
les droites $(1\;,\ 1')$ ; $(2\;,\ 2')$ ; $(3\;,\ 3')$...
L'axe optique $(1\;,\ 1')$ perpendiculaire à la lentille est son axe optique principal $(A.O.P.)$
N.B.
Pour une lentille, il existe une infinité d'axes optiques.
III-3 Les foyers.
Une lentille possède toujours deux points focaux que l'on appelle les foyers de la lentille.
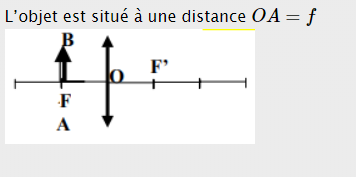
III.3-1 Le foyer - Objet F:
C'est l'objet dont l'image par la lentille est à l'infini.
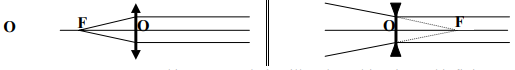
III.3-2 Le foyer - image F':
C'est l'image, par la lentille, d'un objet situé à l'infini.
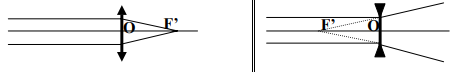
Remarques
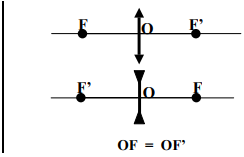
$\bullet\ $ Le foyer - objet $F$ est du coté des rayons incidents pour la lentille convergente et du coté des rayons émergents pour la lentille divergente
$\bullet\ $ Le foyer - image $F'$ est du coté des rayons émergents pour la lentille convergente et du coté des rayons incidents pour la lentille divergente.
$\bullet\ $ Ces foyers $F$ et $F'$ sont symétriques par rapport à la lentille et situés sur son axe optique.
Les rayons particuliers d'une lentille.
a) l'axe optique secondaire
Il passe par un point de l'objet et par le centre optique et n'est pas dévié
b) le rayon incident parallèle à l'axe optique principal :
Il sort de la lentille en passant ou son prolongement passerait par le foyer - image $F'$
c) Le rayon incident passant ou dont le prolongement passerait par le foyer - objet $F$
Il émerge parallèle à l'axe optique principal.
III-4 La distance focale.
La distance focale $f$ est la distance qui sépare le centre optique $O$ de chacun des foyers de la lentille $\left[f=OF=OF'\right]$
N.B.
La distance focale $f$ est une grandeur algébrique :
$\begin{array} {lcl} f &> 0& \text{ pour la lentille convergente }\\ f &< 0&\text{ pour la lentille divergente}\end{array}$
III-5 La convergence ou vergence
La convergence ou vergence $C$ d'une lentille est l'inverse de sa distance focale.
$\left[C=\dfrac{1}{f}\right]$
$\begin{array} {lcl} C \text{ est en dioptrie}(δ) & C > 0 & \text{ pour la lentille convergente}\\ f \text{ en mètre (m)} & C < 0& \text{pour la lentille divergente} \end{array}$
IV- L'image donnée par une lentille
Partout où on la trouve, la lentille sert à donner ou à améliorer une image.
Exemple :
Observer et caractériser l'image donné par une lentille d'un objet réel $AB$ placé perpendiculairement à son axe optique principal à différentes distances de son centre optique.
N.B.
Les principales conclusions et solutions de cet exercice sont à obtenir à partir :
$\begin{array} {lcl} &➭& \text{ d'observations expérimentales}\\ &➭& \text{ de constructions graphiques} \end{array}$

Caractéristiques : l'image $A'B'$ de l'objet $AB$ est :
.........................................................................................................................................
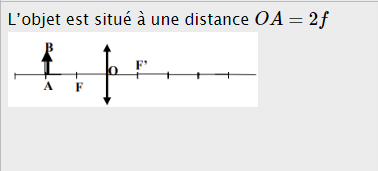
Caractéristiques : l'image $A'B'$ de l'objet $AB$ est :
................................................................................................................................................................

Caractéristiques : l'image $A'B'$ de l'objet $AB$ est :
..................................................................................................................................................................
Caractéristiques : l'image $A'B'$ de l'objet $AB$ est :
..................................................................................................................................................................
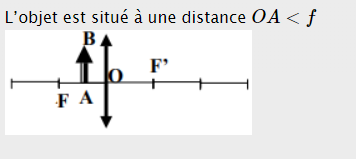
Caractéristiques : l'image $A'B'$ de l'objet $AB$ est :
.....................................................................................................................................................................
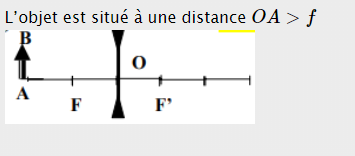
Caractéristiques : l'image $A'B'$ de l'objet $AB$ est :
...................................................................................................................................................................
IV-1 Construction de l'image.
4.1-1 Relever les données numériques de l'énoncé et adopter une échelle convenable.
4.1-2 Représenter correctement la lentille par son symbole.
4.1-3 Indiquer le centre optique $O$ et tracer l'axe optique principal.
4.1-4 Placer les foyers $F$ et $F'$ suivant l'échelle adoptée.
4.1-5 Placer l'objet comme indiqué dans l'énoncé suivant l'échelle adoptée.
On obtient alors l'image de chaque point de l'objet par la rencontre de deux des trois rayons particuliers issus de ce point.
IV-2 Les caractéristiques de l'image.
Caractériser ou donner les caractéristiques d'une image c'est :
$-\ $ indiquer la nature (réelle ou virtuelle) de l'image.
$-\ $ préciser la position de l'image (droite ou renversée) par rapport à l'objet.
$-\ $ comparer la grandeur (taille) de l'image à celle de l'objet.
$-\ $ calculer l'agrandissement de l'image.
$-\ $ situer l'image (position de l'image par rapport à celle de l'objet)
Exemple :
Un objet réel $AB$ de hauteur $10\,cm$ est placé perpendiculairement à l'axe optique principal d'une lentille de distance focale $f=+20\,cm.$
Le point $A$ est sur l'axe optique principal à $50\,cm$ de son centre optique $O.$
Construire et caractériser l'image $A'B'$ de l'objet réel $AB$ donnée par cette lentille.
Données
$\left\{
\begin{array}{rl}
AB=10\text{ cm} \\
f=+20\text{ cm}\\
OA=60\text{ cm}
\end{array}
\right. \text{ Echelle }\frac{1}{10} \left\{
\begin{array}{rl}
AB=1\text{ cm} \\
f=2\text{ cm}\\
OA=6 \text{ cm}
\end{array}
\right.$
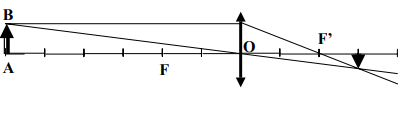
L'image $A'B'$ de l'objet $AB$ est :
$-\ $ Réelle
$-\ $ Renversée
$-\ $ Plus petite que l'objet $\left(A'B'=\dfrac{1}{2} AB\right)$
$$γ=\dfrac{A'B}{AB}=\dfrac{1}{2}$$
$-\ $ sur le côté opposé $OA'=\dfrac{1}{2}OA$
V- Applications :
Quelles utilisations pratiques de lentilles ?
V-1 La vision correcte.
La vision d'un objet est correcte quand on image se forme sur la tache jaune située sur la rétine. Cette image est obtenue grâce à la lentille naturelle qu'est le cristallin.
La netteté de l'image est rendue possible grâce à l'accommodation qui permet au cristallin de faire varier sa convergence.
V-2 Anomalies et corrections de l'œil.
D'origines diverses des anomalies de la vue adviennent et sont corrigées par le port de lentilles sous forme généralement de verres correcteurs.
V.2-1 La myopie
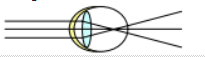
Le mal : Le cristallin de l'œil myope est trop convergent ; sa distance focale est alors courte : l'image se forme avant la rétine.
L'œil voit flou.
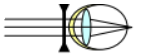
La correction : La correction d'une telle anomalie,la myopie, nécessite le port de lentilles divergentes.
V.2-2 l'hypermétropie
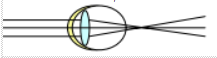
Le mal : L'œil hypermétrope n'est pas assez convergent ; son cristallin a une distance focale longue : l'image se forme derrière la rétine, elle est floue.
La correction : L'hypermétropie se corrige par le port de lentilles convergentes
V.2-3 La presbytie
En vieillissant, le cristallin de l'œil presbyte perd de son élasticité ; son pouvoir d'accommodation diminue : l'image est floue.
Le presbyte comme l'hypermétrope voient nettement les objets éloignés : les personnes atteintes de ces anomalies peuvent conduire leurs voitures sans leurs lunettes de corrections mais ils ne peuvent lire leurs journaux sans correction.
La presbytie se corrige avec des lentilles convergentes.
V-4 L'appareil photographique.
L'appareil photographique est une chambre noire ayant une pellicule photographique ou film comme écran et un objectif formé de lentilles mobiles à son ouverture réglable.
La netteté de l'image, plus petite que l'objet, sur la pellicule, est obtenue grâce à la translation des lentilles mobiles : c'est la mise au point.
V-5 L'appareil de projection.
Un projecteur est un appareil qui, grâce aux lentilles logées dans son objectif, donne d'un objet petit, la diapositive, une image grande sur un écran.