Exercices sur les forces 3e
Classe:
Troisième
Exercice 1
Compléter le texte ci-dessous en ajoutant les mots ou groupe de mots manquants
1) Une intensité : c'est :$\ldots$ exprimée en $\ldots\ldots$
2) Une droite d'action : c'est $\ldots$ ; elle peut être $\ldots$, $\ \ldots$, $\ldots\ldots$
3) On mesure la valeur d'une force à l'aide d'un $\ldots\ldots\ldots$
Exercice 2
Représenter par un vecteur chacune des forces suivantes :
1) Le poids d'une plaque métallique pesant $4.75\;N$
2) La force de traction de $525\;N$ avec laquelle une remorque est déplacée horizontalement.
Exercice 3
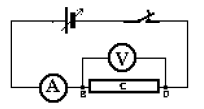
La caisse $C$ de poids $20\;N$ est en équilibre sur une table tel que indiqué par le schéma ci-contre. $A$ et $B$ sont deux charges pesant chacune $0.5\;kg$
1) Reprendre le schéma en représentant toutes les forces agissant sur la caisse $C$
2) Représenter le poids de chacune des deux charges.
3) Donner l'intensité de chacune de ces force

Exercice 4
Le poids d'un objet est une force.
1) Donner sa définition et dites c'est quelle sorte de force ?
2) Indiquer et préciser ses caractéristiques.
Exercice 5
Un objet de masse $500\;g$ est suspendu à un ressort et pend.
1) Représenter, sur un schéma, les forces qui lui sont appliquées
2) Donner, en les précisant, les caractéristiques de chacune de ces forces.
Exercice 6
Faites, sur un schéma, l'inventaire de toutes les forces qui s'appliquent sur une voiture roulant à vitesse constante sur une route horizontale.
Activités : Conditions d'équilibre d'un solide
Une plaque de polystyrène de poids négligeable est soumise à l'action de deux forces par l'intermédiaire de deux fils tendus.
Les deux cylindres accrochés aux deux poulies ont pour masse $50\;g.$
On donne $g=10N\cdot kg^{-1}$
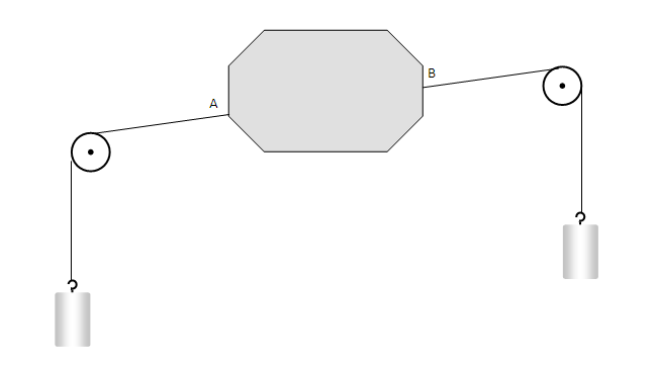
1) Calculer l'intensité du poids de chaque cylindre
2) Représenter le poids des deux cylindres en prenant comme échelle $1\;cm$ pour $0.25N$ puis les forces exercées en $A$ et $B$ en conservant la même échelle.
On notera $\overrightarrow{F}_{1/S}$ la force exercée en $A$ et $\overrightarrow{F}_{2/S}$ la force exercée en $B.$
3) Pourquoi dit-on que dans ce cas la plaque est en équilibre ?
4) Compléter le tableau :
$$\begin{array}{|c|c|c|c|c|} \hline \text{Force}&\text{Point d'application}&\text{Direction}&\text{Sens}&\text{Intensité }(N)\\ \hline \overrightarrow{F}_{1/S}& & & &\\ \hline \overrightarrow{F}_{2/S}& & & & \\ \hline \end{array}$$
5) Déduis du tableau une relation entre $\overrightarrow{F}_{1/S}\ $ et $\ \overrightarrow{F}_{2/S}\ $ ?
Exercice 7 Effets d'une action mécanique
1) Donner trois effets possibles d'une action mécanique exercée sur un objet.
2) Citer un exemple pour chaque effet
Exercice 8 Types d'actions mécaniques
1) Cite deux exemples d'une action de contact et deux exemples d'une action à distance
2) Cite un exemple d'une action localisée et un exemple d'une action répartie.
Exercice 9 Reconnaissance de types d'actions mécaniques
Classe les types d'action en action de contact et en action à distance :
Action exercée par un pied sur un ballon.
Action exercée par un marteau sur un clou.
Action exercée par la Terre sur une mangue qui tombe d'un manguier.
Action exercée par le vent sur une voile de bateau.
Action exercée par un homme tirant sur la laisse d'un chien.
Action exercée par un aimant sur une bille d'acier passant à sa proximité.
$$\begin{array}{|c|c|} \hline \text{Action de contact}&\text{Action à distance}\\ \hline &\\ \hline &\\ \hline &\\ \hline \end{array}$$
Exercice 10 Caractéristiques d'une force
1) Citer les quatre caractéristiques d'une force représentant une action localisée.
2) Comment représente-t-on une force ?
3) Quel appareil mesure la valeur d'une force ?
Exercice 11 Représentation d'une force
Une force a une intensité de $30N.$
1) Représente cette force en utilisant les échelles suivantes :
$1^{er}$ cas : direction verticale et sens vers le haut ; échelle : $1\;cm$ pour $5N$ ;
$2^{ième}$ cas : direction horizontale et sens vers la droite ; échelle : $1\;cm$ pour $6N$
$3^{ième}$ cas : direction faisant un angle de $30^{\circ}$ par rapport à l'horizontale et sens vers le haut. échelle : $1\;cm$ pour $10N$
2) Donne l'intensité d'une force représentée par un vecteur de longueur $5\;cm$ à chacune des échelles précédentes
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Source:
irempt.ucad.sn & ADEM