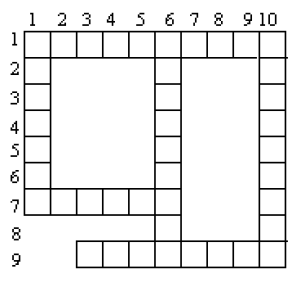
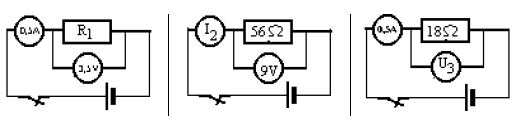
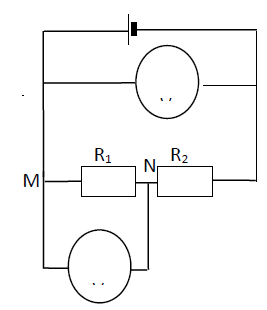
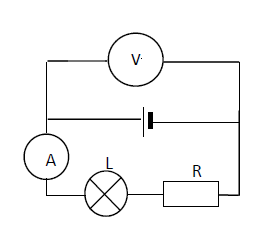
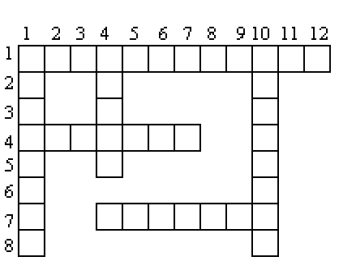
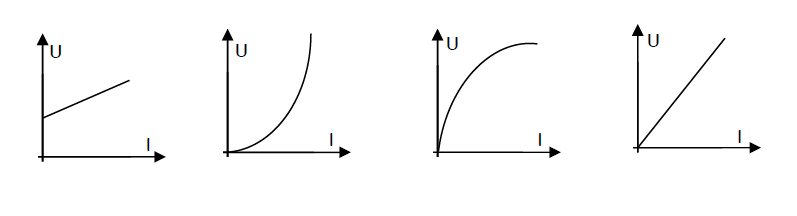indiquer les mots permettant de remplir la grille ci-contre.
1) Donner deux exemples de transformations de l'énergie électrique en énergie calorifique.
2) Quelle est la forme d'énergie contenue dans un arc tendu ? En quelle forme d'énergie se transforme-t-elle à la lâchée de la flèche ?
Une automobile de masse $m=1\;\text{tonne}$ roule sur une route horizontale et rectiligne à la vitesse $v=144\;km/h.$
1) Après avoir défini l'énergie cinétique, la calculer en kilo joules dans le cas de cette voiture.
2 En réalité, le moteur développe une énergie totale de $0.8\;kWh$, en déduire, alors, son rendement.
Un objet de masse $1\;kg$ est soulevé d'une hauteur de $10\;m$ au bout d'une corde.
1) Calculer le travail mécanique qu'il a fallu fournir pour soulever cet objet.
Un courant constant d'intensité $I=3\;A$ passe pendant $45\;min$ dans un conducteur de résistance $R=40\;\Omega.$ Calculer en joules et en calories la chaleur dégagée par effet joule.
Une centrale électrique nucléaire fournit à un réseau une puissance électrique de $1000\;MW.$ Sachant que la puissance totale du combustible nucléaire fournie à la centrale est de $2800\;MW$, trouver le rendement de cette centrale.
Pendant un orage, la foudre qui jaillit entre un nuage et le sol, résulte d'un courant moyen de $10\;kA$ circulant sous une tension de $20\;MV$ pendant $0.1\;s$. Quelles sont la puissance et l'énergie électrique mises en jeu ?
Une automobile a une consommation moyenne de $7.5\;L$ aux $100\;km$ parcourus en $1\;h$. Or la combustion d'un litre d'essence dégage une énergie thermique évaluée à $35\;10^{6}\;J$.
1) Calculer l'énergie thermique fournie à cette automobile.
2) La puissance effective de cette voiture, du point de vue mécanique est évaluée à $18\;KW$. Quel est le rendement de l'automobile ?
Activités
Sur une ampoule, Momar lit l'information $15W.$
Il souhaite déterminer la tension nominale de la lampe.
Pour cela, il réalise un montage potentiométrique permettant de mesurer la tension électrique aux bornes de la lampe et l'intensité du courant qui la traverse.
1) Réaliser le schéma du montage.
2) Il obtient les résultats suivants :
$$\begin{array}{|l|c|c|c|} \hline &\text{Mesure }1&\text{Mesure }2&\text{Mesure }3\\ \hline \text{Tension}&6V&12V&15V\\ \hline \text{Intensité}&0.86A&1.25A&1.41A\\ \hline\text{Puissance électrique reçue}& & &\\ \hline \end{array}$$
a) Pour chaque série de mesures, calculer la puissance reçue par la lampe.
Utilise le tableau de mesures pour déterminer la tension nominale de la lampe.
Justifie la réponse.
b) compare la tension appliquée à la lampe lors de la mesure $1$ avec sa tension nominale.
La lampe va-t-elle briller normalement ou faiblement ?
Exercice 11 Types de conversion d'énergie
Recopier et compléter les phrases suivantes :
L'énergie que possède un corps suspendu à une certaine hauteur du sol est appelée$\ldots\ldots$
L'énergie cinétique est la forme d'énergie que possède un système en$\ldots\ldots$
L'énergie mécanique d'un corps est la somme de son$\ldots\ldots$et de son$\ldots\ldots$
Au cours du mouvement de chute d'un objet, son énergie$\ldots\ldots$est convertie en énergie$\ldots\ldots$
Un chargeur de portable convertit l'énergie$\ldots\ldots$en énergie$\ldots\ldots$
Les photopiles transforment l'énergie$\ldots\ldots$en énergie électrique
Une pile transforme l'énergie$\ldots\ldots$en énergie$\ldots\ldots$; un fer à repasser électrique transforme l'énergie$\ldots\ldots$en$\ldots\ldots$
Le$\ldots\ldots$d'un moteur est le rapport de l'énergie utile à l'énergie absorbée.
Exercice 12 Conversions
Un champion de tennis a réalisé un service en communiquant à une balle de masse $m=55\;g$ une vitesse de $217\;km.h^{-1}$
1) Convertis cette vitesse en $m\cdot s^{-1}.$
2) Déduis-en l'énergie cinétique fournie à la balle lors de ce service.
Exercice 13 énergie potentielle
Une mangue de masse $m=120\;g$ est située sur un arbre à la hauteur $h=3.2\,m.$
Déterminer l'énergie potentielle de pesanteur de cette mangue.
Donnée : $g=9.8\;N\cdot Kg^{-1}$
Exercice 14 Calcul d'une vitesse
1) Calcule l'énergie cinétique d'un camion, de masse $30$ tonnes, roulant en ville à $30\,km\cdot h^{-1}.$
2) A quelle vitesse devrait rouler une voiture de masse $1300\,Kg$ pour avoir la même énergie cinétique ?
Exercice 15 effet joule
Un conducteur ohmique de résistance $R=100\Omega$ est traversé par un courant d'intensité
$I=25\,mA$ pendant une durée $t=5$ minutes.
1) Qu'est-ce que l'effet Joule ?
2) Calculer la puissance Joule pour ce conducteur ohmique.
3) Calculer l'énergie dissipée par effet Joule pour ce conducteur ohmique en joules et en $kWh.$
Exercice 16 puissance et consommation
Un appartement possède les équipements suivants :
$7$ lampes de $9\;W$, $4$ ventilateurs de $75\;W$, un réfrigérateur de $120\;W$, un téléviseur de $200\;W$ et un fer à repasser de $1.2\;kW.$
1) Quelle est la puissance électrique totale de cet appartement si tous les appareils fonctionnent ?
2) Le tableau suivant donne le temps moyen de fonctionnement de chaque appareil.
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Appareils}&\text{Lampe}&\text{réfrigérateur}&\text{Téléviseur}&\text{Fer à repasser}&\text{Ventilateur}\\ \hline \text{temps}&4\,h&18\,h&8\,h\ 30\,min&15\,min&6\,h\\ \hline \end{array}$$
Calcule, en kilowattheure, l'énergie électrique consommée en $60$ jours.
3) La SENELEC vend en moyenne le $kWh$ à $113$ F
Calcule le prix à payer pour une consommation bimensuelle.
4) Chaque appareil transforme de l'énergie électrique en d'autres formes d'énergies.
Donne ces autres formes d'énergies pour la lampe, le fer à repasser et le ventilateur.
Exercice 17 Lampe à basse consommation
Pour éclairer une maison, on dispose de $8$ lampes à incandescence de puissance $40\,W$ chacune.
Pour une durée de fonctionnement de $4\,h$ par jour, calculer la consommation électrique bimensuelle de cette maison en $KWh.$
On remplace les $8$ lampes par des lampes fluo compactes de puissance $11\,W.$
Pour la même durée de fonctionnement, calculer la consommation électrique bimensuelle de cette maison.
1) Conclus.
2) Quel est l'impact, sur l'environnement, de l'utilisation de telles lampes ?
Exercice 18 rendement d'une transformation d'énergie
Un four électrique convertit une énergie électrique en énergie thermique servant à chauffer les aliments.
On fournit une énergie électrique de $2\,KWh$ à un four.
L'énergie thermique effectivement récupérée pour chauffer les aliments est de $1.9\,KWh.$
1) Sous quelles formes se trouve l'énergie électrique convertie ?
2) Calculer le rendement de la conversion en énergie thermique.
Exercice 19 relation $U_{max}$, $P_{max}$ et de $R.$
Les constructeurs indiquent pour les conducteurs ohmiques la puissance électrique maximale permise.
Si on dépasse la valeur indiquée, le composant peut être détérioré.
Un conducteur ohmique $(R=33\Omega)$ est caractérisé par une puissance maximale permise, $P_{max}=0.5\,W.$
1) Exprimer l'intensité maximale permise $I_{max}$ en fonction de $P_{max}$ et de $R.$
2) Exprimer la tension maximale permise $U_{max}$ en fonction de $P_{max}$ et de $R.$
3) Peut-on brancher ce conducteur ohmique dans un circuit où la tension à ses bornes serait de $24\,V$ ?
Exercice 20 estimation d'énergie
Un élève veut déterminer l'énergie électrique consommée par son fer à repasser.
Il ne dispose que d'une montre.
Peut-il réaliser son souhait ?
Si la réponse est oui, indiquer la méthode à utiliser.
Exercice supplémentaire Vérification d'informations trouvées sur une facture.
Votre papa reçoit la facture d'électricité ci-dessous.
Il vous demande de lui expliquer certaines informations.
1) Indique-lui les données suivantes :
a) la puissance souscrite ;
b) la consommation en $KWh.$
2) Explique-lui comment cette consommation en $KWh$ est calculée.
3) Effectue les calculs qui permettent de vérifier les montants des trois tranches et le montant total TTC facturé par SENELEC.
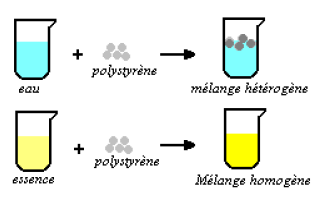
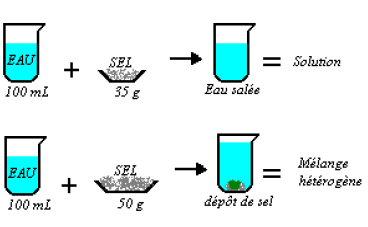 dans un solvant.
dans un solvant.
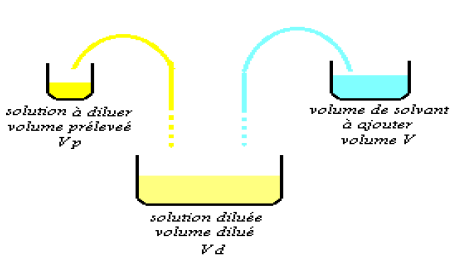 diminue alors sa concentration.
diminue alors sa concentration.