La cinématique est l'étude des mouvements sans tenir compte des forces qui les engendrent ou les modifient.
I. Définitions
$\centerdot\ \ $ Référentiel
Un référentiel que l'on peut noter $(\mathcal{R})$ est un solide de référence, muni d'un repère d'espace et de temps, par rapport auquel on étudie un mouvement.
On peut citer par exemple :
$-\ \ $ Le référentiel terrestre ou référentiel du laboratoire : C'est un référentiel dont le repère d'espace est lié aux objets fixes sur la terre ou au solide de référence que caractérise le laboratoire.
$-\ \ $ Le référentiel héliocentrique : C'est un référentiel constitué d'un repère d'espace dont l'origine est le centre du soleil et les trois axes dirigés vers trois étoiles éloignées supposées fixes.
$-\ \ $ Le référentiel géocentrique : C'est un référentiel dont le repère d'espace a pour origine le centre de la terre et les axes dirigés vers trois étoiles éloignées supposées fixes.
$-\ \ $ Plus loin nous verrons aussi le référentiel galiléen ; référentiel dans lequel un point matériel isolé ou pseudo-isolé est en mouvement rectiligne uniforme, s'il n'est pas au repos.
$\centerdot\ \ $ Mouvement
Un point matériel $M$ est en mouvement par rapport à un référentiel si sa position varie avec le temps.
Lorsque cette position est fixe au cours du temps, on dira que le point $M$ est immobile ou au repos par rapport au référentiel choisi.
Remarque
Pour décrire un mouvement, il faut toujours préciser le référentiel dans lequel on étudie ce mouvement.
$\centerdot\ \ $ Trajectoire
C'est la courbe décrite au cours du temps par un point matériel $M$ en mouvement par rapport à un référentiel choisi.
II. Grandeurs cinématiques
II.1. Vecteur position
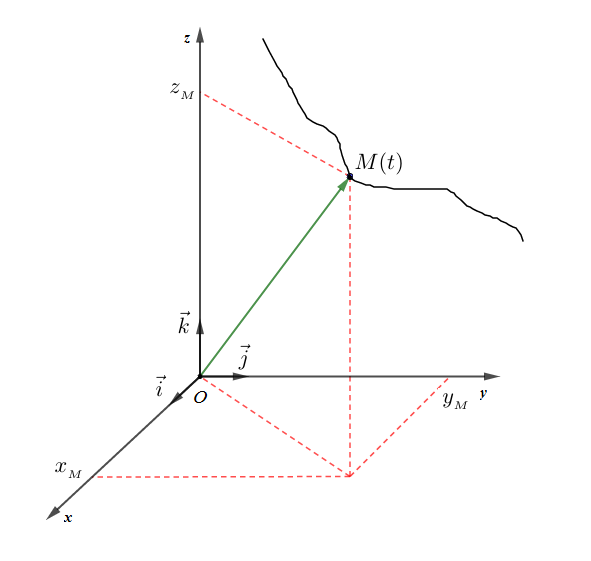
Soit $M(t)$ la position d'un point matériel à l'instant $t$ sur sa trajectoire et soit $O$ origine du repère. On appelle vecteur position le vecteur $\overrightarrow{OM}$ tel que : $$\boxed{\overrightarrow{OM}=\overrightarrow{OM}(t)}$$
II.2. Systèmes de coordonnées
Un point matériel peut être repéré par une, deux ou trois coordonnées selon qu'il se situe respectivement sur une ligne, dans un plan ou dans l'espace.
II.2.1. Coordonnées cartésiennes
Soit $(O\;;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ un repère d'espace et $M$ un point de l'espace, on appelle coordonnées cartésiennes de $M$ les trois réels $x\;,\ y$ et $z$ tels que : $$\boxed{\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}}$$
Comme à l'instant $t\;\ \overrightarrow{OM}=\overrightarrow{OM}(t)$ alors : $$\boxed{\overrightarrow{OM}=x(t)\vec{i}+y(t)\vec{j}+z(t)\vec{k}}$$
Remarque : $||\overrightarrow{OM}||=\sqrt{x^{2}+y^{2}+z^{2}}$
II.2.2. Abscisse curviligne
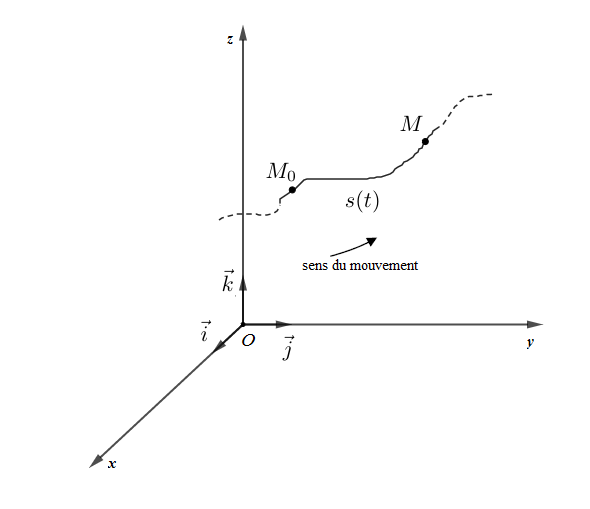
Considérons un point matériel décrivant une trajectoire $(\mathcal{C}).$ Soit $M_{0}$ sa position sur $(\mathcal{C})$ à l'instant $t_{0}$ et $M$ sa position à l'instant $t.$
On appelle abscisse curviligne de $M$ notée $s=s(t)$ l'arc entre $M_{0}$ et $M.$ On a : $$\boxed{s=\overset{\displaystyle\frown}{M_{0}M}}$$
$M_{0}$ est la position initiale du point matériel ou origine du mouvement ; la trajectoire étant orientée de $M_{0}$ vers $M.$
II.2.3. Coordonnées polaires
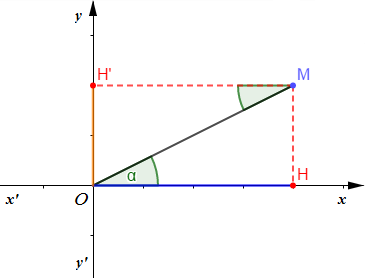
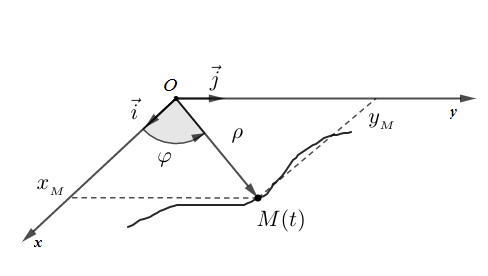
La position d'un point matériel $M$ se trouvant, à l'instant $t$, dans un plan $xOy$ est repérée par $\rho(t)=||\overrightarrow{OM}||$ et par $\varphi=(\widehat{\vec{i}\;,\ \overrightarrow{OM}}).$
$$\left\lbrace\begin{array}{rcl} x_{M}(t)&=&\rho(t)\cos\varphi\\y_{M}(t)&=&\rho(t)\sin\varphi\end{array}\right.$$
$\rho$ et $\varphi$ sont appelés coordonnées polaires de $M.$
II.3. Vecteur vitesse
Considérons un point matériel décrivant une trajectoire $(\mathcal{C}).$
II.3.1. Vecteur vitesse moyenne
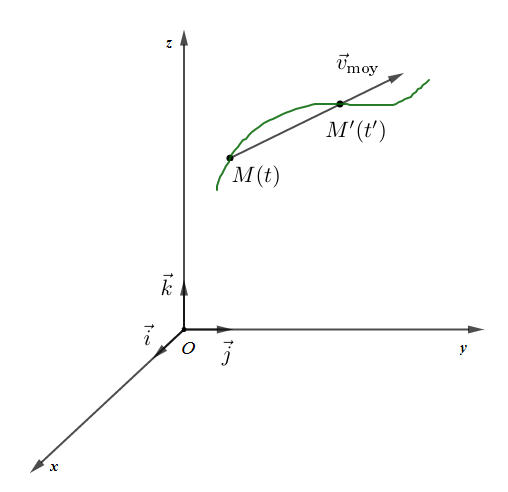
Soit $M$ la position du mobile à l'instant $t$ et $M'$ sa position sur $(\mathcal{C})$ à l'instant $t'.$ On appelle vecteur vitesse moyenne de $M$ le vecteur $\vec{v}_{\text{moy}}$ défini par :
$$\boxed{\vec{v}_{\text{moy}}=\dfrac{\overrightarrow{MM'}}{t'-t}}$$
$-\ \ $ Sens : de $M$ vers $M'$
$-\ \ $ Module : $||\vec{v}_{\text{moy}}||=\dfrac{||\overrightarrow{MM'}||}{|t'-t|}$ en $(m.s^{-1})$
Remarque
La vitesse moyenne est la distance parcourue par le mobile par unité de temps.
II.3.2. Vecteur vitesse instantanée
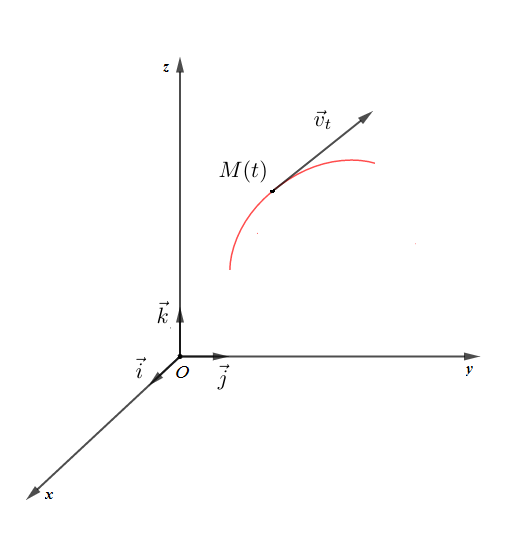
Le vecteur vitesse instantanée d'un point matériel $M$ est la dérivée par rapport au temps du vecteur position $\overrightarrow{OM}\ :$
$$\boxed{\vec{v}_{t}=\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}}$$
$\vec{v}_{t}$ est tangent à la trajectoire au point $M.$
Remarque
La vitesse instantanée exprimée en $m.s^{-1}$ est la vitesse du mobile à l'instant $t.$
En effet, lorsque $t'$ tend vers $t$ alors, $M'$ va aussi tendre vers $M.$
Posons $t'-t=\Delta t$ donc, $t'=t+\Delta t$
Soit $\vec{v}_{t}=\lim\limits_{\Delta t\rightarrow 0}\dfrac{\overrightarrow{MM'}}{\Delta t}.$
On sait que
$\begin{array}{rcl}\overrightarrow{MM'}&=&\overrightarrow{MO}+\overrightarrow{OM'}\\\\&=&\overrightarrow{OM'}-\overrightarrow{OM}\quad\text{or le mobile est à la position }M'\text{ à l'instant }t'\\\\&=&\overrightarrow{OM}(t')-\overrightarrow{OM}(t)\quad\text{avec }\ t'=t+\Delta t\\\\&=&\overrightarrow{OM}(t+\Delta t)-\overrightarrow{OM}(t) \end{array}$
Donc
$\begin{array}{rcl}\vec{v}_{t}&=&\lim\limits_{\Delta t\rightarrow 0}\dfrac{\overrightarrow{MM'}}{\Delta t}\\ \\&=&\lim\limits_{\Delta t\rightarrow 0}\dfrac{\overrightarrow{OM}(t+\Delta t)-\overrightarrow{OM}(t)}{\Delta t}\\ \\&=&\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}\quad\text{d'après le cours de mathématiques sur la dérivée}\end{array}$
Ainsi : $\vec{v}_{t}=\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}$
Composantes de la vitesse en coordonnées cartésiennes
On a :
$\begin{array}{rcl}\vec{v}_{t}&=&\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}\quad\text{or }\ \overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}=x(t)\vec{i}+y(t)\vec{j}+z(t)\vec{k}\\ \\&=&\dfrac{\mathrm{d}x}{\mathrm{d}t}\vec{i}+\dfrac{\mathrm{d}y}{\mathrm{d}t}\vec{j}+\dfrac{\mathrm{d}z}{\mathrm{d}t}\vec{k}\end{array}$
D'où, $$\boxed{\vec{v}_{t}=\dfrac{\mathrm{d}x}{\mathrm{d}t}\vec{i}+\dfrac{\mathrm{d}y}{\mathrm{d}t}\vec{j}+\dfrac{\mathrm{d}z}{\mathrm{d}t}\vec{k}}$$
En notant $\ \dot{x}=\dfrac{\mathrm{d}x}{\mathrm{d}t}\;,\ \dot{y}=\dfrac{\mathrm{d}y}{\mathrm{d}t}\ \text{ et }\ \dot{z}=\dfrac{\mathrm{d}z}{\mathrm{d}t}\;,\ \vec{v}_{t}$ peut encore s'écrire sous la forme : $$\boxed{\vec{v}_{t}=\dot{x}\vec{i}+\dot{y}\vec{j}+\dot{z}\vec{k}}$$
Remarque
$\vec{v}_{t}=v_{x}\vec{i}+v_{y}\vec{j}+v_{z}\vec{k}\ $ avec $\ v_{x}=\dot{x}\;,\ v_{y}=\dot{y}\ \text{ et }\ v_{z}=\dot{z}$
II.4. Vecteur accélération
L'accélération $\vec{a}_{t}$ d'un mobile $M$ à l'instant $t$ est la dérivée par rapport au temps du vecteur vitesse $\vec{v}_{t}\ :$
$$\boxed{\vec{a}_{t}=\dfrac{\mathrm{d}\vec{v}_{t}}{\mathrm{d}t}}$$
Comme $\vec{v}_{t}=\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}$ alors, $\vec{a}_{t}$ peut encore s'écrire : $$\boxed{\vec{a}_{t}=\dfrac{\mathrm{d}^{2}\overrightarrow{OM}}{\mathrm{d}t^{2}}}$$
En effet,
$\begin{array}{rcl}\vec{a}_{t}&=&\lim\limits_{\Delta t\rightarrow 0}\dfrac{\vec{v}_{t'}-\vec{v}_{t}}{\Delta t}\quad\text{avec }\ t'=t+\Delta t\\ \\&=&\lim\limits_{\Delta t\rightarrow 0}\dfrac{\vec{v}_{t+\Delta t}-\vec{v}_{t}}{\Delta t}\\ \\&=&\dfrac{\mathrm{d}\vec{v}_{t}}{\mathrm{d}t}\quad\text{or }\ \vec{v}_{t}=\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}\\ \\&=&\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}\right)\\ \\&=&\dfrac{\mathrm{d}^{2}\overrightarrow{OM}}{\mathrm{d}t^{2}}\end{array}$
D'où, $\vec{a}_{t}=\dfrac{\mathrm{d}\vec{v}_{t}}{\mathrm{d}t}=\dfrac{\mathrm{d}^{2}\overrightarrow{OM}}{\mathrm{d}t^{2}}$
Composantes de l'accélération en coordonnées cartésiennes
On a :
$\begin{array}{rcl}\vec{a}_{t}&=&\dfrac{\mathrm{d}^{2}\overrightarrow{OM}}{\mathrm{d}t^{2}}\quad\text{or }\ \overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}\\ \\&=&\dfrac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\vec{i}+\dfrac{\mathrm{d}^{2}y}{\mathrm{d}t^{2}}\vec{j}+\dfrac{\mathrm{d}^{2}z}{\mathrm{d}t^{2}}\vec{k}\end{array}$
D'où, $$\boxed{\vec{a}_{t}=\dfrac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\vec{i}+\dfrac{\mathrm{d}^{2}y}{\mathrm{d}t^{2}}\vec{j}+\dfrac{\mathrm{d}^{2}z}{\mathrm{d}t^{2}}\vec{k}}$$
$\vec{a}_{t}$ peut encore s'écrire sous la forme : $$\boxed{\vec{a}_{t}=\ddot{x}\vec{i}+\ddot{y}\vec{j}+\ddot{z}\vec{k}}$$
avec $\ \ddot{x}=\dfrac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\;,\ \ddot{y}=\dfrac{\mathrm{d}^{2}y}{\mathrm{d}t^{2}}\ \text{ et }\ \ddot{z}=\dfrac{\mathrm{d}^{2}z}{\mathrm{d}t^{2}}$
Remarque
On peut aussi écrire $\vec{a}_{t}=a_{x}\vec{i}+a_{y}\vec{j}+a_{z}\vec{k}\ $ avec $\ a_{x}=\ddot{x}\;,\ a_{y}=\ddot{y}\ \text{ et }\ a_{z}=\ddot{z}$
Composantes de l'accélération dans la base de Frenet
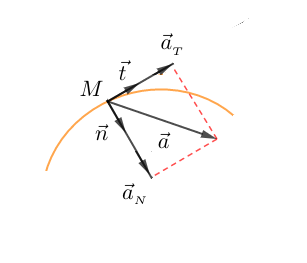
Considérons un point matériel en mouvement curviligne sur une trajectoire $(\mathcal{C}).$ Soit $M$ la position du mobile sur $(\mathcal{C})$ à l'instant $t$ et soit $\vec{T}$ un vecteur unitaire porté par la tangente en $M$ et $\vec{N}$ la normale à $\vec{T}$ dirigée vers le centre de courbure.
Le couple de vecteurs $(\vec{T}\;,\ \vec{N})$ ainsi définie est appelé base de Frenet.
L'accélération $\vec{a}_{t}$ peut alors s'écrire dans cette base sous la forme : $$\boxed{\vec{a}_{t}=a_{_{T}}\vec{T}+a_{_{N}}\vec{N}}$$
avec $a_{_{T}}=\dfrac{\mathrm{d}v}{\mathrm{d}t}\ $ et $\ a_{_{N}}=\dfrac{v^{2}}{R}$ où $R$ est le rayon de courbure.
$-\ \ a_{_{T}}$ est l'accélération tangentielle
$-\ \ a_{_{N}}$ est appelé accélération normale ou centripète.
On obtient ainsi : $$\boxed{\vec{a}_{t}=\dfrac{\mathrm{d}v}{\mathrm{d}t}\vec{T}+\dfrac{v^{2}}{R}\vec{N}}$$
Exercice d'application
Un mobile $M$, à l'instant $t$, est repéré par ses coordonnées cartésiennes : $$x(t)=3t+4\;;\quad y(t)=-5t^{2}+2t+1\;;\quad z(t)=3$$
1) Donner l'expression de sa vitesse et calculer sa valeur aux dates $t_{0}=0\;s\;,\ t_{1}=1\;s$
2) Donner l'expression de son accélération puis calculer sa valeur aux dates $t_{0}=0\;s\;,\ t_{1}=1\;s$
Résolution
1) Expression de la vitesse
On a : $\vec{v}_{t}=\dfrac{\mathrm{d}x}{\mathrm{d}t}\vec{i}+\dfrac{\mathrm{d}y}{\mathrm{d}t}\vec{j}+\dfrac{\mathrm{d}z}{\mathrm{d}t}\vec{k}$ avec $\dfrac{\mathrm{d}x}{\mathrm{d}t}=3\;,\ \dfrac{\mathrm{d}y}{\mathrm{d}t}=-10t+2\ \text{ et }\ \dfrac{\mathrm{d}z}{\mathrm{d}t}=0$
Donc, $$\boxed{\vec{v}_{t}=3\vec{i}-(10t-2)\vec{j}}$$
A $t_{0}=0\;s\;,\ \vec{v}_{0}=3\vec{i}+2\vec{j}$
Donc, $||\vec{v}_{0}||=\sqrt{3^{2}+2^{2}}=\sqrt{13}\;m.s^{-1}$
A $t_{1}=1\;s\;,\ \vec{v}_{1}=3\vec{i}-8\vec{j}$
Donc, $||\vec{v}_{1}||=\sqrt{3^{2}+(-8)^{2}}=\sqrt{73}\;m.s^{-1}$
2) Expression de l'accélération
On a :
$\begin{array}{rcl}\vec{a}_{t}&=&\dfrac{\mathrm{d}\vec{v}_{t}}{\mathrm{d}t}\\\\&=&\dfrac{\mathrm{d}(3\vec{i}-(10t-2)\vec{j})}{\mathrm{d}t}\\ \\&=&\dfrac{\mathrm{d}}{\mathrm{d}t}3\vec{i}-\dfrac{\mathrm{d}(10t-2)}{\mathrm{d}t}\vec{j}\\ \\&=&-10\vec{j}\end{array}$
D'où, $$\boxed{\vec{a}_{t}=-10\vec{j}}$$
Nous constatons que $\vec{a}_{t}$ est une constante.
Par suite, aux dates $t_{0}=0\;s$ et $t_{1}=1\;s\;,\ \vec{a}_{0}=\vec{a}_{1}=-10\vec{j}$
D'où, $||\vec{a}_{0}||=||\vec{a}_{1}||=\sqrt{(-10)^{2}}=10\;m.s^{-2}$
III. Mouvements rectilignes
III.1. Définitions
$\centerdot\ \ $ Un mouvement est dit rectiligne si, et seulement si, la trajectoire est une droite.
$\centerdot\ \ $ Un mouvement est dit uniforme si la norme du vecteur vitesse instantanée $||\vec{v}_{t}||$ du mobile est constante.
$\centerdot\ \ $ Un point matériel est animé d'un mouvement rectiligne uniforme $(MRU)$ si, et seulement si, son vecteur vitesse instantanée $\vec{v}_{t}$ reste constant.
$\centerdot\ \ $ Un mobile est en mouvement rectiligne uniformément varié $(MRUV)$ si, et seulement si, son accélération $\vec{a}_{t}$ est constante.
III.2. Mouvement rectiligne uniformément varié $(MRUV)$
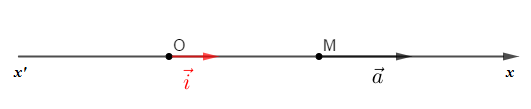
La trajectoire est une droite. Afin de repérer la position d'un mobile sur cette trajectoire nous utilisons l'axe $(x'Ox)$ comme repère d'espace.
Ainsi, un point matériel $M$ sera repéré, à l'instant $t$, par une seule coordonnée $x.$ Le vecteur position s'écrit alors : $$\overrightarrow{OM}=x\vec{i}$$
Considérons un mobile $M$ en mouvement rectiligne uniformément varié avec une vitesse $v_{x}$ à l'instant $t.$
Le mouvement étant rectiligne et uniformément varié alors, l'accélération $\vec{a}_{x}$ est constante.
Or, $a=\dfrac{\mathrm{d}v_{x}}{\mathrm{d}t}$ par suite, $\mathrm{d}v_{x}=a\mathrm{d}t$
Ce qui donne, par passage aux primitives : $$\int \mathrm{d}v_{x}=\int a\mathrm{d}t=a\int \mathrm{d}t$$
Ainsi, d'après cours de mathématiques 1er, $v_{x}=at+\text{cst}$
La constante $\text{(cst)}$ est déterminée à partir des conditions initiales : soit à l'instant initia $t_{0}$, le mobile $M$ est à la position $x_{0}$ avec une vitesse $v_{0}.$
Donc, $v_{0}=at_{0}+\text{cst}\ \Rightarrow\ \text{cst}=v_{0}-at_{0}$
Par conséquent : $$\boxed{v_{x}=a(t-t_{0})+v_{0}}$$
En particulier, lorsque $t_{0}=0$ on obtient : $$\boxed{v_{x}=at+v_{0}}$$
Par ailleurs, on sait que : $v_{x}=\dfrac{\mathrm{d}x}{\mathrm{d}t}=a(t-t_{0})+v_{0}$ donc, $\mathrm{d}x=(a(t-t_{0})+v_{0})\mathrm{d}t$
Par passage aux primitives, on obtient : $$\int\mathrm{d}x=\int(a(t-t_{0})+v_{0})\mathrm{d}t=a\int t\mathrm{d}t-at_{0}\int \mathrm{d}t+v_{0}\int\mathrm{d}t$$
D'où, $x=\dfrac{1}{2}at^{2}+(v_{0}-at_{0})t+\text{cst}$
Or, d'après conditions initiales, $x=x_{0}\ $ à $\ t=t_{0}$
Donc, $x_{0}=\dfrac{1}{2}at_{0}^{2}+(v_{0}-at_{0})t_{0}+\text{cst}$
$\begin{array}{rcl} x_{0}&=&\dfrac{1}{2}at_{0}^{2}+(v_{0}-at_{0})t_{0}+\text{cst}\\ \\&=&\dfrac{1}{2}at_{0}^{2}+v_{0}t_{0}-at_{0}^{2}+\text{cst}\\ \\&=&-\dfrac{1}{2}at_{0}^{2}+v_{0}t_{0}+\text{cst}\\ \\\Rightarrow\ \text{cst}&=&\dfrac{1}{2}at_{0}^{2}-v_{0}t_{0}+x_{0}\end{array}$
Par suite,
$\begin{array}{rcl} x&=&\dfrac{1}{2}at^{2}+(v_{0}-at_{0})t+\dfrac{1}{2}at_{0}^{2}-v_{0}t_{0}+x_{0}\\ \\&=&\dfrac{1}{2}\left( at^{2}+at_{0}^{2}-2at_{0}t\right)+v_{0}t-v_{0}t_{0}+x_{0}\\ \\&=&\dfrac{1}{2}a(t-t_{0})^{2}+v_{0}(t-t_{0})+x_{0}\end{array}$
Par conséquent, $$\boxed{x(t)=\dfrac{1}{2}a(t-t_{0})^{2}+v_{0}(t-t_{0})+x_{0}}$$
Cette équation est appelée équation horaire du mobile. Elle donne l'évolution de la coordonnée du point matériel en fonction du temps.
Elle permet donc de calculer l'abscisse $x$ du mobile à chaque instant $t$, connaissant les conditions initiales $(t_{0}\;,\ x_{0}\text{ et } v_{0})$ ainsi que l'accélération $a.$
Particulièrement, lorsque $t_{0}=0$, l'équation horaire devient : $$\boxed{x(t)=\dfrac{1}{2}at^{2}+v_{0}t+x_{0}}$$
Relation entre l'abscisse $x$ et la vitesse $v_{x}$
Choisissons l'instant initial $t_{0}=0$ et considérons les équations (1) et (2) suivantes : $$(1)\ :\ v_{x}=at+v_{0}\quad\text{et}\quad(2)\ :\ x=\dfrac{1}{2}at^{2}+v_{0}t+x_{0}$$
L'équation (1) donne : $t=\dfrac{v_{x}-v_{0}}{a}.$ En remplaçant cette expression de $t$ dans l'équation (2) on obtient :
$\begin{array}{rcl} x&=&\dfrac{1}{2}at^{2}+v_{0}t+x_{0}\\\\&=&\dfrac{1}{2}a\left(\dfrac{v_{x}-v_{0}}{a}\right)^{2}+v_{0}\left(\dfrac{v_{x}-v_{0}}{a}\right)+x_{0}\\ \\&=&\dfrac{1}{2}a\left(\dfrac{v_{x}^{2}-2v_{x}v_{0}+v_{0}^{2}}{a^{2}}\right)+\dfrac{v_{0}v_{x}-v_{0}^{2}}{a}+x_{0}\\ \\&=&\dfrac{1}{2}.\dfrac{v_{x}^{2}-2v_{x}v_{0}+v_{0}^{2}+2v_{0}v_{x}-2v_{0}^{2}}{a}+x_{0}\\ \\&=&\dfrac{v_{x}^{2}-v_{0}^{2}}{2a}+x_{0}\end{array}$
Ce qui donne alors, $\ x-x_{0}=\dfrac{v_{x}^{2}-v_{0}^{2}}{2a}\ $ ; soit : $$\boxed{v_{x}^{2}-v_{0}^{2}=2a(x-x_{0})}$$
Exercice d'application
Une voiture roule sur une route rectiligne avec une vitesse initiale de $10\;m.s^{-1}$ et une accélération constante de $0.8\;m.s^{-2}.$
1) Calculer sa vitesse au bout de $5\;mn.$
2) Calculer la distance parcourue entre les instants $t_{1}=2\;s\ $ et $\ t_{2}=5\;s.$
3) Calculer la vitesse de la voiture après un parcours de $100\;m.$
Résolution
On est en face d'un mouvement rectiligne uniformément varié $(MRUV).$
Choisissons $t_{0}=0\ $ et $\ x_{0}=0$ comme conditions initiales.
1) Calcul de la vitesse $v_{x}$ au bout de $5\;mn.$
On a : $v_{x}=at+v_{0}\ $ avec $\ t=5\times 60=300\;s$
A.N : $v_{x}=0.8\times 300+10=250\;m.s^{-1}$
2) Calcul de la distance parcourue entre les instants $t_{1}=2\;s\ $ et $\ t_{2}=5\;s.$
D'après l'équation horaire de la voiture, on a : $$x=\dfrac{1}{2}at^{2}+v_{0}t+x_{0}$$
A.N : pour $t=t_{1}=2\;s\;,\ x_{1}=\dfrac{1}{2}0.8\times 2^{2}+10\times 2=21.6\;m$
pour $t=t_{2}=5\;s\;,\ x_{2}=\dfrac{1}{2}0.8\times 5^{2}+10\times 5=60\;m$
La distance parcourue est alors donnée par : $D=x_{2}-x_{1}$
A.N : $D=60-21.6=38.4\;m$
3) Calcul de la vitesse $v_{x}$ après un parcours de $100\;m.$
On sait que : $v_{x}^{2}-v_{0}^{2}=2a(x-x_{0})\ \Rightarrow\ v_{x}=\sqrt{v_{0}^{2}+2a(x-x_{0})}$
A.N : $v_{x}=\sqrt{10^{2}+2\times 0.8\times 100}=16.12\;m.s^{-1}$
III.3. Mouvement rectiligne uniforme $(MRU)$
C'est un cas particulier du mouvement rectiligne uniformément varié ; ici la vitesse est une constante et donc, l'accélération est nulle.
On a : $v_{x}=v_{0}=v\;;\ \forall\;t\ $ et $\ a=\dfrac{\mathrm{d}v_{x}}{\mathrm{d}t}=0$
Par conséquent, l'équation horaire du mobile sera donnée par : $$\boxed{x(t)=v(t-t_{0})+x_{0}}$$
Exercice d'application
Le mouvement d'un mobile est défini par les équations horaires suivantes : $$x(t)=t+3\;;\quad y(t)=2t+1$$
Déterminer l'équation de la trajectoire du mobile et la norme du vecteur vitesse. En déduire la nature du mouvement.
Résolution
D'après l'équation horaire $x(t)$ on a : $$x=t+3\ \Rightarrow\ t=x-3$$
En remplaçant l'expression de $t$ dans l'équation de $y(t)$ on aura : $$y=2(x-3)+1=2x-5$$
D'où, l'équation de la trajectoire du mobile donnée par : $$\boxed{y=2x-5}$$
C'est une équation de droite. Ce qui signifie que la trajectoire est une droite. Par suite, le mouvement est rectiligne.
Par ailleurs, $\vec{v}_{t}=\dfrac{\mathrm{d}x}{\mathrm{d}t}\vec{i}+\dfrac{\mathrm{d}y}{\mathrm{d}t}\vec{j}=\vec{i}+2\vec{j}$
Donc, $||\vec{v}_{t}||=\sqrt{1^{2}+2^{2}}=\sqrt{5}\;m.s^{-1}$ qui est une constante.
Ce qui montre que le mouvement est uniforme.
Et par conséquent, le mobile est animé d'un mouvement rectiligne et uniforme.
III.4. Mouvement rectiligne sinusoïdal
Il est caractérisé par un mouvement d'allers-retours sur une portion de droite.
Ce mouvement borné et non-uniforme, est défini par l'équation horaire : $$\boxed{x(t)=x_{m}\cos(\omega t+\varphi)\quad\text{ou}\quad x(t)=x_{m}\sin(\omega t+\varphi)}$$
$\centerdot\ \ x_{m}$ est l'amplitude maximale
$\centerdot\ \ \omega$ est la pulsation
$\centerdot\ \ \varphi$ est la phase à l'origine.
Le mobile est ainsi animé d'un mouvement périodique de période $T=\dfrac{2\pi}{\omega}$
L'expression de la vitesse est donnée par : $$v_{x}=\dfrac{\mathrm{d}x}{\mathrm{d}t}=-x_{m}\omega\sin(\omega t+\varphi)$$
L'accélération a pour expression :
$\begin{array}{rcl} a_{x}&=&\dfrac{\mathrm{d}v_{x}}{\mathrm{d}t}\\\\&=&-x_{m}\omega^{2}\cos(\omega t+\varphi)\\ \\&=&-\omega^{2}x\end{array}$
Comme $a_{x}=\ddot{x}\ $ alors, $\ \ddot{x}=-\omega^{2}x$
D'où, l'équation du mouvement définie par : $$\boxed{\ddot{x}+\omega^{2}x=0}$$
Remarque
L'accélération est toujours dirigée vers le centre constituant la position d'équilibre : $$\vec{a}=-\omega^{2}x\vec{i}$$
IV. Mouvements circulaires
IV.1. Définition
Un point matériel est animé d'un mouvement circulaire si sa trajectoire est un cercle ou un arc de cercle.
On utilise l'abscisse curviligne $s(t)$ pour le repérage de la position du mobile.
Expression de la vitesse angulaire
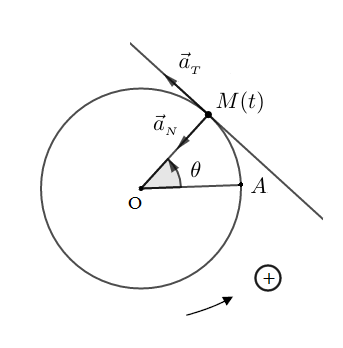
Soit $s=\overset{\displaystyle\frown}{AM}$ l'abscisse curviligne du mobile à l'instant $t$ et $\theta=(\widehat{\overrightarrow{OA}\;,\ \overrightarrow{OM}}).$ On a :
$\begin{array}{rcl} v&=&\dfrac{\mathrm{d}s}{\mathrm{d}t}\quad\text{or }\ s=R\theta\\ \\&=&\dfrac{\mathrm{d}R\theta}{\mathrm{d}t}\\ \\&=&R\dfrac{\mathrm{d}\theta}{\mathrm{d}t}\\ \\&=&R\dot{\theta}\end{array}$
Donc, $v=R\dot{\theta}$ et par suite, $$\boxed{\dot{\theta}=\dfrac{v}{R}}$$
$\dot{\theta}=\omega$ est la vitesse angulaire du mobile exprimée en $\text{rad}.s^{-1}$
Expression de l'accélération angulaire
Dans la base de Frenet, l'accélération est donnée par :
$$\vec{a}=a_{_{T}}\vec{T}+a_{_{N}}\vec{N}$$
avec $a_{_{N}}=\dfrac{v^{2}}{R}=R\dot{\theta}^{2}\ $ et $\ a_{_{T}}=\dfrac{\mathrm{d}v}{\mathrm{d}t}.$ Soit alors :
$\begin{array}{rcl} a_{_{T}}&=&\dfrac{\mathrm{d}v}{\mathrm{d}t}\\\\&=&\dfrac{\mathrm{d}R\dot{\theta}}{\mathrm{d}t}\\ \\&=&R\dfrac{\mathrm{d}\dot{\theta}}{\mathrm{d}t}\\ \\&=&R\ddot{\theta}\end{array}$
Donc, $a_{_{T}}=R\ddot{\theta}$ et par suite, $$\boxed{\ddot{\theta}=\dfrac{a_{_{T}}}{R}}$$
$\ddot{\theta}$ est l'accélération angulaire du mobile exprimée en $\text{rad}.s^{-2}$
IV.2. Mouvement circulaire uniformément varié
Le mouvement étant circulaire et uniformément varié alors, l'accélération $a_{_{T}}$ est constante.
Comme $\ddot{\theta}=\dfrac{a_{_{T}}}{R}$ alors, $\ddot{\theta}$ est une constante.
Or, $\ddot{\theta}=\dfrac{\mathrm{d}\dot{\theta}}{\mathrm{d}t}$ par suite, $\mathrm{d}\dot{\theta}=\ddot{\theta}\mathrm{d}t$
On obtient, par passage aux primitives : $$\int \mathrm{d}\dot{\theta}=\int \ddot{\theta}\mathrm{d}t=\ddot{\theta}\int \mathrm{d}t$$
Ce qui donne : $\dot{\theta}=\ddot{\theta}t+\text{cst}$
La constante $\text{(cst)}$ étant déterminée à partir des conditions initiales : soit à l'instant initial $t_{0}$, le mobile est à la position $M_{0}$ avec une vitesse angulaire $\dot{\theta}_{0}.$
Ainsi, $\text{cst}=\dot{\theta}_{0}-\ddot{\theta}_{0}t_{0}$
D'où : $$\boxed{\dot{\theta}=\ddot{\theta}(t-t_{0})+\dot{\theta}_{0}}$$
En particulier, si $t_{0}=0$ on obtient : $$\boxed{\dot{\theta}=\ddot{\theta}t+\dot{\theta}_{0}}$$
Par ailleurs, on sait que : $\dot{\theta}=\dfrac{\mathrm{d}\theta}{\mathrm{d}t}=\ddot{\theta}(t-t_{0})+\dot{\theta}_{0}$ donc, $\mathrm{d}\theta=(\ddot{\theta}(t-t_{0})+\dot{\theta}_{0})\mathrm{d}t$
Ce qui donne, par passage aux primitives : $$\int\mathrm{d}\theta=\int(\ddot{\theta}(t-t_{0})+\dot{\theta}_{0})\mathrm{d}t$$
D'où, $\theta=\dfrac{1}{2}\ddot{\theta}t^{2}+(\dot{\theta}_{0}-\ddot{\theta}t_{0})t+\text{cst}$
Or, d'après conditions initiales, $\theta=\theta_{0}\ $ à $\ t=t_{0}$
Ce qui entraîne : $\text{cst}=\dfrac{1}{2}\ddot{\theta}t_{0}^{2}-\dot{\theta}_{0}t_{0}+\theta_{0}$
Par conséquent, $$\boxed{\theta(t)=\dfrac{1}{2}\ddot{\theta}(t-t_{0})^{2}+\dot{\theta}_{0}(t-t_{0})+\theta_{0}}$$
Particulièrement, lorsque $t_{0}=0$, l'équation devient : $$\boxed{\theta(t)=\dfrac{1}{2}\ddot{\theta}t^{2}+\dot{\theta}_{0}t+\theta_{0}}$$
IV.3. Mouvement circulaire uniforme
Dans ce ce cas la vitesse est constante et donc, $a_{_{T}}=0\ $ et $\ a_{_{N}}=\dfrac{v^{2}}{R}=\text{cst}.$
La position du mobile est alors repérée par son abscisse curviligne $s(t).$
On a : $v=\dfrac{\mathrm{d}s}{\mathrm{d}t}\ \Rightarrow\ \mathrm{d}s=v\mathrm{d}t$
Par passage aux primitives, on obtient :
$$\int\mathrm{d}s=\int v\mathrm{d}t$$
Ce qui donne : $$\boxed{s(t)=v(t-t_{0})+s_{0}}$$
Exercice d'application
Un mobile est animé d'un mouvement circulaire de rayon de courbure $R=0.5\;m$ et d'équation : $$s(t)=3t+1$$
Calculer les composantes et la valeur de l'accélération pour $t=2\;s.$
Résolution
La trajectoire étant curviligne alors, l'accélération $\vec{a}$ du mobile, à l'instant $t$, sera donnée par : $$\vec{a}=a_{_{T}}\vec{T}+a_{_{N}}\vec{N}$$
Soit $a_{_{T}}=\dfrac{\mathrm{d}v}{\mathrm{d}t}\ $ avec, $\ v=\dfrac{\mathrm{d}s}{\mathrm{d}t}$
Or, $\ s(t)=3t+1\ $ donc, $\ v=\dfrac{\mathrm{d}(3t+1)}{\mathrm{d}t}=3\;m.s^{-1}$
Ainsi, $a_{_{T}}=0$ puisque $v$ est constante.
Aussi, $a_{_{N}}=\dfrac{v^{2}}{R}$
A.N : $a_{_{N}}=\dfrac{3^{2}}{0.5}=18\;m.s^{-2}$
D'où, $||\vec{a}||=\sqrt{a_{_{T}}^{2}+a_{_{N}}^{2}}=18\;m.s^{-2}$ pour n'importe quelle date $t.$
V. Mouvement accéléré - mouvement décéléré
$\centerdot\ \ $ Un mouvement est accéléré si, et seulement si, $$\boxed{\vec{v}\cdot\vec{a}>0}$$
$\centerdot\ \ $ Un mouvement est décéléré si, et seulement si, $$\boxed{\vec{v}\cdot\vec{a}<0}$$
$\centerdot\ \ $ Un mouvement est uniforme si, et seulement si, $$\boxed{\vec{v}\cdot\vec{a}=0}$$
VI. Composition des vitesses
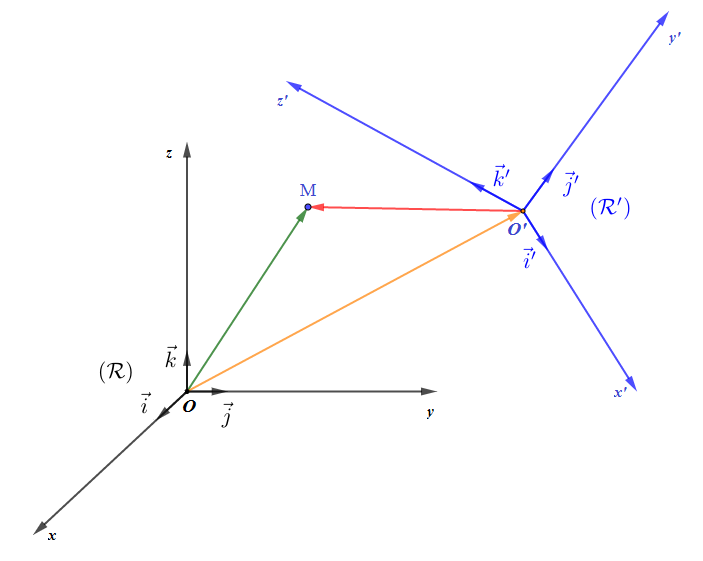
Soit $\mathcal{R}(O\;;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ un référentiel fixe (ou absolu) et $\mathcal{R}'(O'\;;\ \vec{i}'\;,\ \vec{j}'\;,\ \vec{k}')$ un référentiel mobile (ou relatif) et soit $M$ un point matériel mobile par rapport à $(\mathcal{R})$ et par rapport à $(\mathcal{R}')$ tel que : $$\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}\quad\text{et}\quad\overrightarrow{O'M}=x'\vec{i}'+y'\vec{j}'+z'\vec{k}'$$
Soit $\vec{v}_{a}$ la vitesse absolue du mobile dans le référentiel absolu $(\mathcal{R})$ et $\vec{v}_{r}$ sa vitesse relative dans le référentiel relatif $(\mathcal{R}').$
$\vec{v}_{a}=\vec{v}_{_{M/\mathcal{R}}}=\left(\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}\right)_{\mathcal{R}}$
$\vec{v}_{r}=\vec{v}_{_{M/\mathcal{R}'}}=\left(\dfrac{\mathrm{d}\overrightarrow{O'M}}{\mathrm{d}t}\right)_{\mathcal{R}'}$
Or, $\ \overrightarrow{OM}=\overrightarrow{OO'}+\overrightarrow{O'M}\ $ donc, $\ \dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}=\dfrac{\mathrm{d}\overrightarrow{OO'}}{\mathrm{d}t}+\dfrac{\mathrm{d}\overrightarrow{O'M}}{\mathrm{d}t}$
D'après la loi de composition des vitesses on a : $$\boxed{\vec{v}_{a}=\vec{v}_{r}+\vec{v}_{e}}$$
où $\vec{v}_{e}$, encore appelée vitesse d'entrainement, est la vitesse du référentiel mobile $(\mathcal{R}')$ par rapport au référentiel fixe $(\mathcal{R}).$