Physique

Notion de réaction chimique - 4e

Classe: 
Quatrième
 

A Situation problématique

Observons le fonctionnement d'une lampe à carbure ou lampe acétylénique.

 

 
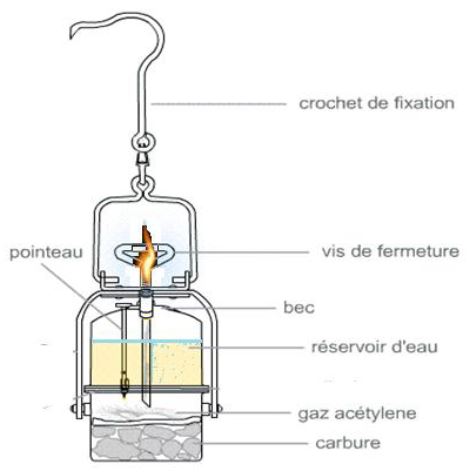
Les lampes à carbure sont constituées de deux cuves : 
 
la première sert de réservoir d'eau, et l'autre contient des morceaux de carbure de calcium.
 
Lorsque l'eau est versée sur le carbure par l'intermédiaire du pointeau, on observe alors le dégagement d'un gaz inflammable appelé acétylène qui produit une lumière très intense lorsqu'il brûle.
 
Le texte ci-dessus est une description simple du fonctionnement d'une lampe à carbure
 
a) Quels corps utilise-t-on pour le fonctionnement de la lampe ?
 
b) Quels sont les corps qui apparaissent lors de ce fonctionnement ?
 
c) Le phénomène observé est-il physique ou chimique ?

Contenus

I- Exemples de réaction chimique

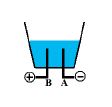
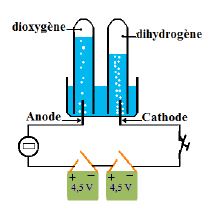
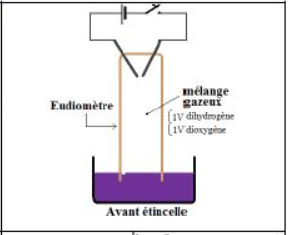
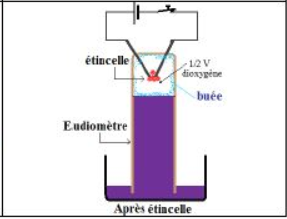
I-1. Electrolyse de l'eau


 

 
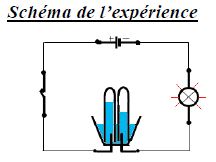
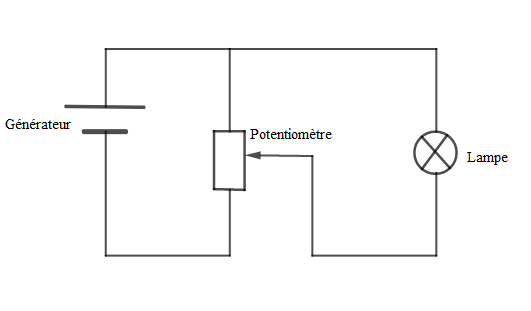
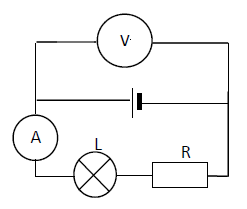
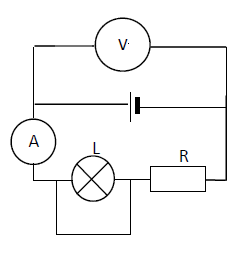
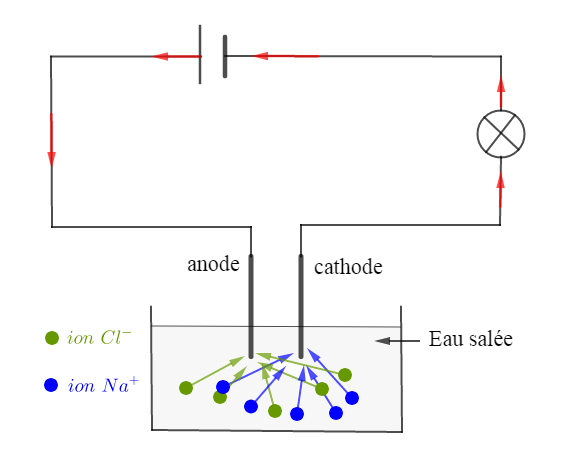
On remplit un électrolyseur avec de l'eau. 
 
Ajoutons quelques gouttes d'acide. 
 
Lorsqu'on ferme l'interrupteur, la lampe s'allume ; le courant passe. 
 
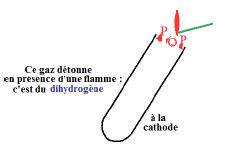
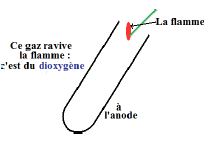
On observe un dégagement de bulles au niveau des électrodes :
 
ces gaz sont le dihydrogène et le dioxygène. 
 
Ainsi l'eau est décomposée par le courant électrique pour donner ces deux gaz.

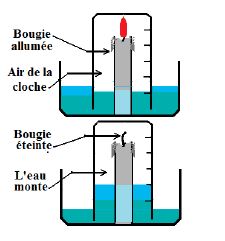
I-2. Combustion du carbone dans un flacon de dioxygène.

On réalise la combustion d'un morceau de charbon dans un flacon contenant de l'eau de chaux.
 
Après la combustion on observe le dégagement d'une fumée et l'eau de chaux contenue dans le flacon se trouble :
 
la combustion s'accompagne alors d'un dégagement de gaz carbonique qui trouble l'eau de chaux.
 
Dans le dioxygène, le carbone brûle et donne du dioxyde de carbone (gaz carbonique).

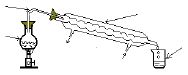
I-3. Action de l'acide sur le calcaire

Introduisons dans un tube à essai contenant de l'acide chlorhydrique un petit morceau de calcaire.
 
On observe une effervescence. 
 
Le gaz qui se dégage trouble l'eau de chaux. De plus, le ballon est légèrement chaud.
 
Lorsque l'acide chlorhydrique attaque le calcaire il se dégage du gaz carbonique. 
 
D'autres expériences montrent la formation aussi d'eau et du chlorure de calcium. 
 
Il se produit un dégagement de chaleur.

I-4. Combustion du mélange fer-soufre

Préparons un mélange intime de $7\;g$ de fer et $4\;g$ de soufre.
 
Chauffons à une extrémité du mélange. On observe une propagation de la combustion du mélange fer-soufre.
 
On obtient à la fin un corps grisâtre qui n'est pas attiré par un aimant : c'est du sulfure de fer.

II- Définitions :

Une réaction chimique est une transformation de corps purs en d'autres corps purs.
 
Les corps qui réagissent et qui disparaissent sont appelés réactifs. 
 
Les corps purs qui se forment ou qui apparaissent lors de la réaction sont les produits de la réaction

 

 

III- Caractéristiques d'une réaction

III-1. Aspects énergétiques

La réaction entre l'acide chlorhydrique et le calcaire s'accompagne d'un dégagement de chaleur : 
 
la réaction est dite exothermique.
 
Certaines réactions se déroulent en absorbant de la chaleur : 
 
ces réactions sont dites endothermiques. 
 
Pour d'autres, aucun effet thermique n'est observé : 
 
on a une réaction athermique.

III-2. La loi de conservation :

a) Combustion fer-soufre

                                                         
 
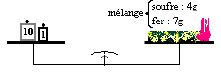
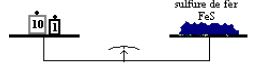
La réaction entre $7\;g$ de fer et $4\;g$ de soufre donne $11\;g$ de sulfure de fer. 
 
Cette expérience montre que la somme des masses des réactifs ayant disparu est égale à celle des produits apparus (le sulfure de fer).

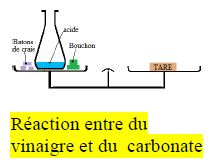
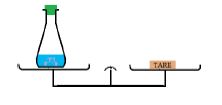
b) Réaction acide-calcaire


                                                       


 

 
La balance est en équilibre avant la réaction et reste toujours en équilibre à la fin de la réaction. 
 
La masse reste invariable au cours de la transformation : 
 
la masse se conserve au cours d'une réaction chimique.

Interprétation

Au cours d'une réaction chimique, il y a une conservation de la matière. 
 
La matière étant constituée d'atomes, il y a alors conservation des atomes présents dans les molécules des différents réactifs. 
 
Les atomes présents dans les réactifs se sont réorganisés pour donner les produits.

 

 

IV- Représentation d'une réaction chimique

On utilise les formules chimiques des réactifs et des produits pour représenter une réaction chimique. 
 
On obtient une écriture symbolique appelée équation bilan.

IV-1. L'équation de la réaction :

Elle indique les différents corps (réactifs et produits) qui entre en jeu au cours de la réaction : 
 
c'est une représentation qualitative de la réaction. 
 
Les réactifs sont écrits à gauche et les produits à droite. 
 
Réactifs et produits sont séparés par une flèche qui indique le sens de la transformation

Exemples :

$\centerdot$ L'électrolyse de l'eau
$$H_{2}O\Longrightarrow H_{2}+O_{2}$$
 
$\centerdot$ La combustion du carbone
$$C+O_{2}\Longrightarrow CO_{2}$$
 
$\centerdot$ L'action de l'acide sur le calcaire
$$HCl+CaCO_{3}\Longrightarrow CaCl_{2}+H_{2}O+CO_{2}$$
 
$\centerdot$ La combustion du mélange fer-soufre
$$Fe+S\Longrightarrow Fe$$

Remarque :

$\centerdot$ Les réactifs sont à gauche de la flèche et les produits à droite.
 
$\centerdot$ la conservation de la matière n'est pas toujours vérifiée avec l'équation de la réaction. 
 
Dans ce cas, l'équation est dite non équilibrée (électrolyse de l'eau).

IV-2. L'équation bilan :

La réaction étant caractérisée par la conservation de la matière, sa représentation doit alors satisfaire à cette loi. 
 
L'équation de la réaction est corrigée si nécessaire : on obtient alors une équation bilan équilibrée.
 
L'équation bilan équilibrée conserve :
 
$\centerdot$ Les éléments chimiques : on a les mêmes éléments chimiques dans les réactifs que dans les produits.
 
$\centerdot$ Le nombre d'atomes de chaque élément chimique : pour un élément donné, on a le même nombre d'atomes dans les réactifs que dans les produits.

Conséquence : 

la masse des réactifs ayant disparu est égale à celle des produits apparus.

Exemples d'équation bilan :

$\centerdot\ $ Electrolyse de l'eau
$$2H_{2}O\Longrightarrow 2H_{2}+O_{2}$$
 
$\centerdot\ $ Action de l'acide chlorhydrique sur le calcaire
$$2HCl+CaCO_{3}\Longrightarrow CaCl_{2}+H_{2}O+CO_{2}$$
 
Les nombres utilisés pour équilibrer l'équation de la réaction sont appelés coefficients stoechiométriques.

L'équation bilan montre :

$\centerdot\ $  Au niveau microscopique, dans quelles proportions les espèces chimiques (atomes, molécules et ions) se combinent et disparaissent pour les réactifs et se forment pour les produits.
 
$\centerdot\ $  Au niveau macroscopique, dans quelles proportions les moles d'espèces chimiques se combinent et disparaissent pour les réactifs et se forment pour les produits.

Exemples :

$\centerdot\ $  L'équation de l'électrolyse de l'eau indique :
 
Au niveau microscopique que $2$ molécules d'eau se sont décomposées pour donner $2$ molécules de dihydrogène et une molécule de dioxygène
 
Au niveau macroscopique, $2$ moles d'eau ont donné $2$ moles de dihydrogène et une mole de dioxygène.
 
$\centerdot\ $ L'action de l'acide chlorhydrique sur le calcaire montre que :
 
Au niveau microscopique, $2$ molécules d'acide se combinent avec une molécule de calcaire pour donner une molécule de chlorure de calcium, une molécule d'eau et une molécule de gaz carbonique
 
Au niveau macroscopique, 2 moles d'acide se combinent avec une mole de calcaire pour donner une mole de chlorure de calcium, une mole d'eau et une mole de gaz carbonique

B- Le problème de chimie

1) Énoncé

Une électrolyse de l'eau $(H_{2}O)$ a permis de recueillir $56\;ml$ de dioxygène $(O_{2})$ dans les conditions normales. 
 
Trouver :
 
a) La masse d'eau décomposée.
 
b) Le volume de dihydrogène $(H_{2})$ recueilli simultanément.

2) Corrigé

$2 H_{2}O\longrightarrow 2 H_{2}+O_{2}$
$2\;mol\qquad 2\;mol\quad 1\;mol$
$n_{H_{2}O}\ ?\qquad n H_{2}\ ?\quad n O_{2}=$
 
le nombre de mole dans $56\;ml$ de $O_{2}$ est :
 
$n_{O_{2}}=\dfrac{v}{V}\rightarrow n_{O_{2}}=\dfrac{56\cdot 10^{-3}}{22.4}=2.5\cdot 10^{-3}mol$ 
 
a) La masse d'eau décomposée est :
 
$m_{H_{2}O}=n\cdot M$
 
$2\;mol\longrightarrow 1\;mol$
 
$n_{H_{2}O}$ ? $\longrightarrow n_{O_{2}}=n_{H_{2}O}=\dfrac{n_{O_{2}}\times 2}{1}=2 n_{O_{2}}$
 
$n_{H_{2}O}=\dfrac{n_{O_{2}}\times 2}{1}2\;n_{O_{2}}$
 
$n_{H_{2}O}=2\times 2.5\cdot 10^{-3}=5\cdot 10^{-3}mol$
 
$M(H_{2}O)=2M(H)+M(O)\rightarrow M(H_{2}O)=2\times 1\times 16=2+16=18\;g/mol$
 
$m_{H_{2}O}=5\cdot 10^{-3}\times 18=9\cdot 10^{-2}g$
 
b) Le volume de dihydrogène recueilli est de $v_{H_{2}}=n\cdot V\text{ avec }V=22.4\;mol/L$
 
$2\;mol\longrightarrow 1\;mol$
 
$n_{H_{2}}$ ? $\longrightarrow n_{O_{2}}=$
 
$n_{H_{2}}=\dfrac{n_{O_{2}}\times 2}{1}=2\times n_{O_{2}}$
 
$n_{H_{2}}=2\times 2.5\cdot 10^{-3}=5\cdot 10^{-3}mol$
 
$v_{H^{2}}=5\cdot 10^{-3}\times 22.4=112\cdot 10^{-3}L$

L'essentiel du cours

$\centerdot$ La réaction chimique transforme certains corps purs appelés réactifs en d'autres corps purs appelés produits.
 
$\centerdot$ La réaction chimique est représentée par une équation bilan qui satisfait à la loi de conservation de la matière et montre dans quelles proportions les réactifs se combinent et les produits se forment.
 
$\centerdot$ L'équation bilan permet de résoudre des problèmes de chimie.
 
Source: 
irempt.ucad.sn

Série d'exercices sur les Moles et grandeurs molaires - 4e

Classe: 
Quatrième
 

Exercice 1

Compléter le texte suivant en ajoutant les mots ou groupes de mots manquants
 
a) L'unité internationale de quantité de matière est la $\ldots\ldots$ Dans une mole on dénombre $\ldots\ldots$ particules identiques.
 
Une $\ldots\ldots$ d'atomes contient $6.02\cdot 10^{23}$ atomes.
 
b) Une mole de $\ldots\ldots$ est un nombre de molécules égal à $\ldots\ldots$ molécules.
 
c) On appelle $\ldots\ldots$ la masse d'une mole. 
 
On exprime la masse molaire en $\ldots\ldots$
 
La $\ldots\ldots$ est la masse d'une mole d'atomes.
 
La masse $\ldots\ldots$ ou $\ldots\ldots$ .est la masse d'une mole de molécules.
 
d) Pour obtenir la masse molaire d'un corps, on fait $\ldots\ldots$ des masses molaires atomiques des atomes qui le composent.
 
e) Le volume molaire est le volume $\ldots\ldots$ d'un corps gazeux.
 
Il n'est défini que pour les $\ldots\ldots$
 
Le volume molaire d'un corps gazeux, dans les conditions normales de pression et de température, $\ldots\ldots$

Exercice 2

Une mole d'eau pèse $18\;g$ ; trouver le nombre de moles contenues dans les différentes masses d'eau suivantes :
 
1) : $7.2\;g$ 
 
2) : $9\;mg$
 
3) : $360\;g$
 
4) : $20\;g$
 
5) : $1\;kg$

Exercice 3 

Calculer la masse molaire de chacun des corps notés ci-dessous.
 
1) $O_{3}$
 
2) $H_{2}SO_{4}$
 
3) $AlCl_{3}$
 
4) $HCl$
 
5) $NaOH$
 
6) $Al_{2}(SO_{4})_{3}$
 
7) $C_{4}H_{10}$
 
8) $S_{2}$
 
9) $ZnSO_{4}$
 
10) $Fe_{3}O_{4}$
 
11) $Ca(OH)_{2}$
 
12) $CaCO_{3}$
 
13) $Ca(HCO_{3})_{2}$
 
14) $HNO_{3}$

Exercice 4 

Calculer le nombre de moles contenu dans chacune des quantités suivantes.
 
1) $980\;mg$ d'acide sulfurique $H_{2}SO_{4}$
 
2) $1\;kg$ de sucre (glucose) $C_{6}H_{12}O_{6}$
 
3) $460\;g$ d'alcool éthylique $C_{2}H_{5}OH$
 
4) $336\;mL$ de gaz butane $C_{4}H_{10}$
 
5) $4.48\;L$ de gaz dioxyde de carbone $CO_{2}$
 
6) $6.84\;g$ de sucre (saccharose) $C_{11}H_{22}O_{11}$

Exercice 5 

Trouver le volume occupé dans les conditions normales par
 
1) $3.6\;g$ de gaz méthane $CH_{4}$
 
3) $320\;mg$ de dioxygène $O_{2}$
 
3) $3.65\;mg$ de gaz chlorhydrique $HCl$
 
4) $22\;g$ de dioxyde de carbone $CO_{2}$

Exercice 6 

Trouver la masse de :
 
1) $140\;mL$ de gaz chlorhydrique $HCl$
 
2) $1.12\;L$ de dihydrogène $H_{2}$
 
3) $17.92\;mL$ de gaz méthane $CH_{4}$
 
4) $2.8\;L$ de dioxygène $O_{2}$
 

Exercice 7 Maitrise de connaissance

Recopie et complète les phrases par les mots ou groupes de mots convenables.
 
La $\ldots\ldots$ est l'unité de quantité de matière. 
 
Une mole d'atomes contient $N$ $\ldots\ldots$ $N$ est appelé $\ldots\ldots$
 
La masse molaire d'un corps est la masse d'une $\ldots\ldots$ d'atomes de ce corps. 
 
Le volume $\ldots\ldots$ d'un gaz est le volume occupé par une $\ldots\ldots$ de ce gaz. 
 
Dans les conditions normales de température et de pression, le volume molaire d'un gaz est de $\ldots\ldots$ $L\cdot mol^{-1}.$ 
 
Des volumes égaux de différents gaz mesurés dans les mêmes conditions de température et de pression renferment la même $\ldots\ldots$ de matière.

Exercice 8 Entités et quantité de matière

1) Détermine la quantité de matière d'un échantillon contenant :
 
a) $2.43\times 10^{21}$ atomes de carbone ;
 
b) $8.35\times 10^{24}$ molécules d'eau
 
2) Détermine le nombre $N$ de molécules contenues dans les échantillons suivants :
 
a) $5.25\times 10^{-3}$ mol de glucose ;
 
b) $11.2\;L$ de chlorure d'hydrogène mesuré dans les $C.N.T.P.$

Exercice 9 Volume et quantité de matière

Calcule les nombres de moles que renferment les échantillons ci-dessous :
 
Volume $v=67.2\;L$ de dioxygène $\left(O_{2}\right)$ ;
 
Volume $v'=56\;cm^{3}$ de diazote $\left(N_{2}\right)$

Exercice 10 Volume molaire

On prépare au laboratoire un volume $v=3\;L$ de dioxygène de masse $m=4\;g.$
 
Déterminer le volume molaire dans les conditions de l'expérience.

Exercice 11 Masse et quantité de matière

Complète le tableau en calculant $M\text{ et }n$
$$\begin{array}{|l|l|c|c|c|} \hline \text{Nom}&\text{Formule}&M\left(g\cdot mol^{-1}\right)&m&n(mol)\\ \hline \text{Chlorure de sodium}&NaCl& &50\;g&\\ \hline \text{Saccharose}&C_{12}H_{22}O_{11}& &0.25\;kg& \\ \hline \text{Acide lactique}&C_{3}H_{6}O_{3}& &10\;mg&\\ \hline \text{Ethanol}&C_{2}H_{6}O& &100\;g&\\ \hline \end{array}$$

Exercice 12

Le sucre est un solide moléculaire constitué de saccharose de formule $C_{12}H_{2}2O_{11}.$ 
 
Un sachet de sucre en poudre a une masse $m=5\;g.$
 
Calcule la masse molaire moléculaire du saccharose.
 
Calcule la quantité de matière en saccharose.
 
Déduis-en le nombre de molécules de saccharose contenues dans le sachet.

Exercice 13 Synthèse d'un ester

Un chimiste synthétise un ester à odeur de banane utilisé pour parfumer certains sirops ou confiseries. 
 
Il introduit dans un ballon, en prenant les précautions nécessaires, les quantités de matière $n_{1}=0.50$ mol d'alcool isoamylique $\left(C_{5}H_{12}O\right)$ et $n_{2}=0.10$ mol d'acide acétique $\left(C_{2}H_{4}O_{2}\right).$
 
Quels volumes $V_{1}\text{ et }V_{2}$ d'alcool et d'acide doit-il prélever ?
 
Données : 
 
Masse volumique de l'alcool isoamylique $\rho_{1}=0.810\;g\cdot mL^{-1}$ ; masse volumique de l'eau $\rho_{e}=1.0\;g\cdot mL^{-1}$ ; densité de l'acide acétique : $d=1.05$

Exercice supplémentaire

La Grotte du Chien

Le dioxyde de carbone peut se former dans les profondeurs terrestres lorsque certains types de roches réagissent entre eux à l'état liquide. 
 
Pendant leurs éruptions, les volcans actifs sont capables de restituer de grandes quantités de gaz, et même dans les zones de volcans éteints depuis longtemps, du dioxyde de
carbone peut s'échapper de fissures dans les roches. 
 
La plus célèbre, peut-être, de ces types de source de dioxyde de carbone est la Grotte du Chien (Grottadel Cane), près de Naples en Italie.
 
Au cours des siècles passés, quand des gens entraient dans la grotte avec leur chien, le chien suffoquait alors que rien n'arrivait à son propriétaire $\ldots\ldots\ldots\ldots\ldots\ldots$$\ldots\ldots\ldots\ldots$
 
Comment expliquer que le chien suffoque alors que rien n'arrive à son propriétaire ?
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

Source: 
irempt.ucad.sn & ADEM

Mole et grandeurs molaires - 4e

Classe: 
Quatrième
 

Activité 

Un  grain de riz a une masse de $0.02\;g$, combien de grains y a-t-il dans $1\;kg$ ? 
 
S'il faut 1 s pour compter un grain, quel temps mettra-t-on pour compter le nombre de grain dans un $kg$ ? 
 
Est-il raisonnable qu'un commerçant vende du riz en comptant les grains ?

Réponse :

$50\ 000$ grains ; $t=50\ 000\,s=13\,h\ 53\,min\ 20\,s.$
 
Pour mesurer des quantités de riz, le commerçant a besoin d'une unité de mesure appropriée telle que le kilogramme ou des pots.
 
Chaque unité contient un nombre élevé de grains. 
 
Par exemple $1\,Kg$ de riz contient $50\ 000$ grains de riz.
 
Le chimiste, dans ses expériences travaille avec des atomes, des ions ou des molécules qui sont infiniment petits comparés aux grains de riz.
 
Les grains de matière (atomes, ions, molécules...) sont infiniment petits à l'échelle humaine, leur manipulation ne peut se faire que par groupes. 
 
Les chimistes ont adopté une unité de mesure de la quantité de matière qui correspond à un nombre fixe de grains de matière identiques. Cette unité est la mole.

I- La mole

I-1. Notion de mole

Activité 1

Trouver le nombre d'atomes contenu dans un échantillon de $12\;g$ de carbone, sachant qu'un atome de carbone pèse $1.993\cdot 10^{-23}g.$
 
Le nombre d'atomes dans un $kg$ de carbone est :
 
$N_{C}=\dfrac{m_{C}}{m_{At}}.$
 
$N_{C}=\dfrac{12}{1.993\cdot 10^{-23}}=6.02\cdot 10^{-23}$
 
$N_{C}=6.02\cdot 10^{23}$ atomes=$6.02\cdot 10^{23}$ atomes
 
Soit six cent deux mille milliards de milliards d'atomes dans $1\;g$ de carbone.
 
Le décompte de telles particules oblige les chimistes à utiliser des quantités de matière appelés moles.

Activité 2

Remplir le tableau ci-dessous :
$$\begin{array}{|c|c|c|c|} \hline \text{Corps}&\text{Masse d'un grain}&\text{Masse de l'échantillon}&\text{Nombre de particules}\\ &\text{de matière}& &\\ \hline \text{carbone}&1.99\cdot 10^{-23}g&12\;g&6.02\cdot 10^{23}\\ \hline \text{Eau}&2.99\cdot 10^{-23}g&18\;g& \\ \hline \text{Fer}&9.30\cdot 10^{-23}g&56\;g& \\ \hline \text{soufre}&5.32\cdot 10^{-23}g&32\;g& \\ \hline \end{array}$$

Constat :

Le nombre de particules (atomes ou molécules) trouvé reste pratiquement constant.

Conclusion 

Les échantillons d'eau de fer et de soufre contiennent approximativement le même nombre de particules que $12$ grammes de carbone. Ce nombre constitue une mole de particules.
 
$\centerdot\ $ une mole d'eau pèse $18\;g$
 
$\centerdot\ $ une mole de carbone pèse $12\;g$
 
$\centerdot\ $ une mole de fer pèse $56\;g$
 
$\centerdot\ $ une mole de soufre pèse $32\;g$
 
Le nombre d'atomes dans $12\;g$ de carbone est appelé mole.

I-2. La constante d'Avogadro

$12\;g$ de carbone contiennent approximativement $6.02\cdot 10^{23}$ atomes. 
 
Ce nombre est appelé nombre d'Avogadro, on le note $\mathcal{N}.$
$$\boxed{\text{Nombre d'Avogadro}=\mathcal{N}=6.02\cdot 10^{23}}$$

Définition 

Une mole est un ensemble de particules identiques contenant $6.02\cdot 10^{23}$ particules.

Exemples :

Une mole d'eau contient $6.02\cdot 10^{23}$ molécules
 
Une mole de fer contient $6.02\cdot 10^{23}$ atomes.
 
Une mole de dioxygène contient $6.02\cdot 10^{23}$ molécules.
 
Une mole de dioxyde de carbone (gaz carbonique) contient $6.02\cdot 10^{23}$ molécules.
 
Une mole de carbone contient $6.02\cdot 10^{23}$ atomes.
 
Une mole de riz contient $6.02\cdot 10^{23}$ grains de riz.

Conclusion 

Le nombre constant $\left(6.02\cdot 10^{23}\right)$ particules que l'on dénombre dans une mole est la constante d'Avogadro. 
 
Elle est notée $\mathcal{N}$ et vaut 602 000 milliards de milliards.
$$\mathcal{N}=6.02\cdot 10^{23}$$

NB : 

La constante d'Avogadro est le nombre d'atomes contenus dans $12\;g$ de carbone $12$

Définition

La mole est l'unité internationale de quantité de matière.
 
Son symbole est : mol.

II- Grandeurs molaires

Pour travailler avec des quantités de matière constituées de molécules, d'atomes ou d'ions avec nos instruments habituels de mesures telles que la balance, on les regroupe par paquet de matière :
 
chaque paquet contenant $\mathcal{N}$ particules.

II-1. Mole de particules

La mole s'applique aussi bien pour les atomes que pour les molécules ou les grains de riz.

Mole d'atomes

Une mole d'atomes est un nombre d'atomes égal à $\mathcal{N}$ atomes c'est à dire $6.02\cdot 10^{23}$ atomes.
$$1\text{ mol d'atomes}=\mathcal{N}\text{ atomes}=6.02\cdot 10^{23}\text{ atomes}$$

Mole de molécules

Une mole de molécules est un nombre de molécules égal à $\mathcal{N}$ molécules c'est à dire $6.02\cdot 10^{23}$ molécules.
$$1\text{ mol de molécules}=\mathcal{N}\text{ molécules }=6.02\cdot 10^{23}\text{ molécules}.$$

Mole de riz

Une mole de riz est un nombre de grains de riz égal à $\mathcal{N}$ grains c'est à dire $6.02\cdot 10^{23}$ grains.
$$1\text{ mol riz}=\mathcal{N}\text{ grains }=6.02\cdot 10^{23}\text{ grains.}$$

II-2. La masse molaire

C'est la masse d'une mole. 
 
On la note $M$ et on l'exprime en $g/mol$ ou $g\cdot mol^{-1}$

II-3. Masse molaire atomique

La masse molaire atomique est la masse d'une mole d'atomes. 
 
On la note par $M$ (symbole de l'élément chimique).

Exemple :

$M(Fe)=56\;g\cdot mol^{-1}$
 
$M(O)=16\;g\cdot mol^{-1}$
 
$M(H)=1\;g\cdot mol^{-1}$

II-4. Masse molaire moléculaire

II-4.1. Définition

La masse molaire moléculaire ou masse molaire est la masse d'une mole de molécules. 
 
On la note $M$(symbole de la molécule).

Exemples 

$M(H_{2}O)=18\;g\cdot mol^{-1}$
 
$M(H_{2})=2\;g\cdot mol^{-1}$
 
$M(NaOH)=40\;g\cdot mol^{-1}$

II-4.2. Calcul de la masse molaire

Pour obtenir la masse molaire d'un corps, on fait la somme des masses molaires atomiques des atomes qui le composent.

Exemples

\begin{eqnarray} M(H_{2}O) &= &2 M(H)+M(O)\nonumber\\ &=& 2\times 1+1\times 16\nonumber\\ &=& 2+16\nonumber\\ &=& 18\;g\cdot mol^{-1}\nonumber \end{eqnarray}
 
\begin{eqnarray} M(NaOH) &= & M(Na)+M(O)+M(H)\nonumber\\ &=& 1\times 23+1\times 16+1\times 1\nonumber\\ &=& 23+16+ 1 \nonumber\\ &=& 40\;g\cdot mol^{-1}\nonumber \end{eqnarray}

III- Le volume molaire d'un gaz

Le volume molaire $V_{m}$ est le volume d'une mole d'un corps gazeux. 
 
Il n'est défini que pour les corps gazeux. 
 
Il s'exprime en $L\cdot mol^{-1}$

III-1. Le volume molaire dans les conditions normales

Dans les conditions dites normales $(0^{\circ}$C, $76\;cm$ de mercure..), une mole de gaz occupe $22.4\;L.$
 
On note $V_{0}=22.4\;L\cdot mol^{-1}$

III-2. La densité par rapport à l'air

La densité par rapport à l'air des corps gazeux est souvent définie par rapport à l'air c'est le rapport entre la masse d'un volume de gaz sur la masse d'un égal volume d'air pris dans les mêmes conditions.
 
Elle est égale au rapport de la masse molaire $M$ du corps gazeux sur la masse d'un égal volume d'air soit $29\;g$ pour la mole d'air.
$$d=\dfrac{M}{29}$$

IV- Applications

Calcul de la quantité $n$ de matière

1) dans une masse $m_{x}$ d'un corps $X$

Le nombre de mole $n_{x}$ contenu dans une masse $m_{x}$ d'un corps $X$ est donné par :
$$\boxed{n_{x}=\dfrac{m}{M(X)}}$$

Exemple : 

le nombre de mole dans $7.2\;g$ d'eau est :
 
$n_{H_{2}O}=\dfrac{m}{M(H_{2}O)}=m_{H_{2}O}=7.2\;g$
 
$M(H_{2}O)=2.1+1.16=18\;g/mol$
 
$n_{H_{2}O}=\dfrac{7.2}{18}=0.4\;mol$

Conséquences : calcul de la masse d'un corps $X$

La masse $m_{x}$ d'un corps $X$ peut être calculée à partir de :
$$\boxed{m_{x}=n_{x}\cdot M(X)}$$

Exemple : 

la masse de 0.5 mol de $CO_{2}$ est :
 
$m_{CO_{2}}=n_{CO_{2}}\cdot M(CO_{2})$
 
$n_{CO_{2}}=0.5\;mol$
 
$M_{(CO_{2})}=M(C)+2M(O)$
 
$M_{(CO_{2})}=1.12+2.16=12+32=44\;g/mol.$
 
$m_{CO_{2}}=0.5\cdot 44=22\;g$

2) dans le volume $V$ d'un corps gazeux.

Le nombre de mole $n$ contenu dans un volume $V$ d'un corps gazeux est :
$$\boxed{n_{g}=\dfrac{v_{g}}{v}}$$

Exemple : 

le nombre de mole contenu dans 1.12 L de dihydrogène dans les conditions normales
 
$n_{H_{2}}=\dfrac{v_{H_{2}}}{v}$
 
$v_{H_{2}}=1.12\;L$
 
$v=22.4\;L/mol$
 
$n_{H_{2}}=\dfrac{1.12}{22.4}=0.05\;mol$

Conséquence : Calcul du volume $V_{g}$ d'un corps gazeux

Le volume $V_{g}$ d'un corps gazeux est donné par :
$$\boxed{V_{g}=n_{g}\cdot V}$$

Exemple : 

le volume occupé par 0.1 mol de butane dans les conditions normales est :
 
$V_{C_{4}H_{10}}=n_{C_{4}H_{10}}\cdot V$
 
$n_{C_{4}H_{10}}=0.1\;mol$
 
$v=22.4\;L/mol$
 
$V_{C_{4}H_{10}}=0.1\cdot 22.4=2.24\;L$

L'essentiel du cours

Mole : La mole (mol) est l'unité de quantité de matière
 
Constante d'Avogadro : Le nombre constant $\left(6.02\cdot 10^{23}\right)$ particules que l'on dénombre dans une mole est la constante d'Avogadro.
 
Elle est notée $\mathcal{N}$ et vaut 602 000 milliards de milliards.
 
Mole d'atomes : 1 mol d'atomes=$\mathcal{N}$ atomes=$6.02\cdot 10^{23}$ atomes
 
Mole de molécules : 1 mol de molécules=$\mathcal{N}$ molécules=$6.02\cdot 10^{23}$ molécules.
 
Masse molaire : C'est la masse d'une mole, on l'exprime en $g/mol=g\cdot mol^{-1}$
 
Masse molaire atomique : C'est la masse d'une mole d'atomes, on l'exprime en $g/mol=g\cdot mol^{-1}$
 
Masse molaire moléculaire : C'est la masse d'une mole de molécules, on l'exprime en $g/mol=g\cdot mol^{-1}$
 
Volume molaire : C'est le volume d'une mole d'un corps gazeux, on l'exprime en $L/mol=L\cdot mol$
 
Source: 
irempt.ucad.sn

Série d'exercices sur les Mélanges et corps purs - 4e

Classe: 
Quatrième
 

Exercice 1   

Encadrer la lettre correspondant à la bonne réponse.
 
Un mélange dans lequel on peut distinguer les différents constituants à l'œil nu est un mélange dit
 
a) Homogène
 
b) hétérogène
 
c) stable

Exercice 2     

On dispose des mélanges suivants :
 
a) eau de mer ;
 
b) eau de ruissellement ;
 
c) eau minérale ;
 
d) jus de bissap ;
 
e) fer+soufre ;
 
f) huile+eau
 
Compléter le tableau ci-dessous en écrivant la lettre correspondant à chaque mélange dans la colonne qui convient
$$\begin{array}{|c|c|} \hline \text{Mélange homogène}&\text{Mélange hétérogène}\\ \hline &\\ \hline \end{array}$$

Exercice 3    

a) eau de mer ; 
 
b) eau de ruissellement ;
 
c) eau minérale ; 
 
d) jus de bissap ;
 
e) fer+soufre ; 
 
f) huile+eau
 
Donner pour chaque mélange la méthode de séparation appropriée
$$\begin{array}{|c|c|} \hline \text{Mélanges}&\text{Méthodes de séparations}\\ \hline &\\ \hline \end{array}$$
 
Choisir la bonne réponse On peut séparer l'eau et le sucre par
 
$\centerdot\ $ Décantation
 
$\centerdot\ $ Filtration
 
$\centerdot\ $ Distillation

Exercice 4   

Compléter le texte par les mots suivants :
 
filtration, potable, hétérogène, décantation.
 
Une ménagère a ramené de l'eau du fleuve.
 
Cette eau est un mélange$\ldots$.
 
Elle la laisse au repos dans la bassine pendant une demi-heure, des substances étrangères se déposent au fond du récipient par$\ldots$.
 
elle verse l'eau dans un canari à travers un morceau à gaze. L'opération s'appelle la $\ldots$. 
 
Le filtrat est un mélange $\ldots$
 
Puis, elle y introduit quelques gouttes d'eau de javel pour rendre l'eau$\ldots$. 

Exercice 5     

La chambre de Samba a les dimensions suivantes : $3\;m\;;\ 3.30\;m\;;\ 3.5\;m.$
 
1) Quel volume d'air renferme cette chambre.
 
2) Calculer le volume de dioxygène disponible pour samba.
 
3) Calculer le volume de diazote présent dans la chambre de Samba

Exercice 6    

Comment peut-on, à partir d'une eau boueuse et salée, obtenir :
 
1) Une eau limpide et salée ?
 
2) Une eau limpide non salée ?

Exercice 7    

Recopier et mettre une croix devant la bonne réponse.
 
1) On peut distinguer deux constituants d'un mélange
 
$\centerdot\ $ homogène 
 
$\centerdot\ $ hétérogène
 
2) La filtration permet de séparer les constituants d'un mélange 
 
$\centerdot\ $ homogène
 
$\centerdot\ $ hétérogène.
 
3) Pour séparer les constituants d'un mélange homogène, on peut utiliser 
 
$\centerdot$ une décantation 
 
$\centerdot\ $ une distillation.
 
4) Lorsqu'on laisse reposer un mélange, on réalise 
 
$\centerdot\ $ une décantation 
 
$\centerdot\ $ une distillation.

Exercice 8      

Modou explique à Fatou comment on fabrique du '' Café Touba '' : il lui indique les trois (3) étapes que comprend cette préparation.
 
$1^{ère}$ étape : mettre de l'eau dans une cafetière, porter l'eau à l'ébullition puis ajouter la poudre de  ''Café Touba'' et attendre quelles minutes.
 
$2^{ème}$ étape : Faire passer le mélange obtenu à travers un tissu pour recueillir la partie liquide.
 
$3^{ème}$ étape : Ajouter du sucre à volonté et remuer à l'aide d'une cuillère. 
 
Le ''Café Touba'' est prêt.
 
Quel type de mélange obtient-on à la fin de la $1^{ère}$ étape ?
 
Quelle est la méthode de séparation utilisée dans la $2^{ème}$ étape ?
 
Comment appelle-t-on, en chimie, le liquide obtenu ; est-ce un corps pur ?
 
Quel type de mélange obtient-on à la fin de la $3^{ème}$ étape ? 
 
Justifier votre réponse. 

Exercice 9     

Le schéma ci-dessous est celui de la distillation de l'eau salée.
 
1) Donner les éléments manquants des annotations
 
2) Indiquer les changements d'états physiques qu'on y rencontre et préciser à quel niveau ?
 
3) Quel est le corps obtenu, donner quelques unes de ses propriétés ?

 

 

Exercice 10     

Le schéma ci dessous est un élément du montage expérimental de l'électrolyse de l'eau.
 
1) Préciser les noms respectifs des électrodes $A\text{ et }B.$
 
2) Quels gaz recueille-t-on sur l'électrode $A$ et sur l'électrode $B$ ?
 
3) Comment caractérise-t-on chacun des gaz 

 Exercice 11    

Fais correspondre par une flèche chaque expression à la bonne réponse.
$$\begin{array}{|lcr|} \hline \text{Mélange}&\qquad\qquad&\text{Mélange dans lequel on ne peut pas}\\ &\qquad\qquad&\text{distinguer ses différents constituants}\\ \\ \text{Corps pur simple}&\qquad\qquad&\text{Association de deux ou de plusieurs}\\ &\qquad\qquad&\text{substances}\\ \\ \text{Mélange homogène}&\qquad\qquad&\text{Transformation qui ne modifie pas la}\\ &\qquad\qquad&\text{nature des corps}\\ \\ \text{Corps pur composé}&\qquad\qquad&\text{Association de plusieurs substances}\\ &\qquad\qquad&\text{qu'on peut distinguer}\\ \\ \text{Mélange hétérogène}&\qquad\qquad&\text{Un corps qui peut se décomposer en}\\ &\qquad\qquad&\text{d'autres corps}\\ \\ &\qquad\qquad&\text{Un corps qui ne peut pas se}\\ &\qquad\qquad&\text{décomposer en d'autres corps}\\ \hline \end{array}$$

Exercice 12    

On dispose des mélanges suivants :
 
$\centerdot\ $ eau de mer
 
$\centerdot\ $ eau de ruissellement
 
$\centerdot\ $ eau minérale
 
$\centerdot\ $ jus de bissap
 
$\centerdot\ $ fer+souffre
 
$\centerdot\ $ huile+eau
 
Reproduis le tableau ci-dessous et écris chaque mélange dans la colonne qui convient
$$\begin{array}{|c|c|} \hline \text{Mélange homogène}&\text{Mélange hétérogène}\\ \hline &\\ &\\ &\\ &\\ &\\ \hline \end{array}$$

Exercice 13      

Recopie et complète les phrases ci-dessous avec les expressions suivantes :
 
filtration, mélange homogène, mélange hétérogène, décantation, distillation, de l'eau.
 
1) Dans un jus d'orange, il y a de la pulpe d'orange, du sucre, et ......... La pulpe se dépose : 
 
le jus d'orange constitue un .......... 
 
Le jus filtré est un ...........
 
2) La boue se dépose au fond d'un lac par ......... 
 
L'eau qui pénètre dans le sol, traverse les couches de sable par ........... et devient limpide.
 
3) Lors d'une pénurie d'eau, une ménagère puise de l'eau dans un puits.
 
Cette eau est un mélange ........... 
 
Elle la laisse au repos dans un récipient pendant quelques minutes. 
 
Des particules lourdes se déposent au fond du récipient par ..........
 
Elle transvase l'eau dans une bassine à travers un morceau de gaze pour retenir les particules légères : 
 
cette opération appelée .......... ; elle donne un mélange .........

Exercice 14    

Propose une méthode de séparation appropriée pour chacun des mélanges ci-dessous.
 
1) Fer et soufre
 
2) Eau et sucre
 
3) Eau et huile
 
4) Farine et grain de mil
 
5) Sable et eau

Exercice 15     

Recopie le tableau et indique la nature (corps pur, mélange, corps pur simple, corps pur composé) de la substance.
$$\begin{array}{|c|c|} \hline \text{Substance}&\text{Nature de la substance}\\ \hline \text{Eau salée}&\\ \hline \text{Jus de bissap}&\\ \hline \text{Pain}&\\ \hline \text{Dioxyde de carbone}&\\ \hline \text{Eau distillée}&\\ \hline \text{dioxygène}&\\ \hline \end{array}$$

Exercice 16     

Au cours d'une électrolyse de l'eau pure, un élève a recueilli $12.5\;cm^{3}$ d'un gaz qui rallume un brin incandescent.
 
1) Donne le nom de ce gaz ? A quelle électrode a-t-il été recueilli ?
 
2) Quel autre gaz doit-il recueillir à l'autre électrode ? 
 
Comment l'identifie-t-on ? 
 
Précise son volume.

Exercice 17     

Dans un eudiomètre, on mélange $40\;cm^{3}$ de dioxygène et $40\;cm^{3}$ de dihydrogène.
 
On fait jaillir une étincelle électrique dans le mélange.
 
1) Montre qu'il reste un gaz à la fin de l'opération.
 
2) Détermine le volume du gaz restant.

Exercice 18     

Recopie et complète les phrases ci-dessous
 
1) A la pression atmosphérique normale, la vaporisation et la ........ de l'eau pure se produisent à la même température constante égale à .........
 
2) La fusion et la .......... de l'eau pure se produisent à la température constante égale à ..........
 
3) Pour un corps .........., la température d'ébullition et la température de fusion sont des constantes physiques.

Exercice 19      

Une chambre fermée a les dimensions suivantes :
 
$\text{Longueur}=3.50\;m\;;\text{ largeur}=3.20\;m\text{ et hauteur}=3.10\;m.$
 
1) Calcule le volume d'air contenu dans la salle.
 
2) Déduis-en les volumes de dioxygène et de diazote contenus dans la salle.

Exercice 20     

Lorsqu'on sort une bouteille d'eau du réfrigérateur, ses parois extérieures se recouvrent de gouttelettes d'eau (buée). 
 
Sachant que l'air contient de la vapeur d'eau, explique la provenance de cette buée.

Exercice supplémentaire     

Exploitation d'un document
 
L'eau douce est rare dans les contrées désertiques ; or certaines d'entre elles, comme les pays du golfe persique, ont à leur portée d'immenses quantités d'eau de mer. 
 
Cette inépuisable réserve d'eau, hélas, est inutilisable telle quelle, en raison de la présence du sel qui la rend impropre à la consommation et à l'irrigation des terres agricoles. 
 
Aussi a-t-on pensé obtenir de l'eau douce à partir de l'eau de mer. 
 
Le dessalement de l'eau de mer peut être pratiqué dans les usines situées à proximité des rivages. 
 
L'eau de mer d'abord est portée à ébullition, puis la vapeur obtenue est liquéfiée.
 
1) Donne un titre à ce texte.
 
2) Nomme la technique utilisée pour rendre l'eau de mer propre à l'irrigation.
 
3) Relève dans le texte les passages qui relatent les différentes étapes de cette technique.
 
4) Précise la nature du corps obtenu.
 
5) Quelles mesures doit-on effectuer pour vérifier la pureté du corps recueilli ? 
 
Donne les résultats attendus.
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 
Source: 
irempt.ucad.sn & ADEM

Mélanges et corps purs - 4e

Classe: 
Quatrième
 

Activité 1 :

Eau limpide, Eau potable, mélanges
 
On dispose de béchers contenant :
 
1) de l'eau de robinet
 
2) de l'eau boueuse
 
3) de l'eau salée
 
4) de l'eau minérale
 
5) de l'eau de puits
 
a) Observer et décrire le contenu de chaque bécher.
 
b) Marquer d'une croix les cases qui permettent de caractériser les contenus par les mots limpide, potable, pur, mélange.
$$\begin{array}{|l|c|c|c|c|} \hline &\text{limpide}&\text{potable}&\text{pure}&\text{mélange}\\ \hline \text{Eau de robinet}& & & &\\ \hline \text{Eau boueuse}& & & &\\ \hline \text{Eau salée}& & & &\\ \hline \text{Eau de puits}& & & & \\ \hline \end{array}$$

Activité 2 : 

Vaporisation d'une eau minérale

Verser $2\;cm^{3}$ d'eau minérale environ dans un tube à essai, puis chauffer jusqu'à l'évaporation totale. 
 
Observer les parois du tube à essai et noter les constats

 

 
$L'évaporation\ de\ l'eau\ de\ mer\ dans\ les\ marais\ salants\ permet\ de\ recueillir\ des\ quantités\ énormes\ de\ sel$
$dans\ les\ régions\ de\ Kaolack\ et\ de\ Fatick$

I- Notion de mélange

I-1. Notion de mélange

Les eaux naturelles (l'eau boueuse, l'eau des fleuves, des océans, l'eau de pluie, celles des puits et l'eau minérale) contiennent en quantités plus ou moins importantes des substances étrangères.
 
Ce sont des mélanges. 
 
Un mélange est composé de plusieurs constituants différents. 
 
On distingue deux types de mélanges : des mélanges dont on ne peut pas distinguer les différents constituants et d'autres dont on peut distinguer les constituants.

I-2. Mélanges homogènes

L'eau salée contient du sel. Le jus de bissap contient du sucre et du bissap dissouts dans l'eau. Cependant on ne pas distinguer l'eau du sel : 
 
l'eau salée est un mélange homogène.
 
Un mélange est dit homogène si on ne peut pas distinguer à l'œil nu ses différentes parties.

Exemple : 

jus de bissap, eau sucrée, eau minérale, air$\ldots$

 

 
$Bras\ de\ mer\ :\ Le\ Saloum$
$Des\ quantités\ énormes\ de\ sel\ sont$
$dissoutes\ dans\ l'eau\ de\ mer$

I- 3. Mélanges hétérogènes

Un mélange est dit hétérogène si on peut distinguer à l'œil nu ses différentes parties.

Exemples : 

eau de ruissellement (eau boueuse), eau+huile, sable+ciment$\ldots$

II- Méthodes de séparation des mélanges

II- 1. Cas des mélanges hétérogènes

Dans une eau boueuse on distingue des particules solides en suspension dans l'eau. 
 
On peut obtenir une eau limpide à partir de cette eau boueuse. 
 
Il existe plusieurs méthodes physiques pour séparer les différents constituants du mélange hétérogène

II- 1.1. La décantation

Introduisons dans une ampoule à décanter un mélange eau plus huile.
 
Agitons puis laissons reposer le mélange.
 
Au bout d'un certain temps on observe une séparation entre l'huile et l'eau. 
 
L'huile étant plus légère que l'eau, flotte au dessus de celle-ci.
 
On dit qu'on a décanté le mélange hétérogène. 
 
La décantation consiste à laisser reposer le mélange.
 
Il se produit une séparation entre les différentes phases du mélange.

Remarque : 

laissons décanter une eau trouble contenant des particules solides en suspension. 
 
Au bout d'un certain temps on remarque que les particules solides se déposent au fond du récipient.
 
$\centerdot$ On complète la décantation par un transvasement pour récupérer la partie liquide (voir schéma).

 
                                                                                                   

 
$\centerdot$ Au laboratoire, on utilise une ampoule à décanter pour séparer les constituants d'un mélange de liquides non miscibles (exemples mélange eau-huile)

II-1.2. La filtration

La filtration est un procédé qui permet de séparer les différents constituants d'un mélange hétérogène solide-liquide. 
 
Pour cela on verse le mélange hétérogène à travers un papier filtre. 
 
Le liquide qui traverse le filtre est appelé filtrat ; c'est un mélange homogène. 
 
Les particules solides sont retenues par le papier filtre (voir schéma).

 
                                                                                                              

 

II- 2. Séparation des constituants des mélanges homogènes

On ne peut séparer les constituants d'un mélange homogène ni par la décantation, ni par la filtration. 
 
D'autres procédés sont utilisés. 
 
Ils sont basés sur les propriétés physiques telles que la température d'ébullition et la température de congélation.

II-2.1. La distillation

Dans un ballon on chauffe de l'eau salée. 
 
Au cours du chauffage, la température augmente et garde une valeur constante égale à $100^{\circ}$C pendant l'ébullition. 
 
La vapeur qui se dégage est liquéfiée dans un réfrigérant appelé aussi condenseur. 
 
Le liquide recueilli dans le bécher est appelé distillat : c'est de l'eau pure.

 
 
                                                                                         

 
Distiller un liquide, c'est le vaporiser puis le liquéfier. La distillation permet de séparer les différents constituants d'un mélange homogène.
 

 

 

II-2.2. Autres méthodes de séparations 

Il existe d'autres méthodes de séparation parmi lesquelles on peut citer :
 
$\centerdot$ Pour les mélanges solide-solide, on a : 
 
le triage, le vannage, la ventilation, le tamisage, le criblage, la centrifugation$\ldots$
 
$\centerdot$ Pour les liquides : distillation fractionnée, congélation fractionnée,

Applications

La distillation fractionnée du pétrole ou des gaz naturels est effectuée par les sociétés de raffinage.
 
En chauffant le pétrole brut, à différents étages qui correspondent à des températures différentes, on récupère divers produits dont l'essence, le gasoil, le fuel, le kérosène, le mazout, le goudron.

II-2.3. Propriétés physiques des corps purs

a) Les constantes physiques d'un corps pur

Durant l'ébullition, la température de la vapeur d'eau reste constante à $100^{\circ}$C.
 
Cette température correspond à la température d'ébullition de l'eau ; c'est une constante physique pour l'eau.
 
Il existe d'autres constantes physiques pour l'eau parmi lesquelles on peut citer : 
 
la température de fusion, la température d'ébullition la masse volumique$\ldots$,
 
Le tableau ci-dessous donne quelques valeurs des constantes physiques de l'eau
$$\begin{array}{|c|c|c|} \hline \text{Température d'ébullition}&\text{Température de fusion}&\text{Masse volumique}\\ \hline 100^{\circ}C&0^{\circ}C&1000\;kg\cdot m^{-3}\\ \hline \end{array}$$
 
Tout corps pur est caractérisé par ses constantes physiques.

Exemples : 

Valeurs des constantes physiques de quelques corps purs
$$\begin{array}{|c|c|c|c|} \hline &\text{Aluminium}&\text{éthanol}&\text{eau}\\ \hline \text{Température}&2518.9&78&100\\ \text{d'ébullition}(^{\circ}C)& & &\\ \hline\text{Température de}&660&-117&0\\ \text{congélation}(^{\circ}C)& & &\\ \hline \text{Masse volumique}&2700&810&1000\\ \left(kg/m^{3}\right)& & &\\ \hline \end{array}$$

b) Critères de pureté

Pour vérifier la pureté d'un corps pur, on mesure ses constantes physiques. 
 
On compare les résultats avec les valeurs données dans les tables des constantes physiques.

III- Autres exemples de mélanges

III- 1. Un mélange gazeux : l'air

L'air qui nous entoure nous permet de respirer et de faire la combustion de plusieurs corps, en particulier pour la cuisson des aliments que nous mangeons.

III- 1.1. Expérience

Une bougie allumée est plantée dans une cuve contenant de l'eau, puis coiffée d'une éprouvette graduée. L'éprouvette est remplie d'air.
 
Au bout de quelques instants
 
$-\ $ La bougie s'éteint
 
$-\ $ L'eau de la cuve remonte à 1/5 du volume de l'éprouvette.

 
                                                                                                 

 
La bougie est éteinte du fait que le dioxygène, constituant de l'air qui entretient la combustion est totalement consommée.
 
L'eau de la cuve est remontée dans l'éprouvette pour remplacer le dioxygène consommé.

III- 1.2. Conclusion  

L'air est constitué de 1/5 de dioxygène et 4/5 de diazote. 
 
D'autres expériences permettent de montrer que l'air sec est un mélange gazeux dont la composition volumique est :
 
$\centerdot\ 78\%$ de diazote
 
$\centerdot\ 21\%$ de dioxygène
 
$\centerdot\ 1\%$ de gaz rares

III- 2. mélanges de solides

D'autres procédés physiques de séparation sont utilisés lorsque tous les constituants du mélange sont des solides.
 
$-\ $ triage mécanique : mélange sable+grain de sel
 
$-\ $ magnétique : fer+sable

IV- Analyse et synthèse de l'eau

IV- 1. Analyse de l'eau

IV- 1.1. Analyse de l'eau pure

a) Expérience

On réalise le montage ci-contre

 
                                                                                                   

 
Le circuit comprend :
 
$\centerdot$ deux piles de $4.5\;V$ montées en série
 
$\centerdot$ une lampe à incandescence
 
$\centerdot$ une cuve à électrolyseur contenant de l'eau pure et deux tubes essais remplis d'eau pure et renversés sur les électrodes.

b) Observations

La lampe reste éteinte car l'eau pure ne conduit pratiquement pas le courant électrique. 
 
On ajoute une solution de soude dans l'électrolyseur, la lampe s'allume et on constate que : 
 
des bulles de gaz se dégagent au niveau des électrodes.
   
Le gaz qui se dégage à l'électrode reliée à la borne négative (cathode) détonne en présence d'une flamme : 
 
c'est du dihydrogène (voir schéma).

 
                                                        

 
Le gaz qui se dégage à l'électrode reliée à la borne positive (anode) rallume une bûchette en incandescence : 
 
c'est du dioxygène (voir schéma).

 
                                                                

 
Le volume de dihydrogène est le double de celui de dioxygène.
 
On peut expérimentalement vérifier que la quantité de soude initialement ajoutée se retrouve intégralement à la fin de l'électrolyse.
 
Par contre la quantité d'eau a diminué.

c) Interprétation des résultats

Au passage du courant électrique l'eau s'est décomposée pour donner du dioxygène et du dihydrogène qui sont d'autres corps purs.
 
La décomposition de l'eau par le courant électrique est appelé électrolyse de l'eau. Ce procédé est une transformation chimique.

d) Conclusion

L'eau est un corps pur qu'on peut décomposer en d'autres corps : 
 
l'eau est un corps pur composé. 
 
Par contre le dihydrogène et le dioxygène ne peuvent pas être décomposés en d'autres corps purs :
 
ce sont des corps purs simples.

Définitions

Un corps pur simple est un corps pur qu'on ne peut pas décomposer en d'autres corps purs.

Exemples : 

dihydrogène, dioxygène, cuivre, zinc, plomb, soufre...
 
Un corps pur composé est un corps qu'on peut décomposer en plusieurs corps purs simples

Exemples : 

eau pure, dioxyde de carbone, oxyde d'aluminium...

IV- 2. Synthèse de l'eau pure

IV- 2.1. Synthèse qualitative : Expérience de CAVENDISH

a) Protocole expérimentale

                                       
                                       

 
Un courant de dihydrogène est produit par l'action d'une solution d'acide sulfurique sur de la grenaille de zinc. 
 
A l'aide d'une flamme on effectue la combustion du dihydrogène dans le dioxygène de l'air contenu dans une éprouvette.

b) Observation

Une buée de vapeur d'eau se forme sur la paroi de l'éprouvette

c) Interprétation

Le dihydrogène brûle dans le dioxygène pour donner de l'eau.
 
La formation de l'eau à partir de dihydrogène et de dioxygène est appelée synthèse de l'eau.

IV- 2.2. Synthèse quantitative : Synthèse à l'eudiomètre


 

      
On introduit dans un eudiomètre, renversé dans une cuve contenant du mercure, un mélange gazeux constitué de $1$ volume de dihydrogène et $1$ volume de dioxygène.
 
Une étincelle électrique déclenche la combustion du mélange.
 


 

Après le passage de l'étincelle électrique, le mercure remonte dans l'eudiomètre et il se forme une buée sur la paroi intérieur : c'est de la vapeur d'eau.
 
Il reste dans l'eudiomètre un volume $V/2$ de gaz.
 
Ce gaz peut rallumer une brindille en incandescence : c'est du dioxygène

NB : 

Un volume $V$ de dihydrogène s'est combiné avec un volume $V/2$ de dioxygène pour donner de l'eau.

Conclusion

Dans l'eau on ne trouve donc que l'oxygène et le l'hydrogène. 
 
L'eau est un corps pur composé.

L'essentiel du cours

Mélanges

Un mélange est un ensemble composé de plusieurs constituants différents.

Mélanges hétérogènes

Des constituants du mélange peuvent être distingués à l'œil nu.

Mélanges homogènes

Les constituants du mélange homogène ne peuvent pas être distingués à l'œil nu. 
 
Les corps étrangers sont dissous. 
 
On a une solution.

Méthodes de séparation des mélanges

$\centerdot$ la décantation permet de séparer un mélange hétérogène liquide-liquide non miscibles en ses différents composants.
 
Pour cela on utilise une ampoule à décanter.
 
Si on a un mélange solide-liquide, les particules solides se déposent au fond du récipient.
 
$\centerdot$ la filtration permet de séparer les particules solides et le filtrat qui est un mélange homogène
 
$\centerdot$ La distillation permet de séparer les différents constituants d'un mélange homogène. 
 
Le distillat est un corps pur.

Composition de l'air

L'air sec est un mélange gazeux contenant $78\%$ de diazote, $21\%$ de dioxygène et $1\%$ de gaz rares

Corps purs

Un corps pur est une substance dont les critères de pureté sont déterminés. 
 
Ces valeurs sont des constantes physiques (température de fusion, température d'ébullition, masse volumique...)

Corps purs simple

Un corps pur simple est un corps pur que l'on ne peut pas décomposer en d'autres corps purs.

Corps purs composé

Un corps pur composé est un corps pur qui peut être décomposé pour donner d'autres corps purs
          
Source: 
irempt.ucad.sn

Solution des exercices : Énergie et rendement 3e

Classe: 
Troisième
 

Exercice 1 

 
 
 
 

Exercice 2 

1) Deux exemples de transformations de l'énergie électrique en énergie calorifique
 
$-\ $ Cuisinière électrique 
 
$-\ $ Four électrique
 
2) L'énergie contenue dans un arc tendu est l'énergie élastique. A la lâchée de la flèche, elle se transforme en énergie mécanique.

Exercice 4 

Un objet de masse $1\;kg$ est soulevé d'une hauteur de $10\;m$ au bout d'une corde.
 
1) Calculons le travail mécanique fourni
 
On a : $W=m\times g\times h$
 
A.N : $W=1\times 10\times 10=100$
 
Donc, $$\boxed{W=100\;j}$$
 
2) Il possède alors de l'énergie mécanique

Exercice 5 

Un courant constant d'intensité $I=3\;A$ passe pendant $45\;min$ dans un conducteur de résistance $R=40\;\Omega.$
 
Calculons la chaleur dégagée par effet joule :
 
$-\ $ en joules
 
On a : $E=RI^{2}t$
 
A.N : $E=40\times 3^{2}\times 45\times 60=972000$
 
Donc, $$\boxed{E=972000\;j}$$
 
$-\ $ en calories
 
On a : 
 
$\begin{array}{rcl} 1\;cal&\longrightarrow&4.18\;j \\ E_{(cal)}&\longrightarrow&972000\;j\end{array}$
 
Donc, en appliquant la règle de proportionnalité, on obtient :
 
$\dfrac{E_{(cal)}}{1}=\dfrac{972000}{4.18}\ \Rightarrow\ E_{(cal)}=\dfrac{972000}{4.18}=232535.885$
 
D'où  $$\boxed{E_{(cal)}=232535.885\;cal}$$

Exercice 6

Une centrale électrique nucléaire fournit à un réseau une puissance électrique de $1000\;MW.$
 
Trouvons le rendement de cette centrale, sachant que la puissance totale du combustible nucléaire fournie à la centrale est de $2800\;MW.$
 
On a : $r=\dfrac{P_{s}}{P_{e}}$ 
 
avec $P_{s}$ la puissance sortante et $P_{e}$ celle entrante
 
A.N : $r=\dfrac{1000}{2800}=0.357$
 
Donc, $$\boxed{r=0.357}$$

Exercice 7

Pendant un orage, la foudre qui jaillit entre un nuage et le sol, résulte d'un courant moyen de $10\;kA$ circulant sous une tension de $20\;MV$ pendant $0.1\;s.$
 
Calculons a puissance et l'énergie électrique mises en jeu
 
$-\ $ Calcul de la puissance :
 
On a : $P=UI$
 
A.N : $P=20\;10^{6}\times 10\;10^{3}=2\;10^{11}$
 
Donc, $$\boxed{P=2\;10^{11}\;w}$$
 
$-\ $ Calcul de l'énergie
 
On a : $E=P\times t$
 
A.N : $E=2\;10^{11}\times 0.1=2\;10^{10}$
 
Donc, $$\boxed{E=2\;10^{10}\;j}$$

Exercice 9

Une grue soulève une charge de $600\;N$, d'une hauteur de $30\;cm$ en une minute.
 
Déterminons le travail effectué 
 
On a : $W=F\times d$
 
A.N : $W=600\times 30\;10^{-2}=180$
 
Donc, $$\boxed{W=180\;j}$$
 
Déterminons la puissance développée
 
On a : $P=\dfrac{W}{t}$ or $t=1\;mn=60\;s$
 
A.N : $P=\dfrac{180}{60}=3$
 
Donc, $$\boxed{P=3\;W}$$

Exercice 10 

Un train met $1\;h\;30\;mn\;50\;s$ pour relier 2 villes distantes de $209\;km.$ L'intensité de la force de travail de traction de la locomotive sur les wagons est $F=4.41\;10^{4}\;N.$
 
1) Calculons la vitesse moyenne de ce train 
 
$-\ $ en $m/s$ 
 
On a : $V=\dfrac{d}{t}$

Convertissons la distance $d$ en mètre et le temps $t$ en seconde.
 
On a : $d=209\;km=209\;10^{3}\;m\ $ et
 
$\begin{array}{rcl} t&=&1\;h\;30\;mn\;50\;s\\&=&1\times 60\times 60+30\times 60+50\\&=&5450\;s\end{array}$
 
A.N : $V=\dfrac{209\;10^{3}}{5450}=38.348$
 
Donc, $$\boxed{V=38.348\;m/s}$$
 
$-\ $ en $km/h.$ 
 
On a : $V=\dfrac{d}{t}$
 
avec, $d=209\;km\ $ et
 
$\begin{array}{rcl} t&=&1\;h\;30\;mn\;50\;s\\ \\&=&1+\dfrac{30}{60}+\dfrac{50}{3600}\\ \\&=&1.513889\;h\end{array}$
 
A.N : $V=\dfrac{209}{1.513889}=138.055$
 
Donc, $$\boxed{V=138.055\;km/h}$$
 
2) Calculons le travail mécanique effectué par cette force. 
 
On a : $W=F\times d$
 
A.N : $W=4.41\;10^{4}\times 209\;10^{3}=92.169\;10^{8}$
 
Donc, $$\boxed{W=92.169\;10^{8}\;j}$$
 
3) Calculons la puissance mécanique développée en Chevaux.
 
On a : $P=\dfrac{W}{t}$
 
A.N : $P=\dfrac{92.169\;10^{8}}{5450}=1691174.312\;W\ $ or, $\ 1\;kW=1.341\;Ch$
 
Donc, $P=1691174.312\;10^{-3}\times 1.341=2267.8$
 
D'où, $$\boxed{P=2267.8\;Ch}$$
 
Autre méthode 
 
On a : $P=F\times V$
 
A.N : $P=4.41\;10^{4}\times 38.348=1691146.8\;W$ or $1\;kW=1.341\;Ch$
 
Donc, $P=1691146.8\;10^{-3}\times 1.341=2267.8$
 
D'où, $$\boxed{P=2267.8\;Ch}$$

Activités

Sur une ampoule, Momar lit l'information $15W.$
 
Il souhaite déterminer la tension nominale de la lampe. 
 
Pour cela, il réalise un montage potentiométrique permettant de mesurer la tension électrique aux bornes de la lampe et l'intensité du courant qui la traverse.
 
Il obtient les résultats suivants :
$$\begin{array}{|l|c|c|c|} \hline &\text{Mesure }1&\text{Mesure }2&\text{Mesure }3\\ \hline \text{Tension}&6\;V&12\;V&15\;V\\ \hline \text{Intensité}&0.86\;A&1.25A&1.41\;A\\ \hline\text{Puissance électrique reçue}& & &\\ \hline \end{array}$$
1) Réalisons le schéma du montage.

 

 
2) a) Pour chaque série de mesures, calculons la puissance reçue par la lampe. Les résultats sont récapitulés dans le tableau ci-dessous :
$$\begin{array}{|l|c|c|c|} \hline &\text{Mesure }1&\text{Mesure }2&\text{Mesure }3\\ \hline \text{Tension}&6\;V&12\;V&15\;V\\ \hline \text{Intensité}&0.86\;A&1.25A&1.41\;A\\ \hline\text{Puissance électrique reçue}&5.16\;W&15\;W&21.15\;W\\ \hline \end{array}$$
D'après le tableau, la tension nominale de la lampe est égale à $12\;V.$ 
 
En effet, sur l' ampoule, il est inscrit $15\;W.$ Or, parmi toutes les mesures, seule la mesure 2 donne une puissance électrique égale à cette valeur inscrite. Par conséquent, la mesure 2 donne les valeurs (tension et intensité) nominale de la lampe.
 
b) La tension appliquée à la lampe lors de la mesure 1 est égale à $6\;V$, elle est donc inférieure à la tension nominale qui est de $12\;V.$
 
La tension appliquée à la lampe étant à la tension nominale alors, la lampe brillera, mais faiblement.

Exercice 11

Recopions et complétons les phrases suivantes :
 
L'énergie que possède un corps suspendu à une certaine hauteur du sol est appelée énergie potentielle.
 
L'énergie cinétique est la forme d'énergie que possède un système en mouvement.
 
L'énergie mécanique d'un corps est la somme de son énergie potentielle et de son énergie cinétique.
 
Au cour du mouvement de chute d'un objet, son énergie potentielle est convertie en énergie cinétique.
 
Un chargeur de portable convertit l'énergie électrique en énergie chimique.
 
Les photopiles transforment l'énergie lumineux en énergie électrique.
 
Une pile transforme l'énergie chimique en énergie électrique ; un fer à repasser électrique transforme l'énergie électrique en énergie thermique.
 
Le rendement d'un moteur est le rapport de l'énergie utile à l'énergie absorbée.

Exercice 12

Un champion de tennis a réalisé un service en communiquant à une balle de masse $m=55\;g$ une vitesse de $217\;km.h^{-1}$
 
1) Convertissons cette vitesse en $m\cdot s^{-1}$
 
On sait que : $1\;km=10^{3}\;m\ $ et $\ 1\;h=3600\;s$
 
Donc,
 
$\begin{array}{rcl} 217\;km/h&=&\dfrac{217\;km}{1\;h}\\ \\&=&\dfrac{217\cdot10^{3}\;m}{3600\;s} \\ \\&=&\dfrac{217\;m}{3.6\;s}\\ \\&=&\dfrac{60.277\;m}{1\;s}\\ \\&=&60.277\;m.s^{-1}\end{array}$
 
D'où, $$\boxed{v=60.277\;m.s^{-1}}$$
       
2) En déduisons l'énergie cinétique fournie à la balle.
 
L'énergie cinétique fournie à la balle est donnée par la relation :
$$E_{c}=\dfrac{1}{2}\times m\times v^{2}$$
avec, $m=55\;g=55\cdot 10^{-3}\;kg\ $ et $\ v=60.277\;m.s^{-1}$
 
Ainsi : $E_{c}=\dfrac{1}{2}\times 55\cdot 10^{-3}\times(60.277)^{2}=99.916$
 
D'où, $$\boxed{E_{c}=99.916\;J}$$
 

Exercice 13

Une mangue de masse $m=120\;g$ est située sur un arbre à la hauteur $h=3.2\;m$
 
Déterminons l'énergie potentielle de pesanteur de cette mangue
 
Soit : $E_{p}=m\times g\times h\ $ avec, $\ m=120\;g=120\cdot 10^{-3}\;kg$
 
A.N : $E_{p}=120\cdot 10^{-3}\times 9.8\times 3.2=3.76$
 
Donc, $$\boxed{E_{p}=3.76\;J}$$
 

Exercice 14

1) Calculons l'énergie cinétique d'un camion, de masse $30$ tonnes, roulant en ville à $30\;km.h^{-1}$ Soit :
$$E_{c}=\dfrac{1}{2}m\times v^{2}$$
Convertissons la masse $m$ en kilogramme et la vitesse en $m.s^{-1}$
 
On a : $1\text{ tonne}=10^{3}\;kg\ $ donc, $\ m=30\text{ tonne}=30\cdot 10^{3}\;kg$
 
aussi, $1\;km.h^{-1}=\dfrac{1000\;m}{3600\;s}=0.277\;m.s^{-1}\ $ donc, $\ 30\;km.h^{-1}=30\times 0.277\;m.s^{-1}=8.31\;m.s^{-1}$
 
avec, $m=30\text{ tonne}=30\cdot 10^{3}\;kg$
 
Ainsi : $E_{c}=\dfrac{30\cdot 10^{3}\times(8.31)^{2}}{2}=1035841.5$
 
D'où, $$\boxed{E_{c}=1035841.5\;J}$$
 
2) Déterminons la vitesse avec laquelle une voiture de masse $1300\;kg$ devrait rouler pour avoir la même énergie cinétique
 
Comme $E_{c}=\dfrac{1}{2}m\times v^{2}\ $ alors, $m\times v^{2}=2\times E_{c}$
 
Ce qui donne : $v^{2}=\dfrac{2\times E_{c}}{m}$
 
Par suite, $v=\sqrt{\dfrac{2\times E_{c}}{m}}$
 
A.N : $v=\sqrt{\dfrac{2\times 1035841.5}{1300}}=39.92$
 
D'où, $$\boxed{v=39.92\;m.s^{-1}}$$

Exercice 15

Un conducteur ohmique de résistance $R=100\;\Omega$ est traversé par un courant d'intensité
 
$I=25\;mA$ pendant une durée $t=5\text{ minutes.}$
 
1) L'effet Joule est la caractéristique d'un conducteur à dégagé de la chaleur par passage du courant électrique.
 
2) Calculons la puissance Joule pour ce conducteur ohmique. 
 
Soit : $P=U\times I\ $ or, d'après la loi d'Ohm, $U=R\times I$
 
Donc, en remplaçant $U$ par $R\times I$, on obtient :
$$P=R\times I^{2}$$
A.N : $P=100\times (25\cdot10^{-3})^{2}=0.0625$
 
D'où, $$\boxed{P=0.0625\;W}$$
 
3) Calculons l'énergie dissipée par effet Joule pour ce conducteur ohmique en joules et en $kWh.$
 
$-\ $ énergie en joule
 
On a : $E=U\times I\times t\ $ or, $\ U\times I=P$
 
Donc, $E=P\times t\ $ avec, $\ t=5\;mn=5\times 60\;s=300\;s$
 
A.N : $E=0.0625\times 300=18.75$
 
Ainsi, $$\boxed{E=18.75\;J}$$
 
$-\ $ énergie en $kWh$ :
 
On a : $1\;kWh=10^{3}\;Wh\ $ et $\ 1\;Wh=3600\;J$
 
alors,
 
$\begin{array}{rcl} 1\;kWh&=&10^{3}\;Wh\\ \\&=&3600\;10^{3}\;J\\ \\&=&3.6\;10^{6}\;J\end{array}$
           
A.N : $E=\dfrac{18.75}{3.6\;10^{6}}=5.208\;10^{-6}$
 
D'où, $$\boxed{E=5.208\;10^{-6}\;kWh}$$

Exercice 16

Un appartement possède les équipements suivants : 
 
7 lampes de $9\;W$, 4 ventilateurs de $75\;W$, un réfrigérateur de $120\;W$, un téléviseur de $200\;W$ et un fer à repasser de $1.2\;kW$
 
1) Déterminons la puissance électrique totale de cet appartement si tous les appareils fonctionnent. Soit :
$$P_{\text{Totale}}=P_{\text{lampes}}+P_{\text{ventil}}+P_{\text{réfrig}}+P_{\text{télé}}+P_{\text{fer}}$$
Ainsi,
 
$\begin{array}{rcl} P_{\text{Totale}}&=&7\times 9+4\times 75+120+200+1.2\;10^{3}\\&=&63+300+120+200+1200\\&=&1883\end{array}$
 
D'où, $$\boxed{P_{\text{Totale}}=1883\;W}$$
 
2) Le tableau suivant donne le temps moyen de fonctionnement de chaque appareil.
$$\begin{array}{|l|c|c|c|c|c|}\hline\text{Appareils}&\text{Lampe}&\text{réfrigérateur}&\text{Téléviseur}&\text{Fer à repasser}&\text{Ventilateur}\\ \hline\text{temps}&4\,h&18\,h&8\,h\ 30\,min&15\,min&6\,h\\ \hline\end{array}$$
 
Calculons, en kilowattheure, l'énergie électrique consommée en $60$ jours.
 
On sait que l'énergie consommée est donnée par : $E=P\times t$
 
Calculons l'énergie consommée par chaque appareil en 60 jours :
 
$-\ $ Lampes
 
Une lampe fonctionne en moyenne $4\,h$ par jour pour une puissance de $9\;W=9.10^{-3}\;kW$
 
Donc, l'énergie consommée par les 7 lampes pour une durée de 60 jours est donnée par :
 
$E_{\text{lampes}}=7\times 9.10^{-3}\times 4\times 60=15.2$
 
Ainsi, $E_{\text{lampes}}=15.2\;kWh$
 
$-\ $ Réfrigérateur
 
Le réfrigérateur, avec une puissance de $120\;W=120.10^{-3}\;kW$, fonctionne en moyenne $18\,h$ par jour. 
 
Donc, pour 60 jours, on a :
 
$E_{\text{réfrig}}=120.10^{-3}\times 18\times 60=129.6\;kWh$
 
D'où, $E_{\text{réfrig}}=129.6\;kWh$
 
$-\ $ Téléviseur
 
Le téléviseur, avec une puissance de $200\;W=200.10^{-3}\;kW$, fonctionne en moyenne $8\,h\ 30\,mn$ par jour ; soit : $8\,h+\dfrac{1}{2}\,h=8\,h+0.5\,h=8.5\,h$
 
Par suite, la consommation en 60 jours est donnée par :
 
$E_{\text{télé}}=200.10^{-3}\times 8.5\times 60=102$
 
Ainsi, $E_{\text{télé}}=102\;kWh$
 
$-\ $ Fer à repasser
 
Le fer à repasser fonctionne en moyenne $15\,mn$ par jour, soit : $\dfrac{1}{4}\,h=0.25\,h$
 
Donc, $E_{\text{fer}}=1.2\times 0.25\times 60=18$
 
Ainsi, $E_{\text{fer}}=18\;kWh$
 
$-\ $ ventilateurs
 
Un ventilateur, avec une puissance de $75\;W=75.10^{-3}\;kW$, fonctionne en moyenne $6\,h$ par jour.
 
Donc, l'énergie consommée par les 4 ventilateurs pour une durée de 60 jours est donnée par :
 
$E_{\text{ventil}}=4\times 75.10^{-3}\times 6\times 60=108$
 
Ce qui donne, $E_{\text{ventil}}=108\;kWh$
 
Ainsi, l'énergie électrique totale consommée en $60$ jours est donnée par :
$$E_{\text{Totale}}=E_{\text{lampes}}+E_{\text{réfrig}}+E_{\text{télé}}+E_{\text{fer}}+E_{\text{ventil}}$$
A.N : $E_{\text{Totale}}=15.2+129.6+102+18+108=372.8$
 
D'où, $$\boxed{E_{\text{Totale}}=372.8\;kWh}$$
 
3) Calculons le prix à payer pour une consommation bimensuelle.
 
La consommation bimensuelle est une consommation de deux mois ; soit 60 jours.
 
Comme la $\text{SENELEC}$ vend en moyenne le $kWh\ $ à $\ 113\text{ F}$ alors, le prix à payer pour une consommation de 60 jours sera donné par :
$$\text{Prix}=113\times E_{\text{Totale}}$$
 
A.N : $\text{Prix}=113\times 372.8=42126.4$
 
D'où, $$\boxed{\text{Prix}=42126.4\text{ F}}$$
 
4) Chaque appareil transforme de l'énergie électrique en d'autres formes d'énergies. 
 
Donnons ces autres formes d'énergies pour la lampe, le fer à repasser et le ventilateur.
 
$-\ $ Pour la lampe ; l'énergie électrique est transformée en énergie lumineux.
 
$-\ $ Pour le fer à repasser ; l'énergie électrique est transformée en énergie thermique.
 
$-\ $ Pour le ventilateur ; l'énergie électrique est transformée en énergie cinétique.
 

 

Auteur: 
Aliou ndiaye

Solution des exercices : Association de conducteurs ohmiques 3e

Classe: 
Troisième
 

Exercice 1 

Complétons le tableau
 
$$\begin{array}{|c|c|c|c|}\hline R_{1}&R_{2}&R_{e}&\text{Types} \\(\text{en }\Omega)&(\text{en }\Omega)&(\text{en }\Omega)&\text{d'association} \\ \hline 680&820&1500&\text{Série} \\ \hline 39.53&68&25&\text{Parallèle} \\ \hline 470&33&503&\text{Série} \\ \hline 51&46&24.985&\text{Parallèle} \\ \hline 56&56&28&\text{Parallèle} \\ \hline\end{array}$$

Exercice 2

Nous disposons de deux lots de résistances $R_{1}\ $ et $\ R_{2}$ telles que $R_{1}=33\;\Omega\ $ et $\ R_{2}=47\;\Omega.$ Indiquons, en précisant le type d'association, le nombre de résistances de chaque que nous utilisons :
 
1) Pour avoir une résistance équivalente $R_{AB}$ de $100\;\Omega$, nous allons utiliser le type d'association ci-dessous
 
 
2) Pour avoir une résistance équivalente $R_{AB}$ de $113\;\Omega$, nous pouvons utiliser le type d'association ci-dessous 
 
 
3) Pour avoir une résistance équivalente $R_{AB}$ de $130\;\Omega$, nous allons utiliser le type d'association ci-dessous
 

Exercice 3 

1) $R_{1}=22\;\Omega$ et $R_{2}=33\;\Omega$ montées en série, trouvons la résistance équivalente
 
On a : $R_{e}=R_{1}+R_{2}$
 
A.N : $R_{e}=22+33=55$
 
Donc, $$\boxed{R_{e}=55\;\Omega}$$
2) $R_{1}=22\;\Omega$ et $R_{2}=33\;\Omega$ montées en parallèle, trouvons alors la résistance équivalente
 
On a : $\dfrac{1}{R_{e}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}$
 
Donc, $\dfrac{1}{R_{e}}=\dfrac{R_{2}+R_{1}}{R_{1}.R_{2}}$
 
D'où, $R_{e}=\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}$
 
A.N : $R_{e}=\dfrac{22\times 33}{22+33}=13.2$
 
Ainsi, $$\boxed{R_{e}=13.2\;\Omega}$$

Exercice 4 

Pour que la résistance du groupement obtenu soit de $11\;\Omega$ il faudra associer les conducteurs en parallèle. Plus précisément, si on met trois conducteurs identiques de résistance $33\;\Omega$ en parallèle on obtient une résistance équivalente de $11\;\Omega.$
 
En effet, on a : $\dfrac{1}{R_{e}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}$
 
Or, $R_{1}=R_{2}=R_{3}=33\;\Omega$
 
Donc, $\dfrac{1}{R_{e}}=\dfrac{1}{33}+\dfrac{1}{33}+\dfrac{1}{33}=\dfrac{3}{33}=\dfrac{1}{11}$
 
D'où, $R_{e}=11\;\Omega$

Exercice 5 

1) Calculons la résistance $R_{2}$ du fil chauffant de cette lampe.
 
On a : $U=R_{2}I\ \Rightarrow\ R_{2}=\dfrac{U}{I}$
 
A.N : $R_{2}=\dfrac{4.5}{0.2}=22.5$
 
Donc, $$\boxed{R_{2}=22.5\;\Omega}$$
2) Trouvons la résistance équivalente à cette association.
 
On a : $\dfrac{1}{R_{e}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}$
 
Donc, $\dfrac{1}{R_{e}}=\dfrac{R_{2}+R_{1}}{R_{1}.R_{2}}$
 
D'où, $R_{e}=\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}$
 
A.N : $R_{e}=\dfrac{22.5\times 27}{22.5+27}=12.27$
 
Ainsi, $$\boxed{R_{e}=12.27\;\Omega}$$

Exercice 6 

Soit le dipôle $AB$ constitué de conducteurs groupés comme indiqué dans le schéma suivant.
Trouvons la résistance équivalente du dipôle $AB$ ainsi obtenu sachant que
$$R_{1}=10\;\Omega\;;\  R_{2}=20\;\Omega\;;\ R_{3}=6\;\Omega\text{ et }R_{4}=9\;\Omega$$

 
$R_{2}$ et $R_{3}$ sont montées en série donc soit $R'$ leur résistance équivalente.
 
On a : $R'=R_{2}+R_{3}$

 

 
Le groupement $(R_{2}\;,\ R_{3})$ ou encore $R'$ étant monté en parallèle avec $R_{4}$ alors, en considérant $R''$ comme la résistance équivalente, on aura :
 
$\dfrac{1}{R''}=\dfrac{1}{R'}+\dfrac{1}{R_{4}}$
 
Donc, $\dfrac{1}{R''}=\dfrac{R_{4}+R'}{R'.R_{4}}$
 
D'où, $R''=\dfrac{(R_{2}+R_{3}).R_{4}}{(R_{2}+R_{3})+R_{4}}$

 

 
Enfin, le groupement $(R_{2}\;,\ R_{3}\;,\ R_{4})$ ou encore $R''$ étant monté en série avec $R_{1}$ alors, la résistance équivalente du dipôle $AB$ sera donnée par :
$$R_{AB}=R_{1}+R''$$
Or, $R''=\dfrac{(R_{2}+R_{3}).R_{4}}{(R_{2}+R_{3})+R_{4}}$
 
Donc, $R_{AB}=R_{1}+\dfrac{(R_{2}+R_{3}).R_{4}}{(R_{2}+R_{3})+R_{4}}=R_{1}+\dfrac{R_{4}(R_{2}+R_{3})}{R_{2}+R_{3}+R_{4}}$

 

 
Par suite,
$$R_{AB}=R_{1}+\dfrac{R_{4}(R_{2}+R_{3})}{R_{2}+R_{3}+R_{4}}$$
A.N : $R_{AB}=10+\dfrac{9(20+6)}{20+6+9}=16.685$
 
D'où, $$\boxed{R_{AB}=16.685\;\Omega}$$

Exercice 7

Des résistors de résistances respectives $R_{1}=12\;\Omega\;;\ R_{2}=R_{4}=6\;\Omega\ $ et $\ R_{3}=3\;\Omega$ sont groupés entre $A\ $ et $\ B$ comme indiqué par le schéma.
 

 
1) Trouvons la résistance du dipôle $AB$ ainsi constitué.
 
La configuration du dipôle $AB$ permet de constater que :
 
$-\ \ R_{_{1}}\ $ et $\ R_{_{2}}$ sont montées en parallèle
 
$-\ \ R_{_{3}}\ $ et $\ R_{_{4}}$ sont montées en parallèle
 
$-\ $ Les groupements $(R_{_{1}}\;,\ R_{_{2}})\ $ et $\ (R_{_{3}}\;,\ R_{_{4}})$ sont montés en série
 
Soient $R_{_{eA}}$ la résistance équivalente du groupement $(R_{_{1}}\;,\ R_{_{2}})\ $ et $\ R_{_{eB}}$ la résistance équivalente à l'association des résistances $R_{_{3}}\ $ et $\ R_{_{4}}$
 
On a alors : $\dfrac{1}{R_{_{eA}}}=\dfrac{1}{R_{_{1}}}+\dfrac{1}{R_{_{2}}}=\dfrac{R_{_{2}}+R_{_{1}}}{R_{_{1}}.R_{_{2}}}$
 
Donc, $R_{_{eA}}=\dfrac{R_{_{1}}.R_{_{2}}}{R_{_{1}}+R_{_{2}}}$
 
A.N : $R_{_{eA}}=\dfrac{12\times 6}{12+6}=\dfrac{72}{18}=4\;\Omega$
 
De la même manière : $\dfrac{1}{R_{_{eB}}}=\dfrac{1}{R_{_{3}}}+\dfrac{1}{R_{_{4}}}=\dfrac{R_{_{4}}+R_{_{3}}}{R_{_{3}}.R_{_{4}}}$
 
Donc, $R_{_{eB}}=\dfrac{R_{_{3}}.R_{_{4}}}{R_{_{3}}+R_{_{4}}}$
 
A.N : $R_{_{eB}}=\dfrac{3\times 6}{3+6}=\dfrac{18}{9}=2\;\Omega$
 
On obtient alors le schéma suivant :
 
 
Soit $R_{_{e}}$ la résistance du dipôle $AB$
 
Comme $R_{_{eA}}\ $ et $\ R_{_{eB}}$ sont montées en série alors,
$$R_{_{e}}=R_{_{eA}}+R_{_{eB}}$$
 
A.N : $R_{_{e}}=4+2=6$
 
Ainsi,$$\boxed{R_{_{e}}=6\;\Omega}$$
 
2) A ce dipôle, on applique une tension de $6\;V$, déterminons l'intensité du courant débité par le générateur dans chacun des cas suivants.
 
a) Les interrupteurs $K_{1}\ $ et $\ K_{2}$ fermés.
 
Le circuit équivalent se présente comme suit :
 
 
D'après la loi d'Ohm, on a : $U_{_{AB}}=R_{_{e}}.I$
 
Donc, $I=\dfrac{U_{_{AB}}}{R_{_{e}}}$
 
A.N : $I=\dfrac{6}{6}=1$
 
D'où, $$\boxed{I=1\;A}$$
 
b) L'interrupteur $K_{1}$ fermé et l'interrupteur $K_{2}$ ouvert.
 
Donc, aucun courant ne traverse $R_{_{4}}$ et le circuit devient :
 
 
On constate que le groupement $(R_{_{1}}\;,\ R_{_{2}})$ est en série avec $R_{_{3}}$
 
Donc, d'après la loi d'Ohm : $U_{_{AB}}=(R_{_{eA}}+R_{_{3}}).I$
 
Par suite, $I=\dfrac{U_{_{AB}}}{R_{_{eA}}+R_{_{3}}}$
 
A.N : $I=\dfrac{6}{4+3}=\dfrac{6}{7}=0.857$
 
D'où, $$\boxed{I=0.857\;A}$$
 
c) l'interrupteur $K_{1}$ ouvert et L'interrupteur $K_{2}$ fermé
 
Donc, aucun courant ne traverse $R_{_{2}}$ et le circuit se présente comme suit :
 
 
Ainsi, le groupement $(R_{_{3}}\;,\ R_{_{4}})$ est en série avec $R_{_{1}}$
 
Alors, d'après la loi d'Ohm on a : $U_{_{AB}}=(R_{_{eB}}+R_{_{1}}).I$
 
Donc, $I=\dfrac{U_{_{AB}}}{R_{_{eB}}+R_{_{1}}}$
 
A.N : $I=\dfrac{6}{2+12}=\dfrac{6}{14}=0.428$
 
D'où, $$\boxed{I=0.428\;A}$$
 
d) Les interrupteurs $K_{1}\ $ et $\ K_{2}$ ouverts.
 
Aucun courant ne traverse $R_{_{2}}\ $ et $\ R_{_{4}}.$ On obtient alors le circuit suivant :
 
 
Ainsi, $R_{_{1}}\ $ et $\ R_{_{3}}$ sont en série.
 
Par suite, d'après la loi d'Ohm : $U_{_{AB}}=(R_{_{1}}+R_{_{3}}).I$
 
D'où, $I=\dfrac{U_{_{AB}}}{R_{_{1}}+R_{_{3}}}$
 
A.N : $I=\dfrac{6}{12+3}=\dfrac{6}{15}=0.4$
 
D'où, $$\boxed{I=0.4\;A}$$
 
3) Calculons les intensités $I_{_{1}}\;;\ I_{_{2}}\;;\ I_{_{3}}\ $ et $\ I_{_{4}}$ pour $K_{1}\ $ et $\ K_{2}$ fermés.
 
Lorsqu'on ferme $K_{1}\ $ et $\ K_{2}$, on obtient les relations suivantes sur les tensions :
$$U_{_{R_{1}}}=U_{_{R_{2}}}=U_{_{eA}}$$
$$U_{_{R_{3}}}=U_{_{R_{4}}}=U_{_{eB}}$$
 
Comme $U_{_{R_{1}}}=R_{_{1}}.I_{_{1}}\ $ et $\ U_{_{eA}}=R_{_{eA}}.I$ alors, $R_{_{1}}.I_{_{1}}=R_{_{eA}}.I$
 
Ce qui donne : $I_{_{1}}=\dfrac{R_{_{eA}}.I}{R_{_{1}}}$
 
A.N : $I_{_{1}}=\dfrac{4\times 1}{12}=\dfrac{4}{12}=0.333$
 
Donc, $$\boxed{I_{_{1}}=0.333\;A}$$
 
Pour déterminer $I_{_{2}}$, on applique la loi des nœuds :
$$I=I_{_{1}}+I_{_{2}}$$
Par suite, $I_{_{2}}=I-I_{_{1}}$
 
A.N : $I_{_{2}}=1-0.333=0.667$
 
Ainsi, $$\boxed{I_{_{2}}=0.667\;A}$$
 
De la même manière, d'après la loi d'Ohm, on a :
$$U_{_{R_{3}}}=R_{_{3}}.I_{_{3}}\ \text{ et }\ U_{_{eB}}=R_{_{eB}}.I$$
Ainsi, $R_{_{3}}.I_{_{3}}=R_{_{eB}}.I$
 
Par suite, $I_{_{3}}=\dfrac{R_{_{eB}}.I}{R_{_{3}}}$
 
A.N : $I_{_{3}}=\dfrac{2\times 1}{3}=\dfrac{2}{3}=0.667$
 
D'où, $$\boxed{I_{_{3}}=0.667\;A}$$
 
D'après la loi des nœuds, on a :
$$I=I_{_{3}}+I_{_{4}}$$
Ce qui donne : $I_{_{4}}=I-I_{_{3}}$
 
A.N : $I_{_{4}}=1-0.667=0.333$
 
Donc, $$\boxed{I_{_{4}}=0.333\;A}$$

Exercice 8 


 
 
 

Auteur: 
Aliou ndiaye

Solution des exercices : La loi d'Ohm 3e

Classe: 
Troisième
 

Exercice 1 

1) Trouvons la résistance du fil chauffant.
 
On a : $P=R\times I^{2}\ \Rightarrow\ R=\dfrac{P}{I^{2}}$
 
A.N : $R=\dfrac{500}{4^{2}}=31.25$

Donc, $$\boxed{R=31.25\;\Omega}$$
2) Calculons la tension à ses bornes.
 
On a : $U=R\times I$
 
A.N : $U=31.25\times 4=125$

Donc, $$\boxed{U=125\;V}$$

Exercice 2 

1) Calcul de la tension
 
On a : $U=R\times I$
 
A.N : $U=47\times 0.12=5.64$

Donc, $$\boxed{U=5.64\;V}$$
2) Calculons l'intensité du courant qui traverse le conducteur, sachant que la tension à ses bornes a été doublée.
 
Soit : $U'=R.I'$
 
Or, $\ U'=2U$ donc en remplaçant $U'$ par $2U$, on obtient : $2U=R.I'$
 
Par suite, $\dfrac{2U}{R}=I'$
 
Comme $\dfrac{U}{R}=I$ alors,
$$I'=2I$$
A.N : $I'=2\times 0.12=0.24$

Donc, $$\boxed{I'=0.24\;A}$$

Exercice 3 

1) Trouvons la valeur de la résistance.
 
On a : $U=R\times I\ \Rightarrow\ R=\dfrac{U}{I}$
 
A.N : $R=\dfrac{6}{160\;10^{-3}}=37.5$

Donc, $$\boxed{R=37.5\;\Omega}$$
2) La puissance électrique consommée est de :
 
$P=R\times I^{2}$
 
A.N : $P=37.5\times(160\;10^{-3})^{2}=0.96$
 
Donc, $$\boxed{P=0.96\;W}$$

Exercice 4 

1) Signification de ces indications :
 
$6\;V$ : la tension électrique 
 
$1\;W$ : la puissance électrique
 
2) Calculons l'intensité du courant qui traverse la lampe quand elle fonctionne normalement.
 
On a : $P=R.I^{2}=R\times I\times I$
 
Or, $\ R.I=U$ donc, $P=U.I$
 
Ce qui donne : $I=\dfrac{P}{U}$
 
A.N : $I=\dfrac{1}{6}=0.166$
 
Donc, $$\boxed{I=0.166\;A}$$
3) Calculons la valeur de la résistance.
 
On a : $R=\dfrac{U}{I}$
 
A.N : $R=\dfrac{6}{0.166}=36.14$
 
Donc, $$\boxed{R=36.14\;\Omega}$$
 
4) $R\text{ (à chaud) }=36.14\;\Omega\;,\ R\text{ (à froid) }=8\;\Omega.$
 
La résistance augmente avec la température.

Exercice 5 Caractéristique d'un conducteur ohmique 

1) Caractéristique intensité - tension de ce conducteur.

 
 
$\begin{array}{rcl}\text{Echelle }\ :\ 1\;cm&\longrightarrow&100\;mA \\ 1\;cm&\longrightarrow&5\;V\end{array}$
 
2) Déduisons de cette courbe la valeur de la résistance du conducteur.
 
La courbe représentative est une application linéaire $(U=RI)$ de coefficient linéaire $R.$
 
Soit $B$ et $D$ deux points de cette droite.
 
Alors, on a : 
 
$R=\dfrac{y_{D}-y_{B}}{x_{D}-x_{B}}=\dfrac{3-1.6}{4.53-2.43}=\dfrac{1.4}{2.1}=066$
 
Donc, $$\boxed{R=0.66\;\Omega}$$

Exercice 6 

 

 
 
1) D'après les montages ci-dessus, l'ampèremètre $A_{1}$ donne le même indicateur $(320\;mA)$ que l'ampèremètre $A_{2}$ car le circuit est en série. 
 
2) Donnons la valeur de la résistance $R$ si la tension de la pile vaut $6\;V$.
 
On a : $U=R\times I\ \Rightarrow\ R=\dfrac{U}{I}$
 
A.N : $R=\dfrac{6}{320\;10^{-3}}=18.75$
 
Donc, $$\boxed{R=18.75\;\Omega}$$

Exercice 7 

$\begin{array}{rcl}\text{Echelle }\ :\ 1\;cm&\longrightarrow&0.1\;A \\ 1\;cm&\longrightarrow&1\;V\end{array}$
 
1) D'après le graphique ci-dessus, nous constatons que les représentations $C_{1}$ et $C_{2}$ sont des droites et donc des applications linéaires de coefficient linéaire respectif $R_{1}$ et $R_{2}.$
 
Or, nous remarquons que $C_{1}$ est au dessus de $C_{2}$, donc cela signifie que coefficient linéaire de $C_{1}$ est supérieur au coefficient linéaire $C_{2}.$
 
Ainsi, on a : $R_{1}>R_{2}$
 
2) Donnons la valeur de la résistance $R_{1}$
 
La représentation de $C_{1}$ étant une droite de coefficient linéaire respectif $R_{1}$, alors en prenant deux points $A$ et $B$ de cette droite on obtient :
 
$R_{1}=\dfrac{y_{B}-y_{A}}{x_{B}-x_{A}}=\dfrac{5-4}{0.1-0.08}=\dfrac{1}{0.02}=50$
 
D'où $$\boxed{R_{1}=50\;\Omega}$$

Exercice 8 

Indiquons la valeur manquante dans chacun des cas suivants
 
$R_{1}=\dfrac{3.5}{0.5}=7\;\Omega$

 

 
 
$I_{2}=\dfrac{9}{56}=0.16\;A$

 

 
 
$U_{3}=18\times 0.5=9\;V$

 

 

Exercice 9 Loi d'Ohm

1) Énonçons la loi d'Ohm : La tension $U$ aux bornes d'un conducteur Ohmique est égale au produit de sa résistance $R$ par l'intensité $I$ du courant qui le traverse.
 
2) La relation entre $U\;,\ I\ $ et $\ R$ est donnée par : en précisant les unités :
$$U=R\times I$$
avec $U$ en volt $(V)\;,\ R$ en Ohm $(\Omega)$ et $I$ en ampère $(A)$
 
3) Considérons les graphes ci-dessous :

 

 
On sait que la relation entre $U\;,\ I\ $ et $\ R$, donnée par $U=R\times I$, traduit une relation linéaire qui peut être représentée par une droite passant par l'origine du repère.
 
Donc, c'est le graphe $n^{\circ}4$ qui correspond à la relation entre $U\;,\ I\ $ et $\ R$ dans le cas d'un conducteur ohmique.

Exercice 10

On considère le schéma du montage suivant appelé pont diviseur de tension.

 

 
$U_{e}$ mesurée par le voltmètre $V$ est appelée tension d'entrée et $U_{s}$ mesurée par $V_{1}$ tension de sortie.
 
1) Montrons que $\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}}{(R_{1}+R_{2})}$
 
Soit : $U_{1}$ la tension aux bornes de $R_{1}$ et $U_{2}$ celle aux bornes de $R_{2}.$
 
$R_{1}\ $ et $\ R_{2}$ sont montées en série or, la tension aux bornes d'un groupement en série est égale à la somme des tensions.
 
Donc, $U_{e}=U_{1}+U_{2}\ $ avec : $U_{1}=R_{1}.I\ $ et $\ U_{2}=R_{2}I$ d'après la loi d'Ohm.
 
Par suite, $U_{e}=R_{1}.I+R_{2}.I=(R_{1}+R_{2})I$
 
De plus, $V_{1}$ mesure en même temps la tension de sortie $(U_{s})$ et la tension aux bornes de $R_{1}.$
 
Donc, $U_{s}=U_{1}=R_{1}.I$
 
Ainsi, $\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}.I}{(R_{1}+R_{2})I}$
 
D'où, $\boxed{\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}}{(R_{1}+R_{2})}}$
 
2) Calculons la tension $(U_{s})$ à la sortie entre les points $M\ $ et $\ N$
 
On sait que : $\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}}{(R_{1}+R_{2})}$
 
Ce qui donne alors : $U_{s}=\dfrac{R_{1}\times U_{e}}{(R_{1}+R_{2})}$
 
avec $R_{1}=60\;\Omega\;;\ R_{2}=180\;\Omega\ $ et $\ U_{e}=12\;V$
 
A.N : $U_{s}=\dfrac{60\times 12}{(60+180)}=3$
 
D'où, $$\boxed{U_{s}=3\;V}$$
 
3) Rôle d'un pont diviseur de tension :
 
Le pont diviseur de tension est un montage électronique simple permettant de diviser une tension d'entrée afin de créer une tension qui soit proportionnelle à cette tension d'entrée.

Exercice 11

On monte en série un générateur fournissant une tension constante $U=6.4\;V$, un résistor de résistance $R=10\;\Omega$ et une lampe $L.$
 
L'intensité du courant $I=0.25\;A$

 

 
1) Calculons la tension $U_{1}$ entre les bornes du résistor $R.$
 
D'après la loi d'Ohm, on a : $U_{1}=R.I$
 
A.N : $U_{1}=10\times 0.25=2.5$
 
D'où, $$\boxed{U_{1}=2.5\;V}$$
 
2) Calculons la tension $U_{2}$ entre les bornes de la lampe.
 
Le résistor et la lampe étant montés en série alors, la tension aux bornes de l'ensemble est égale à la somme des tensions.
 
Donc, $U=U_{1}+U_{2}$
 
Par suite, $U_{2}=U-U_{1}$
 
A.N : $U_{2}=6.4-2.5=3.9$
 
Ainsi, $$\boxed{U_{2}=3.9\;V}$$
 
3) On place un fil de connexion en dérivation aux bornes de la lampe.

 

 
Lorsqu'on place un fil de connexion de résistance nulle en dérivation aux bornes de la lampe alors, le courant passe par le chemin le plus facile à franchir ; le fil.
 
Par conséquent, aucun courant ne passe par la lampe.
 
D'où : $U_{2}=0\;V$ 
 
4) Comme aucun courant ne traverse la lampe alors, $I_{_{L}}=0\;A$ et donc, la lampe ne brille pas.
 
5) Calculons l'intensité du courant qui traverse la résistance.
 
Le fil de connexion étant placé en dérivation aux bornes de la lampe alors, d'après la loi des nœuds, on a :
$$I_{_{L}}+I_{_{\text{fil}}}=I_{_{R}}$$
Or, $I_{_{L}}=0\ $ et $\ I_{_{\text{fil}}}=I$
 
Donc, $I_{_{R}}=I_{_{\text{fil}}}=I$
 
D'où, $$\boxed{I_{R}=0.25\;A}$$
 
 

Auteur: 
Aliou ndiaye

Solution des exercices : Le courant électrique 3e

Classe: 
Troisième
 

Exercice 1 

 

Exercice 2 

1) Trouvons la quantité d'électricité ainsi transportée.
 
On a : $I=\dfrac{q}{t}\ \Rightarrow\ q=I\times t\ $ avec, $t=2\;h=2\times 60\times 60=7\,200\;s$
 
A.N : $q=1\;10^{-3}\times 7\,200=7.2$
 
Donc $$\boxed{q=7.2\;C}$$
 
2) Calculons le nombre d'électrons correspondant.
 
On a : $q=n.e\ \Rightarrow\ n=\dfrac{q}{e}$
 
A.N : $n=\dfrac{7.2}{1.6\;10^{-19}}=4.5\;10^{19}$
 
Donc $$\boxed{n=4.5\;10^{19}}$$

Exercice 3 

1) Calculons en ampère-heure $(Ah)$, la quantité d'électricité en mouvement.
 
On a : $q=I\times t\ $ avec, $\ I=3\;mA=3\;10^{-3}\;A\ $ et $\ t=1\;h$
 
A.N : $q=3\;10^{-3}\times 1=3\;10^{-3}$
 
Donc $$\boxed{q=3\;10^{-3}\;Ah}$$
 
2) Calculons le nombres de charges électriques en circulation pendant une minute.
 
On a : $q(Amn)=\dfrac{q(Ah)}{60}$
 
A.N : $q(Amn)=\dfrac{3\;10^{-3}}{60}=5\;10^{-5}\;Amn$
 
Or, $q=n.e\ \Rightarrow\ n=\dfrac{q}{e}$
 
A.N : $n=\dfrac{5\;10^{-5}}{1.6\;10^{-19}}=3.125\;10^{14}$
 
Donc $$\boxed{n=3.125\;10^{14}}$$
Leur nature : ce sont des électrons.

Exercice 4 

1) Trouvons le nombre d'électrons qui traversent ce circuit pendant ce temps.
 
On a : $q=n.e\ \Rightarrow\ n=\dfrac{q}{e}$
 
A.N : $n=\dfrac{30}{1.6\;10^{-19}}=1.875\;10^{20}$
 
Donc $$\boxed{n=1.875\;10^{20}}$$
 
2) L'intensité du courant électrique dans ce circuit est donnée par
 
$I=\dfrac{q}{t}$
 
A.N : $I=\dfrac{30}{60}=0.5$
 
Donc $$\boxed{I=0.5\;A}$$

Exercice 5

1) Donnons la nature du courant électrique dans chacun des cas suivants :
 
$-\ $ Dans un conducteur métallique, le courant est produit par un déplacement d'électrons.
 
$-\ $ Dans un électrolyte, le courant est dû à un déplacement d'ions.
 
2) Reproduisons le schéma et représentons le sens du courant électrique par des flèches rouges entre les dipôles et dans l'électrolyseur ; indiquons sur chaque ion par une flèche en bleu le sens de déplacement des porteurs de charge positive et en vert le sens de déplacement des porteurs de charge négative.

 

 
 

Exercice 6

Dans le circuit ci-dessous, toutes les lampes sont identiques.

 

 
Le rhéostat permet de maintenir constante l'intensité délivrée par le générateur $I=300\;mA$ pour chaque expérience.
 
1) Indiquons le sens du courant dans chaque branche

 

 
2) Dans ce circuit, il y a quatre nœuds : $M\;;\ N\;;\ O\;;\ P$
 
Énonçons la loi des nœuds : l'intensité des courants qui arrivent à un nœud est toujours égale à celle des courants qui en partent.
 
3) Pour chacun des cas suivants, indiquons les valeurs affichées par les ampèremètres $A\;,\ A_{1}\ $ et $\ A_{2}.$
 
Premier cas : on ferme l'interrupteur $K_{1}$ seul. Alors, la branche $NK_{2}O$ ne marche plus. Donc, $I_{2}=0$
 
Par suite, l'ampèremètre $A_{2}$ affiche $0\;mA$
 
$I=300\;mA$ donc, l'ampèremètre $A$ affiche $300\;mA$
 
$-\ $ Au niveau du nœud $P$, on a : $I=I_{3}+I_{4}$
 
$-\ $ Au niveau du nœud $O$, on a : $I_{4}=I_{1}+I_{2}$
 
Or, $I_{2}=0\ $ donc, $I_{4}=I_{1}$
 
De plus les lampes sont toutes identiques.
 
Ainsi, $I_{3}=I_{1}$ et par suite, $I_{1}=\dfrac{I}{2}=\dfrac{300}{2}=150$
 
Donc, $I_{1}=150\;mA$
 
D'où, l'ampèremètre $A_{1}$ affiche $150\;mA$
 
Deuxième cas : on ferme $K_{2}$ seul.
 
On procède comme dans le premier cas, on obtient alors :
 
$A_{1}$ affiche $0\;mA$
 
$A$ affiche $300\;mA$
 
$A_{2}$ affiche $150\;mA$
 
Troisième cas : on ferme $K_{1}$ et $K_{2}.$
 
Toutes les lampes étant identiques donc, on obtient la même intensité au niveau de chaque lampe.
 
Cette intensité est donc égale à $\dfrac{I}{3}=\dfrac{300}{3}=100\;mA$
 
Ainsi, les ampèremètre $A_{1}\ $ et $\ A_{2}$ affichent $100\;mA$
 
l'ampèremètre $A$ étant traversé par $I=300\;mA$ donc, il affiche $300\;mA$

Exercice 7

Une quantité d'électricité $Q=1800\;C$ traverse un circuit pendant une durée $t=3\;\text{minutes}.$
 
1) Trouvons la valeur de l'intensité $I$
 
On sait que la quantité d'électricité $Q$ qui traverse un circuit pendant une durée $t$ est donnée par :
$$Q=I\times t$$
Ce qui donne : $I=\dfrac{Q}{t}$
 
Comme le temps $t$ est exprimé en minutes alors, on va d'abord le convertir en secondes :
 
On a : $1\;mn\rightarrow 60\;s$ donc, $3\;mn\rightarrow 3\times 60\;s=180\;s$
 
Par suite : $I=\dfrac{1800}{180}=10$
 
D'où, $$\boxed{I=10\;A}$$
 
2) Trouvons le nombre d'électrons qui traversent le circuit par seconde
 
On a : $Q=I\times t$
 
De plus, $Q$ peut encore s'exprimer par : $Q=n\times e$
 
Donc, on obtient l'égalité suivante :
$$n\times e=I\times t$$
Par suite, $n=\dfrac{I\times t}{e}\ $ avec, $I=10\;A\ $ et $\ t=1\;s$
 
A.N : $n=\dfrac{10}{1.6\;10^{-19}}=6.25\,10^{19}$
 
Ainsi, $6.25\,10^{19}$ électrons traversent le circuit chaque seconde.
 

Exercice 8

Un fil électrique est parcouru par un courant d'intensité $I=3\;mA.$
 
1) Trouvons la quantité d'électricité traversant le circuit pendant une minute
 
On sait que la quantité d'électricité traversant un fil électrique est parcouru par un courant d'intensité $I$ pendant une durée $t$ est donnée par :
$$Q=I\times t$$
Or, $t=1\;mn=60\;s\ $ et $\ I=3\;mA=3\cdot 10^{-3}\;A$
 
A.N : $Q=3\cdot 10^{-3}\times 60=0.18$
 
D'où, $$\boxed{Q=0.18\;C}$$
 
2) Trouvons le nombres de charges électriques en circulation pendant une minute et précisons leur nature
 
La quantité d'électricité $Q$ traversant ce fil électrique peut encore s'exprimer par :
$$Q=n\times e$$
Ce qui donne alors : $n=\dfrac{Q}{e}$
 
A.N : $n=\dfrac{0.18}{1.6\cdot10^{-19}}$
 
D'où, $1.125\cdot 10^{18}$ charges électriques sont en circulation dans le fil pendant durée égale à une minute.
 
Ces charges électriques sont des électrons.

Exercice 9

Le nombre d'électrons qui traverse la section d'un circuit est $2\cdot 10^{18}$ pour une intensité de $2.5\;mA$
 
1) Trouvons la quantité d'électricité qui traverse ce circuit.
 
Soit : $Q=n\times e$
 
A.N : $Q=2\cdot 10^{18}\times 1.6\;10^{-19}$
 
D'où, $$\boxed{Q=0.32\;C}$$
 
2) Déterminons alors la durée de passage du courant électrique dans ce circuit.
 
On sait que la quantité d'électricité qui traverse un circuit parcouru par un courant d'intensité $I$ peut encore s'écrire :
$$Q=I\times t$$
Ainsi, $t=\dfrac{Q}{I}$
 
A.N : $t=\dfrac{0.32}{2.5\;10^{-3}}=128$
 
Donc, $$\boxed{t=128\;s}$$

Exercice 10

On considère les deux circuits ci-dessous.

 

 
1) Le circuit étant à chaque fois fermé, expliquons ce qui se passe si le filament d'une lampe se détériore :
 
$-\ $ Pour le circuit 1 : le montage est en série. Alors, si un filament se détériore toutes les lampes s'éteignent car, le circuit est ouvert et le courant ne circule plus.
 
$-\ $ Pour le circuit 2 : le montage est en parallèle. Donc, les lampes ne sont pas traversées par le même courant. Ainsi, si le filament de l'une des lampes se détériore alors, cette lampe s'éteint. Par contre, l'autre lampe s'allume puisque sa branche reste fermée.
 
2) Pour installer deux ampoules dans un couloir, le meilleur montage est celui en dérivation : circuit 2
 
Parce que, avec ce montage, si l'une des lampes se détériore, l'autre peut encore continuer à fonctionner. D'où, l'avantage de ce montage.
 
Par contre, pour le montage 2, la détérioration de l'une des lampes entraine systématiquement le non fonctionnement de l'autre.

Exercice 11

Le circuit ci-dessous comprend un fusible de $500\;mA$, une pile de $4.5\;V$, une première lampe $L_{1}$ portant les indications $4.5\;V\;-\;0.15\;A$ et une deuxième lampe $L_{2}$ dont les indications sont : $4.5\;V\;-\;350\;mA.$

 

 
1) Les indications sur les lampes signifient la tension et l'intensité du courant appropriés à chaque lampe pour son bon fonctionnement.
 
2) Si on ferme $K_{1}$ seul, l'ampèremètre affichera $0.15\;A$ car, c'est la seule valeur de l'intensité suffisante à la lampe pour qu'elle s'allume.
 
En effet, d'après la loi des nœuds, le courant $I$ mesuré par l'ampèremètre est donné par :
$$I=I_{1}+I_{2}$$
$K_{2}$ étant ouvert donc, aucun courant ne passe par $L_{2}.$
 
D'où, $I_{2}=0$ et par suite, $I=I_{1}$
 
Par conséquent, l'ampèremètre $(A)$ affichera $I_{1}=0.15\;A$
 
3) Si les deux interrupteurs $K_{1}\ $ et $\ K_{2}$ sont fermés, alors l'ampèremètre indiquera $500\;mA$ car, c'est la somme des deux intensités parcourant les deux lampes.
 
En effet, au niveau le nœud $M$, en appliquant la loi des nœuds, on obtient :
 
$\begin{array}{rcl} I&=&I_{1}+I_{2}\\&=&0.15\;A+350\;mA\\&=&150\;mA+350\;mA\\&=&500\;mA\end{array}$
 
Donc, $I=500\;mA$
 
Comme l'ampèremètre $(A)$ mesure l'intensité $I$ alors, il affichera $500\;mA$
 
4) Les deux interrupteurs $K_{1}\ $ et $\ K_{2}$ restant fermés, en remplaçant $L_{1}$ par une lampe portant les indications : $4.5\;V\;-\;0.25\;A$ et en appliquant la loi des nœuds, on obtient une intensité $I$ donnée par :
 
$\begin{array}{rcl} I&=&I_{1}+I_{2}\\&=&0.25\;A+350\;mA\\&=&250\;mA+350\;mA\\&=&600\;mA\end{array}$
 
Ainsi, le courant mesuré par l'ampèremètre est d'intensité $I=600\;mA$
 
On remarque que cette valeur est supérieure à l'intensité maximale $(500\;mA)$ pouvant traverser la fusible.
 
Par conséquent, la fusible va se griller par fusion et le circuit s'ouvre.
 
5) Le rôle du fusible est d'ouvrir un circuit électrique lorsque l'intensité du courant électrique dans celui-ci atteint une valeur donnée pendant un certain temps.
 
On l'appelle fusible du fait qu'il y a fusion d'un filament conducteur sous l'effet de son élévation de température provoquée par la surintensité. 

 

 

 

 

 

Auteur: 
Aliou ndiaye

Solution des exercices : La résistance électrique 3e

Classe: 
Troisième

Exercice 1 

1) Trouvons la résistance $R_{1}$ du rouleau de fil métallique.
 
On a : $R_{1}=\dfrac{\rho\times \ell}{s}\ $ or, $\ s=\pi r^{2}=\pi\dfrac{d^{2}}{4}$
 
A.N : $R_{1}=\dfrac{1.6\;10^{-8}\times 100\times 4}{\pi(0.2\;10^{-3})^{2}}=50.929$
 
D'où, $$\boxed{R_{1}=50.929\;\Omega}$$
 
2) Calculons la longueur de fil nécessaire
 
On a : $R=\dfrac{\rho\times \ell}{s}\ \Rightarrow\ \ell=\dfrac{R\times s}{\rho}$
 
A.N : $\ell=\dfrac{20\times(0.2\;10^{-3})^{2}\times\pi}{4\times 1.6\;10^{-8}}=39.269$
 
Donc, $$\boxed{\ell=39.269\;m}$$

Exercice 2 

1) Trouvons la résistivité de ce cuivre.
 
On a : $R=\dfrac{\rho\times \ell}{s}\ \Rightarrow\ \rho=\dfrac{R\times s}{\ell}$
 
Or, $s=\pi r^{2}=\pi\dfrac{d^{2}}{4}\ $ donc, $\rho=\dfrac{R\times\pi d^{2}}{4\ell}$
 
A.N : $\rho=\dfrac{6\times\pi\times(0.2\;10^{-3})^{2}}{4\times 10}=1.884\;10^{-8}$
 
D'où, $$\boxed{\rho=1.884\;10^{-8}\;\Omega.m}$$
 
2) Calculons la résistance du fil de connexion obtenu.
 
On a : $R=\dfrac{\rho\times \ell}{s}$ sachant que $1\;mm^{2}=10^{-6}\;m^{2}$
 
A.N : $R=\dfrac{1.884\;10^{-8}\times 0.5}{10^{-6}}=9.42\;10^{-3}$
 
Ainsi, $$\boxed{R=9.42\;10^{-3}\;\Omega}$$

Exercice 3 

Calculons la longueur qu'il faudra prendre 
 
On a : $R=\dfrac{\rho\times \ell}{s}\ \Rightarrow\ \ell=\dfrac{R\times s}{\rho}$
 
Comme $s=\pi r^{2}=\pi\dfrac{d^{2}}{4}$ alors, $\ell=\dfrac{R\times\pi d^{2}}{4\rho}$
 
A.N : $\ell=\dfrac{40\times\pi\times(0.6\;10^{-3})^{2}}{4\times 10^{4}\times 10^{-2}}=11.309$
 
D'où, $$\boxed{\ell=11.309\;m}$$
 
En effet, on a : $\rho$ en $\Omega.cm$, ce qui fait qu'on doit convertir en $\Omega.m$.
 
Donc, $10^{-4}\;\Omega.m=10^{-4}\;\Omega(10^{-2}\;m)=(10^{-4})(10^{-2})\;\Omega.m$

Exercice 4 

1) Trouvons la résistance $R$ de ce fil conducteur.
 
On a : $R=\dfrac{\rho\times \ell}{s}$ 
 
A.N : $R=\dfrac{1.6\;10^{-8}\times 2}{0.16\;10^{-6}}=0.2$
 
D'où, $$\boxed{R=0.2\;\Omega}$$
 
2) Calculons la résistance d'un fil de même nature, de même longueur et de section double
 
Soit : $s'=2\times s=2\times 0.16\;mm^{2}$
 
Alors on a : $R'=\dfrac{\rho\times \ell}{s'}$ 
 
A.N : $R'=\dfrac{1.6\;10^{-8}\times 2}{2\times 0.16\;10^{-6}}=0.1$
 
Donc, $$\boxed{R'=0.1\;\Omega}$$

Exercice 5 

Un fil homogène a une résistance $R=20\;\Omega$. Trouvons :
 
1) La résistance $R_{1}$ d'un fil de même nature, de même section et dont la longueur est doublée.
 
On a : $R=\dfrac{\rho\times \ell}{s}$ 
 
Alors,
 
$\begin{array}{rcl} R_{1}&=&\dfrac{\rho\times 2\ell}{s}\\ \\&=&\dfrac{\rho\times \ell}{s}\times 2 \\ \\&=&2R\end{array}$
 
A.N : $R_{1}=2\times 20=40$
 
Ainsi, $$\boxed{R_{1}=40\;\Omega}$$
 
2) La résistance $R_{2}$ d'un fil de même nature, de même longueur et dont le diamètre est doublé
 
On a : $R=\dfrac{\rho\times \ell}{s}\ $ avec, $\ s=\pi r^{2}=\dfrac{\pi d^{2}}{4}\qquad\left(r=\dfrac{d}{2}\right)$ 
 
Donc, $R=\dfrac{\rho\times \ell}{\dfrac{\pi\times d^{2}}{4}}=\dfrac{4\times\rho\times \ell}{\pi\times d^{2}}$
 
D'où,
 
$\begin{array}{rcl} R_{2}&=&\dfrac{\rho\times \ell}{\dfrac{\pi\times d'^{2}}{4}}\\ \\&=&\dfrac{4\times\rho\times \ell}{\pi\times d'^{2}}\quad\text{avec }\ d'=2d \\ \\&=&\dfrac{4\times\rho\times \ell}{\pi\times(2d)^{2}} \\ \\&=&\dfrac{4\times\rho\times \ell}{4\times\pi\times d^{2}} \\ \\&=&\dfrac{R}{4}\end{array}$
 
A.N : $R_{2}=\dfrac{20}{4}=5$
 
D'où, $$\boxed{R_{2}=5\;\Omega}$$
 
3) La résistance $R_{3}$ d'un fil de même nature et dont la longueur et le rayon sont doublés.
 
On a : $R=\dfrac{\rho\times \ell}{s}\ $ avec, $\ s=\pi r^{2}.\ $ Donc : $R=\dfrac{\rho\times \ell}{\pi r^{2}}$
 
Ainsi,
 
$\begin{array}{rcl} R_{3}&=&\dfrac{\rho\times(2\ell)}{\pi\times(2r)^{2}}\\ \\&=&\dfrac{2\times\rho\times \ell}{4\times\pi\times r^{2}} \\ \\&=&\dfrac{2}{4}R \\ \\&=&\dfrac{R}{2}\end{array}$
 
A.N : $R_{3}=\dfrac{20}{2}=10$
 
D'où, $$\boxed{R_{3}=10\;\Omega}$$
 
4) La résistance $R_{4}$ d'un fil de même nature et dont la longueur et la section sont doublées. 
 
On a : $R=\dfrac{\rho\times \ell}{s}$ 
 
Alors,
 
$\begin{array}{rcl} R_{4}&=&\dfrac{\rho\times(2\ell)}{(2s)}\\ \\&=&\dfrac{2\times\rho\times \ell}{2\times s} \\ \\&=&\dfrac{\rho\times \ell}{s} \\ \\&=&R\end{array}$
 
Ainsi, $$\boxed{R_{4}=20\;\Omega}$$

Exercice 6 Contrôle de connaissances

Recopier et compléter les phrases ci-dessous.
 
La résistance est la grandeur qui caractérise la propriété d'un dipôle à s'opposer plus ou moins au passage du courant électrique. 
 
La tension aux bornes d'un conducteur ohmique est égale au produit de la résistance de ce conducteur et de l'intensité qui le traverse. 
 
L'unité $S.I$ de la résistance est l'ohm ; son symbole est $\Omega.$
 
La caractéristique intensité tension d'un conducteur ohmique est une droite qui passe par l'origine des axes.
 

Exercice 8 Variation d'une résistance avec sa longueur ou sa section

Un fil homogène a une résistance $R=20\;\Omega.$
 
1) Trouvons la résistance $R_{1}$ d'un fil de même nature, de même section dont la longueur est doublée.
 
Soit $\ell$ la longueur du fil de résistance $R\ $ et $\ \ell'$ la longueur du fil de résistance $R_{1}.$
 
Alors : $R=\dfrac{\rho\times \ell}{s}\ $ et $\ R_{1}=\dfrac{\rho\times \ell'}{s}$
 
Or, $\ell'=2\ell$ donc,
 
$\begin{array}{rcl} R_{1}&=&\dfrac{\rho\times \ell'}{s}\\ \\&=&\dfrac{\rho\times 2\ell}{s}\\ \\&=&2\times\dfrac{\rho\times \ell}{s}\\ \\&=&2\times R\end{array}$
 
Donc, $R_{1}=2R$
 
A.N : $R_{1}=2\times 20=40$
 
D'où, $$\boxed{R_{1}=40\;\Omega}$$
2) Trouvons la résistance $R_{2}$ d'un fil de même nature dont la longueur et la section sont doublées.
 
Soient $\ell\ $ et $\ s$ la longueur et la section du fil de résistance $R\ $ et $\ \ell''\ $ et $\ s''$ la longueur et la section du fil de résistance $R_{2}.$
 
On a : $R=\dfrac{\rho\times \ell}{s}\ $ et $\ R_{2}=\dfrac{\rho\times \ell''}{s''}$
 
Comme $\ell''=2\ell\ $ et $\ s''=2s$ alors,
 
$\begin{array}{rcl} R_{2}&=&\dfrac{\rho\times \ell''}{s''}\\ \\&=&\dfrac{\rho\times 2\ell}{2s}\\ \\&=&\dfrac{2\times\rho\times\ell}{2\times s}\\ \\&=&\dfrac{\rho\times\ell}{s}\\ \\&=&R\end{array}$
 
Ainsi, $R_{2}=R$
 
D'où, $$\boxed{R_{2}=20\;\Omega}$$

Exercice 9 Interpréter un résultat d'une mesure

Un élève mesure la résistance d'un fil de connexion avec un ohmmètre.
 
Il place le curseur sur le calibre le plus élevé, la valeur affichée est $1.$
 
On peut donc en déduire que le fil de connexion a une résistance $R$ donnée par :
$$R=1\times\text{Calibre le plus élevé}$$
En effet, en plaçant le curseur sur le calibre le plus élevé, le ohmmètre affiche une valeur significative égale à $1.$
 
Donc, cette valeur multipliée par celle du calibre donnera la valeur de la résistance.

Exercice 10 Résistance du corps humain

Entre deux points du corps humain, la résistance électrique qui peut être mesurée est plus faible si le corps est mouillé que s'il est sec.
 
1) Soumis à une tension déterminée, un corps est traversé par un courant de plus forte intensité lorsqu'il est mouillé que lorsqu'il est sec.
 
En effet, soit $I_{1}$ l'intensité du courant traversant le corps sec de résistance $R_{1}\ $ et $\ I_{2}$ l'intensité du courant traversant le corps mouillé de résistance $R_{2}.$
 
On soumet à ce corps une tension $U.$
 
D'après la loi d'Ohm, on a :
$$\left\lbrace\begin{array}{rcl} U&=&R_{1}I_{1}\\ \\U&=&R_{2}I_{2}\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{rcl} I_{1}&=&\dfrac{U}{R_{1}}\\ \\I_{2}&=&\dfrac{U}{R_{2}}\end{array}\right.$$
Or, $R_{2}<R_{1}$ donc,
 
$\begin{array}{rcl}\dfrac{1}{R_{2}}>\dfrac{1}{R_{1}}&\Rightarrow&\dfrac{U}{R_{2}}>\dfrac{U}{R_{1}}\\ \\&\Rightarrow&I_{2}>I_{1}\end{array}$
 
Ainsi, $\boxed{I_{2}>I_{1}}$
 
Par conséquent, un corps est traversé par un courant de plus forte intensité lorsqu'il est mouillé que lorsqu'il est sec.
 
2) Pour réduire les risques d'électrocution, il faut éviter que le corps soit mouillé.

Pour les Exercices 11 et 12, voir le corrigé sur les associations de conducteurs ohmiques

Auteur: 
Aliou ndiaye

Pages