Physique

Série d'exercice : Généralité sur la chimie organique - 1L

Classe: 
Première
 

Exercice 1 

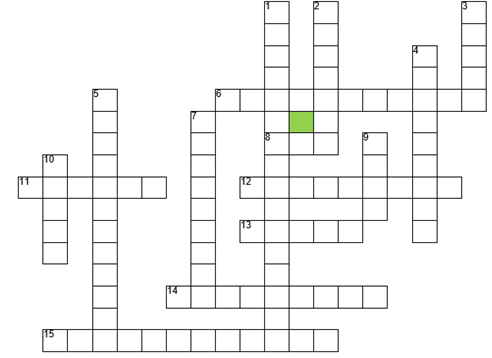
Mots croises
 

 
Horizontal 
 
5. Premier composé organique synthétisé 
 
9. Elle s'oppose à la synthèse
 
10. Élément dont sa présence est prouvée, dans un composé organique, par la formation de l'ammoniac lors d'une réaction chimique 
   
12. Son étude permet déterminer la nature des éléments présents dans un composé organique
 
13. Écriture simplifiée d'une formule développée
 
Vertical
 
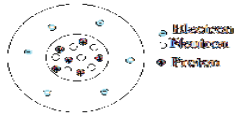
1. Élément qui définit la chimie organique (ou élément présent dans tous les composés organiques 
 
2. Dans cette formule, les toutes liaisons sont représentées 
 
3. Elle renseigne sur le nombre d'atomes présents dans une molécule 
  
4. Ces isomères qui se distinguent par la position d'une liaison multiple 
  
6. Étude qui donne le nombre d'atomes présents dans une molécule organique
  
7. Élément dont sa présence est prouvée dans un composé organique par formation de l'eau lors d'une combustion   
 
8. Chimie de l'élément carbone   
 
11. Isomères qui diffèrent l'enchaînement des atomes de carbone        

Exercice 2

Choisir la bonne réponse 
 
1. La liaison covalente provient de :
 
a. la mise en commun de deux électrons célibataires par deux atomes ;
 
b. l'attraction électromagnétique des atomes
 
c. des effets électroniques dans les molécules
 
2. On définit les isomères chimiques comme :
 
a. des espèces chimiques de même formule brute mais qui diffèrent par leurs structures
 
b. des structures qui se ressemblent
 
c. des structures superposables avec leur image dans un miroir.
 
3. En chimie organique, les isomères, qui existent, sont :
 
a. deux types (isomère de constitution et stéréoisomère / spatiale)
 
b. trois types (squelette, position et fonction) ;
 
c. deux types (configuration et conformation)
 
4. L'analyse élémentaire quantitative d'une substance permet de déterminer : 
 
a. a masse molaire de cette substance ;
 
b. la nature des éléments qui constituent cette substance ;
 
c. le nombre de mole d'atomes de chaque élément contenu dans cette substance.
 
5. La somme des masses des éléments constitutifs d'un échantillon d'une substance est:
 
a. supérieure à la masse de l'échantillon analysé
 
b. inférieure à la masse de l'échantillon analysé
 
c. égale à la masse de l'échantillon analysé aux erreurs d'expérience près.
 
6. Pour déterminer la formule brute d'une substance il suffit de connaître:
 
a. les résultats de l'analyse élémentaire qualitative de la substance
 
b. les résultats de l'analyse élémentaire quantitative de la substance
 
c. la masse molaire et les résultats de l'analyse élémentaires qualitative et quantitative de lasubstance

Exercice 3

Compléter ce texte avec les mots ou groupe de mots suivants : oxydes de carbone ; organique ; biologique ; chimie ; minérale ; carbone ;combustibles ; chimie organique ; caractère minéral ; végétale ; animal ; carbures.
 
A l'origine, la$\ldots\ldots\ldots$étudiait les substances des êtres vivants appartenant au monde$\ldots\ldots\ldots$ou végétal. 
 
Elle s'opposait à la chimie$\ldots\ldots\ldots$(chimie inorganique) qui se consacrait aux substances extraites du monde minéral, c'est-à-dire provenant des roches, des eaux naturelles, de l'atmosphère.
 
Ce n'est qu'en $1828$ Wöhler (chimiste allemand) réussit à créer l'urée substance$\ldots\ldots\ldots$à partir d'un composé minéral$\ldots\ldots\ldots$
 
On comprit alors que la chimie organique obéissait aux mêmes règles que la$\ldots\ldots\ldots$minérale
 
Mais la distinction demeure en raison entre autres des propriétés particulières des composés organiques par rapport aux composés minéraux. 
 
Ainsi les composés organiques (pétroles, gaz naturel, alcool...) sont presque$\ldots\ldots\ldots$, ce qui est rarement le cas des composés minéraux
 
La chimie organique est la chimie des composés du$\ldots\ldots\ldots$Certains sont d'origine naturelle, animale ou k$\ldots\ldots\ldots$d'où l'appellation "organique" (s'oppose à la chimie minérale). 
 
Les médicaments, matières plastiques, fibres synthétiques, peintures, additifs alimentaires sont des produits de la$\ldots\ldots\ldots$obtenus par synthèse, c'est à dire par formation d'une molécule à partir de molécules plus simples.
 
En fait il faut en exclure le carbone, les$\ldots\ldots\ldots$les carbonates, les cyanures les$\ldots\ldots\ldots$qui ont tous un$\ldots\ldots\ldots$

Exercice 4

Lire attentivement ce texte avant de répondre aux questions :
 
En $1800$, la chimie s'était fermement établie parmi les sciences ; au cours de la décennie suivante, les scientifiques se sont vivement intéressés à l'étude de la composition des substances et à la manière dont elles pouvaient être modifiées. 
 
Par suite de recherches, ils ont commencé à faire la distinction entre deux genres de composés : ceux qui étaient issus de sources végétales ou animales ont été appelés composés organiques, et ceux qui provenaient de constituants minéraux de la Terre ont été appelés « inorganiques ».
 
Les chimistes connaissaient l'existence de très nombreux composés organiques telles que les teintures, les savons, le vinaigre, le sucre, les parfums, les gommes et le caoutchouc, pour n' en mentionner que quelques-uns, mais ils n'arrivaient pas à expliquer comment tant décomposes pouvaient être faits à partir de quelques éléments seulement...()
 
Jusqu'alors, on n'avait jamais synthétisé un composé organique à partir de matières inorganiques ; par conséquent, de nombreux scientifiques croyaient que les composés organiques se formaient sous l'influence d'une « force vitale ». 
 
En $1828$, Friedrich Wöhler a fait une découverte remarquable.
 
Il a essayé de fabriquer du cyanate d'ammonium au moyen d'une réaction de décomposition double, dans une solution de chlorure d'ammonium et de cyanate d'argent.
 
Or, ces deux composés étaient considérés comme étant « inorganiques ».
 
Cependant, au lieu d'obtenir du cyanate d'ammonium, il a produit des cristaux d'urée, un composé organique
 
Au cours des années qui ont suivi cette découverte et après que l'acide acétique et plusieurs autres composés organiques eurent été fabriqués à partir de matières inorganiques, la validité de la « force vitale » a été mise en doute. 
 
Avec le temps, de plus en plus de composés organiques ont été synthétisés à partir de matières inorganiques. 
 
Il est devenu évident qu'il n'était pas nécessaire que tous les composés organiques soient associés à des organismes vivants. 
 
Au milieu des années $1850$, on a compris que le facteur commun à tous les composés organiques était le carbone. 
 
Maintenant, les chimistes disent simplement que les composés organiques sont ceux qui contiennent du carbone, sauf les oxydes de carbone, les carbonates,les carbures et les cyanures. 
 
Ces exceptions, en plus de toutes les autres substances connues,sont dites inorganiques. 
 
Trois à quatre millions de composés organiques sont connus tan disque seulement cinquante mille composés inorganiques sont connus 
 
1. Donner un titre à ce texte
 
2. Le texte fait allusion au premier composé organique fabriqué. 
 
Lequel ? 
 
Et quels sont les composés minéraux utilisés pour cette synthèse 
 
3. Citer les composés organiques et les composés minéraux
 
4. Quelle est la chimie qui s'opposait à la chimie organique ?
 
5. Définir la chimie organique                          

Exercice 5

Classer ces composés en composés minéraux ou organique
 
$CH_{4}$ ;
 
$CO_{2}$ ;
 
$C_{2}H_{6}$ ;
 
$CO$ ;
 
$CaCO_{3}$ ;
 
$C_{2}H_{4}$ ;
 
$C_{3}H_{6}$ ; 
 
$C_{5}H_{12}$ ;
 
$HCN$ ;
 
$CaCO_{3}$ ; 
 
$C_{55}H_{72}N_{4}O_{5}Mg$ ;
 
$CH_{4}ON_{2}$ ;
 
$CH_{3}C1$ ;
 
$HNO_{3}$

Exercice 6

Les composés $C_{2}H_{4}$, $C_{3}H_{6}$, $C_{4}H_{8}$, $C_{6}H_{12}$, contiennent tous une même proportion de môles d'atomes de carbone et de môles d'atomes d'hydrogène (une môle d'atomes de carbone pour deux môles d'atomes d'hydrogène).
 
Quelle est la donnée qui permet de distinguer ces quatre composés ?
 
1. La masse atomique relative des éléments
 
2. La masse moléculaire relative du composé
 
3. La constante d'Avogadro
 
4. La masse de l'échantillon considéré

Exercice 7

L'acide acétique (présent notamment dans le vinaigre) a pour formule brute : $C_{2}H_{4}O_{2}$
 
1. Quelle est la masse molaire moléculaire de l'acide acétique ?
 
2. Déterminer les pourcentages en masse de chaque élément présent dans ce composé.
 
On donne les masses molaires atomiques suivantes : 
 
$M(C)=12.0\,g\cdot mol^{-1}$ ;
 
$M(H)=1.0\,g\cdot mol^{-1}$ ;
 
$M(O)=16.0\,g\cdot mol^{-1}$

Exercice 8

La formule de la chlorophylle est $C_{55}H_{72}N_{4}O_{5}Mg.$
 
1. Calculer le pourcentage massique de magnésium contenu dans la chlorophylle.
 
2. Sachant que $0.5\,kg$ de feuilles contient environ $1\,g$ de chlorophylle, calculer la masse de magnésium absorbée lorsqu'on mange $100\,g$ de feuilles, sous forme de salade par exemple.
 
3. Quel est le nombre correspondant d'atomes de magnésium ?

Exercice 9

Un composé organique $A$ est formé de carbone, d'hydrogène et d'oxygène. 
 
La composition centésimale massique de ce composé est la suivante : 
 
$C\ :\ 54.5\%$ ;
 
$H\ :\ 9.1\%$ ;
 
$O\ :\ 36.4\%.$
 
Sa densité de vapeur par rapport à l'air est $d=3.03.$
 
1. Calculer la masse molaire de ce composé
 
2. Déterminer sa formule brute
 
3. Le composé $A$ brûle dans le dioxygène. 
 
Il se forme du dioxyde de carbone et de l'eau.
 
3.1. Écrire l'équation bilan de la réaction chimique
 
3.2. On fait brûler une masse $m=3.4\,g$ de $A.$ 
 
Calculer le volume de dioxygène nécessaire pour que la combustion soit complète.
 
Données : 
 
$V_{m}=22.4L\cdot mol^{-1}$ ; 
 
$M(H)=g\cdot mol^{-1}$ ; 
 
$M(C)=12\,g\cdot mol^{-1}$ ; 
 
$M(O)=16\,g\cdot mol^{-1}$ ; 
 
$\rho_{\,\text{air}}=1.293\,g\cdot L^{-1}$

Exercice 10

L'analyse élémentaire d'un composé organique montre qu'il contient $84\%$ de carbone et $16\%$ d'hydrogène. 
 
Choisir, parmi les formules moléculaires suivantes, celle en accord avec cette composition.
 
1. $C_{6}H_{14}O_{2}$
 
2. $C_{6}H_{10}$
 
3. $CH_{4}O$
 
4. $C_{14}H_{22}$
 
5. $C_{7}H_{16}$

Exercice 11

1. Écrire les formules semi-développées des composés moléculaires suivants : $C_{2}H_{6}$ ; $C_{2}H_{4}$ ; $CH_{4}O$ ; $C_{3}H_{9}N$ ; $C_{2}H_{4}O_{2}.$
 
2. L'analyse quantique d'un composé A indique qu'il est formé en masse de $40\%$ de carbone, de $6\%$  d'hydrogène et de $53\%$ d'oxygène. 
 
Ces données suffisent-elle pour déterminer la formule $A$ ? 
 
Quelle est la formule brute la plus simple ?
 
3. La composition centésimale est, en masse, la suivante pour la saccharine :  $45\%$ de carbone ; $2.7\%$ d'hydrogène ; $26.2\%$ d'oxygène ; $7.7$  d'azote ; $17.5\%$ de soufre.
 
Sachant que la molécule comporte un seul atome de soufre, trouver la formule brute de la saccharine.

Exercice 12

Parmi les substances gazeuses dérivées du carbone, on en connait :
 
$-\ $une $X$, contenant $42.2\%$ en masse de carbone, ainsi que de l'oxygène. 
 
La densité de ce composé $X$ par rapport à l'air vaut $0.967$ ;
 
$-\ $une $Y$, contenant $92.5\%$ en masse de carbone, ainsi que de l'hydrogène. 
 
La densité de ce composé $Y$ par rapport à l'air vaut $0.898$ ; 
 
$-\ $une $Z$, contenant $81.8\%$ 81, en masse de carbone, ainsi que de l'hydrogène. 
 
La densité de ce composé $Z$ par rapport à l'air vaut $1.519.$
 
1. Quelles sont les masses moléculaires relatives des composés $X$, $Y$ et $Z$ ?
 
2. Quelles sont les masses d'un litre de chacun des composés gazeux $X$, $Y$ et $Z$ pris dans les conditions normales de température et de pression $\left(t=0 ^{\circ}C\;,p=1\text{atm ou }101325 P_{a}\right)$ ?
 
3. Déterminer les formules moléculaires des trois composés $X$, $Y$ et $Z.$
 
Masses atomiques : $M_{N}=14\;g\cdot mol^{-1}$ ; $M_{O}=16$ ; $g\;\cdot mol^{-1}$ ; $M_{At}=40\;g\cdot mol^{-1}$

Exercice 13

1. Établir la relation qui permet de calculer la masse molaire d'un composé gazeux à partir de sa densité.
 
On rappelle que la densité d d'un gaz par rapport à l'air est égale à :
 
$d=\dfrac{\text{masse d'un volume de ce gaz}}{\text{masse d'un même volume d'air}}$
 
Les masses sont déterminées dans les mêmes conditions de température et de pression.
 
2. Calculer la masse molaire d'un composé gazeux dont la densité est égale à $2.83.$
 
La masse volumique de l'air est égale à $1.29\;g\cdot L^{-1}$

Exercice 14

La combustion d'un échantillon de $0.084\;g$ d'un composé ne contenant que du carbone et de l'hydrogène a donné une augmentation de masse d'un flacon laveur à l'eau de chaux de $0.265\;g$ et du flacon laveur à l'acide sulfurique concentré de $0.106\;g.$
 
1. Calculer la masse de carbone et la masse d'hydrogène contenues dans l'échantillon.
 
2. Calculer le pourcentage massique de chaque élément.

Exercice 15

On considère un composé organique $(A)$ ne renfermant que du carbone, de l'hydrogène et de l'oxygène.
 
La combustion complète d'un échantillon de $(A)$ de masse $m$ égale à $0.373\;g$ a donné $0.886\;g$ d'un gaz qui trouble l'eau de chaux et $.453\;g$ d'eau.
 
1. Calculer les masses de carbone, d'hydrogène et d'oxygène contenues dans l'échantillon.
 
2. Déterminer la formule brute de (A) sachant que sa masse molaire est égale à $74\;g\cdot mol^{-1}$

Exercice 16

La composition en masse du camphre est : 
 
$78.9\%$ de carbone, $10.5\%$ d'hydrogène et $10.5\%$ d'oxygène.
 
Déterminer sa formule brute sachant que sa masse molaire est égale à $152\\;g\cdot mol^{-1}$

Exercice 17 

La composition en masse d'un composé organique ne contenant que du carbone, de l'hydrogène, de l'azote et de l'oxygène a donné les résultats suivants :
 
$40.6\%$ de carbone ; 
 
$8.47\%$ d'hydrogène et $23.7\%$ d'azote
 
Déterminer sa formule brute sachant que sa masse molaire est égale à $59\;g\cdot mol^{-1}$

Exercice 18

Un composé organique contient du carbone, de l'hydrogène et, éventuellement, de l'oxygène.
 
Pour déterminer la formule moléculaire de ce composé, on a réalisé les deux expériences suivantes :
 
$-\ $la combustion complète de $0.74\;g$ du composé a fourni $1.76\;g$ de dioxyde de carbone et $0.9\;g$ d'eau ;
 
$-\ $ la vaporisation de $0.111\;g$ de ce composé a fourni, à $21^{\circ}C$ , un volume de $35.6\;ml$ sous une pression de $102791 Pa\left(\text{ou }1.014_{\text{atm}}\right).$
 
1. Déterminer la composition centésimale de ce composé
 
2. Calculer sa masse molaire
 
3. Déterminer sa formule moléculaire
 
4. Écrire les formules moléculaires semi-développées de $5$ isomères non cycliques

Exercice 19

Le glucose est un sucre contenant uniquement les éléments carbone, hydrogène et oxygène. 
 
Une analyse centésimale a permis de déterminer les pourcentages en masse suivants : $\%c=40.0$ $\%H+6.7$ $\%O %C=40,0 %H=6,7 %O=53,3$
 
$(\%C représente le pourcentage en masse de l'élément carbone dans le glucose).$
 
Sachant que le glucose a une masse molaire moléculaire de $180.0\;g\cdot mol^{-1}$, quelle est sa formule brute ?
 
On donne les masses molaires atomiques suivantes :$M(C)=12.0\;g\cdot mol^{-1}$ ; $M(H)=1.0\;g\cdot mol^{-1}$ ; $M(O)=16.0\;g\cdot mol^{-1}$

Exercice 20

Pour effectuer l'analyse centésimale élémentaire d'un composé organique de formule brute $C_{x}H_{y}O_{z}$ de masse molaire moléculaire $M=46\;g\cdot mol^{-1}$, on prélève un échantillon de $230\;mg.$
 
On le chauffe en présence d'un excès d'oxyde de cuivre de formule $C_{u}O.$
 
Dans ces conditions, on obtient du dioxyde de carbone, de l'eau et du cuivre métallique. 
 
Une fois la transformation chimique terminée, on a obtenu $44\;mg$ de dioxyde de carbone et $270\;mg$d'eau.
 
1. Écrire l'équation de la réaction modélisant cette transformation chimique.
 
2. Quelle quantité de matière du composé organique contenait l'échantillon utilisé ?
 
3. Exprimer en fonction de $x$ la quantité de matière de dioxyde de carbone et en fonction de $y$ la quantité de matière d'eau produite au cours de la transformation chimique.
 
4. En déduire les valeurs de $x$, $y$ et z ainsi que la formule brute du composé organique étudié.
 
5. Déterminer les pourcentages en masse de chaque élément présent dans ce composé.
 
On donne les masses molaires atomiques suivantes :
 
$M(C)=12.0\;g\cdot mol^{-1}$ ; $M(H)=1.0\,g\cdot mol^{-1}$ ; $M(O)=16.0\cdot mol^{-1}$

Exercice 21

Le chlorhydrate de kétamine est une molécule utilisée comme anesthésique général en médecine humaine et en médecine vétérinaire.
 
Sa formule brute peut s'écrire sous la forme $C_{x}H_{y}C1_{z}N_{t}O_{e}$ 
 
L'analyse quantitative du composé donne les pourcentages massiques suivants : $\%c=65.68$  ;  $\%H=6.78$  ;  $\%N=5.89$  ;  $\%C1=14.91$  ;  
 
1. En déduire la composition centésimale molaire de l'élément oxygène
 
2. Déterminer la formule brute du chlorhydrate de kétamine
 
On donne :

Masse molaire du chlorhydrate de kétamine : $M=237.725\;g\cdot mol$ 

Exercice 22

La composition en masse d'un composé organique ne contenant que du carbone, de l'hydrogène et de l'oxygène a donné les résultats suivants :
 
$52.17\%$ de carbone ; $13.04\%$ d'hydrogène et $34.79\%$ d'oxygène.
 
La densité de la vapeur de ce composé par rapport à l'air est égale à $1.58.$
 
1. Déterminer la masse molaire de ce composé.
 
2. En déduire sa formule brute

Exercice 23

L'analyse quantitative d'un hydrocarbure $C_{x}H_{y}$ montre qu'il contient 
 
$85.7\%$ de carbone.
 
1. Calculer le rapport $\dfrac{x}{y}$
 
2. En déduire la formule brute de cet hydrocarbure sachant que sa densité de vapeur par rapport à l'air est  $d=1.93.$
 
3. Écrire toutes les formules semi-développées possibles de cet hydrocarbure.

Exercice 24

La combustion complète de $10\;mL$ d'un hydrocarbure gazeux nécessite $50\;mL$ d'oxygène et fournit de l'eau et $3\;mL$ de dioxyde de carbone. Les volumes sont mesurés dans les mêmes conditions de température et de pression.
 
1. Déterminer la formule brute de cet hydrocarbure.
 
2. Écrire sa formule semi-développée.

Exercice 25

La combustion complète de $0.01\;mole$ d'un composé organique constitué de carbone, d'hydrogène et d'oxygène nécessite $1.08\;L$ de dioxygène et donne $1.32\;g$ de dioxyde de carbone et $0.72\;g$ d'eau.
 
Le volume molaire des gaz dans les conditions de l'expérience est égal à  $24\;L\cdot mol^{-1}.$
 
1. Écrire l'équation chimique de la réaction de combustion.
 
2. Déterminer la formule brute de ce composé.
 
3. Écrire les formules semi-développées des isomères correspondant à cette formule brut.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Travail et Puissance Mécaniques - 1L

 

Exercice 1

Exercice 2

Choisissons la ou les bonne(s) réponse(s)
 
1. Dans le système international d'unités, le travail d'une force est exprimé en :
$$\boxed{\text{c.}\quad\text{joule }(J)}$$
 
2. Le travail d'une force constante dont le point d'application se déplace rectilignement de $A$ à $B$ peut être :
$$\boxed{\text{a.}\quad\text{positif}}$$ 
                                                 
$$\boxed{\text{b.}\quad\text{négatif}}$$
                                                 
3. Le travail $W$ d'une force constante faisant un angle $\alpha$ avec la trajectoire rectiligne de son point d'application est nul lorsque :
$$\boxed{\text{c.}\quad\alpha=90^{\circ}}$$
 
4. Le travail $W$ d'une force constante faisant un angle $\alpha$ avec la trajectoire rectiligne de son point d'application est positif lorsque :
$$\boxed{\text{b.}\quad 0^{\circ}<\alpha<90^{\circ}}$$
 
5. Le travail $W$ d'une force constante faisant un angle $\alpha$ avec la trajectoire rectiligne de son point d'application est négatif lorsque :
$$\boxed{\text{d.}\quad 90^{\circ}<\alpha<180^{\circ}}$$
 
6. Lorsque le travail d'une force est négatif, on dit que ce travail est :
$$\boxed{\text{b.}\quad\text{résistant}}$$
 
7. La force de frottement a un travail :
$$\boxed{\text{a.}\quad\text{toujous négatif}}$$
 
8. Lorsqu'un objet tombe en chute libre, le travail du poids est :
$$\boxed{\text{a.}\quad\text{positif}}.$$
 
9. Une force est dite conservative si :
$$\boxed{\text{b.}\quad\text{le travail de cette force est indépendant du trajet suivi par le système.}}$$
 
10. Le travail d'une force perpendiculaire au déplacement est :
$$\boxed{\text{c.}\quad\text{nul}}$$
 
11. Le travail du poids d'un objet :
 
 
 
12. Une force constante est appliquée à un solide en mouvement de translation, celle-ci transfert de l'énergie au solide sous forme de travail. 
 
 

Exercice 3

Questions de compréhension (les réponses doivent être justifiées)
 
1. Le travail d'une force peut être nul si la force est perpendiculaire au déplacement
 
2. Le travail d'une force ne dépend pas de la vitesse du déplacement, mais des intensités de la force et du déplacement et de l'angle que la force fait avec le déplacement
 
3. Une pierre tombe du haut d'une falaise. 
 
Le travail de son poids est moteur car la force  favorise le déplacement
 
4. Le travail effectué par une force de frottement est  résistant car la force de frottement s'oppose au déplacement  

Exercice 4

Choisissons, parmi les propositions suivantes :
 
1. Le travail d'une force appliquée à un objet animé d'un mouvement de translation rectiligne est nul si :
 
b. La direction de la force est perpendiculaire au vecteur déplacement de son point d'application ;
 
2. Un solide est animé d'un mouvement de translation rectiligne uniforme. 
 
Il est soumis à deux forces constantes :
 
c. la somme des travaux de ces deux forces n'est pas nulle ;
 
3. le travail d'une force constante est moteur si :
 
c. Le vecteur force est de même direction et de même sens que le vecteur déplacement.

 

Poids, Masse d'un corps : Relation Poids-Masse - 2nd L

Classe: 
Seconde
 

I. Interaction Terre-objet :

1. Le poids d'un corps

1.1. Observations

Un objet lâché sans vitesse initiale tombe et se dirige vers la Terre.
 
Une balle lancée verticalement vers le haut atteint une hauteur limite puis retombe.
 
Un projectile lancé de façon quelconque décrit une trajectoire courbe et finit par atteindre le sol.
 
Ces observations montrent que la Terre exerce une force sur tout objet placé dans son environnement immédiat.

1.2. Définition

Le poids d'un corps est la force d'attraction que la Terre exerce sur ce corps.

2. Caractéristiques du poids

Les caractéristiques du poids d'un corps sont :
 
 
$\blacktriangleright\ $Son point d'application
 
Son point d'application est le centre de gravité $G.$
 
Toutes les verticales passant par un point quelconque de suspension $S$ du corps concourent en point $G$ appelé centre de gravité
 
Le point $G$ dépend de la répartition de la matière dans le volume de l'objet
 
$\blacktriangleright\ $Sa direction
 
La verticale du lieu où se trouve le corps
 
$\blacktriangleright\ $Son sens
 
Le sens est du haut vers le bas
 
$\blacktriangleright\ $Son intensité
 
C'est sa grandeur poids $P$

3. Mesure et unité

L'appareil servant à la mesure du poids d'un corps est le dynamomètre.
 
Le poids $P$ s'exprime en newtons $(N)$

4. Représentation vectorielle

Le poids est une grandeur vectorielle. 
 
On le représente par un vecteur en respectant ses caractéristiques.
 

II. Masse, masse volumique et densité.

1. La masse d'un corps

1.1. Définition

La masse d'un corps est une grandeur physique représentant la quantité de matière contenue dans ce corps.

1.2. Caractéristiques de la masse d'un corps

La masse d'un corps est une grandeur scalaire positive, extensive, invariable, et indépendante du lieu.

1.3. Mesures et unités

1.3. 1. Mesures

1.3.1.1. Appareil de mesure

La masse d'un corps est mesurée à l'aide d'une balance.

Exemples de balance :

                                      

1.3.1.2. Types de mesure

1.3.1.2.1. Mesure par la simple pesée

La simple est réalisée lorsqu'une grande pesée n'est pas nécessaire
 
On utilise, par exemple une balance de Roberval. 
 
Sur l'un des plateaux, on place l'objet dont on veut mesurer sa masse et on met sur l'autre plateau des masses marquées jusqu'à ce que la balance soit équilibrée.

1.3.1.2.2. Mesure par la double pesée

La double pesée permet de mesurer des masses même si la balance utilisée n'est pas juste.
 
On utilise, une balance précise, par exemple, un trébuchet.
 
Pour peser l'objet dont on cherche la masse $m$, on effectue deux pesées avec la même tare $T$ (double pesée à tare constante). 
 
La tare est un objet quelconque, par exemple une masse marquée dont la masse est supérieure à la masse m à mesurer.
 
Première pesée : la tare est placée dans l'un des plateaux, l'objet à peser (masse m) dans l'autre plateau et on équilibre la balance au zéro avec des masses marquées $\left(m_{1}\right)$ à côté de l'objet dont on cherche la masse.
 
Deuxième pesée : on conserve la tare et on équilibre la balance au zéro en plaçant des masses marquées dans le plateau contenant l'objet après avoir vidé de son contenu.
 
La valeur cherchée $m$ s'obtient par la relation : $m+m_{1}=m_{2}\Leftrightarrow\boxed{m=m_{2}-m_{1}}$

1.3.2. Unité de la masse

L'unité de masse dans le Système International (S.I) est le kilogramme $\left(\text{symbole : }kg\right)$
 
On utilise également les multiples et les sous-multiples du kilogramme.
$$\begin{array}{|c|c|c|c|} \hline \text{Multiples }&\text{Unité et symbole}&\text{Valeur en kilogramme}&\text{Valeur en gramme}\\ \hline &\text{La tonne (t)}&10^{3}kg&10^{6}g\\ \hline &\text{Le quintal (q)}&10^{2}kg&10^{5}g\\ \hline &\text{Dizaine de kilogramme (10)}&10^{1}kg&10^{4}g\\ \hline \text{Sous-multiples}&\text{Hectogramme (hg)}&10^{-1}kg&10^{3}g\\ \hline &\text{Décagramme(dag)}&10^{-2}kg&10^{2}g\\ \hline &\text{Gramme (g)}&10^{-3}kg&1g\\ \hline &\text{Décigramme (dg)}&10^{-4}kg&10^{-1}g\\ \hline &\text{Centigramme (cg)}&10^{-5}kg&10^{-2}g\\ \hline &\text{Miligramme (mg)}&10^{-6}kg&10^{-3}g\\ \hline &\text{Microgramme }(\mu g)&10^{-9}kg&10^{-6}g\\ \hline &\text{Nanogramme (ng)}&10^{-12}kg&10^{-9}g\\ \hline \end{array}$$
 
Quelques ordres de grandeurs de masses quelques corps ou particules
 
Masse du proton : $m_{p}=1.672\cdot10^{-27}kg$ ; 
 
masse du neutron :  $m_{n}=1.674\cdot10^{-27}kg$ ;
 
Masse de la Terre : $m_{T}=6\cdot10^{24}kg$ : 
 
masse du Soleil : $m_{S}=2\cdot10^{30}kg$

Définition du kilogramme

Le kilogramme est la masse de l'objet dénommé kilogramme-étalon et conservé au Pavillon de Breteuil à Sèvres.

1. Masse volumique d'un corps

Des corps ayant le même volume ont généralement des masses différentes. 
 
Pour caractériser un corps, on peut utiliser une grandeur physique appelée masse volumique.

1.1. Définition

La masse volumique d'un corps, à température donnée, est la masse de l'unité de volume de ce corps à cette température.

Remarque :

La masse volumique d'une substance dépend des conditions dans lesquelles elle se trouve, elle varie en fonction de la température et de la pression, surtout pour les gaz, mais aussi pour les liquides et les solides.

1.2. Unités de la masse volumique

La masse volumique s'exprime, dans le Système International, en kilogrammes par mètre cube $\left(\text{symbole : }kgm^{-3}\right)$
 
Les unités usuelles sont : le gramme par centimètre cube $\left(g\cdot cm^{-3}\right)$ ; 
 
le kilogramme par décimètre cube $\left(kg\cdot dm^{-3}\right)$ ; 
 
la tonne par mètre cube $\left(t\cdot m^{-3}\right)$

Remarque :

$-\ $Le Kilogramme par litre $(Kg/L)$, le gramme par millilitre $(g/mL)$, le kilogramme par décimètre cube $\left(kg/dm^{3}\right)$ et le gramme par centimètre cube $\left(g/cm^{3}\right)$ sont équivalents : 
$$1g/L=1g/L=1Kg/dm^{3}=1g/cm^{3}$$

1.3. Mesure de la masse volumique d'un corps

1.3.3. Masse volumique des gaz

Tout comme pour les liquides et les solides, il est possible de calculer la masse volumique d'un gaz en divisant la mesure de sa masse par celle de son volume.
$$\rho\dfrac{m}{V}$$

1.3.4 Masse volumique de quelques stances

$$\begin{array}{|l|l|l|l|l|l|l|l|} \hline \text{Métal}&\text{Aluminium}&\text{Argent}&\text{Laiton (alliage)}&\text{Cuivre}&\text{Fer}&\text{Plomb}&\text{Or}\\ \hline \rho\text{ en }g\cdot cm^{-3}&2.7&10.5&7.3-8.4&8.9&7.9&11.4&19.3\\ \hline \end{array}$$

3. Densité d'un corps

3.1. Observations

Un glaçon flotte sur l'eau, un tronc d'arbre flotte sur la rivière.
 
Au contraire une roche, un morceau de fer, une bille de plomb tombent au fond de l'eau. 
 
Celles qui coulent ont une masse volumique plus grande que la masse volumique de l'eau. 
 
Au contraire, les substances qui flottent ont une masse volumique plus petite que celle de l'eau.
 
Comparer la masse volumique d'une substance à celle de l'eau permet donc de faire des prévisions pour savoir si la substance flotte ou non.
 
Il est pratique d'introduire une notion : la densité.

3.2. Définition

$\blacktriangleright\ $ La densité d'un corps est le rapport de la masse de ce corps à la masse d'un égal volume d'un corps pris comme référence pris à la même température.
$$\boxed{d=\dfrac{m}{m_{\,\text{ref}}}}$$
 
Comme $m=\rho V$ et $m_{\;\text{ref}}=\rho_{\,\text{ref}}V$
 
$\blacktriangleright\ $La densité d'un corps est le rapport de sa masse volumique à la masse volumique d'un corps pris comme référence.
$$\boxed{d=\dfrac{\rho}{\rho_{\,\text{ref}}}}$$
 
$-\ $Pour les solides et les liquides, le corps de référence est l'eau :
$$\boxed{d=\dfrac{\rho}{\rho_{\,\text{eau}}}}$$
 
$-\ $Pour les gaz, le corps de référence est l'air : 
$$\boxed{d=\dfrac{\rho}{\rho_{\,\text{air}}}}$$

3.3. Densité de quelques substances

Le tableau ci-dessous résume la densité de quelques substances 
$$\begin{array}{|l|l|l|l|l|l|l|} \hline \text{Substance}&\text{Fer}&\text{Aluminium}&\text{Cuivre}&\text{Ethanol}&\text{Caoutchoue}&\text{Glace}\\ \hline \text{Densité}&7.86&2.7&8.92&0798&0.92\text{ à }0.99&\text{0.917}\\ \hline \end{array}$$
 
L'acier a une densité de l'ordre de celle du fer suivant sa composition.

Remarque

Un corps flotte dans l'eau lorsque la densité est inférieure à $1$ et coule lorsque la densité est supérieure à $1$

IV. Relation entre corps et masse

1. Expérience

A l'aide d'une balance et d'un dynamomètre, mesurons respectivement la masse et le poids de différents objets. 
 
 
On obtient le tableau de valeur suivants : 
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|} \hline \text{Masse }m(kg)&0.1&0.2&0.3&0.4&0.5&0.6&0.7&0.8&0.9&1\\ \hline \text{Poids } P(N)&0.98&1.96&2.94&3.92&4.9&5.88&6.86&7.84&8.82&9.8\\ \hline P/m\ (N/kg)&9.8&9.8&9.8&9.8&9.8&9.8&9.8&9.8&9.8&9.8\\ \hline \end{array}$$
 
$\blacktriangleright\ $Déterminons le rapport $\dfrac{\rho}{m}$
 
On constate en un lieu donné, le poids d'un objet est proportionnel à sa masse.
 
Ce rapport est constant : $\dfrac{\rho}{m}=9.8N\cdot kg^{-1}$
 
Cette constante ou coefficient de proportionnalité est égale à l'intensité $g$ du champ de pesanteur au lieu considéré. 
$$\dfrac{P}{m}=g\Rightarrow\boxed{\begin{array}{lcl} &|&P\text{ en }N\\ P=mg&|&m\text{ en }kg\\ &|&\left(N\cdot kg^{-1}\right) \end{array}}$$
 
$\blacktriangleright\ $Traçons la courbe représentant les variations du poids $P$ en fonction de la masse $m$
 
 
Le graphe représentant le poids $P$ en fonction de la masse $m$ est une droite passant par l'origine de la forme
 
$P=am$ Avec : $a=\dfrac{\Delta P}{\Delta m}=\dfrac{10.8-0}{1.1-0}=9.8N\cdot kg^{-1}=g$ étant le coefficient directeur de la droite
$$a=g\Rightarrow P=mg$$

2. Caractéristiques du vecteur champ de pesanteur

Le poids est une grandeur vectorielle et la masse une grandeur scalaire.
 
Le champ de pesanteur est donc une grandeur vectorielle
$$\overrightarrow{P}=m\overrightarrow{g}$$
Le champ de pesanteur $\overrightarrow{g}$ a les caractéristiques suivantes
 
$\blacktriangleright\ $Direction : la verticale du lieu
 
$\blacktriangleright\ $Sens : vers le bas

3. Variation de l'intensité de la pesanteur

Considérons les tableaux de mesures ci-dessous
$\begin{array}{|l|l|l|l|} \hline \text{Latitude}&\text{Paris}&\text{Pôles Nord}&\text{Equateur}\\ \hline g\left(N\cdot kg^{-1}\right)&9.81&9.83&9.78\\ \hline \end{array}\qquad\quad\begin{array}{|l|l|l|} \hline \text{Altitude}&\text{Chamonix}&\text{Mont Blanc}\\ \hline g\left(N\cdot kg^{-1} \right)&9.809&90.806\\ \hline \end{array}$
 
On constate que l'intensité de la pesanteur varie avec :
 
$-\ $la latitude du lieu considéré
 
$-\ $l'altitude considéré

4. Différences entre le poids et la masse

Il ne faut pas confondre le poids et la masse
 
La masse d'un corps est indépendante du lieu. 
 
Le poids d'un corps dépend du lieu où trouve ce corps
Le poids est une grandeur vectorielle. 
 
La masse est une grandeur scalaire positive
 
La masse s'exprime en kilogramme. Le poids s'exprime en newton.

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercice : Travail et Puissance Mécaniques - 1er L

Classe: 
Première
 

Exercice 1 

Mots croisés :
 
 
Horizontal
 
6. Relative à une puissance qui reflète une vitesse à laquelle un travail est fourni.  
 
8. Se dit du travail d'une force dont la direction de la force est perpendiculaire à celle du déplacement.
      
11. Travail dont la force favorise au déplacement
        
12. Travail d'une force qui s'oppose au déplacement
   
13. Force qui effectue un travail résistant lors que le corps monte
 
14. Partie des sciences physiques qui étudie l'équilibre et le mouvement des corps  
 
15. Ancienne unité de la puissance  
 
Vertical 
 
1. Quantité de travail fournie par intervalle de temps 
    
2. Capacité d'une force à faire déplacer un corps ou un système
   
3. Grandeur physique capable de déformer un corps
 
4. Se rapporte à une force dont sa valeur, son sens et sa direction ne varient pas au cours du temps.
   
5. Se dit d'une force dont le travail ne dépend pas du chemin suivi   
 
7. Quantité de travail fournie par unité de temps 
  
9. Unité de la puissance    
 
10. Unité du travail  

Exercice 2

Choisir la ou les bonne(s) réponse(s)
 
1. Dans le système international d'unités, le travail d'une force est exprimé en :
 
a. newton $(N)$  
 
b. watt $(W)$                           
 
c. joule $(J)$
 
2. Le travail d'une force constante dont le point d'application se déplace rectilignement de $A$ à $B$ peut être :
 
a. positif  
 
b. négatif
 
c. nul
 
3. Le travail $W$ d'une force constante faisant un angle $\alpha$ avec la trajectoire rectiligne de son point d'application est nul lorsque :
 
a. $\alpha=0^{\circ}$
 
b. $0^{\circ}<\alpha<90^{\circ}$
 
c. $\alpha=90^{\circ}$
 
d. $90^{\circ}<\alpha<180$
 
4. Le travail $W$ d'une force constante faisant un angle $\alpha$ avec la trajectoire rectiligne de son point d'application est positif lorsque :
 
a. $\alpha=0^{\circ}$
 
b. $0^{\circ}<\alpha<90^{\circ}$
 
c. $\alpha=90^{\circ}$
 
d. $90^{\circ}<\alpha<180$
 
5. Le travail $W$ d'une force constante faisant un angle $\alpha$ avec la trajectoire rectiligne de son point d'application est négatif lorsque :
 
a. $\alpha=0^{\circ}$
 
b. $0^{\circ}<\alpha<90^{\circ}$
                                   
c. $\alpha=90^{\circ}$
 
d. $90^{\circ}<\alpha<180^{\circ}$
 
6. Lorsque le travail d'une force est négatif, on dit que ce travail est :
 
a. moteur.
 
b. résistant.
 
7. La force de frottement a un travail :
 
a. toujours négatif.
 
b. toujours positif.        
 
c. toujours nul        
 
d. aucune des réponses précédentes.
 
8. Lorsqu'un objet tombe en chute libre, le travail du poids est :
 
a. positif.                        
 
b. négatif.                                   
 
c. nul.                       
 
d. cela dépend de la météo.
 
9. Une force est dite conservative si :
 
a. le travail de cette force est nul.
 
b. le travail de cette force est indépendant du trajet suivi par le système.
 
c. le travail de cette force est indépendant de l'état initial du système.
 
d. le travail de cette force est indépendant de l'état final du système.
 
10. Le travail d'une force perpendiculaire au déplacement est : 
 
a. positif ;                                                       
 
b. négatif ;                                            
 
c. nul. 
 
11. Le travail du poids d'un objet :
 
a. dépend de sa masse ; dépend du chemin suivi ; 
 
b. dépend seulement de l'altitude du point de départ et d'arrivée ;  
 
c. est résistant lors d'une montée ;              
 
d. est nul lors d'un mouvement de translation horizontal
 
12. Une force constante est appliquée à un solide en mouvement de translation, celle-ci transfert de l'énergie au solide sous forme de travail. 
 
a. la puissance moyenne est d'autant plus grande que la durée du transfert est grande. 
 
b. la puissance moyenne est proportionnelle à la force appliquée.
 
c. la puissance moyenne s'exprime en watt. 
 
d. pour une durée donnée, si on veut doubler la vitesse du solide il faut alors une puissance moyenne transférée deux fois plus grande.

Exercice 3

Questions de compréhension (les réponses doivent être justifiées)
 
1. Le travail d'une force peut-il être nul ?
 
2. Le travail d'une force dépend-il de la vitesse du déplacement ?
 
3. Une pierre tombe du haut d'une falaise. 
 
Le travail de son poids est-il moteur ou résistant ?
 
4. Le travail effectué par une force de frottement est-il moteur ou résistant ?

Exercice 4

Choisir, parmi les propositions suivantes :
 
1. Le travail d'une force appliquée à un objet animé d'un mouvement de translation rectiligne est nul si :
 
a. Le point d'application de la force se déplace à vitesse constante ;
 
b. La direction de la force est perpendiculaire au vecteur déplacement de son point d'application ;
 
c. La trajectoire est perpendiculaire au vecteur force.
 
2. Un solide est animé d'un mouvement de translation rectiligne uniforme. 
 
Il est soumis à deux forces constantes :
 
a. le travail de chacune des forces est nul ;                           
 
b. le travail de la somme des forces est nul ;
 
c. la somme des travaux de ces deux forces n'est pas nulle ;
 
3. le travail d'une force constante est moteur si :
 
a. la direction de cette force est colinéaire au déplacement rectiligne de son point d'application ;
 
b. l'angle entre le vecteur force et le vecteur déplacement est inférieur à $90^{\circ}$ ;
 
c. Le vecteur force est de même direction et de même sens que le vecteur déplacement

Exercice 5

1. Calculer le travail du poids d'un objet de masse $102\,g$ lors d'une chute de un mètre.
 
2. Calculer le travail fourni par un cheval qui exerce sur une voiture une traction constante de $700\,N$ le long d'un parcours horizontal de $6\,km$
 
3. Une personne d'un poids de $500\,N$ monte dans un ascenseur du rez de chaussée au cinquième étage puis redescend au troisième étage.
 
Calculer le travail effectué par son poids si la hauteur d'un étage est de trois mètres.

Exercice 6

1. Un moteur de $3\,KW$ de puissance fonctionne pendant $2$ heures.
 
Calculer le travail effectué.
 
2. Un homme monte un sac de $60\,kg$ à $20$ mètres de hauteur en $3$ minutes.
 
2.1. Calculer le travail qu'il effectue.
 
2.2. Quelle puissance développe-t-il ?
 
3. Une chute d'eau débite $200\,m^{3}$ d'eau par minute : 
 
la hauteur de la chute est de $30\,m.$
 
Calculer la puissance de cette chute.
 
4. Par l'intermédiaire d'un câble qui fait un angle de $30^{\circ}$ avec la direction de la voie, on applique une force de traction de $400\,N$ à des wagons.
 
Quel est le travail accompli pour parcourir $400\,m$ ?
 
5. Un moteur d'une puissance de $7.36\,Kw$ est utilisé pour soulever une charge de $500\,kg$ à une hauteur de $8\,m$
 
Quel temps le moteur met-il pour effectuer ce travail ?

Exercice 7

Deux jumeaux de même masse $m=75.0\,kg$ montent au $5^{ème}$ étage d'un immeuble en partant du rez-de-chaussée. 
 
Le jumeau $A$ emprunte l'ascenseur et le jumeau $B$ l'escalier. 
 
La distance entre le plancher durez-de-chaussée et le plancher du $5^{éme}$ est de $16.5\,m.$
 
1. Quel est le travail du poids de $A$ au cours de l'opération ?
 
1.1. Quel est celui de $B$ ?
 
1.2. Dans quel référentiel sont-ils définis ?
 
2. Quel est le travail correspondant au poids de $A$ dans le référentiel de l'ascenseur ?

Exercice 8

Une voiture de masse $1.5$ tonne roule à la vitesse constante de $108\,km/h$ sur un sol horizontal.
 
1. Faire le bilan des forces qu'elle subit et préciser quelles forces font un travail moteur, un travail résistant et celle qui font un travail nul.
 
2. La force de frottement vaut $1800N.$ 
 
Calculer le travail du poids et de la force motrice sur un trajet de $10\,km$
 
3. Calculer la puissance de la voiture.
 
4. Reprendre l'exercice en supposant que la voiture monte un col avec une pente de $10\%$

Exercice 9

L'eau d'un barrage est amenée à la turbine de la centrale électrique par une conduite forcée. 
 
La dénivellation entre le barrage et la turbine est $h=800\,m$
 
1. Déterminer le travail du poids de $1.0\,m$ d'eau entre le barrage et la turbine.
 
2. Déterminer la puissance $P$ de cette chute d'eau si son débit est $D=30\,m^{3}\cdot s^{-1}$
 
3. On admet que toute la puissance de la chute d'eau est transformée en puissance électrique par l'alternateur relié à la turbine. 
 
Quel devrait être le débit $D'$ d'une chute d'eau de même dénivellation pour que sa puissance soit celle d'un réacteur nucléaire de $1000\,MW$ ?

Exercice 10

Choisir la bonne réponse
 
Une force est conservative si :
 
a. son travail est nul
 
b. l'énergie mécanique est constante 
 
c. son travail ne dépend pas du chemin suivi                      
 
d. elle est constante
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Sidy Mouhamed Ndiaye

Interactions entre Objet : La Force - 2nd L

Classe: 
Seconde
 

I. Interaction entre objets

Une interaction implique que deux objets exercent une action l'un sur l'autre. 
 
Il existe deux formes d'interactions ou d'actions mécaniques : l'interaction de contact et l'interaction à distance

1. Interaction de contact

Une action est dite de contact si le point d'application se situe au point de contact entre les deux les objets

2. Interaction à distance

Elle correspond à une force qui s'exerce entre deux objets séparés par une distance

II. La force

1. Observations

Au cours d'un match de football entre deux équipes $A$ et $B$, un joueur de l'équipe de $A$ tire un coup franc
 
Le gardien de but de l'équipe $B$ peut, soit arrêter la balle, soit la dévier. 
 
Le joueur met ainsi en mouvement et le gardien de but modifie ce mouvement. 
 
Tous les deux ont exercé une action mécanique sur la balle
 
Un objet accroché à un ressort le déforme.
 
Le ressort, quant à lui, maintient l'objet au repos
 
Le ressort exercice une action mécanique sur l'objet. 
 
Il en va de même de l'objet sur le ressort

Remarque

La déformation peut ne pas être visible. 
 
C'est le cas, par exemple, d'un livre posé sur la table
 
Nous attribuerons tous les effets observés lors des situations précédentes, effets dynamiques et effets statiques à la même cause.
 
Cette cause commune est appelée force.

2. Définition 

Une force est toute cause capable :
 
$-\ $de mettre un corps en mouvement ou de modifier le mouvement d'un corps (effets dynamiques)
 
$-\ $de déformer un corps ou de le maintenir au repos (effets statiques)

3. Caractéristiques et représentation

3.1. Les caractéristiques d'une force

Les caractéristiques de cette force sont :
 
$-\ $Le point d'application :
 
C'est le point sur lequel la force exercice
 
$-\ $La direction
 
C'est la droite suivant laquelle la force agit
 
$-\ $Le sens
 
Le sens d'une force est le sens de déplacement que cette force tend à produire
 
$-\ $La valeur ou l'intensité
 
C'est la grandeur de la force
 
L'intensité ou la norme est d'autant plus grande que ses effets sur le déplacement ou la déformation d'un corps sont plus importants
 
Dans le Système International, l'unité de la force est le newton (symbole : $N)$
 
L'intensité de la force se mesure à l'aide d'un appareil appelé dynamomètre.
 
Il existe deux de dynamomètres : un dynamomètre simple et un dynamomètre circulaire.
 
 

3.2. Représentation d'une force

Les caractéristiques d'une force sont celles d'un vecteur : la force est une grandeur vectorielle
 

4. Exemples de forces

4.1. Forces de contact et forces à distance

4.1.1. Forces de contact

Elles se manifestent lorsqu'un corps est contact avec un autre corps

4.1.1. Les tensions

 
C'est la force exercée par ce fil sur un solide accroché à l'une de ses extrémités.
 
$\blacktriangleright\ $Point d'application : point d'attache
 
$\blacktriangleright\ $Direction : celle du fil tendu.
 
$\blacktriangleright\ $Sens : du point d'attache vers le fil
 
$\blacktriangleright\ $Intensité : égale à celle de la force exercée par l'objet accroché sur le fil
 
 
C'est la force exercée par ce ressort sur un solide accroché à l'une de ses extrémités.
 
$\blacktriangleright\ $Point d'application : point d'attache
 
$\blacktriangleright\ $Direction : celle du ressort tendu.
 
$\blacktriangleright\ $Sens : du point d'attache vers le ressort
 
$\blacktriangleright\ $Intensité : égale à celle de la force exercée par l'objet accroché sur le ressort
 
$T=k\left|1_{0}-1\right|$ Avec $k$ : constante de raideur du ressort en newtons $(N)\ ;\ 1$ : allongement du ressort et $1_{0}$ longueur à vide du ressort en mètres $(m)$

4.1.2. Les réactions

Dans le cas d'un objet posé sur un support, le support exerce une force sur l'objet (la réaction du support)
 
 
 
 

4.1.2. Forces de contact

On appelle forces à distances des forces qui exercent entre objets séparés par une distance.

Exemples : 

Les forces de gravitation, les forces magnétiques, les forces électriques
 
 
 

4.2. Forces localisées et forces réparties

4.2.1. Forces localisées

Une force est localisée sur un corps qu'on connait la position exacte à partir de laquelle elle exerce

Exemples : 

Les tensions, la réaction d'un crochet

4.2.2. Forces réparties

Une force est dite répartie si elle n'agit pas en un point, mais sur une surface

Exemples : 

L'action du vent sur la voile d'un bateau ; ou celle de la Terre sur un corps (elle s'exerce sur toutes les parties du corps)

Remarque :

Il est souvent possible de remplacer une force répartie par une force localisée ayant le même effet

III. Le principe des interactions

1. Observations

 
Le livre exerce une force $\overrightarrow{F}_{L/T}$ sur la table appelée action.
 
La table réagit en exerçant une force $\overrightarrow{F}_{T/L}$ sur le livre appelée réaction.

2. Énoncé du principe

Lorsqu'un solide $S_{1}$ est en interaction avec un solide $S_{2}$, la force $\overrightarrow{F}_{1}$ exercée par le solide $S_{1}$ sur le solide $S_{2}$ (action) est égale à l'opposé de la force $\overrightarrow{F}_{2}$ exercée par le solide $S_{2}$ sur le solide $S_{1}$ (réaction)
 
Les deux forces $\overrightarrow{F}_{1}$ et $\overrightarrow{F}_{2}$ ont la même droite d'action.
$$\boxed{\overrightarrow{F}_{1}=-\overrightarrow{F}_{2}}\quad\text{ou }\quad\boxed{\overrightarrow{F}_{1}+\overrightarrow{F}_{2}=0}$$
 
Auteur: 
Sidy Mouhamed Ndiaye

Le Circuit Électrique - 2nd L

Classe: 
Seconde
 

I. Circuit électrique

1. Générateurs et récepteur

1.1. Expérience

Nous nous proposons d'allumer la lampe nous pouvons pour cela allumer la lampe d'une façon beaucoup plus commode l'ampoule est montée sur son support puis reliée par des fils métalliques a la pile.
 
 
Le circuit électrique ainsi réalisé comporte :
 
$-\ $un appareil qui produit du courant ; c'est la pile
 
La pile est un générateur de courant
 
$-\ $un appareil qui reçoit le courant fourni par la pile ; c'est la lampe
 
La lampe est un récepteur de courant

1.2. Conclusion

Un circuit électrique est généralement constitué d'une chaine de générateur (s) et de récepteur (s) reliés par les fils conducteurs

Remarque :

Un circuit doit comporter au moins un générateur

2. Exemples de circuits électriques

2.1 Dipôles et symboles

La lampe, la pile possèdent chacun deux bornes ce sont des dipôles électriques
 
Ils sont représentés conventionnellement par des symboles
 
Symboles de quelques dipôles
 

2.2 Schéma du circuit

Un circuit électrique peut être schématisé à l'aide des symboles normalises

Exemple

2.3. Conducteurs et isolants

2.3.1. Expérience

Réalisons le circuit électrique fermé suivant en lui intercalant divers objets 
 
 
$$\begin{array}{|l|l|l|} \hline \text{Objet}&\text{Substance}&\text{Eat de la lampe}\\ \hline \text{Stylo à bille}&\text{Plastique}&\text{Lampe éteinte}\\ \hline \text{Fil de fer}&\text{Fer}&\text{Lampe éteinte}\\ \hline \end{array}$$

Conclusion

Le fil de fer, comme tous les métaux laissent passer le courant électrique. 
 
Ce sont des conducteurs électriques le stylo à bille (en plastique) le bois sec, le plastique le verre tout comme l'air ne laissent pas passer le courant électrique. 
 
Ce sont des isolants électriques

2.4. Les types de circuits

2.4.1. Le circuit série

Dans un circuit série, les dipôles sont reliés les uns à la suite des autres par des fils de connexion formant ainsi une seule boucle

Exemple

Remarques

$-\ $Un circuit est série est constituée d'une boule
 
$-\ $Dans un circuit série, lorsqu'on dipôle ne fonctionne pas le courant ne circule plus et les autres dipôles ne fonctionnent pas

2.4.2. Le circuit en dérivation ou en parallèle

 
Un circuit en dérivation ou en parallèle est un montage électrique dans lequel on peut trouver au moins deux boucles

Remarques

Dans un circuit en dérivation, si un dipôle ne fonctionne pas, les autres dipôles continuent de fonctionner
 
Un circuit en dérivation comporte des nœuds et des branches :
 
$-\ $Un nœud est un point où aboutissent au moins trois fils conducteurs $($exemple ; les nœuds $A$ et $B)$
 
$-\ $une branche est une portion de circuit compris entre deux nœuds
 
La branche qui contient le générateur est branche principale $(AKGB)$
 
Les autres branches sont des branches dérivées $(ALB$ et $DEC)$

2.4.3. Le circuit électrique de la bicyclette

 
 
L'observation du circuit d'une bicyclette montre qu'il est apparemment composé de deux lampes (phare et le feu arrière), d'une génératrice (la dynamo) et deux fils conducteurs
 
Si l'on schématise ce montage, on constate alors qu'il ne peut manifestement pas fonctionner : il n'est pas fermé
 
Il existe nécessairement entre les points $1$, $2$ et $3$ une liaison électrique qui n'est pas constitué par un fil
 
Cette liaison est assurée par le cadre métallique donc par un conducteur de la bicyclette. 
 
On dit que le circuit se ferme par le cadre ou encore par la masse

II. Les effets du courant électrique

Réalisons le circuit suivant
 

1. Effet calorifique

Si on ferme l'interrupteur la lampe s'allume et dégage de la chaleur.
 
La chaleur de la lampe est due au passage du courant qui chauffe et porte à incandescence le filament de la lampe c'est l'effet calorifique

2. Effet chimique

Si on ferme l'interrupteur, il apparait aux électrodes de l'électrolyseur contenant un électrolyte des dégagements de gaz : c'est l'effet chimique

3. Effet magnétique

Lorsque fait passer un courant dans un conducteur $AB$ placé au voisinage d'une aiguille aimantée, la position de cette dernière est modifiée comme dans le cas de la déviation de l'aiguille aimantée placé au voisinage d'un aimant. 
 
C'est l'effet magnétique

III. Sens conventionnel et nature du courant électrique

1. Sens conventionnel du courant électrique

Si nous fermons l'interrupteur, le courant se manifeste par trois effets: l'effet thermique, l'effet magnétique et l'effet chimique, l'inversion des branchements sur les bornes du générateur entraîne l'inversion des effets magnétique et chimique.
 
Nous pouvons donc dire, d'après les observations, que l'effet chimique et l'effet magnétique du courant électrique sont polarisés (ils dépendent du sens du courant électrique).
 
L'effet thermique est quand à lui non polarisé.
 
Pour le sens conventionnel, à l'extérieur d'un générateur, le courant circule de la borne positive du générateur vers la borne négative du générateur

2. Nature du courant électrique

2.1. Dans les conducteurs métalliques

2.1.1. Observations

Lorsqu'on ferme l'interrupteur le faisceau d'électrons du tube de Crookes et le conducteur (tige métallique) dévient dans le même sens : 
 
Dans la tige de cuivre le courant électrique est dû à une circulation d'électrons

2.1.2. Conclusion

Dans un conducteur métallique les porteurs de charges sont des électrons de conduction
 
Ils se déplacent en sens inverse conventionnel du courant électrique 

2.2. Dans les électrolytes

2.2.1. Observations

Si on ferme l'interrupteur les ions positifs $Cu^{2+}$ migrent vers l'électrode négative (cathode) et les ions négatifs $\left(Cr_{2}O_{7}^{2-}\right)$ vers l'électrode positive. 
 
Cette migration des ions est à l'origine de la circulation du courant électrique dans l'électrolyte.

2.2. 2. Conclusion

Dans un électrolyte les porteurs de charge sont des ions : les cations et les anions
 
Le sens conventionnel du courant est le sens de déplacement de porteurs de charge positive.

III. Dangers du courant électrique

Le corps humain n'est pas un excellent conducteur mais, dans certains cas, un courant électrique peut le traverser. 
 
On distingue deux types d'accidents : l'électrisation et l'électrocution.

1. L'électrisation

Une personne est électrisée si elle est traversée par un courant électrique. 
 
Cela peut entraîner de graves brûlures, la tétanisation des muscles et des contractions rapides et irrégulières du cœur.

2. Électrocution

Il y a électrocution lorsque le courant entraîne la mort. 
 
Les effets du courant électrique dépendent de divers facteurs : état de santé, âge, durée de l'électrisation, conditions d'humidité et surtout de la valeur de la tension électrique $($ension de sécurité $24V).$
 
Auteur: 
Sidy Mouhamed Ndiaye

Mouvement - Vitesse - 2nd L

Classe: 
Seconde

I. Mouvement

1. Notion de mouvement

 
Lorsqu'une voiture démarre, ses roues tournent, sa carrosserie se déplace par rapport à la route et les tous objets fixes sur la terre.
 
Un corps est en mouvement lorsqu'il change de position dans le temps par rapport à d'autres corps.

2. Relativité du mouvement

Le mouvement et l'immobilité sont des notions toutes relatives.
 
Un objet $A$ peut être en mouvement par rapport à un objet $B$ mais immobile par rapport à un objet $C.$
 
Ces observations montrent bien que l'état de mouvement ou de repos d'un corps dépend de l'objet de référence choisi appelé référentiel. 
 
On dit que le mouvement a un caractère relatif : C'est la relativité du mouvement.

II. Référentiels et repères

1. Référentiels

1.1. Définition

Un référentiel est un solide (ou un ensemble de solides) par rapport auquel le mouvement est étudié.

1.2. Exemples de référentiels

1.2.1. Référentiel héliocentrique

Il a pour origine le centre du système solaire et trois axes dirigés vers trois étoiles fixes.
 
Il est généralement utilisé des astres ou des planètes du système solaire 
 
 

1.2.2. Référentiel géocentrique

Il a pour origine le centre de la Terre et comprend trois axes dirigés vers trois étoiles fixes, parallèles à ceux du référentiel héliocentrique. 
 
Il est généralement utilisé pour l'étude du mouvement d'un satellite de la Terre.
 
 

1.2.3. Référentiel terrestre
 

Le solide de référence est la Terre. 
 
Il est utilisé dans le cadre des études mécaniques effectuées dans un laboratoire ou à partir du sol.
 
L'objet de référence peut être un arbre, un mur, une table d'expérience... etc 
 
Le référentiel terrestre est encore appelé référentiel de laboratoire 
 
 

2. Repères d'espace et de temps

Pour décrire le mouvement d'un point mobile, il faut le situer dans l'espace et dans le temps ; d'où la nécessité de choisir un repère d'espace et repère de temps 

2.1. Notion de point mobile

Tout objet en mouvement est appelé objet mobile. 
 
Cet objet est considéré comme point mobile si l'étude, sur une distance grande par rapport à ses dimensions porte sur son mouvement global

2.2. Repères d'espaces

Le repère d'espace permet de repérer d'un mobile.
 
Il est lié au référentiel d'étude
 
Le choix du repère d'espace se ramène au choix d'un système d'axes liés à la référence
 
Le repère d'espace peut être :

2.2.1. Le repère cartésien

Dans l'espace tout point $M$ est repéré par ses coordonnées ou ses composantes $x$, $y$ et $z$ ; le vecteur position est : 
$$\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}$$
 
 
Dans le plan, le point $M$ est repéré par ses coordonnées $x$ et $y$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}+y\vec{j}$$
 
 
Sur un axe, le point $M$ est repéré par sa coordonnée $x$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}$$
 
 

2.2.2. Le repère curviligne

Le mobile est repéré par son abscisse curviligne $S=\overset{\displaystyle\frown}{OM}$
 
 

2.2.3. Le repère angulaire

Le repère est constitué par un point origine $O$ associé à une base $\vec{i}$
 
 
La position du mobile est déterminé par :
 
$-\ $ la norme $S$ du vecteur  :   
 
$-\ $ l'angle polaire 

2.3. Repère de temps

$\blacktriangleright\ $ On peut distinguer deux aspects du temps :
 
$-\ $ l'instant, la date où se produit l'événement. 
 
Chaque instant est caractérisé par un nombre algébrique $t$ appelée date
 
$-\ $ la durée du phénomène qui mesure l'intervalle de temps entre le début et la fin du phénomène 
 
Deux évènements liant lieu à des dates $t_{i}$ et $t_{f}$ sont séparés par une durée ou intervalle de temps que l'on note : 
 
Dans le système l'unité de temps est la seconde $($symbole : $s)$
 
$\blacktriangleright\ $ Le repère de temps est l'association :
 
$-\ $ d'un instant origine ou origine des temps que l'on choisit arbitrairement
 
$-\ $ d'une unité de temps associé à un compteur de temps : le chronomètre ou l'horloge

3. Trajectoire

Dans un référentiel donné, la trajectoire d'un point mobile est l'ensemble des positions successivement occupées par ce point mobile

Remarque :

$\blacktriangleright\ $ Si la trajectoire est :
 
$-\ $ une droite, le mouvement est rectiligne ;
 
$-\ $ un cercle, le mouvement est circulaire ;
 
$-\ $ une courbe quelconque, le mouvement est curviligne
 
$\blacktriangleright\ $ La trajectoire d'un point mobile est relatif à un référentiel c'est-à-dire, elle dépend du référentiel 
 
Par exemple, la valve d'un vélo en mouvement décrit par rapport au sol, une courbe appelée cycloïde alors que, par rapport à l'axe de la roue, elle décrit un mouvement circulaire
 
Par rapport à la roue, elle est immobile

 
 

III. Vitesse

Dans la vie courante, la distance parcourue et la durée du parcours sont toujours associées

1. Vitesse moyenne

Dans un référentiel donné, la vitesse moyenne d'un point ou d'un objet entre deux instants $t_{i}$ et $t_{f}$ est le rapport de la distance $d$ parcourue par ce point par la durée du parcours $\Delta\,t=t_{f}-t_{i}$ :
$$\begin{array}{l|l} &d=\text{distance parcourue (en m)}\\ \boxed{V_{M}=\dfrac{d}{\Delta\,t}=\dfrac{d}{t_{f}-t_{i}}}&\Delta\,t=t_{f}-t_{i}=\text{durée du parcours (en s)}\\ &V_{M}=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$
$\blacktriangleright\ $ Si la vitesse augmente, le mouvement est accéléré ;
 
$\blacktriangleright\ $ Si la vitesse diminue, le mouvement est ralenti ou décéléré ou retard 
 
$\blacktriangleright\ $ Si la vitesse est constante, le mouvement est uniforme.

Remarque : 

$\blacktriangleright\ $ Il est fréquent d'exprimer une vitesse en kilomètre par heure
$$V(\text{en }m\cdot s^{-1})\stackrel{\times 3.6}{\longrightarrow}V(\text{en }km\cdot h^{-1})$$
$$V(\text{en }m\cdot s^{-1})\stackrel{\div 3.6}{\longleftarrow}V(\text{en }km\cdot h^{-1})$$
$\blacktriangleright\ $ La vitesse moyenne donne une information globale sur le parcours mais ne permet pas de savoir comment il a été : freinage, accélération, arrêt 

2. Vitesse instantanée 

2.1. Définition 

La vitesse instantanée d'un point mobile $M$ est la vitesse à l'instant $t$
 
Pratiquement cette vitesse instantanée du point mobile, à la date $t$, est égale à sa vitesse moyenne calculée pendant un intervalle très court encadrant l'instant $t$ considérée
$$\begin{array}{l|l} &i\neq 0\\ \boxed{V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}}&t_{i+1}-t_{i-1}=\text{durée du parcours (en s)}\\& V_{i}(t_{i})=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$

2.2. Détermination pratique

Le document ci-dessous est une production de l'enregistrement, à intervalle de temps réguliers $\tau$ du mouvement d'un mobile $M$
 
 
Déterminons les expressions des vitesses instantanées $V_{1}\;,\ V_{2}\;,\ V_{3}\ $ et $\ V_{6}$
 
De manière générale :
$$V_{i}=V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$$
 
$V_{1}=V_{1}(t_{1})=\dfrac{M_{0}M_{2}}{t_{2}-t_{0}}=\dfrac{M_{0}M_{2}}{2\tau}$ ;
 
$V_{2}=V_{2}(t_{2})=\dfrac{M_{1}M_{3}}{t_{3}-t_{1}}=\dfrac{M_{1}M_{3}}{2\tau}$ ;
 
$V_{3}=V_{3}(t_{3})=\dfrac{M_{2}M_{4}}{t_{4}-t_{2}}=\dfrac{M_{2}M_{4}}{2\tau}$ ;
 
$V_{6}=V_{6}(t_{6})=\dfrac{M_{5}M_{7}}{t_{7}-t_{5}}=\dfrac{M_{5}M_{7}}{2\tau}$ 

3. Vecteur vitesse instantanée

La valeur de la vitesse instantanée est insuffisante pour caractériser le mouvement d'un point mobile 
 
Elle n'indique pas la direction du mouvement, le sens du mouvement 
 
Pour ces informations, il faut introduire le vecteur vitesse instantanée 

3.1. Définition 

Le vecteur vitesse instantanée est pratiquement définie par la relation : 
$$\overrightarrow{V}_{i}=\overrightarrow{V}_{i}(t_{i})=\dfrac{\overrightarrow{M_{i-1}M_{i+1}}}{t_{i+1}-t_{i-1}}\quad\text{ avec }i\neq 0$$

Exemple :

3.2. Caractéristiques du vecteur vitesse instantanée

Les caractéristiques du vecteur vitesse instantanée au point $M$ sont 
 
$\surd\ $ le point $M$
 
$\surd\ $ tangente à la trajectoire au point $M$
 
$\surd\ $ Sens : celui du mouvement
 
$\surd\ $ Norme : la valeur $V_{i}=V_{i}(t)=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$
 
 

IV. Étude de quelques mouvements

1. Mouvement rectiligne

1.1. Définition

$-\ $ Un mobile est en mouvement rectiligne uniforme s'il se déplace sur une droite avec un vecteur vitesse constant.

Remarque :

Un mobile est en mouvement rectiligne si le mobile parcourt des distances égales pendant des durées égales.
 
 

1.2. Loi horaire

Par définition :
 
$\begin{array}{rcrcl} V=\dfrac{MM_{0}}{t-t_{0}}=\dfrac{x-x_{0}}{t-t_{0}}&\Rightarrow&x-x_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&x&=&V(t-t_{0})+x_{0} \end{array}$
 
Si $t_{0}=0$ alors, $x=V(t-0)+x_{0}$
 
Par suite, $x=Vt+x_{0}$
 
Ainsi, $x$ est une fonction affine du temps

2. Mouvement rectiligne varié

2.1. Définition

$-\ $ Un mobile est en mouvement rectiligne varié s'il se déplace sur une droite avec un vecteur vitesse de module variable.

2.2. Mouvement accéléré et mouvement décéléré 

Le mouvement est accéléré si le module du vecteur vitesse croit ; le mouvement est décéléré ou retardé si le module du vecteur vitesse décroit.

Remarque :

$-\ $ Un mobile est en mouvement rectiligne accéléré si le mobile parcourt des distances de plus en plus grandes pendant des durées égales 
 
 
$-\ $ Un mobile est en mouvement rectiligne décéléré ou retardé si le mobile parcourt des distances de plus en plus petites pendant des durées égales
 
 
Le mouvement est uniformément varié si la vitesse est une fonction affine du temps.

3. Mouvement circulaire uniforme

3.1. Définition

$-\ $ Un mobile est en mouvement circulaire uniforme s'il se déplace sur un cercle avec un vecteur vitesse de module constant.
 

 
Le vecteur vitesse varie en direction et en sens.

3.2. Loi horaire

Par définition :
 
$\begin{array}{rcrcl} V=\dfrac{\overset{\displaystyle\frown}{M_{0}M}}{t-t_{0}}=\dfrac{S-S_{0}}{t-t_{0}}&\Rightarrow&S-S_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&S&=&V(t-t_{0})+S_{0}\end{array}$
 
Par suite, si $t_{0}=0$ alors, $S=Vt+S_{0}$
 
Il est une relation entre l'abscisse curviligne et l'angle : $S=R\theta$

3.3. La période du mouvement

La durée pour effectuer un tour est appelée période que l'on note $T.$
 
Le mouvement étant uniforme 
$$V=\dfrac{d}{\Delta t}=\dfrac{2\pi R}{T}\Rightarrow T=\dfrac{2\pi R}{V}$$
 
$T$ est constant, car $R$ est fixe et $V$ est constant

3.3. La fréquence du mouvement

La fréquence du mouvement représente le nombre de périodes par seconde 
$$N=\dfrac{1}{T}\quad\text{ ou }\quad N=\dfrac{V}{2\pi R}$$
La fréquence $N$ s'exprime en hertz $($symbole : $Hz)$

V. Mouvement de translation et de rotation d'un solide

1. Mouvement de translation d'un solide

1.1. Définition

Un solide (ou objet indéformable) effectue un mouvement de translation lorsque n'importe quel segment de ce solide se déplace en conservant sa direction. 

1.2. Les différents types de translation

La translation peut être :
 
$-\ $ rectiligne : chaque point du solide décrit une droite
 
$-\ $ curviligne : chaque du solide décrit une courbe
 
$-\ $ circulaire : chaque du solide décrit un cercle  

2. Mouvement de rotation d'un solide

2.1. Définition

Un solide est un mouvement de rotation si les points d'un mobile en rotation décrivent des cercles ou des arcs de cercle centrés sur la même droite, appelée axe de rotation. 
 
Cet axe est perpendiculaire aux plans du cercle.

2.2. Vitesse angulaire

La vitesse angulaire est l'angle balayé par seconde
$$\begin{array}{l|l} &\alpha\text{ angle radians (rad)}\\\boxed{\omega=\dfrac{\alpha}{\Delta t}}&\Delta t=t_{f}-t_{i}=\text{durée en seconde (s)}\\&\omega=\text{vitesse angulaire en radians par seconde }(rad\cdot s^{-1}) \end{array}$$

2.3. Relation entre vitesse d'un point et vitesse angulaire

Par définition :
 
$v=\dfrac{S}{\Delta t}=\dfrac{R\alpha}{\Delta t}=R\dfrac{\alpha}{\Delta t}$
 
Or, $\omega=\dfrac{\alpha}{\Delta t}$ donc, $v=R\omega$

I. Mouvement

1. Notion de mouvement

 
Lorsqu'une voiture démarre, ses roues tournent, sa carrosserie se déplace par rapport à la route et les tous objets fixes sur la terre.
 
Un corps est en mouvement lorsqu'il change de position dans le temps par rapport à d'autres corps.

2. Relativité du mouvement

Le mouvement et l'immobilité sont des notions toutes relatives.
 
Un objet $A$ peut être en mouvement par rapport à un objet $B$ mais immobile par rapport à un objet $C.$
 
Ces observations montrent bien que l'état de mouvement ou de repos d'un corps dépend de l'objet de référence choisi appelé référentiel. 
 
On dit que le mouvement a un caractère relatif : C'est la relativité du mouvement.

II. Référentiels et repères

1. Référentiels

1.1. Définition

Un référentiel est un solide (ou un ensemble de solides) par rapport auquel le mouvement est étudié.

1.2. Exemples de référentiels

1.2.1. Référentiel héliocentrique

Il a pour origine le centre du système solaire et trois axes dirigés vers trois étoiles fixes.
 
Il est généralement utilisé des astres ou des planètes du système solaire 
 
 

1.2.2. Référentiel géocentrique

Il a pour origine le centre de la Terre et comprend trois axes dirigés vers trois étoiles fixes, parallèles à ceux du référentiel héliocentrique. 
 
Il est généralement utilisé pour l'étude du mouvement d'un satellite de la Terre.
 
 

1.2.3. Référentiel terrestre
 

Le solide de référence est la Terre. 
 
Il est utilisé dans le cadre des études mécaniques effectuées dans un laboratoire ou à partir du sol.
 
L'objet de référence peut être un arbre, un mur, une table d'expérience... etc 
 
Le référentiel terrestre est encore appelé référentiel de laboratoire 
 
 

2. Repères d'espace et de temps

Pour décrire le mouvement d'un point mobile, il faut le situer dans l'espace et dans le temps ; d'où la nécessité de choisir un repère d'espace et repère de temps 

2.1. Notion de point mobile

Tout objet en mouvement est appelé objet mobile. 
 
Cet objet est considéré comme point mobile si l'étude, sur une distance grande par rapport à ses dimensions porte sur son mouvement global

2.2. Repères d'espaces

Le repère d'espace permet de repérer d'un mobile.
 
Il est lié au référentiel d'étude
 
Le choix du repère d'espace se ramène au choix d'un système d'axes liés à la référence
 
Le repère d'espace peut être :

2.2.1. Le repère cartésien

Dans l'espace tout point $M$ est repéré par ses coordonnées ou ses composantes $x$, $y$ et $z$ ; le vecteur position est : 
$$\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}$$
 
 
Dans le plan, le point $M$ est repéré par ses coordonnées $x$ et $y$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}+y\vec{j}$$
 
 
Sur un axe, le point $M$ est repéré par sa coordonnée $x$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}$$
 
 

2.2.2. Le repère curviligne

Le mobile est repéré par son abscisse curviligne $S=\overset{\displaystyle\frown}{OM}$
 
 

2.2.3. Le repère angulaire

Le repère est constitué par un point origine $O$ associé à une base $\vec{i}$
 
 
La position du mobile est déterminé par :
 
$-\ $ la norme $S$ du vecteur  :   
 
$-\ $ l'angle polaire 

2.3. Repère de temps

$\blacktriangleright\ $ On peut distinguer deux aspects du temps :
 
$-\ $ l'instant, la date où se produit l'événement. 
 
Chaque instant est caractérisé par un nombre algébrique $t$ appelée date
 
$-\ $ la durée du phénomène qui mesure l'intervalle de temps entre le début et la fin du phénomène 
 
Deux évènements liant lieu à des dates $t_{i}$ et $t_{f}$ sont séparés par une durée ou intervalle de temps que l'on note : 
 
Dans le système l'unité de temps est la seconde $($symbole : $s)$
 
$\blacktriangleright\ $ Le repère de temps est l'association :
 
$-\ $ d'un instant origine ou origine des temps que l'on choisit arbitrairement
 
$-\ $ d'une unité de temps associé à un compteur de temps : le chronomètre ou l'horloge

3. Trajectoire

Dans un référentiel donné, la trajectoire d'un point mobile est l'ensemble des positions successivement occupées par ce point mobile

Remarque :

$\blacktriangleright\ $ Si la trajectoire est :
 
$-\ $ une droite, le mouvement est rectiligne ;
 
$-\ $ un cercle, le mouvement est circulaire ;
 
$-\ $ une courbe quelconque, le mouvement est curviligne
 
$\blacktriangleright\ $ La trajectoire d'un point mobile est relatif à un référentiel c'est-à-dire, elle dépend du référentiel 
 
Par exemple, la valve d'un vélo en mouvement décrit par rapport au sol, une courbe appelée cycloïde alors que, par rapport à l'axe de la roue, elle décrit un mouvement circulaire
 
Par rapport à la roue, elle est immobile

 
 

III. Vitesse

Dans la vie courante, la distance parcourue et la durée du parcours sont toujours associées

1. Vitesse moyenne

Dans un référentiel donné, la vitesse moyenne d'un point ou d'un objet entre deux instants $t_{i}$ et $t_{f}$ est le rapport de la distance $d$ parcourue par ce point par la durée du parcours $\Delta\,t=t_{f}-t_{i}$ :
$$\begin{array}{l|l} &d=\text{distance parcourue (en m)}\\ \boxed{V_{M}=\dfrac{d}{\Delta\,t}=\dfrac{d}{t_{f}-t_{i}}}&\Delta\,t=t_{f}-t_{i}=\text{durée du parcours (en s)}\\ &V_{M}=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$
$\blacktriangleright\ $ Si la vitesse augmente, le mouvement est accéléré ;
 
$\blacktriangleright\ $ Si la vitesse diminue, le mouvement est ralenti ou décéléré ou retard 
 
$\blacktriangleright\ $ Si la vitesse est constante, le mouvement est uniforme.

Remarque : 

$\blacktriangleright\ $ Il est fréquent d'exprimer une vitesse en kilomètre par heure
$$V(\text{en }m\cdot s^{-1})\stackrel{\times 3.6}{\longrightarrow}V(\text{en }km\cdot h^{-1})$$
$$V(\text{en }m\cdot s^{-1})\stackrel{\div 3.6}{\longleftarrow}V(\text{en }km\cdot h^{-1})$$
$\blacktriangleright\ $ La vitesse moyenne donne une information globale sur le parcours mais ne permet pas de savoir comment il a été : freinage, accélération, arrêt 

2. Vitesse instantanée 

2.1. Définition 

La vitesse instantanée d'un point mobile $M$ est la vitesse à l'instant $t$
 
Pratiquement cette vitesse instantanée du point mobile, à la date $t$, est égale à sa vitesse moyenne calculée pendant un intervalle très court encadrant l'instant $t$ considérée
$$\begin{array}{l|l} &i\neq 0\\ \boxed{V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}}&t_{i+1}-t_{i-1}=\text{durée du parcours (en s)}\\& V_{i}(t_{i})=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$

2.2. Détermination pratique

Le document ci-dessous est une production de l'enregistrement, à intervalle de temps réguliers $\tau$ du mouvement d'un mobile $M$
 
 
Déterminons les expressions des vitesses instantanées $V_{1}\;,\ V_{2}\;,\ V_{3}\ $ et $\ V_{6}$
 
De manière générale :
$$V_{i}=V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$$
 
$V_{1}=V_{1}(t_{1})=\dfrac{M_{0}M_{2}}{t_{2}-t_{0}}=\dfrac{M_{0}M_{2}}{2\tau}$ ;
 
$V_{2}=V_{2}(t_{2})=\dfrac{M_{1}M_{3}}{t_{3}-t_{1}}=\dfrac{M_{1}M_{3}}{2\tau}$ ;
 
$V_{3}=V_{3}(t_{3})=\dfrac{M_{2}M_{4}}{t_{4}-t_{2}}=\dfrac{M_{2}M_{4}}{2\tau}$ ;
 
$V_{6}=V_{6}(t_{6})=\dfrac{M_{5}M_{7}}{t_{7}-t_{5}}=\dfrac{M_{5}M_{7}}{2\tau}$ 

3. Vecteur vitesse instantanée

La valeur de la vitesse instantanée est insuffisante pour caractériser le mouvement d'un point mobile 
 
Elle n'indique pas la direction du mouvement, le sens du mouvement 
 
Pour ces informations, il faut introduire le vecteur vitesse instantanée 

3.1. Définition 

Le vecteur vitesse instantanée est pratiquement définie par la relation : 
$$\overrightarrow{V}_{i}=\overrightarrow{V}_{i}(t_{i})=\dfrac{\overrightarrow{M_{i-1}M_{i+1}}}{t_{i+1}-t_{i-1}}\quad\text{ avec }i\neq 0$$

Exemple :

3.2. Caractéristiques du vecteur vitesse instantanée

Les caractéristiques du vecteur vitesse instantanée au point $M$ sont 
 
$\surd\ $ le point $M$
 
$\surd\ $ tangente à la trajectoire au point $M$
 
$\surd\ $ Sens : celui du mouvement
 
$\surd\ $ Norme : la valeur $V_{i}=V_{i}(t)=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$
 
 

IV. Étude de quelques mouvements

1. Mouvement rectiligne

1.1. Définition

$-\ $ Un mobile est en mouvement rectiligne uniforme s'il se déplace sur une droite avec un vecteur vitesse constant.

Remarque :

Un mobile est en mouvement rectiligne si le mobile parcourt des distances égales pendant des durées égales.
 
 

1.2. Loi horaire

Par définition :
 
$\begin{array}{rcrcl} V=\dfrac{MM_{0}}{t-t_{0}}=\dfrac{x-x_{0}}{t-t_{0}}&\Rightarrow&x-x_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&x&=&V(t-t_{0})+x_{0} \end{array}$
 
Si $t_{0}=0$ alors, $x=V(t-0)+x_{0}$
 
Par suite, $x=Vt+x_{0}$
 
Ainsi, $x$ est une fonction affine du temps

2. Mouvement rectiligne varié

2.1. Définition

$-\ $ Un mobile est en mouvement rectiligne varié s'il se déplace sur une droite avec un vecteur vitesse de module variable.

2.2. Mouvement accéléré et mouvement décéléré 

Le mouvement est accéléré si le module du vecteur vitesse croit ; le mouvement est décéléré ou retardé si le module du vecteur vitesse décroit.

Remarque :

$-\ $ Un mobile est en mouvement rectiligne accéléré si le mobile parcourt des distances de plus en plus grandes pendant des durées égales 
 
 
$-\ $ Un mobile est en mouvement rectiligne décéléré ou retardé si le mobile parcourt des distances de plus en plus petites pendant des durées égales
 
 
Le mouvement est uniformément varié si la vitesse est une fonction affine du temps.

3. Mouvement circulaire uniforme

3.1. Définition

$-\ $ Un mobile est en mouvement circulaire uniforme s'il se déplace sur un cercle avec un vecteur vitesse de module constant.
 

 
Le vecteur vitesse varie en direction et en sens.

3.2. Loi horaire

Par définition :
 
$\begin{array}{rcrcl} V=\dfrac{\overset{\displaystyle\frown}{M_{0}M}}{t-t_{0}}=\dfrac{S-S_{0}}{t-t_{0}}&\Rightarrow&S-S_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&S&=&V(t-t_{0})+S_{0}\end{array}$
 
Par suite, si $t_{0}=0$ alors, $S=Vt+S_{0}$
 
Il est une relation entre l'abscisse curviligne et l'angle : $S=R\theta$

3.3. La période du mouvement

La durée pour effectuer un tour est appelée période que l'on note $T.$
 
Le mouvement étant uniforme 
$$V=\dfrac{d}{\Delta t}=\dfrac{2\pi R}{T}\Rightarrow T=\dfrac{2\pi R}{V}$$
 
$T$ est constant, car $R$ est fixe et $V$ est constant

3.3. La fréquence du mouvement

La fréquence du mouvement représente le nombre de périodes par seconde 
$$N=\dfrac{1}{T}\quad\text{ ou }\quad N=\dfrac{V}{2\pi R}$$
La fréquence $N$ s'exprime en hertz $($symbole : $Hz)$

V. Mouvement de translation et de rotation d'un solide

1. Mouvement de translation d'un solide

1.1. Définition

Un solide (ou objet indéformable) effectue un mouvement de translation lorsque n'importe quel segment de ce solide se déplace en conservant sa direction. 

1.2. Les différents types de translation

La translation peut être :
 
$-\ $ rectiligne : chaque point du solide décrit une droite
 
$-\ $ curviligne : chaque du solide décrit une courbe
 
$-\ $ circulaire : chaque du solide décrit un cercle  

2. Mouvement de rotation d'un solide

2.1. Définition

Un solide est un mouvement de rotation si les points d'un mobile en rotation décrivent des cercles ou des arcs de cercle centrés sur la même droite, appelée axe de rotation. 
 
Cet axe est perpendiculaire aux plans du cercle.

2.2. Vitesse angulaire

La vitesse angulaire est l'angle balayé par seconde
$$\begin{array}{l|l} &\alpha\text{ angle radians (rad)}\\\boxed{\omega=\dfrac{\alpha}{\Delta t}}&\Delta t=t_{f}-t_{i}=\text{durée en seconde (s)}\\&\omega=\text{vitesse angulaire en radians par seconde }(rad\cdot s^{-1}) \end{array}$$

2.3. Relation entre vitesse d'un point et vitesse angulaire

Par définition :
 
$v=\dfrac{S}{\Delta t}=\dfrac{R\alpha}{\Delta t}=R\dfrac{\alpha}{\Delta t}$
 
Or, $\omega=\dfrac{\alpha}{\Delta t}$ donc, $v=R\omega$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

L'électricité dans notre environnement - 2nd L

Classe: 
Seconde
 

I. Phénomènes d'électrisation

1. Électrisation par frottement

1.1. Expérience

$-\ $Un bâton en verre bien sèche, frotté à l'aide d'un morceau de drap en soie ou en laine, tenue à la main, attire de petits morceaux de papier.
 
$-\ $On obtient le même résultat si on remplace le bâton en verre par un bâton d'ébonite et si on répète la même opération.
 
 
Les corps frottés sont également capables d'attirer des cheveux ou un mince filet d'eau qui coule d'un robinet.
 
Les corps frottés sont également capables d'attirer des cheveux ou un mince filet d'eau qui coule d'un robinet.

1.2. Conclusion

Il est possible d'électriser ou de charger d'électricité la matière en la frottant.
 
Ce phénomène s'appelle l'électrisation par frottement.
 
Des corps électrisés peuvent attirer d'autres corps plus légers.

2. Électrisation par contact

2.1. Expérience

On constitue, à présent, un pendule électrostatique en suspendant au fil de soie une boule de polystyrène recouverte d'une matière conductrice. 
 
Celle-ci est initialement neutre. 
 
Approchons un bâton en verre, électrisée par frottement, de la boule jusqu'au contact.
 
On constate que la boule est repoussée sous l'effet de son interaction avec la partie électrisée de la tige
 

2.2. Conclusion

Un corps qui, après contact avec un autre corps électrique, acquiert la propriété d'attirer des corps légers a été électrisé par contact

3. Électrisation par influence

3.1. Expérience

L'électroscope est constitué d'une tige métallique qui comporte à son extrémité inférieure deux feuilles d'or très minces qui tombent librement.
 
Un plateau ou une boule métallique sont fixés à l'extrémité supérieure et l'ensemble est enfermé dans une cage métallique vitrée.
 
Le bâton d'ébonite, chargé négativement, est approché du plateau.
 
On constate les feuilles d'or du pendule se repoussent.
 
Si on éloigne l'ébonite, l'ensemble (plateau, tige, feuilles) retrouve sa neutralité ; les feuilles de l'électroscope reprennent leur position verticale initiale
 

3.2. Conclusion 

Les deux feuilles se repoussent parce qu'elles sont électrisées sous l'influence du bâton
 
Un corps peut être électrisé par influence en rapprochant un autre corps électrique

II. Les Charges électriques 

1. Les deux espèces d'électricité

1.1. Expérience

Les pendules sont constitués d'une potence, fixée sur un socle en bois, à laquelle est relié un fil de soie sans torsion.
 
 
Suspendons, en son milieu, un bâton d'ébonite dont une extrémité a été électrisé par frottement.
 
Approchons de cette extrémité la partie électrisée, par la même méthode, d'un second bâton d'ébonite.
 
L'interaction de ces parties électrisées se traduit par une répulsion.
 
Répétons la même expérience, en remplaçant les bâtons d'ébonite par des tiges de verre électrisées comme précédemment. 
 
Là encore l'interaction se traduit par une répulsion.
 
Dans une troisième expérience, on met en présence l'extrémité électrisée du bâton d'ébonite et celle de la tige de verre électrisée.
 
Il en résulte, à présent, une attraction

1.2. Interprétation

Ces expériences mettent en évidence deux types d'électricité :
 
La première apparait dans le verre : c'est l'électricité vitreuse à laquelle on a attribué arbitrairement un signe positif.
 
La seconde se manifeste dans l'ébonite et d'autres résines : c'est l'électricité résineuse ; on lui a attribué un signe négatif.
 
En outre, ces expériences montrent que :
 
$-\ $deux corps chargés d'une électricité de même signe, positive ou négative, se repoussent ;
 
$-\ $deux corps chargés de signes contraires s'attirent
 
Un corps qui n'est pas chargé est neutre.

2. La quantité de charge électrique

La quantité de charge électrique est mesurée en coulomb $C.$
 
Comme un atome est électriquement neutre, la valeur absolue de la charge d'un électron est égale à celle d'un proton. 
 
Cette charge élémentaire, notée $e$, vaut $e=1.602\cdot10^{-19}C$
 
Toute autre charge électrique $Q$ est un multiple entier de la charge élémentaire :
$$Q=ne\;,\ n\in\mathbb{Z}$$

III. Interprétation électronique de l'électrisation

1. Structure de la matière

La matière est constituée d'atomes
 
Un atome peut être considéré comme se composant de deux parties :
 
$-\ $un noyau, constitué de protons chargés positivement et de neutrons électriquement neutres ;
 
$-\ $une enveloppe, appelée nuage électronique, constituée d'électrons chargés négativement
 

Remarque

Un atome électriquement neutre contient autant d'électrons que de protons, la charge des protons et des électrons étant la même en valeur absolue.

2. Électrisation par frottement

Avant le frottement les corps sont électriquement neutres.
 
En les frottant on agit sur les atomes situés à la surface des corps.
 
Les électrons les moins liés sont arrachés d'un des corps et sont transférés sur l'autre. 
 
L'un des corps a un défaut d'électrons : il est chargé positivement.
 
L'autre présente un excès d'électrons et est chargé négativement.
 
 
Un bâton d'ébonite par exemple arrache des électrons au chiffon de laine et se charge négativement.
 
Il est important de remarquer que la charge électrique ne peut être ni créée, ni détruit
 
Les corps s'électrisent uniquement par transfert d'électrons
 
Lorsqu'on corps est électrisé par frottement, il y a lieu un transfert de charges : les électrons les plus faiblement liés sont transférés d'un corps à l'autre.
 
Ainsi :
 
$-\ $un corps chargé positivement présente un défaut d'électrons ;
 
$-\ $un corps chargé négativement présente un excès d'électrons.

3. Électrisation par contact

Lors d'une électrisation par contact, il y a aussi un transfert de charges :
 
$-\ $un corps chargé négativement transmet des électrons au corps initialement neutre ;
 
$-\ $un corps chargé positivement arrache des électrons au corps initialement neutre
 

4. Électrisation par influence

Lorsqu'on approche un corps chargé du corps neutre, les électrons libres sont attirés Il s'établit un déséquilibre des charges dans le corps neutre : les électrons sont en excès du côté du corps positif, ils sont en défaut du côté opposé. 
 
Il y a donc séparation des charges à l'intérieur du corps neutre.
 
La région plus près du corps chargé sera chargée négativement, le côté opposé sera chargé positivement.
 
Dès qu'on éloigne le corps chargé, les électrons se répartissent de nouveau de façon uniforme dans le corps neutre.
 
 
L'électroscope est électrisé par influence, les électrons sont repoussés vers la partie inférieure de l'électroscope.
 
L'électroscope reste neutre et les  électrons retrouvent leur disposition initiale si on éloigne la baguette.

Remarque :

Cette observation permet d'expliquer pourquoi des petits bouts de papier sont attirés par un corps chargé

IV. Conducteurs et isolants

1. Conducteurs

1.1. Expérience

Électrisons par frottement (ou par contact) une règle en plexiglas.
 
Intercalons entre la règle et la boule une tige en carbone (crayon taillé des deux bouts), posée sur un support isolant.
 
Remplaçons la tige en carbone par une tige en cuivre puis, par une tige en aluminium
 

1.1.1. Observation

La boule est repoussée dans le cas du cuivre, de l'aluminium et du carbone
 
La boule s'électrise positivement par contact avec les tiges en cuivre, en aluminium et en carbone

1.1.2. Interprétation

Par contact avec la règle en plexiglas, la tige en cuivre (ou en aluminium ou en carbone) s'électrise positivement en cédant des électrons à la règle. 
 
Ces électrons ayant quitté la tige font apparaitre une charge positive sur toute la tige.
 
La charge positive qui apparaît sur le cuivre (ou l'aluminium ou le carbone) n'est pas localisée à la zone touchée par la règle.
 
L'extrémité de la tige, en contact avec la boule, arrache des électrons à cette dernière, l'amenant ainsi à devenir chargée positivement ce qui explique la répulsion.
 
Le cuivre, l'aluminium et le carbone sont des matériaux qui laissent circuler les électrons ; ils sont appelés des conducteurs

1.2. Conclusion

Les conducteurs sont des matériaux dont les charges électriques internes (électrons libres) se déplacent librement.

Exemples de conducteurs : 

tous les métaux, le carbone

2. Isolants électriques

2.1. Expérience

Reprenons la même expérience en remplaçant la tige en carbone par une autre en verre, puis en bois, puis en $P.V.C$, enfin en plexiglas.

2.1.1. Observation

La boule garde sa position dans le cas du bois, du verre, du $P.V.C$ et du plexiglas.
 
La boule ne s'électrise pas, malgré le contact avec les autres tiges.

2.1.2. Interprétation

Le bois, le plexiglas, le verre et le $P.V.C$ sont des matériaux qui ne permettent pas une circulation des électrons (la charge électrique reste localisée au bout des tiges du côté de la règle en plexiglas) ils sont appelés des isolants.

2.2. Conclusion

Les isolants électriques sont des matériaux dont les charges électriques internes (électrons libres) ne se déplacent pas librement

Exemples d'isolants : 

le verre, l'ébonite, le Plexiglas, le caoutchouc, la porcelaine.

V. Histoire de l'électricité

L'histoire de l'électricité débute durant l'Antiquité, avec la découverte des propriétés attractives de l'ambre frottée, et continue de s'écrire aujourd'hui encore avec plusieurs thèmes d'actualité: moteurs électriques, batteries rechargeables, panneaux solaires, etc.

1. Découverte de l'électricité

L'électricité est un phénomène physique qui a toujours existé, c'est le résultat d'échange d'énergie comme les éclairs. 
 
L'électricité provient du mot Grec « électron » qui désigne l'ambre jaune. 
 
C'est une résine fossile qui possède des propriétés électrostatiques.

2. Début de l'étude de l'électricité

Ce n'est qu'à partir du $18^{eme}$ siècle, qu'elle a commencé à être étudiée par les scientifiques, pour en comprendre ses mécanismes et établir des lois. 
 
En $1752$, Benjamin Franklin démontre que la foudre est un phénomène dû à l'électricité et invente le paratonnerre pour s'en protéger.
 
En $1785$, Charles Colomb présente un deuxième mémoire à l'académie des Sciences, dans lequel il expose la loi selon laquelle les corps chargés électriquement interagissent.
 
En $1799$, Alessandro Volta invente la pile électrique en empilant alternativement des disques de métaux différents (cuivre, zinc) séparés par des disques de feutre imbibés d'acide.
 
En $1820$, Hans Eristian Ansted découvre la relation entre électricité et magnétisme, qui sera mise en forme par James Clerk Maxwell.
 
Peter Barlow $(1776-1862)$ construit en $1822$ ce qui peut être considéré comme le premier moteur électrique de l'histoire : la « roue de Barlow » qui est un simple disque métallique découpé en étoile et dont les extrémités plongent dans un godet contenant du mercure qui assure l'arrivée du courant.
 
Gustave Froment $(1815-1865)$ construit la première machine à résultat variable en $1845.$
 
En $1869$, le Belge Gramme invente la dynamo, qui est la base de la production de l'électricité.
 
En $1869$, Thomas Alva Edison invente la première lampe électrique à incandescence qui reste allumée $45$ heures.
 
En $1883$, Marcel de Prez réalise une expérience de transport d'électricité entre Vizille et Grenoble sur une distance de $14\,km$ en courant continu, pour éclairer la halle du centre ville de Grenoble.
 
Dans la même année, Lucien Gaulard invente un transformateur qui permet d'élever la tension délivrée par un alternateur et facilite ainsi le transport de l'énergie électrique par des lignes à haute tension.
 
En $1886$, George Westinghouse impose le courant alternatif pour la distribution de l'électricité dans tout le territoire des pays développés.
 
La ville lumière de Bourganeuf en Creuse est la première en France, même en Europe, à inaugurer un éclairage électrique de l'ensemble des rues.
 
En $1890$, mise en service de la première locomotive électrique de métro à Londres.
 
En $1991$, en Allemagne, première installation de transmission de courant triphasé entre une centrale hydraulique et Francfort de $175\,km.$
 
Auteur: 
Sidy Mouhamed Ndiaye

Quantité de matière - 2nd L

Classe: 
Seconde

I. Quantité de matière

1. Mole 

1.1 Nécessité de changement d'échelle

L'échelle infiniment petit ou échelle microscopique permet de considérer un seul de carbone dont la masse est voisine $m_{\text{atome}}=2.0\cdot 10^{-23}g$
 
A notre échelle ou échelle macroscopique, c'est la masse de quelques grammes de charbon essentiellement de carbone que nous utilisons pour faire la combustion 
 
Déterminons le nombre d'atomes de carbone contenu dans une masse de charbon $m_{\text{Charbon}}=84g$
$$N=\dfrac{84}{2.0\cdot 10^{-23}}\Rightarrow\,N=42\cdot 10^{23}\text{atomes de carbone}$$ 
 
Ce nombre est considérable !
 
En considérant que l'on puisse voir ces atomes, il faudrait plusieurs siècles aux habitants de toute la Terre pour les compter !

1.2 La mole, unité de la quantité de matière

1.2.1 Observations

Pour faciliter le comptage d'un grand d'objets, ceux-ci sont regroupés en paquets
 
Ainsi les feuilles de papier ne sont pas vendues à l'unité. Elles sont conditionnées en rame de $500$ feuilles 
 
 
De même, il est commode de regrouper les atomes en paquets d'atomes comportant toujours le même nombre d'atomes 
 
Les chimistes sont amenés à utiliser une nouvelle grandeur physique la quantité de matière dont l'unité est la mole (symbole mol)

2.1.2 Définition de la mole

La mole est la quantité de matière d'un système contenant autant d'entités élémentaires qu'il y a d'atomes dans $12g$ de carbone $12$

Remarque :

Lorsqu'on emploi la mole, les entités élémentaires doivent être spécifiées (atomes, molécules, ions, etc...). 
 
Ces entités élémentaires peuvent être des atomes, molécules, ions, des électrons, des protons etc...
 
1.3 La constante d'Avogadro
 
Nombre d'atomes dans $12g$ de carbone $\left(_{6}^{12}C\right)$
 
$m\left(_{6}^{12}C\right)=Am_{p}\longrightarrow\;1\text{ atome}$
 
$m=12g\longrightarrow\;N\text{ atomes}$
 
\begin{eqnarray} N&=&\dfrac{m}{A\cdot m_{p}}\nonumber\\\\ &=&\dfrac{12\cdot 10^{-3}}{12\times 1.66\cdot 10^{-27}}\nonumber\\\\\Rightarrow\,N&=&6.02\cdot 10^{23}\text{ atomes} \end{eqnarray}  
   
Le nombre $6.02\cdot 10^{23}$ porte le nom de constante d'Avogadro. 
 
On note cette constante : $N_{A}=6.02\cdot 10^{23}mol^{-1}$ $($ce qui signifie $6.02\cdot 10^{23}$ entités par mole$)$
 
Une mole d'atomes (ou d'ions ou de molécules...) contient $6.02\cdot 10^{23}$ atomes (ou ions, ou molécules).
 
Conséquence : le nombre $N$ d'entités élémentaires contenues dans un système est proportionnel à la quantité de matière $n$ correspondante : 
$$N=n\times\,N_{A}\quad\text{Ou}\quad n=\dfrac{N}{N_{A}}$$

Exercice d'application 

1. Quel est le nombre de moles de molécules d'eau contenu dans $12.7\cdot 10^{24}$ molécules d'eau
 
2. Quel est le nombre d'ions chlorure $Cl^{-}$ contenu dans $1.5\,mol$ de chlorure de sodium $NaCl$
 
On donne : $N_{A}=6.02\cdot 10^{23}mol^{-1}$

Résolution 

1. Nombre de moles d'eau

\begin{eqnarray} n&=&\dfrac{N}{N_{A}}\nonumber\\\\ &=&\dfrac{12.7\cdot 10^{24}}{6.02\cdot 10^{23}}\nonumber\\\\\Rightarrow\,n &=&21.1\,mol \end{eqnarray}

2. Le nombre d'ions chlorure 

\begin{eqnarray} N&=&n\times N_{A}\nonumber\\\\ &=&1.5\times 6.02\cdot 10^{23}\nonumber\\\\\Rightarrow\,N &=&9.0\cdot 10^{23}\text{ions} \end{eqnarray}

2. Masses molaires

La mase molaire d'une espèce chimique est la masse d'une mole de cette espèce chimique.
 
Elle s'exprime en grammes par mole $($symbole : $mol^{-1})$

2.1 Masse molaire atomique

La masse molaire atomique d'une espèce chimique est la masse d'une mole d'atomes de cette espèce chimique. 
 
Elle s'exprime en grammes par mole $($symbole : $mol^{-1})$

Exemple : 

La masse molaire atomique du fer est $M(Fe)=56\,g\cdot mol^{-1}.$
 
On peut déterminer la masse molaire atomique moyenne d'un élément constitué d'isotopes 

Exemple : 

$$\begin{array}{|l|c|c|} \hline \text{Isotope}&\text{Chlore }35&\text{Chlore }37\\ \hline \text{Pourcentage}&75.8\%&24.2\%\\ \hline \text{Masse}& &\\ \text{d'une mole}&35.0&37.0\\ \text{en gramme}& &\\ \hline\end{array}$$
 
\begin{eqnarray} M &=&\dfrac{35.0\times 75.8}{100}+\dfrac{37.0\times 24.2}{100}\nonumber\\\\\Rightarrow\,M&=&35.5\,g\cdot mol^{-1} \end{eqnarray}

Remarque

Les valeurs des masses molaires atomiques sont indiquées pour chaque élément dans le tableau de classification périodique des éléments.

Exemples : 

$M_{H}=1.0\,g\cdot mol^{-1}$ ;
 
$M_{C}=12.0\,g\cdot mol^{-1}$ ;
 
$M_{O}=16.0\,g\cdot mol^{-1}$ ;
 
$M_{N}=14.0\,g\cdot mol^{-1}$

2.2. Masse molaire moléculaire

La masse molaire moléculaire ou masse molaire d'une espèce chimique moléculaire représente la masse d'une mole de ses molécules.
 
Elle est égale à la somme des masses molaires atomiques des éléments constituant la molécule.
 
Elle s'exprime en grammes par mole $\left(\text{symbole}\ :\ mol^{-1}\right)$
 
La masse molaire moléculaire d'un composé est la masse d'une mole de molécules de ce composé.

Exemples

\begin{eqnarray} M\left(H_{2}O\right)&=&2\cdot M_{H}+M_{O}\nonumber\\\\&=&2\times 1.0+16.0\nonumber\\\\&=&18\,g\cdot mol^{-1} \end{eqnarray}
 
\begin{eqnarray} M\left(C_{2}H_{6}O\right)&=&2\cdot M_{c}+6\cdot M_{H}+M_{O}\nonumber\\\\&=&2\times 12.0+6\times 1.0\nonumber\\\\&=&46.0\,g\cdot mol^{-1} \end{eqnarray}
 
2.3. Masse molaire ionique
 
La masse molaire ionique est la masse d'une mole d’'ions de l'espèce 
considérée.
 
On peut négliger la masse des électrons par rapport à celle du noyau

Exemples 

\begin{eqnarray} M\left(Cl^{-}\right)&=&M_{ci}\nonumber\\\\&=&35.5\,g\cdot mol^{-1} \end{eqnarray}
 
\begin{eqnarray} M_{Al(OH)_{4}^{-}}&=&M_{AL}+4M_{O}+4M_{H}\nonumber\\\\&=&27+4\times 16+4\times 1\nonumber\\\\\Rightarrow M_{Al}(OH)_{4}^{-}\nonumber\\\\&=&95\,\cdot mol^{-1} \end{eqnarray}

3. Relation entre masse et quantité de matière

La quantité de matière $m$ d'un composé de masse $m$ et de masse molaire $ M$ est donnée par la relation : 
$$n=\dfrac{m}{M}\quad\text{OU}\quad m=n\times M$$

Exercice d'application : 

Calculer la quantité de matière contenue dans une masse d'eau de $360\,g.$
 
On donne : Masse molaire moléculaire de l'eau $M_{H_{2}O}=18\,g\cdot mol^{-1}$
 
\begin{eqnarray} n_{H_{2}O}&=&\dfrac{m_{H_{2}O}}{M_{H_{4}}O}\nonumber\\\\&=&\dfrac{360}{18}\nonumber\\\\\Rightarrow\,n_{B_{2}O}&=&20\,mol \end{eqnarray}

4. Volume molaire

4.1. Définition 

Le volume molaire d'un gaz est le volume occupé par une mole de ce gaz dans des conditions de pression et de température données.
 
Le volume molaire d'un gaz se note $V_{m}$, on l'exprime en litres par mole $\left(\text{symbole}\ :\ L\cdot mol^{-1}\right)$

4.2 Expression du volume molaire 

$$PV=nRT$$
 
$$\text{Pour }n=1mol\Rightarrow\,PV_{m}=RT\Rightarrow\,V_{m}=\dfrac{RT}{P}$$
 
On définit conventionnellement des conditions de référence appelées Conditions Normales de Température et de Pression $(C.N.T.P)$
 
\begin{eqnarray} \text{Dans les C.N.T.P : }\left\lbrace\begin{array}{lllll} T&=&0^{\circ}C&=&273K\\ P&=&10^{5}Pa& & \end{array}\right. &\Rightarrow &V_{m}=\dfrac{8.314\cdot 10^{3}\times 273}{10^{5}}\nonumber\\\\&\Rightarrow &V_{m}=22.4\,L\cdot mol^{-1} \end{eqnarray}
 
\begin{eqnarray} \text{Dans les conditions ordinaires : }\left\lbrace\begin{array}{lllll} T&=&24^{\circ}C&=&297K\\ P&=&10^{5}Pa& & \end{array}\right. &\Rightarrow &V_{m}\dfrac{8.314\cdot 10^{3}\times 297}{10^{5}}\nonumber\\\\ &\Rightarrow &V_{m}=24\,L\cdot mol^{-1} \end{eqnarray}

4.3. Relation entre le volume molaire et la quantité matière

La quantité de matière d'un gaz se note $n$ de volume $V$ et $V_{m}$ représente le volume molaire
$$\left\lbrace\begin{array}{lcl} 1\,mol &\longrightarrow &V_{m}\\ n\,mol &\longrightarrow &V \end{array}\right.$$
 
$\Rightarrow\,n=\dfrac{V}{V_{m}}\quad\text{ou}\quad V=n\cdot V_{m}$
 
$n\quad\text{en}\quad mol\ ;\ V\quad\text{en}\quad L\quad\text{et}\quad V_{m}\quad\text{en}\quad L\cdot mol^{-1}$

5. La densité d d'un gaz densité par rapport à l'air

$-\ $La densité du gaz est donc égale à la masse d'un certain volume de ce gaz divisée par la masse du même volume d'air, les volumes étant mesurés dans les mêmes conditions de température et de pression.
$$d=\dfrac{m}{m_{\text{air}}}$$
 
$-\ $On définit également la densité $d$ d'un gaz comme le rapport de la masse volumique du gaz sur la masse volumique du gaz de référence : l'air.
$$d=\dfrac{\rho}{\rho_{\text{air}}}$$
 
$-\ $La densité est une grandeur sans unité.
 
$-\ $Si on s'intéresse à $1\,mol$ du gaz : il occupe le volume molaire et sa masse est $M$, masse molaire du gaz la masse du même volume d'air est sensiblement de $29\,g$ dans les $C.N.T.P$
 
$\begin{array}{lll} d&=&\dfrac{\rho}{\rho_{\text{air}}}\\\\&=&\dfrac{\rho\cdot V_{m}}{\rho_{\text{air}}V_{m}}\\\\\Rightarrow d&=&\dfrac{M}{29} \end{array}$

Exercice d'application

Une bouteille de gaz contient une masse $m=420\,g$ d'un corps liquide de formule $C_{x}H_{y}$ et de masse molaire $M=58\,g\cdot mol^{-1}$
 
1. Déterminer la quantité de matière du gaz présent dans la bouteille
 
2. Calculer le volume occupé par ce corps liquide. 
 
On donne la masse volumique de ce liquide $\rho=0.6\,g\cdot mL^{-1}$
 
3. Le détendeur permet d'abaisser la pression et le liquide sort de la bouteille à l'état gazeux
 
3.1. Calculer le volume molaire du gaz à $25^{\circ}C$ et sous la pression de $1$ bar
 
3.2. Quel volume peut-on récupérer à la température de $25^{\circ}C$ et sous la pression normale
 
3.3. Peut-on espérer vider complètement la bouteille de son gaz ? 
 
Pourquoi ?
 
4. Le corps $17.2\%$ en masse d'hydrogène .
 
Donner sa formule brute et les formules semi-développées possibles
 
Auteur: 
Sidy Mouhamed Ndiaye

Structure de la Matière, Quantité de Matière - 2nd L

Classe: 
Seconde
 
 
I. Structure de la matière
 
1. Molécule et élément chimique
 
1.1. Molécule
 
1.1.1. Observation
 
Le dihydrogène es un gaz est formé de petites particules toutes identiques, animées de mouvements incessants et désordonnés, auxquelles on donne le nom de molécules. 
 
1.1.2. Définition
 
La molécule est plus petite partie d'un corps pur (simple ou composé) qui conserve toutes les propriétés chimiques de ce corps et qui puisse exister à l'état libre.
 
2. Élément chimique
 
2.1. Mise en évidence de l'élément carbone
 
2.1.1. Pyrolyse du bois 
 
fig17
 
La pyrolyse du bois donne du charbon de bois
 
2.1.2. Pyrolyse du sucre
 
La pyrolyse du sucre donne un solide noir appelé charbon de sucre
 
fig18
 
2.1.3. Conclusion
 
Le charbon de bois (produit de la pyrolyse du bois), le solide noir (résidu de la pyrolyse du sucre) contiennent un constituant commun : le carbone 
 
2.2. Définition de l'élément chimique
 
Un élément chimique est un constituant commun à tous les corps qui le contiennent
 
Remarque :
 
$-\ $Les corps purs simples sont formés d'un seul élément
 
Exemples : 
 
Le dihydrogène est formé de l'élément hydrogène ; le dioxygène est formé de l'élément oxygène.
 
$-\ $Les corps purs composés sont formés de plusieurs éléments.
 
Exemples : 
 
L'oxyde de dihydrogène (eau) est formé de l'élément oxygène et de l'élément hydrogène ; le dioxyde de carbone (gaz carbonique) est formé de l'élément oxygène et de l'élément carbone.
 
2.3. Notation chimique 
 
Pour faciliter l'étude de la chimie, les éléments sont représentés par des symboles.
 
Généralement, on utilise la première lettre majuscule du nom (français, latin, grec, étranger...)
 
Lorsque plusieurs éléments commencent par la même lettre, on ajoute une seconde lettre minuscule pour les différencier.
 
Symboles de quelques éléments chimiques
$$\begin{array}{|l|c|c|c|c|c|c|c|c|} \hline \text{Elément}&\text{Hydrogène}&\text{Carbone}\text{Fer}&\text{Sodium}&\text{Azode}&\text{Oxygène}&\text{Fluor}&\text{Calcium}\\ \hline \text{Symbole}&H&C&F&Na&N&O&F&Ca\\ \hline \end{array}$$
 
2.4. Classification périodique des éléments chimiques
 
2.4.1. Principe de la classification 
 
$-\ $Les éléments chimiques sont classés par numéro atomique $Z$ croissant.
 
$-\ $Les éléments dont les atomes ont le même nombre d'électrons sur leur couche externe sont disposés dans une même colonne verticale et constituent un groupe ou une famille.
 
$-\ $Chaque ligne ou période correspond au remplissage d'une couche électronique.
 
2.4.2. Tableau simplifiée de la classification périodique
 
Le tableau simplifié comporte trois lignes ou périodes et huit colonnes ou groupes.
 
fig19
 
2.4.3. Intérêt de la classification périodique
 
Les atomes des éléments de même colonne ont le même nombre d'électrons périphériques. 
 
Ils ont des propriétés chimiques semblables et forment un groupe ou famille.
 
Considérons quelques exemples :
 
2.4.3.1. La famille des métaux alcalins
 
$-\ $A l'exception de l'hydrogène, les éléments de la première colonne constituent le groupe des alcalins.
 
$-\ $Ils ont la même structure électronique externe. 
 
Ils possèdent un électron sur la couche électronique externe.
 
$Li$ (Lithium) ; 
 
$Na$ (Sodium) ; 
 
$K$ (Potassium)
 
$-\ $Les corps simples correspondant à ces éléments sont appelés les métaux alcalins.
 
$-\ $Ce sont des corps mous, légers à l'éclat métallique, très réactifs chimiquement.
 
$-\ $Ils sont oxydés par le dioxygène de l'air. 
 
Il faut les conserver dans le pétrole, à l'abri de l'air.
 
2.4.3.2. La famille des Halogènes.
 
$-\ $Les éléments de la septième colonne constituent la famille des halogènes.  
 
Ces éléments possèdent la même structure électronique externe à sept électrons.
 
$F$ (Fluor) ; 
 
$C1$ (Chlore) ; 
 
$Br$ (brome) ; 
 
$I$ (iode)
 
$-\ $Ils existent sous la forme de molécules diatomiques :
 
$-\ $Le difluor, le dichlore (gaz jaune-vert), le dibrome (liquide jaune-orangé), le diiode (solide violet foncé).
 
2.4.3.3. La famille des gaz nobles.
 
$-\ $Ce sont les éléments de la dernière colonne.
 
$-\ $L'hélium mis à part, ils possèdent une structure externe à huit électrons appelée octet d'électrons.
 
$He$ (Hélium) ; $Ne$ (Néon) ; $Ar$ (Argon)
 
$-\ $Ils possèdent une grande stabilité chimique. 
 
Ce sont des gaz monoatomiques, on les appelle les gaz rares ou gaz inertes.
 
3. Atome et ion
 
3.1. Atome
 
3.1.1. Définition
 
Un atome est la plus petite partie d'un corps simple pouvant se combiner chimiquement avec un autre.
 
3.1.2. Dimensions et constituants. 
 
3.1.2.1. Dimensions
 
L'atome est représenté par une sphère infiniment petite.
 
Le diamètre de l'atome est de l'ordre de l'Angstrom $\left(\text{symbole };\ A^{\circ}\right)$ ; $1A^{\circ}=10^{-15}\,m$
 
3.1.2.2. Les constituants de l'atome
 
3.1.2.2.1. Le modèle atomique
 
L'atome peut être modélisé par une structure présentant un noyau autour duquel existe une zone dans laquelle on peut trouver les électrons. 
 
Cette partie de l'atome est appelée nuage électronique.
 
fig20
 
3.1.2.2.2. Les caractéristiques des constituants de l'atome
 
Les expériences montrent que l'atome est constitué de protons, de neutrons et d'électrons
$$\begin{array}{|l|c|c|} \hline \text{Particule}&\text{Masse}&\text{Charge}\\ \hline \text{Proton}&m_{p}=1.672\cdot10^{-26}\,kg&q_{p}=1.6\cdot10^{-19}C\\
\hline \text{Neutron}&m_{n}=1.674\cdot10^{-26}\,kg&q_{n}=0C\\ \hline \text{Electron}&m_{e}=9.1\cdot10^{-31}\,kg&q_{e}=-1.6\cdot10^{-19}C\\ \hline
\end{array}$$
 
Remarque :
 
$-\ $La masse $m_{p}=m_{n}=1836\,m_{e}$
 
La masse des électrons est $836$ fois plus petite que celle du proton ; donc négligeable par rapport à celle-ci
 
$-\ $Les charges des protons et des électrons sont identiques et ces particules sont en même nombre dans l'atome ; l'atome est donc électriquement neutre.
 
3.1.3. Structure électronique
 
3.1.3.1. Le noyau
 
Le noyau est constitué de deux types de particules : les neutrons et les protons.
 
Ces deux types particules constituants du noyau sont appelés nucléons.
 
Chaque atome est caractérisé par :
 
$-\ $le nombre de protons $Z$ qu'il renferme. 
 
Ce nombre est aussi appelé numéro atomique ou nombre de charge
 
$-\ $le nombre de nucléons $A$ qu'il renferme. 
 
Ce nombre est aussi appelé nombre de masse : $A=Z+N$
 
$N$ étant le nombre de neutrons 
 
On symbolise le noyau des atomes par 
 
fig21
 
$A=Z+N=$ nombre de masse d'un noyau, c'est le nombre de nucléons (protons + neutrons) qu'il contient.
 
$Z=$ numéro atomique d'un noyau, c'est le nombre de protons qu'il contient.
 
Exemple : 
 
$_{6}^{12}C$ ; 
 
$_{8}^{16}O$ ;
 
$_{1}^{1}H$ ; 
 
$_{7}^{14}N$
 
Remarque :
 
Des atomes sont dits isotopes lorsqu'ils renferment le même nombre de protons mais de nombre de nucléons (ou nombre de neutrons) différents 
 
Exemple :
 
$_{6}^{12}C$, $_{6}^{13}C$ et $_{6}^{14}C$ ;
 
$_{1}^{1}H$, $_{1}^{2}H$ et $_{1}^{3}H$
 
3.1.3.2. Le nuage électronique 
 
3.1.3.2.1. Notion du niveau d'énergie
 
Les électrons d'un atome sont répartis en couche de niveau d'énergie différent. 
 
Pour arracher les électrons d'une même couche, il faut lui fournir la même énergie. 
 
On dit que les électrons d'une même couche ont le même niveau d'énergie 
 
Les couches sont désignées par des lettres $K\;,\ L\;,\ M\;,\ N\;,\  O\;,\ P\;,\ Q\ldots\ldots$
 
A chaque couche correspond un nombre entier positif $n$
$$\begin{array}{|l|c|c|c|c|c|c|c|} \hline n&1&2&3&4&5&6&7\\ \hline \text{Lettre}&K&L&M&N&O&P&Q\\ \hline \end{array}$$
 
3.1.3.2.2. Règle de remplissage des couches
 
La répartition des électrons d'un atome sur les différentes couches ou niveaux d'énergie obéit à deux règles :
 
$-\ $la première règle : le nombre maximal d'électrons pouvant appartenir à une couche est : $N=2n^{2}$
 
Exemples :
 
Couche $K$ :
 
$N=2\times 1^{2}\Rightarrow\;N=2\text{élections}$
 
Couche $L$ : 
 
$N=2\times 2^{2}\Rightarrow\;N=8\text{élections}$
 
Couche $M$ : 
 
$N=2\times 3^{2}\Rightarrow\;N=18\text{élections}$
 
$-\ $La deuxième règle : on remplit successivement les couches dans l'ordre $K\;,\ L\;,\ M\;,\ N\ldots$
 
Une couche ne commence à se remplir que si la précédente est saturée 
 
3.1.3.2.3. La configuration électronique 
 
Pour donner la structure électronique ou la configuration électronique, on représente tous les électrons par des points $(\cdot)$ dans des cases portant autant de places disponibles dans une couche déterminée.
 
fig22
 
Exemple 
 
fig23
 
fig24
 
fig25
 
fig26
 
3.1.3.2.4. La formule électronique
 
On écrit la lettre qui correspond à chaque couche et on indique en exposant en haut à droite le nombre d'électrons par couche.
 
Exemples :
 
$H(Z=1)\ :\ K^{1}$ ;
 
$He(Z=2)\ :\ K^{2}$ ;
 
$Li(Z=3)\ :\  K^{2}L^{1}$ ;
 
$C(Z=6)\ :\ K^{2}L^{4}$ ;
 
$O(Z=8)\ :\ K^{2}L^{6}$ ; 
 
$Al(Z=13)\ :\ K^{2}L^{8}M^{3}$
 
3.1.3.3 Structure de Lewis d'un atome
 
La représentation de Lewis permet de mettre en évidence les électrons de la couche externe ou couche périphérique. 
 
Les électrons célibataires sont représentés par des points $(.)$ ; les doublets sont représentés par un tiret $(-)$ placé autour de l'élément considéré
 
Exemples :
 
fig27

 

Auteur: 
Sidy Mouhamed Ndiaye

Pages