Physique

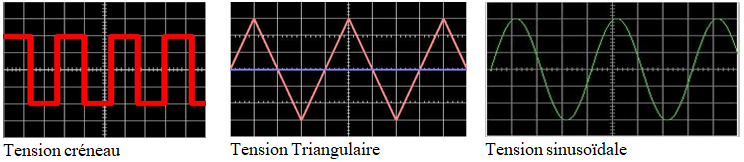
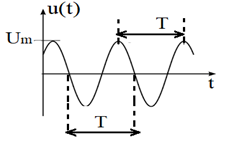
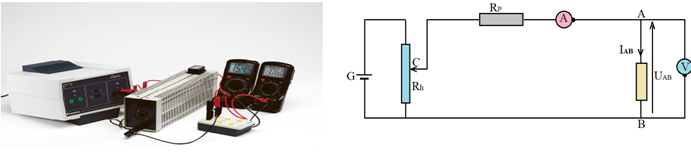
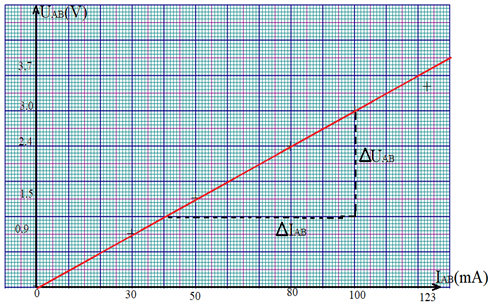
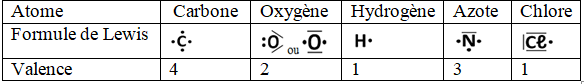L'électricité dans notre environnement - 2nd L

Classe: 
Seconde L
 

I. Phénomènes d'électrisation

1. Électrisation par frottement

1.1. Expérience

$-\ $Un bâton en verre bien sèche, frotté à l'aide d'un morceau de drap en soie ou en laine, tenue à la main, attire de petits morceaux de papier 
 
$-\ $On obtient le même résultat si on remplace le bâton en verre par un bâton d'ébonite et si on répète la même opération.
 
 
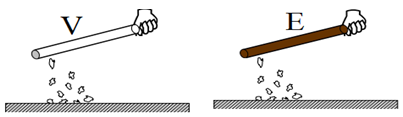
Les corps frottés sont également capables d'attirer des cheveux ou un mince filet d'eau qui coule d'un robinet.
 
Les corps frottés sont également capables d'attirer des cheveux ou un mince filet d'eau qui coule d'un robinet. 

1.2. Conclusion 

Il est possible d'électriser ou de charger d'électricité la matière en la frottant.
 
Ce phénomène s'appelle l'électrisation par frottement.
 
Des corps électrisés peuvent attirer d'autres corps plus légers.

2. Électrisation par contact

2.1. Expérience

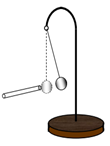
On constitue, à présent, un pendule électrostatique en suspendant au fil de soie une boule de polystyrène recouverte d'une matière conductrice. Celle-ci est initialement neutre. Approchons un bâton en verre, électrisée par frottement, de la boule jusqu'au contact. 
 
On constate que la boule est repoussée sous l'effet de son interaction avec la partie électrisée de la tige
 

2.2. Conclusion 

Un corps qui, après contact avec un autre corps électrique, acquiert la propriété d'attirer des corps légers a été électrisé par contact

3  Électrisation par influence 

3.1. Expérience

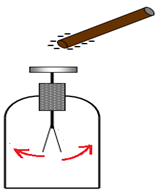
L'électroscope est constitué d'une tige métallique qui comporte à son extrémité inférieure deux feuilles d'or très minces qui tombent librement.
 
Un plateau ou une boule métallique sont fixés à l'extrémité supérieure et l'ensemble est enfermé dans une cage métallique vitrée. 
 
Le bâton d'ébonite, chargé négativement, est approché du plateau. 
 
On constate les feuilles d'or du pendule se repoussent.
 
Si on éloigne l'ébonite, l'ensemble (plateau, tige, feuilles) retrouve sa neutralité ; les feuilles de l'électroscope reprennent leur position verticale initiale
 
 

3.2. Conclusion 

Les deux feuilles se repoussent parce qu'elles sont électrisées sous l'influence du bâton
 
Un corps peut être électrisé par influence en rapprochant un autre corps électrique 

II. Les Charges électriques 

1. Les deux espèces d'électricité 

1.1. Expérience

Les pendules sont constitués d'une potence, fixée sur un socle en bois, à laquelle est relié un fil de soie sans torsion. 
 
Suspendons, en son milieu, un bâton d'ébonite dont une extrémité a été électrisé par frottement.
 
Approchons de cette extrémité la partie électrisée, par la même méthode, d'un second bâton d'ébonite. L'interaction de ces parties électrisées se traduit par une répulsion.
 
 
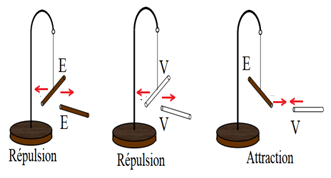
Répétons la même expérience, en remplaçant les bâtons d'ébonite par des tiges de verre électrisées comme précédemment. Là encore l'interaction se traduit par une répulsion.
 
Dans une troisième expérience, on met en présence l'extrémité électrisée du bâton d'ébonite et celle de la tige de verre électrisée. Il en résulte, à présent, une attraction

1.2. Interprétation

Ces expériences mettent en évidence deux types d'électricité :
 
La première apparait dans le verre : c'est l'électricité vitreuse à laquelle on a attribué arbitrairement un signe positif.
 
La seconde se manifeste dans l'ébonite et d'autres résines : c'est l'électricité résineuse ; on lui a attribué un signe négatif.
 
En outre, ces expériences montrent que : 
 
$-\ $deux corps chargés d'une électricité de même signe, positive ou négative, se repoussent ; 
 
$-\ $deux corps chargés de signes contraires s'attirent 
 
Un corps qui n'est pas chargé est neutre.

2. La quantité de charge électrique

La quantité de charge électrique est mesurée en coulomb $(C).$
 
Comme un atome est électriquement neutre, la valeur absolue de la charge d'un électron est égale à celle d'un proton. Cette charge élémentaire, notée e, vaut $e=1.602\cdot 10^{-19}C.$
 
Toute autre charge électrique Q est un multiple entier de la charge élémentaire :

III. Interprétation électronique de l'électrisation

1. Structure de la matière

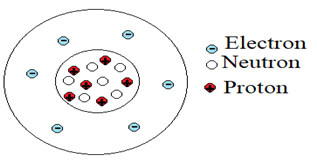
La matière est constituée d'atomes
 
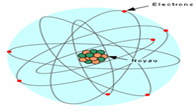
Un atome peut être considéré comme se composant de deux parties : 
 
$-\ $un noyau, constitué de protons chargés positivement et de neutrons électriquement neutres ;
 
$-\ $une enveloppe, appelée nuage électronique, constituée d'électrons chargés négativement

Remarque

Un atome électriquement neutre contient autant d'électrons que de protons, la charge des protons et des électrons étant la même en valeur absolue. 

2. Électrisation par frottement.

Avant le frottement les corps sont électriquement neutres.
 
En les frottant on agit sur les atomes situés à la surface des corps.
 
Les électrons les moins liés sont arrachés d'un des corps et sont transférés sur l'autre.
 
L'un des corps a un défaut d'électrons : il est chargé positivement.
 
L'autre présente un excès d'électrons et est chargé négativement.
 
 
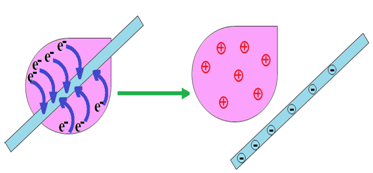
Un bâton d'ébonite par exemple arrache des électrons au chiffon de laine et se charge négativement.
 
Il est important de remarquer que la charge électrique ne peut être ni créée, ni détruite.
 
Les corps n'électrisent uniquement par transfert d'électrons
 
Lorsqu'un corps est électrisé par frottement, il y a lieu un transfert de charges: les électrons les plus faiblement liés sont transférés d'un corps à l'autre.
 
Ainsi :
 
$-\ $un corps chargé positivement présente un défaut d'électrons ;
 
$-\ $un corps chargé négativement présente un excès d'électrons.

3. Électrisation par contact.

Lors d'une électrisation par contact, il y a aussi un transfert de charges :
 
$-\ $un corps chargé négativement transmet des électrons au corps initialement neutre ;
 
$-\ $un corps chargé positivement arrache des électrons au corps initialement neutre.

4. Électrisation par influence

Lorsqu'on approche un corps chargé du corps neutre, les électrons libres sont attirés.
 
Il s'établit un déséquilibre des charges dans le corps neutre : les électrons sont en excès du côté du corps positif, ils sont en défaut du côté opposé.
 
Il y a donc séparation des charges à l'intérieur du corps neutre.
 
La région plus près du corps chargé sera chargée négativement, le côté opposé sera chargé positivement.
 
Dès qu'on éloigne le corps chargé, les électrons se répartissent de nouveau de façon uniforme dans le corps neutre.
 
L'électroscope est électrisé par influence, les électrons sont repoussés vers la partie inférieure de l'électroscope.
 
L'électroscope reste neutre et les électrons retrouvent leur disposition initiale si on éloigne la baguette.

Remarque

Cette observation permet d'expliquer pourquoi des petits bouts de papier sont attirés par un corps chargé

II. Conducteurs et isolants.

1. Conducteurs

1.1. Expérience

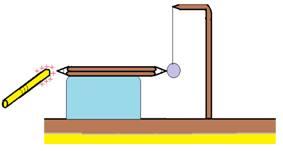
Électrisons par frottement (ou par contact) une règle en plexiglas.
 
Intercalons entre la règle et la boule une tige en carbone (crayon taillé des deux bouts), posée sur un support isolant.
 
Remplaçons la tige en carbone par une tige en cuivre puis, par une tige en aluminium
 

1.1.1. Observation 

La boule est repoussée dans le cas du cuivre, de l'aluminium et du carbone.
 
La boule s'électrise positivement par contact avec les tiges en cuivre, en aluminium et en carbone.

1.1.2. Interprétation

Par contact avec la règle en plexiglas, la tige en cuivre (ou en aluminium ou en carbone) s'électrise positivement en cédant des électrons à la règle.
 
Ces électrons ayant quitté la tige font apparaitre une charge positive sur toute la tige.
 
La charge positive qui apparaît sur le cuivre (ou l'aluminium ou le carbone) n'est pas localisée à la zone touchée par la règle.
 
L'extrémité de la tige, en contact avec la boule, arrache des électrons à cette dernière, l'amenant ainsi à devenir chargée positivement ce qui explique la répulsion.
 
Le cuivre, l'aluminium et le carbone sont des matériaux qui laissent circuler les électrons ; ils sont appelés des conducteurs.

1.2. Conclusion

Les conducteurs sont des matériaux dont les charges électriques internes (électrons libres) se déplacent librement.
 
Exemples de conducteurs : tous les métaux, le carbone

2. Isolants électriques

2.1. Expérience

Reprenons la même expérience en remplaçant la tige en carbone par une autre en verre, puis en bois, puis en $P.V.C$, enfin en plexiglas.

2.1.1. Observation

La boule garde sa position dans le cas du bois, du verre, du $P.V.C$ et du plexiglas.
 
La boule ne s'électrise pas, malgré le contact avec les autres tiges

2.1.2. Interprétation

Le bois, le plexiglas, le verre et le $P.V.C$ sont des matériaux qui ne permettent pas une circulation des électrons (la charge électrique reste localisée au bout des tiges du côté de la règle en plexiglas) ils sont appelés des isolants.

2.2. Conclusion

Les isolants électriques sont des matériaux dont les charges électriques internes (électrons libres) ne se déplacent pas librement

Exemples d'isolants :

le verre, l'ébonite, le Plexiglas, le caoutchouc, la porcelaine.

IV. Histoire de l'électricité

L'histoire de l'électricité débute durant l'Antiquité, avec la découverte des propriétés attractives de l'ambre frottée, et continue de s'écrire aujourd'hui encore avec plusieurs thèmes d'actualité : moteurs électriques, batteries rechargeables, panneaux solaires, etc.

1.Découverte de l'électricité

L'électricité est un phénomène physique qui a toujours existé, c'est le résultat d'échange d'énergie comme les éclairs.
 
L'électricité provient du mot Grec « électron » qui désigne l'ambre jaune.
 
C'est une résine fossile qui possède des propriétés électrostatiques.

2. Début de l'étude de l'électricité                                                           

Ce n'est qu'à partir du $18^{ème}$ siècle, qu'elle a commencé à être étudiée par les scientifiques, pour en comprendre ses mécanismes et établir des lois. 
 
En $1752$, Benjamin Franklin démontre que la foudre est un phénomène dû à l'électricité et invente le paratonnerre pour s'en protéger.
 
En $1785$, Charles Colomb présente un deuxième mémoire à l'académie des Sciences, dans lequel il expose la loi selon laquelle les corps chargés électriquement interagissent.
 
En $1799$, Alessandro Volta invente la pile électrique en empilant alternativement des disques de métaux différents (cuivre, zinc) séparés par des disques de feutre imbibés d'acide.
 
En $1820$, Hans Eristian Ansted découvre la relation entre électricité et magnétisme, qui sera mise en forme par James Clerk Maxwell.
 
Peter Barlow $(1776-1862)$ construit en $1822$ ce qui peut être considéré comme le premier moteur électrique de l'histoire : la « roue de Barlow » qui est un simple disque métallique découpé en étoile et dont les extrémités plongent dans un godet contenant du mercure qui assure l'arrivée du courant.
 
Gustave Froment $(1815-1865)$ construit la première machine à résultat variable en $1845.$
 
En $1869$, le Belge Gramme invente la dynamo, qui est la base de la production de l'électricité.
 
En $1879$, Thomas Alva Edison invente la première lampe électrique à incandescence qui reste allumée $45$ heures.
 
En $1883$, Marcel de Prez réalise une expérience de transport d'électricité entre Vizille et Grenoble sur une distance de $14\,km$ en courant continu, pour éclairer la halle du centre ville de Grenoble.
 
Dans la même année, Lucien Gaulard invente un transformateur qui permet d'élever la tension délivrée par un alternateur et facilite ainsi le transport de l'énergie électrique par des lignes à haute tension.
 
En $1886$, George Westinghouse impose le courant alternatif pour la distribution de l'électricité dans tout le territoire des pays développés.
 
La ville lumière de Bourganeuf en Creuse est la première en France, même en Europe, à inaugurer un éclairage électrique de l'ensemble des rues.
 
En La $1890$, mise en service de la première locomotive électrique de métro à Londres.
 
En $1891$, en Allemagne, première installation  de transmission de courant triphasé entre une centrale hydraulique et Francfort de $175\,km$
 
Auteur: 
Sidy Mouhamed Ndiaye

Le Circuit Électrique

 

I. Circuit électrique

1. Générateurs et récepteurs

1.1. Expérience

Nous nous proposons d'allumer la lampe nous pouvons pour cela allumer la lampe d'une façon beaucoup plus commode l'ampoule est montée sur son support puis reliée par des fils métalliques a la pile.
 
 
Le circuit électrique ainsi réalisé comporte :
 
$-\ $un appareil qui produit du courant ; c'est la pile
 
La pile est un générateur de courant
 
$-\ $un appareil qui reçoit le courant fourni par la pile ; c'est la lampe
 
La lampe est un récepteur de courant

1.2. Conclusion

Un circuit électrique est généralement constitué d'une chaine de générateur $(s)$ et de récepteur $(s)$ reliés par les fils conducteurs

Remarque :

Un circuit doit comporter au moins un générateur

2. Exemples de circuits électriques

2.1 Dipôles et symboles

La lampe, la pile possèdent chacun deux bornes ce sont des dipôles électriques
 
Ils sont représentés conventionnellement par des symboles
 
Symboles de quelques dipôles 
 
 

2.2 Schéma du circuit

Un circuit électrique peut être schématisé à l'aide des symboles normalises

Exemple

 

2.3. Conducteurs et isolants

2.3.1. Expérience

Réalisons le circuit électrique fermé suivant en lui intercalant divers objets
 
 
 
$$\begin{array}{|l|l|l|} \hline \text{Objet}&\text{Substance}&\text{Etat de la lampe}\\ \hline \text{Stylo à bille}&\text{Plastique}&\text{lampe éteinte}\\ \hline \text{Fil de fer}&\text{Fer}&\text{Lampe éteinte}\\ \hline \end{array}$$

Conclusion

Le fil de fer, comme tous les métaux laissent passer le courant électrique.
 
Ce sont des conducteurs électriques le stylo à bille (en plastique) le bois sec, le plastique le verre tout comme l'air ne laissent pas passer le courant électrique.
 
Ce sont des isolants électriques

2.4. Les types de circuits

2.4.1. Le circuit série

Dans un circuit série, les dipôles sont reliés les uns à la suite des autres par des fils de connexion formant ainsi une seule boucle

Exemple

 

Remarques

$-\ $Un circuit est série est constituée d'une boule
 
$-\ $Dans un circuit série, lorsqu'on dipôle ne fonctionne pas le courant ne circule plus et les autres dipôles ne fonctionnent pas

2.4.2. Le circuit en dérivation ou en parallèle

 
Un circuit en dérivation ou en parallèle est un montage électrique dans lequel on peut trouver au moins deux boucles

Remarques

Dans un circuit en dérivation, si un dipôle ne fonctionne pas, les autres dipôles continuent de fonctionner
 
Un circuit en dérivation comporte des nœuds et des branches :
 
$-\ $Un nœud est un point où aboutissent au moins trois fils conducteurs $\left(\text{exemple ; les nœuds }A\text{ et }B\right)$
 
$-\ $une branche est une portion de circuit compris entre deux nœuds 
 
La branche qui contient le générateur est branche principale $(AKGB)$
  
Les autres branches sont des branches dérivées $(ALB$ et $DEC)$

2.4.3. Le circuit électrique de la bicyclette

 
 
L'observation du circuit d'une bicyclette montre qu'il est apparemment composé de deux lampes (phare et le feu arrière), d'une génératrice (la dynamo) et deux fils conducteurs
 
Si l'on schématise ce montage, on constate alors qu'il ne peut manifestement pas fonctionner : il n'est pas fermé
 
Il existe nécessairement entre les points $1.2$ et $3$ une liaison électrique qui n'est pas constitué par un fil
 
Cette liaison est assurée par le cadre métallique donc par un conducteur de la bicyclette. 
 
On dit que le circuit se ferme par le cadre ou encore par la masse

II. Les effets du courant électrique

Réalisons le circuit suivant
 
 

1. Effet calorifique

Si on ferme l'interrupteur la lampe s'allume et dégage de la chaleur.
 
La chaleur de la lampe est due au passage du courant qui chauffe et porte à incandescence le filament de la lampe c'est l'effet calorifique

2. Effet chimique

Si on ferme l'interrupteur, il apparait aux électrodes de l'électrolyseur contenant un électrolyte des dégagements de gaz : c'est l'effet chimique

3. Effet magnétique

Lorsqu'on fait passer un courant dans un conducteur $AB$ placé au voisinage d'une aiguille aimantée, la position de cette dernière est modifiée comme dans le cas de la déviation de l'aiguille aimantée placé au voisinage d'un aimant.
 
C'est l'effet magnétique

III. Sens conventionnel et nature du courant électrique

1. Sens conventionnel du courant électrique

Si nous fermons l'interrupteur, le courant se manifeste par trois effets :
 
l'effet thermique, l'effet magnétique et l'effet chimique,L'inversion des branchements sur les bornes du générateur entraîne l'inversion des effets magnétique et chimique.
 
L'inversion des branchements sur les bornes du générateur entraîne l'inversion des effets magnétique et chimique.
 
Nous pouvons donc dire, d'après les observations, que l'effet chimique et l'effet magnétique du courant électrique sont polarisés (ils dépendent du sens du courant électrique).
 
L'effet thermique est quant à lui non polarisé.
 
Pour le sens conventionnel, à l'extérieur d'un générateur, le courant circule de la borne positive du générateur vers la borne négative du générateur

2.  Nature du courant électrique

2.1. Dans les conducteurs métalliques

 

2.1.1. Observations

Lorsqu'on ferme l'interrupteur le faisceau d'électrons du tube de Crookes et le conducteur (tige métallique) dévient dans le même sens : Dans la tige de cuivre le courant électrique est dû à une circulation d'électrons

2.1.2. Conclusion

Dans un conducteur métallique les porteurs de charges sont des électrons de conduction
 
Ils se déplacent en sens inverse conventionnel du courant électrique

2.2. Dans les électrolytes 

 

2.2.1. Observations

Si on ferme l'interrupteur les ions positifs $Cu^{2+}$ migrent vers l'électrode négative (cathode) et les ions négatifs  vers l'électrode positive.
 
Cette migration des ions est à l'origine de la circulation du courant électrique dans l'électrolyte.

2.2.2. Conclusion

Dans un électrolyte les porteurs de charge sont des ions : les cations et les anions
 
Le sens conventionnel du courant est le sens de déplacement de porteurs de charge positive.

III. Dangers du courant électrique.

Le corps humain n'est pas un excellent conducteur mais, dans certains cas, un courant électrique peut le traverser. 
 
On distingue deux types d'accidents : l'électrisation et l'électrocution.

1. L'électrisation

Une personne est électrisée si elle est traversée par un courant électrique.
 
Cela peut entraîner de graves brûlures, la tétanisation des muscles et des contractions rapides et irrégulières du cœur.

2. Électrocution

Il y a électrocution lorsque le courant entraîne la mort.
 
Les effets du courant électrique dépendent de divers facteurs : état de santé, âge, durée de l'électrisation, conditions d'humidité et surtout de la valeur de la tension électrique $\left(\text{tension de sécurité}= 24V\right).$
 

Structure de la matière - 2nd L

Classe: 
Seconde
 

I. Structure de la matière

1. Molécule et élément chimique

1.1 Molécule

1.1.1 Observation

Le dihydrogène es un gaz est formé de petites particules toutes identiques, animées de mouvements incessants et désordonnés, auxquelles on donne le nom de molécules. 

1.1.2 Définition 

La molécule est plus petite partie d'un corps pur (simple ou composé) qui conserve toutes les propriétés chimiques de ce corps et qui puisse exister à l'état libre.

2. Clément chimique

2.1 Mise en évidence de l'élément carbone

2.1.1 Pyrolyse du bois 

 
La pyrolyse du bois donne du charbon de bois

2.1.2 Pyrolyse du sucre

La pyrolyse du sucre donne un solide noir appelé charbon de sucre
 
 

2.1.3 Conclusion

Le charbon de bois (produit de la pyrolyse du bois), le solide noir (résidu de la pyrolyse du sucre) contiennent un constituant commun : le carbone 

2.2 Définition de l'élément chimique

Un élément chimique est un constituant commun à tous les corps qui le contiennent

Remarque :

$-\ $Les corps purs simples sont formés d'un seul élément

Exemples : 

le dihydrogène est formé de l'élément hydrogène ; le dioxygène est formé de l'élément oxygène
 
$-\ $Les corps purs composés sont formés de plusieurs éléments

Exemples : 

L'oxyde de dihydrogène (eau) est formé de l'élément oxygène et de l'élément hydrogène ; le dioxyde de carbone (gaz carbonique) est formé de l'élément oxygène et de l'élément carbone

2.3 Notation chimique

Pour faciliter l'étude de la chimie, les éléments sont représentés par des symboles 
 
Généralement, on utilise la première lettre majuscule du nom (français, latin, grec, étranger...)
 
Lorsque plusieurs éléments commencent par la même lettre, on ajoute une seconde lettre minuscule pour les différencier
Symboles de quelques éléments chimiques
$$\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline \text{Elément}&\text{Hydrogène}&\text{Carbone}&\text{Fer}&\text{Sodium}&\text{Azote}&\text{Oxygène}&\text{Fluor}&\text{Calcium}\\ \hline \text{Symbole}&H&C&F&Na&N&O&F&Fa\\ \hline \end{array}$$

2.4 Classification périodique des éléments chimiques

2.4.1 Principe de la classification 

$-\ $Les éléments chimiques sont classés par numéro atomique Z croissant 
 
$-\ $Les éléments dont les atomes ont le même nombre d'électrons sur leur couche externe sont disposés dans une même colonne verticale et constituent un groupe ou une famille
 
$-\ $Chaque ligne ou période correspond au remplissage d'une couche électronique

2.4.2 Tableau simplifiée de la classification périodique

Le tableau simplifié comporte trois lignes ou périodes et huit colonnes ou groupes
 
 

2.4.3 Intérêt de la classification périodique 

Les atomes des éléments de même colonne ont le même nombre d'électrons périphériques. Ils ont des propriétés chimiques semblables et forment un groupe ou famille 
 
Considérons quelques exemples :

2.4.3.1 La famille des métaux alcalins

$-\ $A l'exception de l'hydrogène, les éléments de la première colonne constituent le groupe des alcalins.
 
$-\ $Ils ont la même structure électronique externe. Ils possèdent un électron sur la couche électronique externe. 
 
$Li$ (Lithium) ;

$Na$ (Sodium) ;

$K$ (Potassium)

 
$-\ $Les corps simples correspondant à ces éléments sont appelés les métaux alcalins.
 
$-\ $Ce sont des corps mous, légers à l'éclat métallique, très réactifs chimiquement.
 
$-\ $Ils sont oxydés par le dioxygène de l'air. Il faut les conserver dans le pétrole, à l'abri de l'air.

2.4.3.2 La famille des Halogènes

$-\ $Les éléments de la septième colonne constituent la famille des halogènes. Ces éléments possèdent la même structure électronique externe à sept électrons.
 
$F$ (Fluor) ;

$Cl$ (Chlore) ;

$Br$ (brome) ;

$I$ (iode)

 
$-\ $Ils existent sous la forme de molécules diatomiques :
 
$-\ $Le difluor, le dichlore (gaz jaune-vert), le dibrome (liquide jaune-orangé), le diiode (solide violet foncé).

2.4.3.3 La famille des gaz nobles

$-\ $Ce sont les éléments de la dernière colonne.
 
$-\ $L'hélium mis à part, ils possèdent une structure externe à huit électrons appelée octet d'électrons.
 
$He$ (Hélium) ;

$Ne$ (Néon) ;

$Ar$ (Argon)

 
$-\ $Ils possèdent une grande stabilité chimique. Ce sont des gaz monoatomiques, on les appelle les gaz rares ou gaz inertes

3. Atome et ion

3.1 Atome 

3.1.1 Définition 

Un atome est la plus petite partie d'un corps simple pouvant se combiner chimiquement avec un autre.

3.1.2 Dimensions et constituants

3.1.2.1 Dimensions

L'atome est représenté par une sphère infiniment petite. Le diamètre de l'atome est de l'ordre de l'Angstrom $($symbole ; $A^{\circ})$ ; $1A^{\circ}=10^{-15}m$

3.1.2.2 Les constituants de l'atome

3.1.2.2.1 Le modèle atomique

L'atome peut être modélisé par une structure présentant un noyau autour duquel existe une zone dans laquelle on peut trouver les électrons. Cette partie de l'atome est appelée nuage électronique
 
 

3.1.2.2.2 Les caractéristiques des constituants de l'atome

Les expériences montrent que l'atome est constitué de protons, de neutrons et d'électrons
$$\begin{array}{|l|l|l|} \hline \text{Particule}&\text{Masse}&\text{Charge}\\ \hline \text{Proton}&m_{p}=1.672\cdot 10^{-26}Kg&q_{p}=1.6\cdot 10^{-19}C\\ \hline \text{Neutron}&m_{n}=1.674\cdot 10^{-26}Kg&q_{n}=0C\\ \hline \text{Electron}&m_{e}=9.1\cdot 10^{-31}Kg&q_{e}=-1.6\cdot 10^{-19}C\\ \hline \end{array}$$

Remarque :

$-\ $La masse $m_{P}=m_{n}=1836m_{e}.$
 
La masse des électrons est $1836$ fois plus petite que celle du proton ; donc négligeable par rapport à celle-ci
 
$-\ $Les charges des protons et des électrons sont identiques et ces particules sont en même nombre dans l'atome ; l'atome est donc électriquement neutre 

3.1.3 Structure électronique 

3.1.3.1 Le noyau 

Le noyau est constitué de deux types de particules : les neutrons et les protons .Ces deux types particules constituants du noyau sont appelés nucléons 
 
Chaque atome est caractérisé par :
 
$-\ $le nombre de protons $Z$ qu'il renferme. Ce nombre est aussi appelé numéro atomique ou nombre de charge
 
$-\ $le nombre de nucléons $A$ qu'il renferme. Ce nombre est aussi appelé nombre de masse : $A=Z+N$
 
$N$ étant le nombre de neutrons 
 
On symbolise le noyau des atomes par :
 
$_{Z}^{A}X$ $A=Z+N=$ nombre de masse d'un noyau, c'est le nombre de nucléons (protons + neutrons) qu'il contient.
 
$Z=$ numéro atomique d'un noyau, c'est le nombre de protons qu'il contient.

Exemples : 

$_{6}^{12}C$ ;

$_{8}^{16}O$ ;

$_{1}^{1}H$ ;

$_{7}^{14}N$

Remarque :

Des atomes sont dits isotopes lorsqu'ils renferment le même nombre de protons mais de nombre de nucléons (ou nombre de neutrons) différents 

Exemples :

$_{6}^{12}C$, $_{6}^{13}C$ et $_{6}^{14}C$ ;

$_{1}^{1}H$, $_{1}^{2}H$ et $_{1}^{3}H$ 

3.1.3.2 Le nuage électronique 

3.1.3.2.1 Notion du niveau d'énergie

Les électrons d'un atome sont répartis en couche de niveau d'énergie différent. Pour arracher les électrons d'une même couche, il faut lui fournir la même énergie. On dit que les électrons d'une même couche ont le même niveau d'énergie 
 
Les couches sont désignées par des lettres $K$, $L$, $M$, $N$, $O$, $P$, $Q\ldots$
 
A chaque couche correspond un nombre entier positif $n$ 
$$\begin{array}{|l|c|c|c|c|c|c|c|} \hline n&1&2&3&4&5&6&7\\ \hline \text{Lettre}&K&L&M&N&O&P&Q\\ \hline \end{array}$$

3.1.3.2.2 Règle de remplissage des couches

La répartition des électrons d'un atome sur les différentes couches ou niveaux d'énergie obéit à deux règles :
 
$-\ $la première règle : le nombre maximal d'électrons pouvant appartenir à une couche est : $N=2n^{2}$

Exemples :

Couche $K$ : $N=2\times 1^{2}\Rightarrow\;N=2$ électrons
 
Couche $L$ : $N=2\times 2^{2}\Rightarrow\;N=$ électrons
 
Couche $M$ : $N=2\times 3^{2}\Rightarrow\;N=18$ électrons
 
$-\ $la deuxième règle : on remplit successivement les couches dans l'ordre $K$, $L$, $M$, $N\ldots\ldots$
 
Une couche ne commence à se remplir que si la précédente est saturée 

3.1.3.2.3 La configuration électronique 

Pour donner la structure électronique ou la configuration électronique, on représente tous les électrons par des points $(.)$ dans des cases portant autant de places disponibles dans une couche déterminée
 

Exemples :

 

3.1.3.2.4 La formule électronique

On écrit la lettre qui correspond à chaque couche et on indique en exposant en haut à droite le nombre d'électrons par couche

Exemples :

$H$ $(Z=1)$ : $K^{1}$ ;

$He$ $(Z=2)$ : $K^{2}$ ;

$Li$ $(Z=3)$ : $K^{2}L^{1}$ ;

$C$ $(Z=6)$ : $K^{2}L^{4}$ ;

$O$ $(Z=8)$ : $K^{2}L^{6}$ ;

$Al$ $(Z=13)$ : $K^{2}L^{8}M^{3}$

3.1.3.3 Structure de Lewis d'un atome

La représentation de Lewis permet de mettre en évidence les électrons de la couche externe ou couche périphérique. Les électrons célibataires sont représentés par des points $(.)$ ; les doublets sont représentés par un tiret $(-)$ placé autour de l'élément considéré

Exemples :

3.1.4 Valence d'un atome

Le nombre d'électrons célibataires que possède l'élément est la valence
 
 
Hydrogène : monovalent ; 
 
Oxygène : divalent ; 
 
Azote : trivalent ; 
 
Carbone : Tétravalent.

3.1.4 Masse de l'atome

La masse $M$ de l'atome est donnée la relation suivante :
 
$M=m_{\text{noyau}}+m_{\text{éléctrons}}\Rightarrow\boxed{M=Zm_{p}+Nm_{n} +Zm_{e}}$
 
\begin{eqnarray} \text{Si }m_{p}&=&m_{n}\nonumber\\\\\Rightarrow\,M &=&Zm_{p}+Nm_{p}+Zm_{e}\nonumber\\\\\Rightarrow\,M&=&(Z+N)m_{p}+Zm_{e}\nonumber\\\\\Rightarrow\,M&=&Am_{p}+Zm_{e} \end{eqnarray}
 
Si on néglige la masse des électrons $\Rightarrow\,M=Am_{p}$

3.1.5 Structure lacunaire de l'atome

La matière de l'atome est essentiellement concentrée dans son noyau. Les électrons tournent autour du noyau. Les distances séparant le noyau des électrons sont très grandes. Ainsi, la plus grandes partie (volume) est constituée de vide. On dit que l'atome a une structure lacunaire

3.2 Les ions monoatomiques

Certains atomes peuvent perdre ou gagner des électrons et deviennent des ions simples

3.2.1 Les cations

Un cation ou ion positif provient d'un atome qui a perdu un ou plusieurs électron(s)

Exemples : 

$Na\longrightarrow\;Na^{+}+e^{-}$             
 
$Al\longrightarrow\;Al^{3+}+3e^{-}$      
 
$B\longrightarrow\;B^{3+}+3e^{-}$
 
$Mg\longrightarrow\;Mg^{2+}+2e^{-}$          
 
$H\longrightarrow\;H^{+}+e^{-}$          
 
$Li\longrightarrow\;Li^{+}+e^{-}$
 
De manière générale : $M\longrightarrow\;M^{n+}+ne^{-}$

3.2.2 Les anions

Un anion ou ion négatif provient d'un atome qui a gagné un ou plusieurs électron(s)

Exemples :

$Cl+e^{-}\longrightarrow\;Cl^{-}$ ;  
 
$P+3e^{-}\longrightarrow\;P^{3-}$ ;  
 
$N+3e^{-}\longrightarrow\;N^{3-}$ ; 
 
$O+2e^{-}\longrightarrow\;O^{2-}$ ; 
 
$F+e^{-}\longrightarrow\;F^{-}$ ; 
 
$H+e^{-}\longrightarrow\;H^{-}$
 
De manière générale :

$M+ne^{-}\longrightarrow\;M^{n-}$

4. Liaison chimique 

Exceptés, les gaz rares, les éléments chimiques n'existent pas l'état libre mais en combinaison pour former des édifices moléculaires

4.1 Liaison covalente ou liaison de covalence

4.1.1 Définition

La liaison de covalence (ou liaison covalente) résulte de la mise en commun par deux atomes d'une ou plusieurs paires d'électrons célibataires appelées doublets de liaison ou doublets liants

Exemple :

 

4.1.2 La valence d'un atome

La valence d'un atome est le nombre de liaisons de covalence qu'il peut former 
 
Le nombre de liaisons covalentes que peut former un atome est égal au nombre d'électrons qu'il doit acquérir pour saturer sa couche externe à un octet d'électrons (ou un duet pour l'atome d'hydrogène).
 
Le nombre de liaisons $n_{L}$ peut être calculé par la relation : 
$$n=n_{\text{max}}-p$$
 
$n_{\text{max}}$ : nombre d'électrons pour saturer la couche externe et $p$ : nombre d'électrons périphériques d'un atome 
 
Pour les couches $K$ : $n=2-p$
 
Pour les couches $L$ et $M$ : $n=8-p$

Exemples

$$\begin{array}{|l|l|l|l|} \hline \text{Atome}&Z&\text{Formule}&\text{Nombre}\\ & &\text{électronique}&\text{de liaisons}\\ \hline \text{Hydrogène }H&1&(K)^{1}&n=2-1=1\\ \hline \text{Chlore }Cl&17&(K)^{2}(L)^{8}(M)^{7}&n=8-7=1\\ \hline \text{Oxygène }O&8&(K)^{2}(L)^{6}&n=8-6=2\\ \hline \text{Azote }N&7&(K)^{2}(L)^{5}&n=8-5=3\\ \hline \text{Carbone }C&6&(K)^{2}(L)^{4}&n=8-4=4\\ \hline \end{array}$$
 
$\surd$ Le nombre des doublets non liants $n_{d}$ est : $n_{d}=\left(p-n_{L}\right)/2$
 

4.1.3 Formule brute d'une molécule 

La formule brute d'une molécule est constituée des symboles des éléments qui composent cette molécule affectés en indice de coefficients indiquant leur nombre dans la molécule

Exemples :   

$H_{2}$, $O_{2}$, $Cl_{2}$, $NH_{3}$, $CH_{4}$, $C_{2}H_{6}$

4.1.4 Atomicité d'une molécule 

L'atomicité d'une molécule représente le nombre de d'atomes qu'elle comporte
$$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{Molécule}&H_{2}&NH_{3}&CH_{4}&C_{2}H_{6}&KMnO_{4}&K_{2}Cr_{2}O_{7}\\ \hline \text{Atomicité}&2&4&5&6&11\\ \hline \end{array}$$

4.1.5 Représentation de Lewis d'une molécule

La représentation de Lewis d'une molécule est une représentation des atomes et de tous les doublets d'électrons périphériques liants et non-liants de cette molécule

Exemples :

4.1.6 Formule développée et formule semi-développée

4.1.6.1 Formule développée

La formule développée d'une molécule est une représentation de Lewis de la molécule où les doublets non liants ne sont pas représentés

Exemples 

4.2 Liaison covalente polarisée et liaison dative

4.2.1 L'électronégativité

$-\ $L'électronégativité est la tendance d’un atome à capter des électrons. 
 
Elle traduit l'aptitude de l'atome à attirer les électrons des liaisons 

Remarque : 

L'électronégative augmente de la gauche vers la droite le long d'une période et du bas vers le haut le long d'une colonne dans la classification périodique 
 
Le fluor est l'élément le plus électronégatif
 
$-\ $L'électropositivité est la tendance d'un élément chimique à céder des électrons

4.2.2 Liaison covalente polarisée

Une liaison entre deux atomes, $A$ et $B$, ayant des électronégativités différentes est polarisée : ils forment une liaison covalente polarisée (ou polaire) 
 
Les électrons ne sont alors pas répartis de manière symétrique entre les deux atomes. On considère alors que :
 
$-\ $L'atome $A$ porte un excès de charges négatives $\left(\text{noté }\delta^{-}\right)$ ;
 
$-\ $L'atome $B$ porte un défaut de charges négatives $\left(\text{noté }\delta^{+}\right).$
 
Les symboles $\delta^{-}$ et $\delta^{+}$ représentent des fractions de la charge élémentaire $e$ $\left(e=1.6\cdot 10^{-19}C\right)$ : on parle de charges partielles (négative ou positive) sur la liaison

Exemples :

 
$-\ $Dans une liaison polaire, le barycentre des charges électriques $(-)$ n'est pas confondu avec celui des charges électriques $(+).$
 
$-\ $Plus la différence d'électronégativité entre les deux atomes est importante, plus la liaison est polarisée

4.2.3 Liaison covalente dative

C'est une liaison covalente dans laquelle le doublet d'électrons de la liaison à partager est apporté par un seul atome.  L'atome qui donne le doublet s'appelle donneur, l'autre s'appelle accepteur.  
 
La liaison dative se représente par une flèche allant du donneur à l'accepteur. Une fois formée, cette liaison est égale aux autres liaisons covalentes.

Exemple :

 

4.3 Liaison ionique

4.3.1 Définition

La liaison ionique est une liaison établie par attraction électrostatique entre deux ions de signes opposés dans les composés ioniques.
 
Sa cohésion est assurée par la force de l'attraction électrostatique qui unit les deux ions

4.3.2 Le cristal ionique

4.3.2.1 Formule ionique et formule statistique d'un solide ionique

4.3.2.1.1 La formule ionique 

La formule ionique représente un ensemble électriquement neutre écrit avec des ions constituant le composé

Exemples :

$-\ $Chlorure de sodium $\left(Na^{+}\ ;\ Cl^{-}\right)$ ou $\left(Na^{+}+Cl^{-}\right)$
 
$-\ $Fluorure de calcium $\left(Ca^{2+}\ ;\ 2F^{-}\right)$ ou $\left(Ca^{2+}+2F^{-}\right)$
 
$-\ $Chlorure de magnésium $\left(Mg^{2+}\ ;\ 2Cl^{-}\right)$ ou $\left(Mg^{2+}+2Cl^{-}\right)$
 
$-\ $Sulfate de sodium $\left(2Na^{+}\ ;\ SO_{4}^{2-}\right)$ ou $\left(2Na^{+}+SO_{4}^{2-}\right)$

4.3.2.1 La formule statistique 

La formule statistique d'un composé ionique représente un ensemble électriquement neutre et indique la proportion de chacun des ions (cations et anions) qui la compose

Exemples :

$-\ $Chlorure de sodium : $NaCl$
  
$-\ $Fluorure de calcium : $CaF_{2}$
 
$-\ $Chlorure de magnésium : $MgCl_{2}$
 
$-\ $Sulfate de sodium : $Na_{2}SO_{4}$

4.3.3 Nomenclature de quelques ions 

$$\begin{array}{|l|l|l|} \hline &\text{CATIONS}&\text{ANIONS}\\ \hline\\ \text{Ion portant une seule charge}&H^{+}\text{ proton}&F^{-}\text{ ion fluorure} &Na^{+}\text{ ion sodium}&NO_{3}^{-}\text{ ion nitrate}\\ &Ag^{+}\text{ ion argent}&Cl^{-}\text{ ion chlorure}\\ &H_{3}O^{+}\text{ ion hydronium}&HO^{-}\text{ ion hydroxyde}\\ &K^{+}\text{ ion potassium}&MnO_{4}^{-}\text{ ion permanganate}\\ &NH_{4}^{+}\text{ ion ammonium}&\\ \hline \text{Ion portant deux charges}&Mg^{2+}\text{ ion magnésium}&O^{2-}\text{ ion oxyde}\\ &Ca^{2+}\text{ ion calcium}&S^{2-}\text{ ion sulfure}\\ &Ba^{2+}\text{ ion baryum}&SO_{3}^{2-}\text{ ion sulfite}\\ &Fe^{2+}\text{ ion fer II}&SO_{4}^{2-}\text{ ion sulfate}\\ &Ni^{2+}\text{ ion nickel}&CO_{3}^{2-}\text{ ion carbonate}\\ &Cu^{2+}\text{ ion cuivre II}&Cr_{2}O_{7}^{2-}\text{ ion dichromate}\\ &Zn^{2+}\text{ ion zinc}&S_{2}O_{3}^{2-}\text{ ion thiosulfate}\\ &Sn^{2+}\text{ ion étain}&S_{4}O_{6}^{2-}\text{ ion tétrathionate}\\ &Pb^{2+}\text{ ion plomb}&\\ \hline \text{Ion portant trois charges}&Al^{3+}\text{ ion aluminium}&PO_{4}^{3-}\text{ ion phosphate}\\ &Fe^{3+}\text{ ion fer III}&N^{3-}\text{ ion nitrure}\\ &Au^{3+}\text{ ion or}&\\ \hline \text{Ion portant quatre charges}&P^{4+}\text{ ion platine IV}&C^{4-}\text{ ion carbure}\\ \hline \end{array}$$

4.4 Structure des corps

4.4.1 Corps à structure moléculaire

Un corps pur à structure moléculaire est corps est formé uniquement d'une seule espèce chimique. Cette espèce chimique est représentée par des molécules qui sont formées par des atomes liés entre eux par des liaisons chimiques.
 
Si les atomes constituant ces molécules sont identiques, on est donc en présence de molécules simples. 

Exemples :

La molécule d'hydrogène $H_{2}$ formée par deux atomes d'hydrogène. 
 
La molécule d'oxygène $O_{2}$ formée par deux atomes d'oxygène.  
 
Si les atomes constituant ces molécules ne sont pas identiques, on est donc en présence de molécules composées. 

Exemples :

La molécule de dioxyde de carbone $CO_{2}$ formée de  deux atomes d'oxygène et un atome de carbone. 
 
La molécule d'eau $H_{2}O$ formée de deux atomes d'hydrogène et un atome d'oxygène.

4.4.2 Corps à structure atomique

Ces corps purs à structure atomique sont des corps qui existent dans la nature sous forme d'atomes.
 
Les atomes qui constituent les corps purs à structure atomique sont indépendants les uns des autres, c'est à dire, il n'existe aucune liaison entre eux.

Exemples :

Les gaz rares, les métaux sont des corps à structure atomique 

4.4.3 Corps à structure ionique

Un corps à structure ionique est formé par un assemblage géométrique simple d'ions chargés positivement, les cations, et d'ions chargés négativement, les anions liés entre par des forces d'origine essentiellement électrostatique.

Notion d'intensité et de tension - 2nd L

Classe: 
Seconde
 

I. Intensité d'intensité du courant électrique

1. Notion d'intensité électrique

1.1 Variation des effets et intensité

Réalisons un circuit électrique constitué : 
 
$-\ $d'un générateur
 
$-\ $de deux récepteurs : l'ampoule $(L)$, la cuve à l'électrolyse $(C)$, contenant de l'eau distillée
 
$-\ $d'un interrupteur $(K)$
 
$-\ $reliés par des fils conducteurs
 
 
On ferme l'interrupteur la lampe reste éteinte, il ne passe rien dans la cuve
On ajoute quelques gouttes de soude dans l'eau de la cuve :
 
$-\ $l'ampoule s'allume
 
$-\ $des bulles de gaz se dégagent aux électrons de la cuve 
Ces effets du courant deviennent plus importants que le courant est intense ou son intensité a augmenté

1.2 Définition de l'intensité

 
Si en une durée t exprimée en seconde(s). $N$ nombre de charges qui traverse une section de conducteur métallique
 
Le débit de porteurs de charges est défini par la relation
 
$$D=\dfrac{N}{t}$$
 
Si ce débit est constant, l'intensité $I$ d'un courant continu est le rapport de la valeur absolue de la quantité d'électricité $Q$ sur la durée de passage $t$
$$\begin{array}{lcl} D&=&\dfrac{Q}{t}\\\\\text{or }Q&=&N_{e}\\\\\Rightarrow\,I&=&\dfrac{N_{e}}{t}\\\\\Rightarrow\,I&=&D_{e} \end{array}$$

1.3 Ordre grandeur de quelques intensités 

$$\begin{array}{|l|l|l|l|l|l|} \hline \text{Foudre}&\text{Génératrice de}&\text{Démarreur}&\text{Plaque}&\text{Lampe}&\text{Montre}\\ &\text{centrale électrique}&\text{de voiture}&\text{ de cuisson}&\text{halogène}&\text{à quartz}\\ \hline \text{Jusqu'à }200KA&5KA&50A&2\text{ à }20A&1\text{ à }2A&\text{Quelques }nA\\ \hline \end{array}$$

2. Mesure de l'intensité du courant électrique

2.1 Représentation des ampèremètres

L'ampèremètre est un appareil qui permet de mesurer l'intensité du courant électrique 
 
On distingue deux types d'ampèremètres :
 
$-\ $les ampèremètres à aiguilles
 
$-\ $les ampèremètres numériques (ou digitaux)
 
Pour mesurer des courants d'intensité très faible ou déceler simplement le passage du courant électrique on utilise le galvanomètre
 
 
L'ampèremètre est schématisé par le symbole : 
 
 
L'ampèremètre comporte deux parties essentielles :
 
$-\ $un cadran
 
$-\ $des calibres $(3A.$ $1A...$etc$)$
 
Le calibre d'un ampèremètre indique l'intensité maximale pour laquelle l'aiguille est en fin de course
 
$-\ $des divisions

2.2 Branchement et précautions

2.2.1 Branchement

Pour mesurer l'intensité du courant électrique qui traverse un dipôle $D$ placé dans un circuit
 
On ouvre :
 
$-\ $le circuit immédiatement avant (ou après) $D$ et on intercale l'ampèremètre
 
$-\ $l'ampèremètre et le dipôle $D$ sont en série.
 
 
De nombreux appareils ampèremètres sont polarisés. Le courant électrique doit entrer dans l'ampèremètre par la borne positive et sortir par la borne négative

2.2.2 Précaution

Lors d'une mesure il est important pour ne pas détériorer l'ampèremètre d'essayer d'abord les calibres les plus élevés, on effectuera ensuite la mesure avec le calibre qui donne la déviation la plus nette.

2.3 Lecture et intensité de mesure

2.3.1 Lecture

Les grandeurs déviation $n$ et l'intensité I sont proportionnelles et on associe
 
$\text{Calibre}\ \longrightarrow\ N\text{ avec }N\ :\ \text{nombre total de division}$
 
$I\ \longrightarrow\ n\text{ avec }n\ :\ \text{nombre de divisions lues}$
 
$$I=\text{Calibre}\times\dfrac{n}{N}$$

Exemple

Le cadran d'ampèremètre comporte $100$ décisions équidistantes on l'utilise sur le calibre $300\,mA.$
 
Quelle est la valeur de l'intensité du courant quand l'aiguille s'arrête sur la division $80.$

Solution                                                                              

La valeur de l'intensité du courant
 
\begin{eqnarray} I&=&\text{Calibre}\times\dfrac{n}{N}\nonumber\\\\ &=&300\times\dfrac{80}{100}\nonumber\\\\\Rightarrow\,I&=&240mA \end{eqnarray} 

Remarque 

Dans le cas des ampèremètres digitaux la valeur de l'intensité du courant est affichée directement Incertitude de mesure

2.3.2 Classe

La classe de l'ampèremètre est une donnée technique du constructeur permettant d'évaluer l'incertitude absolue sur la mesure de l'intensité 
$$\Delta I=\text{Classe}\times\dfrac{\text{Calibre}}{100}$$

2.4 Présentation du résultat de la mesure de l'intensité

Par définition :  
 
$I=I_{0}\pm\Delta I$ ou
 
$I=I_{0}-\Delta I\leq\,I\leq\,I_{0}+\Delta I$

3. Propriétés de l'intensité du courant électrique

3.1 Unicité de l'intensité du courant électrique dans un circuit en série

3.1.1 Observation

Les ampèremètres $A_{1}$, $A_{2}$ et $A_{3}$ montrent les intensités $I_{1}$, $I_{2}$ et $I_{3}$ on constate que les ampèremètres indiquent la même valeur $I_{1}=I_{2}=I_{3}=I$
 
 
Mettre un dipôle supplémentaire en série dans le circuit produit une diminution de l'intensité

3.1.2 Conclusion

$-\ $Dans un circuit en série l'intensité du courant électrique est la même en tout point du circuit : c'est la loi de l'unicité de l'intensité du courant électrique.
 
$-\ $Quand on ajoute un récepteur en série dans le circuit l'intensité du courant électrique diminue

3.2 Loi des nœuds dans un circuit en dérivation

3.2.1 Observation

L'ampèremètre $A_{1}$ mesure l'intensité du courant dans la branche principale $A_{2}$ mesure l'intensité $I_{2}$ du courant dans une branche en dérivation et $A_{3}$ L'intensité $I_{3}$ du courant dans une autre branche en dérivation
 
Nous constatons que $I_{2}+I_{3}=I_{1}$
  
Si l'on devise un dipôle il ne fonctionne pas et l'autre continue à fonctionner
 

3.2.2 Conclusion

Dans un circuit en dérivation l'intensité du courant de la branche principale est égale à la somme des intensités des courants dans les branches en dérivation
 
Ce résultat ne généralise également au cas où plusieurs courant arrivent au nœud et ou plusieurs courants partent.
 
La somme des intensités des courants qui arrivent à un nœud est égale à la somme des intensités des courants qui partent c'est la loi des nœuds 

II. Tension électrique 

1. Notion de tension électrique

 

1.1 Observations

Dans une pile neuve il existe une importante dissymétrie entre les bornes plus et moins.
 
Sur la borne $-$ se trouve un excès d'électrons et la borne $+$ un déficit d'électrons
 
En revanche dans une pile usagée (utilisée) cette dissymétrie est très faible. 
 
On dit que la tension entre les bornes de la pile neuve est supérieure à celle qui existe entre les bornes de la pile usagée

1.2 Définition

La tension électrique caractérise la dissymétrie électrique de deux points d'un circuit :
 
Elle est nécessaire pour qu'un courant circule enterre ces deux points

1.3 Tension électrique grandeur algébrique

Relions deux points $A$ et $B$ par un fil conducteur.
 
Si le courant circule de $A$ vers $B$ à travers ce conducteur nous dirons la tension $U_{AB}$ entre $A$ et $B$ à travers ce conducteur est positive $\left(U_{AB}>0\right)$
 
Si au contraire le courant circule de $B$ vers $A$ nous dirons que la tension $U_{BA}$ entre $A$ et $B$ est négative $\left(U_{AB}<0\right)$ 
 
S'il ne circule aucun courant, la tension est nulle $(UAB=0)$

Conclusion :

La tension électrique entre deux points $A$ et $B$ d'un circuit est une grandeur algébrique

1.4 Tension représentée par une fléchée

Par convention on note $U_{AB}$ la tension entre les points $A$ et $B$ et on le représente par un segment fléché vers $A$
 
Cette flèche est dessinée à côté du symbole 
 
 

Remarque :

Cette flèche n'est pas vecteur mais seulement une représentation conventionnelle

1.5 Unités

Dans le Système International la tension s'exprime en volt $(V)$
 
On utilise également les multiples et les sous-multiples du volt 
 
Quelques multiples et sous-multiples du volt
$$\begin{array}{|l|l|} \hline \text{Multiples}&\text{Sous-multiples}\\ \hline \text{Mégavolt : }1MV=10^{6}V&\text{Déci volt : }1dV=10^{-1}V\\ \text{Kilovolt : }1kV=10^{3}V&\text{Centi volt : }1cV=10^{-2}V\\ \text{Hecto volt : }1hV=10^{2}V&\text{Millivolt : }1mV=10^{-3}V\\ \text{décavolt : }1daV=10^{1}V&\text{Microvolt : }1\mu V=10^{-6}V\\ \hline \end{array}$$

1.6 Ordre de Grandeurs de quelques tensions

$$\begin{array}{|l|l|l|l|} \hline \text{Tensions aux bornes}&\text{Réseau d'éclairage}&\text{Ligne de transmission}&\text{Tension entre les nuages}\\ \text{d'une pile}&\text{urbain}&\text{électrique}&\text{pendant l'orage}\\ \hline 4.5V&110V\text{ à }220V&500000V&100.000.000V\\ \hline \end{array}$$

2. Mesure de tension électrique

2.1 Utilisation du voltmètre 

On distingue deux types de voltmètres pour la mesure des tensions électriques
 
$-\ $les voltmètres à aiguille
 
$-\ $les voltmètres numériques (digitaux)
 
 
Le voltmètre est schématisé par le symbole :
 

2.1.1 Le branchement du voltmètre 

Le principe d'utilisation du voltmètre est la même que celui de l'ampèremètre a la différence que le voltmètre est branché en dérivation ou en parallèle
 

2.1.2 Lecture de la tension électrique

La tension mesurée aux bornes d'un dipôle à l'aide d'un voltmètre à aiguille a pour expression
$$I=\text{Calibre}\times\dfrac{n}{N}$$
 
$n$ : nombre de divisions devant lesquels s'immobilise l'aiguille
 
$N$ : nombre total de divisions sur le cadran

2.1.3 Incertitude de mesure

Tout comme l'intensité du courant électrique l'incertitude des classes que l'on commet en mesurant une tension électrique est définie par la relation suivante
 
$$\boxed{\Delta U=\dfrac{\text{Calibre}\times\text{Clase}}{100}}$$
 
La précision de la mesure est donnée par $\dfrac{\Delta U}{U}$

2.2 Utilisation l'oscilloscope

On peut mesurer la tension entre deux points $A$ et $B$ a l'aide de l'oscilloscope
 
Mesure
 
Soit un dipôle de borne $A$ et $B$ relions $A$ à une borne $Y$ et $B$ a la masse $M$ : Le spot initialement en $0$ subit une déviation $Y$
 
Nous poserons : $U_{AB}=Ky$                
 
$K$ est la sensibilité verticale en $V/div$
 
Si $U_{AB}$ supérieur à $0$, $y$ supérieur a aussi à $0$
 
 
La lecture de la déviation $y$ permet de calculer $U_{AB}$ la valeur de $k$ lue directement

Remarque

On peut vérifier facilement la tension entre deux points d'un même fil de connexion est nul

3. Propriétés des tensions

3.1 Loi d'additivité des tensions


 
Mesurons les tensions $U_{PN}$, $U_{AD}$, $U_{AB}$, $U_{BC}$ et $U_{CD}$
 
On constate :
$$U_{PN}=U_{AD}=U_{AB}+U_{BC}+U_{CD}$$
   
La tension aux bornes d'une association de dipôles montés en série est égale à la somme des tensions aux bornes de chacun des dipôles

3.2 Unicité de la tension entre deux points

 
Mesurons les tensions $U_{PN}$, $U_{AB}$, $U_{BC}$ et $U_{DE}$
 
On constate :   
$$U_{PN}=U_{AB}=U_{BC}=U_{DE}$$
 
La tension est la même aux bornes de plusieurs dipôles montés en dérivation ou parallèle 

4. Tensions variables

4.1 Tension continue et tension variable

Une tension qui ne varie pas au cours du temps ni en grandeur ni en signe est dite continue
 
En revanche quand le signe ou la valeur de la tension change elle est variable
 
Exemples de tensions variables
 
Certains générateurs sont conçus pour fournir des tensions variables particulaires dont la trace sur l'eau a la forme
 
 

Remarque

Certaines Tensions variables reprennent la même valeur a un intervalle de temps régulier elles sont dites périodiques

4.2 Tension alternative

Une Tension alternative est une tension qui prend alternativement des valeurs positives et négatives 

Exemples : 

tension créneau, tension triangulaire et tension sinusoïdale

4.3 Tension sinusoïdale

4.3.1 Définition

Une tension est dite sinusoïdale si la courbe représentant la tension $U$ en fonction du temps est une courbe régulière appelé sinusoïde

4.3.2 Caractéristiques d une tension sinusoïdale

 
La tension sinusoïdale est caractérisée par :
 
La période $T$ ou la fréquence $N$
 
La période $T$ est plus petit intervalle de temps au bout duquel la tension se reproduit identique à elle-même
 
La fréquence $N$ est le nombre de périodes par unité de temps
$$N=\dfrac{1}{T}$$
 
Elle s'exprime en Hertz $(Hz)$
 
La tension maximale ou la tension efficace 
 
La tension maximale se déduit de la déviation maximale 
$$M_{\text{MAX}}=Ky_{\text{MAX}}$$
 
La tension maximale est liée à la tension efficace par la relation :
$$U_{\text{MAX}}=U\sqrt{2}$$
 
$U_{\text{MAX}}$ et $U$ étant respectivement la tension maximale et la tension efficace

5. Convention récepteur et mesure de sécurité

5.1 Convention Récepteur

Considérons un dipôle $D$ parcouru par un courant
 
Soient $A$ et $B$ les deux bornes du dipôle
 
Orientons arbitrairement le dipôle de $A$ vers $B$ pour algébriser l'intensité du courant traversant le dipôle que nous noterons alors $U_{AB}$
 
Dans la convention récepteur la flèche qui symbolise l'orientation du dipôle pour l'intensité et celle qui représente la tension à considérer sont de sens contraire

5.2 Mesure de Sécurité

5.2.1 Le danger du courant électrique de la tension électrique

Dans une installation domestique la tension aux bornes de la prise est de $220V$ à $380V$
 
Le seuil de tension dangereuse (mortelle) est de $50V$ et de $24V$ dans un local humide.
 
La tension dans les branchements domestiques étant de $220V$ à $380V$, il y'a un danger réel à toucher un fil de phase
 
L'électrocution se produit lorsqu'on touche un fil de phase.
 
N'étant pas soi-même isolé du sol. Les risques d'électrocution sont plus grands lorsque l'on est mouillé ou quand le sol est mouillé

5.2.2 Les règles de sécurité

$-\ $L'isolation des conducteurs doit être rigoureuse
 
$-\ $S'abstenir de manipuler des appareils électriques quand on est mouillé. 
 
Pour changer une ampoule de salle de bain prendre soin de très isoles du sol de manière qu'entre les pieds et le sol aucun corps ne puisse conduire des charges électriques.
 
$-\ $Débrancher tout appareil électrique avant démontage
 
$-\ $vérifier que la fiche de terre des appareils qui en comportent est bien mise à la terre

III. Loi d'ohm

1. Caractéristique d'un résistor ou d'un conducteur ohmique

1.1 Définition

On appelle caractéristique d'un dipôle la représentation (très souvent expérimentale) d'une relation fonctionnelle entre deux grandeurs physiques
 
En électricité quand les grandeurs sont la tension $U$ et l'intensité $I$
 
$-\ $La caractéristique tension-intensité d'un dipôle est la courbe représentant les variations de l'intensité $I$ dans le dipôle en fonction de la tension $U$ à ses bornes $I=f(u)$
 
$-\ $La caractéristique intensité-tension d'un dipôle est la courbe représentant les variations de la tension $U$ à ses bornes en fonction de l'intensité $I$ du courant qui le traverse

1.2 Expérience

Montage
 
Considérons le montage suivant
 
 
le rhéostat $R_{h}$ on fait varier $I_{AB}$ lue sur l'ampèremètre pour chaque valeur de $I_{AB}$ on lit $U_{AB}$ sur le voltmètre Tracé de la caractéristique
 
En agissant sur
Une expérience permet d'obtenir le tableau de valeurs suivantes
$$\begin{array}{|l|c|c|c|c|c|c|} \hline U_{AB}(V)&0&0.9&1.5&2.4&3.0&3.7\\ \hline I_{AB}(mA)&0&30&50&80&100&123\\ \hline \end{array}$$
 
Ce tableau nous permet de tracer la caractéristique intensité-tension
 
 
La caractéristique intensité-tension d'un résistor ou conducteur ohmique est une droite passant par l'origine limitée à la valeur maximale de $I_{AB}$ supportable par le résistor le résistor est un dipôle passif linéaire
 
On obtiendrait la même courbe en intervertissant les bornes du résistor $U_{AB}=f\left(I_{AB}\right)$ le résistor est un dipôle symétrique
 
Le coefficient directeur de la droite représente une caractéristique du conducteur ohmique : la résistance notée $R$
 
La résistance électrique traduit la propriété des matériaux à s'opposer au déplacement des électrons 
Dans l'expérience décrite :
 
\begin{eqnarray} R&=&\dfrac{\Delta U_{AB}}{\Delta I_{AB}}\nonumber\\\\ &=&\dfrac{3-1.2}{(100-40)\cdot 10^{-3}}\nonumber\\\\\Rightarrow\,R&=&30\Omega \end{eqnarray}

2. Loi d'ohm

Énoncé :
 
La tension appliquée aux bornes d'un conducteur ohmique est une fonction linéaire de l'intensité qui le traverse 
$$\boxed{U=RI}$$
 

Solution des exercices : Effet Photoélectrique - Ts

Classe: 
Terminale
 

Exercice 1

a) Calcul du travail d'extraction $W_{O}$
 
$\begin{array}{lll} W_{0}&=&E-E_{C}\\\\&=&\dfrac{h_{C}}{\lambda}-E_{C}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3.00\cdot 10^{8}}{0.150\cdot 10^{-6}\times 1.6\cdot 10^{-19}}-4.8\\\\\Rightarrow\,W_{0}&=&3.5eV \end{array}$
 
b) Nature du métal 
 
$\begin{array}{lll} \lambda_{0}&=&\dfrac{h_{C}}{W_{0}}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3.00\cdot 10^{8}}{3.5\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\lambda_{0}&=&3.5\cdot 10^{-7}\\\\&=&0.35\mu m \end{array}$
 
La longueur d'onde seuil correspond à celle du zinc ; le métal est le zinc
 
c) Tension nécessaire pour arrêter cette émission
 
$\begin{array}{lll} e\left|U\right|&=&E_{C}\\\\\Rightarrow\,e\left|U\right|&=&4.8eV\\\\\Rightarrow\left|U\right|&=&4.8V\\\\\Rightarrow\,U&=&-4.8V \end{array}$
 
d) Pour augmenter la vitesse maximale d'émission, il faut changer la longueur d'onde de la lumière en la diminuant. 

Exercice 2

1) Description d'une cellule photoélectrique dite cellule photoémissive à vide.
 
 
a) Énergie d'extraction $W_{O}$ d'un électron 
 
$\begin{array}{lll} W_{0}&=&\dfrac{h_{C}}{\lambda_{0}}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{0.66\cdot 10^{-6}}\\\\\Rightarrow\,W_{0}&=&3.0\cdot 10^{-19}J \end{array}$ 
 
b) Détermination de l'énergie cinétique maximale $E_{C}$ d'un électron émis au niveau de la cathode. 
 
$\begin{array}{lll} E_{C}&=&\dfrac{h_{C}}{\lambda}-W_{0}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{0.44\cdot 10^{-6}}-3.0\cdot 10^{-19}\\\\\Rightarrow\,E_{C}&=&4.5\cdot 10^{-19}J\\\\E_{C}&=&\dfrac{4.5\cdot 10^{-19}}{1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{C}&=&2.0eV \end{array}$

Exercice 3

1) Expression de l'énergie cinétique de l'électron en fonction de la fréquence $\lambda$ et du travail d'extraction $W_{O}$
 
$E_{C}=\dfrac{h_{C}}{\lambda}-W_{0}$
 
2) Schéma du montage utilisé.
 
 
Expression de la tension d'arrêt en fonction de $\lambda$ et $W_{0}$
 
\begin{eqnarray} eU &=&hv-W_{0}\nonumber\\\\\Rightarrow\,U&=&\dfrac{h}{e}v-\dfrac{W_{0}}{e} \end{eqnarray}
 
3) Calcul des fréquences $\lambda$ des radiations utilisées  
 
\begin{eqnarray} v&=&\dfrac{c}{\lambda}\nonumber\\\\&=&\dfrac{3.0\cdot 10^{8}}{0.60\cdot 10^{-6}}\nonumber\\\\\Rightarrow\,v&=&5\cdot 10^{14}Hz\ ; \end{eqnarray}
 
$v=6\cdot 10^{14}Hz$ ;
 
$v=7.5\cdot 10^{14}Hz$ ;
 
$v=10\cdot 10^{14}Hz$ 
   
4) Tracer la courbe représentant la fonction $U=f(υ)$ 
$$\begin{array}{|l|c|c|c|c|} \hline U(V)&0.19&0.60&1.22&2.26\\ \hline v(Hz)&5\cdot 10^{14}&6\cdot 10^{14}&7.5\cdot 10^{14}&10\cdot 10^{14}\\ \hline \end{array}$$
 
 
Fréquence $υ_{0}$ du seuil photoélectrique du césium.
 
$v_{0}=5\cdot 10^{14}Hz$
 
Longueur d'onde $\lambda_{0}$ du seuil photoélectrique.
 
\begin{eqnarray} \lambda_{0}&=&\dfrac{c}{v_{0}}\nonumber\\\\&=&\dfrac{3\cdot 10^{8}}{5\cdot 10^{14}}\nonumber\\\\\Rightarrow\lambda_{0}&=&0.6\cdot 10^{-6}m \end{eqnarray}

Exercice 4

1) Expression de l'énergie d'un photon de fréquence $\lambda$
 
$E=\dfrac{h_{C}}{\lambda}$ 
  
Expression de l'énergie maximale des électrons émis par la cathode en fonction de $U_{0}$
 
$E_{\text{max}}=eU_{0}$
 
$\begin{array}{lll} E&=&E_{\text{max}}+W_{0}\\\\\Rightarrow\,hv&=&eU_{0}+W_{0}\\\\\Rightarrow\,U_{0}&=&\dfrac{h}{e}v-\dfrac{W_{0}}{e} \end{array}$ 
 
2) Représentation graphique des variations de $U_{0}$ en fonction de $v$
 
 
En déduire le seuil de fréquence $v_{0}$ de la cellule, la constante de Planck $h$ et $W_{0}$ (exprimé en électron-volt)
 
$v_{0}=5\cdot 10^{14}Hz$
 
$U_{0}=\dfrac{h}{e}v-\dfrac{W_{0}}{e}$ C'est une droite de coefficient directeur $\dfrac{h}{e}.$
 
$\begin{array}{lll} \dfrac{h}{e}&=&\dfrac{\Delta U_{0}}{\Delta f}\\\\\Rightarrow\,h&=&e\times\dfrac{\Delta U_{0}}{\Delta f}\\\\&=&1.6\cdot 10^{-19}\times\dfrac{1.52-0}{8.5\cdot 10^{14}-5\cdot 10^{14}}\\\\\Rightarrow\,h&=&6.95\cdot 10^{-34}J\cdot s \end{array}$

Exercice 5

1) Détermination graphique l'équation de la courbe représentant $\left|U_{0}\right|=f\left(\dfrac{1}{\lambda}\right)$
 
 
C'est une de la forme : $\left|U_{0}\right|=a\dfrac{1}{\lambda}+b$
 
$\begin{array}{lll} a&=&\dfrac{\Delta\left|U_{0}\right|}{\Delta\left(\dfrac{1}{\lambda}\right)}\\\\&=&\dfrac{1.5-0}{(3-1.5)\times 10^{6}}\\\\\Rightarrow\,a&=&10^{-6} \end{array}$                                                                                                                                                                                                                                                                                                                                  
 
$\begin{array}{lll} \left|U_{0}\right|&=&0\\\\\Rightarrow\,a\dfrac{1}{\lambda}+b&=&0\\\\\Rightarrow\,b&=&-a\dfrac{1}{\lambda}\\\\&=&-10^{-6}\times 1.5\cdot 10^{6}\\\\\Rightarrow\,b&=&-1.5V\\\\\Rightarrow\left|U_{0}\right|&=&10^{-6}\dfrac{1}{\lambda}-1.5 \end{array}$
 
2) a) Relation entre le potentiel d'arrêt $U_{0}$, le travail d'extraction $W_{0}$ d'un électron du métal de la cathode et l'énergie $W$ d'un photon incident.
 
$W=W_{0}+E_{C}=e\left|U_{0}\right|+W_{0}$
 
Expression de $\left|U_{0}\right|$ en fonction de $\dfrac{1}{\lambda}$ 
 
$\begin{array}{lll} W&=&e\left|U_{0}\right|+W_{0}\\\\\Rightarrow\dfrac{h_{C}}{\lambda}&=&e\left|U_{0}\right|+W_{0}\\\\\Rightarrow\left|U_{0}\right|&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda}-\dfrac{W_{0}}{e} \end{array}$
 
b) Détermination de la valeur approchée de la constante de Planck $h$
 
$\left|U_{0}\right|=10^{-6}\dfrac{1}{\lambda}-1.5\ ;$
 
$\begin{array}{lll} \left|U_{0}\right|&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda}-\dfrac{W_{0}}{e}\\\\\Rightarrow\dfrac{h_{C}}{e}&=&a\\\\\Rightarrow\,h&=&\dfrac{ae}{c}\\\\&=&\dfrac{10^{-6}\times 1.6\cdot 10^{-19}}{3\cdot 10^{8}}\\\\\Rightarrow\,h&=&5.4\cdot 10^{-34}J\cdot s\end{array}$ 
 
Calcul de $W_{0}$
 
$-\dfrac{W_{0}}{e}=-1.5\Rightarrow\,W_{0}=1.5eV$
 
3) a) Calcul de l'énergie $W$
 
$\begin{array}{lll} W&=&\dfrac{h_{C}}{\lambda}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{0.588\cdot 10^{-6}}\\\\\Rightarrow\,W&=&3.4\cdot 10^{-19}J \end{array}$
 
d) Calcul de la vitesse maximale d'émission d'un électron par la cathode
 
$\begin{array}{lll} E_{C}&=&W-W_{0}\\\\\Rightarrow\dfrac{1}{2}mv^{2}\Rightarrow\,v&=&\sqrt{\dfrac{2}{m}\left(W-W_{0}\right)}\\\\&=&\sqrt{\dfrac{2}{9.1\cdot 10^{-31}}\left(3.4\cdot 10^{-19}-1.5\times 1.6\cdot 10^{-19}\right)}\\\\\Rightarrow\,v&=&4.7\cdot 10^{5}m\cdot s^{-1} \end{array}$

Exercice 6

1) Valeur $\lambda_{0}$ de la longueur d'onde du seuil photoélectrique
 
$\begin{array}{lll} W_{0}&=&\dfrac{h_{C}}{\lambda_{0}}\\\\\Rightarrow\lambda_{0}&=&\dfrac{h\times c}{W_{0}}&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{2.5\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\lambda_{0}&=&497nm \end{array}$
 
2) a) Les valeurs de $\lambda_{1}$ et $\lambda_{2}$
 
Les électrons sont extraits du métal que si les longueurs d'onde des photons incidents sont inférieures à la longueur d'onde seuil $\lambda\leq\lambda_{0}$
 
$\lambda_{1}=413.7nm$ ;
 
$\lambda_{2}=451.4nm$ ;
  
b) Montrons que l'expression du potentiel d'arrêt s'écrit $U_{0}=-\dfrac{E_{C}}{e}$
 
Le théorème de l'énergie cinétique appliqué l'électron s'écrit :
 
$\begin{array}{lll} \Delta E_{C}&=&\sum\,W_{\overrightarrow{F}}\\\\\Rightarrow\,E_{C}-0&=&-eU_{0}\\\\\Rightarrow\,U_{0}&=&-\dfrac{E_{C}}{e} \end{array}$
  
a) Calcul de la valeur du potentiel d'arrêt correspondant à chacune des deux radiations
 
$\begin{array}{lll} U_{01}&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda_{1}}-\dfrac{W_{0}}{e}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{413.7\cdot 10^{-9}\times 1.6\cdot 10^{-19}}-2.5\\\\\Rightarrow\,U_{01}&=&0.50V \end{array}$
 
$\begin{array}{lll} U_{02}&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda_{2}}-\dfrac{W_{0}}{e}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{451.4\cdot 10^{-9}\times 1.6\cdot 10^{-19}}-2.5\\\\\Rightarrow\,U_{02}&=&0.25V \end{array}$
 
3) Détermination de la valeur du potentiel d'arrêt correspondant à cette expérience
 
$U_{0}=U_{01}=0.50V.$ Car c'est la valeur la plus élevée.
 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Solution des exercices : Interférences lumineuses - Ts

Classe: 
Terminale
 

Exercice 1

1) Établissement de l'expression de la différence de marche au pots $M$ de l'écran
 
 
\begin{eqnarray} \delta &=&\left(SS_{2}+S_{2}M\right)-\left(SS_{1}+S_{1}M\right)\nonumber\\\\&=&S_{2}M-S_{1}M\ ;\ \left(SS_{2}=SS_{1}\right) \end{eqnarray}
 
\begin{eqnarray} S_{2}M^{2}&=&d_{2}^{2}\nonumber\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}\ ; \end{eqnarray}
 
\begin{eqnarray} S_{1}M^{2}&=&d_{1}^{2}\nonumber\\\\&=&D^{2}+\left(x-\dfrac{a}{2}\right)^{2} \end{eqnarray}
 
\begin{eqnarray} d_{2}^{2}-d_{1}^{2}&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-\left(D^{2}+\left(x-\dfrac{a}{2}\right)^{2}\right)\nonumber\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-D^{2}-\left(x-\dfrac{a}{2}\right)^{2}\nonumber\\\\\left(d_{2}-d_{1}\right)\left(d_{2}+d_{1}\right)&=&\left(\left(x+\dfrac{a}{2}\right)+\left(x-\dfrac{a}{2}\right)\right)\left(\left(x+\dfrac{a}{2}\right)-\left(x-\dfrac{a}{2}\right)\right)\nonumber\\\\&=&2ax \end{eqnarray}
 
Les grandeurs $x$ et $a$ sont petites devant la grandeur $D.$ Dans ces conditions, 
 
\begin{eqnarray} d_{2}+d_{1}&=&2D\nonumber\\\\\Rightarrow\delta &=& d_{2}-d_{1}\nonumber\\\\ &=&\dfrac{ax}{D} \end{eqnarray}
 
2) Détermination de la distance entre les deux sources
 
$x_{n}=\dfrac{n\lambda D}{a}$
 
\begin{eqnarray} x_{9}-x_{6}&=&\dfrac{9\lambda D}{a}-\left(-\dfrac{6\lambda D}{a}\right)\nonumber\\\\&=&\dfrac{15\lambda D}{a}\nonumber\\\\&=&d\nonumber\\\\\Rightarrow a&=&\dfrac{15\lambda D}{d}\nonumber\\\\&=&\dfrac{15\times 0.6\cdot10^{-6}\times 2.5}{1.5\cdot 10^{-2}}\nonumber\\\\\Rightarrow a&=&1.5\cdot 10^{-3}m\nonumber\\\\&=&1.5mm \end{eqnarray}
 
3) Détermination de la nature de la frange en point $P$ de $E$ distant de $2.5mm$ de la frange centrale
 
\begin{eqnarray} x_{n}-0&=&\dfrac{n\lambda D}{a}-0\nonumber\\\\&=&d\nonumber\\\\\Rightarrow n&=&\dfrac{ad}{\lambda D}\nonumber\\\\&=&\dfrac{1.5\cdot10^{-3}\times2.5\cdot10^{-3}}{2.5\times0.6\cdot10^{-6}}\nonumber\\\\\Rightarrow n=\dfrac{5}{2} \end{eqnarray}
 
l'ordre d'interférence est un demi-entier ; la frange au point $P$ est une frange sombre 

Exercice 2

1) Les vibration lumineuses issues des fentes $f_{1}$ et $f_{2}$ sont cohérentes et en phase puisqu'elle sont d'une même sources
 
2) Expression du retard en fonction de $d_{1}$ et de la vitesse $c$de la lumière dans l'air
 
$t_{1}=\dfrac{d_{1}}{c}$ 
 
3) Expression du retard en fonction de $d_{2}$ de la vitesse $c$ de la lumière dans l'air
 
$t_{2}=\dfrac{d_{2}}{c}$
 
4) Conditions le point $M$ sera :
 
Sur frange brillante : 
 
$d_{2}-d_{1}=k\lambda$
 
Sur une frange sombre : $d_{2}-d_{1}=\left(k+\dfrac{1}{2}\right)\lambda$
 
5) Que peut-on dire des points $M$ suivants :
$d_{2}-d_{1}=0$ ; $M$ est le milieu d'une frange centrale.  
 
$-\ d_{2}-d_{1}=3.20\mu m$ : 
 
$\begin{array}{lll} k&=&\dfrac{d_{2}-d_{2}}{\lambda}\\\\&=&\dfrac{3.20}{0.64\cdot 10}\\\\\Rightarrow\,k&=&5 \end{array}$
 
$M$ est le milieu d'une frange brillante.
 
$-\ d_{2}-d_{1}=2.24\mu m$ : 
 
\begin{eqnarray} k&=&\dfrac{d_{2}-d_{2}}{\lambda}\nonumber\\\\ &=&\dfrac{2.24}{0.64\cdot 10}\nonumber\\\\\Rightarrow k &=&\dfrac{7}{2}\nonumber\\\\ &=&\left(3+\dfrac{1}{2}\right) \end{eqnarray}
 
$M$ est le milieu d'une frange sombre.

Exercice 3

1) a) Le phénomène qui se produit à la sortie de chaque fente est le phénomène de diffraction
 
L'aspect ondulatoire de la lumière est mis en évidence. 
 
b) Pour obtenir des interférences lumineuses, il est nécessaire d'utiliser un dispositif fournissant deux images d'une même source et les faisceaux issus de ces sources secondaires produisent des interférences lumineuses  
 
c) Schéma et représentation de la marche des faisceaux lumineux issus des fentes $F_{1}$ et $F_{2}.$
 
 
2) a) On observe sur l'écran des zones alternativement sombres et claires appelées franges d'interférences. Ces franges, sur l'écran, sont pratiquement rectilignes, parallèles, équidistantes et au plan de figure.
 
La frange centrale qui se forme en $O$ est une frange brillante claire.
 
b) Valeur de $\lambda.$
 
$\begin{array}{lll} l&=&\dfrac{5\lambda D}{a}\\\\\Rightarrow\lambda&=&\dfrac{al}{5D}\\\\&=&\dfrac{1.5\cdot 10^{-3}\times 8\cdot 10^{-3}}{5\times 2}\\\\\Rightarrow\lambda&=&1.2\cdot 10^{-6}m\\\\&=&1.2\mu m \end{array}$
 
3) Distance $x$ où se produit la première coïncidence de franges brillantes 
 
$x_{1}=\dfrac{k_{1}\lambda_{1}D}{a}$ ;
 
$x_{2}=\dfrac{k_{2}\lambda_{2}D}{a}$
 
$\begin{array}{lll}  x_{1}&=&x_{2}\\\\\Rightarrow\dfrac{k_{1}\lambda_{1}D}{a}\\\\&=&\dfrac{k_{2}\lambda_{2}D}{a}\\\\\Rightarrow\dfrac{k_{1}}{k_{2}} &=&\dfrac{\lambda_{2}}{\lambda_{1}}\\\\&=&\dfrac{0.54}{0.60}\\\\&=&\dfrac{9}{10}\\\\\Rightarrow\,k_{1}&=&9\ ;\\\\k_{2}&=&10\\\\k_{2}=10\Rightarrow\,x_{2}&=&\dfrac{10\lambda_{2}D}{a}\\\\&=&\dfrac{10\times 0.54\cdot 10^{-6}\times 2}{1.5\cdot 10^{-3}}\\\\\Rightarrow\,x_{2}&=&7.2mm \end{array}$

Exercice 4

Dispositif expérimental
 
 
1) Interprétation de la formation des franges brillantes et obscures.
 
Les franges brillantes (ou interférences constructives) résultent de la superposition de deux vibrations lumineuses qui arrivent en phase. C'est-à-dire la différence de marche en un point est un multiple entier de la longueur d'onde  
 
Les franges obscures (ou interférences destructives) résultent de la superposition de deux vibrations lumineuses qui arrivent en opposition de phase. C'est-à-dire la différence de marche en un point est un multiple demi- entier de la longueur d'onde  
 
2) Différence de marche aux 2 fentes d'un point $M$ de l'écran
 
$\begin{array}{lll} \delta &=&\left(SS_{2}+S_{2}M\right)-\left(SS_{1}+S_{1}M\right)\\\\&=&S_{2}M-S_{1}M\\\\SS_{2}&=&SS_{1} \end{array}$
 
$\begin{array}{lll} S_{2}M^{2}&=&d_{2}^{2}\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}\ ; \end{array}$
 
$\begin{array}{lll} S_{1}M^{2}&=&d_{1}^{2}\\\\&=&D^{2}+\left(x-\dfrac{a}{2}\right)^{2} \end{array}$
 
\begin{eqnarray} d_{2}^{2}-d_{1}^{2}&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-\left(D^{2}+\left(x-\dfrac{a}{2}\right)^{2}\right)\nonumber\\\\&=&D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-D^{2}-\left(x-\dfrac{a}{2}\right)^{2}\nonumber\\\\\left(d_{2}-d_{1}\right)\left(d_{2}+d_{1}\right)&=&\left(\left(x+\dfrac{a}{2}\right)+\left(x-\dfrac{a}{2}\right)\right)\left(\left(x+\dfrac{a}{2}\right)-\left(x-\dfrac{a}{2}\right)\right)\nonumber\\\\&=&2ax \end{eqnarray}
 
Les grandeurs $x$ et $a$ sont petites devant la grandeur $D.$ Dans ces conditions, 
 
$\begin{array}{lll} d_{2}+d_{1}&=&2D\\\\\Rightarrow\delta &=&d_{2}-d_{1}\\\\&=&\dfrac{ax}{D} \end{array}$
 
La position des franges brillantes correspond à :
 
\begin{eqnarray} \dfrac{ax}{D}&=&k\lambda\nonumber\\\\\Rightarrow\,x_{k}&=&\dfrac{k\lambda D}{a} \end{eqnarray}
  
La position des franges obscures correspond à :  
 
\begin{eqnarray} \dfrac{ax}{D}&=&\left(k+\dfrac{1}{2}\right)\lambda\nonumber\\\\\Rightarrow\,x_{k}&=&\left(k+\dfrac{1}{2}\right)\dfrac{\lambda D}{a} \end{eqnarray}
 
5) Calcul de la longueur d'onde et de la fréquence de la lumière émise par le laser, 
 
$\begin{array}{lll} x_{6}&=&\dfrac{6\lambda D}{a}\\\\\Rightarrow\lambda &=&\dfrac{ax_{n}}{6D}\\\\&=&\dfrac{0.5\cdot 10^{-3}\times 12.7\cdot 10^{-3}}{6\times 2}\\\\\Rightarrow\lambda&=&5.29\cdot 10^{-7}m \end{array}$
 
$\begin{array}{lll} v&=&\dfrac{c}{\lambda}\\\\&=&\dfrac{3\cdot 10^{8}}{5.29\cdot 10^{-7}}\\\\\Rightarrow\,v&=&5.67\cdot 10^{14}Hz \end{array}$
 
6) La longueur d'onde est une caractéristique du milieu de propagation, elle change donc avec le milieu.
 
La fréquence est une caractéristique de l’onde ; elle ne change donc pas le milieu de propagation.
 
Calcul de la nouvelle valeur de la longueur d'onde
 
$\begin{array}{lll} \lambda &=&\dfrac{c}{v}\\\\&=&\dfrac{200000\cdot 10^{3}}{5.67\cdot 10^{14}}\\\\\Rightarrow\lambda &=&3.47\cdot 10^{-7}m \end{array}$

Exercice 5

1) On observe sur l'écran $K$ une figure des franges d'interférences, c'est-à-dire des bandes étroites alternativement colorées (franges brillantes) et noires (franges sombres) équidistantes, parallèles et parallèles aux fentes
 
2) Établissement de la formule donnant $a$ en fonction de $\lambda$, $N$, $d$ et $L$
 
$\begin{array}{lll} L&=&\dfrac{N\lambda d}{a}\\\\\Rightarrow\,a&=&\dfrac{N\lambda d}{L} \end{array}$
 
Calcul de $a$
 
$\begin{array}{lll} a&=&\dfrac{N\lambda d}{L}\\\\&=&\dfrac{7\times 0.55\cdot 10^{-6}\times 1.20}{7.2\cdot 10^{-3}}\\\\\Rightarrow\,a&=&0.64mm \end{array}$
 
3) En augmentant l'intervalle $a=F_{1}F_{2}$, l'intervalle $L$ séparant $N$ franges brillantes consécutives augmente et on observe sur l'écran un étalement du phénomène d'interférence (à revoir)
 
Valeur limite $a'$ de la distance $F_{1}F_{2}$ séparant les deux fentes 
 
$\begin{array}{lll} i&=&\dfrac{\lambda d}{a'}\\\\\Rightarrow\,a'&=&\dfrac{\lambda d}{i}\\\\&=&\dfrac{0.55\cdot 10^{-6}\times 1.20}{0.2\cdot 10^{-3}}\\\\\Rightarrow\,a'&=&0.33mm \end{array}$
 
4) Nombre de franges brillantes observées sur l'intervalle $L$
 
$\begin{array}{lll} L&=&\dfrac{N\lambda d}{a}\\\\\Rightarrow\,N&=&\dfrac{aL}{\lambda d}\\\\&=&\dfrac{7.2\cdot 10^{-3}\times 0.33\cdot 10^{-3}}{0.55\cdot 10^{-6}\times 1.20}\\\\\Rightarrow\,N&=&4\text{franges brillantes} \end{array}$

Exercice 6

1) 1) Relation donnant $\lambda$ en fonction de $a$, $d$, $l$ et $N$
 
$\begin{array}{lll} l&=&\dfrac{N\lambda d}{a}\\\\\Rightarrow\lambda&=&\dfrac{al}{Nd}\\\\&=&\dfrac{2.00\cdot 10^{-3}\times 4.00\cdot 10^{-3}}{12\times 1.00}\\\\\Rightarrow\lambda &=&6.67\cdot 10^{-7}m \end{array}$
 
1) 2) Nouvelle longueur $l.$
 
$\begin{array}{lll} n_{0}&=&\dfrac{\lambda}{\lambda'}\\\\\Rightarrow\lambda'&=&\dfrac{\lambda}{n_{0}} \end{array}$
 
$\begin{array}{lll} l&=&\dfrac{N\lambda' d}{a}\\\\&=&\dfrac{N\lambda d}{an_{0}}\\\\&=&\dfrac{12\times 6.67\cdot 10^{-7}\times 1.00}{2.00\cdot 10^{-3}\times 1.30}\\\\\Rightarrow\,l&=&3.1mm \end{array}$

Exercice 7

1) Pour plus de précision on mesure la distance correspondant à $6$ interfranges plutôt que celle mesurant $1$ interfrange
$$\begin{array}{|l|c|c|c|c|c|} \hline \text{Couleur}&\text{Bleu}&\text{Vert}&\text{Jaune}&\text{Orange}&\text{Rouge}\\\hline 6i&14.1&15.6&17.4&18.3&19.5\\\hline\lambda(\mu m)&0.47&0.52&0.58&0.61&0.65\\\hline \end{array}$$
 
3) Tracé de la courbe représentative de la fonction $i=f(\lambda).$
$$\begin{array}{|l|c|c|c|c|c|} \hline \text{Couleur}&\text{Bleu}&\text{Vert}&\text{Jaune}&\text{Orange}&\text{Rouge}\\\hline 6i&14.1&15.6&17.4&18.3&19.5\\\hline\lambda(\mu m)&0.47&0.52&0.58&0.61&0.65\\\hline i&2.35&2.6&2.9&3.05&3.25\\\hline \end{array}$$
 
 
4) La courbe $i=f(\lambda)$ représentant est une droite. La relation $i=\lambda\dfrac{D}{a}$ est en accord avec la courbe obtenue précédemment.
 
5) Il faudrait réduire la largeur des fentes $F_{1}$ et $F_{2}$ ; augmenter la distance fentes-écran du dispositif expérimental pour obtenir des mesures avec une plus grande précision
 
6) Valeur de l'interfrange obtenu avec une radiation de longueur d'onde $0.50\mu m$
 
$\begin{array}{lll} i&=&a\lambda\\\\\Rightarrow\,a&=&\dfrac{\Delta i}{\Delta\lambda}\\\\&=&\dfrac{3.25-2.35}{0.65-0.47}\\\\\Rightarrow\,a&=&5\\\\\Rightarrow\,i&=&5\lambda \end{array}$
 
$\begin{array}{lll} \lambda &=&0.50\mu m\\\\\Rightarrow\,i&=&5\times 0.50\\\\&=&2.5mm \end{array}$
 
7) Pour la déterminer expérimentalement la longueur d'onde inconnue, il suffit de déterminer expérimentalement l'interfrange correspondant à deux franges brillantes ou à deux franges sombres de cette source monochromatique et déduire à partir de la relation $i=5\lambda$ la valeur de la longueur de la source monochromatique

Exercice 8

1) a) Description et explication du phénomène observé sur l'écran $(E).$
 

 

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Solution des exercices : Oscillations Mécaniques - Ts

Classe: 
Terminale
 

Exercice 1

I.
 
1) Équation différentielle du mouvement du corps $M$
 
 
Système étudié : le corps
 
Référentiel d'étude : terrestre supposé galiléen
 
Bilan des forces extérieurs appliquées : le poids $\overrightarrow{P}$ ; la tension $\overrightarrow{T}$ ; la réaction $\overrightarrow{R}$ ; du plan horizontal
 
Le Théorème du centre d'inertie s'écrit : $\overrightarrow{P}+\overrightarrow{T}+\overrightarrow{R}=m\vec{a}$
 
En projetant suivant l'axe $(Ox)$ ; il vient : 
 
\begin{eqnarray} 0-kx &=& m\ddot{x}\nonumber\\\\\Rightarrow\ddot{x}+\dfrac{k}{m}x&=&0 \end{eqnarray}  
 
est l'équation différentielle du mouvement de $M$ où $\ddot{x}+\omega^{2}x=0\text{ avec }\omega=\sqrt{\dfrac{k}{m}}$
 
2) Détermination de l'équation horaire du mouvement du corps $M$ 
 
a) Cas : $t=0$ ; $x=x_{0}>0$ et la vitesse initiale de $M$ est nulle
 
L'équation différentielle admet comme solution : $x=x_{m}\cos\left(\omega t\varphi\right)$
 
\begin{eqnarray} \text{A}\quad t&=&0\nonumber\\\\\Rightarrow x(0)&=& x_{m}\cos\left(\omega\times 0+\varphi\right)\nonumber\\\\ &=& x_{m}\cos\varphi\nonumber\\\\ &=& x_{0}>0 \end{eqnarray}   
 
$x=-\omega x_{m}\sin\left(\omega t+\varphi\right)$
 
\begin{eqnarray} \dot{x}(0)&=& -\omega x_{m}\sin\left(\omega\times 0+\varphi\right)\nonumber\\\\&=& -\omega x_{m}\sin\varphi\nonumber\\\\&=&0\nonumber\\\\\Rightarrow\varphi &=&0\nonumber\\\\\text{ou}\quad\varphi &=&\pi\nonumber\\\\\text{or à}\quad t=0\ ;\ \cos\varphi>0\nonumber\\\\\Rightarrow\varphi &=&0\nonumber\\\\\Rightarrow x_{m}\cos 0 &=& x_{0}\nonumber\\\\\Rightarrow x_{m}&=& x_{0}\nonumber\\\\\text{d'où}\quad x&=& x_{0}\cos\omega t \end{eqnarray}
 
b) cas : $t=0$ le corps $M$ est en $x=x_{0}$ et la vitesse de $M$ est $\vec{v}=v_{0}\vec{e}_{x}$ avec $v_{0}>0$
 
$\begin{array}{lcr} \text{A}\quad t=0\Rightarrow\;x(0)&=&x_{m}\cos\left(\omega\times 0+\varphi\right)\\\\&=&x_{m}\cos\varphi\\\\&=&x_{0} \end{array}$
 
$\begin{array}{lcr} \dot{x}(0)&=&-\omega\,x_{m}\sin\left(\omega\times 0+\varphi\right)\\\\&=&-\omega\,x_{m}\sin\varphi\\\\&=&v_{0}>0\\\\\Rightarrow\sin\varphi&<&0\\\\\dfrac{-\omega\,x_{m}\sin\varphi}{x_{m}\cos\varphi}&=&\dfrac{v_{0}}{x_{0}}\\\\\Rightarrow\tan\varphi&=&-\dfrac{v_{0}}{\omega\,x_{0}}\\\\\Rightarrow\varphi&=&\tan^{-1}\left(-\dfrac{v_{0}} {\omega\,x_{0}}\right)\\\\\Rightarrow\,x&=&x_{m}\cos\left(\omega\,t+\tan^{-1}\left(-\dfrac{v_{0}}{\omega\,x_{0}}\right)\right) \end{array}$
 
II.
 
1) Détermination de la position d'équilibre du corps $M.$
 
Système étudier : le corps
 
Référentiel d'étude : terrestre supposé galiléen
 
Bilan des forces extérieurs appliqués : le poids $\overrightarrow{P}$ ; la tension $\overrightarrow{T}$
 
La condition d'équilibre  s'écrit : 
 
$\begin{array}{lcr} \overrightarrow{P}+\overrightarrow{T}&=&\overrightarrow{0}\\\\\Rightarrow\;mg-k\left(l-l_{0}\right)&=&0 \end{array}$
 
2) Équation différentielle du mouvement de $M$
 
En mouvement : 
 
$\begin{array}{lcr} \overrightarrow{P}+\overrightarrow{T}&=&m\vec{a}\\\\\Rightarrow\;mg-k\left(l+x-l_{0}\right)&=&m\ddot{x}\\\\\Rightarrow\;mg-k\left(l-l_{0}\right)-kx&=&m\ddot{x}\\\\\Rightarrow\;\ddot{x}+\dfrac{k}{m}x&=&0 \end{array}$

Exercice 2 : Oscillations d'un pendule simple

1) Conservation de l'énergie
 
a) Expression de l'énergie cinétique $E_{C}(\dot{\theta})$, de l'énergie potentielle de pesanteur $E_{P}(\theta)$ et de l'énergie totale $E.$
 
$E_{P}(\theta)=mg\left(l-\cos\theta\right)$
 
$\begin{array}{lcr} E_{C}(\dot{\theta})&=&\dfrac{1}{2}mv^{2}\\\\\text{or }v&=&1\dot{\theta}\\\\\Rightarrow\;E_{C}(\dot{\theta})&=&\dfrac{1}{2}ml^{2}\dot{\theta}^{2} \end{array}$
 
$\begin{array}{lcr} E_{m}&=&E_{P}(\theta)+E_{C}(\dot{\theta})\\\\&=&mg\left(l-\cos\theta\right)+\dfrac{1}{2}ml^{2}\dot{\theta}^{2} \end{array}$
 
$\begin{array}{lcr} \text{A}\quad t=0\quad E_{m0}&=&E_{P}\left(\theta_{0}\right)+E_{C}\left(\dot{\theta_{0}}\right)\\\\&=&mg\left(l-\cos\theta_{0}\right)\\\\&=&mg\left(l-\cos\theta_{0}\right)\\\\&=&\text{cte} \end{array}$
 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Solutions des exercices : Oscillations électriques libres et forcées - Ts

Classe: 
Terminale
 

Exercice 1

1) a) Expression de $Q_{0}$ en fonction de $U_{0}$ et $C.$
 
$Q_{0}=CU_{0}$
 
b) Expression de $E_{0}$ en fonction de $Q_{0}$ et $C.$
 
$E_{0}=\dfrac{1}{2}CU_{0}$
 
2) a) Expression de l'énergie électromagnétique $E$ en fonction de $L$, $C$, $q$ et $i.$
 
$E=\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}Li^{2}$
 
b) Montrons que l'énergie électromagnétique se conserve et elle est égale à $\dfrac{Q_{0}^{2}}{2C}$
 
Le circuit électrique ne comporte que des dipôles non dissipatifs (condensateur et bobine) ; donc l'énergie électromagnétique se conserve et est égale à l'énergie initialement emmagasinée par le condensateur : $E_{0}=\dfrac{1}{2}\dfrac{Q_{0}^{2}}{C}$
 
Équation différentielle des oscillations électriques.
 
$\begin{array}{rcl} E_{0}&=&E\\\\&=&\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}Li^{2}\\\\\Rightarrow\dfrac{\mathrm{d}E_{0}}{\mathrm{d}t}&=&\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{1}{2}+\dfrac{1}{2}Li^{2}\right)\\\\&=&0\\\\\Rightarrow\dfrac{1}{2C}\times 2q\dfrac{\mathrm{d}q}{\mathrm{d}t}+\dfrac{1}{2}L\times 2i\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&0\\\\\text{or }\dfrac{\mathrm{d}q}{\mathrm{d}t}&=&i\\\\&=&\dot{q}\\\\\text{et }\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&\ddot{q}\\\\\Rightarrow\dot{q}\left(\dfrac{q}{C}+L\ddot{q}\right)&=&0\\\\\text{comme }\dot{q}\text{ n'est pas toujours nul}\\\\\Rightarrow\dfrac{q}{C}+L\ddot{q}&=&0 \end{array}$
 
c) Détermination de l'expression de la période propre $T_{0}$ en fonction de $L$ et $C.$
 
$T_{0}=2\pi\sqrt{LC}$
 
d) Expression de la charge $q$ en fonction du temps.
 
$\begin{array}{rcl} q&=&q_{m}\cos\left(\omega_{0}t+\varphi\right)\\\\&=&q_{m}\cos\left(\dfrac{2\pi}{T_{0}}t+\varphi\right) \end{array}$
 
$\begin{array}{rcl} \text{A }q&=&q_{m}\cos\varphi\\\\&=&q_{m}\\\\&=&Q_{0}\\\\\Rightarrow\cos\varphi&=&1\\\\\Rightarrow\varphi&=&0\\\\\Rightarrow\,q&=&Q_{0}\cos\dfrac{2\pi}{T_{0}}t \end{array}$
 
3. Montrons que l'expression l'énergie $E_{L}$ en fonction du temps s'écrit : 
 
$\begin{array}{rcl} E_{L}&=&\dfrac{E_{0}}{2}\left[1+\cos\left(\dfrac{4\pi}{T_{0}}t+\pi\right)\right]\\\\\,E_{L}&=&\dfrac{1}{2}Li^{2}\\\\&=&\dfrac{1}{2}L\ddot{q}^{2}\\\\&=&\dfrac{1}{2}L\left(-\dfrac{2\pi}{T_{0}}Q_{0}\sin\dfrac{2\pi}{T_{0}}t\right)^{2}\\\\&=&\dfrac{1}{2}L\dfrac{4\pi^{2}}{T_{0}^{2}}Q_{0}^{2}\sin^{2}\dfrac{2\pi}{T_{0}}t\sin^{2}\alpha\\\\&=&\dfrac{1-\cos 2\alpha}{2}\\\\\Rightarrow\,E_{L}&=&\dfrac{1}{2}L\dfrac{4\pi^{2}}{T_{0}^{2}}Q_{0}^{2} \end{array}$
 
4) a) Valeurs de $L$ et de $_{E0}.$
 
$\begin{array}{rcl} E_{0}&=&2\cdot 10^{-3}J\\\\ E8{0}&=&2\cdot 10^{-3}J\\\\\Rightarrow\,E_{0}&=&\dfrac{1}{2}Li^{2}\\\\\Rightarrow\,L&=&\dfrac{2E_{0}}{i^{2}}\\\\&=&\dfrac{2\times 2\cdot 10^{-3}}{(0.2)^{2}}\\\\\Rightarrow\,L&=&10^{-1}H \end{array}$
 
b) Valeur de $T_{0}.$
 
$T_{0}=2\pi\cdot 10^{-4}s$
 
5) Détermination de $C$, $Q_{0}$ et $U_{0}.$
 
$\begin{array}{rcl} T_{0}&=&2\pi\sqrt{LC}\\\\\Rightarrow\,LC&=&\dfrac{T_{0}^{2}}{4\pi^{2}}\\\\\Rightarrow\,C&=&\dfrac{T_{0}^{2}}{4\pi^{2}L}\\\\&=&\dfrac{\left(2\pi\cdot 10^{-4}\right)^{2}}{4\pi^{2}\times 2\cdot 10^{-2}}\\\\\Rightarrow\,C&=&5\cdot 10^{-5}F \end{array}$
 
$\begin{array}{rcl} E_{0}&=&\dfrac{1}{2}L\dfrac{4\pi^{2 }}{T_{0}^{2}}Q_{0}^{2}\\\\\Rightarrow\,Q_{0}&=&\sqrt{\dfrac{2E_{0}T_{0}^{2}}{4\pi^{2}}L}\\\\&=&\sqrt{\dfrac{2\times 2\cdot 10^{-3}\times\left(2\pi 10^{-4}\right)^{2}}{4\pi^{2}\times 2\cdot 10^{-2}}}\\\\\Rightarrow\,Q_{0}&=&4.47\cdot 10^{-5}C \end{array}$
 
$\begin{array}{rcl} U_{0}&=&\dfrac{Q_{0}}{C}\\\\&=&\dfrac{4.47\cdot 10^{-5}}{5\cdot 10^{-7}}\\\\\Rightarrow\,U_{0}&=&89.4V \end{array}$

Exercice 2

A. L'interrupteur $K$ est dans la position (1) 
 
1) Le phénomène observé est la charge du condensateur
 
2) Allure de la courbe de variation de la tension aux bornes du condensateur en fonction du temps.
 
 
B. L'interrupteur $K$ est basculé dans la position (2) 
 
 
1) a) Établissement de l'équation différentielle qui régit les oscillations de la charge $q(t).$
 
La loi d'additivité des tensions s'écrit : $U_{C}+U_{L}=0$ 
 
$\begin{array}{rcl} U_{C}&=&\dfrac{q}{C}\ ;\\\\ U_{L}&=&L\dfrac{\mathrm{d}i}{\mathrm{d}t}\ ;\\\\ i&=&\dfrac{\mathrm{d}q}{\mathrm{d}t}\\\\&=&\dot{q}\ ;\\\\\dfrac{\mathrm{d}i}{\mathrm{d}t}\\\\&=&\ddot{q}\\\\\Rightarrow\dfrac{q}{C}+L\ddot{q}\\\\&=&0\\\\\Rightarrow\ddot{q}+\dfrac{q}{LC}\\\\&=&0 \end{array}$
 
b) Montrons que $q(t)=Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)$ peut être une solution de l'équation différentielle
 
$\begin{array}{rcl} q(t)&=&Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\\\\\Rightarrow\,q(t)&=&\omega_{0}Q_{m}\cos\left(\omega_{0}t+\varphi_{q}\right)\\\\\Rightarrow\ddot{q}t&&=&-\omega_{0}^{2}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\\\\\ddot{q}+\dfrac{q}{LC}&=&0\\\\\Rightarrow-\omega_{0}^{2}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)+\dfrac{1}{LC}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\\\\&=&0\\\\\Rightarrow\left(-\omega_{0}^{2}+\dfrac{1}{LC}\right)Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)&=&0\\\\\Rightarrow-\omega_{0}^{2}+\dfrac{1}{LC}&=&0\\\\\Rightarrow-\omega_{0}^{2}Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)&=&0\\\\\Rightarrow-\omega_{0}^{2}+\dfrac{1}{LC}&=&0\\\\\Rightarrow\omega_{0}^{2}&=&\dfrac{1}{LC}\\\\\Rightarrow\omega_{0}&=&\sqrt{\dfrac{1}{LC}} \end{array}$
   
2) a) Montrons que le circuit $(L\;,\ C)$ est conservatif  
 
$\begin{array}{rcl} E_{C}+E_{L}&=&\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}Li^{2}\\\\&=&\dfrac{1}{2}\dfrac{q^{2}}{C}+\dfrac{1}{2}L\dot{q^{2}}\\\\&=&\dfrac{1}{2}\dfrac{\left(Q_{m}\sin\left(\omega_{0}t+\varphi_{q}\right)\right)^{2}}{C}+\dfrac{1}{2}L\left(\omega_{0}Q_{m}\cos\left(\omega_{0}t+\varphi_{q}\right)\right)^{2}\\\\\Rightarrow\,E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\sin^{2}\left(\omega_{0}t+\varphi_{q}\right)+\dfrac{1}{2}L\omega_{0}^{2}Q_{m}^{2}\cos^{2}\left(\omega_{0}t+\varphi_{q}\right)\\\\\text{or}\quad \omega_{0}^{2}&=&\dfrac{1}{LC}\\\\\Rightarrow\,E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\sin^{2}\left(\omega_{0}t+\varphi_{q}\right)+\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\cos^{2}\left(\omega_{0}t+\varphi_{q}\right)\\\\&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\left(\sin^{2}\left(\omega_{0}t+\varphi_{q}\right)+\cos^{2}\left(\omega_{0}t+\varphi_{q}\right)\right)\\\\\Rightarrow\,E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C} \end{array}$
 
Et l'énergie totale est constante ; le circuit $(L\;,\ C)$ est donc conservatif  
 
b) Montrons que l'énergie électrique emmagasinée dans le condensateur en fonction de $i^{2}$ est de la forme $E_{e}= Q_{m}^{2}-\dfrac{1}{2} L\cdot i^{2}$
 
$\begin{array}{rcl} E&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}\\\\&=&E_{e}+E_{L}\\\\\Rightarrow\,E_{e}&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}-E_{L}\\\\\Rightarrow\,E_{e}&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}-\dfrac{1}{2}Li^{2} \end{array}$
 
c) Justifions théoriquement l'allure de la courbe  
 
D'après la loi d'additivité des tensions : $U_{C}+U_{L}=0$
 
$\Rightarrow\,U_{L}=-U_{C}\Rightarrow\,U_{L}=-\dfrac{q}{C}$
 
La courbe représentant la tension $U_{L}$ aux bornes de la bobine en fonction de la charge $q$  une droite passant par l'origine de pente négative. Ce que l'allure de la courbe confirme
 
3) Détermination :
 
a) L'inductance $L$ de la bobine.
 
$\begin{array}{rcl} E_{e}&=&\dfrac{1}{2}\dfrac{Q_{m}^{2}}{C}-\dfrac{1}{2}Li^{2}\\\\\Rightarrow\dfrac{\Delta E_{e}}{\Delta i^{2}}&=&-\dfrac{1}{2}L\\\\\Rightarrow\,L&=&-\dfrac{2\Delta E_{e}}{\Delta i^{2}}\\\\&=&-\dfrac{2\left(0-5\cdot 10^{-4}\right)}{(10-0)\cdot 10^{-4}}\\\\\Rightarrow\,L&=&1H \end{array}$
 
b) La capacité C du condensateur.

 

 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Solutions des exercices : Étude du Dipôle RC - Ts

Classe: 
Terminale
 

Exercice 1

1) Schéma du montage ; 
 
 
2) Établissement de la relation entre $I$, $C$, $U_{C}$ et $t.$
 
$U_{C}=\dfrac{q}{C}\text{ or }q=It\Rightarrow\,U_{C}\dfrac{I}{C}t$ 
 
3) Détermination de la valeur de la capacité $C$ du condensateur
 
La courbe représentant la tension $U_{C}$ aux du condensateur en fonction du temps $t$ est une droite qui passe par l'origine de coefficient directeur $\dfrac{I}{C}$
 
$\begin{array}{rcl} \dfrac{I}{C}&=&\dfrac{\Delta U_{C}}{\Delta t}\\\\\Rightarrow\,C&=&I\dfrac{\Delta t}{\Delta U_{C}}\\\\&=&0.5\cdot 10^{-3}\times\dfrac{15-0}{3.5-0}\\\\\Rightarrow\,C&=&2.1\cdot 10^{-3}F \end{array}$
 
4) a) Calcul de la tension de claquage du condensateur.
 
$\begin{array}{rcl} U_{C}&=&\dfrac{I}{C}t_{\text{max}}\\\\&=&0.5\cdot 10^{-3}\times\dfrac{2\times 60}{2.1\cdot 10^{-3}}\\\\\Rightarrow\,U_{C}&=&28.6V \end{array}$
 
b) L'énergie électrique maximale emmagasinée par le condensateur
 
$\begin{array}{rcl} E_{\text{max}}&=&\dfrac{1}{2}CU_{C}^{2}\\\\&=&\dfrac{1}{2}\times 2.1\cdot 10^{-3}\times(28.6)^{2}\\\\\Rightarrow\,E_{\text{max}}&=&0.86J \end{array}$

Exercice 2

1) a) L'interrupteur en position $1$ correspond à la charge du condensateur ; en position $2$ correspond à la décharge du condensateur 
 
1) b) La fig2 correspond la charge du condensateur, car la charge d'un condensateur est proportionnelle à l'intensité du courant délivré par le générateur de courant.
 
2) a) Calcul de la charge du condensateur à la date $40s.$
 
$\begin{array}{rcl} Q&=&It\\\\&=&10^{-6}\times 40\\\\\Rightarrow\,Q&=&40\cdot 10^{-6}C \end{array}$
 
2) b) Valeur de l'énergie emmagasinée par le condensateur à la date $40s$
 
$\begin{array}{rcl} E&=&\dfrac{1}{2}QU_{C}\\\\&=&\dfrac{1}{2}\times 40\cdot 10^{-6}\times 40\\\\\Rightarrow\,E&=&80\cdot 10^{-3}J \end{array}$
 
2) c) La capacité du condensateur
 
$\begin{array}{rcl} E&=&\dfrac{1}{2}CU_{C}^{2}\\\\\Rightarrow\,C&=&\dfrac{2E}{U_{C}^{2}}\\\\&=&\dfrac{2\times 80\cdot 10^{-3}}{40^{2}}\\\\\Rightarrow\,C&=&10\cdot 10^{-3}F \end{array}$ 
 
3. a. Détermination de la permittivité électrique absolue $\varepsilon$ du diélectrique de ce condensateur.
 
$\begin{array}{rcl} C&=&\dfrac{\varepsilon S}{e}\\\\\Rightarrow\varepsilon&=&\dfrac{e\times C}{S}\\\\&=&\dfrac{0.02\cdot 10^{-3}\times 10\cdot 10^{-3}}{0.1}\\\\\Rightarrow\varepsilon&=&2\cdot 10^{-8}(S.I) \end{array}$
 
b) $\begin{array}{rcl} \varepsilon_{r}&=&\dfrac{\varepsilon}{\varepsilon_{0}}\\\\&=&\dfrac{2\cdot 10^{-8}}{8.85\cdot 10^{-12}}\\\\\Rightarrow\varepsilon_{r}&=&2.3\cdot 10^{3} \end{array}$

Exercice 3

1) a) Précisons le graphe correspondant à la charge $q=f(t)$ et celui correspondant à la tension $u_{R1}=g(t).$
 
Lorsque le condensateur est chargé, l'intensité du courant de charge est nulle. En conséquence, le graphe représentant la charge est croissant ; tandis que celui représentant le courant décroissant.
 
Le graphe de la fig3 représente la charge $q=f(t)$ et la fig4 celui de la tension $u_{R1}=g(t)$ image du courant.
 
b) Établissement de la relation entre $q$, $u_{R1}$, $E$ et $C$
 
La loi d'additivité des tensions s'écrit : 
 
$\begin{array}{rcl} u_{C}+u_{R1}&=&E\\\\\text{or }u_{C}&=&\dfrac{q}{C}\\\\\Rightarrow\dfrac{q}{C}+u_{R1}&=&E\\\\\Rightarrow\,u_{R1}&=&E-\dfrac{q}{C} \end{array}$
 
c) Montrons qu'à la date $t=0$, la tension $u_{R1}$ est égale à $E.$ 
 
$\begin{array}{rcl} u_{R1}&=&E-\dfrac{q}{C}\\\\\text{or }t=0\ ;\ q=0\\\\\Rightarrow\,u_{R1}&=&E \end{array}$
 
Valeur de $u_{R1}$
 
$u_{R1}=2\times 5=10V$
 
d) Valeur de la charge électrique maximale $Q_{\text{max}}$ du condensateur
 
$\begin{array}{rcl} Q_{\text{max}}&=&5\times 2\cdot 10^{-4}\\\\&=&10^{-3}C \end{array}$
 
2) a) Définition la constante de temps $\tau$ d'un dipôle $RC$
 
La constante de temps $\tau$ correspond au temps de charge ou de décharge d'un condensateur et est égal : $\tau=RC$  
 
Montrons que $\tau$ est un temps
 
$\begin{array}{rcl} \tau&=&R\times C\\\\&=&\dfrac{U}{I}\times\dfrac{Q}{U}\\\\&=&\dfrac{Q}{I}\\\\&=&\dfrac{It}{I}\\\\&=&t \end{array}$
 
b) Montrons que l'équation différentielle régissant les variations de $u_{R1}$ au cours du temps peut s'écrire sous la forme
$$\tau_{1}\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}=0$$
 
La loi d'additivité des tensions s'écrit :  
 
$u_{C}+u_{R1}=E$
 
or $u_{C}=\dfrac{q}{C}$
 
et $u_{R1}=R_{1}i\Rightarrow\,i=\dfrac{u_{R1}}{R_{1}}$
 
$\begin{array}{rcl} \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{q}{C}+u_{R1}\right)&=&\dfrac{\mathrm{d}}{\mathrm{d}t}E\\\\\Rightarrow\dfrac{1}{C}\dfrac{\mathrm{d}q}{\mathrm{d}t}&=&0\\\\\Rightarrow\dfrac{1} {C}i+\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}&=0\\\\\Rightarrow\dfrac{u_{R_{1}}}{R_{1}C}+\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}&=&0\\\\\Rightarrow\,R_{1}C\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}&=&0\\\\\Rightarrow\tau_{1}\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}&=&0\ ;\\\\\text{avec }\tau_{1}&=&R_{1}C \end{array}$
 
c) Détermination de $A$ et $\alpha.$
 
$u_{R1}=Ae^{-\alpha t}$ ;
 
$\tau_{1}\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}=0$

 

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Solutions des exercices : Induction Magnétique - Étude d'un dipôle RL - Ts

Classe: 
Terminale
 

Exercice 1

I
 
 
1) Le phénomène observé est l'induction électromagnétique
 
2) Le sens de circulation du courant induit dans la bobine. (Voir schéma)
 
3) L'inducteur, source du champ magnétique, est l'aimant droit.
 
L'induit, siège du courant induit, est la bobine.
 
II
 
1) a) Montrons que la bobine est le siège d'un phénomène d'auto-induction
 
Le circuit est le siège d'un courant d'intensité variable. Le courant crée, en tout point de la bobine, un champ magnétique variable à travers le circuit lui-même. Cette variation s'accompagne d'une f.é.m. ou d'un courant d'un courant d'auto-induction.
 
b) Montrons que la tension aux bornes de la bobine est : $u_{AB}=\dfrac{-L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}$
 
 
$u_{AB}=L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
 
$\begin{array}{rcl} u_{CB}&=&-Ri\\\\\Rightarrow\,i&=&-\dfrac{u_{CB}}{R}\\\\\Rightarrow\,u_{AB}&=&L\dfrac{\mathrm{d}\left(-\dfrac{u_{CB}}{R}\right)}{\mathrm{d}t}\\\\\Rightarrow\,u_{AB}&=&-\dfrac{L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t} \end{array}$
 
c) Justifions littéralement l'allure de la tension sur la voie $Y_{A}$
 
La tension aux bornes résistor est triangulaire de la forme : $u_{CB}=at+b$
 
$\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}=a\Rightarrow\,u_{AB}=-\dfrac{L}{R}a$ 
 
La bobine transforme une tension triangulaire en tension carrée ; d'où l'allure de la tension sur la voie $Y_{A}$
 
2) a) Calcul de la période $T$ et la de fréquence $N$ des tensions
 
$T=0.2\cdot 10^{-3}\times 8\Rightarrow\,T=1.6\cdot 10^{-3}s$
 
$N=\dfrac{1}{1.6\cdot 10^{-3}}$
 
$\Rightarrow\,N=625Hz$
 
b) Détermination des expressions de $u_{AB}$ et de $u_{CB}$ en fonction du temps.
 
$\begin{array}{rcl} u_{AB}&=&1\times 0.2\\\\\Rightarrow\,u_{AB}&=&0.2V \end{array} $
 
$\begin{array}{rcl} u_{CB}&=&2\times 2\\\\\Rightarrow\,u_{CB}&=&4V \end{array} $
 
c) Valeur de l'inductance $L$ de la bobine
 
$\begin{array}{rcl} u_{AB}&=&-\dfrac{L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}\\\\\Rightarrow\,L&=&-Ru_{AB}\dfrac{\mathrm{d}t}{\mathrm{d}u_{CB}}\\\\&=&-10\cdot 10^{3}\times 0.2\times\left(\dfrac{0.8\cdot 10^{-3}}{-4}\right)\\\\\Rightarrow\,L&=&0.4H \end{array}$
 
Signification physique de l'inductance :
 
L'inductance est une grandeur physique caractérisant l'aptitude d'une bobine à modérer les variations de tout courant électrique qui y circule.

Exercice 2

 
1) a) Représentation du champ magnétique créé par la bobine $B_{2}.$ (voir figure)
 
b) Énoncé la loi de Lenz. 
 
Toute variation de flux à travers un circuit fermé entraine la circulation d'un courant induit qui, par ses effets électromagnétiques, s'oppose à la cause qui lui a donné naissance.  
 
Représentation du champ magnétique induit dans la bobine $B_{1}.$ (voir figure)
 
Le sens du courant induit. (voir figure)
 
c) La bobine $B_{2}$ est l'inducteur et $B_{1}$ l'induit
 
2) a) En diminuant l'intensité du courant débitée par le générateur la valeur du champ magnétique créé par la bobine $B_{2}$ diminue.
 
b) Représentation du champ magnétique créé par $B_{2}$ et de celui qui est induit dans $B_{1}.$
 
 
c) Sens du courant induit dans $B_{1}.$ (voir figure)
 
3) Représentation du  champ magnétique induit dans la bobine $B_{1}$ lorsque on modifie les bornes générateur
 
 

Exercice 3

1) Schéma de principe du montage 
 
 
2) La tension aux bornes de la résistance permet d'observer l'allure de $i(t)$ car cette tension est proportionnelle à l'intensité du courant électrique. A une constante $R$ près, la voie $Y_{B}$ visualise les variations de l'intensité.
  
3) Détermination de la période $T$ de l'intensité du courant
 
$T=4\times 0.5\cdot 10^{-3}\Rightarrow\,R=2\cdot 10^{-3}s$
 
4) Détermination de l'amplitude $I_{m}$ (valeur maximale atteinte) de l'intensité du courant
 
$\begin{array}{rcl} u_{CB}&=&RI_{m}\\\\\Rightarrow\,I_{m}&=&\dfrac{u_{CB}}{R}\\\\&=&\dfrac{2\times 4}{10\cdot 10^{3}}\\\\\Rightarrow\,I_{m}&=&80\cdot 10^{-3}A \end{array}$ 
 
5) a) Détermination de la valeur de la tension $u_{L}$
 
$u_{L}=3\times 0.1\Rightarrow\,u_{L}=0.3V$
 
b) Détermination de la valeur de la dérivée par rapport au temps de l'intensité du courant
 
$\begin{array}{rcl} u_{CB}&=&-Ri\\\\\Rightarrow\,i&=&-\dfrac{u_{CB}}{R}\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&-\dfrac{1}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}\\\\&=&-\dfrac{1}{10\cdot 10^{3}}\dfrac{(-4-4)}{10^{-3}}\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&0.8A\cdot s^{-1} \end{array}$
 
c) Valeur de $L$ de l'inductance de la bobine.
 
$\begin{array}{rcl} u_{L}&=&L\dfrac{\mathrm{d}i}{\mathrm{d}t}\\\\\Rightarrow\,L&=&u_{L}\dfrac{\mathrm{d}t}{\mathrm{d}i}\\\\&=&0.3\times\dfrac{l}{0.8}\\\\\Rightarrow\,L&=&0.4H \end{array}$

Exercice 4

1) Détermination de la direction et le sens du vecteur champ magnétique. ( Voir figure)
 
 
2) a) Sens positif et tracé du vecteur surface $\overrightarrow{S}.$
    
b) Détermination de l'expression du flux magnétique à travers le circuit.  
 
$\Phi=\overrightarrow{B}\cdot\overrightarrow{S}=BS\cos\left(\overrightarrow{B}\cdot\overrightarrow{S}\right)$
 
or $\cos\left(\overrightarrow{B}\cdot\overrightarrow{S}\right)=\cos 0=0$
 
$\Rightarrow\Phi=BS$
 
Montrons que ce flux s'écrit sous la forme : $\Phi=B\cdot L\cdot V\cdot t$
 
$\Phi=BS$
 
or $S=MN\times CM=L\times Vt$
 
$\Rightarrow\Phi=BLVt$ 
 
3) a) Calcul de la force électromotrice induite
 
$\begin{array}{rcl} e&=&-\dfrac{\mathrm{d}\Phi}{\mathrm{d}t}\\\\\text{or}\quad\Phi&=&BLVt\\\\\Rightarrow\,e&=&-BLV\\\\&=&-1\times 25\cdot 10^{-2}\times 10\\\\\Rightarrow\,e&=&-0.25V \end{array}$
 
b) Calcul de l'intensité $i$ du courant induit
 
$\begin{array}{rcl} e&=&ri\\\\\Rightarrow\,i&=&\dfrac{e}{r}\\\\&=&\dfrac{-0.25}{0.5}\\\\\Rightarrow\,i&=&*-0.25A \end{array}$
 
c) Détermination du sens du courant induit. 
 
Le sens du courant induit est de sens contraire du sens positif
 
d) Représentation de $i$ sur le schéma. (voir figure)

Exercice 5

1) a) Établissement de l'expression de l'inductance $L$ du solénoïde.
 
 
$\begin{array}{rcl} \Phi&=&N\overrightarrow{B}\cdot\overrightarrow{S}\\\\&=&N\overrightarrow{B}\cdot S\vec{n}\\\\&=&NBs\\\\&=&\dfrac{\mu_{0}N^{2}S}{l}i\\\\&=&Li\\\\\Rightarrow\,L&=&\dfrac{\mu_{0}N^{2}S}{l} \end{array}$
 
Calcul de la valeur de l'inductance
 
$\begin{array}{rcl} L&=&\dfrac{\mu_{0}N^{2}S}{l}\\\\&=&\dfrac{\mu_{0}N^{2}\pi R^{2}}{l}\\\\&=&\dfrac{4\pi 10^{-7}\times\left(10^{3}\right)^{2}\pi\times\left(5\cdot 10^{-2}\right)^{2}}{40\cdot 10^{-2}}\\\\\Rightarrow\,L&=&0.025H \end{array}$
 
b) Expression de $i(t)$ dans chaque intervalle de temps. 
 
$t\in\left[0\ ;\ 2ms\right]$ ;
 
$\begin{array}{rcl} i_{0}&=&0\ ;\\\\ a&=&\dfrac{\Delta i}{\Delta t}\\\\&=&\dfrac{0.04-0}{2}\\\\&=&2\cdot 10^{-2}\\\\\Rightarrow\,i(t)&=&2\cdot 10^{-2}t \end{array}$
 
$t\in\left[2ms\ ;\ 6ms\right]$ ;
 
$\begin{array}{rcl} i_{0}&=&0.04\cdot 10^{-3}\ ;\\\\ a&=&\dfrac{\Delta i}{\Delta t}\\\\&=&\dfrac{0-0.4}{6-2}\\\\&=& 10^{-2}\\\\\Rightarrow\,i(t)&=&-10^{-2}t+0.04\cdot 10^{-3} \end{array}$
 
c) Le phénomène qui se produit dans le solénoïde est le phénomène d'induction.
 
Le solénoïde est le siège d'un courant d'intensité variable, donc une variation du flux qui entraine la création d'un courant induit ou d'une f.é.m induite. 
 
d) Calcul de la f.é.m. induite dans le solénoïde dans des intervalles de temps 
 
$e=-L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
 
$\begin{array}{rcl} [0\ ;\ 2ms]\ ;\ i{t}&=&2\cdot 10^{-2}t\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&2\cdot 10^{-2}\\\\\Rightarrow\,e&=&-0.025\times 2\cdot 10^{-2}\\\\\Rightarrow\,e&=&-50\cdot 10^{-2}V \end{array}$
 
$\begin{array}{rcl} [2ms\ ;\ 6ms]\ ;\ i{t}&=&-10^{-2}t+0.04\cdot 10^{-3}t\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&-10^{-2}\\\\\Rightarrow\,e&=&-0.025\times -10^{-2}\\\\\Rightarrow\,e&=&-25\cdot 10^{-3}V \end{array}$
 
b) Représentation de f.é.m. au cours du temps. (voir figure) 
 
 
2) a) Représentation du sens du courant induit et du sens du courant principal. sur la spire et sur le solénoïde dans chacun des intervalles
 
 
3) a) Calcul de la tension aux bornes du solénoïde.
 
$u_{S}=ri$

 

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Pages