Vous êtes ici

Physique

Solutions des exercices : Loi de Laplace - Ts

Classe:

Terminale

Exercice 1

1) Sens d'inclinaison de la tige $AN.$ (Voir figure)

2) a) Caractéristiques de la force de la place $\overrightarrow{F}$ qui agit sur la tige $AN$

Direction ; point d'application $($milieu de la tige $AN)$ ; sens : (voir figure)

Intensité :

$\begin{array}{rcl} F&=&I_{2}IB_{1} \\ \\&=&5\times 4\cdot 10^{-2}\times 0.3\\ \\\Rightarrow F&=&-2 0.06N \end{array}$

b) Représentation de $\overrightarrow{F}$ (voir figure)

c) Détermination de la masse de la tige $AN$

La tige $AN$ est soumise aux forces : $\overrightarrow{F}$ ; $\overrightarrow{P}$ ; $\overrightarrow{R}$

La condition d'équilibre s'écrit :

$\begin{array}{rcl} M_{A}\left(\overrightarrow{P}\right)+M_{A}\left(\overrightarrow{F}\right)+M_{A}\left(\overrightarrow{R}\right)&=&\vec{0} \\ \\\Rightarrow\,-mg\dfrac{L\sin\theta}{2}+I_{2}lB_{1}\dfrac{L}{2}+0&=& 0\\ \\\Rightarrow m&=&\dfrac{I_{2}IB_{1}}{g\sin\theta}\\\\&=&\dfrac{5\times 4\cdot 10^{-2}\times 0.3}{10\sin 10^{\circ}}\\\\\Rightarrow\,m&=&0.035Kg \end{array}$

3) a) Il y a une interaction entre les deux tiges

La tige $OM$ parcouru un courant $I_{1}$ crée au voisinage un champ magnétique $\overrightarrow{B_{1}}$ de la tige $AN$ qui, à son tour parcourue par $I_{2}$, subit une force

La tige $AN$ parcouru un courant $I_{2}$ crée au voisinage un champ magnétique $\overrightarrow{B_{2}}$ de la tige $OM$ qui, à son tour parcourue par $I_{1}$, subit une force $\overrightarrow{F_{1}}$

b) $I_{1}$ s'agit d'une interaction attractive.

c) La tige $OM$ est inclinée vers la tige $AN.$

d) Détermination de la valeur du champ $\overrightarrow{B_{2}}$

$B_{2}=\dfrac{\mu_{0}I}{2\pi MN}$

Exercice 2

1) Représentation des forces exercées sur le fil.

2) Sens du courant électrique. (Voir figure)

3) Calcul de l'angle $\alpha$

La condition d'équilibre appliquée à la tige s'écrit :

$\begin{array}{rcl} M_{O}\left(\overrightarrow{P}\right)+M_{O}\left(\overrightarrow{F}\right)+M_{O}\left(\overrightarrow{R}\right)&=&0 \\\\\Rightarrow\,-mg\dfrac{l\sin\alpha}{2}+IlB\dfrac{l}{2}+0&=& 0\\ \\\Rightarrow\sin\alpha&=&\dfrac{IlB}{mg}\\\\&=&\dfrac{5\times 25\cdot 10^{-2}\times 0.05}{10\times 8\cdot 10^{-3}}\\\\\Rightarrow\sin\alpha&=&0.78\\ \\ \alpha&=&51^{\circ} \end{array}$

Exercice 3

1) Tracé de la courbe $m=f(I).$

2) Établissement de la relation théorique $m=f(I).$

La balance est soumise aux forces : $\overrightarrow{F_{1}}$ ; $\overrightarrow{F_{2}}$ ; $\overrightarrow{F_{3}}$ ; $\overrightarrow{P}$ et $\overrightarrow{R}$

$\begin{array}{rcl} M_{\Delta}\left(\overrightarrow{P}\right)+M_{\Delta}\left(\overrightarrow{F_{1}}\right)+M_{\Delta}\left(\overrightarrow{F_{2}}\right)+M_{\Delta}\left(\overrightarrow{F_{3}}\right)+M_{\Delta}\left(\overrightarrow{R}\right)&=&0 \\ \\\Rightarrow\,-mgd'+0+ILBd+0+0&=& 0\\ \\\Rightarrow\,m&=&\dfrac{ILBd}{gd'} \end{array}$

3) Valeur du champ magnétique

Le graphe est une droite qui passe par l’origine de pente positive

$m=\dfrac{ILBd}{gd'}$

or $d'=\dfrac{5}{4}d$

$\Rightarrow\,m=\dfrac{4LB}{5g}I$

$\begin{array}{rcl} \Rightarrow\dfrac{4LB}{5g}&=&\dfrac{\Delta m}{\Delta I}\\ \\\Rightarrow\,B&=&\dfrac{5g\Delta m}{4L\Delta I}\\ \\&=&\dfrac{5\times 10\left(1\cdot 10^{-3}-0\right)}{4\times 2\cdot 10^{-2}(5-0)}\\ \\\Rightarrow\,B&=&0.125T \end{array}$

3) La masse maximale supportable par la balance

$\begin{array}{rcl} m&=&\dfrac{4\times2\cdot 10^{-2}\times 0.125}{5\times 10}\times 12\\\\\Rightarrow\,m&=&2.4g \end{array}$

La masse maximale supportable par la balance est inférieure $m=2.45g$ ; donc la balance ne peut pas supporter une telle masse.

Exercice 4

1) Représentation des forces qui exercent sur la barre $\overrightarrow{P}.$

Sens de $\overrightarrow{B}$ (voir schéma)

a) La condition la condition d'équilibre de la barre $MN$ s'écrit :

$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}=\vec{0}$

b) Expression de la norme de $B$ en fonction de $I_{1}$, $L$, $m$, $g$ et $\theta.$

Pour que la barre reste en équilibre.

$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}=\vec{0}$

En projetant la relation suivant l'axe $xx'$

$\begin{array}{rcl} -mg\sin\theta+I_{1}LB+0&=&0\\\\\Rightarrow\,B&=&\dfrac{mg\sin\theta}{I_{1}L} \end{array}$

Montrons que $B=68mT.$

$\begin{array}{rcl} B&=&\dfrac{mg\sin\theta}{I_{1}L}\\\\&=&\dfrac{10\cdot 10^{-3}\times 10\times\sin 20^{\circ}}{10\times 0.05}\\\\\Rightarrow\,B&=&68mT \end{array}$

3) a) Représentation des forces qui exercent sur la barre $MN.$

b) La condition d'équilibre de la barre s'écrit :

$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}+\overrightarrow{T}=\vec{0}$

Valeur de la constante de raideur $k$ du ressort.

En projetant la relation suivant l'axe $xx'$

$\begin{array}{rcl} -mg\sin\theta+I_{1}LB+0-k\Delta l&=&0\\\\\Rightarrow\,k&=&\dfrac{I_{2}LB-mg\sin\theta}{\Delta l}\\\\k&=&\dfrac{15\times 0.05\times 68\cdot 10^{-3}-10\cdot 10^{-3}\times 10\times\sin 20^{\circ}}{3.6\cdot 10^{-3}}\\\\\Rightarrow\,k&=&4.7N\cdot m^{-1} \end{array}$

Exercice 5

1) a) Sens du courant traversant la tige. Voir figure

b) Caractéristiques de la force de la place exercée sur la tige

$\bullet\ $Point d'application : milieu $AC$

$\bullet\ $Direction : perpendiculaire à la tige

$\bullet\ $Sens : voir figure

$\bullet\ $Intensité :

$\begin{array}{rcl} F&=&I_{1}lB_{1}\\\\&=&10\times 10\cdot 10^{-2}\times 0.1\\\\\Rightarrow\,F&=&0.1N \end{array}$

2) a) Bilan des forces qui exercent sur la tige : $\overrightarrow{P}$ ; $\overrightarrow{F}$ ; $\overrightarrow{R}$ et $\overrightarrow{T}$

b) Détermination de l'allongement du ressort $\Delta l.$

Le théorème des moments appliqué à la tige s'écrit :

$\begin{array}{rcl} M_{O}\left(\overrightarrow{P}\right)+M_{O}\left(\overrightarrow{F}\right)+M_{O}\left(\overrightarrow{T}\right)+M_{O}\left(\overrightarrow{R}\right)&=&0\\\\\Rightarrow -mg\dfrac{L}{2}\sin\alpha+I_{1}lB_{1}\left(L-\dfrac{l}{2}\right)+0-k\Delta ll\cos\alpha&=&0\\\\\Delta l&=&\dfrac{I_{1}lB_{1}\left(L-\dfrac{l}{2}-mg\dfrac{L}{2}\sin\alpha}{kl\cos\alpha}\\\\&=&\dfrac{10\times 10\cdot 10^{-2}\times 0.1\left(40\cdot 10^{-2}-5\cdot 10^{-2}\right)-10\cdot 10^{-3}\times 10\times 20\cdot 10^{-2}\times\sin 8^{\circ}}{23\times 10\cdot 10^{-2}\times\cos 8^{\circ}}\\ \\\Rightarrow\Delta l&=&0.014m \end{array}$

3) a) Bilan des forces qui exercent sur la tige : $\overrightarrow{P}$ ; $\overrightarrow{F}$ et $\overrightarrow{R}$

b) Détermination de la valeur du champ magnétique $\overrightarrow{B_{2}}.$

$\begin{array}{rcl} M_{O}\left(\overrightarrow{P}\right)+M_{O}\left(\overrightarrow{F}\right)+M_{O}\left(\overrightarrow{R}\right)&=&0\\\\\Rightarrow-mg\dfrac{L}{2}\sin\alpha+I_{1}l\left(B_{1}-B_{2}\right)\left(L-\dfrac{1}{2}\right)+0&=&0\\\\\Rightarrow\,B_{2}&=&B_{1}-\dfrac{mg\dfrac{L}{2}\sin\alpha}{I_{1}l\left(L-\dfrac{l}{2}\right)}\\\\&=&0.1-\dfrac{10\cdot 10^{-3}\times 10\times 20\cdot 10^{-2}\times\sin 4^{\circ}}{10\times 10\cdot 10^{-2}\times\left(40\cdot 10^{-2}-5\cdot 10^{-2}\right)}\\\\\Rightarrow\,B_{2}&=&0.096T \end{array}$

4) a) Caractéristiques de la force de Laplace

$\bullet\ $Point d'application : milieu $AC$

$\bullet\ $Direction : la verticale

$\bullet\ $Sens : de haut en bas

$\bullet\ $Intensité : $F=I_{3}lB_{3}$

b) Le courant $I_{3}$ circule de $O$ vers $A$

Calcul de la valeur de $I_{3}$

$\begin{array}{rcl} M_{O'}\left(\overrightarrow{P}\right)+M_{O'}\left(\overrightarrow{F}\right)+M_{O'}\left(\overrightarrow{R}\right)&=&0\\\\\Rightarrow-m_{0}gO'P+I_{3}lB_{3}O'A+0&=&0\\\\(O'P=O'A)\Rightarrow-m_{0}gO'P+I_{3}lB_{3}O'A+0&=&0\\\\\Rightarrow\,I_{3}&=&\dfrac{m_{0}g}{lB_{3}}\\\\&=&\dfrac{4\cdot 10^{-3}\times 10}{10\cdot 10^{-2}\times 5\cdot 10^{-2}}\\\\\Rightarrow\,I_{3}&=&4A \end{array}$

Exercice 6

1) a) Représentation des forces qui s'exercent sur la tige $(T)$

b) L'allongement du ressort est dû à la force à la tension du fil de direction verticale et de sens ascendant.

c) Le champ magnétique $\overrightarrow{B}$ est de direction verticale et de sens ascendant. Ce champ est dirigé suivant l'axe nord-sud.

2) a) Montrons que l'équation de la courbe est de la forme : $I=ax$

Système étudié : la tige

Référentiel d'étude : terrestre supposé galiléen

Bilan des forces appliquées :

$\overrightarrow{P}=m\overrightarrow{g}$ ; $\overrightarrow{T_{f}}$ ; $\overrightarrow{R}$

$\overrightarrow{F}=i\overrightarrow{L}\wedge\overrightarrow{B}$

La condition d'équilibre s'écrit :

$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}+\overrightarrow{T_{f}}=\vec{0}$

En projetant la relation suivant $\overrightarrow{F}$ force de Laplace

$0+0-T_{f}+F=0$ ; $F=ILB$

Le fil est inextensible et le poids de la poulie est négligeable :

$\begin{array}{rcl} T_{f}&=&T\\\\&=&kx\\\\\Rightarrow-kx+ILB&=&0\\\\\Rightarrow\,ILB&=&kx\\\\\Rightarrow\,I&=&\dfrac{k}{LB}x\\\\&=&ax\\\\\Rightarrow\,a&=&\dfrac{k}{LB} \end{array} $

b) Le graphe représentant $I$ en fonction de $x$ est une droite dont sa pente ou son coefficient directeur est a :

$\begin{array}{rcl} a&=&\dfrac{\Delta I}{\Delta x}\\\\&=&\dfrac{5-0}{2.5\cdot 10^{-3}-0}\\\\\Rightarrow\,a&=&2\cdot 10^{3}A\cdot m^{-1} \end{array}$

c) Relation qui lie $B$, $I$, $k$, $x$ et $L$

$I=\dfrac{k}{LB}x=ax$

$\begin{array}{rcl} a&=&\dfrac{k}{LB}\\\\\Rightarrow\,B&=&\dfrac{k}{aL}\\\\&=&\dfrac{10}{2\cdot 10^{3}\times 10\cdot 10^{-2}}\\\\\Rightarrow\,B&=&0.05T \end{array}$

3) a) Représentation des forces qui s'exercent sur la tige.

b) Montrons que la masse $m$ de la tige $(T)$ est donnée par l'expression : $m=\dfrac{IBL}{g\sin\alpha}$

Le système est en équilibre, la condition d'équilibre s'écrit :

$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}=\vec{0}$

La projection de la relation suivant $CE$ :

$\begin{array}{rcl} -mg\sin\alpha+ILB+0&=&0\\\\\Rightarrow\,mg\sin\alpha&=&ILB\\\\\Rightarrow\,m&=&\dfrac{ILB}{g\sin\alpha} \end{array}$

c) Calcul de la valeur de la masse $m$

$\begin{array}{rcl} m&=&\dfrac{ILB}{g\sin\alpha}\\\\&=&\dfrac{1\times 10\cdot 10^{-2}\times 0.05}{9.8\times\sin 15^{\circ}}\\\\\Rightarrow\,m&=&1.97\cdot 10^{-3}Kg \end{array}$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Solutions des exercices : Mouvement d'une particule chargée dans un champ magnétique uniforme - Ts

Classe:

Terminale

Exercice 1

1) a) Détermination de l'expression littérale de la vitesse $v$ en $A$ d'un ion de masse $m$ et de charge $q$ en fonction de $m$, $e$ et $U$

Système étudié : l'ion

Référentiel d'étude : terrestre

Bilan des forces appliquées :

$-\ $la force électrique $\overrightarrow{F}$

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force électrique

Le théorème de l'énergie cinétique entre $S$ et $A$ s'écrit :

\begin{eqnarray} \Delta E_{C} &=&\sum\,W_{\overrightarrow{F}_{\text{EXT}}}\nonumber\\\\\Rightarrow E_{CA}-E_{CS} &=&W_{SA}\left(\overrightarrow{F}\right)\nonumber\\\\\Rightarrow\dfrac{1}{2}mv_{A}^{2}-0 &=&2eU\nonumber\\\\\Rightarrow v_{A} &=&\sqrt{\dfrac{2eU}{m}} \end{eqnarray}

b) Montrons que les deux ions $_{80}^{200}Hg^{2+}$ et $_{80}^{202}Hg^{2+}$ émis par $S$ arrivent en $A$ avec des vitesses différentes.

Ayant la même charge et accélérés par le même champ, la vitesse des ions ne dépend que de leur masse. Ce qui explique bien la différence de vitesse des ions lorsqu'ils arrivent en $A.$

2) a) Établissement de l'expression de $R$ en fonction de $m$, $e$, $||\overrightarrow{B}||$ et $||\overrightarrow{V}||$ puis en fonction de $m$, $e$, $||\overrightarrow{B}||$ et $U.$

Système étudié : l'ion

Référentiel d'étude : terrestre supposé galiléen

Bilan des forces appliquées :

$-\ $la force magnétique $\overrightarrow{F}_{m}$

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force magnétique

La deuxième de Newton s'écrit :

$\overrightarrow{F}_{m}=m\vec{a}$

$\Rightarrow\,2e\vec{v}\wedge\overrightarrow{B}$

$\Rightarrow\,\vec{a}=\dfrac{2e\vec{v}\wedge\overrightarrow{B}}{m}$

\begin{eqnarray} \vec{v}\perp\overrightarrow{F_{_{m}}}\Rightarrow\vec{a}_{t} &=&\vec{0}\nonumber\\\\\Rightarrow\vec{a} &=&\overrightarrow{a}_{n}\nonumber\\\\\Rightarrow\,a_{n} &=&\dfrac{v^{2}}{R}\nonumber\\\\ &=&\dfrac{2evB}{m}\nonumber\\\\\Rightarrow R &=&\dfrac{mv}{2eB}\nonumber\\\\\text{or}\quad v &=&\sqrt{\dfrac{2eU}{m}}\nonumber\\\\\Rightarrow R &=&\dfrac{m\sqrt{\dfrac{2eU}{m}}}{2eB}\nonumber\\\\\Rightarrow R &=&\dfrac{1}{2B}\sqrt{\dfrac{2mU}{e}} \end{eqnarray}

b) Calcul de $R_{1}$ et $R_{2}$

\begin{eqnarray} R_{1} &=&\dfrac{1}{2B}\sqrt{\dfrac{2m_{1}U}{e}}\nonumber\\\\ &=&\dfrac{1}{2\times 0.2}\sqrt{\dfrac{2\times 3.32\cdot 10^{-25}\times 600}{1.6\cdot 10^{-19}}}\nonumber\\\\\Rightarrow R_{1} &=&0.124\,m \end{eqnarray}

\begin{eqnarray} R_{2} &=&\dfrac{1}{2B}\sqrt{\dfrac{2m_{2}U}{e}}\nonumber\\\\ &=&\dfrac{1}{2\times 0.2}\sqrt{\dfrac{2\times 3.35\cdot 10^{-25}\times 600}{1.6\cdot 10^{-19}}}\nonumber\\\\\Rightarrow R_{2} &=&0.125\,m \end{eqnarray}

La distance $IF$ entre les deux points d'impact

\begin{eqnarray} IF &=& 2\left(R_{2}-R_{1}\right)\nonumber\\\\ &=&2(0.125-0.124)\nonumber\\\\\Rightarrow IF &=&0.002\,m \end{eqnarray}

Exercice 2

1.1. Expression de la force agissant sur le proton en $O$

$\overrightarrow{F}_{m}=q_{P}\overrightarrow{v_{0}}\wedge\overrightarrow{B}$ soit en module $F_{m}=q_{P}v_{0} B$

1.2. Montrons que la valeur de la vitesse est constante

\begin{eqnarray} \vec{v}\perp\overrightarrow{F_{m}}\Rightarrow\vec{a}_{t} &=&\vec{0}\nonumber\\\\\Rightarrow\,a_{t} &=&\dfrac{\mathrm{d}v}{\mathrm{d}\mathrm{t}}\nonumber\\\\ &=&0\nonumber\\\\\Rightarrow v &=&cte \end{eqnarray}

1.3. Montrons que la trajectoire est circulaire de rayon $R_{0}=\dfrac{m_{P}}{q_{P}B}V_{0}$

\begin{eqnarray} \overrightarrow{a_{t}} &=& \vec{0}\nonumber\\\\\Rightarrow\overrightarrow{a} &=&\overrightarrow{a_{n}}\nonumber\\\\\Rightarrow\,a_{n} &=&\dfrac{v_{0}^{2}}{R_{0}}\nonumber\\\\ &=&\dfrac{q_{P}v_{0}B}{m}\nonumber\\\\\Rightarrow\,R_{0} &=&\dfrac{m_{P}v_{0}}{q_{P}B} \end{eqnarray}

Le rayon est constant, le mouvement est donc circulaire

2.1. Expression de la longueur parcourue par un proton sur le demi-tour de rayon $R_{0}$

$$l=\pi\,R_{0}=\dfrac{\pi m_{P}v_{0}}{q_{P}B}$$

2.2. Expression du temps t mis par ce proton pour effectuer ce demi-tour

\begin{eqnarray} t &=&\dfrac{l}{v_{0}}\nonumber\\\\ &=&\dfrac{\dfrac{\pi m_{P}v_{0}}{q_{P}B}}{v_{0}}\nonumber\\\\\Rightarrow\,t &=&\dfrac{\pi m_{P}}{q_{P}B} \end{eqnarray}

2.3. Ce temps est indépendant de la vitesse d'entrée du proton dans le «dee»

Calcul de la valeur de $t.$

\begin{eqnarray} \Rightarrow\,t &=&\dfrac{\pi m_{P}}{q_{P}B}\nonumber\\\\ &=&\dfrac{\pi\times 1.67\cdot 10^{-27}}{1.6\cdot 10^{-19}\times 1.0}\nonumber\\\\\Rightarrow t &=&3.3\cdot 10^{-8}s \end{eqnarray}

3. Calcul de la fréquence $f$

\begin{eqnarray} f &=&\dfrac{1}{2t}\nonumber\\\\ &=&\dfrac{1}{2\times 3.3\cdot 10^{-8}}\nonumber\\\\\Rightarrow f &=&15\cdot 10^{-8}s \end{eqnarray}

4.1. Expression littérale de la variation d'énergie cinétique $\Delta E_{c}$ du proton

Le théorème de l'énergie cinétique s'écrit :

\begin{eqnarray} \Delta E_{c} &=&\sum\,W_{\overrightarrow{F}_{\text{EXT}}}\nonumber\\\\\Rightarrow\Delta E_{c} &=& W_{SA}\left(\overrightarrow{F}\right)\nonumber\\\\ &=& q_{P}U_{M} \end{eqnarray}

Calcul de la variation d'énergie cinétique $\Delta E_{c}$ du proton

\begin{eqnarray} \Delta E_{c} &=&q_{P}U_{M}\nonumber\\\\ &=& 1.6\cdot 10^{-19}\times 2\cdot 10^{3}\nonumber\\\\\Rightarrow\Delta E_{c} &=& 3.2\cdot 10^{-16}J \end{eqnarray}

\begin{eqnarray} \Delta E_{c} &=&\dfrac{q_{P}U_{M}}{e}\nonumber\\\\\Rightarrow\Delta E_{c} &=& 2\cdot 10^{3}eV \end{eqnarray}

$\left(e=q_{P}=1.6\cdot 10^{-19}C\right)$

4.2. Le rayon de la trajectoire du proton augmente à chaque fois qu'il traverse l'intervalle étroit puisque le rayon de la trajectoire augmente avec la vitesse.

5. Calcul du nombre de tours que le proton décrits dans le cyclotron.

Le nombre de tours correspond à l'énergie finale de la particule divisée par l'énergie acquise à chaque tour.

\begin{eqnarray} n &=&\dfrac{\Delta E_{cf}}{2\Delta E_{c}}\nonumber\\\\ &=&\dfrac{\dfrac{1}{2}m_{P}v^{2}-0}{2\Delta E_{c}}\nonumber\\\\\Rightarrow n &=&\dfrac{1.67\cdot 10^{-27}\times\left(2\cdot 10^{7}\right)^{2}}{4\times 3.2\cdot 10^{-16}}\nonumber\\\\ &=& 552\text{tours} \end{eqnarray}

6. Calcul de la valeur du rayon

\begin{eqnarray} R &=&\dfrac{m_{P}v}{q_{P}B}\nonumber\\\\ &=&\dfrac{1.67\cdot 10^{-27}\times 2\cdot 10^{7}}{1.6\cdot 10^{-19}\times 1.0}\nonumber\\\\\Rightarrow R &=&0.21\,m \end{eqnarray}

Exercice 3 : Utilisation d'un spectrographe de masse

1) Expression de la force magnétique s'exerçant sur l'ion $X^{+}.$

$\overrightarrow{F_{m}}=e\vec{v}\wedge\overrightarrow{B}$ soit en module $F_{m}=evB$

Représentation sur un schéma du vecteur force $\overrightarrow{F_{m}}$ (Voir figure)

Sens du vecteur champ magnétique $\overrightarrow{B}$ (Voir figure)

2) Démontrons que le mouvement de l'ion $X^{+}$ dans la zone $IV$ est plan et uniforme

Système étudié : l'ion

Référentiel d'étude : terrestre supposé galiléen

Bilan des forces appliquées :

$-\ $la force magnétique $\overrightarrow{F_{m}}$

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force magnétique

Le théorème du centre d'inertie s'écrit :

\begin{eqnarray} \overrightarrow{F_{m}} &=&m\vec{a}\nonumber\\\\\Rightarrow e\vec{v}\wedge\overrightarrow{B}\nonumber\\\\ &=&m\vec{a}\nonumber\\\\\Rightarrow \vec{a} &=&\dfrac{e\vec{v}\wedge\overrightarrow{B}}{m} \end{eqnarray}

$\vec{a}\perp\overrightarrow{B}\ ;\ \vec{v}\perp\overrightarrow{B}\text{ et }\vec{a}\perp\overrightarrow{v}$

La trajectoire est contenue dans un plan orthogonal $\overrightarrow{B}.$

Le mouvement est donc plan.

$\vec{a}\perp\vec{v}\Rightarrow\overrightarrow{a_{t}}=\vec{0}$

$\Rightarrow\,a_{t}=\dfrac{\mathrm{d}v}{\mathrm{d}t}=0\Rightarrow\,v=cte$

Le mouvement est uniforme

3) Montrons que l'ion $X^{+}$ décrit dans cette zone un arc de cercle.

\begin{eqnarray} \overrightarrow{a_{t}} &=&\vec{0}\nonumber\\\\\Rightarrow\overrightarrow{a_{n}} &=&\overrightarrow{a}\nonumber\\\\\Rightarrow a_{n} &=&a\nonumber\\\\\Rightarrow\dfrac{v'^{2}}{R} &=&\dfrac{ev'B}{m}\nonumber\\\\\Rightarrow\,R &=&\dfrac{mv'}{eB}\nonumber\\\\ &=& cte \end{eqnarray}

L'ion $X^{+}$ décrit donc dans cette zone un arc de cercle

4) Expression le rayon du cercle trajectoire en fonction de $U'$, $m$, $e$ et $B.$

\begin{eqnarray} R &=&\dfrac{mv'}{eB}\nonumber\\\\\text{or }v' &=&\sqrt{\dfrac{2eU'}{m}}\nonumber\\\\\Rightarrow\,R &=&\dfrac{m\sqrt{\dfrac{2eU'}{m}}}{eB}\nonumber\\\\\Rightarrow\,R &=&\dfrac{1}{B}\sqrt{\dfrac{2mU'}{e}} \end{eqnarray}

5) Masse de l'ion $X^{+}$

\begin{eqnarray} O_{3}A &=&2R\nonumber\\\\ &=&\dfrac{2}{B}\sqrt{\dfrac{2mU'}{e}}\nonumber\\\\\Rightarrow\,O_{3}A^{2} &=&\dfrac{4}{B^{2}}\times\dfrac{2m U'}{e}\nonumber\\\\\Rightarrow m &=&\dfrac{eB^{2}O_{3}A^{2}}{8U'}\nonumber\\\\ &=&\dfrac{1.6\cdot 10^{-19}\times(1.80)^{2}\times(0.069)^{2}}{8\times 8.00\cdot 10^{3}}\nonumber\\\\\Rightarrow m &=&3.86\cdot 10^{-26}Kg \end{eqnarray}

Identification de la substance $X.$

\begin{eqnarray} m &=& Am_{P}\nonumber\\\\\Rightarrow A &=&\dfrac{m}{m_{P}}\nonumber\\\\\Rightarrow A &=&\dfrac{3.86\cdot 10^{-26}}{1.67\cdot 10^{-27}}\nonumber\\\\ &=&23 \end{eqnarray}

L'élément est le sodium de symbole $Na$

Exercice 4 : spectromètre de masse

a) Valeur du champ électrique $\overrightarrow{E}$

Les particules ne sont pas déviées lorsque les deux forces électrique et magnétique auxquelles sont soumises se compensent.

\begin{eqnarray} \overrightarrow{F_{e}}+\overrightarrow{F_{m}} &=&\vec{0}\nonumber\\\\\Rightarrow q\overrightarrow{E}+q\vec{v}\wedge\overrightarrow{B} &=&\vec{0}\nonumber\\\\\Rightarrow\overrightarrow{E} &=&-\vec{v}\wedge\overrightarrow{B}\nonumber\\\\\Rightarrow\,E &=&vB\nonumber\\\\\Rightarrow\,v &=&\dfrac{E}{B}\nonumber\\\\ &=&\dfrac{6.4\cdot 10^{6}}{0.32}\nonumber\\\\\Rightarrow\,v &=&20.10^{6}m\cdot s^{-1} \end{eqnarray}

Il ne se passe rien si q change de signe puisque cette vitesse est indépendante de la charge.

b) i) Montons que les particules de même rapport $\dfrac{q}{m}$ décrivent des trajectoires circulaires de même rayon $R.$

\begin{eqnarray} \overrightarrow{F_{m}} &=&q\vec{v}\wedge\overrightarrow{B}\nonumber\\\\ &=&m\vec{a}\nonumber\\\\\Rightarrow|q|vB &=&ma_{n}\nonumber\\\\\Rightarrow|q|vB &=&m\dfrac{|v^{2}|}{R}\nonumber\\\\\Rightarrow\dfrac{|q|}{m} &=&\dfrac{v}{RB} \end{eqnarray}

$v=cte\;,\ m=cte\ ;\ \text{si }\dfrac{|q|}{m}=cte\Rightarrow\,R=cte$

Les particules de même rapport $q/m$ décrivent des trajectoires circulaires de même rayon $R.$

Calcul de $R.$

Le signe $q$ détermine le sens de la déviation.

ii) Montrons que $R=\left(d^{2}+a^{2}\right)/2d.$

\begin{eqnarray} R^{2} &=&a^{2}+x^{2}\nonumber\\\\\text{ or }R &=&d+X\nonumber\\\\\Rightarrow X &=&R-d\nonumber\\\\\Rightarrow R^{2} &=&a^{2}+(R-d)^{2}\nonumber\\\\\Rightarrow R^{2} &=&a^{2}+R^{2}-2dR+d^{2}\nonumber\\\\\Rightarrow 2dR &=&a^{2}+d^{2}\nonumber\\\\\Rightarrow R &=&\dfrac{a^{2}+d^{2}}{2d} \end{eqnarray}

Valeur de $q/m$

\begin{eqnarray} \dfrac{q}{m} &=&\dfrac{v}{RB}\nonumber\\\\ &=&\dfrac{2dv}{B\left(a^{2}+d^{2}\right)}\nonumber\\\\ &=&\dfrac{2\times 10\cdot 10^{-2}\times 20\cdot 10^{6}}{0.32\times\left(\left(5.0\cdot 10^{-2}\right)^{2}+\left(10\cdot 10^{-2}\right)^{2}\right)}\nonumber\\\\\Rightarrow\dfrac{q}{m} &=&48\cdot 10^{6}CKg^{-1} \end{eqnarray}

Identification des particules

\begin{eqnarray} \dfrac{q}{m} &=& 48\cdot 10^{6}CKg^{-1}\nonumber\\\\\Rightarrow m &=&\dfrac{q}{48\cdot 10^{6}}\nonumber\\\\\Rightarrow Am_{P} &=&\dfrac{q}{48\cdot 10^{6}}\nonumber\\\\ A &=&\dfrac{q}{48\cdot 10^{6}m_{P}}\nonumber\\\\ &=&\dfrac{q}{48\cdot 10^{6}\times 1830m_{e}}\nonumber\\\\ &=&\dfrac{1.6\cdot 10^{-19}}{48\cdot 10^{6}\times 1830\times 9.1\cdot 10^{-31}}\nonumber\\\\\Rightarrow A &=&2 \end{eqnarray}

Les particules sont des deutériums

Exercice 5

1) Établissement de l'expression de $r_{1}$ et $r_{2}$ en fonction de $q$, $m$, $B$ et des vitesses respectives $v_{1}$ et $v_{2}$ de la particule.

\begin{eqnarray} F_{m} &=&ma_{n}\nonumber\\\\ &=&\dfrac{mv^{2}}{r}\nonumber\\\\ &=&qvB\nonumber\\\\\Rightarrow\,r &=&\dfrac{mv}{qB}_nonumber\\\\\Rightarrow\,r_{1} &=&\dfrac{mv_{1}}{qB}\nonumber\\\\\text{et}\quad r_{2} &=&\dfrac{mv_{2}}{qB} \end{eqnarray}

\begin{eqnarray} \dfrac{r_{1}}{3} &=&r_{2}\nonumber\\\\\Rightarrow r_{2} &=&3r_{1}\nonumber\\\\\Rightarrow r_{2} &>& r_{1}\nonumber\\\\\Rightarrow\dfrac{mv_{2}}{qB} &>&\dfrac{mv_{1}}{qB}\nonumber\\\\\Rightarrow v_{2} &>& v_{1} \end{eqnarray}

Lorsque la particule ralentit, sa vitesse diminue. La particule se déplace de $II$ vers de $I$

Détermination de $v_{1}$ et $v_{2}.$

$v_{2}=2\cdot 10^{7}m\cdot s^{-1}$

$r=\dfrac{mv}{qB}\Rightarrow\dfrac{qB}{m}=\dfrac{v}{r}$

\begin{eqnarray} \dfrac{v_{1}}{r_{1}} &=&\dfrac{v_{2}}{r_{2}}\nonumber\\\\\Rightarrow v_{1} &=&\dfrac{r_{1}v_{2}}{r_{2}}\nonumber\\\\ &=&\dfrac{1}{3}\times 2\cdot 10^{7}\nonumber\\\\\Rightarrow v_{1} &=& 6.7\cdot 10^{6}m\cdot s^{-1} \end{eqnarray}

2) Le signe de la particule est positif. Le trièdre doit être direct et la particule se déplace de $II$ vers de $I$

3) Calcul de la charge massique $\dfrac{q}{m}$

\begin{eqnarray} \dfrac{q}{m} &=&\dfrac{v}{r_{2}B}\nonumber\\\\ &=&\dfrac{2.0\cdot 10^{7}}{3\times 14\cdot 10^{-2}\times 0.50}\nonumber\\\\\Rightarrow\dfrac{q}{m} &=&9.5\cdot 10^{7}CKg^{-1} \end{eqnarray}

Identification de la particule

\begin{eqnarray} \dfrac{q}{m} &=&9.5\cdot 10^{7}CKg^{-1}\nonumber\\\\\Rightarrow q &=&9.5\cdot 10^{7}m\nonumber\\\\\Rightarrow Ze &=&9.5\cdot 10^{7}m\nonumber\\\\\Rightarrow Z &=&\dfrac{9.5\cdot 10^{7}m}{e}\nonumber\\\\ &=&\dfrac{9.5\cdot 10^{7}\times 1.67\cdot 10^{-27}}{1.6\cdot 10^{-19}} \end{eqnarray}

$Z=1$ La particule est un proton

Exercice 6

1) a) La tension doit être établie de façon que la plaque $P_{2}$ soit chargée négativement.

b) Montrons que l'énergie cinétique, est indépendante de l'isotope envisagé.

Système étudié : l'ion

Référentiel d'étude : terrestre

Bilan des forces appliquées :

$-\ $la force électrique $\overrightarrow{F}$

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force électrique

Le théorème de l'énergie cinétique entre $P_{1}$ et $P_{2}$ s'écrit :

\begin{eqnarray} \Delta E_{c} &=& W\left(\overrightarrow{F}\right)\nonumber\\\\ &=&2eU\nonumber\\\\\Rightarrow E_{C_{p_{2}}}-0 &=&2eU\nonumber\\\\\Rightarrow E_{C_{p_{2}}} &=&2eU \end{eqnarray}

L'énergie cinétique, ne dépend que de la tension accélératrice

\begin{eqnarray} E_{C_{p_{2}}} &=& 2eU\nonumber\\\\ &=&2\times 1.6\cdot 10^{-19}\times 1000\nonumber\\\\\Rightarrow\,E_{C_{p_{2}}} &=&3.2\cdot 10^{-16}J \end{eqnarray}

c) Calcul de la vitesse acquise par les ions $_{54}^{129}Xe^{+}$

\begin{eqnarray} \dfrac{1}{2}mv^{2} &=& E_{C_{p_{2}}}\nonumber\\\\\Rightarrow\,v &=&\sqrt{\dfrac{2E_{C_{p_{2}}}}{129m_{P}}}\nonumber\\\\ &=&\sqrt{\dfrac{2\times 3.2\cdot 10^{-16}}{129\times 1.67\cdot 10^{-27}}}\nonumber\\\\\Rightarrow\,v &=&5.45\cdot 10^{4}m\cdot s^{-1} \end{eqnarray}

d) Expression, en fonction de $x$ et $v$, de la vitesse $v'$ acquise par les ions $_{54}^{x}Xe^{+}$ en $O_{2}$

$\dfrac{1}{2}\times 129m_{P}v^{2}=2eU$ ;

\begin{eqnarray} \dfrac{1}{2}xm_{P}v'^{2} &=& 2eU\nonumber\\\\\Rightarrow\dfrac{1}{2}xm_{P}v'^{2} &=&\dfrac{1}{2}\times 129m_{P}v^{2}\nonumber\\\\\Rightarrow\,v' &=&v\sqrt{\dfrac{129}{x}} \end{eqnarray}

2) Séparation des ions

a) Montrons que le mouvement est plan, circulaire et uniforme

Système étudié : l'ion

Référentiel d'étude : terrestre supposé galiléen

Bilan des forces appliquées :

$-\ $la force magnétique $\overrightarrow{F_{m}}$

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force magnétique

Le théorème de centre d'inertie s'écrit :

\begin{eqnarray} \overrightarrow{F_{m}} &=&m\vec{a}\nonumber\\\\\Rightarrow\,e\vec{v}\wedge\overrightarrow{B} &=&m\vec{a}\nonumber\\\\\Rightarrow\vec{a} &=&\dfrac{e\vec{v}\wedge\overrightarrow{B}}{m} \end{eqnarray}

$\vec{a}\perp\overrightarrow{B}\ ;\ \vec{v}\perp\overrightarrow{B}\quad\text{et}\quad\vec{a}\perp\vec{v}$

La trajectoire est contenue dans un plan orthogonal $\overrightarrow{B}$

Le mouvement est donc plan

\begin{eqnarray} \vec{a}\perp\vec{v}\Rightarrow\vec{a_{t}} &=&\vec{0}\nonumber\\\\\Rightarrow\,a_{t} &=&\dfrac{\mathrm{d}v}{\mathrm{d}t}\nonumber\\\\ &=&0\nonumber\\\\\Rightarrow\,v &=&cte \end{eqnarray}

Le mouvement est uniforme

\begin{eqnarray} \vec{a_{t}} &=&\vec{0}\nonumber\\\\\Rightarrow\,\vec{a_{n}} &=&\vec{a}\nonumber\\\\\Rightarrow\,a_{n} &=& a\nonumber\\\\\Rightarrow\dfrac{v^{2}}{R} &=&\dfrac{evB}{m}\nonumber\\\\\Rightarrow\,R &=&\dfrac{mv}{eB}\nonumber\\\\ &=&cte \end{eqnarray}

Le mouvement est circulaire

Expression du rayon de courbure $R.$

\begin{eqnarray} R &=&\dfrac{mv}{eB}\nonumber\\\\ &=&\dfrac{129\times 1.67\cdot 10^{-27}\times 5.45\cdot 10^{4}}{1.6\cdot 10^{-19}\times 0.1}\nonumber\\\\\Rightarrow\,R &=&0.734m \end{eqnarray}

b) Valeur de $x$

\begin{eqnarray} AB &=&2R'-2R\nonumber\\\\ &=&2\left(\dfrac{xm_{P}v'}{eB}-\dfrac{129m_{P}v}{eB}\right)\nonumber\\\\ &=& 2\left(\dfrac{xm_{P}}{eB}v\sqrt{\dfrac{129}{x}}-\dfrac{129m_{P}v}{eB}\right)\nonumber\\\\ &=&2\left(\dfrac{m_{P}}{eB}v\sqrt{129x}-\dfrac{129m_{P}v}{eB}\right)\nonumber\\\\\Rightarrow\dfrac{m_{P}}{eB}v\sqrt{129x} &=&\dfrac{AB}{2}+\dfrac{129m_{P}v}{eB}\nonumber\\\\\Rightarrow\sqrt{129x} &=&\dfrac{eB\cdot AB}{2m_{P}v}+129\nonumber\\\\\Rightarrow\,x &=&\dfrac{1}{129}\left(\dfrac{eB\cdot AB}{2m_{P}v}+129\right)^{2}\nonumber\\\\ &=&\dfrac{1}{129}\left(\dfrac{1.6\cdot 10^{-19}\times 0.1\times 8\cdot 10^{-2}}{2\times 1.67\cdot 10^{-27}\times 5.45\cdot 10^{4}}+129\right)^{2}\nonumber\\\\\Rightarrow\,x &=&143 \end{eqnarray}

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Solutions des exercices : Réactions Nucléaire - Ts

Classe:

Troisième

Exercice 1

1.1. Cette réaction de désintégration correspondant à la radioactivité $\alpha$ car la particule émise est l'hélium.

1.2. Expression littérale du défaut de masse $\Delta m$ du noyau de symbole $_{Z}^{A}X$ et de masse $m_{X}$

$\Delta m=Zm_{P}+(A-Z)m_{n}-m_{X}$

Calcul du défaut de masse du noyau de radium $R_{a}$ en unité de masse atomique $u$

\begin{eqnarray} \Delta m &=& Zm_{P}+(A-Z)m_{n}-m_{Pa}\nonumber\\\\ &=& 88\times 1.007+(226-88)\times1.009-225.977\nonumber\\\\\Rightarrow \Delta m &=&1.881u \end{eqnarray}

1.3. Expression de la relation d'équivalence masse-énergie

$\Delta E=\Delta mC^{2}=\left(Zm_{P}+\left(A-Z\right)m_{n}-m_{X}\right)C^{2}$

1.4. L'énergie de liaison $E_{1}$ d'un noyau est l'énergie qu'il faut fournir à un noyau au repos pour le dissocier en nucléons isolés et immobiles.

Calcul, en joule, de l'énergie de liaison $E_{1}(Rn)$ du noyau de radon.

\begin{eqnarray} E_{1}\left(R_{n}\right) &=&\Delta mE\nonumber\\\\ &=&\dfrac{3.04\cdot 10^{-27}}{1.66054\cdot 10^{-27}}\times 93.5\nonumber\\\\\Rightarrow E_{1}\left(R_{n}\right)&=&1.71\cdot 10^{3}MeV \end{eqnarray}

Énergie de liaison par nucléon $E_{1}/A$ du noyau de radon en $MeV\cdot$nucléon$^{-1}.$

\begin{eqnarray} E_{1}/A &=&\dfrac{E_{1}\left(R_{n}\right)}{A}\nonumber\\\\ &=&\dfrac{1.76\cdot 10^{3}}{222}\nonumber\\\\\Rightarrow E_{1}/A &=&7.93MeV\cdot\text{nucléon}^{-1} \end{eqnarray}

1.5. Expression littérale de la variation d'énergie $\Delta E$ de la réaction en fonction de $m_{Ra}$, $m_{Rn}$ et $m_{He}$

\begin{eqnarray} \Delta E &=&\left(m_{Rn}+m_{He}-m_{Ra}\right)C^{2}\nonumber\\\\\Rightarrow\Delta E &=&(221.970+4.001-225.977)\times 1.66054\cdot 10^{-27}\times\left(3.0\cdot 10^{8}\right)^{2}\nonumber\\\\\Rightarrow\Delta E &=&9.0\cdot 10^{-13}J \end{eqnarray}

Exercice 2

1.1.1. L'observation du diagramme montre que le rhénium 186 est au-dessus de la vallée de stabilité ; zone où les neutrons sont en excès.

L'isotope radioactif possède donc un excès de neutron(s) ou par rapport à un isotope stable du même élément.

1.1.2 La particule émise au cours d'une désintégration $\beta^{-1}$ porte le nom d'électron.

1.1.3 Équation de la désintégration du noyau de rhénium $186.$

$$_{Z}^{186}Re\ \longrightarrow\ _{76}^{A}Os\ +\ _{-1}^{0}e$$

La loi de conservation du nombre de masse s'écrit : $186=A+0\Rightarrow\;A=186$

La loi de conservation du nombre de charge s'écrit : $z=76-1\Rightarrow\;z=75$

L'équation de la désintégration s'écrit finalement : $_{77}^{186}Re\ \longrightarrow\ _{76}^{186}Os\ +\ _{-1}^{0}e$

2.1 La composition du noyau de phosphore $32$

Le phosphore possède 15 protons et $32-15=17$ neutrons

2.2 Vérifions par un calcul la valeur $E$ de l'énergie du rayonnement émis par la désintégration du phosphore $32$

\begin{eqnarray} E &=&\left(m_{S}+m_{e}-m_{p}\right)\dfrac{C^{2}}{e}\nonumber\\\\\text{avec }E &=&1.6\cdot 10^{-19}eV\nonumber\\\\\Rightarrow E &=&\left(5.30763\cdot 10^{-26}+9.1\cdot 10^{-31}-5.30803\cdot 10^{-26}\right)\dfrac{\left(3\cdot 10^{8}\right)^{2}}{1.6\cdot 10^{-19}}\nonumber\\\\ &=&1.7\cdot 10^{6}eV\nonumber\\\\\Rightarrow E&=&1.7MeV \end{eqnarray}

2.3. Lors de cette transformation, le patient n'est pas exposé au rayonnement gamma $(\gamma)$ particulièrement pénétrant.

2.4. Rappel de la loi de décroissance du nombre $N(t)$ de noyaux radioactifs dtun échantillon en fonction de $\lambda$ et $N_{0}$

$$N(t)=N_{0}e^{-\lambda t}$$

2.5. Le temps de demi-vie radioactive $t_{1/2}$ est le temps au bout duquel la moitié des noyaux radioactifs initialement présents s'est désintégrée

Établissement de la relation qui existe entre le temps de la demi-vie et la constante de désintégration radioactive $\lambda$

\begin{eqnarray} N\left(t+t_{1/2}\right) &=&N_{0}e^{-\lambda\left(t+t_{1/2}\right)}\nonumber\\\\ &=&\dfrac{N_{0}e^{-\lambda t}}{2}\nonumber\\\\\Rightarrow e^{-\lambda t_{1/2}} &=&\dfrac{1}{2}\nonumber\\\\\Rightarrow\ln e^{-\lambda t_{1/2}} &=&\ln\dfrac{1}{2}\nonumber\\\\\Rightarrow -\lambda t_{1/2} &=&-\ln 2\nonumber\\\\\Rightarrow\;t_{1/2} &=&\dfrac{\ln 2}{\lambda} \end{eqnarray}

2.6. Vérifions, par un calcul, la valeur approchée du temps de demi-vie proposée dans la carte d'identité

$\begin{array}{rcl} t_{1/2}&=&\dfrac{\ln 2}{\lambda}\\\\&=&\dfrac{\ln 2}{5.6\cdot 10^{-7}\times 24\times 3600}\\\\\Rightarrow\,t_{1/2}&=&14\text{ jours} \end{array}$

Exercice 3

1.1.$\alpha$ représente le noyau d'hélium.

Équation de la réaction nucléaire correspondante

$_{z}^{230}Th\ \longrightarrow\ _{76}^{A}Ra^{\ast}\ +\ _{2}^{4}He$

La loi de conservation du nombre de nucléons s'écrit :

$230=A+4\Rightarrow\,A=230-4=226$

La loi de conservation du nombre de charge s'écrit :

$z=76+2=78$

L'équation de la désintégration s'écrit :

$$_{78}^{230}Th\ \longrightarrow\ _{76}^{226}Ra^{\ast}\ +\ _{2}^{4}He$$

1.2. Le temps de demi-vie radioactive $t_{1/2}$ est le temps au bout duquel la moitié des noyaux radioactifs initialement présents s'est réduite de moitié.

Vérifions que sa valeur est de $7.5\times 10^{4}$ années

$\begin{array}{rcl} N(t)&=&N_{0}e^{-\lambda t_{1/2}}\\\\&=&\dfrac{N_{0}}{2}\\\\\Rightarrow\dfrac{N(t)}{N_{0}}&=&\dfrac{1}{2}\\\\&=&0.5 \end{array}$

Le temps de demi-vie correspond à l'abscisse d'ordonnée $0.5\Rightarrow\,t_{1/2}=7.5\cdot 10^{4}\text{ années}$

1.3. Expression mathématique de la loi de décroissance radioactive

$$N(t)=N_{0}e^{-\lambda t}$$

Calcul de la constante radioactive en année$^{-1}$

$\begin{array}{rcl} \lambda&=&\dfrac{\ln 2}{t_{1/2}}\\\\&=&\dfrac{\ln 2}{7.5\cdot 10^{4}}\\\\\Rightarrow\lambda &=&9.2\cdot 10^{-6}\text{année}^{-1} \end{array}$

1.4. La nature des noyaux est la seule grandeur qui fait varier le temps de demi-vie

1.5. Valeurs de $Z_{4}$ et $Z_{5}$

$_{92}^{238}U\ \longrightarrow\ _{90}^{234}Th\ +\ _{2}^{4}He$ : radioactivité $\alpha$

$_{90}^{234}Th\ \longrightarrow\ _{91}^{234}Pa\ +\ _{-1}^{0}e$ : radioactivité $\beta$

$_{91}^{234}Pa\ \longrightarrow\ _{z_{4}}^{234}U\ \Rightarrow\ _{91}^{234}Pa\ \longrightarrow\ _{92}^{234}U\ +\ _{-1}^{0}e\ \Rightarrow\ z_{4}=92$

$_{z_{4}}^{234}U\ \longrightarrow\ _{z_{5}}^{230}Th\ \Rightarrow\ _{92}^{234}U\ \longrightarrow\ _{90}^{234}Th\ +\ _{2}^{4}He\ \Rightarrow\ z_{5}=90$

1.6.1. Démontrons que $A(t)=\lambda\cdot N(t)$ pour une population de noyaux donnée.

$\begin{array}{rcl} A(t)&=&-\dfrac{\mathrm{d}N(t)}{\mathrm{d}t}\\\\&=&-\dfrac{\mathrm{d}\left(N_{0}e^{-\lambda t}\right)}{\mathrm{d}t}\\\\&=&\lambda N_{0}e^{-\lambda t}\\\\\Rightarrow\,A(t)&=&\lambda N \end{array}$

1.6.2. Déduisons à l'équilibre séculaire, le rapport $N^{230}Th/N^{238}U$ est constant

$A_{1}(t)=\lambda_{1}N^{230}Th$

$A_{2}(t)=\lambda_{2}N^{238}U$

$\begin{array}{rcl} A_{1}&=&A_{2}\\\\\Rightarrow\lambda_{1}N^{230}Th&=&\lambda_{2}N^{238}U\\\\\Rightarrow\dfrac{N^{230}Th}{N^{238}U}&=&\dfrac{\lambda_{2}}{\lambda_{1}}\\\\&=&\text{constant} \end{array} $

Exercice 4

A) 1) Équation de la réaction nucléaire correspondante

$_{94}^{241}Pu\ \longrightarrow\ _{z}^{A}Am\ +\ _{-1}^{0}e$

La loi de conservation du nombre de nucléons s'écrit :

$241=A+0\Rightarrow\,A+241$

La loi de conservation du nombre de charge s'écrit :

$94=z-1\Rightarrow\,z=95$

L'équation de la désintégration s'écrit :

$_{94}^{241}Pu\ \longrightarrow\ _{95}^{241}Am\ +\ _{-1}^{0}e$

2) Détermination de la composition des $Pu$ noyaux $Pu$ et $Am$

$Pu$ possède $94$ protons et $241-94=147$ neutrons

$Am$ possède $241$ protons et $241-95=146$ neutrons

La particule émise $\left(\beta^{-1}\right)$ provient de la désintégration d'un proton $_{1}^{1}p$ en neutron.

$_{0}^{1}n$ et en électron $_{-1}^{0}e\left(\beta^{-1}\right)$ : $\left(_{1}^{1}p\ \longrightarrow\ _{-1}^{0}e\ +\ _{0}^{1}n\right)$

B) 1) Équation de cette désintégration

$_{95}^{241}Am\ \longrightarrow\ _{93}^{237}Np\ +\ _{2}^{4}He$

2) Montrons que cette réaction libère une énergie $W$

$\begin{array}{rcl} \Delta m&=&m_{Np}+m_{\alpha}-m_{Am}\\\\&=&237.0480+4.0015-241.0567\\\\\Rightarrow\Delta m&=&7.2\cdot 10^{-3}u \end{array}$

Cette réaction s'accompagne d'une perte de masse $\Delta m$ ; donc de l'énergie libérée $W.$

Calcul de l'énergie $W$ libérée par la désintégration d'un noyau d'américium.

$\begin{array}{rcl} W&=&\Delta muc^{2}\\\\&=&7.2\cdot 10^{-3}\times 931.5MeV\cdot c^{-2}\times c^{2}\\\\\Rightarrow\,W&=&6.707MeV \end{array}$

3) Calcul des énergies cinétiques $E_{c\alpha}$ et $E_{cNp}$

$\begin{array}{rcl} m_{\alpha}E_{C_{\alpha}}&=&m_{Np}E_{C_{Np}}\\\\\Rightarrow\,E_{C_{\alpha}}&=&\dfrac{m_{Np}}{m_{\alpha}}E_{C_{Np}} \end{array}$

$\begin{array}{rcl} W&=&E_{C_{\alpha}}+E_{C_{Np}}\\\\&=&\dfrac{m_{Np}}{m_{\alpha}}E_{C_{Np}}+E_{C_{Np}}\\\\&=&\left(\dfrac{m_{Np}}{m_{\alpha}}+1\right)E_{C_{Np}}\\\\\Rightarrow\,E_{C_{Np}}&=&\dfrac{W}{\left(\dfrac{m_{Np}}{m_{\alpha}}\right)+1}\\\\&=&\dfrac{6.707}{\left(\dfrac{237.0480}{4.0015}+1\right)}\\\\\Rightarrow\,E_{C_{Np}}&=&2.77\cdot 10^{-2}MeV \end{array}$

$\begin{array}{rcl} E_{C_{\alpha}}&=&\dfrac{W}{\left(\dfrac{m_{\alpha}}{m_{Np}}+1\right)}\\\\&=&\dfrac{6.707}{\left(\dfrac{4.0015}{237.0480}\right)+1}\\\\\Rightarrow\,E_{C_{\alpha}}&=&6.60\cdot 10^{-2}MeV \end{array}$

4) a) L'activité d'une substance radioactive est le nombre de désintégrations par unité de temps.

Elle s'exprime en becquerel $(bq).$

b) Montrons que $-\ln(A)=\lambda t-\ln\left(A_{0}\right).$

$\begin{array}{rcl} A&=&-\dfrac{\mathrm{d}N}{\mathrm{d}t}\\\\&=&-\dfrac{\mathrm{d}\left(N_{0}e^{-\lambda t}\right)}{\mathrm{d}t}\\\\&=&\lambda N_{0}e^{-\lambda t}\\\\&=&A_{0}e^{-\lambda t}\\\\\text{avec }A_{0}&=&\lambda N_{0} \end{array}$

$\begin{array}{rcl} \ln A&=&\ln A_{0}e^{-\lambda t}\\\\&=&\ln A_{0}+\ln e^{-\lambda t}\\\\&=&\ln A_{0}-\lambda t\\\\\Rightarrow-\ln A&=&\lambda t-\ln A_{0} \end{array}$

c) Détermination graphique :

$-\ $de la valeur de la constante radioactive $\lambda$ de $_{95}^{241}Am.$

$\begin{array}{rcl} \lambda&=&\dfrac{\Delta(-\ln A)}{\Delta t}\\\\&=&\dfrac{0-(-1)}{2.066\cdot 10^{11}-0}\\\\\Rightarrow\lambda&=&4.84\cdot 10^{-12}\cdot s^{-1} \end{array}$

La période $T$ est :

$\begin{array}{lll} T&=&\dfrac{\ln 2}{\lambda}\\\\&=&\dfrac{\ln 2}{4.84\cdot 10^{-12}}\\\\\Rightarrow\,T&=&1.43\cdot 10^{11}s \end{array}$

$-\ $L'activité $A_{0}$ de l'échantillon d'américium $_{95}^{241}Am.$

$\begin{array}{lll} -\ln A_{0}&=&-1\\\\\Rightarrow\,A_{0}&=&e^{1}\\\\&=&2.72Bq \end{array}$

Valeur de $N_{0}.$

$\begin{array}{lcr} A_{0}&=&\lambda N_{0}\\\\\Rightarrow\,N_{0}&=&\dfrac{A_{0}}{\lambda}\\\\&=&\dfrac{2.72}{4.84\cdot 10^{-12}}\\\\\Rightarrow\,N_{0}&=&6.07\cdot 10^{11}\text{noyaux} \end{array}$

L'activité actuelle.

$\begin{array}{lcl} -\ln\,A_{\text{actuelle}}&=&0.88\\\\\Rightarrow\,A_{\text{actuelle}}&=&e^{-0.88}\\\\&=&0.415Bq \end{array}$

Calcul de l'âge de l'échantillon d'américium

$\begin{array}{lcr} A_{\text{actuelle}}&=&A_{0}e^{-\lambda t}\\\\\Rightarrow\,t&=&-\dfrac{1}{\lambda}\ln\dfrac{A_{\text{actuelle}}}{A_{0}}\\\\&=&\dfrac{1}{\lambda}\left(-\ln\,A_{\text{actuelle}}+\ln\,A_{0}\right)\\\\&=&\dfrac{1}{4.84\cdot 10^{-12}}(0.88+1)\\\\\Rightarrow\,t&=&4.2\cdot 10^{11}s \end{array}$

Exercice 5

I. Étude de la famille uranium $238$ – plomb $206$

1) a) Un noyau radioactif est un noyau instable qui se désintègre spontanément.

b) Équation de la réaction nucléaire

$_{92}^{238}U\ \longrightarrow\ _{z}^{A}Th\ +\ _{2}^{4}He$

La loi de conservation du nombre de nucléons s'écrit : $238=A+4\Rightarrow\,A=234$

La loi de conservation du nombre de charge s'écrit : $92=z+2\Rightarrow\,z=90$

L'équation de la désintégration s'écrit : $_{92}^{238}U\ \longrightarrow\ _{90}^{234}Th\ +\ _{2}^{4}He$

c) Calcul de l'énergie libérée au cours de cette désintégration en joule puis en $MeV$

$\begin{array}{lcr} \Delta E&=&\left(m_{Th}+m_{He}-m_{U}\right)c^{2}\\\\&=&(234.0436+4.0015-238.0508)\times 1.66\cdot 10^{-27}\times\left(3.0\cdot 10^{8}\right)^{2}\\\\\Rightarrow\Delta E&=&-8.52\cdot 10^{-13}J\\\\\Rightarrow\Delta E&=&\dfrac{-8.52\cdot 10^{-13}J}{1.6\cdot 10^{-19}}\\\\&=&-5.3\cdot 10^{6}eV \end{array}$

2) a) Il s'agit de la radioactivité $\beta^{-}$

La particule émise $(\beta^{-})$ provient de la désintégration d'un proton $_{1}^{1}p$ en neutron. $_{0}^{1}n$ et en électron $_{-1}^{0}e(\beta^{-})$ : $\left(_{1}^{1}p\ \longrightarrow\ _{-1}^{0}e\ +\ _{0}^{1}n\right)$

b) Détermination le nombre de désintégrations $\alpha$ et $\beta^{-}$

$_{92}^{238}U\ \longrightarrow\ _{82}^{206}Pb\ +\ x_{-1}^{0}e\ +\ y_{2}^{4}He$

La loi de conservation du nombre de nucléons s'écrit :

$\begin{array}{lcr} 238&=&8206+4y\\\\\Rightarrow\,y&=&\dfrac{238-206}{4}\\\\&=&8 \end{array}$

La loi de conservation du nombre de charge s'écrit :

$\begin{array}{lcr} 92&=&82-x+2y\\\\\Rightarrow\,x&=&92-82-2y\\\\&=&82+2\times 8-92\\\\\Rightarrow\,x&=&6 \end{array}$

L'équation de la désintégration s'écrit : $_{92}^{238}U\ \longrightarrow\ _{82}^{206}Pb\ +\ 6_{-1}^{0}e\ +\ 8_{2}^{4}He$

II. Géochronologie :

1) a) La quantité initiale $N_{U}(0)$ de noyaux d'uranium

$N_{U}(0)=5\cdot 10^{12}\text{noyaux}$

b) Montrons que $N_{U}(t)$ vérifie l'équation différentielle

$\begin{array}{lcr} \dfrac{\mathrm{d}U_{U}}{\mathrm{d}t}+\lambda N_{U}&=&0\\\\N_{U}&=&N_{U}(0)e^{-\lambda t}\\\\\dfrac{\mathrm{d}N_{U}}{\mathrm{d}t}+\lambda N_{U}&=&\dfrac{\mathrm{d}}{\mathrm{d}t}\left(N_{U}(0)e^{-\lambda t}\right)+\lambda N_{U}(0)e^{-\lambda t}\\\\&=&-\lambda N_{U}(0)e^{-\lambda t}+\lambda N_{U}(0)e^{-\lambda t}\\\\&=&0\\\\\Rightarrow\dfrac{\mathrm{d N_{U}}}{\mathrm{d}t}+\lambda N_{U}&=&0 \end{array}$

c) Montrons que $B=N_{U}(0)$ et que $\lambda=\dfrac{1}{\tau}.$

$\begin{array}{lcr} N_{U}&=&Be^{-\dfrac{t}{\tau}}\\\\\Rightarrow\dfrac{\mathrm{d}N_{U}}{\mathrm{d}t}&=&-\dfrac{1}{\tau}Be^{-\dfrac{t}{\tau}}\\\\\dfrac{\mathrm{d}N_{U}}{\mathrm{d}t}+\lambda N_{U}&=&-\dfrac{1}{\tau}Be^{-\dfrac{t}{\tau}}+\lambdaBe^{-\dfrac{t}{\tau}}\\\\&=&0\\\\\RightarrowBe^{-\dfrac{t}{\tau}}\left(-\dfrac{1}{\tau}+\lambda\right)&=&0\\\\\Rightarrow-\dfrac{1}{\tau}+\lambda&=&0\ (\text{comme }B\neq 0)\\\\\lambda&=&\dfrac{1}{\tau} \end{array}$

d) Détermination à partir du graphe la constante de temps $\tau$ de l'uranium $238$

$\begin{array}{lcr} \dfrac{\mathrm{d}N_{U}}{\mathrm{d}t}&=&-\dfrac{1}{\tau}N_{U}(0)e^{-\dfrac{t}{\tau}}\\\\\Rightarrow\left(\dfrac{\mathrm{d}N_{U}}{\mathrm{d}t}\right)_{t=0}&=&-\dfrac{1}{\tau}N_{U}(0)\\\\&=&\dfrac{\Delta N_{U}}{\Delta t}\\\\\Rightarrow\tau&=&-\dfrac{N_{U}(0)\Delta t}{\Delta N_{U}}\\\\\Rightarrow\tau&=&-\dfrac{5\cdot 10^{12}\left(6.5\cdot 10^{9}-0\right)}{0-5\cdot 10^{12}}\\\\\Rightarrow\tau&=&6.5\cdot 10^{9}\text{années} \end{array}$

Autre méthode : la tangente à l'origine de la courbe coupe l'axe des abscisses au temps $t=\tau=6.5\cdot 10^{9}\text{années}$

e) Le temps de demi-vie radioactive $T$ est le temps au bout duquel la moitié des noyaux radioactifs initialement présents s'est désintégrée.

Relation entre $T$ et $\tau.$

$\begin{array}{lcr} \lambda&=&\dfrac{1}{\tau}T\\\\&=&\dfrac{\ln 2}{\lambda}\\\\\text{or }\lambda&=&\dfrac{1}{\tau}\\\\\Rightarrow\,T&=&\dfrac{\ln 2}{\dfrac{1}{\tau}}\\\\\Rightarrow\,T&=&\tau\ln 2 \end{array}$

Calcul de $T$

$\begin{array}{lcr} T&=&\tau\ln 2\\\\&=&6.5\cdot 10^{9}\times\ln 2\\\\\Rightarrow\,T&=&4.5\cdot 10^{9}\text{années} \end{array}$

Valeur de $T$ par méthode graphique

$T$ correspond à l'abscisse de

$\begin{array}{lcr} \dfrac{N_{U}(0)}{2}\\\\&=&\dfrac{5\cdot 10^{12}}{2}\\\\&=&2.5\cdot 10^{12} \end{array}$

La projection sur des l'axe de temps donne : $T=4.5\cdot 10^{9}\text{années}$

2) a) L'activité radioactive d'une substance radioactive est le nombre de désintégrations par unité de temps.

Calcul, en becquerel, de l'activité initiale de l'uranium $238.$

$\begin{array}{lcr} A_{0}&=&\lambda N_{U}(0)\\\\&=&\dfrac{\ln 2}{T}N_{U}(0)\\\\&=&\dfrac{\ln 2}{4.5\cdot 10^{9}\times 3.15\cdot 10^{7}}\times5\cdot 10^{12}\\\\\Rightarrow\,A_{0}&=&2.4\cdot 10^{-5}Bq \end{array}$

b) Détermination graphique de l'activité de l'uranium à $t=15\cdot 10^{9}$ années

$\begin{array}{lcr} A&=&\lambda N_{U}(0)\\\\&=&\dfrac{\ln 2}{T}N_{U}(0)\\\\&=&\dfrac{\ln 2}{4.5\cdot 10^{9}\times 3.15\cdot 10^{7}}\times 0.5\cdot 10^{12}\\\\\Rightarrow\,A_{0}&=&2.4\cdot 10^{-6}Bq \end{array}$

Par calcul l'activité de l'uranium à $t=15\cdot 10^{9}$ années

$\begin{array}{lcr} A&=&A_{0}e^{-\dfrac{t}{\tau}}\\\\\Rightarrow\,A(t=15\cdot 10^{9}\text{années})&=&2.4\cdot 10^{-5}e^{-\dfrac{15\cdot 10^{9}}{6.5\cdot 10^{9}}}\\\\\Rightarrow\,A&=&2.4\cdot 10^{-6}Bq \end{array}$

3) a) Établissement de la relation entre $N_{U}(t_{\text{Terre}})$, $N_{U}(0)$ et $N_{pb}(t_{\text{Terre}}).$

$\begin{array}{lcr} N_{pb}(t_{\text{Terre}})&=&N_{U}(0)-N_{U}(t_{\text{Terre}})\\\\\Rightarrow\,N_{U}(t_{\text{Terre}})&=&N_{U}(0)-N_{pb}(t_{\text{Terre}}) \end{array}$

Calculer la quantité $N_{U}$

$\begin{array}{lcr} N_{U}(t_{\text{Terre}})&=&N_{U}(0)-N_{Pb}(t_{\text{Terre}})\\\\&=&5\cdot 10^{12}-2.5\cdot 10^{12}\\\\\Rightarrow N_{U}(t_{\text{Terre}})&=&2.5\cdot 10^{12}_text{noyaux} \end{array}$

Détermination de l'âge $t_{\text{Terre}}$ de la Terre.

$\begin{array}{lcr} N_{U}&=&N_{U}(0)e^{\dfrac{-t}{\tau}}\\\\\Rightarrow\,e^{\dfrac{-t}{\tau}}&=&\dfrac{N_{U}}{N_{U}(0)}\\\\\Rightarrow\ln e^{\dfrac{-t}{\tau}}&=&_ln\dfrac{N_{U}}{N_{U}(0)}\\\\\Rightarrow-\dfrac{t}{\tau}&=&\ln\dfrac{N_{U}}{N_{U}(0)}\\\\\Rightarrow\,t_{\text{Terre}}&=&-\tau\ln\dfrac{N_{U}}{N_{U}(0)}\\\\&=&-6.5\cdot 10^{9}\ln\dfrac{2.5\cdot 10^{12}}{5\cdot 10^{12}}\\\\\Rightarrow\,t_{\text{Terre}}&=&4.5\cdot 10^{9}_text{années} \end{array}$

Exercice 6

1) a) Les isotopes sont des atomes qui le même nombre de protons ; mais qui diffèrent par leur nombre de masse.

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Solutions des exercices : Niveaux d'énergie de l'atome - Ts

Classe:

Terminale

Exercice 1

1) Calcul des énergies correspondant à $n=1\;,\ 2\;,\ 3$ et $\infty$

$E_{n}=\dfrac{-13.6}{n^{2}}$

$E_{1}=\dfrac{-13.6}{1^{2}}=-13.6\,eV$

$E_{2}=\dfrac{-13.6}{2^{2}}=-3.40\,eV$

$E_{3}=\dfrac{-13.6}{3^{2}}=-1.51\,eV$

$E_{\infty}=\dfrac{-13.6}{\infty}=0\,eV$

Représentation du diagramme des niveaux d'énergie de l'atome d'hydrogène.

2) L'énergie minimale que l'on doit fournir à un atome d'hydrogène pour qu'il passe de l'état fondamental à un état excité correspond à une transition électronique de l'état fondamental au premier état excité $($niveau $n=2)$

$E=E_{2}-E_{1}=-3.40-(-13.6)$

$\Rightarrow E=10.2eV$

3) Calcul de la longueur d'onde correspondant à cette transition.

\begin{eqnarray} E &=&\dfrac{hC}{\gamma}\nonumber \\\\\Rightarrow\gamma&=&\dfrac{hC}{E}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{10.2\times 1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma &=&1.22\cdot 10^{-7}m \end{eqnarray}

4) Calcul de la longueur d'onde de la radiation susceptible d'ioniser l'atome d'hydrogène

\begin{eqnarray} E_{\infty-E_{1}} &=&\dfrac{hC}{\gamma}\nonumber\\\\\Rightarrow\gamma&=& \dfrac{hC}{E_{\infty}-E_{1}}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{(0-(-13.6))\times 1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma&=&9.13\cdot 10^{-8}m \end{eqnarray}

Exercice 2

1) a) Montrons que le mouvement de l'électron est uniforme

Système étudié : l'électron

Référentiel d'étude : de laboratoire

Bilan des forces appliquées : la force électrostatique $\overrightarrow{F}$ et le poids négligeable $\overrightarrow{P}$ devant la force électrostatique

Le théorème du centre d'inertie s'écrit :

\begin{eqnarray} \overrightarrow{F} &=&m\vec{a}\nonumber\\\\\Rightarrow -\dfrac{ke^{2}}{r^{2}}\overrightarrow{u_{OP}} &=&m\vec{a} \end{eqnarray}

Projetons cette relation dans le repère de Frenet $\left(O\;,\ \overrightarrow{u_{t}}\;,\ \overrightarrow{u_{n}}\right)$

$-\ $suivant : $\overrightarrow{u_{t}}$ :

\begin{eqnarray} 0 &=&ma_{t}\nonumber\\\\\Rightarrow m\dfrac{\mathrm{d}v}{\mathrm{d}t} &=&0\nonumber\\\\\Rightarrow v &=&\text{constante} \end{eqnarray}

; le mouvement est donc uniforme

b) Expression de la vitesse $v$ en fonction de $k$, $e$, $r$ et $m$

$-\ $suivant : $\overrightarrow{u_{n}}$

\begin{eqnarray} \dfrac{ke^{2}}{r^{2}} &=&ma_{n}\nonumber\\\\\Rightarrow m\dfrac{v^{2}}{r} &=&\dfrac{ke^{2}}{r^{2}} \nonumber\\\\\Rightarrow v &=&\sqrt{\dfrac{ke^{2}}{mr}} \end{eqnarray}

c) Expression de l'énergie cinétique en fonction de $k$, $e$, $r$ et $m$

\begin{eqnarray} E_{C} &=&\dfrac{1}{2}mv^{2}\nonumber\\\\ &=&\dfrac{1}{2}m\left(\sqrt{\dfrac{ke^{2}}{mr}}\right)^{2} \nonumber\\\\\Rightarrow E_{C} &=&\dfrac{1}{2}\dfrac{ke^{2}}{r} \end{eqnarray}

d) Exprimer en énergie mécanique $E$ en fonction de $k$, $e$ et $r$

\begin{eqnarray} E &=& E_{C}+E_{P}\nonumber\\\\ &=&\dfrac{1}{2}\dfrac{ke^{2}}{r}-\dfrac{ke^{2}}{r}\nonumber\\\\ &=&\dfrac{1}{2}\dfrac{ke^{2}}{r}-\dfrac{2ke^{2}}{2r} \nonumber\\\\\Rightarrow E &=&-\dfrac{1}{2}\dfrac{ke^{2}}{r}\nonumber\\\\ E_{r\;\rightarrow\;+\infty} &=&-\dfrac{1}{2}\dfrac{ke^{2}}{r}=0 \end{eqnarray}

2) a) Détermination de l'expression de $r_{n}$ en fonction des constantes $k$, $K$, $m$, $e$ et $n.$

\begin{eqnarray} m\dfrac{v^{2}}{r} &=&\dfrac{ke^{2}}{r^{2}}\nonumber\\\\\Rightarrow v^{2}&=&\dfrac{ke^{2}}{mr} \end{eqnarray}

\begin{eqnarray} v_{n}r_{n}&=&\dfrac{nK}{m}\nonumber\\\\\Rightarrow\left(v_{n}r_{n}\right)^{2}&=&\left(\dfrac{nK}{m}\right)^{2}\nonumber\\\\\Rightarrow v_{n}^{2}r_{n}^{2}&=&\dfrac{n^{2}K^{2}}{m^{2}}\nonumber\\\\\Rightarrow \dfrac{ke^{2}}{mr_{n}}r_{n}^{2}&=&\dfrac{n^{2}K^{2}}{m^{2}}\nonumber\\\\\Rightarrow r_{n}&=&\dfrac{n^{2}K^{2}m}{ke^{2}m^{2}}\nonumber\\\\\Rightarrow r_{n}&=&\dfrac{K^{2}}{ke^{2}m}n^{2} \end{eqnarray}

Expression de $r_{n}$ en fonction de $r_{1}.$

\begin{eqnarray} r_{n}&=&\dfrac{K^{2}}{ke^{2}m}n^{2}\nonumber\\\\\Rightarrow r_{1}&=&\dfrac{K^{2}}{ke^{2}m}\nonumber\\\\\Rightarrow r_{n}&=&r_{1}n^{2} \end{eqnarray}

Calculer $r_{1}$

\begin{eqnarray} r_{1}&=&\dfrac{K^{2}}{ke^{2}m}\nonumber\\\\&=&\dfrac{\left(1.054\cdot 10^{-34}\right)^{2}}{9.000\cdot 10^{9}\times\left(1.602\cdot 10^{-19}\right)^{2}\times9.109\cdot 10^{-31}}\nonumber\\\\\Rightarrow r_{1}&=&5.200\cdot 10^{-11}m \end{eqnarray}

b) Détermination de l'expression de $E_{n}$, énergie mécanique de l'électron sur le cercle de rayon $r_{n}$, en fonction de $k$, $K$, $m$, $e$ et $n$

\begin{eqnarray} E&=&-\dfrac{1}{2}\dfrac{ke^{2}}{r}\nonumber\\\\\Rightarrow E_{n}&=&-\dfrac{1}{2}\dfrac{ke^{2}}{\dfrac{K^{2}}{ke^{2}m}}n^{2}\nonumber\\\\\Rightarrow E_{n}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}n^{2}} \end{eqnarray}

Expression de $E_{n}$ en fonction de $E_{1}$

\begin{eqnarray} E_{n}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}n^{2}}\nonumber\\\\\Rightarrow E_{1}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}}\nonumber\\\\\Rightarrow E_{n}&=&-\dfrac{E_{1}}{n^{2}} \end{eqnarray}

c) Calculer $E_{1}$ et $E_{2}$ en électronvolts.

\begin{eqnarray} E_{1}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}}\nonumber\\\\ E_{1}&=&-\dfrac{\left(9.000\cdot 10^{9}\right)^{2}\left(1.602\cdot 10^{-19}\right)^{4}\times 9.109\cdot 10^{-31}}{2\times\left(1.054\cdot 10^{-34}\right)^{2}}\times\dfrac{1}{1.602\cdot 10^{-19}}\left(1eV=1.602\cdot 10^{-19}J\right)\nonumber\\\\\Rightarrow E_{1}&=&-13.6eV \end{eqnarray}

\begin{eqnarray} E_{2}&=&-\dfrac{E_{1}}{2^{2}}\nonumber\\\\ &=&-\dfrac{13.6}{2^{2}}\nonumber\\\\\Rightarrow E_{2}&=&-3.4eV \end{eqnarray}

L'absorption de l'énergie par l'atome d'hydrogène est la cause du passage de l'énergie de l'électron de $E_{1}$ à $E_{2}.$

Exercice 3 L'atome d'hydrogène

1) Le nom du nombre noté $"n"$ qui apparaît dans le diagramme est le nombre quantique principal.

2) On dit qu'un atome est dans son état fondamental lorsqu'il se trouve dans le plus bas niveau d'énergie (niveau stable).

L'état fondamental de l'atome d'hydrogène correspond à $n=1.$

3) Lorsqu'une population d'atomes d'hydrogène est au repos, sans apport d'énergie de la part de l'extérieur, alors ces atomes se trouvent dans l'état fondamental.

4) Le niveau noté : $n=\infty$ représente l'atome à l'état ionisé.

5) Énergie minimale nécessaire pour ioniser un atome d'hydrogène à partir de son état fondamental

$\Delta E=E_{\infty}-E_{1}=0-(-13.6)\Rightarrow\Delta E=13.6eV$

6) Un atome d'hydrogène qui a la configuration électronique $n=3$ n'est pas dans son état fondamental, mais dans un état appelé état excité.

7) L'atome d'hydrogène ne peut pas se trouver dans un état situé entre les niveaux $n=1$ et $n=2$, puisque le premier état excité correspond à $n=2.$

$\bullet\ $On peut exciter cet atome par un photon de lumière dont l'énergie correspond à une transition électronique du niveau $n=3$ à un niveau supérieur.

$\bullet\ $Montrons qu'en se dés excitant vers le niveau $2$, il émet un photon de longueur d'onde : $\lambda=656.1\,nm.$

\begin{eqnarray} E_{2}-E_{3}&=&-\dfrac{hC}{\gamma}\nonumber\\\\\Rightarrow\gamma&=&\dfrac{hC}{E_{3}-E_{2}}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{(-1.51-(-3.40))\times1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma&=&6.567\cdot 10^{-7}m\nonumber\\\\\Rightarrow\gamma&=&656.7nm \end{eqnarray}

Cette radiation est visible, car sa longueur d'onde dans le vide est comprise entre $400\,nm$ et $800\,nm.$

9) Détermination de la transition électronique correspondant à l’émission de cette radiation.

\begin{eqnarray} E_{2}-E_{n}&=&-E\nonumber\\\\\Rightarrow E_{n}&=& E_{2}+E \nonumber\\\\\Rightarrow n^{2} &=&\dfrac{E_{1}}{-E-E_{2}}\nonumber\\\\\Rightarrow n &=& \sqrt{\dfrac{-E_{1}}{E+E_{2}}}\nonumber\\\\\Rightarrow n &=&\sqrt{\dfrac{-13.6}{2.54+(-3.40)}}\nonumber\\\\\Rightarrow n&=&4 \end{eqnarray}

Calcul de la longueur d'onde correspondante

\begin{eqnarray} \dfrac{hC}{\gamma} &=&E\nonumber\\\\\Rightarrow\gamma&=&\dfrac{hC}{E}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{2.54\times 1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma&=&4.89\cdot 10^{-7}m\nonumber\\\\\Rightarrow\gamma&=&489 nm \end{eqnarray}

10) Une lampe à décharge à hydrogène émet un spectre discontinu.

Exercice 4 Niveaux d'énergie de l'atome d'hydrogène

1.1.1 Détermination de l'énergie minimale pour ioniser l'atome d'hydrogène à partir de son état fondamental $(n=1).$

$\begin{array}{rcl} E&=&E_{\infty}-E_{1}\\\\&=&0-\left(-\dfrac{13.6}{1^{2}}\right)\\\\&=&13.6eV \end{array}$

1.1.2 Détermination de l'énergie minimale pour ioniser l'atome d'hydrogène à partir de son état excité $n=2$

$\begin{array}{rcl} E&=&E_{\infty}-E_{2}\\\\&=&0-\left(-\dfrac{13.6}{2^{2}}\right)\\\\&=&3.40eV \end{array}$

1.2 Diagramme des niveaux d'énergie de l'atome d'hydrogène :

2.1. Calcul de la différence d'énergie $\left(E_{3}-E_{1}\right)$ en $eV$

$\begin{array}{rcl} E_{3}-E_{1}&=&\left(E_{3}-E_{2}\right)+\left(E_{2}-E_{1}\right)\\\\&=&\dfrac{h_{C}}{\lambda_{2}}+\dfrac{h_{C}}{\lambda_{1}}\\\\&=&h_{C}\left(\dfrac{1}{\lambda_{2}}+\dfrac{1}{\lambda_{1}}\right)\\\\\Rightarrow\,E_{3}-E_{1}&=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{1.6\cdot 10^{-19}}\left(\dfrac{1}{568.8\cdot 10^{-9}}+\dfrac{1}{589\cdot 10^{-9}}\right)\\\\\,E_{3}-E_{1}&=&4.29eV \end{array}$

2.2 Expression de la longueur d'onde $\lambda$ de ce faisceau en fonction des longueurs d'onde $\lambda_{1}$ et $\lambda_{2}$

\begin{eqnarray} \dfrac{h_{C}}{\lambda} &=&\dfrac{h_{C}}{\lambda_{2}}+\dfrac{h_{C}}{\lambda_{1}}\nonumber\\\\\Rightarrow\dfrac{1}{\lambda} &=&\dfrac{1}{\lambda_{2}}+\dfrac{1}{\lambda_{1}}\nonumber\\\\ &=&\dfrac{\lambda_{2}+\lambda_{1}}{\lambda_{1}\lambda_{2}}\nonumber\\\\\Rightarrow\lambda &=&\dfrac{\lambda_{1}\lambda_{2}}{\lambda_{2}+\lambda_{1}}\nonumber\\\\ &=&\dfrac{589\times 558.8}{568.8+589}\nonumber\\\\\Rightarrow\lambda &=&289.4nm. \end{eqnarray}

Exercice 5

1) L'énergie $E_{0}$ correspond à l'énergie d'ionisation de l'atome dans son état fondamental

2) Relation simple existe entre l'énergie de transition $\Delta E$ d'un niveau $n$ à un niveau $p$ du photon émis ou absorbé

$-\ $Lors de l'absorption d'un photon $n<p$ :

$\begin{array}{rcl} \Delta E &=&\dfrac{h_{C}}{\lambda}\\\\ &=&E_{0}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\\\\\Rightarrow\lambda &=&\dfrac{h_{C}}{E_{0}}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right) \end{array}$

$-\ $Lors de l'absorption d'un photon $n<p$ :

\begin{eqnarray} \Delta E &=& E_{n}-E_{p}\nonumber\\\\ &=&-\dfrac{E_{0}}{n^{2}}-\left(-\dfrac{E_{0}}{p^{2}}\right)\nonumber\\\\ &=& E_{0}\left(\dfrac{1}{p^{2}}-\dfrac{1}{n^{2}}\right) \end{eqnarray}

et la longueur d'onde du photon émis

$\begin{array}{rcl} E&=&E_{n}-E_{p}\\\\&=&-\dfrac{h_{C}}{\lambda}\\\\&=&\left(-\dfrac{E_{0}}{n^{2}}-\left(-\dfrac{E_{0}}{p^{2}}\right)\right)\\\\&=&E_{0}\left(-\dfrac{1}{n^{2}}+\dfrac{1}{p^{2}}\right)\\\\\Rightarrow\lambda&=&\dfrac{h_{C}}{E_{0}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)} \end{array}$

3) a) Montrons que pour une transition d'un niveau $p$ à un niveau $n$ tel que $p>n$, on peut écrire la relation $\dfrac{1}{\lambda}=R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right).$

Lors d'une transition d'un niveau $p$ à un niveau $n$ tel que $p>n$

\begin{eqnarray} \Delta E &=&E_{n}-E_{p}\nonumber\\\\ &=&-\dfrac{h_{C}}{\lambda}\nonumber\\\\ &=&\left(-\dfrac{E_{0}}{n^{2}}-\left(-\dfrac{E_{0}}{p^{2}}\right)\right)\nonumber\\\\ &=&E_{0}\left(-\dfrac{1}{n^{2}}+\dfrac{1}{p^{2}}\right)\nonumber\\\\\Rightarrow\dfrac{1}{\lambda} &=&\dfrac{E_{0}}{\lambda}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\nonumber\\\\\Rightarrow\dfrac{1}{\lambda} &=& R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\nonumber\\\\\text{avec}\quad R_{H} &=&\dfrac{E_{0}}{h_{C}} \end{eqnarray}

b) Vérifions que $R_{H}$ (appelée constante de Rydberg) vaut $R_{H}=1.1\cdot 10^{7}\cdot m^{-1}$

$\begin{array}{rcl} R_{H}&=&\dfrac{E_{0}}{h_{C}}\\\\&=&\dfrac{13.6\times 1.6\cdot 10^{-19}}{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}\\\\\Rightarrow\,R_{H}&=&1.1\cdot 10^{7}\cdot m^{-1} \end{array}$

c) Comparons $\lambda_{3\;,\ 2}$ et $\lambda_{4\;,\ 2}$

$\lambda_{3\;,\ 2}=\dfrac{h_{C}}{\Delta E_{3\;,\ 2}}$

$\lambda_{4\;,\ 2}=\dfrac{h_{C}}{\Delta E_{4\;,\ 2}}$

$\Delta E_{4\;,\ 2}>\Delta E_{3\;,\ 2}\Rightarrow\lambda_{3\;,\ 2}>\lambda_{4\;,\ 2}$

Calcul des valeurs $\lambda_{3\;,\ 2}$ et $\lambda_{4\;,\ 2}$

$\begin{array}{rcl} \dfrac{1}{\lambda}&=&R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\\\\\Rightarrow\lambda&=&\dfrac{1}{R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)} \end{array}$

$\begin{array}{rcl} \lambda_{3\;,\ 2}&=&\dfrac{1}{R_{H}\left(\dfrac{1}{2^{2}}-\dfrac{1}{3^{2}}\right)}\\\\&=&\dfrac{1}{1.1\cdot 10^{7}\left(\dfrac{1}{2^{2}}-\dfrac{1}{3^{2}}\right)}\\\\\Rightarrow\lambda_{3\;,\ 2}&=&6.55\cdot 10^{-7}m \end{array}$

$\begin{array}{rcl} \lambda_{4\;,\ 2}&=&\dfrac{1}{R_{H}\left(\dfrac{1}{2^{2}}-\dfrac{1}{4^{2}}\right)}\\\\&=&\dfrac{1}{1.1\cdot 10^{7}\left(\dfrac{1}{2^{2}}-\dfrac{1}{4^{2}}\right)}\\\\\Rightarrow\lambda_{4\;,\ 2}&=&4.85\cdot 10^{-7}m \end{array}$

4) Lorsqu'on excite L'atome $H$ dans son état fondamental à l'aide d'un photon incident d'énergie $W=13.8eV$ supérieure à l'énergie d'ionisation $E_{0}=13.6eV$, l'atome est ionisé et l'électron est éjecté de l'atome avec une énergie cinétique.

Calcul de l'énergie cinétique $E_{c}$ de l'électron de $H$ éjecté

$\begin{array}{rcl} E_{c}&=&W-E_{0}\\\\&=&13.8-13.6\\\\\Rightarrow\,E_{c}&=&0.2eV \end{array}$

5) Étudions le comportement l'atome d'hydrogène pris à l'état fondamental $\left(E_{1}=-13.6eV\right)$ lorsque l'atome entre en choc inélastique avec un électron ayant une énergie cinétique égale $11eV$

Un gain d'énergie de $11.0eV$ mènerait l'atome d'hydrogène à une énergie de :

$-13.6+11=-2.6eV$

Cette valeur $-2.6eV$ ne correspond à aucun niveau d'énergie de l'atome d'hydrogène. Cette absorption d'énergie est impossible.

L'atome $H$ reste donc au niveau fondamental, l'électron en question n'est pas absorbé.

Exercice 6

1) Couleurs correspondant aux différentes radiations.

Couleur des radiations :

$H_{\alpha}$ : raie rouge

$H_{\beta}$ : radiation bleue

$H_{\lambda}$ : raie indigo

$H_{\delta}$ : raie violette

2.1. La plus petite valeur possible de $n.$

La longueur d'onde est une grandeur positive ; $n$ ne peut donc prendre que des valeurs entières positives définies par $n^{2}-4>0$ donc $n>2.$

La longueur d'onde minimale de la raie correspondante

Elle correspond à $n=3$

$\begin{array}{rcl} \lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{3^{2}}{3^{2}-4}\\\\\Rightarrow\lambda &=&661.9nm\qquad\text{raie}\ H_{\alpha} \end{array}$

2.2. Valeurs prises $n$ pour les autres raies visibles du spectre

$\begin{array}{rcl} n=4\Rightarrow\lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{4^{2}}{4^{2}-4}\\\\\Rightarrow\lambda &=&490.3nm\qquad\text{raie}\ H_{\beta} \end{array}$

$\begin{array}{rcl} n=5\Rightarrow\lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{5^{2}}{5^{2}-4}\\\\\Rightarrow\lambda &=&437.7nm\qquad\text{raie}\ H_{\gamma} \end{array}$

$\begin{array}{rcl} n=6\Rightarrow\lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{6^{2}}{6^{2}-4}\\\\\Rightarrow\lambda &=&413.7nm\qquad\text{raie}\ H_{\delta} \end{array}$

3.1. L'énergie de l'atome ne peut prendre que certaines valeurs bien déterminées (discrètes).

Ces valeurs forment une suite discontinue. On dit que l'énergie de l'atome est quantifiée. $E_{0}$ représente, pour l'atome d'hydrogène, son énergie à l'état fondamental.

3.2. Établissement, en fonction de $n$, de la fréquence $v_{n\;,\ 2}$ des radiations émises lorsque l'atome passe d'un état excité $n>2$ à l'état excité $n=2$

\begin{eqnarray} E_{2}-E_{n} &=&-hv_{n\;,\ 2}\nonumber\\\\\Rightarrow\,v_{n\;,\ 2} &=&\dfrac{E_{n}-E_{2}}{h}\nonumber\\\\&=&\dfrac{E_{0}}{h}\left(-\dfrac{1}{n^{2}}-\left(\dfrac{1}{2^{2}}\right)\right)\nonumber\\\\&=&\dfrac{E_{0}}{h}\left(\dfrac{1}{2^{2}}-\dfrac{1}{n^{2}}\right)\nonumber\\\\&=&\dfrac{E_{0}}{h}\left(\dfrac{1}{4}-\dfrac{1}{n^{2}}\right)\nonumber\\\\\Rightarrow\,v_{n\;,\ 2}&=&\dfrac{E_{0}}{h}\left(\dfrac{n^{2}-4}{4n^{2}}\right)\nonumber\\\\&=&\dfrac{E_{0}}{4h}\left(\dfrac{n^{2}-4}{n^{2}}\right)\nonumber\\\\&=&\dfrac{13.6\times 1.60\cdot 10^{-19}}{4\times 6.62\cdot 10^{-34}}\left(\dfrac{n^{2}-4}{n^{2}}\right)\nonumber\\\\\Rightarrow\,v_{n\;,\ 2}&=&8.22\cdot 10^{14}\left(\dfrac{n^{2}-4}{n^{2}}\right) \end{eqnarray}

3.3. Retrouvons l'expression empirique de Balmer : $\lambda=\lambda_{0}\dfrac{n^{2}}{n^{2}-4}.$

$\begin{array}{rcl} v_{n\;,\ 2}&=&\dfrac{c}{\lambda}\\\\\Rightarrow\lambda&=&\dfrac{c}{v_{n\;,\ 2}}\\\\&=&\dfrac{c}{\dfrac{E_{0}}{4h}\left(\dfrac{n^{2}-4}{n^{2}}\right)}\\\\&=&\dfrac{4h_{C}}{E_{0}}\left(\dfrac{n^{2}}{n^{2}-4}\right)\\\\&=&\lambda_{0}\left(\dfrac{n^{2}}{n^{2}-4}\right) \end{array}$

$\begin{array}{rcl} \lambda_{0}&=&\dfrac{4h_{C}}{E_{0}}\\\\&=&\dfrac{4\times 6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{13.6\times 1.60\cdot 10^{-19}}\\\\\Rightarrow\lambda_{0}&=&3.65\cdot 10^{-7}m\\\\\Rightarrow\lambda_{0}&=&365nm \end{array}$

$\begin{array}{rcl} \lambda&=&\lambda_{0}\left(\dfrac{n^{2}}{n^{2}-4}\right)\\\\&=&\lambda_{0}\dfrac{1}{1-\dfrac{4}{n^{2}}}\,n\rightarrow\;+\infty\\\\\lambda&=&\lambda_{0}\\\\&=&365nm \end{array}$

Cette radiation de longueur d'onde $\lambda_{0}$ est émise lorsque l'atome passe de l'état excité $(n=\infty)$ à l'état excité $n=2.$ $\lambda_{0}$ est la longueur d'onde limite de la série de Balmer.

Cette radiation est située dans le proche $UV.$

3.4. Tracé du diagramme représentant les transitions entre les différents niveaux d'énergie de l'atome d'hydrogène pour les quatre raies $H\alpha$, $H\beta$, $H\lambda$, $H\delta$ de la série de Balmer.

4.1. Énergie cinétique minimale d'un électron projectile susceptible de provoquer par choc l'excitation d'un atome d'hydrogène de son état fondamental à son deuxième état excité

$\begin{array}{rcl} E_{c}&=&E_{3}-E_{1}\\\\&=&-1.51-(-13.6)\\\\\Rightarrow\,E_{c}&=&12.1eV \end{array}$

4.2. Il faudra donc accélérer cet électron, initialement immobile, sous une tension de $12.1V.$

4.3. Détermination des longueurs d'onde des deux photons

La dés-excitation de l'atome se fait avec l'émission successive de deux photons.

$\ast\ $Un photon, d'énergie $hv_{3\;,\ 2}$, est émis lors de la transition du niveau $E_{3}$ vers le niveau $E_{2}$ de l'atome.

$$E_{3}-E_{2}=hv_{3\;,\ 2}$$

La radiation émise correspond à la raie $H\alpha$ de la série de Balmer $\lambda=656.5nm.$

$\ast\ $L'autre photon est émis lors de la transition du niveau $E_{2}$ vers l'état fondamental $E_{1}$

$\begin{array}{rcl} E_{2}-E_{1}&=&hv_{2\;,\ 1}\\\\&=&h\dfrac{c}{\lambda_{2\;,\ 1}}\\\\\Rightarrow\lambda_{2\;,\ 1}&=&\dfrac{hc}{E_{2}-E_{1}}\\\\\lambda_{2\;,\ 1}&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{10.2\times 1.6\cdot 10^{-19}}\\\\&=&1.22\cdot 10^{-7}m\\\\&=&122nm \end{array}$

Ce rayonnement est situé dans l'ultraviolet

Exercice 7 : Étoile Vega et son spectre

1) Le spectre est un spectre discontinu car ce spectre est constitué de raies.

2) L'étoile possède une atmosphère puisque son spectre est inclus à celui du visible.

3) Tracé de $\lambda$ en fonction de $x.$

4) Coefficient directeur et ordonnée à l'origine de la droite.

$\begin{array}{rcl} a&=&\dfrac{\Delta\lambda}{\Delta x}\\\\&=&\dfrac{700-400}{8.5-0}\\\\\Rightarrow\,a&=&35.3nm\cdot cm^{-1} \end{array}$

$\begin{array}{rcl} \lambda&=&ax+b\\\\\Rightarrow\,x&=&0\\\\\Rightarrow\lambda&=&b\\\\&=&400nm \end{array}$

Équation numérique de $\lambda=ax+b$

$\lambda=35.3x+400$

5) Valeurs des longueurs d'onde émises par l'étoile

$\begin{array}{rcl} \lambda&=&35.3x+400\\\\\Rightarrow\,x&=&0\\\\\Rightarrow\lambda&=&400nm \end{array}$

$\begin{array}{rcl} x&=&8.5\\\\\Rightarrow\lambda&=&35.3\times 8.5+400\\\\\Rightarrow\lambda&=&700nm \end{array}$

6) La majeur partie des longueurs d'onde émise par l'hydrogène ou par l'hélium appartiennent au spectre de l'étoile Véga. L'étoile Véga contient de l'hydrogène et de l'hélium, donc de l'atmosphère.

Exercice 8

1) Justification de la discontinuité du spectre d'émission.

Les spectres d'émission de l'atome d'hydrogène observés sont des raies.

a) L'état fondamental de l'atome correspond à l'état stable de l'atome

b) L'énergie d'ionisation de l'atome d'hydrogène est l'énergie minimale qu'il fournir à l'atome d'hydrogène, situé dans son état fondamental, pour lui arracher son électron

$\begin{array}{rcl} E&=&E_{\infty}-E_{1}\\\\&=&0-(-13.6) \end{array}$

2) a) Calcul de la longueur d'onde maximale $\lambda_{\text{max}}$ correspondant à la transition de l'électron d'un niveau $n>2$ au niveau $2.$

Cette longueur d'onde correspond à une transition électronique du niveau $n=3$ au niveau $n=2$

$\begin{array}{rcl} -\dfrac{h_{C}}{\lambda_{\text{max}}}&=&E_{2}-E_{3}\\\\\Rightarrow\lambda&=&\dfrac{h_{C}}{E_{3}-E_{2}}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{1.602\cdot 10^{-19}\times(-1.51-(-3.40))}\\\\\Rightarrow\lambda_{\text{max}}&=&657nm \end{array}$

$\lambda_{\text{max}}\approx\lambda_{4}$

b) Transitions correspondant aux radiations de longueur d'onde $\lambda_{1}$, $\lambda_{2}$ et $\lambda_{3}.$

Les longueurs d'onde appartiennent au spectre visible correspondant à la transition de l'électron d'un niveau $n>2$ au $n.$

$\begin{array}{rcl} \bullet\text{ pour }\lambda&=&\lambda_{1}\\\\\Rightarrow\,E_{n}&=&E_{2}+\dfrac{h_{C}}{\lambda_{1}}\\\\&=&-3.40+\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{410\cdot 10^{-9}\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{n}&=&-0.37eV \end{array}$

La transition correspond au niveau $n=6$ au niveau $n=2$

$\begin{array}{rcl} \bullet\text{ pour }\lambda&=&\lambda_{2}\\\\\Rightarrow\,E_{n}&=&E_{2}+\dfrac{h_{C}}{\lambda_{2}}\\\\&=&-3.40+\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{434.1\cdot 10^{-9}\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{n}&=&-0.5eV \end{array}$

La transition correspond au niveau $n=5$ au niveau $n=2$

$\begin{array}{rcl} \bullet\text{ pour }\lambda&=&\lambda_{3}\\\\\Rightarrow\,E_{n}&=&E_{2}+\dfrac{h_{C}}{\lambda_{3}}\\\\&=&-3.40+\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{486.1\cdot 10^{-9}\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{n}&=&-0.85eV \end{array}$

La transition correspond au niveau $n=4$ au niveau $n=2.$

3) a) Ce photon est absorbé car l'énergie correspondant à la longueur d'onde est égale à la différence d'énergie entre le niveau $n=2$ et le niveau $n=4$

b) L'atome est ionisé si l'énergie absorbée $E$ est supérieure ou égale à l'énergie d'ionisation $E_{0}.$

$E=11eV<E_{0}=13.6eV$ ; l'énergie du photon est inférieure à l'énergie d'ionisation, l'atome ne sera pas ionisé

$E=11eV<E_{0}=13.6eV$ ; l'énergie cinétique de l'électron est inférieure à l'énergie d'ionisation, l'atome ne sera pas ionisé

$E=14.3eV>E_{0}=13.6eV$ ; l'énergie du photon est supérieure à l'énergie d'ionisation, l'atome sera ionisé et l'électron qui l'atome avec l'énergie restante sous d'énergie cinétique.

$\begin{array}{rcl} E_{C}&=&E-E_{0}\\\\&=&14.3-13.6\\\\\Rightarrow\,E_{C}&=&0.7eV \end{array}$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Solution des exercices : Dipôles actifs - 2nd S

Classe:

Seconde

Exercice 9

On réalise le montage suivant :

Les deux générateurs sont identiques et ont pour f.é.m $4.5\;V$ et pour résistance interne $1\;\Omega.$ Les conducteurs ohmiques ont pour résistances $R_{1}=500\;\Omega\ $ et $\ R_{2}=200\;\Omega$

1) La f.é.m. $E$ et la résistance interne $r$ du générateur équivalent aux deux générateurs sont données par :

$E=E_{1}+E_{2}\ $ et $\ r=r_{1}+r_{2}$

Les deux générateurs étant identiques alors, $E_{1}=E_{2}\ $ et $\ r_{1}=r_{2}$

Ainsi, $E=4.5+4.5=9\ $ et $\ r=1+1=2$

D'où, $\boxed{E=9\;V\ \text{ et }\ r=2\;\Omega}$

2) Calculons la résistance équivalente $R$ aux deux résistors $R_{1}\ $ et $\ R_{2}$

Comme les résistors sont montés en parallèle alors, leur résistance équivalente $R$ vérifie :

$\begin{array}{rcl}\dfrac{1}{R}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}&\Rightarrow&\dfrac{1}{R}=\dfrac{R_{1}+R_{2}}{R_{1}\times R_{2}}\\\\&\Rightarrow&R=\dfrac{R_{1}\times R_{2}}{R_{1}+R_{2}}\end{array}$

A.N : $R=\dfrac{500\times 200}{500+200}=142.8$

D'où, $\boxed{R=142.8\;\Omega}$

3) Déduisons-en l'intensité du courant débité par les deux piles et la valeur $U_{_{PN}}$

Considérons le circuit équivalent ci-dessous :

On a : $\left\lbrace\begin{array}{rcl} U_{_{PN}}&=&E-r.I\\\\U_{_{AB}}&=&R.I\end{array}\right.$

Or, $U_{_{PN}}=U_{_{AB}}$

Donc,

$\begin{array}{rcl} E-r.I=R.I&\Rightarrow&R.I+r.I=E\\\\&\Rightarrow&I(R+r)=E\\\\&\Rightarrow&I=\dfrac{E}{R+r}\end{array}$

A.N : $I=\dfrac{9}{142.8+2}=0.062$

Ainsi, $\boxed{I=0.062\;A=62\;mA}$

Par suite,

$\begin{array}{rcl} U_{_{PN}}&=&E-r.I\\\\&=&9-2\times 0.062\\\\&=&8.876\end{array}$

D'où, $\boxed{U_{_{PN}}=8.87\;V}$

4) Déterminons les intensités des courants dans les deux conducteurs ohmiques

On a :

$$U_{_{PN}}=U_{1}=U_{2}$$

Par ailleurs, d'après la loi d'Ohm, on a :

$$U_{1}=R_{1}.I_{1}\ \text{ et }\ U_{2}=R_{2}.I_{2}$$

Par suite,

$\begin{array}{rcl} U_{_{PN}}=R_{1}.I_{1}&\Rightarrow&I_{1}=\dfrac{U_{_{PN}}}{R_{1}}\end{array}$

A.N : $I_{1}=\dfrac{8.87}{500}=0.018$

Ainsi, $\boxed{I_{1}=0.018\;A=18\;mA}$

De la même manière, on :

$\begin{array}{rcl} U_{_{PN}}=R_{2}.I_{2}&\Rightarrow&I_{2}=\dfrac{U_{_{PN}}}{R_{2}}\end{array}$

A.N : $I_{2}=\dfrac{8.87}{200}=0.044$

D'où, $\boxed{I_{2}=0.044\;A=44\;mA}$

On peut aussi utiliser la loi des nœuds pour déterminer le courant $I_{2}.$

En effet, au niveau du nœud $B$, on a :

$$I_{1}+I_{2}=I$$

Ce qui donne,

$\begin{array}{rcl} I_{2}&=&I-I_{1}\\\\&=&0.062-0.018\\\\&=&0.044\end{array}$

D'où, $\boxed{I_{2}=0.044\;A=44\;mA}$

Oscillations électriques libres et oscillations électriques forcées - Ts2

Classe:

Terminale

A. Oscillations électriques libres

La bobine et le condensateur étant capables de stocker puis de redonner de l'énergie, nous nous intéresserons aux échanges énergétiques entre les différents composants d'un tel dipôle qui peut se comporter comme un oscillateur électrique.

I. Les oscillations libres non amorties

1. Production des oscillations électriques libres non amorties

$\ast\ $L'interrupteur $K_{1}$ est fermé, $K_{2}$ est ouvert

On considère le circuit électrique schématisé ci-dessous, lorsque le condensateur se charge complètement, sa charge est maximale $Q_{\text{max}}.$

D'après la loi des tensions : \begin{eqnarray} u_{C} &=& u_{G}\nonumber\\\Rightarrow\dfrac{Q_{\text{max}}}{C}&=&E\nonumber\\\Rightarrow Q_{\text{max}}&=& CE \end{eqnarray}

L'énergie électrique emmagasinée par le condensateur est

$$E_{e}=\dfrac{1}{2}\dfrac{Q_{\text{max}}^{2}}{C}=\dfrac{1}{2}CE^{2}$$

$\ast\ $L'interrupteur $K_{1}$ est ouvert, $K_{2}$ est fermé

Le condensateur se décharge dans une bobine pure, on obtient des oscillations électriques libres non amorties (oscillations sinusoïdales). L'oscillogramme ci-dessous représente les variations de la tension $u^{c}$ aux bornes du condensateur

$T_{0}$ est la période propre du circuit $LC$

2. Équation différentielle

En ouvrant l'interrupteur $K_{1}$ et en fermant l'interrupteur $K_{2}$ le condensateur se décharge à travers la bobine pure.

La loi d'additivité des tensions s'écrit :

Auteur:

Sidy Mouhamed Ndiaye

Les textiles - TL

Classe:

Terminale

La caractéristique d'un textile est d'être composé de fibres et de pouvoir être tissé. Un textile est constitué de macromolécules qui peuvent être :

$-\ $naturelles et provenir :

$\bullet\ $du règne végétal comme la cellulose

$\bullet\ $du règne animal comme la soie et la laine

$-\ $voire du règne minéral comme l'amiante, avant que l'on découvre ses propriétés cancérigènes

$-\ $Artificielles, comme le nylon ou le polyester, macromolécules qui peuvent être filées et tissées.

Les fibres textiles se répartissent en deux grandes catégories : les fibres naturelles et les fibres chimiques. Les fibres textiles chimiques quant à elles se divisent en deux familles : les fibres artificielles et les fibres synthétiques. Les premières proviennent d'une transformation chimique de substances naturelles, généralement de la cellulose, les secondes sont fabriquées à partir de polymères organiques et inorganiques

I. Textiles naturels

1. Généralités

Les fibres naturelles sont obtenues par transformations physiques et mécaniques d'une matière naturelle, sans modiﬁer sa composition. Elles peuvent être d'origine végétale comme le coton ou le lin (les fibres sont issues des fleurs, des graines, des tiges, des feuilles des plantes, de la sève), d'origine animale, comme la laine ou la soie (les fibres sont issues des poils d'animaux et des sécrétions d'insectes), ou encore d'origine minérale (amiante, métaux,...)

2. Exemples de fibres naturelles

2.1. Le coton

Le coton est une fibre naturelle végétale qui entoure les graines d'un arbuste communément appelé cotonnier. Il est constitué de cellulose pure. Le coton est la plus importante des fibres naturelles produites dans le monde (près de la moitié de la consommation mondiale de fibres textiles). On l'apprécie pour sa longueur, sa finesse, son toucher très doux. Il est solide et souple en même temps. En revanche, il a tendance à se froisser facilement

2.2. Le lin

Le lin est une fibre végétale extraite de la tige du linume. Elle a la particularité d'être une fibre longue (plusieurs dizaines de centimètres), solide et brillante, donnant des tissus frais et absorbants, ce qui la rend idéale pour l'été. Par contre le lin a tendance à se froisser facilement

Les fibres peuvent être utilisées pour faire du papier, des cordes, des sacs. Le lin est anallergique, isolant et thermorégulateur.

2.3. La laine

La laine est une fibre textile naturelle d'origine animale. Elle est obtenue à partir de la toison du mouton ou d'autres animaux (chèvre, lapin, chameau, lama, alpaga,...). La laine est utilisée pour son pouvoir d'isolation thermique et son confort, sa nervosité, sa souplesse, son aptitude au feutrage.

Elle est aussi très absorbante, pouvant absorber jusqu'à $30\%$ de son poids. On distingue différentes variétés de laine dont l'alpaga, le cachemire et l'angora.

La laine est utilisée dans les vêtements, couvertures

2.3. La soie

La soie est une fibre d'origine animale. La soie est issue du cocon produit par la chenille du bombyx du mûrier communément appelée ver à soie. Un fil continu, fin, élastique et souple est obtenu. La fibre de soie est très absorbante : elle peut absorber jusqu'à $30\%$ de son poids Infroissable et léger, le fil de soie est très brillant et très doux au toucher. Il est aussi très solide, jusqu'à $3$ fois plus solide que la laine

II. Les fibres textiles chimiques

Les fibres textiles chimiques quant à elles se divisent en deux familles : les fibres artificielles et les fibres

Auteur:

Sidy Mouhamed Ndiaye

Matières plastiques - TL

Classe:

Terminale

Les matières plastiques remplacent de plus en plus les métaux pour la confection d'objets. Elles sont moins denses que les métaux et les objets sont donc moins lourds. D'autre part elles se corrodent beaucoup moins que les métaux et ne sont pratiquement pas attaquées par les acides. On dit qu'elles sont chimiquement inertes.

1. Généralités

1.1. Définition

Les matières plastiques, appelées polymères, sont des matériaux organiques composés de macromolécules (molécules géantes). Elles peuvent être moulées et sont obtenus par une réaction chimique appelée polymérisation

1.2. Quelques propriétés des matières plastiques

Les polymères (résines) obtenus (sous forme de petites billes, de poudre, de granulés) ont des propriétés médiocres. L'adjonction d'adjuvants favorisent la transformation des résines et améliorent les caractéristiques d'utilisation de ces résines :

$-\ $lubrifiants(savon, cire..) pour transformer les résines.

$-\ $stabilisants, antioxydants pour atténuer les effets oxydants $(O_{2}$ de l'air$)$, les effets de la chaleur, les effets de la lumière.

$-\ $plastifiants qui confèrent de la souplesse.

$-\ $colorants qui confèrent l'aspect désiré.

$-\ $antistatiques pour éliminer l'électricité statique.

$-\ $ignifugeants pour retarder la combustion.

$-\ $charges inertes(solides en poudre...farine de bois, craie, fibre de verre..), elles abaissent le prix de revient, elles augmentent la dureté ainsi que la résistance à l'abrasion, elles diminuent le frottement.

$-\ $agents de ténacité, qui améliorent la ténacité, la résistance aux chocs,...

$-\ $etc....

I. Polymères

1. Définition d'un polymère

Un polymère est une macromolécule, c'est-à-dire, une grande molécule constituée d'unités qui se répètent et qui dérivent de monomères.

2. Polymérisation

2.1. Définition

La polymérisation est l'addition des uns des autres des molécules insaturées identiques ou des molécules insaturées différentes. Le composé initial est appelé monomère et le produit obtenu est le polymère.

2.2. Les caractéristiques d'un polymère

Le polymère est caractérisé par :

$-\ $le motif représentant le groupe d'atomes qui se répètent dans la molécule

$-\ $l'indice de polymérisation ou le degré de polymérisation, le nombre de molécules additionnées

3. Les différents types de polymérisation

On distingue la polyaddition et la polycondensation

3.1. Polymérisation par polyaddition

La polyaddition est une réaction de polymérisation au cours de laquelle des molécules insaturées identiques ou non, appelées monomères, s'unissent pour une macromolécule appelée polymère

$$nA\longrightarrow -(-A-)_{n}-\quad\text{ou}\quad nA+nB\longrightarrow -(-AB-)_{n}-$$

$A$ et $B$ sont les momères ;

$-A-$ ou $–AB-$ sont les motifs du polymère

$-(-A-)_{n}$ ou $-(-AB-)_{n}-$

Remarque :

Cette union de molécules monomères insaturées se fait sans élimination d'un produit de réaction

3.2. Polymérisation par polycondensation

La polycondensation est une réaction de polymérisation dans laquelle plusieurs molécules de natures différentes s'unissent pour former un polymère avec élimination de molécules légères

4. Exemples de polymères

4.1. Téréphtalate de polyéthylène $(PET)$

Le polyéthylènetéréphtalate est un produit de polycondensation de l'acide téréphtalique avec l'éthylène glycol. Les polyesters linéaires ont d'abord été utilisés essentiellement pour la fabrication de fibres textiles (tergal, diolen…) ou de films (mylar, terphane...). Mais la tendance actuelle est de développer leurs applications en tant que matières plastiques techniques pour les industries mécaniques et électriques, en raison de leurs propriétés

4.2. Polyéthylène $(PE)$ : le $HP$ et le $BP$

Les polyéthylènes sont des polymères (macromolécules) qui font partie de la famille des polyoléfines. Ils sont issus de la polymérisation de l'éthylène gazeux :

$$nCH_{2}=CH_{2}\longrightarrow -\left(CH_{2}-CH_{2}\right)_{n}-$$

En fait il existe deux variétés :

$-\ $le polyéthylène basse densité $PEBD$, souple, à chaînes ramifiées, dit haute pression $(1000\,atm\;,\ 200^{\circ}C)$

$-\ $le polyéthylène haute densité $PEHD$, dur, peu ramifié, dit basse pression $(10\,atm\;,\ 100^{\circ}C).$

Il existe par ailleurs un autre type de $PE$, le $PEMD$ (moyenne densité), mais c'est en réalité un intermédiaire entre les deux formes et n'a pas de caractéristique particulière ou intéressante qui mérite d'être développée. Il semble juste convenable de voir la répartition entre ces différentes formes sur le document suivant :

4.3. Polypropylène $(PP)$

Le polypropylène est obtenu par polymérisation du propylène. Le polypropylène industriel le plus utilisé est celui où les groupements méthyles sont du même coté $(PP$ isotactique$).$

$$nCH_{2}=CH-CH_{3}\longrightarrow\left(CH_{2}-CH\left(CH_{3}\right)\right)_{n}-$$

4.4. Polytétrafluoroéthylène $(PTFE$ ou Téflon$)$

Il est aussi appelé Teflon. Il est synthétisé par polyaddition du tétrafluoroéthylène.

Le Teflon est semi-cristallin, semi-opaque, et blanc. Il est doux. Il possède des propriétés antiadhésives particulièrement performantes. Le polytétrafluoroéthylèneest facilement déformable et a une forte tendance à l'allongement.

Il possède une faible résistance aux contraintes doublée d'une faible résistance aux radiations. Une résistance chimique remarquable non affectée par la plupart des produits chimiques.

Le polytétrafluoroéthylèneest utilisé pour la fabricationdes roulements, les joints, l'isolation électrique à hautes températures, des revêtements et garnitures non adhésives. Il est également utilisé :

$-\ $dans habillement: antitache

$-\ $en chimie: revêtement des ustensiles

$-\ $comme lubrifiant des pièces mécaniques en mouvement etc...

Équation de réaction de polymérisation

$$nCF_{2}=CF_{2}\longrightarrow\left(CH_{2}-CHCl\right)_{n}-$$

4.5. Polychlorure de vinyle $(PVC$ ou $PCV)$

Il est obtenu par la polymérisation des monomères de chlorure de vinyle. Ce polymère de formule est issu d'une réaction chimique entre de l'éthylène et de l'acide chlorhydrique, en présence d'oxygène, Il peut être soit rigide soit souple selon les ingrédients qu'on lui incorpore.

Équation de réaction de polymérisation

4.6. Polystyrène $(PS)$

Le polystyrène est un plastique dur, cassant et transparent. C'est un produit industriel courant largement diffusé, offrant de très nombreux usages.

On distingue trois types de polystyrènes :

$-\ $le polystyrène "cristal" n'a pas une structure cristalline mais porte ce nom en raison de son aspect transparent. Il polymérise sous forme de perles à haute température en présence d'un adjuvant plastifiant

$-\ $le polystyrène "choc" ou acrylonitrile butadiène styrène est un copolymère formé par du styrène et du polybutadiène. C'est le plus commun de la famille des plastiques styréniques car il est résistant, capable de supporter des impacts plus forts que le polystyrène normal. Cet $ABS$ est employé par l'industrie pour des produits rigides, légers et moulés (bacs à douche).

Le matériau le plus connu de la gamme est le polystyrène expansé $(PSE).$

Il existe deux types de $PSE$ : le polystyrène expansé moulé $(PSE-M)$ obtenu à partir d'un polystyrène "expansible" et le polystyrène expansé extrudé $(PSE-E).$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Production, transport, utilisation de l'énergie électrique - TL

Classe:

Terminale

I. Généralités sur l'énergie

1. Définition

L'énergie désigne la capacité à modifier un état ou à produire un travail ou générant un rayonnement électromagnétique ou de la chaleur.

2. Quelques sources d'énergie

Les énergies sont également parfois classées en fonction de leur source. On peut parler des énergies fossiles (tirées du charbon ou du pétrole, par exemple), de l'énergie nucléaire (qui provient de réactions nucléaires), ou encore des énergies renouvelables, qui sont naturellement régénérées comme l'énergie solaire ou l'énergie éolienne

3. Formes d'énergie

L'énergie peut se présenter sous des formes très diverses :

$-\ $l'énergie mécanique qui se présente sous deux formes : énergie cinétique et énergie potentielle

$-\ $l'énergie thermique ou calorifique

$-\ $l'énergie chimique

$-\ $l'énergie rayonnante ou lumineuse

$-\ $l'énergie nucléaire

$-\ $l'énergie électrique

L'énergie peut passer, dans certains conditions, d'une forme à un autre et vice versa : on dit qu'il y a transformation ou conversion d'énergie

4. Unités d'énergie

Dans le système international, l'énergie s'exprime en joules $(J)$, mais dans le langage courant, elle s'exprime plus souvent en wattheure en kilowatt-heure $(kWh)$ ; la calorie $(Cal)$ ; la thermie $(Th)$

$1Wh=3600J$

$1kWh=106Wh$

$1Cal=4.18J$

$1Th=106J$

II. Production de l'énergie électrique

1. Mise en évidence du phénomène d'induction électromagnétique

1.1. Observation

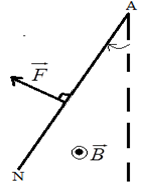
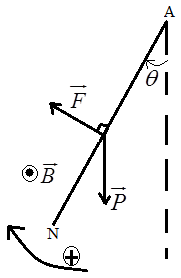
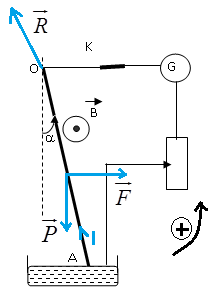
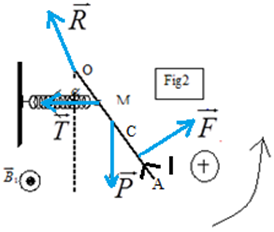
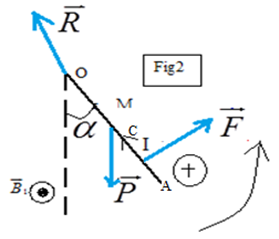
Introduisons un aimant dans une bobine connectée à un galvanomètre (Ampèremètre sensible à cadre mobile, dont l'aiguille dévie soit vers la droite soit vers la gauche selon le sens du courant).

On constate :

$-\ $un courant circule dans la bobine pendant la durée du mouvement de l'aimant.

Retirons l'aimant, un courant circule dans le sens opposé. Maintenons l'aimant immobile dans la bobine ; rien ne se passe.

Maintenons l'aimant fixe et approchons la bobine, un courant circule de la bobine. Maintenons l'aimant toujours immobile, et éloignons la bobine, un courant circule dans la bobine

1.2. Conclusion

Le phénomène observé s'appelle induction électromagnétique. Le courant observé s'appelle courant induit. Son intensité est généralement variable dans le temps.

La bobine dans laquelle le courant induit circule est l'induit ou circuit induit. L'aimant est l'inducteur ou circuit inducteur

De même que tout courant est dû à une tension, le courant induit est dû à une tension induite appelée force électromotrice induite ou $f.é.m.$ induite.

2. Les alternateurs

2.1. Principe de fonctionnement

Le principe d'induction magnétique est généralement expérimenté en déplaçant un aimant permanent dans une bobine. Une tension ou un courant se crée aux bornes de la bobine. Un alternateur fonctionne selon ce

principe : un électroaimant, alimenté par un courant d'excitation, est en rotation à l'intérieur d'une bobine : il produit ainsi une tension alternative ou un courant alternatif.

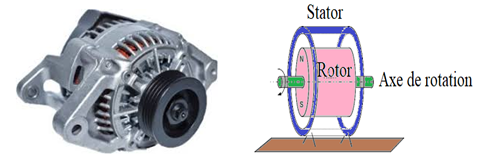
2.2. Constitution d'un alternateur

Un alternateur est constitué de deux parties :

$-\ $le rotor : c'est la partie mobile de l'alternateur. Il est, en général, constitué de plusieurs aimants.

$-\ $le stator : comme son nom l'indique, le stator constitue la partie fixe ou statique, de l'alternateur.

Il s'agit donc le plus souvent de l'induit.

Les enroulements du stator sont fabriqués en fils de cuivre. Chaque spire de fil est isolée des autres spires. Dans le cas des alternateurs monophasés, les enroulements sont reliés en série

2.3. Rôle d'un alternateur

Le rôle de l'alternateur est de convertir de l'énergie mécanique en énergie électrique. L'électricité ainsi produite est utilisée de différentes manières selon les conditions de conduite

3. Les centrales électriques

Une centrale électrique est un site industriel destiné à la production d'électricité. Les centrales électriques alimentent en électricité, au moyen du réseau électrique, les consommateurs, particuliers ou industriels éloignés de la centrale

3.1. Principe de fonctionnement d'une centrale électrique

Le principe général d'une centrale de production électrique est de transformer une source d'énergie primaire en énergie électrique. On peut donc considérer qu'elle est un convertisseur d'énergie

L'énergie primaire à l'origine de la transformation peut être :

$-\ $chimique : issue de la combustion de matériaux fossiles (charbon, gaz naturel, pétrole) ou non-fossiles (biomasse, par exemple) ;

$-\ $mécanique : générée par la force du vent, de l'eau des rivières ou des marées, etc. ;

$-\ $nucléaire : issue de la fission d'atomes d'uranium ou de plutonium ;

$-\ $solaire.

3.2. Fonctionnement technique d'une centrale

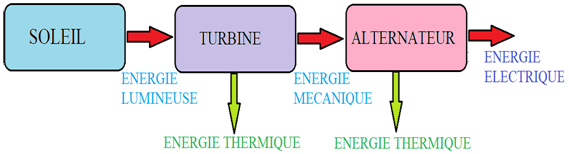
Deux éléments sont essentiels au sein d'une centrale électrique : la turbine et l'alternateur.

La turbine a pour rôle de convertir l'énergie primaire en énergie mécanique. Il s'agit d'une roue munie de palettes ou aubes, qui tournent selon les cas, sous l'action :

$-\ $de l'eau (sous forme liquide ou sous forme de vapeur d'eau sous pression) ;

$-\ $du vent (cas spécifique de l'éolienne).

Selon l'énergie primaire utilisée, différentes technologies de turbines sont possibles :

$-\ $turbine hydraulique ;

$-\ $turbine à vapeur ;

$-\ $turbine à combustion (communément appelée turbine à gaz) ;

$-\ $éolienne.

La turbine est couplée à un alternateur (un grand aimant cerclé d'une bobine) en rotation : celui-ci a pour rôle de convertir l'énergie mécanique produite par la turbine en mouvement, en énergie électrique.

3.3. Les différents types de centrales électriques

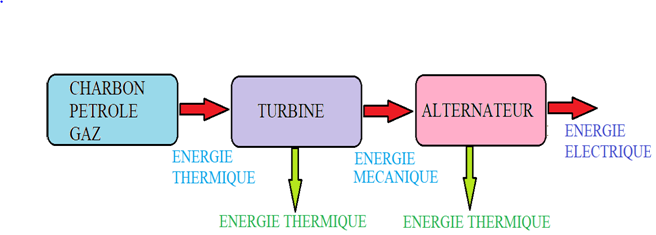
3.3.1. Les centrales thermiques

Les centrales thermiques classiques, également appelées centrales thermiques conventionnelles, sont des centrales à flamme, qui peuvent être alimentées par :

$-\ $une énergie primaire fossile : charbon en fines particules, fioul liquide ou gaz ;

$-\ $une énergie primaire renouvelable, issue de la biomasse : biocarburant, méthane ou bois, par exemple

Fonctionnement

Dans une centrale thermique à flamme, du charbon, du pétrole, du gaz naturel ou une énergie biomasse sont brûlés : l'énergie chimique des combustibles est transformée en énergie thermique.

Cette énergie thermique issue de la combustion permet de chauffer de l'eau dans une chaudière, qui se transforme alors en vapeur d'eau. La vapeur d'eau sous pression et sous haute température met en mouvement la turbine qui entraîne l'alternateur, produisant de l'électricité.

Bilan énergétique

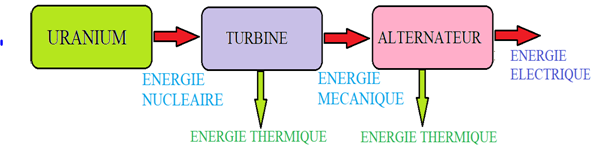
3.3.2. Les centrales nucléaires

Les centrales nucléaires font partie de la famille des centrales thermiques. La principale différence avec les centrales à flamme réside dans la façon de produire la chaleur nécessaire pour chauffer l'eau : ici, ce n'est pas par combustion, mais par fission qu'est générée l'énergie thermique.

Fonctionnement

Après fission (éclatement) des noyaux des atomes d'uranium ou de plutonium dans le réacteur nucléaire, l'énergie nucléaire est convertie en énergie thermique.

L'énergie thermique obtenue permet de chauffer de l'eau liquide pour la transformer en vapeur. La vapeur d'eau sous pression et sous haute température met en mouvement la turbine qui entraîne l'alternateur, produisant ainsi de l'électricité.

Bilan énergétique

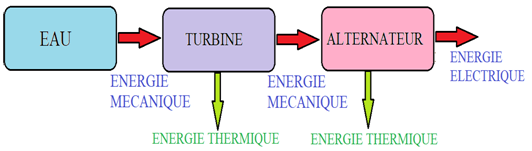
3.3.3. Les centrales hydroélectriques ou hydrauliques

Les centrales hydroélectriques, également appelées centrales hydrauliques, utilisent le mouvement de l'eau pour produire de l'électricité.

Fonctionnement

En effet, c'est la force motrice issue d'une retenue d'eau (barrage au niveau d'un fleuve ou d'une chute, par exemple) qui permet d'activer une turbine, laquelle déclenche la rotation de l'alternateur

Bilan énergétique

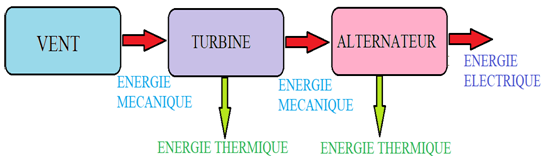
3.3.4. Les centrales éoliennes

L'éolienne utilise l'énergie cinétique du vent pour produire de l'électricité

Fonctionnement

Le mouvement du rotor est transmis à l'arbre principal, qui est couplé à un alternateur par un multiplicateur permettant d'augmenter considérablement la vitesse de rotation.

Cet alternateur convertit ensuite l'énergie mécanique de rotation en énergie électrique

Bilan énergétique

3.3.5. Les centrales solaires ou photovoltaïques

Une centrale solaire thermodynamique permet de transformer l'énergie thermique du rayonnement solaire en chaleur, afin de la convertir ensuite en énergie électrique. Elle est donc particulièrement appropriée aux régions et pays à fort ensoleillement.

Fonctionnement

Les rayonnements du soleil chauffent de l'eau, qui est ainsi transformée en vapeur. Cette vapeur fait tourner une turbine : l'énergie de la turbine est transformée en énergie électrique grâce à un alternateur

Bilan énergétique

III. Énergie et puissances électriques

1. Énergie électrique

1.1. Définition

L'énergie électrique est une énergie disponible sous forme de courant d'électrons (électricité). Cette énergie est utilisée directement pour produire de la lumière ou de la chaleur.

1.2. Expression de l'énergie électrique

L'énergie électrique dans un dipôle, soumis à une tension $U$, parcouru par un courant d'intensité $I$ pendant une durée $\Delta t$ est donnée par la relation :

$$\boxed{E=UI\Delta t}$$

2. Puissance électrique

Pour quantifier cette énergie, on définit la puissance électrique. C'est l'énergie reçue ou cédée par un dipôle par unité de temps. Plus la puissance fournie à un dipôle récepteur est grande, plus le fonctionnement de ce dipôle est efficace.

2.1. Définition

La puissance est une quantité d'énergie échangée (perdue ou gagnée) par unité de temps. Cela correspond à un débit d'énergie

$$\boxed{P=\dfrac{E}{\Delta t}}$$

L'unité S.I. de la puissance est le watt $(W).$ $1W=1J\cdot s^{-1}.$

Exemples

Une ampoule de $40W$ consomme $40J$ d'énergie électrique chaque seconde. Un moteur de $100kW$ fournit $100kJ$ d'énergie mécanique chaque seconde.

Quelques unités usuelles

Le wattheure (énergie)

Le wattheure est l'énergie échangée par un dispositif d'une puissance d'un watt pendant une heure.

$1Wh=3600Ws=3600J$

Le kilowattheure : $1kWh=103Wh$

Puissances électriques de quelques récepteurs et générateurs

$$\begin{array}{|l|c|c|c|} \hline \text{Appareils}&\text{Puissance}&\text{Appareils}&\text{Puissance}\\ \hline \text{Calculatrice de poche}&0.4mW&\text{Fer à repasser}&1kW\\\hline \text{Phare de bicyclette}&2.4W&\text{Téléviseur en couleurs}&80W\\ \hline \text{Congélateur}&150W&\text{Cuisinière électrique}&6kW\\ \hline \text{Locomotive électrique}&3MW&\text{Pile solaire }1cm^{2}&5mW\\ \hline \text{Monocellule}&2W&\text{Dynamo de bicyclette}&3W\\ \hline \text{Générateur de centrale électrique}&300MW&\text{Moteur de TGV}&1MW\\ \hline \end{array}$$

2.2. Puissance moyenne

La présence de bobines dans des appareils entraîne un décalage entre la tension et l'intensité : L'intensité n'est pas maximale en même temps que la tension. Ce décalage intervient dans le calcul de la puissance.

La puissance moyenne aux bornes d'un dipôle s'exprime par la relation :

$$\boxed{P_{m}=KUI}$$

avec $P$ en watts $(W)$ ; $U$ en volts $(V)$ ; $I$ en ampères $A)$

$k$ est appelé le facteur de puissance, avec $k\leq1$ ; $k$ n'a pas d'unité.

Le facteur de puissance est une caractéristique d'un récepteur électrique qui rend compte de son efficacité pour consommer de la puissance lorsqu'il est traversé par un courant.

2.3. Puissance apparente

La puissance apparente est la puissance maximale qui est disponible pour faire fonctionner une installation électrique.

La puissance apparente s'exprime par la relation :

$$\boxed{P_{a}=UI}$$

$U$ en volts $(V)$ ; $I$ en ampères $(A)$ ; $P_{a}$ en voltampère $(VA)$

Relation entre la puissance moyenne et la puissance apparente

$$\boxed{P_{m}=KP_{a}}$$

IV. Les transformateurs

1. Définition

Un transformateur est un composant électrique qui a pour rôle de modifier les valeurs de l'intensité et de la tension appliquées à son entrée par une source alternative en un système de tension et d'intensité de valeurs efficaces différentes, mais de fréquence et de forme identique.

Il est constitué d'enroulements indépendants mais liés par un circuit magnétique (cas d'un transformateur statique)

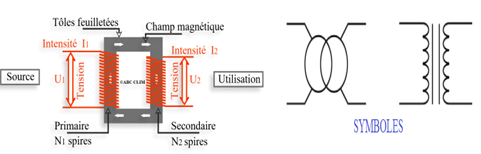
2. Constitution du transformateur

Un transformateur est constitué de :

$-\ $deux enroulements nommés bobines,en fils de cuivre.

Une bobine comportant $N_{1}$ spires appelé primaire, alimentée par un courant de type alternatif de tension $U_{1}$, et d'intensité $I_{1}$ et d'une autre bobine nommée secondaire comportant $N_{2}$ spires, qui fournit, sous la tension $U_{2}$, un courant $I_{2}$ au récepteur.

$-\ $d'un circuit en tôle feuilletée assez fine, son rôle est permettre le transfert au secondaire de l'énergie magnétique crée par le primaire

3. Rapport de transformation

Le rapport de transformation d'un transformateur est le quotient de la valeur efficace de la tension au secondaire à vide par la valeur efficace de la tension au primaire

$$\boxed{r=\dfrac{N_{2}}{N_{1}}=\dfrac{U_{2}}{U_{1}}=\dfrac{I_{1}}{I_{2}}}$$

Si $r>1$, le transformateur est élévateur,

Si $r<1$, il est abaisseur

Si $r=1$, l'appareil est un transformateur d'isolement. (Le transformateur est utilisé comme un isolateur)

Remarque :

Un transformateur est un appareil réversible car, il peut jouer le rôle d'élévateur et d'abaisseur de tension

4. Rendement d'un transformateur

L'énergie ne se perd pas au cours d'une transformation. Elle se conserve. Un radiateur électrique transforme la totalité de l'énergie électrique qu'il reçoit en chaleur.

Un moteur électrique ne transforme pas la totalité de l'énergie qu'il consomme en énergie mécanique. Il produit également de la chaleur. L'énergie électrique consommée est égale à la somme de l'énergie utile et de l'énergie perdue.

$$\boxed{E_{reçu}=E_{utile}+E_{perdu}}$$

Le rendement énergétique est égal au rapport de l'énergie utile fournie et de l'énergie totale consommée.

$$\boxed{r=\dfrac{E_{utile}}{E_{reçu}}}$$

Le rendement s'exprime par la relation :

$\boxed{r=\dfrac{P_{utile}}{P_{reçu}}}$ avec $\boxed{P_{reçu}=P_{utile}=P_{perdu}}$

V. Les lignes électriques

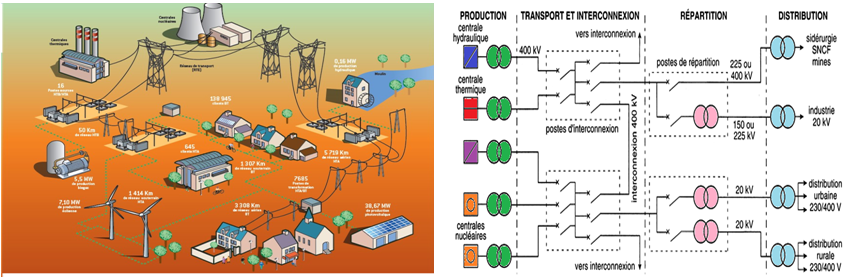
L'énergie produite par les différents sites de production doit être acheminée sur tout le territoire. Cet acheminement est réalisé par des lignes aériennes ou souterraines

1. Les lignes de transport

1.1. Lignes de transport Très Haute Tension $(THT)$

Ce sont les lignes qui relient les centrales éloignées aux centres d'utilisation. On les place dans une catégorie distincte à cause de leurs propriétés spéciales. Ces lignes peuvent atteindre des longueurs de $1000km$ et elles fonctionnent à des tensions allant jusqu'à $765kV.$ Les lignes à courant continu à haute tension sont également incluses dans ce groupe.

1.2. Lignes de transport Haute Tension $(HT)$

Ce sont les lignes reliant les postes de transformation principaux aux centrales de génération.

Elles sont constituées de fils aériens ou de câbles souterrains. Dans cette catégorie, on trouve aussi les lignes servant à échanger de l'énergie entre deux grands réseaux et à augmenter la stabilité de l'ensemble

2. Les lignes de distribution

2.1. Lignes de distribution $MT$

Ce sont des lignes qui relient les clients aux postes de transformation principaux de la compagnie d'électricité

2.2. Lignes de distribution $BT$

Ce sont les lignes et la filerie installées à l'intérieur des édifices, usines et maisons pour alimenter les moteurs, cuisinières, lampes, etc. Dans certaines régions, on utilise un réseau comprenant une grille de câbles souterrains

3. Les pertes en lignes

Le réseau électrique national s'étend sur des milliers de kilomètres de lignes électriques. Ces lignes sont constituées de câbles métalliques très longs qui sont des conducteurs électriques imparfaits. Ainsi, lorsque des courants électriques de forte intensité traversent ces câbles, une partie de l'énergie transportée est transformée en chaleur par effet joule et donc perdue.

Une partie de l'énergie électrique transportée se dissipe par effet joule dans la résistance de la ligne, les pertes en ligne sont données par la relation :

$$\boxed{P_{j}=RI^{2}}$$

$P_{j}$ est la puissance des pertes en ligne en watts $(W)$

$R$ est la résistance de la ligne en ohms $(\Omega)$

$I$ est l'intensité en ligne en ampère $(A).$

La puissance totale transportée :

$$\boxed{P_{T}=UI}$$

$U$ est la tension à transportée

$I$ est l'intensité en ligne

$\Rightarrow I=\dfrac{P_{T}}{U}\Rightarrow P_{J}=\left(\dfrac{P_{T}}{U}\right)^{2}.$

$$\Rightarrow\boxed{P_{J}=R\dfrac{P_{T}^{2}}{U^{2}}}$$

Pour une puissance transportée donnée, les pertes en ligne sont inversement proportionnelles au carré de la tension, ce qui explique l'intérêt de la haute tension. Si la tension est forte, la puissance des pertes en ligne $P_{J}$ sera faible.

Afin de limiter ces pertes d'énergie, il est nécessaire de diminuer l'intensité du courant donc d'augmenter la tension aux bornes de la ligne

VI. Utilisation de l'énergie électrique

1. Réseau électrique

Le réseau électrique est l'infrastructure mettant en relation la production d'électricité et les usages finaux. Il a pour but d'acheminer l'électricité d'un réseau de transport ou de répartition jusqu'aux consommateurs

2. Utilisation domestique

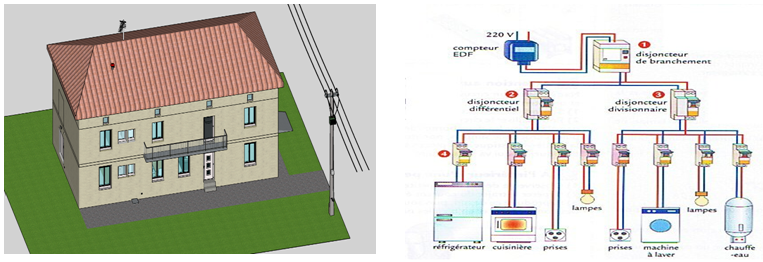
2.1. Installation domestique

L'électricité sert pour l'éclairage, le chauffage ou la climatisation. Elle fait tourner les moteurs électriques, le téléphone, la radiodiffusion, la télévision, la sonorisation, l'informatique, les automates, les communications numériques (internet, réseaux) ont besoin d'électricité.

L'installation électrique doit assurer la protection des personnes et des biens contre les risques électrique.

2.2. Les composants d'une installation électrique

2.2.1. Le compteur électrique

Le compteur électrique sert à mesurer la consommation électrique en $kWh.$ Grâce à lui, les fournisseurs peuvent calculer l'énergie consommée et ensuite établir la facture d'électricité. Selon l'offre tarifaire choisie, le compteur peut indiquer un ou deux index (compteur bi-horaire avec tarif de jour et tarif de nuit).

2.2.2. Le disjoncteur de général

Le disjoncteur général (ou disjoncteur de branchement) protège l'installation électrique et les personnes, c'est lui qui assure la coupure d'urgence en cas de surcharge électrique. Cependant, il ne peut suffire seul à la protection de l'installation électrique.

2.2.3. Le disjoncteur différentiel

Placé dans le tableau électrique, en amont d'un circuit ou d'un groupe de circuits, le disjoncteur différentiel joue le même rôle que le disjoncteur général mais à un second niveau. Il permet ainsi de couper l'alimentation électrique en cas de surtension dans une partie seulement de l'installation.

Le disjoncteur différentiel protège mais également les personnes des risques de décharges.

2.2.4. Le disjoncteur divisionnaire

Le rôle d'un disjoncteur divisionnaire est plus spécifique que celui des autres types de disjoncteurs. Il ne sert qu'à protéger individuellement le circuit qu'il protège contre une surcharge ou un court-circuit. Il n'est pas en mesure de détecter les fuites de courant et d'empêcher une électrisation. C'est pourquoi il doit toujours être secondé par un interrupteur ou un disjoncteur différentiel.

2.2.5. Les fusibles

Les coupe-circuits à fusibles, communément appelés par leur abréviation fusibles, sont des appareils de connexion qui servent à ouvrir le circuit dans lequel ils sont installés et d'interrompre le courant lorsque ce dernier est en surintensité pendant un laps de temps donné. Ces organes de sécurité dont le rôle est d'ouvrir un circuit électrique quand le courant y atteint une valeur d'intensité dangereuse, ramenant ainsi l'intensité à zéro.

Il permet ainsi d'éviter des accidents tels que les départs d'incendie, une défaillance des isolants ou encore la surchauffe d'un appareil électrique.

Les fusibles ne sont pas réarmables comme les disjoncteurs. Si l'un d'eux saute, on coupe le courant du disjoncteur général, ensuite on enlève le fusible défectueux du tableau électrique et on le remplace par un fusible neuf du même ampérage. Par mesure de sécurité, il faut débrancher les appareils de l'habitation pour éviter que le nouveau fusible ne saute au moment de remettre le courant.

2.3. Facturation

Le mode de facturation de l'électricité pour une entreprise correspond au mode de calcul utilisé par le fournisseur pour établir la facture. En cela, il diffère du mode de paiement (carte bleu, chèque, prélèvement bancaire, etc.).

Il existe deux modes de facturation :

$-\ $l'un se basant sur la consommation estimée ;

$-\ $l'autre sur la consommation réelle.

2.3.1. Facture sur la consommation estimée

Une facture dite « estimée » est établie sur la base d'une estimation annuelle de votre consommation. En quelque sorte, l'électricité payée n'est pas celle mesurée par votre compteur électrique.

Pour estimer la consommation de l'entreprise sur l'année, il est possible de prendre en compte :

$-\ $les consommations des années précédentes ;

$-\ $la somme des kilowatts $(kWh)$ consommés par les équipements nécessaires au bon fonctionnement de votre société. Entre également dans le calcul d'autres paramètres, comme l'évolution des prix de l'électricité (production, acheminement et taxes).

2.3.2. Facturation sur la consommation réelle

La facturation au réel permet à l'entreprise de payer tous les mois ou tous les deux mois l'électricité réellement consommée par ses équipes et locaux professionnels. L'usager doit donc relever régulièrement son compteur et transmettre les chiffres à son fournisseur d'électricité. La relève est même facilitée pour les entreprises bénéficiant d'un compteur qui envoie directement les informations à votre opérateur.

3. Les dangers électriques

Tout accident dû à l'électricité est une électrisation. Les risques corporels: causés par un contact direct (avec un conducteur sous tension) ou indirect (avec une masse métallique d'un équipement sous tension).

$-\ $L'électrocution: c'est une électrisation mortelle. Elle fait suite à trop d'électricité passé dans le corps.

$-\ $Contact direct: c'est le contact d'une personne avec des parties normalement sous tension ou avec des

Les risques d'incendie: causés par un court-circuit, une surcharge, un défaut de connexion dans les appareillages et un arc électrique.

Les risques de surtension: causés par une élévation brutale de la tension appliquée aux bornes des appareils utilisés

Auteur:

Sidy Mouhamed Ndiaye

Force et champ électrostatiques - 1er s

Classe:

Première

I. Forces électrostatiques

1. Mise en évidence

Un pendule est constitué d'une potence, fixée sur un socle en bois, à laquelle est relié un fil de soie sans torsion

Suspendons, en son milieu, un bâton d'ébonite dont une extrémité a été électrisée par frottement.

$\blacktriangleright\ $Approchons de cette extrémité la partie électrisée, par la même méthode, d'un second bâton d'ébonite

L'interaction ou la force d'interaction de ces parties électrisées se traduit par une répulsion

$\blacktriangleright\ $Répétons la même expérience, en remplaçant les bâtons d'ébonite par des tiges de verre électrisées comme précédemment.

L'interaction ou la force d'interaction se traduit par une répulsion

$\blacktriangleright\ $Dans une troisième expérience, on met en présence l'extrémité électrisée du bâton d'ébonite et celle de la tige de verre électrisée.

Il en résulte, à présent, une interaction attractive ou une force d'attraction.

2. Loi de coulomb

Deux objets quasi-ponctuels $A$ $($portant la charge électrique $Q_{A})$ et $B$ $($de charge $Q_{B})$ distants de $r$, exercent l'un sur l'autre des forces de même droite de support $(AB=r)$ et de même valeur.

Si $Q_{A}$ et $Q_{B}$ sont de même signe, les forces sont répulsives, si $Q_{A}$ et $Q_{B}$ sont de signes contraires, les forces sont attractives.

$\overrightarrow{F}_{A/B}=-\overrightarrow{F}_{B/A}=\dfrac{Q_{A}Q_{B}}{4\pi\varepsilon_{0}r^{2}}\overrightarrow{u}_{AB}$

ou $\overrightarrow{F}_{A/B}=-\overrightarrow{F}_{B/A}=\dfrac{KQ_{A}Q_{B}}{r^{2}}\overrightarrow{u}_{AB}$

avec $k=\dfrac{1}{4\pi\varepsilon_{0}}=9\cdot 10^{9}S.I$

II. Champ électrostatique

1. Vecteur champ électrique

1.1. Mise en évidence

Approchons de la boule du pendule, l'extrémité frottée d'une baguette en ébonite chargée négativement ; on observe une déviation du fil.

Ceci met en évidence l'existence d'une force d'origine électrique qui agit sur la boule. La présence de la charge portée par le bâton d'ébonite a modifié les propriétés électriques de l'espace environnant. Pour traduire ce changement, on dit que dans la région règne un champ électrique.

1.2. Définition

Un champ électrique règne dans une région de l'espace si, dans cette région, un corps électrisé subit une force électrique.

1.3. Expression du vecteur du champ électrique

1.3.1. Expression du vecteur du champ électrique du champ électrostatique crée par une charge ponctuelle

D'après la loi de Coulomb :

$$\overrightarrow{F}=\dfrac{qq'}{4\pi\epsilon_{0}r^{2}}\vec{i}\quad(1)$$

D'après la définition du champ électrostatique

$$\overrightarrow{F}=q'\overrightarrow{E}\quad(2)$$

$$(1)=(2)\Rightarrow\;\overrightarrow{E}=\dfrac{q}{4\pi\epsilon_{0}r^{2}}\vec{i}$$

Les caractéristiques du vecteur champ électrostatique sont :

$\blacktriangleright\ $Point d'application : un point du lieu considéré, où se trouve la charge $q$ ;

$\blacktriangleright\ $Direction : même direction que

$\blacktriangleright\ $Sens : même sens que si $q>0$, sens opposé sinon ;

$\blacktriangleright\ $Intensité :

$$\boxed{E=\dfrac{F}{|q|}}\quad\text{ou}\quad E=\dfrac{|q|}{4\pi\epsilon_{0}r^{2}}$$

$F=$ force électrostatique exercée par la charge sur la charge $q$ $($en $N)$

$q=$ Valeur de la charge sur laquelle s'applique $F$ $($en $C)$

$E=$ intensité du champ électrostatique en volts par mètre $($en $V\cdot m^{-1})$

Remarque :

L'intensité du champ électrostatique s'exprime en newtons par mètre $($en $N\cdot C^{-1})$

1.3.2. Expression du vecteur du champ électrique du champ électrostatique crée par un ensemble de charges ponctuelles

2. Ligne de champ et spectre du champ électrostatique

2.1. Ligne de champ électrostatique

On appelle lignes de champ les courbes tangentes au vecteur champ en chacun de leurs points. Elles sont orientées dans le sens du vecteur champ. Les lignes de champ dues à une seule charge source $Q.$

Si celle-ci est positive $(+)$ le champ est dirigé de la charge vers l'extérieur.

Si la charge est négative $(-)$, le champ est dirigé de l'extérieur vers la charge.

On peut visualiser les lignes du champ électrique à l'aide de graines de gazon plongées dans un liquide isolant ou des grains de semoule plongés dans l'huile de paraffine. Elles représentent respectivement les lignes de champ de deux charges égales positives et celles de deux charges égales et de signes contraires Cette disposition des lignes de champ donne la nette impression que les charges de même signe se repoussent et que les charges de signes contraires s'attirent. Chaque charge source crée des lignes de champ

La mise en présence de deux charges, d'égale valeur, entraîne une déformation des lignes de champ et on obtient une nouvelle topographie. En chaque point, la ligne de champ est tangente au champ résultant

Remarque :

$\blacktriangleright\ $Les lignes de champ ne se coupent jamais. En effet, le champ électrostatique ne peut pas avoir deux directions différentes en un point de l'espace champ

$\blacktriangleright\ $La forme des lignes de champ rend compte de la direction du champ électrostatique en tout point

2.2. Spectre du champ électrostatique

Un ensemble de lignes de champ constitue un spectre électrique du champ. L'orientation du vecteur champ en un point donné est déterminée par la seule ligne de champ qui passe parce point. Le spectre électrique peut nous renseigner sur l'intensité du champ : plus les lignes de champ sont rapprochées autour d'un point de l'espace, plus le champ en ce point est intense.

Remarque :

$\blacktriangleright\ $Les lignes de champ ne sont pas réelles, mais elles nous aident à mieux visualiser le champ électrique.

$\blacktriangleright\ $Un tube de champ ou tube de forces est une surface formée par des lignes de champ qui s'appuient sur une courbe fermée.

Si on limite le tube de champ par des sections terminales, il constitue une surface fermée.

3. Champ électrique uniforme

Un champ électrostatique est uniforme dans une région de l'espace si le vecteur champ électrostatique est constant ; c'est-à-dire le champ garde la même la direction, le même sens et la même intensité. Le champ électrostatique entre les plaques métalliques planes, parallèles chargées est uniforme.

En saupoudrant la surface de l'huile de paraffine avec les grains de semoule, ces derniers s'orientent en se disposant suivant des droites perpendiculaires aux plaques.

Les droites dessinées par les grains de semoule matérialisent les lignes de champ électrique associées à $\overrightarrow{E}$ ; elles correspondent à des droites parallèles.

Auteur:

Sidy Mouhamed Ndiaye

Vous êtes ici

Physique

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 1

Exercice 2

Exercice 3 : Utilisation d'un spectrographe de masse

Exercice 4 : spectromètre de masse

Exercice 5

Exercice 6

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 1

Exercice 2

Exercice 3 L'atome d'hydrogène

Exercice 4 Niveaux d'énergie de l'atome d'hydrogène

Exercice 5

Exercice 6

Exercice 7 : Étoile Vega et son spectre

Exercice 8

Exercice 9

A. Oscillations électriques libres

I. Les oscillations libres non amorties

1. Production des oscillations électriques libres non amorties

2. Équation différentielle

I. Textiles naturels

1. Généralités

2. Exemples de fibres naturelles

2.1. Le coton

2.2. Le lin

2.3. La laine

2.3. La soie

II. Les fibres textiles chimiques

1. Généralités

1.1. Définition

1.2. Quelques propriétés des matières plastiques

I. Polymères

1. Définition d'un polymère

2. Polymérisation

2.1. Définition

2.2. Les caractéristiques d'un polymère

3. Les différents types de polymérisation

3.1. Polymérisation par polyaddition

Remarque :

3.2. Polymérisation par polycondensation

4. Exemples de polymères

4.1. Téréphtalate de polyéthylène $(PET)$

4.2. Polyéthylène $(PE)$ : le $HP$ et le $BP$

4.3. Polypropylène $(PP)$

4.4. Polytétrafluoroéthylène $(PTFE$ ou Téflon$)$

4.5. Polychlorure de vinyle $(PVC$ ou $PCV)$

4.6. Polystyrène $(PS)$

I. Généralités sur l'énergie

1. Définition

3. Formes d'énergie

4. Unités d'énergie

II. Production de l'énergie électrique

1. Mise en évidence du phénomène d'induction électromagnétique

1.1. Observation

1.2. Conclusion

2. Les alternateurs

2.1. Principe de fonctionnement

2.2. Constitution d'un alternateur

2.3. Rôle d'un alternateur

3. Les centrales électriques

3.1. Principe de fonctionnement d'une centrale électrique

3.2. Fonctionnement technique d'une centrale

3.3. Les différents types de centrales électriques

3.3.1. Les centrales thermiques

3.3.2. Les centrales nucléaires

3.3.3. Les centrales hydroélectriques ou hydrauliques