Série d'exercices : Les alcanes - 1e s
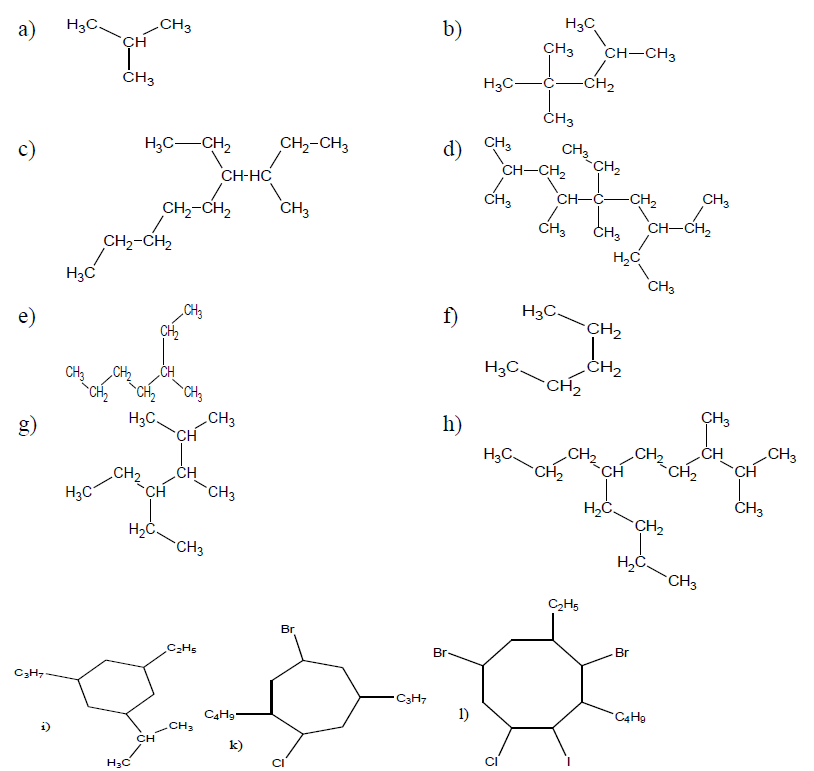
Exercice 1
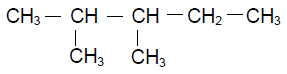
Exercice 2
Exercice 3
Exercice 4
Exercice 5
Exercice 6
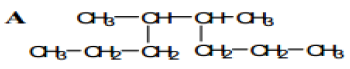



L’histologie étymologiquement est la science des « tissus ». Elle permet de connaitre et de comprendre l’organisation et le fonctionnement des cellules. L’étude des cellules est longue et complexe ; processus qui nécessite les étapes suivantes : prélèvement, fixation, coloration, observation aux microscopes.
Ils sont d’ordre cytologique et tissulaire.
Les cellules isolées ou amas de cellules peuvent être obtenus à partir de :
-Liquide spontanément émis : c’est le cas des urines des crachas, du sang, du pus excrétable par pistule.
-Les cellules desquamantes : spontanément obtenus par raclage, brossage á partir d’organes comme la peau, la joue interne, le col de l’utérus, le nez, les voies respiratoires et biliaires.
- Le ponction à l’aiguille : d’un liquide (liquide céphalorachidien, le kyste) ou d’un organe ou d’une tumeur (ganglions, nodules thyroïdien).
Ils sont effectués selon trois modalités : la biopsie, les pièces opératoires et l’autopsie.
La biopsie : elle consiste à prélever un fragment de tissu sur un être vivant en vue d’un examen anatomo-pathologique au niveau d’organes externes ou internes. La biopsie s’effectue en plusieurs modalités :
-Par ponction à l’aide d’une aiguille ou d’un trocart au niveau de l’organe en question (foie, rein…)
-Par biopsie chirurgicale après anesthésie locale ou générale.
-Au cours d’une endoscopie : la pince est dans ce cas montée sur l’endoscopie (appareil chirurgicale qui permet de visualiser des opérations chirurgicales ou simplement d’observer des organes internes).
Les pièces opératoires on peut obtenir des tissus à partir des pièces opératoires par exérèse (extraction ou retranchement d’un élément étranger ou nuisible du corps humain) partielle ou complète d’un ou de plusieurs organes.
L’autopsie : elle correspond à un examen anatomo-pathologique pratiquer pour un cadavre.
NB : Le prélèvement des cellules végétales est plus facile. Il peut se faire à partir des feuilles, des organes…
Le but de la fixation est de maintenir ou de conserver le prélèvement dans un état aussi proche de l’état vivant. Lors du prélèvement, les cellules déversent des enzymes qui peuvent provoquer leurs morts (autodigestion ou autolyse). De même à l’air libre certains prélèvements peuvent être contaminés par des bactéries qui vont entrainer leur putréfaction.
Ainsi les modes d’action des fixations sont :
L’inhibition de l’autolyse, l’inhibition de la putréfaction, l’inhibition des constituants cellulaires ou tissulaires pour leurs études.
Ce sont des composés qui font précipiter ou coaguler les macromolécules. Les fixateurs chimiques peuvent être simples :
Ex : formol, alcool éthylique, acide acétique, acide picrique…
Ils peuvent aussi être Composés :
Ex :mélange de Bouin (acide acétique + formol + acide picrique + eau), le mélange de carnoy.
Les plus utilisés sont l’azote liquide $(-196^{o}C)$ et la neige carbonique $(-60^{o}C)$.
NB : Les fixateurs les plus communs à microscope optique et les plus utiliser dans le monde sont le Formol $(4%)$,Formaldéhyde$(10%)$.
Les fixateurs maintiennent normal les cellules en reliant les groupements des protéines des cellules.
Les tissus de l’organisme ne sont pas spontanément colorés.Cette caractéristique naturelle rend leur observation difficile. Les colorants présentent des composants acides ou basiques en milieu aqueuse qui forment des sels avec des radicaux ionisés.
Les composants acides colorent les zones tissulaires basophiles alors que les composants basiques colorent ceux acidiphiles.
Il consiste a placé l’échantillon dans un mélange de vert de méthylène-pyronine pendent quelques minutes $(2mm)$ puis à rincer l’échantillon dans l’eau. Les verts de méthylène colorent l’ADN du noyau en vert et la pyronine colore l’ARN en rose.
Il consiste à mettre l’échantillon dans un tube contenant de $HCL$ puis placer dans un bain mari (permet la conservation en une température donnée) a $600^{o}C$ pendent $10 mm$ et enfin à le récupérer et le plonger dans le réactif de SCHIFF.L’ADN se colore en rase.
C’est la coloration la plus utilisée dans l’histopathologie, on l’utilise également en hématologie.L’hématéine est une substance basique qui colore l’ADN du noyau en violet. L’éosine est une substance acide qui colore les protéines cytoplasmiques en rose. Le Safran colore les fibres calogènes en jaunes.
c.La coloration MAY-GRUNWALD GIEMSA (MGG)
Elle est utilisée en hématologie avec les frottis sanguins, les ponctions inflammatoires et les coupes d’organes hématologiques et lymphoïdes.

Elle est de routine en cytologique et en gynécologique.
| Noyau | Coloration |
| Cytoplasme des cellules profondes | Bleue |
| Cytoplasme des cellules superficielles | Rose |
Les principales techniques de séparation des constituants cellulaires sont : la centrifugation, la chromatographie et l’électrophorèse.
Elle est une technique qui utilise la force centrifuge (qui éloigne du centre) ou de centrifugation pour séparer les différents composants d’un mélange.
La force de centrifuge est conduite par la rotation du récipient (centrifugeur).
L’augmentation de la vitesse de centrifugation permet une séparation plus nette des différents constituants du mélange et surtout des macromolécules. On parle d’ultracentrifugation. Elle consiste à verser les mélanges hétérogènes dans le ou les tubes à essai puis à les soumettre en rotation. Sous l’effet de la force centrifuge, des particules sont expulsées dans le fond du tube à essai.
Il existe deux types de centrifugations :
La centrifugation différentielle
Elle permet de séparer les particules en fonction de leur taille par une succession de centrifugation en des temps et des accélérations croissantes.
La centrifugation en gradient de densité
La vitesse de sédimentation d’une particule est en fonction de la différence entre sa densité et celle du milieu ambiant. Dans ce tube de centrifugation, le gradient de centrifugation du milieu ambiant peu changer en modifiant le produit chimique de la solution.
Calcules de la vitesse de rotation pour une centrifugeuse précise :
Le nombreg est la force requise pour obtenir une centrifugation optimale. Il est nommé aussi force centrifuge relative (RCF). La relation qui existe entre la vitesse et la rotation exprimé en tours ou en rotation par minutes (RTM) ; la force centrifuge la distance entre le centre du rotor et le fond du tube (r) est décrite par la formule suivante :
$RTM = 1000√RCF / r x 1,118$
Pour appliquer la formule de calcul on doit :
-identifier la RCF en se référant aux indications fournies par le fabriquant du tube.
-identifier le rayon du rotor de la centrifugeuse, car constatant le mode d’emploi ou en le lisant directement sur le rotor.
Le rayon de rotation d’un rotor est de $86 mm$.
Quelle vitesse faudrait-elle programmer la centrifugeuse pour l’accélération de $1300 g$.
$Rtm = 1000√RCF / r x 1,118$
Rtm = 1000√1300 / 86 x 1,11
V (rtm) = 1000√1300 / 96,148
V (rtm) =3677,1 g.mm$
Elle permet de séparer les éléments d’un mélange ou d’un solvant appelé phase mobile à partir d’un support solide dit phase fine ou stationnaire.
Le principe de la chromatographie repose sur le déplacement différentiel des constituants du mélange sur la phase fine ou solide. En effet ces constituants parcourent ces phases proportionnelles à leurs caractéristiques intrinsèques (poids, taille…) ou à leurs affinités avec la phase stationnaire (selon la polarité).
En fonction de la nature surtout de la phase mobile, on distingue la chromatographie en phase liquide (CPL) et la chromatographie en phase gazeuse (CPG).
Elle est une technique de séparation et d’analyse basée sur la migration différentielle des éléments du mélange.
Le principe est le suivant :
-Les échantillons sont déposés dans des puits préfabriqués au sommet du gel.
-Le tampon est le même dans les réservoires du haut en bas $(pH = 9)$ pour que toutes les protéines aient une charge négative.
-Un courant électrique continue parcourt le gel pendent la durée de migration (ainsi puisque les protéines ont même charges, leur migration dépendra uniquement de leurs poids).
-Après migration, le gel est retiré et les bandes de protéines sont visualisées par :
-Coloration de bleu de Coomasie
-Coloration de nitrate d’argent
C’est une technique de marque consistant à une association d’une molécule vectrice et d’un marqueur radioactif.
Le marqueur radioactif est un atome au noyau instable à cause d’un excès de protons, de neutrons ou les deux.
Ainsi elle émet des rayons gamma qui permettent de préciser sa localisation, le traceur est choisi par sa capacité à se fixer préférentiellement dans tel ou tel type de tissu ou son aptitude à mettre en évidence tel ou tel pathologie. C’est le cas de l’iode qui a tendance à se concentrer sur la thyroïde : l’iode entre dans la formation des hormones thyroïdiennes, ainsi le marquage par l’iode du radioactif permet de vérifier le fonctionnement de la thyroïde, de suivre le chemin des molécules formées.
C’est le cas aussi du glucosequi permet de détecter les cellules tumorales. Ces cellules consomment beaucoup de sucre. Ainsi on peut les mettre en évidence en marquant une substance voisine du glucose appelé fluoro désoxyglucose (FDG). D’autres radios traceurs sont utilisés : il s’agit du sodium radioactif $(Na23)$, du carbone radioactif $(C14)$.
L’étude de la structure de la cellule nécessite son observation. Celle-ci est délicate du fait de la petite taille des éléments de la cellule. Ainsi, elle nécessite alors des microscopes. On distingue deux types de microscopes : le microscope optique et le microscope électronique.
Ils sont des instruments optiques grossissants, munis d’un objectif et de l’oculaire qui permet de grossir l’image d’un objet de petite taille et donc on examine des détails invisibles à l’ œil nu. Il est utilisé en biologie pour observer des cellules et des tissus et en pétrographie (science qui étudie les roches minérales), pour reconnaitre des roches en métallurgie pour analyser la structure d’un métal.
Il y a la partie optique et la partie mécanique.
La partie mécanique : elle est constituée de :
-du socle ou pied : il supporte l’appareil
-La potence : elle permet de tenir l’appareil
-La platine : elle permet de recevoir la préparation, elle est percée d’un trou à son centre et est muni de deux valets qui fixent la préparation.
-Le révolver : il possède les objectifs
-Le (s) tube (s) portent l’oculaire (s)
-Les oculaires : ils sont munis de grossissement
-Les objectifs : ils sont également munis des lentilles (grossissements) qui permettent d’agrandir la préparation.
-La source lumineuse est constituée d’une lampe ou d’un miroir.
La lumière composée de photons passe à travers le condensateur qui concentre le flux lumineux en rayons lumineuses.
La lentille d’un objectif permet un premier agrandissement entre $x40 ; x200$ et $x150$ (en fonction de l’objectif) puis la lentille de l’oculaire qui permet un deuxième agrandissement en générale x4. Ainsi l’œil reçoit une image agrandie
L’agrandissement final (grossissement) est le produit des deux grossissements.
Grossissement $= G$. de l’objectif $x G$. de l’oculaire
Les microscopes optiques ne permettent pas de voir des objets de tailles $< 0,02 U_{m}$ contrairement au microscope électronique. Ce dernier utilise à la place de la lumière un rayonnement électronique (électrons). Il existe deux types de microscopes électroniques :
oLe microscope électronique a transmission (MET)
Le pouvoir de séparation du MET (de $2$ nanomètres a $0,02$ nanomètre) est théoriquement $40000$ fois supérieur à celui du $M_{O}$ et 2million de fois de l’œil.Le MET comprend :
-Un canon a électron
-Un système de détection d’électrons
-des lentilles magnétiques
oLes microscopes électroniques à balayage (MEB)
Le principe du balayage consiste à explorer la surface de l’échantillon et à transmettre le signal du détecteur a un écran cathodique dont le balayage est exactement électronisé et synchronisé avec celui du faisceau.
$\begin{array}{lcl}\dfrac{M_{C_{n}H_{2n+3}N}}{100}&=&\dfrac{14}{\%N}\\&\Rightarrow&M_{C_{n}H_{2n+3}N}&=&\dfrac{14\times 100}{\%N}\\&\Rightarrow&14 n+17&=&\dfrac{14\times 100}{19.18}\\&\Rightarrow&14n+17=73\\&\Rightarrow&n=4\\&\Rightarrow& C_{4}H_{11}N \end{array}$
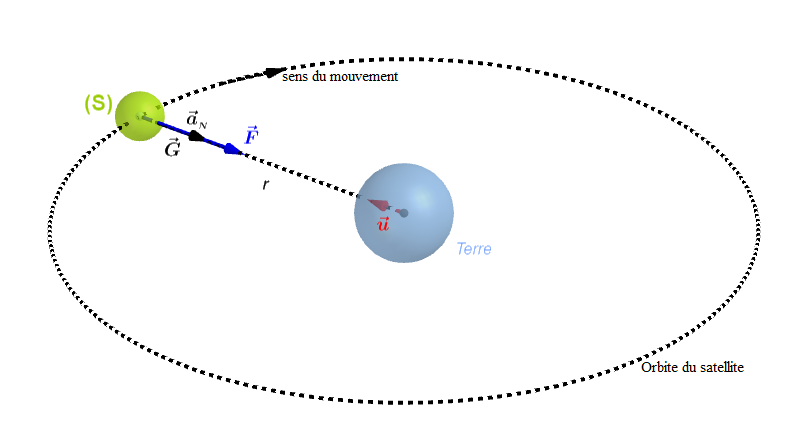
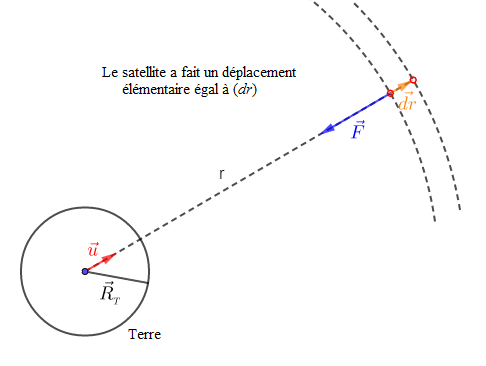
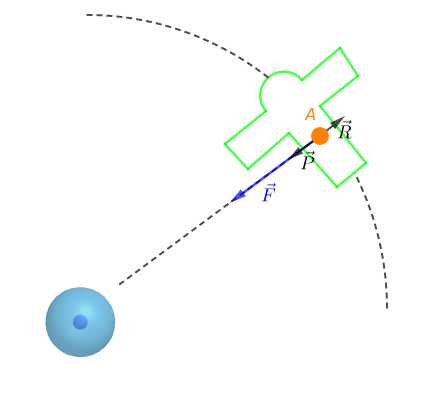
L'énergie mécanique $E_{m}$, d'un satellite sur orbite est donnée par : $$E_{m}=E_{c}+E_{p}$$