Physique

Série d'exercices : Classification quantitative des couples oxydant - réducteur ion métallique/métal - 1er s

Classe: 
Première
 

Exercice 1

On donne les potentiels normaux d'oxydo-réduction $E_{0}$ des couples rédox suivant :
 
$Ag^{+}/Ag\ :\ 0.8\,V$ ;
 
$Zn^{2+}/Cu\ :\ 0.34\,V$ ;
 
$Zn^{2+}/Zn\ :\ -0.76\,V$ ;
 
$Al^{3+}/Al\ :\ -1.66\,V$ ;
 
1) Quel est par convention, le potentiel normal d'oxydo-réduction du couple  
 
2) pour chaque couple rédox, identifier l'oxydant et le réduction ; présenter les résultats sous forme de tableau.
 
3) Écrire pour chacun des couples rédox précédents, la demi-équation de réduction.
 
4) Parmi les couples de réactifs suivants, rechercher ceux qui donneront lieu à une réaction spontanée. 
 
Écrire dans ce cas l'équation d'oxydoréduction correspondante.
 
$Ag^{+}\ +\ Zn$
 
$Cu^{+}\ +\ H^{+}$
 
$Cu\ +\ Ag^{+}$
 
$Zn^{2+}\ +\ H_{2}$
 
$Al\ +\ Cu^{2+}$
 
$Zn\ +\ H^{+}$
 
5) On réalise les piles correspondants aux réaction spontanées de la question précédente.
 
Déterminer dans chaque cas l'anode et la cathode.
 
Calculer la force électromotrice de chacune d'elle.
 
(On présentera les résultats sous formes de tableau).

Exercice 2

1. On réalise le pile constituée
 
$\blacklozenge\ $ d'une tige de fer trempant dans une solution aqueuse de sulfate de fer $(II)$
 
$\blacklozenge\ $ d'une tige de zinc trempant dans une solution aqueuse de sulfate de zinc $(II)$, les deux solutions étant reliées par un pont salin
 
1.1. Écrire les deux demi-équations des couples rédox en présence.
 
Préciser le sens dans lequel chaque réaction a effectivement lieu lorsque la pile débite.
 
1.2. On branche un voltmètre comme indiqué sur la figure.
 
 
Préciser la polarité de la piles ; c'est-à-dire le signe $+$ ou $-$ de chacune des électrodes
 
2. Les constructeurs automobiles utilisent, pour la fabrication des carrosseries, des tôle d'acier galvanisées, assimilables à des plaques de fer sur lesquelles une couche de zinc recouvrant toute la surface a été déposée.
 
2.1. Le zinc empêche-t-il la corrosion du fer ? 
 
Pourquoi ? 
 
La protection reste-t-elle efficace Si, à la suite d'un choc par exemple, la couche de zinc est interrompue ?
 
2.2. A la place du zinc, on dépose de la même manière une couche de chrome sur une tôle de fer. 
 
Le chrome empêche-t-il la corrosion du fer ? 
 
Pourquoi ? 
 
La protection reste-t-elle efficace Si la couche de chrome est interrompue ?
 
2.3. Mêmes questions pour le nickelage des tôles de fer.
 

Exercice 3

On place $m=50\,mg$ de cuivre dans une solution de chlorure d'or $\left(AuCl_{3}\right)$ de volume $V=100\,ml$ et de concentration $c=10^{-2}mol/L.$ 
 
On agite jusqu'à ce que la réaction soit terminée.
 
On sait que les potentiels normaux des couples $Au^{3+}/Au$ et $Cu^{2+}/Cu$ sont respectivement $E_{1}=1.5\,V$ et $E_{2}=0.34\,V.$
 
La masse molaire de $Cu\ :\ M(Cu)=63.5\,g/mol.$
 
1. Montrer que le cuivre est attaqué (justifier la réponse).
 
2. Écrire l'équation-bilan de cette réaction chimique.
 
3. Déterminer le nombre de moles initial $M_{1}$ de moles de cuivre.
 
4. Déterminer le nombre de moles initial $M_{2}$ d'ions $Au^{3+}$ présents dans la solution de chlorure d'or.
 
5. Déterminer le réactif introduit en excès

Exercice 4

1. On se propose de déterminer la durée $t$ pour obtenir un dépôt d'argent.
 
L'intensité $I$ du courant électrique est réglée à $2\,A.$
 
La masse $m$ du dépôt est $1.875\,g.$
 
La valeur absolue de la charge de l'électron $e$ est égale à $1.6\cdot 10^{-19} C.$
 
Le nombre d'Avogadro $N$ a pour valeur $6.02\cdot 10^{23}.$
 
La masse molaire atomique du métal déposé $M$ est égale à $108\,g/mol.$
 
On utilise, pour un dépôt d'argent, la formule suivante $\dfrac{It}{Ne}=\dfrac{m}{M}$ dans laquelle $t$ est en secondes et les autres grandeurs dans les unités indiquées ci-dessus :
 
Calculer le temps $t$ nécessaire à l'opération.
 
2. On indique la classification des métaux selon leur potentiel d'oxydoréduction :
 
 
Après avoir lu le document concernant la Statue de la Liberté de la page suivante, répondre aux questions suivantes :

Document : La Statue de la Liberté en péril : la corrosion

C'est en $1870$ que BARTHOLDI réalise le tout premier modèle de la Statue de la Liberté actuelle.
 
Elle est érigée en pleine mer, au large de Manhattan, sur l'île de Bedloe à New-York. 
 
L'atmosphère qui règne à cet endroit s'explique par un air marin humide et salé, par les vapeurs acides d'une raffinerie de pétrole voisine, par l'air humide et acide exhalé par des millions de visiteurs et l'eau qui pénètre jusqu'à l'ossature de la statue par les fenêtres de la torche.
 
La statue, haute de $93$ mètres, est en feuilles de cuivre de largeur $1.40\,m$ et d'épaisseur $2.37\,mm.$ 
 
Elle est construite avec $8$ tonnes de feuilles de cuivre biseautées. 
 
La statue est soutenue par un pylône en fer auquel se trouve fixé un treillis également en fer pour soutenir l'enveloppe de cuivre. 
 
L'architecte EIFFEL, auteur de l'œuvre, a fait poser un isolant entre le support (fer) et l'enveloppe (cuivre). 
 
L'isolant n'a pas résisté à l'usure du temps : l'humidité s'y est installée, puis fer et cuivre sont entrés en contact. 
 
Il en résulte qu'en de nombreux points de l'enveloppe, plusieurs rivets de cuivre ont sauté en y laissant des trous importants. 
 
La corrosion de la charpente est aggravée par la nature du fer du siècle dernier qui était moins raffiné qu'aujourd'hui. 
 
A la seconde restauration de la statue en $1986$, des solutions mécaniques et électrochimiques ont été apportées pour lui rendre une bouffée d'oxygène
 
2.1. Entre les deux éléments métalliques entrant dans la constitution de la statue, indiquer celui qui possède le plus grand pouvoir réducteur.
 
2.2. Écrire l'équation bilan de l'oxydoréduction de ces deux éléments.
 
2.3. En laboratoire, on réalise une pile électrochimique ayant pour électrodes une lame de fer et une lame de cuivre plongées chacune dans une solution électrolytique comme le montre le schéma ci-dessous.
 
a) Donner le nom du métal constituant l'électrode positive de cette pile.
 
b) Préciser et justifier le sens de circulation des électrons dans le circuit.
 
 
3. Le vieillissement du treillis (de la statue) dans le temps nécessite une protection contre la corrosion.
 
Parmi plusieurs méthodes envisagées, il a été choisi d'installer une anode sacrificielle en zinc. 
 
Expliquer pourquoi le zinc protège le fer et écrire l'équation de la réaction d'oxydoréduction correspondante.
 
4. Pour décaper un lot de pièces en métal ferreux, une entreprise utilise une solution d'acide chlorhydrique de concentration $0.015\,mol/L.$
 
Calculer le $pH$ de cette solution d'acide fort.

Exercice 5

On donne 
 
$E^{\circ}\left(Ni^{2+}/Ni\right)=-0.25\,V$
 
$E^{\circ}\left(Zn^{2+}/Zn\right)=-0.76\,V$ 
 
$E^{\circ}\left(Pb^{2+}/Pb\right)=-0.25\,V$
 
1. On réalise la pile $P_{1}$ symboliser par $Ni|Ni^{2+}\left(0.01\,mol\cdot L^{-1}\right)||Fe^{2+}\left(1\,mol\cdot L^{-1}\right)|Fe.$
 
On constate que le courant circule dans un circuit extérieur de l'électrode de nickel vers l'électrode de fer.
 
1.1. Indiquer la polarité des électrodes. 
 
En déduire les modifications survenues dans chaque compartiment de la pile. 
 
Écrire l'équation de la réaction spontanée, qui se produit dans la pile $P_{1}.$
 
1.2. Monter que le potentiel normal du couple $Fe^{2+}/Fe$ est inférieur à une valeur que l'on déterminera. 
 
En déduire si le fer est attaqué par une solution d'acide ou non ?
 
2. On plonge maintenant une lame de zinc dans une solution contenant des ions $Fe^{2+}.$ 
 
On constate la formation d'un dépôt.
 
2.1. Comparer les potentiels normaux des couples $Fe^{2+}/Fe$ et $Zn^{2+}/Zn.$
 
2.2. Dire si on observe une réaction chimique quand on plonge une lame de fer dans une solution contenant des ions $Pb^{2+}.$
 
3. On réalise la pile $P_{2}$ en associant les deux couples $Fe^{2+}/Fe$ (placé a gauche) $Zn^{2+}/Zn$ (placé a droite)
 
3.1. Donner le symbole de la pile $P_{2}$ et écrire l'équation chimique associé a cette pile.
 
3.2. Calculer $E^{\circ}\left(Fe^{2+}/Fe\right)$ sachant que la f.e.m de la pile $P_{2}$ est $E_{2}=0.32\,V$ quand $\left[Fe^{2+}\right]=1\,mol\cdot L^{-1}$ et $\left[Zn^{2+}\right]=1\,mol\cdot L^{-1}.$

Exercice 6

En utilisant la technique du dosage manganimétrique, on se propose de déterminer la concentration molaire $C_{1}$ d'une solution $(S_{1})$ de sulfate de fer $(II)$ $\left(FeSO_{4}\right)$ de volume $V_{1}=10\,ml.$ 
 
Le matériel dont on dispose est :
 
$-\ $ Une burette graduée
 
$-\ $ Un erlenmeyer
 
$-\ $ Une pipette jaugée de $10\,ml$
 
$-\ $ La solution de permanganate de potassium $KMnO_{4}$ de concentration molaire $C_{2}=0.01\,mol\cdot L^{-1}.$
 
$-\ $ Une solution aqueuse concentrée d'acide sulfurique $H_{2}SO_{4}.$
 
1) Donner le schéma annoté du dispositif en précisant la solution dosant et l'espèce à doser. 
 
Préciser le rôle de $H_{2}SO_{4}$
 
2) a) Écrire l'équation de la réaction rédox qui a lieu lors du dosage
 
b) A l'équivalence rédox, le volume de la solution dosant est $V_{2}=2\,0mL.$
 
c) Comment reconnaître l'équivalence rédox
 
d) déterminer la valeur de $C_{1}$
 
La pile électrochimique schématisée par la figure ci-dessous est constituée par :
 
$-\ $ Une demi-pile formée de la solution $(S_{1})$ dans laquelle on plonge une lame de fer.
 
$-\ $ Une demi-pile formée par une solution de concentration molaire $C_{3}=1\,mol\cdot L^{-1}$ d'ion $Cu^{2+}$ dans laquelle on plonge une lame de cuivre.
 
$-\ $ Un pont salin contenant une solution saturée de nitrate de potassium $\left(K^{+}\;,\ NO^{3-}\right)$
 
$-\ $ Le circuit extérieur à la pile est constitué d'un résistor $R$, d'un interrupteur $K$ et d'un ampèremètre
 
 
1) Donner le symbole de ce schéma de pile ainsi que l'équation chimique associée.
 
2) La f.é.m. de la pile est $E=0.78\,V.$
 
a) Déterminer la polarité des bornes de la pile
 
b) Écrire la transformation chimique qui se produit dans chaque compartiment de la pile après la fermeture de $K.$ 
 
En déduire l'équation bilan de la réaction chimique spontanée quand la pile débite un courant
 
c) Préciser le rôle du pont salin
 
d) Reproduire le schéma de la figure 1 ($K$ fermé) en précisant le sens du courant et des électrons dans le circuit

Exercice 7 : Pile chrome argent

Une pile d'oxydo-réduction est constituée en associant les deux demi-piles suivantes :
 
$-\ $ Une lame de chrome trempant dans $100\,mL$ de solution de nitrate de chrome $III$ de concentration $0.100\,mol\cdot L^{-1}.$
 
$E^{\circ}\left(Cr^{3+}/Cr\right)=-0.74\,V$
 
$-\ $ Un fil d'argent trempant dans $100\,mL$ de solution de nitrate d'argent de concentration $0.100\,mol\cdot L^{-1}.$
 
$E^{\circ}\left(Ag^{+}/Ag\right)=0.80\,V$
 
Les deux demi-piles sont reliées par un pont salin contenant une solution gélifiée de nitrate de potassium $\left(K^{+}+NO^{3-}\right).$
 
1. Définir le "potentiel standard" d'un couple oxydant-réducteur. 
 
Calculer la f.é.m. de cette pile.
 
2. Faire un schéma de la pile en justifiant les polarités des électrodes.
 
Quelles sont les charges qui circulent à l'intérieur et à l'extérieur de la pile, lorsque celle-ci débite ? (Indiquer leur sens de déplacement sur le schéma)
 
3. Écrire les équations-bilan des réactions qui ont lieu dans chaque demi-pile ainsi que l'équation du bilan de la réaction chimique.
 
4. Au cours du fonctionnement de la pile, la masse d'une des électrodes diminue de $80.2\,mg.$
 
4.1. Quelle est cette électrode ?
 
4.2. Calculer la variation de masse de l'autre électrode.
 
4.3. Quelle est alors la concentration $C_{1}$ en ion $Ag^{+}$ ?
 
4.4. Quelle est alors la concentration $C_{2}$ en ion $Cr^{3+}$ ?
 
$\left(M_{Ag}=108\,g\cdot mol^{-1}\text{ et }M_{Cr}=52\,g\cdot mol^{-1}\right)$

Exercice 8 : Gouttière en cuivre ou gouttière en zinc : que choisir ?

Le zinc des gouttières s'abime sous l'action des pluies acides
 
En plongeant une lame de zinc dans une solution aqueuse d'acide, on constate une disparition progressive du métal et un dégagement gazeux (qui explose à la moindre étincelle).

A. Action des pluies acides sur le zinc

Les deux couples oxydant/réducteur mis en jeu sont : $H^{+}(aq)/H_{2}(g)$ de potentiel rédox $E_{0}=0.00\,V$ et $Zn^{2+}(aq)/Zn(s)$ de potentiel rédox $E_{0}=-0.76\,V$
 
1. L'association de ces deux couples constitue une pile.
 
1.1. Quelle serait la borne moins de cette pile ?
 
1.2. Donner la valeur de la force électromotrice E attendue pour cette pile.
 
2. A quelle borne de la pile y a-t-il oxydation ?
 
3. Donner l'équation globale de la réaction de fonctionnement de cette pile.

B. Action des pluies acides sur le cuivre

Les deux couples oxydants/réducteurs mis en jeu sont : $H^{+}(aq)/H_{2}(g)$ de potentiel rédox $E_{0}=0.00\,V$ et $Cu^{2+}(aq)/Cu(s)$ de potentiel rédox $E_{0}=+0.34\,V.$
 
1. L'association de ces deux couples constitue une pile.
 
Quelle est la valeur de la force électromotrice $E$ attendue pour cette pile.
 
2. A quelle borne de la pile y a-t-il réduction ?
 
3. Donner l'équation globale de la réaction de fonctionnement de cette pile.

C. Conclusion

1. Quel est le gaz dégagé qui explose dans l'air à la moindre étincelle lorsque l'on plonge le zinc dans une solution acide ?
 
2. Expliquer pourquoi, indépendamment du coût, la gouttière en cuivre sera préférée à la gouttière en zinc dans les régions ou les pluies acides sont fréquentes

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Classification qualitative des couples oxydant - réducteur ion /métal - 1er s

Classe: 
Première
 

Exercice 1

Une lame de fer plongée dans une solution de sulfate de cuivre $\left(Cu^{2+}\;,\ SO_{4}^{2+}\right)$ se recouvre d'un dépôt de cuivre.
 
Une lame de cuivre plongée dans une solution de nitrate d'argent $\left(Ag^{+}\;,\ NO^{3-}\right)$ se recouvre d'un dépôt d'argent.
 
1) Écrire dans chaque cas, l'équation de la réaction qui se produit.
 
2) Préciser les couples redox mis en jeu.
 
3) Classer les métaux mis en jeu par pouvoir réducteur croissant.
 
4) L'hydrogène est moins réducteur que le fer. 
 
Dire ce qui se passe si on met du fer dans une solution acide.

Exercice 2

On veut étudier le couple $Co^{2+}/Co$ ($Co$ est le cobalt). 
 
On réalise deux expériences.

Expérience a : 

$100\,ml$ d'une solution rose contenant des ions cobalt, de concentration $0.20\,mol\cdot L^{-1}$ sont décolorés par le métal fer et il se forme un dépôt sur le fer

Expérience b : 

Le cobalt métallique donne un dégagement de dihydrogène en milieu acide.
 
1) Expliquer ce qui s'est passé dans les deux expériences ; écrire les équations-bilan des réactions
 
2) Classer qualitativement les trois couples mis en jeu.
 
3) Dans la première expérience quelle est la masse de métal formé ?

Exercice 3

On réalise les expériences suivantes :
 
On observe un dépôt de cuivre sur la partie immergée de la lame de nickel
 
Aucun dépôt n'est observé sur la partie immergée de la lame de nickel
 
1) Écrire la demi-équation du couple rédox qui permet d'expliquer le dépôt de cuivre.
 
2) Écrire la demi-équation du couple rédox qui permet d'où proviennent les électrons de la demi-réaction précédente.
 
3) Écrire l'équation bilan de la réaction chimique traduisant le dépôt métallique.
 
Expliquer pourquoi aucun dépôt n'est observé dans l'expérience 2

Exercice 4

I. On plonge une lame de zinc $Zn$ dans une solution bleue contenant des ions cuivre $(II)$ $Cu^{2+}.$ 
 
Quelques minutes après on observe un dépôt rougeâtre sur la lame de zinc.
 
1) Préciser la nature de ce dépôt.
 
2) Écrire les demi équations électroniques représentant les transformations subies par l'ion $Cu^{2+}$ et le zinc $Zn.$
 
3) Écrire l'équation bilan de la réaction d'oxydo réduction.
 
4) Préciser l'oxydant et le réducteur qui interviennent dans cette réaction.
 
5) La corrosion est un phénomène bien connu des marins. 
 
Les bateaux dont la coque est en acier en sont victimes et doivent en être protégés. 
 
Une méthode de protection consiste à poser à la surface de la coque des blocs de métal que l'on appelle « anodes sacrificielles ». 
 
Pour prévoir les réactions d'oxydoréduction, on peut s'appuyer sur l'échelle de classification électrochimique suivante
 
 
a) Citer les métaux qui peuvent jouer le rôle de « anode sacrificielle ».
 
Justifier la réponse.
 
b) Écrire l'équation bilan de la réaction avec l'une des métaux possible.
 
II. On dispose de $1\,g$ d'un alliage de cuivre et de zinc dont on ne connait pas la composition. 
 
Le cuivre ne réagit pas avec les ions $H_{3}O^{+}$ par contre le zinc réagit .
 
On attaque donc cet alliage avec l'acide chlorhydrique
 
$\left(H_{3}O^{+}\ ;\ Cl^{-}\right)$ en excès, on obtient un dégagement gazeux de dihydrogène $H_{2}$ dont on mesure le volume $V=0.14\,L.$ 
 
1) Sachant que les couples oxydant/réducteur sont $Zn^{2+}/Zn$ ; $H_{3}O^{+}/H_{2}$
 
Écrire les demi-équations électroniques et l'équation bilan de la réaction. 
 
2) a) Calculer la quantité de matière (nombre de moles) de dihydrogène obtenu. 
 
On donne le volume molaire $V_{m}=22.4\,L\cdot mol^{-1}$
 
b) Déterminer la masse de zinc ayant réagit $M(Zn)=65.4\,g\cdot mol^{-1}$
 
3) Déterminer la masse de cuivre contenu dans cet alliage
 
On classe les quatre métaux : Cuivre, Fer, Zinc et Aluminium par ordre croissant du pouvoir réducteur :
 
 
1) Écrire les équations des réactions d'oxydoréductions qui se produisent s'il est possible, en justifiant votre réponse quand on plonge :
 
a) Une lame de fer dans une solution contenant des ions $Au^{3+}$
 
b) Une lame de zinc dans une solution contenant des ions $Cu^{2+}$
 
2) L'acide chlorhydrique $\left(H_{3}O^{+}\right)$ réagit sur le fer en donnant un dégagement de dihydrogène ; une lame de cuivre ne réagit pas avec l'acide chlorhydrique.
 
Placer le dihydrogène sur l'axe de classification électrochimique ci-dessus.

Exercice 5

 
On introduit $1.12\,g$ de fer en poudre dans $100\,mL$ d'une solution aqueuse de sulfate de cuivre $\left(CuSO_{4}\right)$ de molarité égale à $0.2\,mol\cdot L^{-1}.$
 
1) Écrire l'équation de la réaction qui a lieu.
 
2) En supposant que la réaction est totale, calculer
 
a) la masse du solide formé.
 
b) la concentration des ions $Fe^{2+}$ dans la solution.
 
3) On filtre le mélange obtenu. 
 
On ajoute à $50\,mL$ du filtrat $5\,g$ d'un mélange de poudre de zinc, de plomb et d'argent
 
a) Quelle est la réaction qui se produit ?
 
b) Écrire les deux demi-équations électroniques et l'équation bilan de la réaction qui se produit.
 
c) En supposant que la rection est totale et que les réactifs sont pris dans les proportions stoechiométriques, calculer la quantité de matière du métal formé. 
 
En déduire la masse du métal attaqué.
 
4) On filtre le nouveau mélange. 
 
On verse sur le résidu une solution d'acide chlorhydrique en excès. 
 
On recueille $0.672\,L$ de dihydrogène.
 
a) Montrer qu'il se produit deux réactions d'oxydoréduction.
 
b) Préciser les deux couples rédox pour chaque réaction.
 
c) Écrire les demi équations électroniques, en déduire les équations bilan de deux réactions.
 
d) Calculer la masse de chaque métal du mélange (zinc, plomb et argent).
 
On donne : 
 
$M_{Cu}=64\,g\cdot mol^{-1}$ ; $M_{Fe}=56\,g\cdot mol^{-1}$ ; $M_{Zn}=65.3\,g\cdot mol^{-1}$ ; $M_{Pb}=207\,g\cdot mol^{-1}$ ; $V_{M}=24\,L\cdot mol^{-1}$

Exercice 6

Le laiton est un alliage formé de deux métaux le cuivre et le zinc.
 
On fait réagir un échantillon de 15 g de cet alliage sur une solution d'acide chlorhydrique en large excès. 
 
Il se dégage un volume $V=0.9\,L$ de dihydrogène mesuré dans les conditions normales de température et de pression. 
 
En ajoutant au filtrat, une solution d'hydroxyde de sodium , il se forme un précipité.
 
1) En se basant sur l'échelle de la classification électrochimique des métaux, montrer que seul le zinc a réagit.
 
2) Écrire l'équation de la réaction entre le zinc $Zn$ et les ions $H_{3}O^{+}.$
 
Préciser les couples rédox mis en jeu au cours de cette réaction d'oxydoréduction.
 
3) a) Calculer la quantité de matière de dihydrogène recueillie à la fin de la réaction.
 
b) En déduire la quantité de matière de zinc contenue dans l'échantillon.
 
4) a) Calculer la masse du zinc qui a réagi.
 
b) En déduire le pourcentage massique, en zinc et en cuivre, du laiton.
 
On donne :
 
 
$V_{m}=22.4\,L\cdot mol^{-1}\text{ et }M_{Zn}=65.4\,g\cdot mol^{-1}$

Exercice 7

Soit la classification des éléments chimiques par ordre de pouvoir réducteur croissant.
 
 
1) Décrire qu'est ce que se passe dans chaque expérience.
 
a) On plonge une lame de cuivre dans une solution $\left(Ag^{+}\;,\ NO_{3}^{-}\right)$
 
b) On plonge une lame de cuivre dans une solution $\left(Zn^{2+}\;,\ SO_{4}^{2-}\right)$
 
c) Si on plonge une lame d'Aluminium dans une solution $\left(H^{+}\;,\ Cl^{-}\right)$
 
2) Donner l'équation de la réaction lorsqu'il est possible

Exercice 8

On donne les masses molaires en $(g\cdot mol^{-1})$ de : $Fe=56$ et $Ag=108$
 
Dans un volume $V=100\,cm^{3}$ d'une solution aqueuse de nitrate d'argent $\left((Ag^{+}+NO_{3}^{-}\right)$ de concentration molaire $C=1\,mol\cdot L^{-1}$, on ajoute une masse $m=2.24\,g$ de fer en poudre, on constate qu'un dépôt gris scintillant apparaît sur les grains de fer. 
 
Lorsque la réaction atteint son état final on ajoute aux produits formés quelques gouttes d'une solution d'hydroxyde de sodium, on remarque qu'un précipité vert apparaît instantanément.
 
1) a) Identifier les produits de la réaction. 
 
Justifier la réponse.
 
b) Écrire les équations relatives à l'oxydation et à la réduction.
 
$-\ $ En déduire l'équation bilan de la réaction.
 
$-\ $ Préciser les couples rédox mis en jeu au cours de cette réaction.
 
2) a) Calculer la quantité de matière initiale de chacun des réactifs.
 
b) Les réactifs sont-ils en proportions stœchiométriques ? 
 
Si non, quel est le réactif limitant ?
 
c) Calculer, à la fin de la réaction,
 
$-\ $ la concentration molaire des ions présents dans la solution.
 
$-\ $ la masse du dépôt métallique formé.
 
3) Sachant qu'une solution d'acide chlorhydrique réagit avec le fer mais elle est sans action sur l'argent. 
 
Comparer en justifiant la réponse les pouvoirs réducteurs de $Fe$, $Ag$, $H.$ 
 
Les placer sur un axe par ordre de pouvoir réducteur croissant

Exercice 9

On dissout du nitrate de cuivre $II$ $Cu\left(N0_{3}\right)_{2}$, du nitrate d'argent $AgN0_{3}$ et du nitrate d'or $Au\left(NO_{3}\right)_{3}$ dans de l'eau pure de façon à obtenir $300\,ml$ d'une solution $(S).$ 
 
On partage ensuite $(S)$ en trois parties égales.
 
Dans la première partie $(S_{1})$ on place une lame d'argent, on obtient un dépôt d'or de masse $m_{1}=0.394\,g.$ 
 
Dans la deuxième partie $(S_{2})$, on met une lame de cuivre, On obtient un dépôt d'argent et d'or de masse $m_{2}=0.934\,g.$ 
 
Dans la troisième partie $(S_{3})$, on place une lame de zinc on obtient un dépôt d'argent d'or et de cuivre de masse $m_{3}=1.188\,g.$
 
l) a) interpréter ces expériences.
 
b) Écrire les équations des réactions dans $(S_{1})$ et $(S_{2})$, en précisant à chaque fois l'oxydant et le réducteur
 
c) Déduire une classification électrochimique des métaux utilisés.
 
2) Calculer les molarités des ions $Cu^{2+}$, $Ag^{+}$, $Au^{3+}$ et $NO_{3}^{-}$ dans la solution $(S).$
 
On donne : 
 
$Ag=108\,g\cdot mol^{-1}\;,\ Au=197\,g\cdot mol^{-1}\;,\ Cu=63.5\,g\cdot mol^{-1}\;,\ Zn=65\,g\cdot mol^{-1}$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Notion de couples oxydant/réducteur - 1er s

Classe: 
Première
 

Exercice 1

1) Rappeler les définitions des termes oxydant - réducteur - réaction d'oxydoréduction
 
2) Écrire la demi-équation électronique relative aux couples rédox : $Pb^{2+}/Pb-Au^{3+}/Au$
 
3) Dans la réaction spontanée d'oxydoréduction entre la solution de nitrate d'argent et le cuivre
 
a) Quel est l'oxydant ?
 
b) Quel est le réducteur ?
 
c) Quelle est l'espèce chimique qui s'oxyde ?
 
d) Quelle est l'espèce chimique qui est réduite.
 
e) Quels sont les couples redox intervenant dans la réaction ?

Exercice 2

Les ions cadmium $Cd^{2+}$ réagissent avec l'argent métallique $Ag$ pour donner un dépôt de cadmium métallique et des ions argent $Ag^{+}$
 
1) Donner les deux écritures qui symbolisent les transformations subies par les ions cadmium $Cd^{2+}$ et l'argent $Ag.$
 
2) En déduire l'équation bilan de la réaction d'oxydoréduction.
 
3) Préciser l'entité qui joue le rôle d'oxydant et celle qui joue le rôle de réducteur.
 
4) Préciser l'entité qui subit l'oxydation et celle qui subit la réduction

Exercice 3

On donne l'équation suivante :
 
1) Rechercher le nom de l'élément dont le symbole est $Ag.$
 
2) Identifier les deux couples rédox mis en jeu dans cette réaction d'oxydoréduction.
 
3) Écrire les demi-équations d'oxydoréduction correspondant à ces couples.
 
4) Déterminer quels sont, respectivement, l'oxydant et le réducteur dans la transformation étudiée.

Exercice 4

On plonge un clou en fer dans une solution bleue de sulfate de cuivre. 
 
Au bout d'un certain temps, la solution se décolore et le clou se couvre d'un dépôt rouge.
 
1) Quel est le nom de ce dépôt rouge ?
 
2) Pourquoi la coloration bleue a-t-elle disparu ?
 
3) A la solution restante, on ajoute de la soude. 
 
On obtient un précipité vert.
 
Quel ion a-t-on identifié ?
 
4) Sachant que pour l'élément cuivre, la réaction s'écrit : $Cu^{2+}+2e^{-}\ \rightarrow\ Cu$, écrire la réaction pour l'élément fer.
 
5) Écrire la réaction chimique traduisant l'oxydo-réduction.
 
6) Au cours de cette réaction, quel est :
 
$-\ $ l'élément qui est oxydé ?
 
$-\ $ l'élément qui est réduit

Exercice 5

On plonge un clou en fer dans une solution bleue de sulfate de cuivre. 
 
Au bout d'un certain temps, la solution se décolore et le clou se couvre d'un dépôt rouge.
 
1) Quel est le nom de ce dépôt rouge ?
 
2) Pourquoi la coloration bleue a-t-elle disparu ?
 
3) A la solution restante, on ajoute de la soude. 
 
On obtient un précipité vert.
 
Quel ion a-t-on identifié ?
 
4) Sachant que pour l'élément cuivre, la réaction s'écrit : $Cu^{2+}+2e^{-}\ \rightarrow\ Cu$, écrire la réaction pour l'élément fer.
 
5) Écrire la réaction chimique traduisant l'oxydo-réduction.
 
6) Au cours de cette réaction, quel est :
 
$-\ $ l'élément qui est oxydé ?
 
$-\ $ l'élément qui est réduit ?

Exercice 6

$1-\ $ En $TP$, les élèves ajoutent de la limaille de fer dans une solution de sulfate de $II$ ; cuivre $(II)$ $CuSO_{4}$
 
Ils observent la formation d'un dépôt métallique.
 
a) Quelle est la couleur du dépôt formé ?
 
b) Quel est son nom ?
 
c) Écrire la demi-équation électronique de la réaction correspondante.
 
$2-\ $  Dans le but de caractériser les ions en solution, les élèves filtrent la solution et ajoutent dans le filtrat quelques gouttes d'hydroxyde de sodium $\left(Na^{+}+OH^{-}\right).$ 
 
Il se forme un précipité.
 
a) Quelle est la couleur du précipité formé ?
 
b) Quel est son nom ?
 
c) Quelle est sa formule ?
 
d) Quels ions met-il en évidence ?
 
e) Écrire la demi-équation électronique de la réaction correspondante.
 
$3-\ $ Écrire l'équation-bilan de la réaction d'oxydoréduction.

Exercice 7

Pour protéger les coques de navires en acier on utilise des pièces de zinc. 
 
Le zinc métallique est oxydé et le fer de l'acier réduit lors cette réaction chimique.
 
1) Donner le nom de la réaction chimique.
 
2) Écrire les deux demi-équations et indiquer celle qui correspond à l'oxydation et celle qui correspond à la réduction. 
 
Écrire l'équation bilan.
 
Que devient la pièce en zinc ? 
 
Que faut-il faire régulièrement ?

Exercice 8

On ajoute du fer en poudre à $30\,mL$ d'une solution de sulfate de cuivre placée dans un bécher. 
 
Une agitation régulière est effectuée pendant quelques minutes puis on réalise une filtration. 
 
Le filtrat obtenu est limpide et verdâtre. 
 
La poudre recueillie sur le papier filtre est recouverte d'un dépôt métallique rouge.
 
$1-\ $ Quelle était la couleur de la solution initiale ?
 
$2-\ $ A quoi correspond le dépôt métallique rouge ?
 
$3-\ $ Comment peut-on vérifier chimiquement qu'il s'est formé des ions $Fe^{2+}$ au cours de la réaction ?
 
$4-\ $ Écrire les deux demi-équations électroniques intervenant puis l'équation-bilan de la réaction.
 
$5-\ $ Quel est l'oxydant dans cette réaction ? 
 
Quel est réducteur ? 
 
Quelle est l'espèce qui subit une réduction ?
 
Quelle est celle qui subit une oxydation ?

Exercice 9

Pour débarrasser une eau résiduelle des ions mercuriques $\left(Hg^{2+}\right)$ qu'elle contient, il est possible de mettre en œuvre une réaction d'oxydoréduction entre les ions $Hg^{2+}$ et le fer $Fe.$
 
On fait passer $10\,g$ d'une eau à $6\cdot10^{-4}\%$ (en masse) en ion mercurique $\left(Hg^{2+}\right)$ sur du fer en poudre.
 
1) Sachant que le fer se transforme en ion fer $II$ $\left(Fe^{2+}\right)$ et les ions $Hg^{2+}$ passant à l'état atomique $Hg.$
 
Écrire l'équation bilan de la réaction
 
a) Préciser par mis les réactifs l'oxydant et le réducteur. 
 
b) Indiquer les couples rédox mis en jeux.
 
c) Calculer la masse d'ion $Hg^{2+}$ contenus $10\,g$ d'eau.
 
d) Calculer la masse de fer nécessaire pour traiter une tonne de cette eau résiduelle.
 
On donne : $Hg=200\,g\cdot mol^{-1}\ ;\ Fe=56\,g\cdot mol^{-1}.$
 
Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Amplificateur opérationnel - 2nd S

Classe: 
Seconde
 

Exercice 1

 
 
$R_{1}=1\;k\Omega\;,\ R_{2}=12\;k\Omega$

 
 
Calibre : $v_{1}\ :\ 0.2\;V/div\;;\quad v_{2}\ :\ 2\;V/div$
Balayage : $0.5\;ms/div$
 
1) Déterminer $V_{1}\;,\ V_{2}$ et l'amplification du montage $A=\dfrac{V_{2}}{V_{1}}$
 
Comment appelle-t-on ce montage ?
 
2) L'amplificateur Opérationnel fonctionne en régime linéaire .
 
Pourquoi ? Que peut on dire de $v_{d}$ (ou $\varepsilon$) ?
 
3) Que dire des courants $i_{_{R_{1}}}\ $ et $\ i_{_{R_{2}}}.$ Justifier.
 
4) Écrire les lois des mailles d'entrée et de sortie. En déduire $A=\dfrac{V_{2}}{V_{1}}$ en fonction de $R_{1}\ $ et $\ R_{2}.$
 
5) $v_{\text{sat}}=\pm 12\;V.$ Calculer $v_{1_{\text{max}}}$ pour éviter la saturation. 
 
Tracer $v_{2}(t)$ ci-dessous (l'amplitude de $v_{1}$ est maintenant réglée à $1.5\;V).$

 
 
Calibre : $v_{1}\ :\ 0.5\;V/div\;;\quad v_{2}\ :\ 5\;V/div$
Balayage : $0.5\;ms/div$
 

Exercice 2

 

 
On considère le montage ci-dessus pour lequel l'amplificateur opérationnel $(A.O.)$ est supposé idéal.
 
La tension de saturation de l'$A.O.$ est $V_{\text{sat}}=15\;V.$
 
On donne les résistances : $R_{1}=2.2\;k\Omega\;,\ R_{2}=4.7\;k\Omega$
 
La tension d'entrée est $U_{e}=U_{_{AM}}=1.5\;V.$
 
1) Préciser ce qui définit un $A.O.$ idéal.
 
2.1) Montrer qu'avec ce montage un même courant traverse $R_{1}\ $ et $\ R_{2}.$
 
2.2) Établir que, dans les conditions considérées, la tension de sortie $U_{s}=U_{_{SM}}$ est donnée par : $U_{s}=-\dfrac{R_{2}}{R_{1}}U_{e}$
 
2.3) Justifier le nom de montage amplificateur inverseur donné à ce montage.
 
2.4) Calculer la tension de sortie.
 
3) Entre $A\ $ et $\ M$, à l'entrée du montage précédent, on remplace la pile par un générateur de tension réglable. 
 
Compléter le tableau ci-dessous en précisant, pour chaque valeur de la tension d'entrée $U_{e}$ la valeur correspondante de la tension de sortie $U_{s}.$
 
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|}\hline U_{e}(V)&-10&-8.0&-4.0&-2.0&0.0&2.0&4.0&8.0&10\\ \hline U_{s}(V)&&&&&&&&&\\ \hline\end{array}$$
 

Exercice 3

Le montage étudié dans cette partie est représenté sur la figure 1. 
 
L'amplificateur opérationnel $AO_{1}$ utilisé est considéré comme parfait.
 
La caractéristique $V_{s}=f(V_{e})$ du montage est représentée sur la figure 2.
 
La résistance $R_{1}$ est ajustable et $R_{2}=10\;k\Omega.$

 

 

 
1) Montrer qu'en régime linéaire l'amplification du montage peut s'exprimer sous la forme :
$$A=\dfrac{V_{s}}{V_{e}}=-\dfrac{R_{2}}{R_{1}}$$
 
2) En utilisant le résultat précédent et la caractéristique de la figure 2, déterminer la valeur donnée à la résistance $R_{1}.$
 
3) On applique à l'entrée du montage une tension sinusoïdale de valeur efficace $V_{_{E}}=2.0\;V.$ 
 
Un voltmètre est utilisé en en position $AC$ conformément à la figure 3. Quelle est l'indication de cet appareil

 
 

Exercice 4

On réalise avec le même montage deux séries de mesures :

 

 
$\centerdot\ $ première série : le voltmètre $n^{\circ}1$ indique $2.3\;V$ et le voltmètre $n^{\circ}2$ affiche $9.2\;V$ ;
 
$\centerdot\ $ deuxième série : le voltmètre $n^{\circ}1$ indique$4.1\;V$ et le voltmètre $n^{\circ}2$ affiche $13.6\;V$
 
1) Comment s'appelle la tension mesurée par le voltmètre $n^{\circ}1\ ?$
 
2) Comment s'appelle la tension mesurée par le voltmètre $n^{\circ}2\ ?$
 
3) Quel est le coefficient d'amplification du montage ?
 
Justifiez le choix de la série de mesures que vous utilisez pour cette détermination.
 
4) Quelle est la tension de saturation du montage ?
 

Exercice 5

 
 
$R_{1}=10\;k\Omega\;;\quad R_{2}=33\;k\Omega$
 
Pour ce montage, le coefficient d'amplification vaut : $A=-\dfrac{R_{2}}{R_{1}}$ et la tension de saturation $\pm 14\;V$
 
1) On appelle $U_{e}$ la tension d'entrée du montage et $U_{s}$, la tension de sortie.
 
Reporter sur le montage les flèches tension $U_{e}\ $ et $\ U_{s}.$
 
2) Calculer $A.$
 
Lorsque le montage amplificateur fonctionne en régime linéaire, écrire la relation qui existe entre la tension de sortie $U_{s}$ et la tension d'entrée $U_{e}.$
 
3) Compléter le tableau de valeurs :
 
$$\begin{array}{|l|c|c|c|c|c|c|c|}\hline U_{e}(V)&-6&-4&-2&0&1&3&5\\ \hline U_{s}(V)&&&&&&&\\ \hline\end{array}$$
 
4) Construire le graphique de la fonction $U_{s}=f(U_{e})$ ;
 
5) A partir de cette courbe, préciser :
 
$-\ \ $ les valeurs de $U_{e}$ pour lesquelles le régime de fonctionnement est appelé linéaire.
 
$-\ \ $ les valeurs de $U_{e}$ pour lesquelles le régime de fonctionnement est dit saturé
 

Exercice 6

On réalise le montage suivant et on observe les deux oscillogrammes ci-dessous :

 

 
Déterminer :
 
1) la tension de saturation :
 
2) le coefficient d'amplification du montage.
 
Sur le montage, le symbole « masse » figure à la fois la masse du circuit et celle des deux voies de l'oscilloscope.
 
Les réglages initiaux de l'oscilloscope, pour chaque voie, sont tels que la ligne médiane horizontale corresponde à une tension nulle.

 

 
 

Exercice 7


 

 
1) Rappeler les caractéristiques d'un $A.O.$ idéal.
 
2) Quelle relation simple existe-t-il entre la tension $U_{e}$ et la tension $U_{s}\ ?$
 

Exercice 8

A l'aide d'un amplificateur opérationnel alimenté par un générateur $(e_{1}\;,\ 0\;,\ -e_{2})$, nous avons réalisé le montage de la figure ci-dessous

 

 
1) En supposant l'$A.O.$ idéal $(I^{+}=I^{-}=0\;;\ V_{_{E^{+}}}-V_{_{E^{-}}}=0$ montrer que :
$$\dfrac{U_{s}}{e}=\dfrac{R_{1}+R_{2}}{R_{1}}$$
 
Application numérique : $R_{1}=10\;k\Omega\;;\quad R_{2}=100\;k\Omega$
 
2) Avec un $A.O.\ 741$, on a relevé les mesures suivantes :
 
$I_{e}=0.004\;\mu A\;;\ e=0.48\;V\;;\ U_{s}=5.4\;V$
 
$R_{c}=2000\Omega\;;\ e_{1}=15.13\;V\;;\ I_{1}=4.23\;mA\;;\ e_{2}=15.10\;V\;;\ I_{2}=1.50\;mA$
 
Calculer le rapport expérimental $\dfrac{U_{s}}{e}.$
 
Conclure.
 

Exercice 9

Pour le montage de la figure ci-dessous, on donne : 
 
$R_{1}=10\;k\Omega\;;\ R_{2}=4.7\;k\Omega\ $ et $\ R_{3}=2.2\;k\Omega$
 
De plus, la mesure de $i_{c}$ a donné : $i_{c}=2.5\;mA$

 

 
1) l'ampli op fonctionne-t-il en régime linéaire ou saturé ?
 
Justifier.
 
2) calculer l'intensité $i_{e}$ du courant dans la résistance $R_{2}.$
 
3) calculer la tension d'entrée $u_{e}.$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Dipôles actifs - 2nd S

Classe: 
Seconde
 

Exercice 1

Afin de tracer la caractéristique d'un générateur, on relève les mesures suivantes :
 
$$\begin{array}{|l|c|c|c|c|c|c|}\hline U_{_{PN}}(V)&8&7.8&7.6&7.4&7.0&6.7\\ \hline I(A)&0&0.10&0.20&0.30&0.50&0.60\\ \hline\end{array}$$
 
1) Tracer la caractéristique courant-tension de ce générateur
 
2) Déterminer sa f.é.m et sa résistance interne
 
3) Écrire l'équation de cette caractéristique
 
4) Déterminer de manières différentes la tension aux du générateur lorsqu'il débite un courant d'intensité $0.35\;A$
 

Exercice 2

Un circuit est formé d'une pile, un rhéostat, d'un interrupteur $K$ et d'un ampèremètre en série
 
On relie la borne positive de la pile à l'entrée $Y$ d'un oscillographe et la borne négative à la masse $M$
 
On utilise un balayage sur la sensibilité $k=0.5\;V/cm$
 
1) $K$ étant ouvert, l'ordonnée du segment lumineux est $y_{1}=2\;cm$ 
 
$K$ étant fermé, l'ordonnée de ce segment est $y_{2}=1\;cm$
 
Calculer la f.é.m $E$ et la résistance interne $r$ de la pile sachant l'ampèremètre indique $400\;mA$
 
2) On déplace le curseur du rhéostat, l'ordonnée du segment lumineux vaut $y_{3}=9\;mm.$ Quelle est l'indication de l'ampèremètre
 

Exercice 3

Sur le graphe ci-dessous nous avons tracé avec la même échelle les caractéristiques Intensité - tension de deux dipôles $D_{1}\ $ et $\ D_{2}.$

 

 
1) Indiquer la courbe qui correspond au dipôle résistor et celle au dipôle générateur.
 
2.a) Rappeler pour chaque dipôle la loi d’Ohm correspondante. (On notera la tension aux bornes du générateur $U_{_{PN}}\ $ et $\ U_{_{AB}}$ celle aux bornes du résistor)
 
b) Donner le schéma du circuit permettant de tracer la caractéristique Intensité - tension du générateur.
 
c) Déterminer, à partir du graphe, et en justifiant la réponse, les valeurs de la f.é.m. $E$ et de la résistance interne $r$ du générateur et la résistance R du résistor.
 
3) Calculer l'intensité du courant de court-circuit $I_{cc}$ du générateur
 
4) On réalise un circuit en branchant ce générateur aux bornes de ce résistor de résistance $R.$
 
a) Représenter le schéma du circuit.
 
b) Montrer que l'intensité du courant dans le circuit est donnée par $I=\dfrac{E}{r+R}$
 
c) Montrer que $I=\dfrac{10}{6}=1.66\;A$
 

Exercice 4

On associe en série une pile, un rhéostat et une résistance de protection dans le but d'établir la caractéristique de la pile.
 
$$\begin{array}{|l|c|c|c|c|c|c|c|c|}\hline U_{_{PN}}(V)&9.00&8.89&8.78&8.66&8.56&8.35&8.12&8.02\\ \hline I(A)&0&0.1&0.2&0.3&0.4&0.6&0.8&0.9\\ \hline\end{array}$$
 
1) Rappeler la définition de la caractéristique d'un dipôle. Donner les appareils de mesure nécessaire.
 
2) Faire le schéma du montage en précisant le sens conventionnel du courant électrique, en plaçant les appareils de mesure avec leurs bornes de branchement. 
 
On représentera également la tension positive aux bornes de la pile.
 
3) Tracer $U_{_{PN}}=f(I)$ avec l'échelle suivante : $2\;cm$ pour $0.1\;A$ en abscisse $1\;cm$ pour $0.2\;V$ en ordonnée
 
4) Déduire du graphe la force électromotrice $E$ et la résistance interne de la pile en précisant la méthode employée et es unités.
 
5) On relie un générateur linéaire de f.é.m. $E=9.0\;V$ et de résistance interne $r=1.2\Omega$ à une portion de circuit comportant un conducteur ohmique de résistance $R=20\Omega$ associés en série.
 
Déterminer l'intensité du courant électrique circulant dans le circuit
 

Exercice 5

Deux piles sont montées en série 
 
$P_{1}N_{1}$ de paramètres $E_{1}=4.5\;V\;;\ r_{1}=1.5\Omega\;;\ I_{\text{max}}=0.5\;A$
 
$P_{2}N_{2}$ de paramètres $E_{2}=4.5\;V\;;\ r_{2}=1.5\Omega\;;\ I_{\text{max}}=0.6\;A$
 
1) Tracer la caractéristique de chacune de deux piles
 
Échelle : $1\;cm$ pour $0.1\;A$ et $1\;cm$ pour $1\;V$
 
2) Tracer la caractéristique du dipôle équivalent à la série
 
3) Déterminer la f.é.m et la résistance interne de ce dipôle :
 
$-\ \ $ graphiquement
 
$-\ \ $ par calcul
 

Exercice 6

Une batterie de voiture est constituée de six accumulateurs au plomb de f.é.m $2\;V$ et de résistance $0.001\Omega$, montés en série
 
1) Quelle est la f.é.m $E$ de la batterie ?
 
Quelle est sa résistance interne $r\ ?$
 
2) Si par méprise on pose sur les deux bornes de cette batterie une clé métallique $(R=0)$, quelle est l'intensité du courant qui est débité par la batterie ? Conclure.
 

Exercice 7

Afin de tracer la caractéristique d'un pile, on effectue les mesures suivantes :
 
$$\begin{array}{|l|c|c|c|c|}\hline U_{_{PN}}(V)&4.5&4.4&4.3&4.2\\ \hline I(mA)&0&100&200&300\\ \hline\end{array}$$
 
L'intensité maximale admissible par la pile est $I_{\text{max}}=0.8\;A$
 
Cette pile alimente un résistor de résistance $R=5\Omega$ caractérisé par une intensité maximale de $1\;A$
 
1) Tracer sur le même graphe la caractéristique courant-tension de la pile et celle du résistor
 
Échelle : $1\;cm$ pour $100\;mA\ $ et $\ 1.5\;cm$ pour $1\;V$
 
2) Déterminer la f.é.m de la pile et sa résistance interne
 
3) Définir le point de fonctionnement.
 
4) Calculer l'intensité qui traverse le circuit et la tension aux bornes des dipôles
 

Exercice 8

On réalise le montage suivant :

 

 
1) Le voltmètre indique $6\;V$, calculer l'intensité du courant débité par la pile sachant que $R_{1}=2\Omega\ $ et $\ R_{2}=4\Omega$
 
2) En déduire $U_{_{AM}}\ $ et $\ U_{_{BM}}$
 
3) On relie $A$ à l'entrée $Y$ d'un oscillographe et $M$ à la masse, le balayage est supprimé et la sensibilité vaut $k=2\;V/cm.$ Que voit-on sur l'écran ?
 
4) On relie $B$ à l'entrée $Y$ d'un oscillographe et $M$ à la masse, le balayage est supprimé et la sensibilité vaut $k=2\;V/cm.$ Que voit-on sur l'écran ?
 
5) On ouvre l'interrupteur $K$, le voltmètre indique $9\;V$
 
Quelles sont la f.é.m et la résistance interne de la pile ?
 

Exercice 9

On réalise le montage suivant :

 

 
Les deux générateurs sont identiques et ont pour f.é.m $4.5\;V$ et pour résistance interne $1\Omega.$ Les conducteurs ohmiques ont pour résistances $R_{1}=500\Omega\ $ et $\ R_{2}=200\Omega$
 
1) Quelles sont la f.é.m. et la résistance interne du générateur équivalent aux deux générateurs ?
 
2) Quelle est la résistance équivalente aux deux résistors $R_{1}\ $ et $\ R_{2}\ ?$
 
3) En déduire l'intensité du courant débité par les deux piles et la valeur $U_{_{PN}}$
 
4) Quelles sont les intensités des courants dans les deux conducteurs ohmiques ?
 

Exercice 10

On se propose de tracer la caractéristique d'un dipôle actif (voir fig. ci dessous).

 

 
Les mesures réalisées sont les suivantes :
 
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|}\hline U_{_{PN}}(V)&2.0&1.9&1.8&1.6&1.5&1.3&1.3&1.1&1.0\\ \hline I(mA)&0&100&200&300&500&700&800&900&1000\\ \hline\end{array}$$
 
1) Proposer un schéma du circuit ayant permis ce relevé de mesure.
 
2) Tracer la caractéristique U en fonction de I du dipôle. Il sera tenu compte du soin apporté à la réalisation de cette courbe et des éléments attenant à l'élaboration de toute caractéristique.
 
On obtient une caractéristique quasi linéaire. (vous prendrez la meilleure des droites)
 
3) Quel est l'élément du graphique qui permet de vérifier qu'il s'agit bien d'un dipôle actif?
 
4) Comment expérimentalement mesure-t-on une tension à vide ?
 
5) Déterminer, en prenant garde de bien respecter les unités, la force électromotrice et la résistance interne du dit dipôle.
 
6) Comment expérimentalement mesure-t-on la résistance interne d'un dipôle actif?
 

Exercice 11

La tension mesurée aux bornes d'un générateur à vide est $E_{0}=36\;V.$ Lorsqu'il débite dans une charge un courant d'intensité $I=5\;A$, la tension baisse et devient $U=35\;V$
 
On suppose que le fonctionnement du dipôle actif est linéaire entre ces deux points.
 
1) Donner la relation liant $U\;,\ E_{0}\;,\ I$ et la résistance interne $R_{i}.$
 
2) Calculer la résistance interne $R_{i}$ du générateur.
 
On branche aux bornes du générateur une résistance $R.$ Elle est traversée par un courant $I=10\;A.$
 
Faire le schéma de montage.
 
3) Calculer la tension $U$ aux bornes de $R.$
 
4) En déduire la valeur de $R.$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Phénomènes d'électrisation - 2nd S

Classe: 
Seconde
 

Exercice 1

Questions de cours :
 
$\ast\ $ Qu'est ce qu'un corps électrisé ?
 
$\ast\ $ Quels sont les différents modes d'électrisation ?
 
$\ast\ $ Est-ce que tous les corps électrisés sont chargés d'un même signe ? Justifier la réponse.
 
$\ast\ $ Comment peut-on expliquer l'apparition des charges électriques positives sur le verre frotté avec un drap sec ?
 
$\ast\ $ Qu'est ce qu'une décharge électrique ?
 
$\ast\ $ Quelle est la valeur de la charge électrique élémentaire ?
 

Exercice 2

Compléter les phrases suivantes :
 
a) Un corps est dit neutre s'il contient$\ldots\ldots$ de charges $\ldots\ldots$ que de charges $\ldots\ldots$
 
b) On approche un bâton d'ébonite frotté à un bâton de verre frotté, on observe une $\ldots\ldots$c à dire les deux bâtons sont $\ldots\ldots$
 
c) Un bâton en p.v.c frotté porte une charge $\ldots\ldots$ c'est-à-dire il à un $\ldots\ldots$ d'électrons.
 
d) Un corps chargé négativement présente un excès $\ldots\ldots$, entre ce corps et un autre corps de charge opposé il y a $\ldots\ldots.$
 
e) Entre deux corps électrisés se manifestent des actions mutuelles appelées $\ldots\ldots$ ; $\ldots\ldots$ et $\ldots\ldots.$
 
f) Au bout d'une pointe les charges d'un corps électrisé $\ldots\ldots$ très fortement
 

Exercice 3

Compléter le tableau suivant :
 
$$\begin{array}{|l|c|c|c|}\hline&\text{Règle en plexiglas}&\text{Règle en ébonite}&\text{Règle en verre}\\ \hline\text{Règle en plexiglas}&&&\\ \hline\text{Règle en ébonite}&&&\\ \hline\text{Règle en verre}&&&\\ \hline\end{array}$$
 

Exercice 4

Répondre par vrai ou faux sur les propositions suivantes et corriger les fausses d’elles.
 
1) La neutralité électrique de la matière dans son état normal veut dire qu'elle ne renferme aucune charge électrique.
 
2) L'électrisation positive d'un corps résulte du fait qu'il a gagné des charges positives prises au corps avec lequel il a interagi pour s'électriser.
 
3) Un corps électrisé ne peut attirer, par interaction électrique, que d'autres corps électrisés et portant des charges de nature différente de celle qu'il porte lui-même.
 
4) Un corps électrisé ne peut repousser, par interaction électrique, que les corps électrisés et portant des charges électriques de même nature que sa propre charge.
 
5) Pour électriser un corps il est nécessaire de le frotter par un autre corps.
 

Exercice 5

On réalise l'expérience suivante:
 
$C$ est un crayon à papier, dont on a taillé les deux bouts, la mine dépasse à chaque extrémité. $V$ est du verre isolant. On touche l'extrémité $A$ avec un bâton chargé négativement : la boule du pendule s'écarte.

 

 
Pour chaque phrase ci-dessous choisir la bonne expression. (Choix à justifier.)
 
1) La mine est isolante / conductrice.
 
2) Des électrons sont passés de la mine sur le bâton / du bâton sur la mine.
 
3) Des électrons sont passés de la mine sur la boule / de la boule sur la mine.
 
4) La boule s'est chargée négativement / positivement.
 

Exercice 6 

Compléter les phrases suivantes avec ces mots ( deux ; positives, charges ; influence ; trois ; quatre ; négatives ; repousser ; même signe ; contacte ; attirer ; frottement, électrisation ; décharge ; signe contraire)
 
Le peigne, par frottement, à acquis la propriété d'$\ldots\ldots$ les cheveux. Il a subit une $\ldots\ldots.$
 
Il existe $\ldots\ldots$ sortes de $\ldots\ldots$ électriques : $\ldots\ldots$ et $\ldots\ldots.$
 
Des charges électriques de $\ldots\ldots$  s'attirent alors que des charges électriques de $\ldots\ldots$ se repoussent.
 
Il existe $\ldots\ldots$ modes d'électrisation par $\ldots\ldots$ par $\ldots\ldots$ et par $\ldots\ldots$
 

Exercice 7

Quatre tiges $A\;,\ B\;,\ C\ $ et $\ D$ sont électrisées par frottement.
 
$A$ repousse $B$ qui attire $C.\ C$ est une tige en verre qui repousse $D.$
 
1) Quel est le signe des charges électriques apparues sur $A\;,\ B\ $ et $\ D\ ?$
 
2) Quelle interaction existe-t-il entre $A\ $ et $\ C\ ?$ Entre $A\ $ et $\ D\ ?$ Entre $B\ $ et $\ D\ ?$
 

Exercice 8

On dispose d'une petite sphère $A$ recouverte de papier d'aluminium sur laquelle on dépose une charge $q_{_{A}}=10^{-8}\;C.$
 
On approche un corps $B$ portant une charge de valeur absolue $|q_{_{B}}|=10^{-7}\;C$ dont on ne connaît pas le signe. On observe une attraction.

 

 
1) Expliquer pourquoi la sphère $A$ réagit de cette façon ? donner le signe de la charge
 
2) Expliquer comment peut-on déchargé la sphère
 
3) La sphère étant déchargée on rapproche d'elle de nouveau le corps $B.$ Schématiser et expliquer
 

Exercice 9

Quatre tiges $A\;,\ B\;,\ C\ $ et $\ D$ sont électrisées par frottement.
 
$A$ attire $B$ qui repousse $C.\ C$ est une tige en plexiglas qui attire $D.$
 
1) Quel est le signe des charges électriques apparues sur $A\;,\ B\ $ et $\ D\ ?$

 

 
2) Quelle interaction existe-t-il entre :
$$\begin{array}{|l|l|}\hline&\text{Interaction}\\ \hline A\ \boxminus\text{ et }C\ \blacksquare&\\ \hline A\ \boxminus\text{ et }D\ \boxplus&\\ \hline B\ \square\text{ et }D\ \boxplus&\\ \hline\end{array}$$
 

Exercice 10

Dans un orage, un éclair accompagne un transfert de charges entre la terre et un nuage.
 
On suppose que la décharge transfère une charge électrique de 20 coulombs pendant 1 millième de seconde.

 

 
1) Déterminer l'intensité moyenne du courant électrique accompagnant le transfert.
 
2) Quel est le rôle du paratonnerre ?
 
3) La charge totale du nuage étant $-320\;C$, calculer l'excès d'électrons accumulés dans le nuage
 

Exercice 11

On charge séparément par frottement :
 
$-\ \ $ Une règle de verre qui porte alors la charge $q_{1}=2\;10^{-13}\;C$ ;
 
$-\ \ $ Une règle en plastique qui porte alors la charge $q_{2}=-9\;10^{-12}\;C.$
 
On réalise le contact entre les zones électrisées des deux règles.
 
1) Calculer la charge électrique de l'ensemble des deux règles
 
2) En déduire la charge électrique portée par chaque règle après le contacte.
 
3) préciser le sens dans le quel s'est fait le transfert des électrons
 

Exercice 12

Un corps A est électrisé par contact à l'aide d'un bâton de verre initialement frotté sur un drap. La charge portée par le corps $A$ est $q_{_{A}}=12.8\;10^{-9}\;C.$
 
1) Dire si le corps $A$ possède un excès ou un défaut d'électrons.
 
2) Préciser le sens du transfert des électrons entre le verre et le corps $A.$
 
3) Calculer le nombre d'électrons transféré. On donne $e=1.6\;10^{-19}\;C.$
 

Exercice 13

1) Un corps $A$ est chargé positivement. On l'approche d'un autre corps $B$ chargé, il y a attraction. Quel est le signe de la charge du corps $B$ ? Justifier la réponse.
 
2) Le corps $A$ est maintenant mis en contact avec un corps $C$ électriquement neutre.
 
a) Le corps $C$ devient-il chargé ? Si oui que serait le signe de sa charge ?
 
b) Qu'appelle-t-on ce mode d'électrisation ?
 
c) Y a-t-il échange d'électrons ? Si oui, dans quel sens (de $A$ vers $C$ ou de $C$ vers $A)\  ?$
 

Exercice 14

Un bâton d'ébonite frotté par la fourrure acquiert une charge $q=-4.8\;10^{-19}\;C.$
 
1) Donner la définition de l'électrisation.
 
2) Le bâton d'ébonite a-t-il gagné ou perdu des électrons ?
 
3) Déterminer le nombre d'électrons gagnés ou perdus par le bâton d'ébonite ?
 
4) En déduire le nombre d'électrons gagnés ou perdus par la fourrure
 

Exercice 15

On approche du plateau neutre d'un électroscope une baguette d'ébonite préalablement chargée négativement par un chiffon. On observe alors que la feuille métallique se décolle du tronc.

 

 
1) Expliquer de manière concise cette observation.
 
2) Que se passe-t-il ensuite si l'on éloigne la baguette d'ébonite?
 
3) On approche à nouveau la baguette d'ébonite chargée jusqu'à ce qu'elle touche le plateau puis on l'éloigne.
 
Qu'observe-t-on alors ? Pourquoi ?
 
4) On approche alors du plateau (sans le toucher) le chiffon qui a permis de charger la baguette.
 
Qu'observe-t-on ?
 
5) Pourquoi la feuille métallique doit-elle être légère ?
 
6) Quel est le rôle du joint en plastique qui entoure le haut du tronc ?
 

Exercice 16

1) Un bâton $(A)$ initialement neutre, est électrisé par frottement à l'aide d'un chiffon .Sa charge électrique devient $q_{_{A}}=48\;10^{-18}\;C$
 
1.1) Le bâton $(A)$ a-t-il gagné ou perdu des électrons à la suite de l'électrisation ? Justifier
 
1.2) Déterminer le nombre d'électrons gagnés ou perdus par $(A)$
 
2) Un deuxième bâton $(B)$ porte une charge $q_{_{B}}=3.2\;10^{-18}\;C.$ On met en contact l'extrémité chargée de $(A)$ avec l'extrémité chargée de $(B)$
 
2.1) Interpréter le phénomène qui se produit entre les deux bâtons après ce contact
 
2.2) Préciser, en le justifiant, le sens de transfert des électrons
 
2.3. Déterminer la charge de chaque bâton après contact
 

Exercice 17

On frotte l'une des extrémités d'un bâton d'ébonite avec de la fourrure. Cette extrémité frottée devient électrisée et porte une charge $Q=-1.6\;10^{-9}\;C$
 
1) Citer une expérience qui montre que l'extrémité frottée est électrisée
 
2.1) Montrer que le bâton d'ébonite possède un excès d'électrons
 
2.2) Calculer le nombre $n$ d'électrons en excès portés par le bâton d'ébonite
 
On donne : la charge d'un électron $-e=-1.6\;10^{-19}\;C$
 
2.3) D'où proviennent les électrons en excès portés par l'ébonite ?
 
2.4) Donner la valeur de la charge portée par la fourrure
 
3) On rapproche l'extrémité frottée du bâton d'ébonite du plateau d'un électroscope neutre. On observe une déviation de l'aiguille de l'électroscope. Il est donc électrisé
 
3.1) Dire l'électroscope est électrisé par contact ou par influence
 
3.2) Expliquer en s'aidant d'un schéma l'électrisation de l'électroscope. Indiquer sur ce schéma les signes des électricités portées par l'électroscope
 
3.3) A quoi est dû la déviation de l'aiguille de l'électroscope ?
 
4) On met l'extrémité frottée en contact avec le plateau de l'électroscope qui devient électrisé par contact
 
4.1) Quel est le signe de l'électricité portée par l'électroscope ?
 
4.2) Faire un schéma de l'électroscope électrisé
 

Exercice 18

Par contact avec un bâton $P.V.C$ frotté avec une peau de chat, un pendule électrostatique acquiert une charge égale en valeur absolue $10^{-8}\;C.$
 
a) Quel est le signe de la charge du pendule ?
 
b) Au cours du contact, y a-t-il transfert d'électrons du (pendule vers $P.V.C)$ ou du $( P.V.C$ vers pendule) ?
 
c) Trouver le nombre d'électrons transférés
 

Exercice 19

On frotte un bâton d'ébonite avec un drap sec.
 
1) Expliquer l'apparition des charges négatives sur le bâton.
 
2) La charge du bâton est $-64\;10^{-15}\;C$, combien de charges électriques élémentaires négatives porte-t-elle ?
 
On donne la valeur absolue de la charge élémentaire $e=1.6\;10^{-19}\;C$
 
3.a) Montrer que le drap utilisé s'est électrisé ?
 
b) Quelle est la nature de sa charge ?
 
c) Comment peut-on le prouver expérimentalement ?
 
d) donner la valeur de sa charge ?
 

Exercice 20

1) Un bâton de verre frotté avec du nylon perd 100 électrons.
 
Calculer La valeur de sa charge q en coulomb ; on donne $e=1.6\;10^{-19}\;C.$
 
2.a) Une bille initialement neutre est mise en contact avec le bâton de verre, s'électrise.
 
Indiquer le signe de sa charge.
 
b) Indiquer les modes d'électrisation de la bille et du bâton.
 
c) Après le contact, le nombre d'électrons perdu par la bille est $n=35$ électrons. Calculer en coulomb la valeur de la charge de la bille $q'$
 
d) Déduire en le justifiant la valeur en coulomb de la nouvelle charge $q''$ du bâton après le contact
 
3) Comment décharger les deux corps, bâton de verre et bille.
 

Exercice 21

1) Une tige en $P.V.C$ est frottée avec un chiffon de laine. Elle est alors chargée négativement.
 
Que se passe t-il si on l'approche d'un pendule constitué d'une boule légère ?
 
2) La tige possède t-elle un excès d'électrons ou un défaut ? D'où proviennent ces charges ?
 
3) Expliquer à l'aide d'un schéma et de quelques lignes le phénomène que l'on observe. (Il y a 2 arguments essentiels à donner).
 
4) Si nous avions procédé de la même manière avec une tige en cuivre à la place de la tige en plastique, aurait-on pu observer le même phénomène ? Pourquoi ?
 
5) La tige en $P.V.C$ est remplacée par une autre en plexiglas, après frottement avec la laine, elle est approchée de la boule initialement non électrisée, On constate qu'il y a attraction, puis une répulsion tout juste après que la boule se mette en contact avec la tige en plexiglas électrisé.
 
a) Préciser le signe de la charge portée par la tige en plexiglas électrisé par frottement avec de la laine
 
b) Préciser le signe de la charge de la boule du pendule électrostatique juste après le contact avec la tige en plexiglas électrisé.
 
c) Comment expliquer avant contact, l'interaction attractive entre la boule initialement non électrisée et la tige en plexiglas électrisé ?

 

 

Exercice 22

On approche de la boule métallique $(B)$ d'un électroscope (sans la toucher) ; un bâton en ébonite $(E)$ préalablement frottée avec un tissu en laine, nous constatons que les feuilles (très minces et légères d'aluminium) de l'électroscope se repoussent. Voir figure.
 
1) Expliquer la répulsion des feuilles d'aluminium.
 
2) Les feuilles d'aluminium ont-elles subie une électrisation par contact ou par frottement ? Sinon donner un nom à ce mode d'électrisation

 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

 
Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Dosage acide - base - Ts

Classe: 
Terminale
 

Exercice 1

1) Bilan de matière des ions hydronium et hydroxyde :
$$\begin{array}{|c|ccccccc|} \hline \text{Etat du système}&H_{3}O^{+}&\ &+\ OH^{-}&\ &\rightarrow&\ &2H_{2}O\\ \hline \text{Avancement}& &|&nH_{3}O^{+}&|&n_{OH^{-}}&|&n_{H_{2}O}\\ \hline \text{Etat initial}& &|&n_{A}&|&n_{B}&|&\text{Excès}\\ \hline \text{Etat intermédiaire}&x&|&n_{A}-x&|&n_{B}-x&|&\text{Excès}\\ \hline \text{Etat final}&x_{max}&|&n_{A}-x_{max}&|&n_{B}-x_{max}&|&\text{Excès}\\ \hline \end{array}$$
 
$\begin{array}{lcl} n_{B}-x_{max}&=&0\\&\Rightarrow&x_{max}=n_{B} \end{array}$
 
$\begin{array}{lcl} n_{A}-x_{max}&=&0\\&\Rightarrow&x_{max}=n_{A}\\&\Rightarrow& n_{B}=n_{A} \end{array}$
 
2) Calcul de la concentration molaire de la solution après neutralisation :
 
$\bullet\ \ $ $V_{A}=200\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.0.$
 
$\begin{array}{lcl} n_{A}&=&C_{A}V_{A}\\&=&10^{-pH_{A}}V_{A}\\&=&10^{-2}\times200\cdot10^{-3}\\&=&2.0\cdot10^{-3}mol \end{array}$
 
$\begin{array}{lcl} n_{B}&=&C_{B}V_{B}\\&=&10^{-pH_{B}}V_{B}\text{ avec }C_{B}\\&=&\left[OH^{-}\right]\\&=&\dfrac{K_{e}}{10^{-pH_{B}}}\\&=&10^{14+pH_{B}}\\&\Rightarrow&n_{B}=10^{-14+pH_{B}}V_{B}\\&=&10^{-14+12.0}\times200\cdot10^{-3}\\&=&2.0\cdot10^{-3}mol\\&\Rightarrow&\dfrac{n_{A}}{1}=\dfrac{n_{B}}{1} \end{array}$
 
La réaction est totale.
 
La solution est neutre et $pH=7$
 
$\bullet\ \ $ $V_{A}=800\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=500\,mL\;,\ pH_{B}=12.0.$
 
$\begin{array}{lcl} n_{A}&=&C_{A}V_{A}\\&=&10^{-pH_{A}}V_{A}\\&=&10^{-2}\times800\cdot10^{-3}\\&=&8.0\cdot10^{-3}mol \end{array}$
 
$\begin{array}{lcl} n_{B}&=&10^{-14+pH_{B}}V_{B}\\&=&10^{-14+12.0}\times500\cdot10^{-3}\\&=&5.0\cdot10^{-3}mol \end{array}$
 
$\dfrac{n_{A}}{1}>\dfrac{n_{B}}{1}$, l'acide $HCl$ est en excès, la base $NaOH$ est le réactif limitant
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&\dfrac{C_{A}V_{A}-C_{B}V_{B}}{V_{A}+V_{B}}\\&\Rightarrow&pH=-\log\dfrac{C_{A}V_{A}-C_{B}V_{B}}{V_{A}V_{B}}\\&=&-\log\dfrac{8.0\cdot10^{-3}-5.0\cdot10^{-3}}{800\cdot10^{-3}+500\cdot10^{-3}}\\&\Rightarrow&pH=2.6 \end{array}$
 
$\bullet\ \ $ $V_{A}=300\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.3.$
 
$\begin{array}{lcl} n_{A}&=&C_{A}V_{A}\\&=&10^{-pH_{A}}V_{A}\\&=&10^{-2}\times300\cdot10^{-3}\\&=&3.0\cdot10^{-3}mol \end{array}$
 
$\begin{array}{lcl} n_{B}&=&C_{B}V_{B}\\&=&10^{-14+pH_{B}}V_{B}\\&=&10^{-14+12.3}\times200\cdot10^{-3}\\&=&6.0\cdot10^{-3}mol \end{array}$
 
$\dfrac{n_{B}}{1}>\dfrac{n_{A}}{1}$, la base $NaOH$ est en excès, l'acide est le réactif limitant
 
$\begin{array}{lcl} \left[OH^{-}\right]&=&\dfrac{C_{B}V_{B}-C_{A}V_{A}}{V_{A}+V_{B}}\\&\Rightarrow&pH=14+\log\dfrac{C_{B}V_{B}-C_{A}V_{A}}{V_{A}V_{B}}\\&=&14+\log\dfrac{6.0\cdot10^{-3}-3.0\cdot10^{-3}}{300\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&pH=11.3 \end{array}$
 
3) Calcule de la concentration molaire des ions sodium et des ions chorure en solution dans trois cas.
 
$\bullet\ \ $ $V_{A}=200\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.0.$
 
$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-pH_{A}}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times200\cdot10^{-3}}{200\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Cl^{-}\right]=5.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$
 
$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+pH_{B}}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+12}\times200\cdot10^{-3}}{200\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Na^{+}\right]=5.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$
 
$\bullet\ \ $ $V_{A}=800\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=500\,mL\;,\ pH_{B}=12.0.$
 
$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-pH_{A}}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times800\cdot10^{-3}}{800\cdot10^{-3}+500\cdot10^{-3}}\\&\Rightarrow&\left[Cl^{-}\right]=6.2\cdot10^{-3}mol\cdot L^{-1} \end{array}$
 
$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+pH_{B}}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+12}\times500\cdot10^{-3}}{800\cdot10^{-3}+500\cdot10^{-3}}\\&\Rightarrow&\left[Na^{+}\right]=3.8\cdot10^{-3}mol\cdot L^{-1} \end{array}$
 
$\bullet\ \ $ $V_{A}=300\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.3.$
 
$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-pH_{A}}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2.0}\times300\cdot10^{-3}}{300\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Cl^{-}\right]=6.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$
 
$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+pH_{B}}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+12.3}\times200\cdot10^{-3}}{300\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Na^{+}\right]=8.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$

Exercice 2

1) Montrons que la concentration $C$ est voisine de $6\,mol\cdot L^{-1}$
 
$\begin{array}{lcl} C&=&\dfrac{m}{MV}\\&=&\dfrac{20\%m_{S}}{MV}\\&=&\dfrac{20\%\rho\,V}{MV}\\&=&\dfrac{20\%\rho}{M}\\&\Rightarrow&C=\dfrac{0.20\times 1000\times 1.2}{40}\\&\Rightarrow& C=6\,mol\cdot L^{-1} \end{array}$
 
2) Volume de la solution commerciale à prélever.
 
Au cours de la dilution le nombre de la base, le nombre de moles de la base reste constant :
 
$\begin{array}{lcl} n_{B}&=&CV_{0}\\&=&CV\\&\Rightarrow& V_{0}=\dfrac{CV}{C}\\&=&\dfrac{3\cdot 10^{-2}}{C}\\&\Rightarrow& V_{0}5\,mL \end{array}$
 
3) a) Une base est une espèce chimique susceptible de capter au moins un proton
 
b) Calcule du $pH$ de la solution diluée
 
$pH=14+\log\,C=14+\log\,3\cdot 10^{-2}\Rightarrow pH=12.5$
 
4) a) Équation de la réaction :
 
$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O$ ou
 
$HCl\ +\ NaOH\ \rightarrow\ NaCl\ +\ H_{2}O$
 
b) Calcule de la concentration de la solution diluée :
 
$\Rightarrow C_{B}=\dfrac{C_{A}V_{A}}{V_{B}}=\dfrac{1\cdot 10^{-2}\times 15}{5}$
 
$n_{B}=n_{A}\Rightarrow C_{B}V_{B}=C_{A}V_{A}\Rightarrow C_{B}=3\cdot 10^{-2}mol\cdot L^{-1}$
 
On retrouve bien la valeur souhaitée

Exercice 3

 
1) a) Les coordonnées du point d'équivalence : $E\left(pH_{E}=4\ ;\ V_{E}=12.5\,mL\right)$
 
b) Le $pK_{A}$ de la base est : $pK_{A}=6.4$
 
2) Équation de la réaction de dosage :
 
$HCO_{3}^{-}\ +\ H_{3}O^{+}\ \rightarrow\ H_{2}CO_{3}$
 
Concentration molaire de la base :
 
$\begin{array}{lcl} C_{B}&=&\dfrac{C_{A}V_{A}}{V_{B}}\\&=&\dfrac{1\cdot 10^{-1}\times 12.5}{50}\\&\Rightarrow& C_{B}=2.5\cdot 10^{-2}mol\cdot L^{-1} \end{array}$
 
Concentration massique de la base :
 
$\begin{array}{lcl} C_{m_{B}}&=&C_{B}\times M_{HCO_{3}^{-}}\\&=&2.5\cdot 10^{-2}\times(1.0+12+3\times16)\\&\Rightarrow&C_{m_{B}}=1.5\,g\cdot L^{-1} \end{array}$
 
3) Détermination du titre alcalimétrique $T.A.C$
 
$\begin{array}{lcl} C_{B}V_{B}&=&C_{A}V_{A}\\&\Rightarrow&V_{A}=\dfrac{C_{B}V_{B}}{C_{A}}\\&=&\dfrac{2.5\cdot 10^{-2}\times 100}{2\cdot 10^{-2}}\\&\Rightarrow& V_{A}=125\,mL \end{array}$

Exercice 4

 
1) a) La courbe est croissante : on part d'un $pH$ acide et on atteint des $pH$ basiques
 
Cette courbe comporte quatre parties essentielles :
 
     $\bullet\ \ 0\,mL\leq V_{b}\geq 5\,mL$ où le $pH$ croit assez nettement
     
     $\bullet\ \ 5\,mL\leq V_{b}\geq 9\,mL$ où le $pH$ varie peu, la courbe est quasiment rectiligne ;
     
     $\bullet\ \ 9\,mL\leq V_{b}\geq 13\,mL$, où l'on observe une variation de $pH$, brusque mais moins importante que pour l'acide fort
     
     $\bullet\ \ V_{b}\geq 3\,mL$ où le $pH$ varie faiblement et tend vers une asymptote horizontale
 
b) L'acide $AH$ est un acide faible puisque la courbe présente deux points d'inflexion $E$ et $E_{1/2}$
 
2) a) La valeur du $PH$ à l'équivalence est déterminée par méthode des tangentes : $pH=8.8$
 
b) La constante d'acidité $pK_{A}$ du couple $AH/A^{-}$  correspond à l'ordonnée du volume à la demi-équivalence $pK_{A}=4.8$
 
3) Le point d'équivalence d'un tirage ou plus largement  d'une réaction chimique est le point où l'espèce chimique à tirer et l'espèce titrante ont été mélangés dans des proportions stoechiométriques. 
 
A l'équivalence du tirage, ces deux espèces sont complètement consommées et donc leur quantité de matière est nulle.
 
$\bullet\ \ $Calcul de la concentration $C_{A}$ de la solution de l'acide $AH$
 
A l'équivalence :
 
$\begin{array}{lcl} C_{A}V_{A}&=&C_{B}V_{B}\\&\Rightarrow& C_{A}=\dfrac{C_{B}V_{B}}{V_{A}}\\&=&\dfrac{0.1\times 10}{20}\\&\Rightarrow& C_{A}=0.1\,mol\cdot L^{-1} \end{array}$
 
4) a) Équation de la réaction de dosage
$$AH\ +\ OH\ \rightarrow\ A^{-}\ +\ H_{2}O$$
 
Montrons que la réaction est pratiquement totale
 
$\begin{array}{lcl} K_{R}&=&\dfrac{[A^{-}]}{[AH][OH^{-}]}\\&=&\dfrac{[A^{-}]\left[H_{3}O^{+}\right]}{[AH]\left[OH^{-}\right]\left[H_{3}O^{+}\right]}\\&=&\dfrac{K_{A}}{Ke}\\&\Rightarrow&K_{R}=\dfrac{10^{-4.8}}{10^{-14}}\\&=&10^{9.2}\\&\Rightarrow&K_{R}>10^{4} \end{array}$
 
La réaction est pratiquement totale
 
b) A l'équivalence la solution est une solution de base faible : la solution est donc basique
  
c) Vérifions que le $pH$ à l'équivalence $E$ est donné par la relation :
 
$pH_{E}=\left(pKe+pKa+\log\,C'_{AE}\right)$
 
Pour $pKa=4.8\quad C'_{AE}=\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\Rightarrow$
 
$\begin{array}{lcl} pH&=&\dfrac{1}{2}\left(14+pK_{A}+\log\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\right)\\&=&\dfrac{1}{2}\left(14+4.8+\log\dfrac{0.1\times 10}{20+10}\right)\\&\Rightarrow& pH=8.7\\&\Rightarrow&pH_{E}=8.8 \end{array}$
 
5) a)
$\bullet\ \ $Le $Ph$ diminue avec la concentration qui diminue avec la dilution. 
 
Le $pH$ initial de la solution acide augmente donc avec la dilution
 
$\bullet\ \ $La dilution n'a pas d'effet sur le $pH$ à la demi-équivalence, car ce $pH$ est indépendant de la concentration ; car il faut $pH=pK_{A}$
 
$\bullet\ \ $La dilution n'a pas d'effet sur le volume $V_{BE}$ de base versé à l'équivalence car, cette dilution apporte autant ions $H_{3}O^{+}$ que d'ions $OH^{-}$
 
$\bullet\ \ $Le $pH$ à l'équivalence augmente avec la dilution car la concentration diminue
 
b) Calcule du volume $Ve$ d'eau
 
Au cours de la dilution, le nombre moles d'acide reste contant :
 
$\begin{array}{lcl} n_{A}&=&C'_{AE}\left(V_{e}+V_{a}\right)V_{e}\\&=&C_{A}V_{a}\\\Rightarrow V_{e}&=&\left(\dfrac{C_{A}}{C'_{AE}}-1\right)V_{a}\\\Rightarrow V_{e}&=&\left(\dfrac{C_{A}}{10^{2\,pH_{E}-\left(pK_{A}+pK_{e}\right)}}-1\right)V_{a}\\\Rightarrow V_{e}&=&\left(\dfrac{10^{-1}}{10^{2\times(8.8-0.15)-(4.8+14)}}-1\right)V_{a}\\\Rightarrow V_{e}&=&43\,mL \end{array}$
 
6) a) La teinte sensible d'un indicateur coloré correspond à la zone de virage de cet indicateur coloré (ou la teinte sensible est le nom donné à la couleur que prend la solution dans la zone de virage).
 
b) La phénolphtatéine est l'indicateur approprié car le $pH$ à l'équivalence $\left(pH_{E}=8.8\right)$ appartient à la zone de virage cet indicateur $(8.2-10.0)$

Exercice 5

1) Schéma annoté du dispositif
 
 
2) Tracé de la courbe
 
 
3) a) A l'équivalence à $pH_{E}=8.3$ et il s'agit d'un acide faible (pour un dosoge d'un acide fort par une base forte, à l'équivalence, $pH_{E}=7$)
 
b) A la demi-équivalence : $pH=pK_{A}=4.2$ et l'acide est l'acide benzoique
 
c) La valeur du $pH$ initial est : $pH=2.81$
 
$-\ $ Calcule de la concentration $C_{a}$ de l'aide
 
L'acide est faiblement dissocié : 
 
$\begin{array}{lcl} pH&=&\dfrac{1}{2}\left(pK_{A}-\log\,C_{a}\right)\\&\Rightarrow& C_{a}=10^{-2pH+pK_{A}}\\&=&10^{-2\times 2.81+4.2}\\&\Rightarrow& C_{a}=3.8\cdot10^{-2}mol\cdot L^{-1} \end{array}$
 
4) Équation de la réaction du dosage :
 
$C_{6}H_{5}COOH\ +\ OH^{-}\ \rightarrow\ C_{6}H_{5}CO^{-}\ +\ H_{2}O$
 
5) Calcule de la concentration $C_{b}$ de la base :
 
A l'équivalence :
 
$\begin{array}{lcl} n_{b}&=&n_{a}\\&\Rightarrow& C_{a}V_{b}=C_{a}V_{a}\\&\Rightarrow& C_{b}=\dfrac{C_{a}V_{a}}{V_{b}}\\&=&\dfrac{3.8\cdot10^{-2}\times 20}{10}\\&\Rightarrow&C_{b}=7.6\cdot10^{-2}mol\cdot L^{-1} \end{array}$
 
6) Tracé de la courbe
 
 

Exercice 6

1) a) Cette solution est basique car son $pH$ est supérieur à $7$
 
b) L'espèce conjuguée est l'ion ammonium de formule : $NH_{4}^{+}$
 
c) Le couple acide-base auquel appartient l'ammoniac est : $NH_{4}^{+}|NH_{3}$
 
d) Diagramme de prédominance, en fonction de $pH$, des espèce de ce couple
 
 
Le $pH>pK_{A}\;,\ NH_{3}$ est l'espèce prédominante dans la solution $S$
 
2) a) Équation de la réaction support du dosage
 
$H_{3}O^{+}\ +\ NH_{3}\ \rightarrow\ NH_{4}^{+}\ +\ H_{2}O$ ou
 
$HCl\ +\ NH_{3}\ \rightarrow\ NH_{4}^{+}\ +\ Cl^{-}\ +\ H_{2}O$
 
La transformation chimique est rapide et totale
 
b) Expression de la constante d'équilibre $K_{r}$ en fonction de la constante d'acidité $Ka.$
 
$\begin{array}{lcl} K_{r}&=&\dfrac{\left[NH_{4}^{+}\right]}{\left[H_{3}O^{+}\right]\left[NH_{3}\right]}\\&\text{or }K_{A}&=\dfrac{\left[H_{3}O^{+}\right]\left[NH_{3}\right]}{\left[NH_{4}^{+}\right]}\\&\Rightarrow&K_{r}=\dfrac{1}{K_{A}} \end{array}$
 
Calculer sa valeur de la constante de réaction
 
$\begin{array}{lcl} K_{r}&=&\dfrac{1}{K_{A}}\\&=&\dfrac{1}{6.3\cdot10^{-10}}\\&\Rightarrow&K_{r}=1.6\cdot10^{9} \end{array}$
 
$K_{r}\geq 10^{4}$, la réaction est totale
 
c) Détermination de la concentration molaire $C$ de la solution 
 
A l'équivalence :
 
$\begin{array}{lcl} n_{B}&=&n_{A}\\&\Rightarrow& CV=C_{A}V_{A}\\&\Rightarrow& C=\dfrac{C_{A}V_{A}}{V}\\&=&\dfrac{5.00\cdot10^{-1}\times10.8}{10.0}\\&\Rightarrow&C=5.40\cdot10^{-1}mol\cdot L^{-1} \end{array}$
 
Concentration $C_{0}$ de la solution commerciale
 
$\begin{array}{lcl} C&=&\dfrac{C_{0}}{20}\\&\Rightarrow&C_{0}=20C\\&=&20\times5.40\cdot10^{-1}\\&\Rightarrow&C_{0}=10.8\,mol\cdot L^{-1} \end{array}$
 
d) Détermination de l'expression du pourcentage massique de la solution commerciale en fonction de $C_{0}$ ; $M$ et $\mu.$
 
$\begin{array}{lcl} C_{0}&=&\dfrac{m_{NH_{3}}}{M\times V_{\text{Solution}}}\\&=&\dfrac{x\times m_{\text{Solution}}}{M\times V_{\text{Solution}}}\\&=&\dfrac{x\times\mu\times V_{\text{Solution}}}{M\times V_{\text{Solution}}}\\&=&\dfrac{x\times\mu}{M}\\&\Rightarrow& x=\dfrac{C_{0}M}{\mu}\\&=&\dfrac{10.8\times 17}{920}\\&\Rightarrow&x=0.20\ ;\ \text{soit }x=20\% \end{array}$
 
Cette valeur correspond bien au pourcentage massique de l'ammoniac
 
3) a) Détermination les quantités de matière $n_{1}$ d'ammoniac et $n_{2}$ d'acide chlorhydrique introduites
 
$\begin{array}{lcl} n_{1}&=&CV\\&=&5.4\cdot10^{-1}\times10.0\cdot10^{-3}\\&\Rightarrow&n_{1}=5.4\cdot10^{-3}mol \end{array}$
 
$\begin{array}{lcl} n_{2}&=&C_{A}V_{A}\\&=&5.00\cdot10^{-1}\times6.0\cdot10^{-3}\\&\Rightarrow&n_{2}=3.0\cdot10^{-3}mol \end{array}$
 
b) Détermination de l'avancement final, l'avancement maximal à l'aide d'un tableau descriptif de l'évolution du système chimique
$$\begin{array}{|c|c|ccccccc|} \hline \text{Système}&\text{Avancement}&H_{3}O^{+}\ &+&\ NH_{3}\ &\rightarrow&NH_{4}^{+}&+&\ H_{2}O\\ \hline \text{Initial}&x=0&0&|&5.4\cdot10^{-3}&|&0&|&0\\ \hline \text{Intermédiaire}&x&C_{A}V_{A}-x&|&5.4\cdot10^{-3}-x&|&x&|&x\\ \hline \text{Final}&x_{f}&C_{A}V_{A}-x_{f}&|&5.4\cdot10^{-3}-x_{f}&|&x_{f}&|&x_{f}\\ \hline \end{array}$$
 
L'avancement final correspond à :
 
$5.4\cdot10^{-3}-x_{f}=0\Rightarrow x_{f}=5.4\cdot10^{-3}mol$
 
Lorsque la quantité initiale de base introduite est consommée l'avancement est maximal : $x_{f}=x_{max}$
 
c) Montrons que la transformation est quasi-totale
 
$\tau=\dfrac{x_{f}}{n_{B}}=\dfrac{x_{f}}{CV}=\dfrac{5.4\cdot10^{-3}}{5.4\cdot10^{-1}\times10.0\cdot10^{-3}}$
$$\Rightarrow\tau=1$$
 
La transformation est quasi-totale

Exercice 7

1) Schéma annoté du dispositif expérimental
 
 
2) Tracé des courbes $pH_{1}=f\left(V_{B1}\right)$ et $pH_{2}=f\left(V_{B2}\right)$
 
 
3) Identification sur le graphique de l'acide fort et l'acide faible
 
$AH_{1}$ est l'acide fort et $AH_{2}$ est l'acide faible
 
4) Calcule des concentration des deux acides
 
A l'équivalence :
 
$-\ $ acide fort :
 
$\begin{array}{lcl} n_{AH_{1}}&=&n_{b}\\&\Rightarrow&C_{AH_{1}}V_{AH_{1}}\\&=&C_{b}V_{E}\\&\Rightarrow&C_{AH_{1}}=\dfrac{C_{b}V_{E}}{V_{AH_{1}}}\\&\Rightarrow&C_{AH_{1}}=\dfrac{0.1\times10}{10}\\&\Rightarrow&C_{AH_{1}}=10^{-1}mol\cdot L^{-1} \end{array}$
 
$-\ $ acide faible :
 
$\begin{array}{lcl} n_{AH_{2}}&=&n_{b}\\&\Rightarrow&C_{AH_{2}}V_{AH_{2}}\\&=&C_{b}V_{E}\\&\Rightarrow&C_{AH_{2}}=\dfrac{C_{b}V_{E}}{V_{AH_{2}}}\\&\Rightarrow&C_{AH_{2}}=\dfrac{0.1\times10}{10}\\&\Rightarrow&C_{AH_{2}}=10^{-1}mol\cdot L^{-1} \end{array}$
 
5) Détermination du $pK_{A}$ et la constante d'acidité $K_{A}$ de l'acide faible.
 
A la demi-équivalence : $pH=pK_{A}=4.8$
 
$K_{A}=10^{-pK_{A}}=10^{-4.8}=1.6\cdot10^{-5}$
 
6) Valeur $pH$ de la solution acide lorsqu'on continue à ajouter la solution 
 
Après l'équivalence, la solution est basique :
 
$\begin{array}{lcl} pH&=&14+\log\,C'_{b}\\&=&14+\log\dfrac{C_{b}V_{b}-C_{a}V_{a}}{V_{b}+V_{a}}\\&=&14+\log\dfrac{V_{b}\left(C_{b}-C_{a}\dfrac{V_{a}}{V_{b}}\right)}{V_{a}\left(1+\dfrac{V_{a}}{V_{b}}\right)}\\&=&14+\log\dfrac{\left(C_{b}-C_{a}\dfrac{V_{a}}{V_{b}}\right)}{\left(1+\dfrac{V_{a}}{V_{b}}\right)}\\\\&\Rightarrow&pH=14+\log\,C_{b}\\&=&14+\log0.1V_{b}V_{a}\\&\Rightarrow&\dfrac{V_{a}}{V_{b}}\approx 0\\&\Rightarrow&pH=13 \end{array}$

Exercice 8

1) Montrons que la concentration molaire $C$ est voisine de $6\,mol\cdot L^{-1}$
 
$\begin{array}{lcl} C&=&\dfrac{n}{V}\\&=&\dfrac{m}{MV}\\&=&\dfrac{20\%m_{\text{}Solution}}{MV}\\&=&\dfrac{20\%\rho V}{MV}\\&=&\dfrac{20\%\rho}{M}\\&=&\dfrac{20\%\mathrm{d}\rho_{eau}}{M}\\&\Rightarrow&C=\dfrac{0.20\times1.2\times1000}{40}\\&\Rightarrow&C=6\,mol\cdot L^{-1} \end{array}$
 
2) Volume de la solution commerciale à prélever
 
Au cours de la dilution le nombre de moles de la soude reste constant :
 
$\begin{array}{lcl} n_{b}&=&CV\\&=&C'V'\\&\Rightarrow&V=\dfrac{C'V'}{C}\\&\Rightarrow&V=\dfrac{3\cdot10^{-2}\times1}{6}\\&\Rightarrow&V=5\,mL \end{array}$
 
3) a) Une base forte est une base qui s'ionise totalement dans l'eau en donnant des ions $HO^{-}$
 
b) Calcul du pH de la solution diluée 
 
$pH=14+\log\,C'=14+\log3\cdot10^{-2}\Rightarrow pH=12.5$
 
4) a) Équation – bilan de la réaction
$$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O\quad\text{ou}$$
$$HCl\ +\ NaOH\ \rightarrow\ NaCl\ +\ H_{2}O$$
 
b) Calcul de la concentration de la solution diluée
 
A l'équivalence :
 
$\begin{array}{lcl} n_{b}&=&n_{a}\\&=&C_{b}V_{b}\\&=&C_{a}V_{a}\\&\Rightarrow&C_{b}=\dfrac{C_{a}V_{a}}{V_{b}}\\&\Rightarrow&V=\dfrac{10^{-2}\times15}{5}\\&\Rightarrow&C_{b}=3\cdot10^{-2}mol\cdot L^{-1} \end{array}$
 
On retrouve bien la valeur souhaitée.

Exercice 9

1) a) Représentation graphique $pH=f(x)$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline \dfrac{V_{B}}{V_{A}}&\dfrac{1}{5}&\dfrac{1}{4}&\dfrac{1}{3}&\dfrac{1}{2}&1&2&3&4&5\\ \hline x&-0.7&-0.6&-0.5&-0.3&0&0.3&0.5&0.6&0.7\\ \hline pH&3.1&3.2&3.3&3.5&3.8&4.1&4.3&4.4&4.5\\ \hline \end{array}$$
 
 
b) Le graphe représentant le $pH$ en fonction de $x$ est une fonction affine qui peut se mettre sous la forme : $pH=a+bx$
 
$a$ est l'ordonnée à l'origine :
 
$b$ est le coefficient directeur de la droite
 
$\begin{array}{lcl} b&=&\dfrac{\Delta pH}{\Delta x}\\&=&\dfrac{(4.5-3.1)}{(0.7-(-0.7))}\\&\Rightarrow&b=1\\&\Rightarrow&pH=3.8+\log x \end{array}$
 
2) Montrons que pour une même concentration d'acide et de base, $\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}=\dfrac{V_{B}}{V_{A}}$
 
Dans le mélange :
 
$\left[RCOO^{-}\right]=\dfrac{CV_{B}}{V_{A}+V_{B}}$
 
$\begin{array}{lcl} \left[RCOO^{-}\right]&=&\dfrac{CV_{B}}{V_{A}+V_{B}}\\&\Rightarrow&\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}\\&=&\dfrac{\dfrac{CV_{B}}{V_{A}+V_{B}}}{\dfrac{CV_{A}}{V_{A}+V_{B}}}\\&=&\dfrac{CV_{B}}{V_{A}+V_{B}}\times\dfrac{V_{A}+V_{B}}{CV_{A}}\\&\Rightarrow&\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}=\dfrac{V_{B}}{V_{A}} \end{array}$
 
3) a) Expression du $pH$ du mélange obtenu en fonction du $pKa$ et du rapport : $\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}$
 
Équation de la réaction :
 
$RCOOH\ +\ H_{2}O\ \rightarrow\ RCOO^{-}\ +\ H_{3}O^{+}$
 
La constante de réaction s'écrit : 
 
$\begin{array}{lcl}K_{A}=\dfrac{\left[RCOO^{-}\right]\left[H_{3}O^{+}\right]}{\left[RCOOH\right]}\\&\Rightarrow&\log K_{A}=\log\dfrac{\left[RCOO^{-}\right]\left[H_{3}O^{+}\right]}{\left[RCOOH\right]}\\&=&\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}+\log\left[H_{3}O^{+}\right]\\&\Rightarrow&-\log\left[H_{3}O^{+}\right]\\&=&-\log K_{A}+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}\\&\Rightarrow&pH=pK_{A}+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]} \end{array}$
 
b) Le $pKa$ de l'acide
 
$pH=3.8+\log x=pH=3.8+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}$
 
et $pH=pK_{A}+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}$
 
Par identification :
 
$pK_{A}=3.8$

Exercice 10

1.1. Équation- bilan entre l'acide éthanoïque et l'eau
 
$CH_{3}COOH\ +\ H_{2}O\ \rightarrow\ CH_{3}COO^{-}\ +\ H_{3}O^{+}$
 
1.2.1. Expression du $pH$ et calcul du rapport $\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}$
 
$\begin{array}{lcl} pH&=&pKa+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}\\&\Rightarrow&\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}\\&=&10^{pH-pKa}\\&=&10^{3.4-4.78}\\&\Rightarrow&\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}=4.2\cdot10^{-2} \end{array}$
 
1.2.2. Calcul des concentrations molaires des espèces chimiques présentes dans $S_{1}.$
 
Espèces chimiques présentes dans la solution $S_{1}$ :
 
$H_{3}O^{+}\;,\ CH_{3}COOH\;,\ CH_{3}COO^{-}\;,\ H_{2}O\;,\ OH^{-}$
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&10^{-pH}\\&=&10^{-3.4}\\&\Rightarrow&\left[H_{3}O^{+}\right]=3.98\cdot 10^{-4}mol\cdot L^{-1} \end{array}$
 
$\begin{array}{lcl} \left[OH^{-}\right]&=&\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{3.98\cdot10^{-4}}\\&\Rightarrow&\left[OH^{-}\right]=2.5\cdot 10^{-11}mol\cdot L^{-1} \end{array}$
 
Electroneutralité de la solution : $\left[CH_{3}COO^{-}\right]+\left[OH^{-}\right]=\left[H_{3}O^{+}\right]$ solution acide, on néglige les ions $\left[OH^{-}\right]\Rightarrow\left[CH_{3}COO^{-}\right]=\left[H_{3}O^{+}\right]=3.98\cdot10^{-4}mol\cdot L^{-1}$
 
$\begin{array}{lcl}\left[CH_{3}COOH\right]&=&\dfrac{\left[CH_{3}COO^{-}\right]}{4.2\cdot10^{-2}}\\&=&\dfrac{3.98\cdot10^{-4}}{4.2\cdot10^{-2}}\\&\Rightarrow&\left[CH_{3}COOH\right]=9.5\cdot10^{-3}mol\cdot L^{-1}\end{array}$
 
1.2.3. Concentration $C_{A}$ de la solution $S_{1}$
 
La concentration de la matière s'écrit :
 
$\left[CH_{3}COOH\right]+\left[CH_{3}COO^{-}\right]=C_{A}$
 
la dissociation de l'acide étant faible $\Rightarrow C_{A}\approx\left[CH_{3}COOH\right]=9.5\cdot10^{-3}mol\cdot L^{-1}$
 
1.2.4. Détermination de la masse $m$ introduite
 
$\begin{array}{lcl} m&=&n\times M\\&=&C_{A}V\times M\\&=&9.5\cdot10^{-3}\times 1\times(12\times2+4\times1+16\times2)\\&\Rightarrow&m=0.75\,g \end{array}$
 
2.1. Les espèces chimiques présentes dans $S_{2}$ :
 
$H_{3}O^{+}\;,\ CH_{3}COOH\;,\ CH_{3}CO^{-}\;,\ H_{2}O\;,\ OH^{-}$
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&10^{-pH}\\&=&10^{-8.4}\\&\Rightarrow&\left[H_{3}O^{+}\right]=3.98\cdot10^{-9}mol\cdot L^{-1} \end{array}$
 
$\begin{array}{lcl} \left[OH^{-}\right]&=&\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{3.98\cdot 10^{-9}}\\&\Rightarrow&\left[OH^{-}\right]=2.5\cdot 10^{-6}mol\cdot L^{-1} \end{array}$
 
$\left[Na^{+}\right]=C_{B}=10^{-2}mol\cdot L^{-1}$
 
Electroneutralité de la solution :
 
$\left[CH_{3}COO^{-}\right]+\left[OH^{-}\right]=\left[H_{3}O^{+}\right]+\left[Na^{+}\right]$, 
 
on néglige les concentrations des ions $H_{3}O^{+}$ et $OH^{-}$ devant celle des ions $Na^{+}$
 
$\Rightarrow\left[CH_{3}COO^{-}\right]\approx\left[Na^{+}\right]=C_{B}=10^{-2}mol\cdot L^{-1}$
 
La concentration de la matière s'écrit :
 
$\begin{array}{lcl} \left[CH_{3}COOH\right]+\left[CH_{3}COO^{-}\right]&=&C_{B}\\&\Rightarrow&\left[CH_{3}COOH\right]&=&C_{B}-\left[CH_{3}COO^{-}\right]\\&\approx&0mol\cdot L^{-1} \end{array}$
 
2.3.  Calcul de la valeur $pKa$ du couple acide/base
 
$\begin{array}{lcl} pH&=&\dfrac{1}{2}\left(14+pK_{A}+\log\,C_{B}\right)\\&\Rightarrow&pK_{A}=2pH-14-\log\,C_{B}\\&\Rightarrow&pK_{A}=2\times 8.4-14-\log\,10^{-2}\\&\Rightarrow&pK_{A}=4.8 \end{array}$
 
Les valeurs de $pKa$ sont équivalentes
 
3.1. Montrons que :
 
$\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
 
Electroneutralité de la solution :
 
$\left[CH_{3}COO^{-}\right]+\left[OH^{-}\right]=\left[H_{3}O^{+}\right]+\left[Na^{+}\right]$
 
on néglige les concentrations des ions $H_{3}O^{+}$ et $OH^{-}$ devant celle des ions $Na^{+}$
 
$\begin{array}{lcl} \Rightarrow\left[CH_{3}COO^{-}\right]&\approx&\left[Na^{+}\right]\\&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times 20}{20+20}\\&=&5\cdot 10^{-3}mol\cdot L^{-1} \end{array}$
 
$\begin{array}{lcl} \left[CH_{3}COOH\right]&=&\dfrac{10^{-2}\times V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times 20}{30+20}\\&=&5\cdot 10^{-3}mol\cdot L^{-1}\\&\Rightarrow&\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right] \end{array}$
 
3.2.  $pH$ de la solution $S$
 
$pH=pKa+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}$
 
or $\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
 
$\Rightarrow\,pH=pKa=4.75$
 
3.3. Nom et propriétés de la solution
 
La solution est une solution tampon et, le $pH$ varie peu lors de l'addition modérée d'un acide fort ou d'une base forte ; ou lors d'une dilution.

Exercice 11

1.1 Détermination du volume $V_{0}$ de la solution commerciale
 
Le nombre de moles de l'acide ne varie pas :
 
$C_{0}V_{0}=C_{a}V_{a}$
 
$\Rightarrow\,V_{0}=\dfrac{C_{a}V_{a}}{C_{0}}$ or
 
$\begin{array}{lcl} C_{0}&=&\dfrac{m}{MV_{S}}\\&=&\dfrac{99\%m_{S}}{MV_{S}}\\&=&\dfrac{99\%\rho\,V_{S}}{MV_{S}}\\&=&\dfrac{99\%\rho}{M}\\&\Rightarrow&V_{0}=\dfrac{C_{a}V_{a}}{\dfrac{99\%\rho}{M}}\\&=&\dfrac{C_{a}V_{a}M}{99\%\rho}\\&=&\dfrac{0.1\times 1\times 60}{0.99\times 1050}\\&\Rightarrow&V_{0}=5.8\,mL \end{array}$
 
1.2 Équation bilan de la réaction de l'acide éthanoïque avec l'eau
 
$CH_{3}COOH+H_{2}O\ \rightarrow\ CH_{3}COO^{-}+H_{3}O^{+}$
 
2.1. Détermination de la masse $m_{b}$ d'éthanoate de sodium
 
$m_{B}=C_{b}V_{b}\times M=0.3\times 500\cdot 10^{-3}\times 82$
 
$\Rightarrow\,m_{b}=12.3\,g$
 
2.2. Équation de la dissociation de l'éthanoate de sodium dans l'eau
 
$CH_{3}COONa\ \rightarrow\ CH_{3}COO^{-}+Na^{+}$
 
2.3. Équation de la réaction entre un ion éthanoate et l'eau
 
$CH_{3}COO^{-}+H_{2}O\ \rightarrow\ CH_{3}COOH+OH^{-}$
 
3.1. Propriétés d'une solution tampon
 
Le $pH$ varie peu lors de l'addition modérée d'un acide fort ou d'une base forte ; ou lors d'une dilution
 
3.2. Expression de la constante d'acidité $Ka$ du couple d'acide éthanoïque ion/éthanoate
 
$Ka=\dfrac{\left[CH_{3}COO^{-}\right]\left[H_{3}O^{+}\right]}{\left[CH_{3}COOH\right]}$
 
$\begin{array}{lcl} \log\,Ka&=&\log\dfrac{\left[CH_{3}COO^{-}\right]\left[H_{3}O^{+}\right]}{\left[CH_{3}COOH\right]}\\&\Rightarrow&\log\,Ka=\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}+\log\left[H_{3}O^{+}\right]\\&\Rightarrow&-pKa=-pH+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}\\&\Rightarrow&pH=pKa+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]} \end{array}$
 
3.3.  $pH=pKa$ lorsque $\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
 
3.4. Détermination les volumes d'acide éthanoïque et d'éthanoate de sodium à utiliser
 
$\left[CH_{3}COOH\right]=\dfrac{C_{a}V_{a}}{V_{a}+V_{b}}$ ;
 
$\left[CH_{3}COOH\right]=\dfrac{C_{b}V_{b}}{V_{a}+V_{b}}$ ;
 
$\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
 
$\begin{array}{lcl} \left[CH_{3}COOH\right]&=&\left[CH_{3}COO^{-}\right]\\&\Rightarrow&\dfrac{C_{a}V_{a}}{V_{a}+V_{b}}=\dfrac{C_{b}V_{b}}{V_{a}+V_{b}}\\&\Rightarrow&C_{a}V_{a}=C_{b}V_{b}\\&\Rightarrow&V_{a}=\dfrac{C_{b}}{C_{a}}V_{b}\text{ or }V_{a}+V_{b}=V\\&\Rightarrow&\dfrac{C_{b}}{C_{a}}V_{b}+V_{b}=V\\&\Rightarrow&V_{b}=\dfrac{V}{\dfrac{C_{b}}{C_{a}}}+1\\&=&\dfrac{100}{\dfrac{0.3}{0.1}}+1\\&\Rightarrow&V_{b}=25\,mL \end{array}$
 
$V_{a}=V-V_{b}=100-25\Rightarrow\,V_{a}=75\,mL$
 
4.1.  Tracé de la courbe $pH=f\left(V_{b}\right)$
 
4.2. Détermination graphique des coordonnées du point d'équivalence $E$
 
A l'équivalence : $V_{E}=20\,mL\text{ et }pH_{E}=8.8$
 
4.3. Valeur de la concentration molaire $Ca$ de la solution d'acide éthanoïque
 
$\begin{array}{lcl}C_{a}V_{a}&=&C_{b}V_{E}\\&\Rightarrow&C_{a}=\dfrac{C_{b}V_{E}}{V_{a}}\\&=&\dfrac{0.1\times 20}{20}\\&\Rightarrow&C_{a}=0.1\,mol\cdot L^{-1}  \end{array}$
 
4.4. Valeur du $pKa$ du couple $CH_{3}COOH|CH_{3}COO^{-}$
 
$pKa=4.75$
 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Les hydrocarbures insaturés : alcènes et alcynes - 1er s

Classe: 
Première
 

Exercice 1

A) Nommer les composés instaurés suivants :
 
1) $CH_{3}-CH_{2}-CH=CH-CH_{3}$
 
2) $CH_{3}-CH\left(C_{2}H_{5}\right)-CH=CH-CH_{2}-CH_{3}$
 
3) 
 
4) 
 
5) $CH_{3}-C\equiv C-CH\left(C_{2}H_{5}\right)-CH_{2}-CH_{2}-CH_{3}$
 
6) $CH_{3}-C\equiv C-CH\left(C_{2}H_{5}\right)-CH_{2}-CH_{2}-CH_{3}$
 
7) $CH\equiv C-C\left(CH_{3}\right)_{2}-CH\left(C_{2}H_{5}\right)-CH_{3}$
 
B) Donner les formules des divers corps et leur noms dans les réaction suivantes :
 
$C_{2}H_{5}OH\ \longrightarrow\ W+H_{2}O$
 
$W+Cl_{2}\ \longrightarrow\ X$
 
$X\ \longrightarrow\ Y+HCl$
 
$Y\ \longrightarrow\ Z$ par polymérisation
 
Préciser l'intérêt du polymère obtenu

Exercice 2

Écrire la formule semi-développée des hydrocarbures suivants :
 
a) $3-\text{éthyl}\;,\ 2-\text{méthylpent}-2-\text{ène.}$
 
b) $3.6-\text{diéthyloct}-4-\text{yne.}$
 
c) $2.4-\text{diméthylpent}-2-\text{ène}$
 
d) hex$-2-$yne
 
e) $1.2-$dibromocyclobutène
 
f) $2-\text{chlorobuta}-1.3-\text{diène}$
 
g) vinyclopropane
 
h) $4.6-\text{dipropylnon}-4-\text{ène}$
 
i) $6-\text{métthylpet}-2.4-\text{diyne}$
 
j) $3-\text{éthyl}-1.4-\text{diméthyl}-5-\text{tert}-\text{butyl}-2-\text{vinylcyclohexène}$
 
k) But$-3-$ène
 
l) $\text{Pent}-3-\text{ynec}$
 
m) $2-\text{éthlprop}-1-\text{ène}$
 
n) $2-$méthylcyclopentène 
 
o) buta$-1.3-$diène 
 
p) $Z-2.4-\text{diméthylpent}-2-\text{ène}$
 
q) $E-3.4-\text{diméthylpent}-2-\text{ène}$

Exercice 3

Soit $A$ u hydrocarbure aliphatique insaturé, de masse molaire $M=68\,g\cdot mol^{-1}$, dont la chaine carbonée renferme une triple liaison.
 
a) Trouver la formule brute de l'hydrocarbure $A.$
 
b) trouver tous les isomères possibles de $A$ et les nommer.
 
On donne :
 
$M(H)=1\,g\cdot mol^{-1}\text{ et }M(C)=12\,g\cdot mol^{-1}$

Exercice 4

Un alcène $A$ réagit très rapidement, mole à mole, avec du dibrome.
 
Le produit $B$ obtenu contient $74\%$ (masse) de dibrome.
 
1) Quelle est la masse molaire de $B$ ?
 
2) En déduire la masse molaire et la formule brute de $A.$
 
3) Représenter tous les isomères possible pour $A$ et les nommer ; tenir compte des stéréoisomères s'il y a lieu.
 
4) l'hydratation de $A$ conduit préférentiellement à l'alcool $D$, alors que l'hydratation des isomères de $A$ conduit préférentiellement au même alcool $E$, isomère de $D.$ 
 
En déduire les formules de $A$, $B$, $D$ et $E.$
 
On donne, en $g\cdot mol^{-1}$, les masses molaires : $C\ :\ 12\;,\ H\ :\ 1\;,\ Br\ :\ 80$

Exercice 5

1) Un hydrocarbre aliphatique saturé $(A)$ a une masse molaire moléculaire $M=58\,g\cdot mol^{-1}.$
 
a) Trouver la formule brute de $(A)$
 
b) Écrire les formules semi-développées possibles et donner le nom des différents isomères de $(A).$
 
c) Identifier l'isomère $\left(A_{1}\right)$ de $(A)$ sachant qu'il présente une chaine ramifiée.
 
2) l'action du dibrome $B_{r2}$ sur l'hydrocarbure $\left(A_{1}\right)$ en présence de la lumière, donne un mélange de dérivés bromés dont l'un est un dérivé dibromé noté $(B)$
 
a) Écrire l'équation chimique de la réaction conduisant à la formation de $(B)$ en utilisant les formule brutes.
 
b) Donner toutes les formules semi-développées possibles de $(B)$ et le nom des isomères correspondants
 
c) La structures de l'hydrocarbure de départ $\left(A_{1}\right)$ a-t-elle été modifiée au cours de cette réaction.
 
3) L'un des isomères $\left(B_{1}\right)$ de $(B)$ peut être obtenu par une réaction d'addition du dibrome sur un alcène.
 
a) Trouver la formule brute de cet alcène.
 
b) Écrire la formule semi développée et le nom de cet alcène.
 
c. Écrire l'équation de la réaction d'addition en utilisant les formules brutes.
 
d) la structure de l'hydrocarbure de départ a-t-elle été modifiée au cours de cette réaction ?

Exercice 6

Un hydrocarbure $A$ contient en masse $6$ fois plus de carbone que d'hydrogène.
 
1) a) Déterminer la formule brute générale de cet hydrocarbure.
 
b) A quelle(s) famille(s) d'hydrocarbure appartient-il ?
 
c) Écrire les formules semi-développées possible de $A$ sachant que $A$ renferme $8$ atomes d'hydrogène.
 
2) La chaine carbonée de l'hydrocarbure $A$ est linéaire ; de plus $A$ possède des stéréo-isomère $Z/E.$
 
Représenter ces stéréo-isomères.
 
3) Le craquage de $A$ dans un vapocraqueur conduit à la formation de l'éthylène.
 
a) Toute la quantité de $A$ n'a pas été transformée, déterminer la composition centésimale molaire du mélange gazeux du vapocraqueur à la fin de la réaction sachant que sa densité par rapport à l'air est $d=1.2068.$
 
b) Après refroidissement du mélange, on y ajoute du dichlore ; puis on place le nouveau mélange à l'obscurité.
 
Écrire les formules semi-développées et les noms des produits $B$ et $C$ formés. 
 
$B$ étant le produit issu de l'action du dichlore sur $A.$
 
c) Le chauffage des produits $B$ et $C$ provoque l'élimination d'une molécule de chlorure d'hydrogène $HCl.$ 
 
Le composé $C$ donne le composé $D$ et le chlorure d'hydrogène. 
 
Écrire l'équation bilan.
 
d) Plusieurs molécules du composé $D$ s'additionnent les unes aux autres pour former une macromolécule $E.$
 
Donner la nature de la réaction produite puis le nom et l'intérêt du composé $E.$

Exercice 7 

1) On réalise dans un eudiomètre la combustion d'un volume $V=10\,cm^{3}$ d'un hydrocarbure $A$ en présence de $110\,cm^{3}$ de dioxygène. 
 
Après combustion puis refroidissement, le volume de gaz restant est $90\,cm^{3}$ dont les $50\,cm^{3}$ sont absorbables par le phosphore et le reste par la potasse.
 
a) Écrire l'équation bilan de la réaction de combustion.
 
b) Déterminer le volume de dioxygène entré en réaction et le volume de dioxyde de carbone obtenu.
 
c) Déterminer la formule brute de $A.$
 
d) Écrire les cinq formules semi-développées possibles de $A$ et les nommer.
 
2) a) En l'absence totale de lumière, $A$ réagit avec le dichlore. 
 
Montrer que cela permet d'éliminer deux des cinq isomères de $A.$
 
b) L'hydrogénation de $A$ en présence de nickel conduit à un composé $B$ à chaine carbonée linéaire. 
 
En outre, l'action du chlorure d'hydrogène sur $A$ donne deux composés $C$ et $D$ ; le composé $D$ étant obtenu de façon majoritaire. 
 
Écrire les formules semi-développées et les noms des composés $A$, $B$, $C$ et $D.$
 
c) $A$ présente t-il l'isomérie $Z$ et $E$ ? 
 
Justifier la réponse.
 
3) a) Écrire les équation-bilans des réactions de :
 
$-\ \ A$ avec l'eau
 
$-\ \ A$ avec le dibrome
 
$-\ $ La polymérisation de $A$
 
On donnera le nom des produits obtenus
 
b) De quel alcyne $A'$ peut-on partir pour obtenir $A$ ? 
 
Écrire l'équation de la réaction

Exercice 8

1. Écrire les formules semi-développées des isomères du butène. On précisera le nom de chaque isomère.
 
2.1. Donner la formule brute de l'alcène dont la molécule contient $n$ atomes de carbone.
 
2.2. Exprimer en fonction de $n$ la masse molaire $M$ de cet alcène.
 
2.3.
2.3.1. Un alcène a pour masse molaire $M=70\,g\cdot mol^{-1}.$ 
 
Déterminer, en utilisant le résultat précédent, la formule brute de cet alcène.
 
Quel est son nom ?
 
2.3.2. Cet alcène présente deux stéréoisomères. 
 
En déduire le nom de l'alcène. 
 
Écrire les formules semi-développées de ces deux isomères et préciser leurs noms.
 
Données : masses molaires atomiques :
 
$\bullet$ Carbone : $M_{C}=12\,g/mol$
 
$\bullet$ Hydrogène : $M_{H}=1.0\,g/mol$

Exercice 9

1) Écrire la formule semi-développée de l'acétylène. 
 
A quelle famille de composé appartient-il ?
 
Pourquoi dit-on que c'est un hydrocarbure insaturé ?
 
2) On fait réagir du dichlore sur l'acétylène.
 
Écrire l'équation-bilan de la réaction et nommer le produit $B$ formé.
 
3) On procède à la polymérisation du composé $B.$ 
 
On obtient un polymère $E$ de masse molaire $M_{E}=67.5\,kg/mol.$
 
a) Écrire l'équation de la réaction et nommer le composé $E.$
 
b) Calculer le degré de polymérisation du polymère et donner la $FSD$ de son motif.
 
4) L'hydrogénation de l'acétylène conduit à un composé insaturé $C.$
 
L'hydratation du composé $C$ donne un composé $F.$
 
a) Préciser le catalyseur utilisé pour chacune des réactions.
 
b) Écrire les équations-bilans des différentes réactions.
 
c) A quelles familles de composés, $C$ et $F$ appartiennent-ils ? 
 
Les nommer.
 
Données : $M_{C}=12g\,/mol$ ; $M_{H}=1\,g/mol$

Exercice 10

1) On prépare un alcool $A$ par addition de l'eau sur un alcène ramifié de formule brute $C_{n}H_{2n}$ noté $B.$
 
Écrire l'équation-bilan de la réaction.
 
2) La combustion de $"m"$ grammes de $A$ donne $m_{1}$ grammes de $CO_{2}$ et $m_{2}$ grammes d'eau tel que $\left(m_{1}/m_{2}\right)=88/45.$
 
a) Écrire l'équation de la combustion de $A.$
 
b) En déduire la valeur de $n$ et la $FSD$ de l'alcène $B.$
 
c) Montrer que l'hydratation de $B$ en présence d'acide sulfurique peut conduire théoriquement à la formation de deux alcools. 
 
Préciser le nom et la classe de chacun d'eux.
 
3) En réalité un seul alcool est essentiellement obtenu : lequel ? 
 
Pourquoi ?

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 
Auteur: 
Sidy Mouhamed Ndiaye

MELANGES ET CORPS PURS

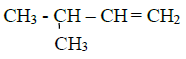
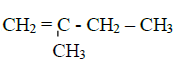
Tous les objets qui nous entourent (êtres vivants, végétaux, minéraux …..) constituent la matière  
Les roches, les arbres, l’air…..etc., ont des exemples de matières  
I. Les états physiques de la matière et changements d’états
1. Etats physiques de la matière  La matière se présente dans la nature sous trois états différents : l’état solide, l'état liquide et l’état gazeux
1.1. L'état solide A l'état solide, un corps possède une forme et un volume propres  Les solides sont incompressibles Moyennant un effort, on  peut changer la forme d’un solide, mais il est pratiquement impossible de faire varier son volume Certains solides sont élastiques, mais chaque  solide à sa limite d’élasticité  Exemples : cahier, bois, fer, charbon….   
1.2. L’état liquide Les liquides n’ont pas de forme propre, mais leur volume est invariable ; ils sont fluides et incompressibles
Exemples : l’eau, pétrole, l’essence, le lait……
 Remarque Les solides en poudre, divisés ou pulvérisés s’écoulent comme les liquides, mais leur surface libre n’est ni plane, ni horizontale comme les liquide  
1.3. L’état gazeux
Les gaz n’ont pas de forme propre, ni de volume propre. Ils sont compressibles, expansibles et élastiques. Ils sont fluides
Exemples : l’air, le dioxyde de carbone, le dioxygéne….
Remarque :  Les solides sont caractérisés  par un état ordonné  et compact. L’état liquide  est désordonné .L'état physique des gaz est désordonné et diffus  
2. Les changements d’état physique
2.1. Définition  Le passage d’un état physique à un autre état physique est appelé changement d’état  
2.2. Digramme de changement d'état
Un changement d’état physique s’effectue toujours à une température constante sous une pression donnée  
3. Les transformations de la matière  
3.1. Phénomène physique Un phénomène physique est une transformation au cours de laquelle la nature de la matière n’est pas altérée (dénaturée ou détruite)
Exemples : la fusion de la glace ; la dilatation des métaux ; la rosée….
3.2. Phénomène chimique
 Un phénomène chimique est une transformation au cours de laquelle la nature de la matière est  altérée (dénaturée ou détruite) Exemples : Action de l’eau  de Javel sur une tache ; la décomposition de la craie par un acide ; feuille de papier brulée …. II. Les mélanges
 1. Définition  Un mélange est un ensemble de deux ou plusieurs constituants Il peut être solide, liquide ou gaz  
 2. Mélange hétérogène Un mélange hétérogène est un mélange dans lequel on peut distinguer à l’ œil nu ses différents constituants  Exemples : $eau_{+} huile ; eau_{+} terre$ ; boissons gazeuses
 3. Mélange homogène Un mélange homogène est un mélange dans lequel on ne peut pas distinguer à l’ œil nu ses différents constituants  Exemples : lait ; sirop ; thé
 Z***c
 4. Méthodes de séparation des constituants d’un mélange
 Il existe de nombreuses méthodes variables de séparation selon la nature du mélange et la nature
 des constituants qui le constituent.
 Parmi ces méthodes, on citer :
 4.1. La  décantation
 La décantation est une de séparation qui consiste à laisser le mélange au repos pour que les particules solides lourdes se déposent au fond du récipient.
En transvasant, on peut séparer le liquide de ces particules. Le produit de la décantation est appelé décantat
 Exemples de décantation
 -Décantation d’un mélange solide-liquide : jus d’orange
 -Décantation d’un mélange liquide-liquide :  
  4.2. La  filtration La filtration est une méthode de séparation qui consiste à faire passer le mélange liquide à travers un filtre .
  Le produit de la filtration est appelé filtrat
4.3. La distillation  
La distillation est une méthode de séparation  basée sur la différence de température d’ébullition.
Elle consiste à vaporiser partiellement un mélange liquide homogène et à condenser
les vapeurs formées pour les séparer Le produit de la distillation est appelé distillat
 Exemple : distillation de l’eau sucrée
Remarque :
Pour séparer les différents constituants de l’air, on le liquéfie en le comprimant. On procède alors à la
distillation de ce liquide Au début de l’ébullition (température de liquéfaction  du diazote liquide $(–196°C)$), il se dégage du diazote, puis le dioxygène lorsque  la température atteint$ -183^{0}C $(température de liquéfaction du dioxygène) L’air est donc un mélange dont l’expérience montre qu’il est constitué de $78%$ de diazote ($4/5$ en volume) , de $21%$ de dioxygène ($1/5$ en volume) et $1%$ d’autres gaz (gaz rares, dioxyde de carbone et de la vapeur d’eau)
4.4. Quelques autres méthodes de séparation
4.4.1.congélation                                                                                                                                                                                                                                                                                                                             C’est une méthode de séparation basée sur la différence de cristallisation (température à laquelle un corps se congèle).
Le corps dont sa température d’ébullition est plus grande est récupéré le premier sous formes de cristaux
4.4.2. Le tamisage Si les grains de différents solides ont  des dimensions différentes, le passage au tamis permet de les séparer
4.4.3. La flottation  On mouille le mélange. Selon le liquide choisi, certaines particules flottent
4.4.4. Le triage magnétique Si un des constituants du mélange contient du fer, les particules de ce constituant sont attirées par l’aimant
III. Corps purs
1. Définition Un corps pur est un corps qu’on ne peut pas fractionner par une méthode quelconque de séparation  
2. Critères  de pureté d’un corps pur Tout corps pur est défini par les constantes physiques parmi lesquelles on citer :
-la masse volumique -les points de changement d’état : température de fusion, d’ébullition, de solidification etc…..
Exemple : Valeurs de quelques constantes physiques de l’eau pure. -masse volumique : $1kg/L$
-température de solidification ou de fusion :  $t=0^{0}C$
-température d’ébullition ou de liquéfaction : $t= 100^{0}C$
3. Corps purs simples et corps purs composés
3.1. Analyse de l’eau   
3.1.1. Définition  Analyser un corps revient à chercher ses constituants par une méthode appropriée
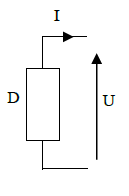
3.1.2. L’électrolyse de l’eau  
Mettons de l’eau additionnée de quelques gouttes d’acide dans le voltamètre (ou cuve à l’électrolyse) et fermons l’interrupteur 
On constate que le courant circule et  des dégagements gazeux au niveau des tubes A l’anode (signe+), le gaz recueilli rallume une buchette presque éteinte. Ce gaz est le dioxygène
A la cathode (signe-), le gaz recueilli a volume deux fois grand et produit une légère détonation en présence d’une allumette enflammée. Ce gaz est le dihydrogène
Conclusion :
-L’eau est décomposé par le courant électrique en dioxygène et en dihydrogène
-Le volume de dihydrogène est le double du volume de dioxygène : dihydrogène dioxygène $V_{dihydrogène}= 2V_{dioxygène} $
-La masse totale des gaz (dihydrogène et dioxygène) est égale à la d’eau disparue : $m_{e}=m_{H}+ m_{o}
eau⎯→ dioxygène   + dihydrogène
18g              16g                 2g $     
Les masses de dihydrogène et de dioxygène sont proportionnelles à la masse d’eau disparue
$\frac{m_{H}}{m_{E}} =\frac{2g}{18g} \Longrightarrow{ m_{H}} = \frac{1}{9}m_{E}
\frac{m_{o}}{m_{E}} =\frac{16g}{18g} \Longrightarrow{m_{o} }= \frac{8}{9}m_{E}$
-Un corps pur qui peut décomposer en deux ou plusieurs corps purs est un corps pur composé
Exemple : l’eau  
-Un corps pur qui ne peut être décomposé en d’autres corps purs est un corps simple
Exemples : le dioxygène et le dihydrogène
3.2. Synthèse de l’eau
3.2.1. Définition
La synthèse de l’eau est la formation de l’eau à partir du mélange du dihydrogène et du dioxygène.
3.2.2. Synthèse eudiométrique
On déclenche des étincelles électriques au niveau des électrodes pour amorcer le processus de synthèse
- La pression des gaz baisse, le niveau de mercure qui va remonter lorsque les deux gaz réagissent en formant une buée (eau) sur la paroi interne du tube eudiométrique.
$dioxygène   + dihydrogène eau ⎯→     
16g                 2g          18g$  
La masse d’eau  produite  est proportionnelle à la masse de dihydrogène ou à la masse de dioxygène
$\frac{m_{E}}{m_{H}} =\frac{18g}{2g} \Longrightarrow{  m_{E} =9m_{E}}
\frac{m_{E}}{m_{O}} =\frac{18g}{16g} \Longrightarrow{m_{E}} = \frac{9}{8}m_{O}$
ELEMENTS, ATOMES, CLASSIFICATION PERIODIQUE DES ELEMENTS
I. Eléments
1. Mise en évidence de l’élément carbone
1.1. Pyrolyse du bois  
La pyrolyse du bois donne du charbon de bois
1.2. Pyrolyse du sucre La pyrolyse du sucre donne un solide noir appelé charbon de sucre
1.3. Conclusion Le charbon de bois (produit de la pyrolyse du bois), le solide noir (résidu de la pyrolyse du sucre) contiennent un constituant commun : le carbone  
2. Définition de l’élément chimique Un élément chimique est un constituant commun  à tous les corps qui le contiennent
Remarque
-Les corps purs simples sont formés d’un seul élément
Exemples : le dihydrogène est formé de l’élément hydrogène ;
le dioxygène est formé de l'élément oxygène
-Les corps purs composés sont formés de plusieurs éléments
Exemples : l’oxyde de dihydrogène (eau) est formé de l’élément oxygène et l'élément hydrogène ;
le dioxyde de carbone (gaz carbonique) est formé de l’élément oxygène et de l'élément carbone
3. Notation de l'élément chimique
Pour faciliter l’étude de la chimie, les éléments sont représentés par des
symboles  Généralement, on utilise la première lettre majuscule du nom (français, latin, grec, étranger….)
Lorsque plusieurs éléments commencent par la même lettre, on ajoute une seconde lettre minuscule  pour les
différencier
Symboles de quelques éléments chimiques
    H C F Na N O F Ca 

Elément  Hydrogène Carbone Fer Sodium Azote Oxygène   Fluor Calcium
Symbole H C F Na N O F Ca

II. Atomes
La matière est faite à partir des particules extrêmement petites appelées atomes.
Les propriétés  chimiques des corps purs peuvent être interprétées à partir d’un modèle unique d’atome  
1. Dimension de l’atome L’atome est représenté par une sphère infiniment petite .
Le diamètre de l’atome est de l’ordre de l’Angstrom (symbole ; A°) ; 1A°=10-15m
2. Les constituants de l’atome
2.1. Le modèle atomique L’atome peut être  modélisé par une structure présentant un noyau autour duquel
 existe une zone dans laquelle on peut trouver les électrons. Cette partie  
 de l’atome est appelée nuage électronique   
 2.2. Les caractéristiques des constituants de l’atome
Les expériences montrent que l’atome est constitué de protons, de neutrons et d’électrons

Particule Masse Charge
Proton $m_{P}=1.672.10^{-26}kg$ $q_{p}=1.6.10^{-19}C$
Neutron $m_{n}=1.674.10^{-26}kg$ $q_{n}=0C$
Electron $m_{e}=9.1.10^{-31}kg$ $q_{e}=-1.6.10^{-19}C$

Remarque :
 -La masse $m_{P}=m_{n}=1836m_{e}$. La masse des électrons est $1836$ fois plus petite que celle du proton ; donc négligeable  par rapport à celle-ci
-Les charges des protons et des électrons sont identiques et ces particules sont en même nombre dans l’atome ; l'atome est donc électriquement neutre   
 3. Structure de l'atome  
 3.1. Le noyau  Le noyau est constitué de deux types de particules : les neutrons et les protons .
 Ces deux types particules constituants du noyau sont appelés nucléons  Chaque atome est caractérisé par :
 -le nombre de protons $Z$ qu’il renferme .Ce nombre est aussi appelé numéro atomique ou nombre de charge
 -le nombre de nucléons $A$ qu’il renferme .Ce nombre est aussi appelé nombre de masse : $A=Z+N
  N$ étant le nombre de neutrons  
  On symbolise le noyau des atomes par :
  $A = Z + N =$ nombre de masse d'un noyau, c'est le nombre de nucléons (protons + neutrons) qu'il contient.
  $Z =$ numéro atomique d'un noyau, c'est le nombre de protons qu'il contient.
Exemples : $^{12}_{6}C;^{16}_{8}O.^{1}_{1}H;^{14}_{7}N$
Exemples : $^{12}_{6}C$
Remarque :
Des atomes sont dits isotopes lorsqu’ils renferment le même  nombre  de protons mais de nombre de
nucléons (ou nombre de neutrons) différents  Exemples :$^{12}_{6}C , ^{13}_{6}C$ et $^{14}_{6}C;^{1}_{1}H,^{2}_{1}H$ et$ ^{3}_{1}H$  
3.2. Le nuage électronique  
3.2.1. Notion du niveau d’énergie
Les électrons d’un atome sont répartis en couche de niveau d’énergie différent. Pour arracher les électrons d’une même couche, il faut lui fournir la même énergie.
On dit que les électrons d’une même  couche  ont le même niveau  d’énergie  
Les couches sont désignées par des lettres $K, L, M, N, O, P, Q……$.
A chaque couche correspond un nombre entier positif$ n$

n $1$ $2$ $3$ $4$ $5$ $6$ $7$
Lettre K L M N O P Q

3.2.2. Règle de remplissage des couches
La répartition des électrons d’un atome sur les différentes couches ou niveaux d’énergie obéit à deux règles :
-la première règle ; le nombre maximal d’électrons pouvant à une couche est :$ N=2n^{2}$
Exemples :
Couche $K : N=2\times{1^{2}}\Longrightarrow{N=2}électrons $
Couche $L : N=2\times{2^{2}}\Longrightarrow{N=8}électrons$
Couche$ M : N=2\times{3^{2}}\Longrightarrow{N=18}électrons$
-la deuxième règle ; on remplit successivement les couches dans l’ordre $K, L, M, N…$..
Une couche ne commence à se remplir que si la précédente est saturée 
3.2.3. La configuration électronique 
Pour donner la structure électronique ou la .configuration électronique, on représente tous les électrons par des points (.) dans des cases portant autant de places disponibles dans une couche déterminée Nature

3.2.3. La formule électronique
On écrit la lettre qui correspond à chaque couche et on indique en exposant en haut à droite le nombre
d’électrons par couche
Exemples : $H (Z=1) :K^{1} ;  He (Z=2) : K^{2} ; Li (Z=3) :K^{2} L^{1}; C (Z=6) :K^{2} L^{4}; O (Z=8) :K^{2} L^{6} Al (Z=13) :K^{2} L^{8}M^{3}$
3.3. Structure de Lewis d’un atome La représentation de Lewis permet de mettre en évidence les électrons de la couche externe ou couche
périphérique. Les électrons célibataires sont représentés par des points (.) ; les doublets sont représentés par
un tiret (-) placé autour de l’élément considéré Exemples

Symbole H C N O P CI Na Ne


3.4. Valence d’un atome
Le nombre d’électrons célibataires que possède l’élément est la valence Symbole H C N O P Cl Représentation de Lewis

4. Masse de l’atome
La masse M de l’atome est la relation suivante :
 $M=m_{mnoyau}+m_{éléctrons}\Longrightarrow{M=Zm_{p}+Nm_{n} +Zm_{e}}$
  Si$ m_{p} =m_{n} \Longrightarrow{M=Zm_{p}+Nm_{p} +Zm_{e}}\Longrightarrow= (Z+N) m_{p} +Zm_{e}\Longrightarrow{  M=Am_{p}} +Zm_{e}$
 Si on néglige la masse des électrons\Longrightarrow{  M=Am_{p}}$  
5. Structure lacunaire de l’atome
 La matière de l’atome est essentiellement concentrée dans son noyau. Les électrons tournent autour du noyau.
Les distances  séparant le noyau des électrons sont très  grandes. Ainsi, la plus grandes partie (volume) est constituée de vide.
On dit que l’atome a une structure lacunaire  
 III. Classification périodique des éléments chimiques
1. Principe de la classification
 -Les éléments chimiques sont classés par numéro atomique $Z$ croissant ;
 -Les éléments dont les atomes ont le même nombre d’électrons sur leur couche externe sont disposés dans une même colonne verticale et constituent un groupe ou une famille
-Chaque ligne ou période correspond au  remplissage  d’une couche électronique
 2. Tableau simplifié  
 Le tableau simplifié comporte trois lignes ou périodes et huit colonnes ou groupe GROUPES

3. Intérêt de la classification périodique 
Les atomes des éléments de même colonne ont le  même nombre d’électrons périphériques. Ils ont des
propriétés chimiques semblables et forment un groupe ou famille  Considérons quelques exemples : 
3.1. La famille des métaux alcalins.
- A l’exception de l’hydrogène, les éléments de la première colonne constituent le groupe des alcalins.
-  Ils ont la même structure électronique externe. Il possède $1$ électron sur la couche électronique externe. 
$Li $(Lithium) ;$ Na$ (Sodium) ; $K$ (Potassium)
- Les corps simples correspondant à ces éléments sont appelés les métaux alcalins.
- Ce sont des corps mous, légers à l’éclat métallique, très réactifs chimiquement.
- Ils sont oxydés par le dioxygène de l’air.
Il faut les conserver dans le pétrole, à l’abri de l’air.
3.2. La famille des Halogènes.
-Les éléments de la 7ième colonne constituent la famille des Halogènes.  
Ces éléments possèdent la même structure électronique externe à $7$ électrons. $F$ (Fluor) ; $Cl$ (Chlore) ; $Br$ (brome) ; $I$ (iode
-Ils existent sous la forme de molécules diatomiques :
-Le difluor, le dichlore (gaz jaune-vert), le dibrome (liquide jaune-orangé), le diiode (solide violet foncé).
3.3. La famille des gaz nobles.
-Ce sont les éléments de la dernière colonne.
- L’Hélium mis à part, ils possèdent une structure externe à huit électrons appelée octet d’électrons. $He$ (Hélium);  $Ne$ (Néon) ; $Ar$ (Argon)  
-Ils possèdent une grande stabilité chimique. Ce sont des gaz monoatomiques, on les appelle les gaz rares ou gaz inertes
4. Les ions monoatomiques  Certains  atomes peuvent perdre ou gagner des électrons et deviennent des ions simples 4.1. Les cations  Un cation ou ion positif provient d’un atome qui a perdu un ou plusieurs électron(s)

 

Solution des exercices : acide - base - Ts

Classe: 
Terminale
 

Exercice 1

1) Masse de carbone, d'hydrogène et d'oxygène contenue dans l'échantillon.
 
$\begin{array}{lcl} \dfrac{m_{C}}{M_{C}}&=&\dfrac{m_{CO_{2}}}{M_{CO_{2}}}\\&\Rightarrow& m_{C}=m_{CO_{2}}\dfrac{M_{C}}{M_{CO_{2}}}\\&=&2.7\times\dfrac{12}{44}\\&\Rightarrow& m_{C}=0.74\,g \end{array}$
 
$\begin{array}{lcl} m_{H}&=&m_{H_{2}O}\dfrac{2M_{H}}{M_{H_{2}O}}\\&=&1.1\times\dfrac{2\times 1.0}{18}\\&\Rightarrow& m_{H}=0.12\,g \end{array}$
 
$\begin{array}{lcl} m_{O}&=&m-\left(m_{C}+m_{H}\right)\\&=&1.35-(0.74+0.12)\\&\Rightarrow& m_{O}=0.49\,g \end{array}$
 
2) a) Pourcentage massique centésimal :
 
$-\ $ en carbone :
 
$\begin{array}{lcl} \%C&=&\dfrac{m_{C}\times 100}{m}\\&=&\dfrac{0.74\times 100}{1.35}\\&\Rightarrow& \%C=55 \end{array}$
 
$-\ $ en hydrogène :
 
$\begin{array}{lcl} \%H&=&\dfrac{m_{H}\times 100}{m}\\&=&\dfrac{0.12\times 100}{1.35}\\&\Rightarrow& \%H=9.0 \end{array}$
 
$-\ $ en oxygène :
 
$\begin{array}{lcl} \%O&=&\dfrac{m_{O}\times 100}{m}\\&=&\dfrac{0.49\times 100}{1.35}\\&\Rightarrow& \%C=36 \end{array}$
 
b) Montrons que la formule de $A$ est $C_{4}H_{8}O_{2}$ 
 
Soit $C_{x}H_{y}O_{z}$ le composé $A$
 
$\begin{array}{lcl} \dfrac{12x}{\%C}&=&\dfrac{y}{\%H}\\&=&\dfrac{16z}{\%O}\\&=&\dfrac{M}{100}\\&\Rightarrow& x=\dfrac{\%C\times M}{12\times 100}\\&=&\dfrac{55\times 88}{12\times 100}\\&\Rightarrow& x=4 \end{array}$
 
$\begin{array}{lcl}\text{Par analogie }y&=&\dfrac{\%H\times M}{1.0\times 100}\\&=&\dfrac{9.0\times 88}{1.0\times 100}\\&\Rightarrow& y=8 \end{array}$
 
$\begin{array}{lcl}z&=&\dfrac{\%O\times M}{16\times 100}\\&=&\dfrac{36\times 88}{16\times 100}\\&\Rightarrow& z=2 \end{array}$
 
D'où la formule brute : $C_{4}H_{8}O_{2}$
 
3) a) Un acide est une entité chimique capable de céder au moins un proton.
 
b)  Équation chimique de la réaction de l'acide dans l'eau
 
$C_{3}H_{7}COOH+H_{2}O\ \rightarrow\ C_{3}H_{7}COO^{-}+H_{3}O^{+}$
 
c) les couples acide-base mis en jeu sont :
 
$H_{3}O^{+}|H_{2}O\text{ et }C_{3}H_{7}COOH|C_{3}H_{7}COO^{-}$
 
d) concentration molaire $C$ de la solution
 
$\begin{array}{lcl} C&=&\dfrac{n}{V}\\&=&\dfrac{0.1}{500\cdot 10^{-3}}\\&\Rightarrow& C=0.2\,mol\cdot L^{-1} \end{array}$

Exercice 2

1) Masse de cristaux à peser pour préparer $S_{o}$
 
$\begin{array}{lcl} m&=&n\times M\\&=&C\times V\times M\\&=&0.1\times 100\cdot 10^{-3}\times(12\times 6+6\times 1.0+2\times 16)\\&\Rightarrow& m=1.1\,g \end{array}$
 
2) a) Équation bilan de la réaction de l'acide benzoique avec l'eau
 
$C_{6}H_{5}COOH+H_{2}O\ \rightarrow\ C_{6}H_{5}COO^{-}+H_{3}O^{+}$
 
Montrons que l'acide benzoique n'est pas un acide fort
 
Pour un acide fort, $pH=-\log\,C$
 
$-\log\,C_{0}=-\log\,0.1=-\log\,10^{-1}=1\neq\,pH(pH=2.6)$
 
L'acide benzoique n'est pas un acide fort.
 
b) Détermination du coefficient de dissociation
 
Electroneutralité de la solution : $\left[H_{3}O^{+}\right]=\left[HO^{-}\right]+\left[C_{6}H_{5}COO^{-}\right]$, solution acide on néglige les ions $HO^{-}$ devant les ions $H_{3}O^{+}\Rightarrow\left[C_{6}H_{5}COO^{-}\right]=\left[H_{3}O^{+}\right]=10^{-pH}$
 
$\begin{array}{lcl} \alpha_{0}&=&\dfrac{\left[C_{6}H_{5}COO^{-}\right]}{C_{0}}\\&=&\dfrac{10^{-pH}}{C_{0}}\\&=&\dfrac{10^{-2.6}}{0.1}\\&\Rightarrow&\alpha_{0}=0.025 \end{array}$
 
3) Le coefficient $\alpha_{1}$ de l'acide dans la solution $S_{1}$
 
$\begin{array}{lcl} \alpha_{1}&=&\dfrac{\left[C_{6}H_{5}COO^{-}\right]}{C_{1}}\\&=&\dfrac{10^{-pH}}{\dfrac{C_{0}}{10}}\\&=&\dfrac{10^{1}\times 10^{-pH}}{C_{0}}\\&=&\dfrac{10^{-pH+1}}{C_{0}}\\&=&\dfrac{10^{-3.1+1}}{0.1}\\&\Rightarrow&\alpha_{1}=0.079 \end{array}$

Conclusion : 

On remarque que $\alpha_{1}>\alpha_{0}$ donc la dissociation augmente avec la dilution

Exercice 3

1) a) Si l'acide benzoique était un acide fort, il réagirait totalement avec l'eau. 
 
Pour une solution de concentration $c=1.0\cdot 10^{-2}mol\cdot L^{-1}\;,\ \left[H_{3}O^{+}\right]=c.$
 
Ici le $pH$ est égale à $3.1$ donc $\left[H_{3}O^{+}\right]=10^{-3.1}mol\cdot L^{-1}=7.9\cdot 10^{-4}mol\cdot L^{-1}\;,\ \left[H_{3}O^{+}\right]\neq c$
 
L'acide benzoique est un acide faible.
 
1) b) $C_{6}H_{5}COOH+H_{2}O\leftrightarrows C_{6}H_{5}COO^{-}+H_{3}O^{+}$
 
$K_{a}=\dfrac{\left[H_{3}O^{+}\right]\left[C_{6}H_{5}COO^{-}\right]}{\left[C_{6}H_{5}COOH\right]}$
 
2)a) Pour une base forte $pH=14+\log\,C$
 
Pour l'ion benzoate est une base faible.
 
2) b) $C_{6}H_{5}COO^{-}+H_{2}O\leftrightarrows C_{6}H_{5}COOH+HO^{-}$
 
$K_{R}=\dfrac{\left[HO^{-}\right]\left[C_{6}H_{5}COOH\right]}{\left[C_{6}H_{5}COO^{-}\right]}=\dfrac{K_{e}}{K_{a}}=1.6\cdot 10^{-10}$
 
3) a) $pH>pK_{a}$ donc la base du couple prédomine :
 
3) b)
 
 
3) c) $C_{6}H_{5}COOH+HO^{-}\longrightarrow\ C_{6}H_{5}COO^{-}+H_{2}O$
 
$$K_{R}=\dfrac{\left[C_{6}H_{5}COO^{-}\right]}{\left[C_{6}H_{5}COOH\right]\left[HO^{-}\right]}=\dfrac{K_{a}}{K_{e}}$$
 
$K_{R}=10^{14-4.2}=6.3\cdot 10^{9}>10^{4}$
 
La constance de réaction est très grande: la réaction peut être considérée comme totale.
 
4) La quantité initiale de chaque espèce n'est pas modifiée lors du mélange. 
 
Les deux solution $S_{1}$ et $S_{2}$ ont la même concentration et on en prélève le même volume ; l'acide benzoique et l'ion benzoate ont donc même concentration dans le mélange.
 
Comme $pH=pKa+\log\dfrac{B}{A}\;,\ \text{or }[B]=[A]\Rightarrow\,pH=pKa=4.2$

Exercice 4

1) a) La formule brute d'un acide carboxylique est :
 
$C_{n}H_{2n+1}COOH\text{ ou }R-COOH$ 
 
Montrons que sa masse molaire s'écrit sous la forme : $M=14n+32$
 
$M=M_{C_{n}H_{2n}O_{2}}=12n+2n+2\times 16=14n+32$
 
b) Formule semi-développée et nom de chaque isomère
 
$M=88\,g\cdot mol^{-1}\Rightarrow 14n+32=88\Rightarrow n=4$
 
D'où $C_{3}H_{7}-COOH$ 
 
$CH_{3}-CH_{2}-CH_{2}-COOH$ : acide butanoique
 
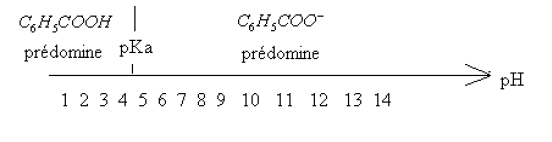
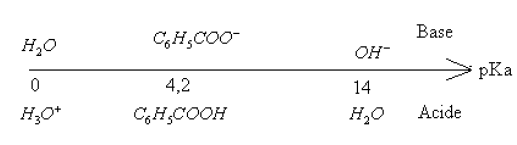
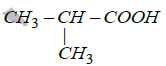  : acide $2-$methylpropanoique
                        
 
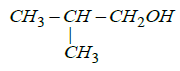2) a) La réaction est une réaction d'oxydation
 
b) Formule semi-développée, nom et classe de l'alcool
 
    : $2-\text{methylpropan}-1-\text{ol}$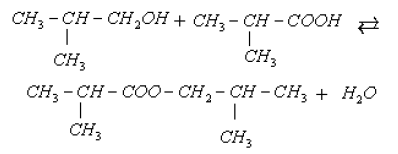
                           
 
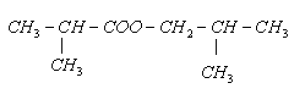Classe : alcool primaire
 
3) a) La réaction est une réaction d'estérification directe
 
b) équation chimique de la réaction
 
 
d) Nom de l'ester formé :
 
 $2-\text{méthylpropate}-2-\text{méthylpropyle}$
                             
                              
4) a) Calcule de la masse $m$
 
$\begin{array}{lcl} m&=&n\times M\\&=& CV\times M\\&=&0.01\times 100\cdot 10^{-3}\times 88\\&\Rightarrow&\boxed{m=88\,mg} \end{array}$
 
b) Calcule de la concentration en ion $H_{3}O^{+}$
 
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&10^{-pH}\\&=&10^{-3.9}\\&\Rightarrow&\left[H_{3}O^{+}\right]=1.3\cdot 10^{-4}mol\cdot L^{-1} \end{array}$
 
Pour un acide fort, $pH=-\log\,C$
 
$-\log\,C=-\log\,0.01=2\neq\,pH(pH=3.9)$
 
L'acide est donc un acide faible
 
c) Équation de dissociation de l'acide $A$ dans l'eau
 
$C_{3}H_{7}COOH+H_{2}O\ \rightarrow\ C_{3}H_{7}COO^{-}+H_{3}O^{+}$

Exercice 5

1) a) Montrons que le méthylamine est une base alors que $B$ est une base forte.
 
Pour une base forte
 
$pH=14+\log\,C$
 
Solution $S_{1}$
 
$-\ $ sans dilution : $pH_{1}=14+\log\,C_{1}=11.85$
 
$\begin{array}{lcl}-\ \text{Avec dilution : }pH_{1}&=&14+\log\dfrac{C_{1}}{10}\\&=&14+\log\,C_{1}-1\\&=&11.85-1\\&=&10.85\neq\,pH_{1}\left(pH_{1}=11.35\right) \end{array}$
 
Dans le méthylamine est une base faible.
 
Solution $S_{2}$ :
 
$-\ $ Sans dilution : $pH_{2}=14+\log\,C_{2}=12$
 
$\begin{array}{lcl}-\ \text{Avec dilution : }pH_{2}&=&14+\log\dfrac{C_{2}}{10}\\&=&14+\log\,C_{2}-1\\&=&12-1\\&=&11\\&=&pH_{2} \end{array}$
 
$B$ est donc une base forte.
 
b) Calcule de la concentration $C_{2}$
 
$\begin{array}{lcl} pH_{2}&=&14+\log\,C_{2}\\&\Rightarrow& C_{2}=10^{pH_{2}-14}\\&=&10^{12-14}\\&\Rightarrow&\boxed{C_{2}=10^{-2}mol\cdot L^{-1}} \end{array}$
 
c) Préparation de la solution
 
2) Établissement de la relation $pH=\dfrac{1}{2}(pKa+pKe+\log\,C)$ vérifiée par la solution $S_{1}.$
 
Espèces chimiques en solution :
 
$H_{3}O^{+}\ ;\ HO^{+}\ ;\ CH_{3}NH_{2}\ ;\ CH_{3}NH_{3}^{+}\ ;\ H_{2}O$
 
Electroneutralité de la solution :
 
$\left[H_{3}O^{+}\right]+\left[CH_{3}NH_{3}^{+}\right]=\left[HO^{-}\right]$
 
$\left[HO^{-}\right]>>\left[H_{3}O^{+}\right]$ (Solution basique)
 
$\Rightarrow\left[CH_{3}NH_{3}^{+}\right]=\left[HO^{-}\right]=\dfrac{K_{e}}{\left[H_{3}O^{+}\right]}$
 
Conservation de la matière :
 
$\left[CH_{3}NH_{3}^{+}\right]+\left[CH_{3}NH_{2}\right]=C$ la base faible se dissocie faiblement
 
$\Rightarrow\left[CH_{3}NH_{2}\right]=C$
 
$\begin{array}{lcl} K_{a}&=&\dfrac{\left[CH_{3}NH_{2}\right]\left[H_{3}O^{+}\right]}{\left[CH_{3}NH_{3}^{+}\right]}\\&=&\dfrac{C\left[H_{3}O^{+}\right]}{\dfrac{K_{e}} {\left[H_{3}O^{+}\right]}}\\&=&\dfrac{C\left[H_{3}O^{+}\right]^{2}}{K_{e}}\\&\Rightarrow&\left[H_{3}O^{+}\right]^{2}=\dfrac{K_{a}\times K_{e}}{C}\\&\Rightarrow&-\log\left[H_{3}O^{+}\right]^{2}=-\log\dfrac{1}{C}\\&\Rightarrow&2pH=pK_{a}+pK_{e}+\log\,C\\&\Rightarrow& pH=\dfrac{1}{2}\left(pK_{a}+pK_{e}+\log\,C\right) \end{array}$
 
3) Valeur du $pK_{a}$
 
Pour $\log\,C=0$ on a $pH=\dfrac{1}{2}\left(pK_{a}+pK_{e}\right)$
 
$\Rightarrow pK_{a}=2pH-pK_{e}$
 
$pK_{a}=2\times 12.35-14=10.7$
 
Concentration de la solution
 
$\begin{array}{lcl}pH&=&\dfrac{1}{2}\left(pK_{a}+pK_{e}+\log\,C\right)\\&\Rightarrow&\log\,C=2pH\left(pK_{a}+pK_{e}\right)\\&\Rightarrow&C=10^{2pH\left(pK_{a}+pK_{e}\right)}\\&=&10^{2\times10.85(10.7+14)}\\&\Rightarrow&C=10^{-3}mol\cdot L^{-1} \end{array}$

Exercice 6

1) a) Un acide est fort, s'il s'ionise totalement dans l'eau.
 
Un acide est faible s'il s'ionise partiellement dans l'eau.
 
b) Pour un acide fort $pH=-\log\,C$
 
Pour une même concentration $C=10^{-2}mol/L\ ;\ pH=-\log\,10^{-2}=2.$
 
Donc on peut conclure que $A_{2}H$ est un acide fort et $A_{1}H$ ; $A_{3}H$ et $A_{4}H$ sont des acides faibles.
 
2) a) Calcule des coefficients de dissociation pour chaque acide faible
 
$AH\ +\ H_{2}O\ \leftrightarrows\ A^{-}\ +\ H_{3}O^{+}$
 
$\alpha=\dfrac{[AH]_{d}}{[AH]_{i}}=\dfrac{[A^{-}]}{C}=\dfrac{\left[H_{3}O^{+}\right]}{C}=\dfrac{10^{-pH}}{C}$
 
$\left\lbrace\begin{array}{lcl} d&:&\text{dissocié}\\ i&:&\text{initial}\end{array}\right.$
 
$\alpha_{1}=\dfrac{10^{-3.4}}{10^{-2}}\Rightarrow\alpha_{1}=0.039$,
 
$\alpha_{3}=\dfrac{10^{-5.6}}{10^{-2}}\Rightarrow\alpha_{3}=0.25\cdot 10^{-3}$,
 
$\alpha_{4}=\dfrac{10^{-2.9}}{10^{-2}}\Rightarrow\alpha_{4}=0.13$
 
$\alpha_{4}>\alpha_{1}>\alpha_{3}.$
 
La force de l'acide croit avec le coefficient de dissociation ; d'où le classement :
 
 
b) Relation entre la constante d'acide $K_{a}$ et le coefficient de dissociation $\alpha$
 
                  $AH\ +\ H_{2}O\ \leftrightarrows\ A^{-}\ +\ H_{3}O^{+}$
 
$t=0$         $C$       excès                              $0$            $0$
 
$t\neq0$    $C-x$     excès                              $x$           $x$
 
$\alpha=\dfrac{x}{C}\Rightarrow x=\alpha\times C$
 
$\begin{array}{lcl} K_{a}&=&\dfrac{\left[H_{3}O^{+}\right][A^{-}]}{[AH]}\\&=&\dfrac{x\times x}{C-x}\\&=&\dfrac{\alpha C\times\alpha C}{C-\alpha\times C}\\&=&C\dfrac{\alpha^{2}}{1-\alpha} \end{array}$
 
c) Calcule de la constante d'acide de chaque acide faible
 
$K_{\alpha_{1}}=C\dfrac{\alpha_{1}^{2}}{1-\alpha_{1}}=10^{-2}\dfrac{0.039^{2}}{1-0.039}=1.6\cdot10^{-5}$,
 
$K_{\alpha_{3}}=C\dfrac{\alpha_{3}^{2}}{1-\alpha_{13}}=10^{-2}\dfrac{\left(0.25\cdot 10^{-3}\right)^{2}}{1-0.25\cdot 10^{-3}}=6.3\cdot10^{-10}$,
 
$K_{\alpha_{4}}=C\dfrac{\alpha_{4}^{2}}{1-\alpha_{4}}=10^{-2}\dfrac{(0.13)^{2}}{1-0.13}=1.9\cdot10^{-4}$,
 
$K_{\alpha_{4}}>K_{\alpha_{1}}>K_{\alpha_{3}}.$
 
La force de l'acide croit avec la constante de dissociation d'ou le classement :
 
 
5) La nouvelle valeur du coefficient de dissociation de $A_{1}H$
 
$\begin{array}{lcl} \alpha_{1}&=&\dfrac{10^{-pH}}{C'}\\&=&\dfrac{10^{-pH}}{\dfrac{C}{10}}\\&=&\dfrac{10^{-pH+1}}{C}\\&=&\dfrac{10^{-3.9+1}}{10^{-10}}\\&=&0.13 \end{array}$
 
$\alpha_{1}>\alpha_{1}.$
 
La dilution a pour effet de déplacer l'équilibre chimique dans le sens de la dissociation de l'acide.
 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Pages