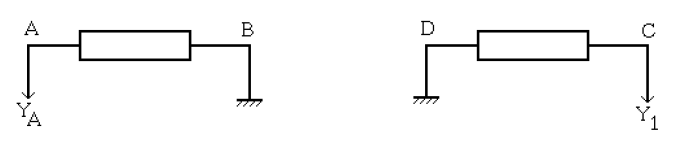Physique

Solutions des exercices : Mélanges et corps purs - 4e

Classe: 
Quatrième
 

Exercice 1

Encadrons la lettre correspondant à la bonne réponse.
 
Un mélange dans lequel on peut distinguer les différents constituants à l'œil nu est un mélange dit
 
a) Homogène
 
$\boxed{\text{b) hétérogène}}$
 
c) stable
 

Exercice 2

On dispose des mélanges suivants :
 
a) eau de mer ;
 
b) eau de ruissellement ;
 
c) eau minérale ;
 
d) jus de bissap ;
 
e) fer+soufre ;
 
f) huile + eau
 
Complétons le tableau ci-dessous en écrivant la lettre correspondant à chaque mélange dans la colonne qui convient
$$\begin{array}{|c|c|} \hline \text{Mélange homogène}&\text{Mélange hétérogène}\\ \hline a\;,\ c\;,\ d&b\;,\ e\;,\ f\\ \hline \end{array}$$
 

Exercice 3

a) eau de mer ;
 
b) eau de ruissellement ;
 
c) eau minérale ;
 
d) jus de bissap ;
 
e) fer + soufre ;
 
f) huile + eau
 
Donnons pour chaque mélange la méthode de séparation appropriée
$$\begin{array}{|c|l|} \hline \text{Mélanges}&\text{Méthodes de séparations}\\ \hline a&\text{Décantation}\\ \hline b&\text{Filtration}\\ \hline c&\text{Distillation fractonnée}\\ \hline d&\text{Distillation fractonnée}\\ \hline e&\text{Triage magnétique}\\ \hline f&\text{Décantation}\\ \hline \end{array}$$
 
Choisissons la bonne réponse.
 
On peut séparer l'eau et le sucre par :
 
$\centerdot\ $ Décantation
 
$\centerdot\ $ Filtration
 
$\boxed{\centerdot\ \text{Distillation}}$

Exercice 4 

Complétons le texte par les mots suivants :
 
filtration, potable, hétérogène, décantation, homogène.
 
Une ménagère a ramené de l'eau du fleuve.
 
Cette eau est un mélange hétérogène.
 
Elle la laisse au repos dans la bassine pendant une demi-heure, des substances étrangères se déposent au fond du récipient par décantation.
 
Elle verse l'eau dans un canari à travers un morceau à gaze. L'opération s'appelle la filtration. 
 
Le filtrat est un mélange homogène.
 
Puis, elle y introduit quelques gouttes d'eau de javel pour rendre l'eau potable. 
 

Exercice 5

La chambre de Samba a les dimensions suivantes :
$$h=3\;m\;;\ \ell=3.30\;m\;;\ L=3.5\;m$$
1) Calculons le volume d'air $V_{\text{air}}$ renfermant cette chambre.
 
La chambre de Samba étant de forme parallélépipédique alors, son volume $V$ est donné par :
 
$\begin{array}{rcl} V&=&L\times\ell\times h\\&=&3.5\times 3.30\times 3\\&=&34.65\;m^{3}\end{array}$
 
Comme le volume d'air renfermant cette chambre est équivalent à $V$ alors, on obtient :
$\boxed{V_{\text{air}}=34.65\;m^{3}}$
 
2) Calculons le volume de dioxygène disponible pour samba.
 
Dans la composition volumique de l'air nous distinguons :
 
$\centerdot\ \ 78\%$ de diazote
 
$\centerdot\ \ 21\%$ de dioxygène
 
$\centerdot\ \ 1\%$ de gaz rare
 
De ce fait, dans les $34.65\;m^{3}$ d'air renfermant la chambre de Samba, les $21\%$ sont du dioxygène.
 
Soit alors $V_{_{O_{2}}}$ ce volume de dioxygène.
 
On a : $V_{_{O_{2}}}=21\%V_{\text{air}}=\dfrac{21\times V_{\text{air}}}{100}$
 
A.N : $V_{_{O_{2}}}=21\%V_{\text{air}}=\dfrac{21\times 34.65}{100}=7.276$
 
D'où, $\boxed{V_{_{O_{2}}}=7.276\;m^{3}}$
 
Ainsi, Samba dispose de $7.276\;m^{3}$ de dioxygène.
 
3) Calculons le volume de diazote présent dans la chambre de Samba
 
Pour calculer ce volume $V_{_{N_{2}}}$ de diazote, on applique la même approche que dans la question 2).
 
Comme $V_{_{N_{2}}}=78\%V_{\text{air}}$ alors, $V_{_{N_{2}}}=\dfrac{78\times 34.65}{100}=27.027$
 
Soit : $\boxed{V_{_{N_{2}}}=27.027\;m^{3}}$
 

Exercice 6

A partir d'une eau boueuse et salée, on peut obtenir :
 
1) une eau limpide et salée, par filtration
 
2) une eau limpide non salée, par distillation
 

Exercice 7

Recopions et mettons une croix devant la bonne réponse.
 
1) On peut distinguer deux constituants d'un mélange
 
$\centerdot\ $ homogène
 
$\centerdot\ $ hétérogène $\ \boxed{\times}$
 
2) La filtration permet de séparer les constituants d'un mélange
 
$\centerdot\ $ homogène
 
$\centerdot\ $ hétérogène $\ \boxed{\times}$
 
3) Pour séparer les constituants d'un mélange homogène, on peut utiliser
 
$\centerdot\ $ une décantation
 
$\centerdot\ $ une distillation $\ \boxed{\times}$
 
4) Lorsqu'on laisse reposer un mélange, on réalise
 
$\centerdot\ $ une décantation $\ \boxed{\times}$
 
$\centerdot\ $ une distillation

Exercice 8

Modou explique à Fatou comment on fabrique du "Café Touba" : il lui indique les trois (3) étapes que comprend cette préparation.
 
$1^{ère}$ étape : mettre de l'eau dans une cafetière, porter l'eau à l'ébullition puis ajouter la poudre de  "Café Touba" et attendre quelles minutes.
 
$2^{ème}$ étape : Faire passer le mélange obtenu à travers un tissu pour recueillir la partie liquide.
 
$3^{ème}$ étape : Ajouter du sucre à volonté et remuer à l'aide d'une cuillère.
 
Le "Café Touba" est prêt.
 
A la fin de la $1^{ère}$ étape, on obtient un mélange hétérogène parce qu'on peut distinguer, à l'œil nu, les particules solides du café dans le mélange.
 
La méthode de séparation utilisée dans la $2^{ème}$ étape est la filtration.
 
En chimie, le liquide obtenu après filtration est appelé : filtrat (qui est un mélange homogène)
 
Le filtrat n'est pas un corps pur.
 
A la fin de la $3^{ème}$ étape, on obtient un mélange homogène.
 
En effet, le filtrat est tout d'abord un mélange homogène et lorsque le sucre ajouté sera dissout dedans, on n'arrivera plus à distinguer, à l'œil nu, le sucre du filtrat.
 
Ce qui veut dire que le mélange final du "Café Touba" est un mélange homogène.

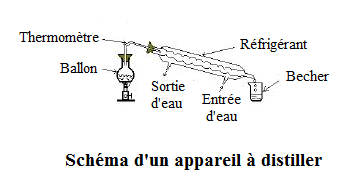
Exercice 9

Le schéma ci-dessous est celui de la distillation de l'eau salée.
 
1) Donnons les éléments manquants des annotations

 

 
2) Les changements d'états physiques qu'on y rencontre sont les suivants :
 
$-\ \ $ La vaporisation
 
Ce changement d'état se produit dans le ballon. L'eau se transforme en vapeur sous l'effet de l'augmentation de la température qui atteint $100^{\circ}C$
 
$-\ \ $ La liquéfaction
 
Ce changement d'état se déroule dans le réfrigérant. Les vapeurs d'eau se refroidissent et se condensent pour donner des gouttes d'eau.
 
3) Le corps obtenu, encore appelé distillat, est de l'eau ; un corps pur dont quelques-unes de ses propriétés sont :
 
$-\ \ $ Température d'ébullition $100^{\circ}C$
 
$-\ \ $ Température de fusion $0^{\circ}C$
 
$-\ \ $ Masse volumique $1000\;kg.m^{-3}$
 

Exercice 10

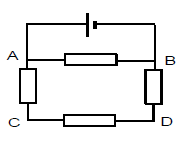
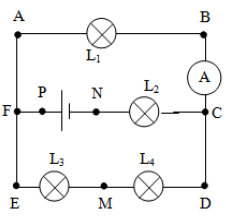
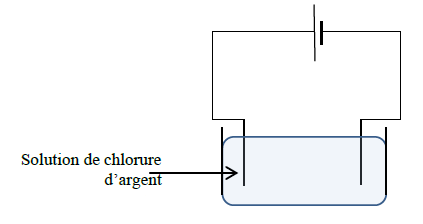
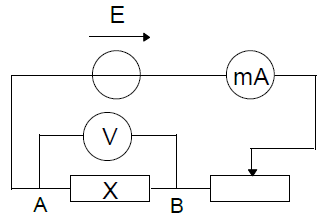
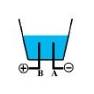
Le schéma ci dessous est un élément du montage expérimental de l'électrolyse de l'eau.

 

 
1) Précisons les noms respectifs des électrodes $A\ $ et $\ B.$
 
$\centerdot\ \ A\ $ est appelé Cathode : c'est l'électrode reliée à la borne négative de l'électrolyseur
 
$\centerdot\ \ B\ $ est appelé Anode : c'est l'électrode reliée à la borne positive de l'électrolyseur
 
2) Le gaz recueilli sur l'électrode $A$ est du dihydrogène et le gaz recueilli sur l'électrode $B$ est du dioxygène.
 
3) Pour mettre en évidence le dihydrogène, on approche une flamme à la cathode $A$, cela provoque alors une détonation. Ce qui montre la présence du dihydrogène.
 
Pour caractériser le dioxygène, on approche une bûchette en incandescence à l'anode $B.$ On constate alors que la bûchette se rallume. Ce qui met en évidence la présence du dioxygène.

Exercice 11

Faisons correspondre par une flèche chaque expression à la bonne réponse.
$$\begin{array}{|lcl|}\hline\text{Mélange}&\longrightarrow&\text{Association de deux ou de plusieurs}\\&&\text{substances}\\ \hline\text{Corps pur simple}&\longrightarrow&\text{Un corps qui ne peut pas se}\\&&\text{décomposer en d'autres corps}\\ \hline\text{Mélange homogène}&\longrightarrow&\text{Mélange dans lequel on ne peut pas}\\&&\text{distinguer ses différents constituants}\\ \hline\text{Corps pur composé}&\longrightarrow&\text{Un corps qui peut se décomposer en}\\&&\text{d'autres corps}\\ \hline\text{Mélange hétérogène}&\longrightarrow&\text{Association de plusieurs substances}\\ &&\text{qu'on peut distinguer}\\ \hline&&\text{Transformation qui ne modifie pas la}\\&&\text{nature des corps}\\ \hline\end{array}$$
 

Exercice 12

On dispose des mélanges suivants :
 
$\centerdot\ $ eau de mer
 
$\centerdot\ $ eau de ruissellement
 
$\centerdot\ $ eau minérale
 
$\centerdot\ $ jus de bissap
 
$\centerdot\ $ fer + souffre
 
$\centerdot\ $ huile + eau
 
Reproduisons le tableau ci-dessous et écrivons chaque mélange dans la colonne qui convient
$$\begin{array}{|l|l|}\hline\text{Mélange homogène}&\text{Mélange hétérogène}\\ \hline\text{eau de mer}&\text{eau de ruissellement}\\ \text{eau minérale}&\text{fer + souffre}\\ \text{jus de bissap}&\text{huile + eau}\\ \hline\end{array}$$
 

Exercice 13

Recopions et complétons les phrases ci-dessous avec les expressions suivantes :
 
filtration, mélange homogène, mélange hétérogène, décantation, distillation, de l'eau.
 
1) Dans un jus d'orange, il y a de la pulpe d'orange, du sucre, et de l'eau. La pulpe se dépose :
 
le jus d'orange constitue un mélange hétérogène.
 
Le jus filtré est un mélange homogène.
 
2) La boue se dépose au fond d'un lac par décantation.
 
L'eau qui pénètre dans le sol, traverse les couches de sable par filtration et devient limpide.
 
3) Lors d'une pénurie d'eau, une ménagère puise de l'eau dans un puits.
 
Cette eau est un mélange hétérogène.
 
Elle la laisse au repos dans un récipient pendant quelques minutes.
 
Des particules lourdes se déposent au fond du récipient par décantation.
 
Elle transvase l'eau dans une bassine à travers un morceau de gaze pour retenir les particules légères :
 
cette opération appelée filtration ; elle donne un mélange homogène.
 

Exercice 14

Proposons une méthode de séparation appropriée pour chacun des mélanges ci-dessous.
 
1) Fer et soufre : Triage magnétique
 
2) Eau et sucre : Distillation
 
3) Eau et huile : Décantation
 
4) Farine et grain de mil : Tamissage
 
5) Sable et eau : Filtration
 

Exercice 15

Recopions le tableau et indiquons la nature (corps pur, mélange, corps pur simple, corps pur composé) de la substance.
$$\begin{array}{|l|l|}\hline\text{Substance}&\text{Nature de la substance}\\ \hline\text{Eau salée}&\text{mélange}\\ \hline\text{Jus de bissap}&\text{mélange}\\ \hline\text{Pain}&\text{mélange}\\ \hline\text{Dioxyde de carbone}&\text{corps pur composé}\\ \hline\text{Eau distillée}&\text{corps pur composé}\\ \hline\text{Dioxygène}&\text{corps pur simple}\\ \hline\end{array}$$

Exercice 16

Au cours d'une électrolyse de l'eau pure, un élève a recueilli $12.5\;cm^{3}$ d'un gaz qui rallume un brin incandescent.
 
1) Le gaz qui rallume un brin incandescent est caractéristique du dioxygène.
 
Il a été recueilli au niveau l'anode.
 
2) A l'autre électrode, plus précisément à la cathode, l'élève doit recueillir du dihydrogène.
 
Pour identifier ce gaz, on approche une flamme à la cathode, cela provoque alors une détonation. Ce qui montre la présence du dihydrogène.
 
Précisons son volume.
 
Pour cette expérience, nous savons que le volume de dihydrogène est le double de celui de dioxygène. Ainsi, 
$$\boxed{V_{_{H_{2}}}=2V_{_{O_{2}}}}$$
avec, $V_{_{O_{2}}}=12.5\;cm^{3}$
 
Par suite, $V_{_{H_{2}}}=2\times 12.5=25$
 
D'où, $\boxed{V_{_{H_{2}}}=25\;cm^{3}}$

Exercice 17

Dans un eudiomètre, on mélange $40\;cm^{3}$ de dioxygène et $40\;cm^{3}$ de dihydrogène.
 
On fait jaillir une étincelle électrique dans le mélange.
 
1) Montrons qu'il reste un gaz à la fin de l'opération.
 
Lorsqu'on fait jaillir une étincelle électrique dans le mélange, on va observer simultanément l'apparition d'une flamme sous l'effet du dioxygène suivie d'une détonation provoquée par la présence du dihydrogène.
 
La réaction qui s'est produite a utilisé des volumes de dioxygène $V_{_{O_{2}}}$ et de dihydrogène $V_{_{H_{2}}}$ tels que :
$$V_{_{H_{2}}}=2V_{_{O_{2}}}$$
Ainsi, pour faire réagir tout le dioxygène, on aura aussi besoin d'un volume de dihydrogène $V_{_{H_{2}}}$ tel que :
 
$\begin{array}{rcl} V_{_{H_{2}}}&=&2V_{_{O_{2}}}\\&=&2\times 40\;cm^{3}\\&=&80\;cm^{3}\end{array}$
 
Or, on ne dispose que de $40\;cm^{3}$ de dihydrogène, dans l'eudiomètre.
 
Donc, il n'y a pas assez de dihydrogène pour faire réagir en même temps tout le dioxygène du mélange.
 
Ce qui fait que tout le dioxygène ne va pas réagir.
 
Et par conséquent, il va encore rester du dioxygène dans l'eudiomètre, à la fin de l'opération.
 
2) Déterminons le volume du gaz restant.
 
D'après la question 1), le gaz restant est du dioxygène. Ce qui veut dire que tout le dihydrogène a réagi.
 
Par suite, le volume de dioxygène réagi $V_{_{O_{2}(\text{réagi})}}$ est tel que :
$$V_{_{H_{2}}}=2V_{_{O_{2}(\text{réagi})}}$$
D'où, $V_{_{O_{2}(\text{réagi})}}=\dfrac{V_{_{H_{2}}}}{2}=\dfrac{40\;cm^{3}}{2}=20\;cm^{3}$
 
Le volume de dioxygène restant $V_{_{O_{2}(\text{restant})}}$ sera donc donné par :
$$V_{_{O_{2}(\text{restant})}}=V_{_{O_{2}}}-V_{_{O_{2}(\text{réagi})}}$$
 
A.N : $V_{_{O_{2}(\text{restant})}}=40-20=20$
 
Ainsi, $\boxed{V_{_{O_{2}(\text{restant})}}=20\;cm^{3}}$
 

Exercice 18

Recopions et complétons les phrases ci-dessous
 
1) A la pression atmosphérique normale, la vaporisation et la liquéfaction de l'eau pure se produisent à la même température constante égale à $100^{\circ}C.$
 
2) La fusion et la solidification de l'eau pure se produisent à la température constante égale à $0^{\circ}C.$
 
3) Pour un corps pur, la température d'ébullition et la température de fusion sont des constantes physiques.

Exercice 19

Une chambre fermée a les dimensions suivantes :
 
Longueur $L=3.50\;m\ $ largeur $\ell=3.20\;m\ $ et hauteur $h=3.10\;m.$
 
1) Calculons le volume d'air contenu dans la salle.
 
Soit $V$ le volume de la salle.
 
Comme l'air remplit toute la salle alors, le volume d'air $V_{\text{air}}$ contenu dans cette salle sera égal au volume $V.$ On a :
$$V_{\text{air}}=V=L\times\ell\times h$$
A.N : $V_{\text{air}}=3.5\times 3.20\times 3.10=34.72$
 
D'où, $\boxed{V_{\text{air}}=34.72\;m^{3}}$
 
2) Déduisons-en les volumes de dioxygène et de diazote contenus dans la salle.
 
L'air contenu dans la salle étant constitué de 1/5 de dioxygène et 4/5 de diazote alors, on a : 
$$V_{_{O_{2}}}=\dfrac{1}{5}V_{\text{air}}\quad\text{et}\quad V_{_{N_{2}}}=\dfrac{4}{5}V_{\text{air}}$$
A.N : $V_{_{O_{2}}}=\dfrac{1}{5}\times 32.72=6.944\quad$ et $\quad V_{_{N_{2}}}=\dfrac{4}{5}\times 32.72=27.776$
 
Ainsi, $\boxed{V_{_{O_{2}}}=6.944\;m^{3}}\quad$ et $\quad \boxed{V_{_{N_{2}}}=27.776\;m^{3}}$

Exercice 20

Lorsqu'on sort une bouteille d'eau du réfrigérateur, ses parois extérieures se recouvrent de gouttelettes d'eau (buée).
 
Expliquons la provenance de cette buée.
 
Dans le réfrigérateur, la température est très basse. Donc, une bouteille d'eau sortie instantanément de ce réfrigérateur conserve la même température.
 
Ainsi, la vapeur d'eau contenu dans l'air, au contact avec les parois extérieures de la bouteille, se refroidit puis se condense pour enfin donner ces gouttelettes d'eau (buée).
 
On dit aussi que la vapeur d'eau contenu dans l'air s'est liquéfiée, au contact des parois extérieures de la bouteille.

Exercice supplémentaire

Exploitation d'un document
 
L'eau douce est rare dans les contrées désertiques ; or certaines d'entre elles, comme les pays du golfe persique, ont à leur portée d'immenses quantités d'eau de mer.
 
Cette inépuisable réserve d'eau, hélas, est inutilisable telle quelle, en raison de la présence du sel qui la rend impropre à la consommation et à l'irrigation des terres agricoles.
 
Aussi a-t-on pensé obtenir de l'eau douce à partir de l'eau de mer.
 
Le dessalement de l'eau de mer peut être pratiqué dans les usines situées à proximité des rivages.
 
L'eau de mer d'abord est portée à ébullition, puis la vapeur obtenue est liquéfiée. 
 
1) Donnons un titre à ce texte : Le dessalement de l'eau de mer
 
2) La technique utilisée pour rendre l'eau de mer propre à l'irrigation est la distillation.
 
3) Les passages du texte qui relatent les différentes étapes de cette technique sont :
 
"L'eau de mer d'abord est portée à ébullition, puis la vapeur obtenue est liquéfiée"
 
4) Après liquéfaction, on obtient un corps pur ; l'eau.
 
5) Les mesures que l'on doit effectuer pour vérifier la pureté du corps recueilli sont :
 
$-\ \ $ Température d'ébullition
 
$-\ \ $ Température de fusion
 
$-\ \ $ Masse volumique
 
Les résultats attendus sont :
 
$-\ \ $ Température d'ébullition $100^{\circ}C$
 
$-\ \ $ Température de fusion $0^{\circ}C$
 
$-\ \ $ Masse volumique $1000\;kg.m^{-3}$
 
 

Auteur: 
Aliou ndiaye

Série d'exercices : Les composés oxygénés - 1er s

Classe: 
Première
 

Exercice 1

Horizontalement

4) Son nom se termine par le suffixe one
 
6) Corps organiques qui renferment les éléments : carbone, hydrogène et oxygène
 
7) Composés oxygénés renferment le groupe carbonyle
 
9) ensemble de caractères chimiques associés à la présence dans une molécule d'un atome ou groupe d'atomes
 
10) Composé organique faisant partie de la famille des composés carbonylés
 
11) Composés oxygènes renfermant deux atomes d'oxygène et donnant un test négatif avec le $B.B.T$

Verticalement

1) Elle permet d'identifier la fonction et le nom du composé organique
 
2) Il caractérisé les aldéhydes et cétones
 
3) Test propre aux aldéhydes
 
5) Isomère de fonction de l'alcool
 
8) Nom générique des composés oxygénés dérivant des alcanes, contenant un groupement hydroxyle

Exercice 2

1) Compléter le tableau suivant :
$$\begin{array}{|c|c|c|} \hline \text{Fonction}&\text{Groupe caractéristique}&\text{Nom du groupe caractéristique}\\ \hline \text{Cétone}& &\\ \hline &-COOH&\\ \hline \text{Alcool}& &\\ \hline &-CHO&\\ \hline \text{Ester}& &\\ \hline \end{array}$$
 
2) Nommer les composés suivants. 
 
(Si c'est un alcool, préciser sa classe).
 
$CH_{3}-CHOH-CH_{2}-CH_{3}$
 
$CH_{3}-CH_{2}-CHO$
 
$CH_{3}-CH_{2}-COH-CH_{2}-CH_{3}$
$CH_{2}$
        $CH_{3}$
        
$CH_{3}-CO-CH_{2}-CH_{3}$
 
$CH_{3}-CH_{2}-CH-COOH$
  $CH_{3}$
  
$CH_{3}-CH_{2}-CH_{2}-CH_{2}-CO-O-CH_{2}-CH_{3}$

Exercice 3

1) Quel groupe caractérise un alcool ? 
 
Un aldéhyde ? 
 
Une cétone ?
 
2) Écrire la formules semi-développé de chacun des corps suivants en indiquant à quel groupe fonctionnel ils appartiennent
 
a) Méthanol
 
b) Butanone
 
c) Acide propanoique
 
d) Butanoate de méthyle
 
e) Butanal
 
f) Pentan$-2-$ol
 
g) $-2-$méthylpropan$-2-$ol
 
h) Acide$-2-$méthylpropanoique
 
i) Pentan$-3-$on
 
j) Butanoate d'éthyle
 
3) A quelle famille de composés organiques appartiennent les molécules suivantes (donner leur nom) :
 
$CH_{3}-CH_{2}-CH_{2}-CH_{2}-CH_{2}-CH_{2}-CHOH-CH_{3}$
 
$CH_{3}-CH_{2}-CH_{2}-CH_{2}-COOH-CH_{3}$
 
$CH_{3}-CH_{2}-CO-CH_{2}-CH_{2}-CH_{3}$
 
$CH_{2}-COH\left(CH_{3}\right)-CH_{3}$
 
$CH_{3}-CH_{2}-CH_{2}-CH\left(C_{2}H_{5}\right)-CO-CH_{3}$
 
$CH_{3}-CH_{2}-CH_{2}-CH\left(C{2}H_{5}\right)-CH_{2}OH$
 
$CH_{2}-CH\left(C{2}H_{5}\right)-CHO$

Exercice 4 : Étiquetage imprécis

La composition d'un liquide lave-glace mentionne la présence en proportion importante d'un composé $A$ de formule $C_{3}H_{8}O.$ 
 
Afin de lever le doute sur l'imprécision apportée par cette seule formule brute, le professeur propose à ses élèves de réaliser deux expériences :
 
$-\ $ oxydation ménagée de quelques $mL$ de liquide $A$ avec oxydant en défaut ;
 
$-\ $ analyse des produits de l'oxydation ménagée de $A.$ 
 
Le test avec la $2.4-DNPH$ est positif, mais celui avec la liqueur de Felhing est négatif.
 
1) Montrer que la formule brute $C_{3}H_{8}O$ conduit à deux formules semi-développées.
 
2) Nommer les deux isomères. 
 
Quel est leur groupe caractéristique ? 
 
Préciser leur classe.
 
3) Quel groupe caractéristique est mis en évidence dans les produits de l'oxydation de $A$ ? 
 
Justifier votre réponse.
 
4) Conclure sur la formule semi-développée du composé $A.$ 
 
Justifier.
 
5) On déshydrate $A.$ 
 
Nommer le composé obtenu et écrire l'équation bilan de la réaction.

Exercice 5 Identification de composés oxygénés

On dispose de cinq flacons contenant des liquides inconnus $A$, $B$, $C$, $D$ et $E$, tous différents mais de formule brute $C_{3}H_{x}O_{y}.$
 
Chaque composé ne présente qu'un seul groupe caractéristique oxygéné.
 
Les chaînes carbonées de ces composés ne contiennent ni double liaison, ni cycle.
 
Parmi les cinq composés, deux sont des alcools. 
 
L'oxydation de $A$ conduit à $C$ ou $D$ ; celle de $B$ conduit à $E.$
 
1) Ces données sont-elles suffisantes pour identifier les cinq composés ?
 
2) Le composé $C$ réagit avec la liqueur de Fehling, contrairement à $D.$ 
 
En déduire la formule semi-développée et le nom de ces cinq composés.

Exercice 6 : Pourcentage massique et formule d'alcools

On appelle pourcentage massique $P$ d'un élément dans une molécule, le quotient de la masse de cet élément dans une mole de molécules par la masse molaire de la molécule.
 
On considère un alcool $A$ qui a la même chaîne carbonée qu'un alcane comportant $n$ atomes de carbone.
 
1. Exprimer la formule brute de l'alcool en fonction de $n.$
 
2. En déduire l'expression de la masse molaire de $A$ en fonction de $n.$
 
3. Le pourcentage massique de l'élément oxygène dans la molécule $A$ est $P(O)=26.7\%.$
 
3.1 Déterminer la valeur de $n$ et la formule brute de $A.$ 
 
En déduire les formules semi-développées possibles pour $A.$
 
Identifier $A$ sachant que c'est un alcool primaire.

Exercice 7

L'analyse élémentaire d'un composé organique formé seulement de carbone, d'hydrogène et d'oxygène a montré qu'il contient $60\%$ en masse de carbone et $13.3\%$ d'hydrogène.
 
Sa masse molaire moléculaire est $M=60\,g\cdot mol^{-1}.$
 
1. Déterminer sa formule brute.
 
2. On réalise la combustion complète d'une masse $m=1.2\,g$ de ce composé.
 
2.1 Écrire l'équation de la réaction.
 
2.2 Calculer la masse de carbone et d'hydrogène dans cet échantillon.
 
2.3 En déduire la masse d'eau et le volume de dioxyde de carbone obtenus quand la réaction est terminée.
 
3. Donner les formules semi développées possibles de ce composé.
 
Donnée : 
 
$Mc=12\,g\cdot mol^{-1}$ ;
 
$Mo=16\,g\cdot mol^{-1}$ ; 
 
$MH=1\,g\cdot mol^{-1}$ ; 
 
$Vm=24\,L\cdot mol^{-1}$

Exercice 8

Deux alcools aliphatiques saturés isomères $(A_{1})$ et $(A_{2})$ ont une même masse molaire $M=74\,g\cdot mol^{-1}$
 
1. Montrer que leur formule brute est $C_{4}H_{10}O.$
 
2. On réalise leur oxydation ménagée par une solution de bichromate de potassium acidifiée.
 
$A_{1}$ ne donne rien
 
$A_{2}$ donne un composé $B_{2}$
 
$B_{2}$ donne un test positif avec la $D.N.P.H$ et un test négatif avec le réactif de Schiff.
 
2.1 Préciser en le justifiant la classe de chacun des alcools $(A_{1})$ et $A.$
 
2.2 Donner la formule semi développées et le nom de $B_{2}.$
 
2.3 Donner la formule semi développées et le nom de $A_{1}$ et $A_{2}$
 
3. On réalise la déshydratation intramoléculaire de $A_{1}$ en présence de l'acide sulfurique.
 
On obtient un composé organique $C_{1}.$
 
3.1 Écrire l'équation de la réaction en utilisant les formules semis développées.
 
3.2 Préciser le nom de $C_{1}$ et dire, comment on peut l'identifier ?

Exercice 9

La combustion complète, par le dioxygène, de $0.1\,mol$ d'un alcool saturé $A$ : 
 
$C_{n}H_{2n+2}O$ a entraîné la formation de $6.72\,L$ de dioxyde de carbone, mesuré dans les conditions normales.
 
1. a) Écrire l'équation de combustion. 
 
En déduire la formule brute de cet alcool.
 
b) Donner la formule semi-développée et le nom de chacun des isomères possibles.
 
2. On dispose de deux réactifs :
 
$-\ $ une solution de $D.N.P.H$ ;
 
$-\ $ une solution de liqueur de Fehling.
 
a) Que permettent de tester ces réactifs ?
 
b) Ayant isolé entité chimique provenant de l'oxydation ménagée de $A$, peut-on, en utilisant ces réactifs, identifier sans ambiguïté l'alcool $A$ ?
 
3. a) L'alcool $A$ a été obtenu par hydratation d'un alcène. 
 
Lequel ?
 
b) Préciser si cette hydratation conduit à un ou plusieurs des isomères trouvés à la question 1.
 
Donner les équations chimiques de cette hydratation.
 
On donne : $V_{0}=22.4\,L$ (volume molaire dans les conditions normales)

Exercice 10

1. On prépare un alcool $A$ par addition d'eau sur un alcène $B$ de formule brute $C_{n}H_{2n}.$
 
Écrire l'équation de la réaction.
 
2. La combustion complète de $m\,(g)$ de $A$ donne une masse $m_{1}\,(g)$ de dioxyde de carbone et une $m_{2}\,(g)$ d'eau telles que :
 
$\dfrac{m_{1}}{m_{2}}=\dfrac{11}{6}$
 
2.1 Écrire l'équation de la réaction de combustion de $A.$
 
2.2 En déduire la valeur de $n$ et les formules brutes de $A$ et $B.$
 
2.3 Écrire les formules semi-développées de $A$ et $B.$
 
3. Par oxydation ménagée de $A$ on obtient un composé $A'.$ 
 
On fait réagir une masse $m$ de $A'$ sur la liqueur de Fehling. 
 
Après chauffage on obtient un précipité rouge brique de masse molaire $143\,g\cdot mol^{-1}$ qu'on recueille, sèche et pèse.
 
3. Nommer les produits $A$ et $A'.$

Exercice 11

On considère un monoalcool aliphatique saturé de masse molaire moléculaire $M=74\,g\cdot mol^{-1}.$
 
1) Déterminer la formule brute de cet alcool. 
 
2) Donner la formule semi-développée, le nom et la classe de chacun des alcools isomères correspondant à cette formule brute. 
 
3) On désire identifier trois de ces isomères désignées respectivement par $A$, $B$ et $C.$ 
 
Pour cela, on les soumet à une oxydation ménagée par une solution acidifiée de permanganate de potassium. 
 
Les résultats observés sont répertoriés dans le tableau suivant :
$$\begin{array}{|c|c|c|c|} \hline \text{Isomérie}&A&B&C\\ \hline \text{Couleur de la}&\text{violette}&\text{incolore}&\text{incolore}\\ \text{solution}& & & \\ \hline\text{Produits}&\text{rien}&D&E\text{ et }F\\ \hline \end{array}$$
 
Les ions permanganate $MnO_{4}^{-}$ (violets) se réduisent pour donner des ions manganèse $Mn^{2+}$ (incolores) 
 
3) a) Peut on identifier un isomère ? 
 
Si oui lequel ? 
 
Justifier la réponse. 
 
On réalise sur les produits $D$, $E$ et $F$ les tests dont les résultats sont consignés dans le tableau suivant :
$$\begin{array}{|c|c|c|} \hline \text{Réactif}&\text{Test à la }2.4-D.N.P.H&\text{Test au réactif de Schiff}\\ \hline D&\text{Positif}&\text{Négatif}\\ \hline E&\text{Négatif}&\text{Négatif}\\ \hline F&\text{Positif}&\text{Positif}\\ \hline \end{array}$$
 
3) b) Que met en évidence un test positif à la $2.4-D.N.P.H$ ? 
 
Est-il suffisant pour identifier $D$ et $F$ ?
 
3) c) Que met en évidence un test positif au réactif de Schiff ?
 
3) d) Déduire la fonction chimique de chacun des composés $D$, $E$ et $F.$
 
Identifier les alcools $B$ et $C$ sachant quel alcool $C$ possède une chaine ramifiée

Exercice 12 

On réalise en présence d'acide sulfurique, l'hydratation du propène. 
 
1. Montrer que l'on peut prévoir théoriquement la formation de deux alcools $(A_{1})$ et $(A_{2}).$ 
 
Préciser le nom et la classe de chacun d'eux. 
 
2. L'oxydation ménagée de l'alcool $(A_{1})$, avec le bichromate de potassium $K_{2}Cr_{2}O_{7}$ en milieu acide ; donne un produit $(B_{1})$ et l'alcool $(A_{2})$ donne un produit $(B_{2}).$ 
 
$(B_{1})$ et $(B_{2})$ donnent un précipité jaune avec le $2.4-D.N.P.H.$ 
 
Seul $(B_{2})$ rosit le réactif de Schiff. 
 
2.1 Quelle est la fonction chimique du produit $(B_{2})$ ? 
 
Donner son nom et sa formule semi-développée. 
 
2.2 Identifier l'alcool $(A_{2}).$ 
 
Justifier. 
 
2.3 Identifier l'alcool $(A_{1})$ ? 
 
En déduire la fonction chimique, le nom et la formule semi-développée du produit $(B_{1}).$ 
 
3. Un acide carboxylique $(C)$ peut être obtenu par oxydation ménagée de l'un de deux alcools $(A_{1})$ et $(A_{2})$ précédents. 
 
3.1 De quel alcool s'agit-il ? 
 
Justifier. 
 
3.2 Donner le nom et la formule semi-développée de l'acide $(C)$ obtenu

Exercice 13

Un composé organique ne contenant que du carbone, de l'hydrogène et de l'oxygène a une masse molaire de $74\,g/mol.$ 
 
On prélève $1.48\,g$ de ce composé et on le fait réagir dans un eudiomètre avec un excès de dioxygène. 
 
L'analyse des gaz obtenus donne les résultats suivants :
 
$\bullet\ $ masse de dioxyde de carbone : $3.52\,g.$
 
$\bullet\ $ masse d'eau : $1.8\,g.$
 
1. Quelle est la formule bute de ce composé
 
2. Ce composé peut être obtenu par addition d'eau sur un hydrocarbure $A.$
 
2.1 A quelle famille d'hydrocarbures appartient $A$ ? 
 
Donner sa formule brute.
 
2.2 Donner les isomères de $A$ et identifier ceux qui présentent une isomère $Z–E.$
 
2.3 Après avoir rappelé la règle de Markovnikov, identifier le(s) composé(s) $A$ qui respecte(nt) cette règle ; appliquer cette règle dans l'addition du chlorure d'hydrogène sur un isomère (de votre choix ) de $A.$
 
3. Le composé $A$ est obtenu par hydrogénation catalytique d'un autre hydrocarbure $B.$
 
3.1 A quelle famille précise appartient le composé $B$ ?
 
3.2 Écrire l'équation-bilan de la réaction d'hydrogénation de $B$ donnant $A$ en précisant la nature la nature du catalyseur.
 
3.3 Quel hydrocarbure obtient-on si l'hydrogénation de $B$ a lieu en présence de nickel comme catalyseur. 
 
Écrire l'équation-bilan de cette réaction.
 
$O\ :\ 16\,g/mol\ ;\ C\ :\ 12\,g/mol\ ;\ H\ :\ 1\,g/mol$
 
Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Les composés aromatiques - 1er s

Classe: 
Première

Exercice 1

1. Nommer les composés aromatiques
 
 
2. Donner la formule semi-développée des composés aromatiques
 
2.1  $1\;,\ 3.5-\text{triméthylbenzène}$
 
2.2  $1-$bromo$-4-$chlorobenzène
 
2.3  Fluorobenzène
 
2.4  $1.4-$dibromo$-2-$méthylbenzène
 
2.5. Hexylbenzène

Exercice 2

On considère un mélange de composés aromatiques renfermant le benzène et le styrène.
 
$1-\ $ Donner la formule développée du styrène.
 
$1-\ $ Dans $10\,cm^{3}$ du mélange, on introduit un peu de bromure de fer $III$ puis, goutte à goute et en agitant, du dibrome pur tant que la coloration brun-rouge ne persiste pas. 
 
Le dégagement qui se produit est envoyé barboter dans une solution de nitrate d'argent, ou il provoque la formation d'un précipité blanc jaunâtre. 
 
On admettra que les conditions opératoires ne permettent pas de polysubtitutions sur les noyaux benzéniques. 
 
Le volume de dibrome versé est $V_{Br2}=8.4\,cm^{3}.$
 
Le précipité obtenu est filtré, séché et pesé ; sa masse est $m=19.1\,g$
 
a) Écrire les équations-bilan de toutes les réaction mises en jeu dans cette manipulation.
 
b) Déterminer les compositions molaire et volumique du mélange étudié.
 
c) Déterminer la masse volumique du styrène
 
Données :
 
Masse molaires en $g\cdot mol^{-1}$,
 
les masses molaires : $C\ :\ 12\;,\ H\ :\ 1\;,\ O\ :\ 16\;,\ N\ :\ 14\;,\ Ag\ :\ 108\;,\ Br\ :\ 80$
 
Masse volumique du benzène est : $\mu_{b}=880\,kg\cdot m^{-3}$
 
Masse volumique du dibrome : $\mu_{Br2}=3250\,kg\cdot m^{-3}$

Exercice 3

1) Le Xylène est le nom courant du diméthylbenzène.
 
Combien a-t-il d'isomère ? 
 
Les nommer.
 
2) Le propène peut fixer une molécule de chlorure d'hydrogène. 
 
Quelles sont les formules semi-développées des deux produits que l'on obtient ?
 
En fait, on obtient un seul corps : le plus symétrique des deux. 
 
Donner son nom systématique.
 
3) Traité par le corps obtenu en 2) en présence de chlorure d'aluminium anhydre, le metaxylène donne réaction de substitution au cours de laquelle un groupe isopropyle $\left(CH_{3}\right)_{2}CH-$ remplace un atome d'hydrogène du cycle benzénique. 
 
Combien d'isomères peut-on obtenir ? 
 
Compte tenu de "l'encombrement" du groupe isopropyle quel sera l'isomère le plus abondant ?
 
4) La nitration de cet isomère conduit à un produit dont la composition massique centésimale est la suivante :
 
$C\ :\ 46.6\%\ ;\ H\ :\ 4.6\%\ ;\ N\ :\ 14.8\%\ ;\ O\ :\ 33.9\%.$
 
Détermine sa formule brute. 
 
Sa masse molaire et sa formule semi-développée.
 
On donne : $M_{H}=1$ ; $M_{C}=12$ ; $M_{N}=14$ ; $M_{O}=16$ en $g/mol.$

Exercice 4

Le toluène de formule brute $C_{7}H_{8}$ est un composé aromatique. 
 
C'est un liquide qui sert à la fabrication des colorants, des solvants et des explosifs tel que le $2\;,\ 4\;,\ 6-$trinitrotoluène connu sous le nom de $T.N.T.$
 
$1-\ $ Écrire les formules semi-développées du toluène et de $T.N.T$ puis donner le nom systématique du toluène.
 
$2-\ $ Le $T.N.T$ est synthétisé par action de l'acide nitrique $HNO_{3}$ sur le toluène en présence de l'acide sulfurique.
 
a) Écrire l'équation bilan de cette réaction. 
 
Est-ce une réaction d'addition ou de substitution ?
 
b) Calculer la masse de toluène nécessaire à la synthèse de une tonne de $T.N.T.$
 
c) Lorsqu'il explose, le $T.N.T$ se décompose en donnant le diazote, la vapeur d'eau, le monoxyde de carbone et le carbone et un dégagement de chaleur. 
 
Écrire l'équation bilan de la réaction d'explosion et calculer la masse de carbone produit par l'explosion de $100$ de $T.N.T.$
 
$3-\ $ A un mélange équimolaire de dichlore et de toluène dans un flacon placé à l'obscurité, on y ajoute le chlorure d'aluminium anhydre. 
 
Le mélange de dichlore et de toluène d'un autre flacon $F_{1}$ exposé à la lumière contient un excès de dichlore.
 
a) Après la disparition de la coloration verte, on introduit dans chaque flacon le papier $pH.$ 
 
Qu'observe-t-on ?
 
b) Donner la formule semi-développée et le nom du composé organique formé dans le flacon $F_{2}$
 
Est-il un composé aromatique ?
 
c) Trois composés chlorés se forment dans le flacon $F_{1}.$ 
 
Écrire leurs formules semi-développées et les nommer
 
Données : 
 
masse molaire moléculaire en $C\ :\ 12\;,\ H\ :\ 1.0\;,\ Cl\ :\ 35.5\;,\ O\ :\ 16\;,\ N\ :\ 14$

Exercice 5

Un composé $A$, de formule brute $C_{8}H_{10}$, possède les propriétés suivantes : en présence de brome, et avec du fer, $A$ donne un produit de substitution contenant $43\%$ de brome ; par hydrogénation de $A$, en présence d'un catalyseur on obtient $C_{8}H_{16}$
 
1) Que peut-on déduire, quant à la nature du produit ? 
 
Montrer que l'action du brome est une monosubstitution
 
2) Proposer les différentes formules développées de $A$ et (il y en a quatre) et donner leurs noms
 
3) Afin de choisir et de préciser la formule développée de $A$, on effectue une déshydrogénation de $A$ en $B.$ 
 
Ce dernier corps a pour formule $C_{8}H_{8}$ et décolore l'eau de brome.
 
Préciser alors la formule de $B.$
 
4) On indique que $B$ est une styrène.
 
Préciser la formule de $A.$
 
5) Combien existe-il de dérivés monobromés de $A.$ (bromation sur le cycle aromatique) ?
 
Écrire les formules semi-développées de ceux-ci. 
 
On donne les masses atomiques : $M_{Br}=80\,g\cdot mol^{-1}$ ; $M_{H}=1.0\,g\cdot mol^{-1}$ ; $M_{C}=12\,g\cdot mol^{-1}$

Exercice 6

On effectue la nitration du toluène (méthyl-benzène).
 
1) Dans les conditions de l'expérience on obtient un dérivé nitré, le trinitrotoluène (connu sous le nom de $T.N.T$). 
 
Écrire l'équation-bilan de la réaction.
 
2) Quelle est la masse de toluène nécessaire pour obtenir une masse de $1\,Kg$ de trinitrotoluène, le rendement étant de $90\%.$

Exercice 7

En présence de chlorure d'aluminium, le benzène réagit sur le chloroéthane pour donner un dégagement de chlorure d'hydrogène et un hydrocarbure $A$, dont le pourcentage massique en en carbone est de $90.6\%.$
 
1) Quelle est la formule brute de $A$ ?
 
2) Écrire l'équation-bilan de la réaction et la formule développée de $A.$
 
Par chauffage en présence d'un catalyseur, $A$ se déshydrogène facilement en $B.$
 
Le produit obtenu comporte $92.3\%$ (en masse) de carbone. 
 
Quelle est sa formule développée ?
 
Ce corps se polymérise très facilement.
 
3) Quel est le motif du polymère obtenu ?

Exercice 8

En présence de trace de chlorure d'aluminium anhydre utilisé comme catalyseur, le chlorure de méthyle réagit sur le noyau benzénique du benzène pour donner un composé plus connu sous le nom de toluène.
 
1) Écrire et compléter la réaction suivante en précisant le catalyseur : 
 
 
On procède à la combustion de $136\,g$ de toluène. 
 
Quel est le volume d'air nécessaire si la combustion précédente se faisait à la température de $27^{\circ}C$ et à la pression normale ? 
 
On rappelle que l'air contient $20\%$ d'oxygène.

Exercice 9

Par substitution du brome sur le benzène, on fabrique du $1.2–$dibromobenzène.
 
1) Écrire les deux réactions qui permettent d'aboutir à ce produit. 
 
Préciser les conditions expérimentales.
 
On veut fabriquer une masse $m=5.0\,g$ de $1.2–$dibromobenzène. 
 
Sachant que le rendement global de la réaction est égal à $40$, calculer :
 
2.1. La masse de benzène nécessaire.
 
2.2. Le volume de dibrome (supposé gazeux) utilisé.
 
Données :
 
$Br\ :\ 80\,g/mol\ ;\ C\ :\ 12\,g/mol\ ;\ H\ :\ 1\,g/mol\ ;\ V_{m}=24\,L/mol$

Exercice 10

Un hydrocarbure $A$, a pour formule brute $C_{9}H_{12}.$
 
$-\ $ Par hydrogénation, en présence d'un catalyseur, $A$ donne un corps de formule $C_{9}H_{18}.$
 
$-\ $ En présence de dibrome et de trichlorure d'aluminium, $A$ conduit à un produit de substitution $B$ contenant $40.2\%$ en masse de brome.
 
1) Montrer que $A$ renferme un noyau benzénique.
 
2) Montrer que le brome ne se substitue qu'une fois sur $A.$
 
3) Écrire toutes les formules semi-développées de $A.$
 
4) Il n'existe qu'un seul dérivé mononitré de $A.$ 
 
En déduire la formule semi-développée de $A.$

Correction des exercices


Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Généralisation de l'oxydoréduction en solution aqueuse - 1er s

Classe: 
Première
 

Exercice 1

Une solution aqueuse de permanganate de potassium peut oxyder l'eau oxygénée en milieu acide.
 
1) Écrire l'équation de cette réaction d'oxydoréduction sachant que les couples mis en jeu sont :
 
$O_{2}/H_{2}O_{2}\text{ et }MnO_{4}^{-}/Mn^{2+}$
 
2) On utilise $V_{0}=12\,mL$ de solution de permanganate de potassium de concentration $C_{0}=2.0\cdot10^{-2}mol\cdot L^{-1}$ pour oxyder $V=20\,mL$ d'eau oxygénée. 
 
Déterminer la concentration $C$ de l'eau oxygénée

Exercice 2

Identifier les couples rédox mis en jeu et équilibrer les équations dans un milieu acide.
 
$Cr_{2}O_{7}^{2-}\ +\ Hg\ \rightarrow\ Cr^{3+}\ +\ Hg^{2+}$
 
$MnO_{4}^{-}\ +\ H_{2}O_{2}\ \rightarrow\ Mn^{2+}\ +\ O_{2}$
 
$H_{2}O_{2}\ +\ SO_{2}\ \rightarrow\ H_{3}^{O+}\ +\ SO_{4}^{2-}$
 
$Cr_{2}O_{7}^{2-}\ +\ Fe^{2+}\ \rightarrow\ Fe^{3+}\ +\ Cr^{3+}$
 
$H_{2}S\ +\ Fe^{3+}\ \rightarrow\ Fe^{2+}\ +\ Cr^{3+}$
 
$MnO_{4}^{-}\ +\ Cl^{-}\ \rightarrow\ Mn^{2+}\ +\ Cl_{2}$

Exercice 3

On dispose de cristaux de sulfate de fer $II$ hydraté, de formule $FeSO_{4}$, $xH_{2}O$, dans laquelle $x$ désigne un nombre entier que l'on veut déterminer.
 
On dissout une masse $m=1.00\,g$ de ces cristaux dans un peu d'eau acidifiée par de l'acide sulfurique. 
 
On agite pour obtenir une solution $S.$
 
On verse ensuite dans $S$ une solution de permanganate de potassium $\left(K^{+}+MnO_{4}^{-}\right)$ de concentration molaire $c=5.00\cdot10^{-2} mol\cdot L^{-1}.$ 
 
Au début de l'expérience, la couleur rose due aux ions permanganate disparaît immédiatement. 
 
Lorsqu'on a ajouté $14.4\,mL$ de la solution de permanganate dans $S$, on obtient une teinte rose persistante.
 
1) Écrire la réaction d'oxydoréduction responsable de la décoloration.
 
2) Déterminer la quantité de matière de sulfate de fer $II$ hydraté utilisé.
 
3) En déduire la valeur de $x$ et la formule du sulfate de fer $II$ hydraté.
 
Masses molaires atomiques :
 
$Fe\ :\ 56\,g\cdot mol^{-1}\ ;\ Mn\ :\ 55\,g\cdot mol^{-1}$
 
$S\ :\ 32\,g\cdot mol^{-1}\ ;\ O\ :\ 16\,g\cdot mol^{-1}\ ;\ H\ :\ 1\,g\cdot mol^{-1}$
 
$E^{\circ}\left(MnO_{4}^{-}/Mn^{2+}\right)=1.51,V$ ; 
 
$E^{\circ}\left(Fe^{3+}/Fe^{2+}\right)=+0.77\,V$ ; 
 
$E^{\circ}\left(Fe^{2+}/Fe\right)=-0.44\,V$

Exercice 4

On trouve en pharmacie des sachets contenant $0.25\,g$ de permanganate de potassium solide : la dissolution
 
du contenu d'un sachet dans $2.5\,L$ d'eau permet d'obtenir une solution violette qui peut être utilisée comme antiseptique externe.
 
1) À température ordinaire, le permanganate de potassium est un solide gris-violet de formule $KMnO_{4}.$ 
 
Écrire la formule de la solution aqueuse antiseptique.
 
2) Calculer la masse molaire du permanganate de potassium.
 
3) Calculer la concentration massique puis la concentration molaire de la solution obtenue.
 
4) L'ion permanganate $MnO_{4}^{-}$ fait partie du couple rédox $MnO_{4}^{-}/Mn^{2+}.$
 
Recopier les affirmations exactes et éliminez les autres :
 
$-\ $ Les propriétés antiseptiques de la solution sont dues au caractère oxydant de l'ion permanganate.
 
$-\ $ L'ion permanganate est un bon oxydant, ce qui confère à la solution des propriétés antiseptiques.
 
$-\ $ Le caractère réducteur de l'ion $MnO_{4}^{-}$ fait de lui un bon antiseptique externe.
 
$-\ $ L'ion permanganate donne aux solutions aqueuses une coloration violette.
 
5) Écrire la demi-équation correspondant au couple rédox $MnO_{4}^{-}/Mn^{2+}$
 
6) Pourquoi ne faut-il jamais mélanger une solution de permanganate de potassium avec une solution d'acide chlorhydrique ? 
 
Écrire l'équation de la réaction qui a eu lieu.

Informations : 

Le dichlore $Cl_{2}$ est un gaz verdâtre très toxique. 
 
L'ion chlorure du couple $Cl_{2}/Cl^{-}$ est un bon réducteur de l'ion permanganate

Exercice 5

Une solution $(S_{1})$ de sulfate de fer $II$ $\left(Fe\,SO_{4}\right)$ est préparée par dissolution de $3.04\,g$ de soluté de façon à préparer un volume $V=400\,mL.$
 
La solution $(S_{1})$ est abandonnée à l'air ; une partie des ions fer $II$ a été oxydé en ions fer $III.$
 
On désigne par $(S'_{1})$ la nouvelle solution.
 
Pour déterminer le pourcentage des ions fer $II$ oxydés par l'air on procède de la manière suivante :
 
On prélève un volume $V_{1}=20\,mL$ de la solution $(S'_{1})$ auquel on ajoute quelques gouttes d'acide sulfurique et on le fait réagir avec une solution $(S_{2})$ de permanganate de potassium $\left(KMnO_{4}\right)$ de concentration $C_{2}=10^{-2}mol\cdot L^{-1}$
 
Il a fallut versé $V_{2}=8\,mL$ de la solution $(S_{2})$ pour faire régir tous les ion fer $II.$
 
1) a) Calculer le nombre de mol d'ions fer $II$ dans $(S_{1}).$
 
b) Déterminer la concentration $C_{1}$ de la solution $(S_{1}).$
 
2) Calculer la masse de permanganate de potassium utilisée pour préparer $100\,mL$ de $(S_{2}).$
 
3) Écrire les équations d'oxydation et de réduction et déduire l'équation bilan de la réaction rédox qui se produit.
 
4) a) Déterminer le nombre de mole d'ions fer $II$ dans $V_{1}.$
 
b) Calculer le pourcentage de mole d'ions fer $II$ qui ont été oxydés par l'air

Exercice 6

Le dioxyde de soufre $SO_{2}$ est un gaz très soluble dans l'eau. 
 
Pour éviter que le vin ne s'oxyde, les œnologues (spécialistes du vin) ajoutent du dioxyde de soufre au moût de raisin. 
 
Dans un vin blanc, la concentration massique en dioxyde de soufre est limitée : elle ne doit pas excéder $210\,mg\cdot L^{-1}.$ 
 
Pour vérifier la conformité de la concentration de dioxyde de soufre dans le vin, il existe un mode opératoire officiel. 
 
On utilise une solution titrante de diiode de concentration $c_{1}=7.80\cdot10^{-3}moL\cdot L^{-1}.$ 
 
Dans un erlenmeyer, on verse un volume $V_{2}=25.0\cdot mL$ de vin blanc. 
 
On ajoute $2\,mL$ d'acide sulfurique pour acidifier le milieu et $1\,mL$ d'empois d'amidon. 
 
Lors du titrage d'un vin blanc, l'équivalence est obtenue après avoir versé un volume
 
$V_{eq}=6.10\,mL.$
 
1) Dessiner et nommer la verrerie utile pour ce montage.
 
2) Comment repère-t-on ici le volume équivalent ?
 
3) Écrire l'équation de la réaction chimique utilisée comme outil dans ce dosage.
 
4) Déterminer à l'équivalence. la quantité de matière de dioxyde de soufre dissoute dans la prise d'essai...
 
5) Déterminer la concentration molaire puis la concentration massique en $SO_{2}$ du vin titré. 
 
Est-il conforme ?
 
Données : couples oxydant/réducteur 
 
$SO_{4}^{2-}(aq)(\text{incolore})/SO_{2}(aq)(\text{incolore})\text{ et }I_{2}(\text{violet en présence d'amidon})/I^{-}(aq)(\text{incolore})$

Exercice 7

1.1. Mettre en évidence $3$ couples oxydo-réducteurs parmi les espèces de la liste suivante :
 
$Fe^{2+}\;,\ SO_{3}^{2-}\;,\ S_{2}O_{3}^{2-}\;,\ SO_{2}$ ;
 
$S_{4}O_{6}^{2-}\;,\ Fe\;,\ Fe^{3}\;,\ HSO_{3}^{-}\;,\ SO_{3}^{2-}$
 
1.2. Identifier un couple acido-basique qui s'est glissé dans la liste précédente
 
2. On dose un effluent gazeux contenant du dioxyde de soufre à la sortie d'une cheminée industrielle, avant traitement pour rejet à l'air libre.
 
Pour cela on fait barboter un volume de gaz $V_{g}=10\,m^{3}$ dans $V_{1}=250\,mL$ d'eau distillée de façon à dissoudre tous les gaz solubles dans l'eau. 
 
La solution obtenue, versée dans un erlenmeyer est dosée par une solution de permanganate de potassium acidifiée de concentration $C_{2}=1.0\cdot 10^{-3} mol\cdot L^{-1}.$
 
Pour atteindre l'équivalence le volume de permanganate versé $V_{e2}=18.8\,mL.$
 
On donne l'équation de la réaction d'oxydoréduction :
 
$2Mn\,O_{4}^{-}\ +\ 5SO_{2}\ +\ 2H_{2}O\ \rightarrow\ 2Mn^{2+}\ +\ 5SO_{3}^{2-}\ +\ 4H^{+}$ 
 
2.1. Déterminer la quantité de matière d'ions $MnO_{4}^{-}$ ajoutés pour atteindre l'équivalence.
 
2.2. Définir l'équivalence ?
 
2.3. Déterminer la quantité de matière de dioxyde de soufre dans la solution dosée
 
2.4. En déduire la masse de dioxyde de soufre contenue dans un mètre cube d'effluent gazeux.
 
2.5. La norme recommandée par l'O.M.S est $50\,g\cdot m^{-3}.$
 
Ce gaz devra t-il être épuré ?
 
$M(SO_{2})=64\,g\cdot mol^{-1}\ ;\ M(SO_{2})=64\,g\cdot mol^{-1}$

Exercice 8

1) Au milieu acide, l'ion nitrate $NO_{3}$ oxyde le cuivre métallique $Cu$ en $Cu^{2+}$ et il se réduit en monoxyde d'azote $NO.$
 
a) Écrire les équations d'oxydation et de réduction.
 
b) Préciser les couples d'oxydoréduction mis en jeu.
 
c) Déduire l'équation bilan de la réaction.
 
2) Le monoxyde d'azote formé est un gaz incolore, il réagit avec le dioxygène de l'air pour donner le dioxyde d'azote de formule $NO_{2}$ qui est un gaz de couleur rousse.
 
a) Écrire l'équation de la réaction et montrer
 
b) Donner les couples rédox mis en jeu
 
Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Structure de la matière - 4e

Classe: 
Quatrième
 

Exercice 1

Complétons le texte suivant en ajoutant les mots ou groupes de mots manquants.
 
La matière a une structure discontinue. Parmi les corps purs on note des corps moléculaires dont la particule élémentaire est la molécule qui est constituée d'atomes.
 
Chaque type d'atome est appelé élément ; on le représente par un symbole chimique.
 
Un atome qui perd des électrons est appelé cation alors que celui qui en gagne est dit anion.
 

Exercice 2

La plus petite partie d'un corps pur est appelée : Molécule
 

Exercice 3

Soient les formules chimiques suivantes :
$$1)\ CH_{4}\qquad 2)\ O_{2}\qquad 3)\ NaOH$$
 
Donnons les noms des éléments chimiques contenus dans chaque corps purs et donnons le nombre d'atomes de chaque élément.
 
1) $CH_{4}$
 
$-\ \ $ Éléments chimiques :
 
$\centerdot\ \ C\ :$ Carbone
 
$\centerdot\ \ H\ :$ Hydrogène
 
$-\ \ $ Nombre d'atomes :
 
La molécule de $CH_{4}$ renferme 1 atome de carbone $(C)$ et 4 atomes d'hydrogène $(H).$ Ce qui donne 5 atomes au total.
 
2) $O_{2}$
 
$-\ \ $ Éléments chimiques :
 
$\centerdot\ \ O\ :$ Oxygène
 
$-\ \ $ Nombre d'atomes :
 
La molécule de $O_{2}$ renferme 2 atomes d'oxygène $(O).$
 
3) $NaOH$
 
$-\ \ $ Éléments chimiques :
 
$\centerdot\ \ Na\ :$ Sodium
 
$\centerdot\ \ O\ :$ Oxygène
 
$\centerdot\ \ H\ :$ Hydrogène
 
$-\ \ $ Nombre d'atomes :
 
La molécule de $NaOH$ renferme 1 atome de sodium $(Na)$, 1 atome d'oxygène $(O)$ et 1 atome d'hydrogène $(H).$ Ce qui donne au total, 3 atomes.
 

Exercice 4

Soient les formules chimiques suivantes :
 
$N_{2}\;;\ CO_{2}\;;\ Al_{4}C_{3}\;;\ Fe\;;\ O_{3}\;;\ HCl$ ;
 
$CaCO_{3}\;;\ H_{2}\;;\ S\;;\ Pb\;;\ H_{2}SO_{4}$
 
$CHCl_{3}\;;\ O_{2}\;;\ Cu.$
 
Complétons le tableau ci-dessous en écrivant la formule de chaque corps pur dans la colonne qui convient :
$$\begin{array}{|c|c|c|} \hline \text{Corps purs}&\text{Corps purs}&\text{Corps purs}\\ \text{simple}&\text{simple}&\text{Composés}\\ \hline \text{atomiques}&\text{moléculaires}&\\ \hline Fe\;,\ S&N_{2}\;,\ O_{3}&CO_{2}\;;\ Al_{4}C_{3}\\Pb\;,\ Cu&H_{2}\;,\ O_{2}&HCl\;,\ CaCO_{3}\\&&H_{2}SO_{4}\;,\ CHCl_{3}\\ \hline \end{array}$$
 
Donnons la composition de chacun des corps purs composés.
 
$CO_{2}\ :$ 1 atome de carbone $(C)$ et 2 atomes d'oxygène $(O).$
 
$Al_{4}C_{3}\ :$ 4 atomes d'aluminium $(Al)$ et 3 atomes de carbone $(C).$
 
$HCl\ :$ 1 atome d'hydrogène $(H)$ et 1 atome de chlore $(Cl).$
 
$CaCO_{3}\ :$ 1 atome de calcium $(Ca)$, 1 atome de carbone $(C)$ et 3 atomes d'oxygène $(O).$
 
$ H_{2}SO_{4}\ :$ 2 atomes d'hydrogène $(H)$, 1 atome de soufre $(S)$ et 4 atomes d'oxygène $(O).$
 
$CHCl_{3}\ :$ 1 atome de carbone $(C)$, 1 atome d'hydrogène et 3 atomes de chlore $(Cl).$
 

Exercice 5

Complétons le tableau suivant :
$$\begin{array}{|c|c|c|c|} \hline\text{Formule}&\text{Noms}&\text{Nombre}&\text{Nombre}\\ \text{chimique}&\text{éléments}&\text{d'atomes}&\text{total}\\ \text{du corps}&\text{chimiques}&\text{de chaque}&\text{d'atome}\\ \text{pur}&\text{présents}&\text{élément}&\text{dans le}\\ &\text{dans le}& &\text{corps}\\ &\text{corps}& &\\ \hline O_{2}&\text{Oxygène}&2&2\\ \hline NaCl&\text{Sodium}&1&2\\ &\text{Chlore}&1&\\ \hline H_{2}O&\text{Hydrogène}&2&3\\ &\text{Oxygène}&1&\\ \hline Fe_{3}O_{4}&\text{Oxygène}&4&7\\ &\text{Fer}&3&\\ \hline AlCl_{3}&\text{Aluminium}&1&4\\ &\text{Chlore}&3&\\ \hline Al_{2}(SO_{4})_{3}&\text{Aluminium}&2&\\ &\text{Soufre}&3&17\\ &\text{Oxygène}&12=(3\times 4)&\\ \hline Ca(NO_{3})_{2}&\text{Azote}&2&\\ &\text{Calcium}&1&9\\ &\text{Oxygène}&6=(2\times 3)&\\ \hline \end{array}$$

Exercice 6

Complétons cette grille de mots croisés

 
 
 

Exercice 7

Donnons la formule chimique de chacun des corps dont la molécule renferme :
 
$\centerdot\ $ Un atome de carbone et quatre atomes d'hydrogène.
$$CH_{4}$$
 
$\centerdot\ $ Un atome de sodium, un atome d'oxygène et un atome d'hydrogène
$$NaOH$$
 
$\centerdot\ $ Six atomes de carbone, douze atomes d'hydrogène et six atomes d'oxygène.
$$C_{6}H_{12}O_{6}$$
 
$\centerdot\ $ Un atome de calcium, deux atomes d'oxygène et deux atomes d'hydrogène.
$$Ca(OH)_{2}$$
 
$\centerdot\ $ Un atome de carbone et deux atomes d'oxygène.
$$CO_{2}$$

Exercices supplémentaires

Exercice A
 
Écrivons la formule chimique des corps dont les noms sont donnés ci-après : 
 
$\rhd\ $ dioxyde de soufre : $SO_{2}$
 
$\rhd\ $ trioxyde de soufre : $SO_{3}$
 
$\rhd\ $ dioxygène : $O_{2}$
 
$\rhd\ $ trioxygène ou ozone : $O_{3}$
 
$\rhd\ $ monoxyde de carbone : $CO$
 
Exercice B : Savoir distinguer un corps pur simple d'un corps pur composé
 
Choisissez la bonne réponse :
 
$\rhd\ $ l'eau est un corps composé
 
$\rhd\ $ le dihydrogène est un corps simple
 
$\rhd\ $ il existe plusieurs corps simples contenant le même élément $(\text{Faux}$
 

Exercice 8 Maitrise de connaissances

Recopions et complétons les phrases suivantes à l'aide de la liste de termes : 
 
composé ; négativement ; $10^{-10}\;m$ ; neutre ; ion ; simple ; positivement ; noyau ; électrons.
 
Un atome possède un noyau central chargé positivement et des électrons chargés négativement.
 
La charge des électrons compense celle du noyau ; l'atome est donc électriquement neutre.
 
Un ion est un atome qui a gagné ou perdu un ou plusieurs électrons.
 
Les dimensions de l'atome sont de l'ordre de $10^{-10}\;m.$
 
Un corps pur composé est formé d'atomes différents.
 
Un corps pur simple est formé d'atomes identiques.

Exercice 9 Symbole d'un élément chimique

1) Donnons le nom de l'élément correspondant à chacun des symboles suivants :
$$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{Symbole}&Mg&Cl&Al&Ne&Ca&P\\ \hline \text{Nom}&\text{Magnésium}&\text{Chlore}&\text{Aluminium}&\text{Néon}&\text{Calcium}&\text{Phosphore}\\ \hline \end{array}$$
 
2) Donnons le symbole de chacun des éléments chimiques suivants :
$$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{Elément}&\text{oxygène}&\text{hydrogène}&\text{azote}&\text{sodium}&\text{soufre}&\text{potassium}\\ \text{chimique}&&&&&&\\ \hline \text{Symbole}&O&H&N&Na&S&K\\ \hline \end{array}$$
 

Exercice 10 Formule chimique

Écrivons la formule chimique à partir de la composition de la molécule
$$\begin{array}{|l|c|} \hline \text{Composition de la molécule}&\text{Formule du corps pur}\\ \hline \text{2 atomes de chlore}&Cl_{2}\\ \hline \text{1 atome de soufre et 2 atomes d'oxygène}&SO_{2}\\ \hline \text{1 atome de carbone et 2 atomes d'oxygène}&CO_{2}\\ \hline \text{3 atomes d'oxygène}&O_{3}\\ \hline \text{1 atome d'azote et 3 atomes d'hydrogène}&NH_{3}\\ \hline \end{array}$$
 

Exercice 11 Signification d'une formule

Le sucre ou saccharose a pour formule moléculaire : $C_{12}H_{22}O_{11}$
 
Dans le tableau suivant, indiquons le nom et le nombre des différents atomes présents dans la molécule.
$$\begin{array}{|c|c|c|}\hline\text{Atomes présents}&\text{Nom}&\text{Nombre}\\ \hline C&\text{Carbone}&12\\ \hline H&\text{Hydrogène}&22\\ \hline O&\text{Oxygène}&11\\ \hline \end{array}$$
 

Exercice 12 Reconnaissance de formule

On considère les écritures suivantes : $O_{3}\;;\ 2O_{2}\;;\ 2O\;;\ O_{2}.$
 
Représentation des écritures :
 
1) Une molécule de dioxygène est représentée par : $O_{2}$
 
2) Deux atomes d'oxygène séparés sont représentés par : $2O$
 

Exercice 13 Classement selon l'atomicité

Indiquons l'atomicité des molécules suivantes
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|} \hline &N_{2}&HCl&Ne&H_{2}O&CO&O_{3}&He&NO_{2}&Cl_{2}\\ \hline \text{atomicité}&2&2&1&3&2&3&1&3&2\\ \hline \end{array}$$
 

Exercice 14 Corps pur simple et corps pur composé

Recopions et mettons une croix dans la case correspondant à la bonne réponse.
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|} \hline &H_{2}O&He&Cl_{2}&H_{2}&SO_{2}&Ne&NH_{3}&HCl&O_{3}\\ \hline \text{Corps pur simple}&&\times&\times&\times&&\times&&&\times\\ \hline \text{Corps pur composé}&\times&&&&\times&&\times&\times&\\ \hline \end{array}$$

Exercice 15 Entité chimique

On considère les entités chimiques suivantes :
 
$O_{3}\;;\ PO_{4}^{3^{-}}\;;\ SO_{4}^{2^{-}}\;;\ HO^{-}\;;\ NH_{3}\;;\ Fe^{3^{+}}\ \text{ et }\ H_{3}O^{+}.$
 
1) Classons-les en molécules, anions et cations dans le tableau suivant
$$\begin{array}{|c|c|c|}\hline\text{molécules}&\text{anions}&\text{cations}\\ \hline O_{3}\;;\ NH_{3}&PO_{4}^{3^{-}}\;;\ SO_{4}^{2^{-}}\;;\ HO^{-}&Fe^{3^{+}}\;;\ H_{3}O^{+}\\ \hline\end{array}$$
 
2) La charge électrique de chaque entité chimique est donnée dans le tableau ci-dessous
$$\begin{array}{|c|r|}\hline\text{entité chimique}&\text{charge}\\ \hline O_{3}&0\\ \hline NH_{3}&0\\ \hline PO_{4}^{3^{-}}&-3\\ \hline SO_{4}^{2^{-}}&-2\\ \hline HO^{-}&-1\\ \hline Fe^{3^{+}}&+3\\ \hline H_{3}O^{+}&+1\\ \hline\end{array}$$

Exercice 16 "un collier d'or"

Le diamètre d'un atome d'or est environ $0.144\;nm.$
 
Calculons le nombre minimal d'atomes d'or que l'on pourrait placer côte à côte pour obtenir une longueur $40\;cm$
 
Convertissons d'abord en unité internationale :
 
$1\;nm=10^{-9}\;m\ $ donc, $\ 0.144\;nm=0.144\cdot 10^{-9}\;m$
 
$1\;cm=10^{-2}\;m\ $ donc, $\ 40\;cm=40\cdot 10^{-2}\;m$
 
Ensuite, on sait que :
$$\begin{array}{rcl} 1\text{ atome d'or}&\text{occupe}&0.144\;nm\\ n\text{ atomes d'or}&\text{occupe}&40\;cm\end{array}$$
 
Enfin, en considérant les rapports de proportionnalité, on obtient :
 
$\dfrac{n}{1}=\dfrac{40\;cm}{0.144\;nm}.$ Ce qui donne alors : $n=\dfrac{40\;cm}{0.144\;nm}$
 
Or, $\ 0.144\;nm=0.144\cdot 10^{-9}\;m\ $ et $\ 40\;cm=40\cdot 10^{-2}\;m$
 
Donc, en remplaçant par les valeurs converties, on obtient :
 
$\begin{array}{rcl} n&=&\dfrac{40\cdot 10^{-2}\;m}{0.144\cdot 10^{-9}\;m}\\ \\&=&\dfrac{40\cdot 10^{-2}\times 10^{9}}{0.144}\\ \\&=&\dfrac{40\cdot 10^{7}}{0.144}\\ \\&\approx&2777777778\end{array}$
 
Ainsi, pour obtenir une longueur de $40\;cm$ on pourrait placer côte à côte, au minimum, $2777777778$ atomes d'or.

Exercice 17

La masse d'un noyau d'atome de cuivre est de $1.05\times 10^{-25}\;kg.$
 
Celle de l'ensemble de ses électrons est de $2.64\times 10^{-29}\;kg.$
 
1) Comparons la masse du noyau de l'atome de cuivre à celle de ses électrons en calculant le rapport masse noyau/masse des électrons.
 
On a :
 
$\begin{array}{rcl}\dfrac{m_{\text{noyau}}}{m_{\text{électron}}}&=&\dfrac{1.05\times 10^{-25}}{2.64\times 10^{-29}}\\ \\&=&\dfrac{1.05\times 10^{-25}\times 10^{29}}{2.64}\\ \\&=&\dfrac{1.05\times 10^{4}}{2.64}\\ \\&=&3977.27\end{array}$
 
Donc, $\boxed{\dfrac{m_{\text{noyau}}}{m_{\text{électron}}}=3977.27}$
 
Ce qui veut dire encore que : $m_{\text{noyau}}=3977.27\times m_{\text{électron}}$
 
Ainsi, nous constatons que la masse du noyau de l'atome de cuivre fait $3977.27$ fois plus que celle de ses électrons.
 
Par suite, la masse du noyau de l'atome de cuivre est largement supérieure à la masse de ses électrons.
 
2) Explication de la phrase suivante : "la masse de l'atome est concentrée en son noyau".
 
D'après la question précédente, la masse du noyau de l'atome de cuivre est environ $3977.27$ fois plus grande que la masse de l'ensemble de ses électrons.
 
Ce qui signifie que la masse des électrons reste négligeable devant celle du noyau.
 
Par conséquent, toute la masse de l'atome est quasiment déterminée par la masse du noyau.
 
D'où, la phrase suivante : "la masse de l'atome est concentrée en son noyau"
 

Exercice 18 Formule statistique d'un composé

Complétons le tableau ci-dessous en reliant la formule statistique du composé ionique à celles de ses ions.
$$\begin{array}{|c|c|c|c|c|} \hline &Na^{+}&Cu^{2^{+}}&Ca^{2^{+}}&Fe^{3^{+}}\\ \hline Cl^{-}&NaCl&CuCl_{2}&CaCl_{2}&FeCl_{3} \\ \hline SO_{4}^{2^{-}}&Na_{2}SO_{4}&CuSO_{4}&CaSO_{4}&Fe_{2}(SO_{4})_{3}\\ \hline OH^{-}&NaOH&Cu(OH)_{2}&Ca(OH)_{2}&Fe(OH)_{3}\\ \hline NO_{3}^{-}&NaNO_{3}&Cu(NO_{3})_{2}&Ca(NO_{3})_{2}&Fe(NO_{3})_{3}\\ \hline S^{2^{-}}&Na_{2}S&CuS&CaS&Fe_{2}S_{3}\\ \hline \end{array}$$

Auteur: 
Aliou ndiaye

Série d'exercices : Généralités sur le mouvement - 2nd S

Classe: 
Seconde
 

Exercice 1

I. Dans chacun des cas suivants, choisir la bonne réponse.
 
1) Dans le cas d'un mouvement rectiligne uniforme
 
a) le vecteur vitesse est constant.
 
b) la valeur du vecteur vitesse est constante.
 
2) Dans le cas d'un mouvement circulaire uniforme
 
a) le vecteur vitesse est constant
 
b) la valeur du vecteur vitesse est constante.
 
3) Dans le cas d'un mouvement curviligne uniforme:
 
a) le vecteur vitesse est constant
 
b) la valeur du vecteur vitesse est constante.
 
4) Lorsque la valeur du vecteur vitesse est constante
 
a) le mouvement est uniforme
 
b) le mouvement est rectiligne uniforme.
 
5) Lorsque le vecteur vitesse est constant
 
a) le mouvement est uniforme. b. le mouvement est rectiligne uniforme.
 
II. Lorsqu'on éternue, on ferme les yeux involontairement. Le conducteur d'une automobile roulant à $108\;km.h^{-1}$ éternue pendant une demi-seconde. 
 
Quelle distance parcourt-il sans voir la route ?
 

Exercice 2

On étudie la course d'Usain Bolt le Jamaïcain avec précision. On effectue un chronométrage tous les 10 mètres.
 
1) Compléter la colonne position
 
2) Calculer les différentes vitesses instantanées.
 
3) Calculer la vitesse moyenne entre $M_{0}\ $ et $\ M_{3}$, puis entre $M_{4}\ $ et $\ M_{9}$
 
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|}\hline&M_{0}&M_{1}&M_{2}&M_{3}&M_{4}&M_{5}&M_{6}&M_{7}&M_{8}&M_{9}&M_{10}\\ \hline\text{Temps (s)}&0&1.85&2.91&3.82&4.70&5.51&6.37&7.19&8.01&8.87&9.72\\ \hline\text{Position (m)}&0&10&&&&&&&&&\\ \hline\text{Vitesse}&&&&&&&&&&&\\ \text{instantanée}&&&&&&&&&&&\\(m/s)&&&&&&&&&&&\\\hline\end{array}$$

Exercice 3

Un mobile autoporteur est lancé sur une table horizontale : On enregistre les positions successives d'un point $M$ du mobile. 
 
Entre deux positions enregistrées, il s'est écoulé une durée $\Delta t=60\;ms.$
 
L'enregistrement de sa trajectoire est donnée par la figure ci-dessous :
 
$$\begin{array}{|cccccccccccc|}\hline&M_{0}&M_{1}&M_{2}&M_{3}&M_{4}&M_{5}&M_{6}&M_{7}&M_{8}&M_{9}\\&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\&t_{0}&t_{1}&t_{2}&t_{3}&t_{4}&t_{5}&t_{6}&t_{7}&t_{8}&t_{9}\\ \hline\end{array}$$
Échelle : $1\,cm$ sur le schéma représente $2\,cm$ en réalité
 
1)  Nommer les points $M_{0}\;;\ M_{1}\;;\ M_{2}\;;\ \ldots\ (M_{0}$ étant le premier point de la trajectoire).
 
2) Déterminer la nature de la trajectoire du point $M.$
 
3) Déterminer la nature du mouvement du point $M.$
 
4) Calculer la vitesse instantanée aux dates $t_{2}\;,\ t_{4}\ $ et $\ t_{7}.$
 
5) Représenter le vecteur vitesse du mobile aux positions $M_{2}\;,\ M_{4}\ $ et $\ M_{7}$ en précisant l'échelle utilisée.
 
6) Le résultat est-il en accord avec la réponse de la 3e question ?
 
7) Déterminer la vitesse du mobile au point $M_{9}.$
 

Exercice 4 : Mouvement d'un objet

On repère les positions successives d'un point $L$ d'un disque tournant autour d'un axe grâce à une lampe clignotante placée en $L$ et qui émet des éclairs à intervalles réguliers $\tau=20\;ms.$

 

 
1) Quel est la vitesse instantanée de $L$ en $L_{6}\ $ et $\ L_{2}\ ?$
 
Tracer les vecteurs vitesses associés.
 
2) On suppose que le mouvement est circulaire uniforme. Calculer, sans utiliser la règle, la vitesse angulaire du solide.
 
3) Vérifier la relation entre $V\ $ et $\ \omega$, la vitesse angulaire.
 
4) En déduire la période $T$ de rotation.
 
5) Le vecteur vitesse de $L$ est-il constant au cours du temps ?
 

Exercice 5 : Étude du mouvement d'un enfant sur un tremplin

L'enregistrement 1 ci-dessous représente dans le référentiel terrestre les positions $E_{i}$ d'un enfant en rollers sur un tremplin.
 
Ces positions sont inscrites à intervalles de temps égaux $\tau=0.20\;s$
 
1) Sans effectuer de calculs, déterminer les différentes phases du mouvement (uniforme, accéléré, décéléré).
 
Justifier la réponse.
 
2) Déterminer les valeurs de $v_{1}\ $ et $\ v_{8}$, vitesses instantanées du point E aux instants $t_{1}\ $ et $\ t_{8}.$
 
3) Représenter ces vecteurs vitesse en utilisant comme échelle :
 
$1\;cm\longrightarrow 2\;m.s^{-1}$

 

 
Échelle : $1\;cm$ sur le schéma représente $0.5\;m$ en réalité
 

Exercice 6

Sur une table horizontale, un mobile sur coussin d'air est relié à un point fixe $O$ par un fil inextensible.
 
On lance le mobile et on registre à intervalles de temps égaux $\tau=20\;ms$, les positions successives $M_{i}$, du point $M$ situe au centre du mobile. 
 
La première partie du mouvement s'effectue fil tendu, puis celui-ci casse.
 
L'enregistrement obtenu est sur le document ci-dessous.
 
1) on constate au vu de l'enregistrement que le mouvement du point $M$ peut se décomposer en deux phases distinctes.
 
a) donner sous la forme $M_{i}M_{j}$ les deux parties correspondantes à ces deux phases.
 
b) Pour chacune d'elle, donner la nature du mouvement et préciser si le vecteur vitesse du point $M$ est constant.
 
2) Calculer les vitesses des points $M_{5}\ $ et $\ M_{15}.$ Les représenter sur l'enregistrement. 
 
On prendre comme échelle de vitesse : $1\;cm$ représente $0.2\;m/s$
 
3) Sans rapporteur, calculer la vitesse angulaire au point $M_{5}$
 
Enregistrement de la trajectoire du mobile autoporteur

 

 

Exercice 7 : Étude du mouvement d'un solide


 
$$\begin{array}{lrcl}\text{Echelle :}&1\;cm&\longleftrightarrow&5\;cm\\&(\text{ici})&&(\text{réel}) \end{array}$$
 
On a enregistré le mouvement de deux points $A\ $ et $\ B$ d'un même solide se déplaçant sur une surface plane horizontale. 
 
Le dispositif d'enregistrement est fixe par rapport à la table.
 
A l'instant $t=0$ correspondent les positions $A_{0}\ $ et $\ B_{0}$ de $A\ $ et $\ B.$ Entre deux repérages successifs, il s'écoule une durée $\tau=40\;ms.$
 
L'enregistrement est donné ci-dessus.
 
1) Calculer la vitesse instantanée du point $A$ aux instants $t_{2}\ $ et $\ t_{5}.$ Représenter le vecteur vitesse de $A$ aux instants $t_{2}\ $ et $\ t_{5}$ avec l'échelle : $1\;cm$ pour $0.5\;m.s^{-1}$
 
2) Calculer la vitesse instantanée de $B$ aux mêmes instants et représenter les vecteurs vitesses.
 
3) Le centre d'inertie $G$ du solide est situé au milieu du segment $[AB].$ 
 
Déterminer les positions de $G$ aux différents instants de l'enregistrement.
 
4) Indiquer précisément le nom du mouvement de $G.$
 

Exercice 8

Un mobile ponctuel se déplace sur un cercle de rayon $R=0.75\;m$ avec la vitesse angulaire constante $\omega=0.5\times\pi\;rad.s^{-1}$

 

 
1) Quelle est la nature de ce mouvement ?
 
2) Calculer l'abscisse angulaire d'un point $M$ à l'instant $t=2\;s.$
 
Placer le point $M$ sur le cercle.
 
3) Déterminer la vitesse linéaire $V$ du mobile.
 
4) Calculer la période du mouvement. Déduire sa fréquence
 

Exercice 9

Un solide est animé d'un mouvement de translation rectiligne.
 
Le graphe suivant représente les variations de la vitesse $V$ du solide en fonction du temps :
 
1) Si $t_{1}=25\;min\ $ et $\ t_{2}=35\;min$, que peut-on dire du mouvement :
 
1.1) Quand $0<t<t_{1}\ ?$
 
1.2) Quand $t_{1}<t<t_{2}\ ?$
 
1.3) Quand $t>t_{2}\ ?$
 
2) Déterminer la distance parcourue à la date $t_{1}.$

 

 

Exercice 10

I. Deux athlètes $A\ $ et $\ B$ courent sur une piste circulaire longue de $400\;m.$ Ils partent ensemble et se déplacent à des vitesses respectivement égales à $10\;m/s\ $ et $\ 9\;m/s.$
 
1) Au bout de combien de temps auront-ils un tour d'écart ?
 
2) Quelles distances les deux coureurs auront-ils alors parcourues ?
 
II. Un lièvre s'éloigne d'un chasseur selon une ligne droite, sa vitesse est de $36\;km/h.$ 
 
Le chasseur tire lorsque la distance qui le sépare de sa future victime est de $98\;m.$ 
 
Si la vitesse de la balle est de $500\;m/s$, quelle distance pourra encore parcourir le lièvre avant d'être touché ?
 
III. Sur une portion de route rectiligne, un camion passe au point $A$ à midi et se dirige vers le point $B$, distant de $5\;km$, avec une vitesse constante de $54\;km/h.$ A midi et deux minutes, une voiture quitte $B$ pour se diriger vers $A$, à la vitesse constante de $72\;km/h.$
 
A quelle distance de $A$ les deux véhicules vont-ils se croiser ?
 

Exercice 11

Un camion $M_{1}$ quitte une ville $A$ à $8h\;50\;min$ pour se rendre à une ville $B$ avec une vitesse constante $V_{1}=126\;km.h^{-1}$
 
Un autre camion $M_{2}$ quitte ville $B$ à $9\;h$ pour se rendre à la ville $A$ avec une vitesse $V_{2}$ inconnue. La route est supposée rectiligne et la distance entre les deux villes est de $259\;km.$
 
1) Calculer la durée et la distance parcourue par $M_{1}$ avant le départ de $M_{2}.$
 
2) En prenant comme origine des espaces $(x=0)$ la ville $A$ et comme origine des dates $(t=0)$ l'instant de départ du camion $M_{2}.$
 
2.1) Déterminer l'équation horaire $x_{1}$ du camion $M_{1}$
 
2.2) Déterminer en fonction de $V_{2}$ l'équation horaire $x_{2}$ du camion $M_{2}.$
 
3) À quelle date et à quelle heure le camion $M_{1}$ arrivera-t-il à destination?
 
4) Quelle est la vitesse $V_{2}$ du camion $M_{2}$ pour que les deux mobiles arrivent en même temps à destination?
 
5) En supposant que $V_{2}=238\;m.s^{-1}$, en déduire:
 
5.1) La date et l'heure de rencontre des deux camions.
 
5.2) La position de rencontre.
 
6) À quelles dates les deux camions sont-ils distants de $5\;km\ ?$ 
 
Commenter le résultat

 

 

Exercice 12

L'enregistrement du mouvement d'un mobile autoporteur est donné par le schéma ci-dessous 
 
(Échelle : $1\;cm$ pour $1\;cm$)
 
Deux positions consécutives du mobile sont séparées par un intervalle de temps constant $\tau=40\;ms$

 

 
1) Après observation de cet enregistrement, quelle est la nature précise du mouvement ? Justifier la réponse
 
2-1) Mesurer la distance $M_{0}M_{8}$
 
2-2) Déterminer l'intervalle de temps qui sépare les deux positions $M_{0}\ $ et $\ M_{8}$
 
2-3) En déduire la vitesse moyenne du mobile. On arrondira le résultat à $0.01\;m.s^{-1}$
 
3-1) Déterminer les valeurs des vitesses instantanées $v_{1}\;;\ v_{2}\ $ et $\ v_{5}.$
 
3-2) L'observation des vitesses instantanées successives permet-elle d'affirmer que le mouvement du mobile autoporteur est accéléré ?
 
3-3) Représenter les vecteurs vitesses instantanées correspondant aux positions $M_{2}\ $ et $\ M_{5}$ du mobile
 
Échelle : $1\;cm$ pour $0.2\;m.s^{-1}$
 

Exercice 13

Un mobile $M$ effectue le trajet entre $A\ $ et $\ D$ en passant par les points $B\ $ et $\ C$ comme l'indique la figure suivante :

 

 
1) Compléter le tableau suivant en déterminant la nature de la trajectoire ainsi que le type de mouvement correspondant pour chaque partie du trajet
 
$$\begin{array}{|c|c|c|}\hline\text{Partie du trajet}&\text{Nature du trajet}&\text{Nature du mouvement}\\ \hline AB&&\\ \hline BC&&\\ \hline CD&&\\ \hline\end{array}$$
 
2) a) Le mobile parcourt la distance $AB=340\;m$ en $\Delta t_{1}=20\;s.$ 
 
Déterminer sa vitesse moyenne $V_{1}$ sur le trajet $AB.$
 
b) Le mobile effectue le parcours entre $B\ $ et $\ C$ avec une vitesse moyenne $V_{2}=15.7\;m.s^{-1}$ en $\Delta t_{2}=30\;s.$
 
Déterminer la distance du parcours $BC.$
 
c) Le mobile parcourt la distance $CD=143\;m$ avec une vitesse moyenne $V_{3}=14.3\;m.s^{-1}$
 
Déterminer la durée $\Delta t_{3}$ de ce parcours $CD.$
 
3) En déduire la nature du mouvement du mobile sur tout le trajet entre $A\ $ et $\ D$, en justifiant votre réponse.
 
4) Calculer la vitesse moyenne $V_{m}$ du mobile sur tout le trajet entre $A\ $ et $\ D.$
 

Exercice 14

On étudie le mouvement d'un véhicule sur un circuit. 
 
Le diagramme suivant représente les variations de la vitesse du véhicule en fonction du temps.

 

 
1) Étude de la phase I
 
a) Rappeler la définition de la trajectoire d'un mobile.
 
b) Comment évolue la vitesse du véhicule de 0 à 12 secondes ? Justifier
 
c) En déduire la nature du mouvement du véhicule
 
2) Étude la phase II
 
a) Que peut-on dire de la vitesse du véhicule pendant cette phase ?
 
b) Déterminer, à partir du graphique, la vitesse du véhicule et la durée de la phase II.
 
c) Convertir la vitesse du véhicule pendant cette phase en $km.h^{-1}$
 
d) Calculer la distance d parcourue par le véhicule au cours de cette phase.
 
3) Étude de la phase III
 
a) Que peut-on dire de la vitesse du véhicule pendant cette phase ? 
 
Justifier
 
b) Quelle est la nature de mouvement du véhicule au cours de cette phase ?
 
d) Déterminer, à partir du graphique, la vitesse en $m.s^{-1}$ du véhicule au temps $t=30$ secondes

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$


 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Tension électrique - 2nd S

Classe: 
Seconde
 

Exercice 1


 
1) Représenter les tensions $U_{_{PN}}\;,\ U_{_{AB}}\;,\ U_{_{DC}}\ $ et $\ U_{_{DE}}.$
 
2) Quelle est la valeur de $U_{_{AB}}\ ?$
 
3) En déduire la valeur de $I_{1}.$
 
4) Quelle est la valeur de $U_{_{DC}}\ ?$
 
5) Quelle est la valeur de $U_{_{DE}}\ ?$
 
$U_{_{PN}}=20\;V\;;\ I=300\;mA\;;\ I_{2}=200\;mA$
 
Les dipôles $D_{3}\ $ et $\ D_{2}$ sont identiques
 

Exercice 2

1) Nommer dans chaque cas la tension mesurée par l'oscillographe.

 

 
2) On fournit un écran d'oscillographe
 
Les réglages initiaux de l'oscillographe sont tels que la ligne médiane horizontale corresponde à une tension nulle

 

 
2.1) Sur la voie $A$ quelle est la sensibilité utilisée ?
 
2.2) Sur la voie $B$ quelle est la sensibilité utilisée ?
 
2.3) La tension mesurée sur la voie $A$ est-elle positive ou négative ?
 
2.4) La tension mesurée sur la voie $B$ est-elle positive ou négative ?
 
2.5) Quelle est en divisions la déviation observée sur la voie $A\ ?$ En déduire la valeur de la tension mesurée sur la voie $A\ ?$
 
2.6) Quelle est en divisions la déviation observée sur la voie $B\ ?$ En déduire la valeur de la tension mesurée sur la voie $B\ ?$
 

Exercice 3

On a visualisé ci-dessous diverses tensions. La sensibilité verticale est de $2\;V/div$ et la sensibilité horizontale de $2\;ms/div.$
 
1) Indiquer l'oscillogramme qui correspond à une tension continue et celui qui correspond à une tension alternative sinusoïdale.

 

 
2) Pour l'oscillogramme représentant une tension continue, calculer la valeur de la tension qui a été mesurée.
 
3) Pour l'oscillogramme représentant une tension alternative sinusoïdale,
 
a) Déterminer $U_{\text{max}}.$
 
b) Calculer la valeur efficace de la tension.
 
4) Pour l'oscillogramme représentant une tension alternative sinusoïdale, déterminer la période du courant et sa fréquence.
 

Exercice 4

On considère le circuit électrique ci-dessous comportant sept dipôles passifs comme l'indique la figure.

 


 

On donne les mesures suivantes :
$$U_{_{AB}}=4\;V\;;\quad U_{_{FE}}=2\;V\;;\quad U_{_{BC}}=1\;V\quad\text{et}\quad U_{_{ED}}=\dfrac{3}{2}U_{_{BC}}$$
 
1) Calculer les tensions électriques suivantes : $U_{_{BE}}\;;\ U_{_{CE}}\;;\ U_{_{DC}}.$
 
2) En déduire le sens du courant dans la branche $(BE).$
 
3) On donne les valeurs de quelques intensités.

$I=5\;A\;;\ I_{1}=2\;A\;;\ I_{3}=3\;A\ $ et $\ I_{4}=I_{5}$
 
Déterminer les intensités électriques $I_{2}\;;\ I_{4}\;;\ I_{6}\ $ et $\ I_{7}.$
 
4) L'ampèremètre du circuit est de classe 2. Il comporte 100 divisions et porte les calibres $1\;A\;;\ 5\;A\;;\ 10\;A\ $ et $\ 15\;A.$
 
a) Quel est le calibre le mieux adapté à la mesure ? En déduire l'indication de l'aiguille.
 
b) Donner un encadrement de l'intensité mesurée
 

Exercice 5

Pour le montage suivant, on donne les valeurs des tensions :
$$U_{1}=-12\;V\;;\ U_{5}=-3\;V\;;\ U_{7}=4\;V$$
 
Calculer les valeurs des tensions $U_{2}\;;\ U_{3}\;;\ U_{4}\ $ et $\ U_{6}.$

 
 

Exercice 6

On considère le circuit électrique ci-dessous où les trois lampes $L_{1}\;,\ L_{2}\ $ et $\ L_{3}$ de tension nominale $6\;V$ chacune.

 

 
1) Indiquer le sens du courant dans chaque branche.
 
2) L'ampèremètre $A_{1}$ comporte 100 divisions, l'aiguille dévie de 70 divisions, le calibre est de $1\;A.$
 
2.1) Quelle est l'intensité du courant électrique mesuré par l'ampèremètre ?
 
2.2) En déduire l'intensité dans $A_{2}.$
 
3) On donne $I_{2}=0.5\;A$ l'intensité du courant qui traverse la lampe $L_{3}.$
 
3.1) Énoncer la loi des nœuds.
 
3.2) Déterminer l'intensité du courant $I_{1}$ (qui traverse les lampes $L_{1}\ $ et $\ L_{2}).$
 
Les lampes éclairent-elles de la même manière ?
 
4.1) Indiquer sur le schéma comment brancher le voltmètre pour mesurer la tension $U_{_{AB}}$ et préciser les bornes $+\ $ et $\ -$ (du voltmètre).
 
4.2) Le calibre utilisé est $5\;V$ et l'aiguille indique la graduation 60 de l'échelle qui comporte 100 divisions. 
 
Quelle est la valeur de la tension mesurée ?
 
4.3) On donne $U_{_{PN}}=6\;V$, en appliquant la loi des mailles calculer $U_{_{BC}}.$
 
4.4) En déduire la tension aux bornes de la lampe $L_{3}.$
 
4.5) Quelle(s) lampe(s) brille(ent)–t–elle(s) normalement ?
 
4.6) On relie $B\ $ et $\ C$ par un fil de connexion (aux bornes de $L_{2}).$
 
$-\ \ $ Qu'appelle-t-on cette opération ?
 
$-\ \ $ La tension aux bornes de chaque lampe a-t-elle changé ? et quelle sont les lampes brillent normalement dans ce cas ?
 

Exercice 7

 

 
Soit le circuit de la figure ci-dessus. On a mesuré les tensions : 
 
$U_{_{AB}}=5\;V\;;\ U_{_{AC}}=15\;V\;;\ U_{_{AE}}=12\;V\;;\ U_{_{AD}}=20\;V$
 
a) Calculer la valeur des tensions $U_{_{BC}}\;;\ U_{_{BE}}\;;\ U_{_{DE}}\;;\ U_{_{CD}}\;;\ U_{_{EC}}$
 
c) Indiquer le sens des courants dans les 3 branches

 

 
a) Que peut-on dire de la tension $U_{_{AE}}\ ?$
 
b) Calculer toutes les autres tensions.
 
c) Préciser quel est le dipôle générateur dans ce montage.
 

Exercice 8

Calculer les tensions aux bornes des différents dipôles du circuit ci-dessous et les intensités des courants qui les traversent.

 

 
On donne : $U_{_{AB}}=120\;mV\;;\ |U_{_{CD}}|=30\;mV\;;\ U_{_{AD}}=U_{_{DB}}$
 
$I=1\;A\;;\ I_{1}=0.2\;A\;;\ I_{2}=0.5\;A\;;\ I_{6}=0.4\;A$
 

Exercice 9

On considère le circuit de la figure ci-dessous

 

 
1) Sachant que la quantité d'électricité $Q$ qui traverse la section du fil $AF$ pendant une minute est $Q=30\;C$
 
1.1) Calculer le nombre d'électrons qui traverse cette section pendant la même durée
 
1.2) En déduire la valeur de l'intensité du courant $I_{1}$ qui traverse la lampe $L_{1}.$
 
2) L'ampèremètre A comporte 100 divisions et possède les calibres suivant : $5\;A\;;\ 1\;A\;;\ 300\;mA\;;\ 100\;mA.$
 
2.1) Quel est le calibre le plus adapté pour la mesure de l'intensité $I_{1}\ ?$
 
2.2) Devant quelle division l'aiguille de l'ampèremètre s'arrête-t-elle ?
 
3) L'intensité débité par le générateur est $0.8\;A$
 
3.1) Quels sont les points qui sont considérés comme des nœuds ?
 
3.2) Indiquer le sens du courant dans chaque branche
 
Déterminer les valeurs des intensités qui traversent les lampes $L_{2}\;,\ L_{3}\ $ et $\ L_{4}$
 
4) On branche un voltmètre aux bornes de la lampe $L_{1}$, il indique une tension de valeur $4\;V$
 
4.1) Quelle tension indique-t-il $U_{_{AB}}\ $ ou $\ U_{_{BA}}\ ?$ 
 
Schématiser le voltmètre aux bornes de la lampe $L_{1}.$
 
4.2) Sachant que $U_{_{MD}}=1\;V$, déterminer $U_{_{ME}}$
 

Exercice 10

Soit le montage suivant :

 

 
$E=10\;V\;;\ U_{1}=6\;V\;;\ I_{1}=0.1\;A\;;\ I_{2}=30\;mA$
 
1) Établir l'équation du nœud $C.$
 
2) En déduire l'expression de $I_{3}$ en fonction de $I_{1}\ $ et $\ I_{2}.$
 
3) Calculer $I_{3}.$
 
4) Établir l'équation de la maille $(ABCFA).$
 
5) En déduire l'expression de la tension $U_{2}.$
 
6) Calculer $U_{2}.$
 
7) Établir l'équation de la maille $(CDEFC).$
 
8) En déduire l'expression de $U_{3}.$
 
9) Calculer $U_{3}.$
 
10) Vérification de la loi des mailles
 
Établir l'expression de la maille $(ABDEA)$ et montrer que $E=U_{1}+U_{3}.$
 
11) Faire l'application numérique. La loi des mailles est-elle vérifiée ?
 

Exercice 11

Soit le réseau représenté à la figure ci-dessous, comportant un générateur de courant continu. 
 
On mesure les tensions suivantes :
$$U_{_{AB}}=22\;V\;;\ U_{_{BC}}=10\;V\;;\ U_{_{BE}}=6\;V\;;\ U_{_{ED}}=3\;V$$
 
1) Calculer les tensions $U_{_{AE}}\;;\ U_{_{DA}}\;;\ U_{_{CD}}\;;\ U_{_{CE}}\ $ et $\ U_{_{PN}}$
 
2) Dans quel sens le courant circule-t-il dans chaque branche ? (Faire le circuit)
 
3) Lorsqu'on mesure les intensités des courants qui aboutissent au nœud $E$, on trouve que ceux qui arrivent ont la même intensité $I=4\;A.$ En déduire les valeurs des intensités des courants dans les branches $AE\;;\ BE\ $ et $\ DE.$
 
4) L'intensité du courant qui traverse le générateur est $I_{0}=14\;A$, celle dans la branche AB est égale à $5\;A.$
 
En déduire les intensités des courants dans les autres branches du réseau.

 

 

Exercice 12

Soit le circuit électrique ci-dessous.

 

 
On donne : $U_{_{PA}}=2\;V\;;\ U_{_{AC}}=10\;V\ $ et $\ U_{_{AB}}=2U_{_{PA}}.$
 
1) Représenter, par une flèche sur le circuit les tensions suivantes : $U_{_{DE}}\;;\ U_{_{CB}}\ $ et $\ U_{_{CN}}.$ 
 
Donner le signe de chacune de ces tensions.
 
2) Énoncer la loi des mailles.
 
On branche un voltmètre à aiguille entre les bornes du générateur pour mesurer la tension $U_{_{PN}}.$ 
 
Représenter ce voltmètre sur le circuit en indiquant ses deux bornes.
 
3) Le calibre du voltmètre étant fixé à $30\;V$ et l'aiguille s'arrête devant la graduation 14 sur l'échelle 30.
 
Calculer la valeur de $U_{_{PN}}.$ En déduire celle de $U_{_{NP}}.$
 
4) Calculer les valeurs des tensions $U_{_{DE}}\;;\ U_{_{CB}}\ $ et $\ U_{_{CN}}.$
 

Exercice 13

Soit le circuit représenté ci-dessous. Il comporte un générateur et plusieurs lampes. Seules les lampes $(L_{6})\ $ et $\ (L_{7})$ sont identiques.
 
On donne : $I_{1}=0.1\;A\ $ et $\ I_{4}=20\;mA.$
 
$U_{_{AB}}=4\;V\;;\ U_{_{CB}}=-2\;V\;;\ U_{_{GD}}=7\;V\;;\ U_{_{ED}}=-1\;V\ $ et $\ U_{_{GF}}=10\;V.$

 

 
1) Indiquer le sens du courant dans chaque branche du circuit.
 
2) Comparer, en justifiant votre réponse, les valeurs de $I_{2}\ $ et $\ I_{4}$
 
3) Écrire la loi des nœuds au nœud $A.$
 
4) En déduire la valeur de $I_{3}.$
 
5) Indiquer sur le schéma du circuit l'emplacement de l'ampèremètre pour mesurer l'intensité $I_{3}.$
 
6) Calculer $I_{5}\;,\ I_{6}\ $ et $I_{7}.$
 
7) Représenter les tensions $U_{_{AB}}\ $ et $\ U_{_{CB}}.$
 
8) Quelle est la valeur de la tension $U_{_{CD}}\ ?$
 
9) Écrire la loi des mailles dans la maille $ABCDA.$
 
10) Calculer la tension $U_{_{AD}}$ et déduire $U_{_{GA}}.$
 
11) Représenter, sur le schéma du circuit, le branchement du voltmètre qui permet de mesurer la tension $U_{_{GA}}.$
 
12) Comparer, en justifiant votre réponse, les tensions $U_{_{EF}}\ $ et $\ U_{_{HF}}.$
 
13) Déterminer les valeurs des tensions $U_{_{EF}}\ $ et $\ U_{_{HF}}.$
 

Exercice 14

On réalise le montage ci-dessous :

 

 
1) On choisit comme masse dans le circuit le point B. On y relie la borne $COM$ d'un voltmètre.
 
L'autre borne du voltmètre est successivement placée en $A\;,\ C\ $ et $\ D.$
 
On lit alors respectivement sur le voltmètre $15\;V\;,\ 12\;V\ $ et $\ 3\;V.$
 
En déduire les potentiels des points $A\;,\ B\;,\ C\;,\ D$ et la valeur de la tension $U_{_{AD}}.$
 
2) Sur le même circuit, on choisit maintenant le point $C$ comme masse. On y relie la borne $COM$ d'un voltmètre.
 
L'autre borne du voltmètre est successivement placée en $A\;,\ B\;,\ D$
 
On lit alors respectivement sur le voltmètre $3\;V\;,\ -12\;V\ $ et $\ -9\;V.$
 
En déduire les potentiels des points $A\;,\ B\;,\ C\;,\ D$ et la valeur de la tension $U_{_{AD}}.$
 
3) Compléter le tableau récapitulatif :
$$\begin{array}{|l|c|c|c|}\hline&V_{_{A}}(V)&V_{_{D}}(V)&U_{_{AD}}(V)\\ \hline 1^{\text{ère}}\text{ expérience avec masse en } B&&&\\ \hline 2^{\text{ème}}\text{ expérience avec masse en } C&&&\\ \hline\end{array}$$
 
Rédiger votre conclusion
 

Exercice 15

 

 
Sachant que les 3 dipôles rectangulaires ne sont pas des générateurs, calculer les tensions demandées sur les schémas 1 et 2.
 

Exercice 16

 

 
Un générateur maintient entre ses bornes une tension constante $U_{_{PN}}=6.0\;V$ 
 
L'interrupteur étant fermé on mesure : $U_{_{PA}}=2.8\;V\ $ et $\ U_{_{MS}}=1.3\;V$
 
1) Préciser sur le schéma le mode de branchement du voltmètre dans le circuit pour les tensions ci-dessus. Indiquer la borne $COM.$
 
2) Le multimètre comporte plusieurs calibres. Quel est le calibre le mieux adapté à la mesure de $U_{_{MS}}\ ?$
 
a) $20\;V$
 
b) $200\;mV$
 
c) $2\;V$
 
3) Représenter la flèche correspondant à la tension $U_{_{PA}}.$
 
4) Déterminer la tension aux bornes du dipôle $D_{4}.$
 
5) Quelles sont les tensions aux bornes des dipôles $D_{2}\ $ et $\ D_{3}\ ?$
 

Exercice 17

La tension aux bornes du générateur est 6 volts.

 

 
a) Quelle est la tension aux bornes de $L_{3}\ ?$
 
b) La tension aux bornes de $L_{2}$ est $1.5\;V$ Quelle est la tension aux bornes de $L_{1}\ ?$
 
c) On enlève $L_{3}$ les tensions aux bornes de $L_{1}\ $ et $\ L_{2}$ changent-elles ?
 
d) On enlève $L_{1}$, quelle sera la tension aux bornes $L_{3}\ ?$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Intensité du courant électrique - 2nd S

Classe: 
Seconde
 

Exercice 1

On considère le circuit de la figure ci-dessous

 

 
1) Sachant que la quantité d'électricité $Q$ qui traverse la section du fil $AF$ pendant une minute est $Q=30\;C.$
 
a) Calculer le nombre d'électrons qui traverse cette section pendant la même durée.
 
b) En déduire la valeur de l'intensité du courant $I_{1}$ qui traverse la lampe $L_{1}.$
 
2) L'ampèremètre $A$ comporte 100 divisions et possède les calibres suivant :
$$5\;A\;;\quad 1\;A\;;\quad 300\;mA\;;\quad 100\;mA$$
 
a) Quel est le calibre le plus adapté pour la mesure de l'intensité $I_{1}\ ?$
 
b) Devant quelle division l'aiguille de l'ampèremètre s'arrête-t-elle ?
 
3) L'intensité débité par le générateur est $0.8\;A.$
 
a) Quels sont les points qui sont considérés comme des nœuds ?
 
b) Indiquer le sens du courant dans chaque branche.
 
Déterminer les valeurs des intensités qui traversent les lampes $L_{2}\;,\ L_{3}\ $ et $\ L_{4}$
 

Exercice 2

On considère le montage de ma figure représentée ci dessous.

 

 
L'ampèremètre comporte 100 divisions et possède les calibres suivants :
$$3\;A\;;\quad 1\;A\;;\quad 300\;mA\;;\quad 100\;mA\;;\quad 30\;mA\quad\text{et}\quad 10\;mA$$
Lorsqu'on utilise le calibre $300\;mA$,l'aiguille de l'ampèremètre s'arrête devant la graduation 30.
 
1) Calculer l'intensité du courant qui traverse l'ampèremètre en $mA$ et en $A.$
 
2) Quels sont les calibres permettant la mesure de l'intensité $I\ ?$ 
 
Préciser le meilleur calibre.
 
3) Quelle est l'indication de l'aiguille de l'ampèremètre lorsqu'il est utilisé sur le meilleur calibre ?
 
4) Calculer la quantité d'électricité traversant la section du fil conducteur pendant 2 minutes.
 
5) Déduire le nombre d'électrons traversant la section de ce fil pendant 2 minutes.
 

Exercice 3

1) Une pile est capable de libérer une quantité d'électricité $Q=470\;C.$ Elle alimente en électricité une montre à quartz. Il faut changer la pile tous les dix huit mois. (47 millions de secondes)
 
Calculer l'intensité du courant électrique qui passe dans la pile.
 
2) De quelle grandeur l'ampèreheure est-il l'unité ? Convertir l'ampèreheure dans l'unité correspondante du système international.
 
3) L'intensité moyenne qui passe dans la pile d'une calculatrice à cristaux liquides est $I=0.20\;mA.$ La capacité de la pile utilisée est $Q=0.30\;Ah.$
 
Pendant combien de temps peut-on utiliser la calculatrice ?
 
4) Pour sortir de son garage, un automobiliste actionne son démarreur pendant 5 secondes et, ensuite, allume ses phares est ses feux de position pendant 1 minute. L'intensité du courant dans la batterie est respectivement de 30 ampères et de 6 ampères pendant ces opérations.
 
Quelle est la quantité d'électricité totale débitée par la batterie ?

 

 
 

Exercice 4

Dans la portion de circuit de la figure ci-dessous, calculer les intensités $I_{1}\;,\ I_{2}\ $ et $\ I_{3}.$
 
On donne : $I_{4}=7\;A\;,\ I_{5}=2\;A\;,\ I_{6}=3\;A\;,\ I_{7}=5\;A.$

 

 
 

Exercice 5

Dans les trois circuits suivants, compléter en indiquant le sens du courant dans chaque branche. 

Utiliser la loi de distribution du courant pour déterminer les intensités manquantes.

 

 
 

Exercice 6

1) Préciser sur le circuit ci-dessous le sens du courant dans chaque dipôle et énoncer la loi des nœuds.

 

 
2) On donne $I_{1}=3\;A\;,\ I_{2}=5\;A\;,\ I_{5}=1\;A\ $ et $\ I_{6}=3I_{4}$
 
Calculer $I\;,\ I_{3}\;,\ I_{4}\ $ et $\ I_{6}.$
 
3) On désire vérifier la valeur de $I_{1}$ à l'aide d'un ampèremètre de classe 2 possédant 6 calibres :
$$100\;mA\;;\quad 1\;A\;;\quad 2\;A\;;\quad 4\;A\;;\quad 6\;A\;;\quad 10\;A$$ et dont le cadrant comporte 120 divisions.
 
3.1) Quel est le calibre le mieux adapté ? Quelle est la déviation correspondante ?
 
3.2) Calculer l'incertitude absolue $\Delta I$, l'incertitude relative pour la mesure et donner un encadrement de l'intensité.
 

Exercice 7


 

 
Dans le montage ci-dessus les lampes sont identiques. L'ampèremètre indique $0.3\;A$
 
1) Quelle est l'intensité traversant chacune des lampes ?
 
2) Quels sont les nœuds du circuit ci-dessous ?
 
3) Calculer les intensités des courants 
 
On donne : $I_{1}=10\;A\;,\ I_{4}=4\;A\ $ et $\ I_{6}=5\;A$
 
4) Préciser quel est le dipôle générateur dans ce montage

 

 
 

Exercice 8

On considère le circuit électrique suivant.

 

 
1) L'ampèremètre (A) possède 100 divisions, il est utilisé sur le calibre $10\;A$, l'aiguille s'arrête en face de la division 40 et indique l'intensité $I.$
 
a) Préciser le sens de $I$ et calculer sa valeur.
 
b) En déduire la quantité d'électricité qui traverse une section du fil pendant une minute.
 
2) L'ampèremètre $(A_{1})$ possède 30 divisions, l'aiguille indique la graduation $1_{2}$ lorsqu'on l'utilise sur le calibre $3\;A.$
 
Calculer l'intensité $I_{1}$ indiquée par $(A_{1})$
 
3) Déduire la valeur de l'intensité $I_{2}$ indiquée par $(A_{2}).$
 
4) On inverse les branchements du générateur.
 
L'éclat des lampes change-t-il ?
 
5) La lampe $(L_{1})$ est grillée, la lampe $(L_{2})$ continuera-t-elle à briller ? Justifier
 

Exercice 9

Soit le circuit électrique suivant :

 

 
1) Que peut-on dire des deux points $A\ $ et $\ B\ ?$
 
2) Indiquer le sens des courants manquants dans chaque branche du circuit.
 
3) Pour mesurer l'intensité $I$, on utilise un ampèremètre à aiguille dont le calibre est fixé à $10\;A$ et son aiguille indique la graduation 85. 
 
Calculer $I.$
 
4) En appliquant la loi des nœuds, écrire :
 
a) Une relation entre $I\;,\ I_{1}\;,\ I_{2}\ $ et $\ I_{3}$
 
b) Une relation entre $I_{1}\;,\ I_{2}\ $ et $\ I_{4}$
 
c) Une relation entre $I_{3}\;,\ I_{4}\;,\ I_{5}\ $ et $\ I_{6}$
 
5) Sachant que $I_{2}=2\;A\;,\ I_{3}=3\;A\ $ et $I_{6}=1.5\;A$, calculer les intensités manquantes.
 

Exercice 10

Soit les circuits suivants :

 

 
Indiquer sur les schémas les valeurs des intensités dans chaque lampe
 

Exercice 11

On considère le circuit de la figure ci-dessous :

 

 
1) L'ampèremètre $A$ comporte 100 divisions et possède les calibres suivants :
$$5\;A\;;\quad 3\;A\;;\quad 1\;A\;;\quad 300\;mA\;;\quad 100\;mA$$
 
1.1) Quels sont les calibres quand peut utiliser pour mesurer cette intensité $I_{1}\ ?$
 
1.2) Quel est le calibre le plus adapté pour la mesure de l'intensité $I_{1}\ ?$
 
1.3) Devant quelle division l'aiguille de l'ampèremètre $A_{1}$ s'arrête-t-elle ?
 
2) L'intensité du courant débitée par le générateur est $I=0.8\;A$
 
2.1) Quels sont les points qui sont considérés comme des nœuds ?
 
2.2) Indiquer le sens du courant dans chaque branche.
 
Déterminer les valeurs des intensités qui traversent les lampes $L_{2}\;,\ L_{3}\ $ et $\ L_{4}$
 

Exercice 12

On considère le circuit électrique suivant :

 

 
1) Déterminer le nombre de nœuds et le nombre de branches
 
2) Calculer les intensités des courants $I_{1}\;,\ I_{3}\;,\ I_{5}\;,\ I_{8}\;,\ I_{10}\;,\ I_{11}\ $ et $\ I_{12}$ après avoir déterminer le sens des courants
 
On donne : $I_{2}=0.7\;A\;;\ I=0.16\;A\;;\ I_{6}=0.49\;A\;;\ I_{7}=0.12\;A\;;\ I_{9}=0.25\;A$
 

Exercice 13

Sur le circuit ci-dessous, indique par des flèches dans chacune des branches le sens du courant.

 

 
Sur le schéma marque en rouge les nœuds du circuit.
 
On appelle $I_{1}$ le courant qui arrive au nœud, $I_{2}\ $ et $\ I_{3}$ les courants qui partent du nœud.
 
Indique sur le schéma les courants $I_{1}\;,\ I_{2}\ $ et $\ I_{3}.$
 
L'ampèremètre $A_{1}$ situé à coté de la pile indique $I_{1}=1.5\;A$ et l'ampèremètre $A_{2}$ situé entre les deux lampes indique $I_{2}=0.98\;A.$
 
Quelle valeur indique alors le troisième ampèremètre ?
 

Exercice 14

On considère les réseaux suivants dans lesquels certains courants sont connus en intensité et en sens.
 
Déterminer les caractéristiques (intensité et sens) des courants manquants

 

 
 

Exercice 15

1) Une ampoule est traversée par un courant continu de $0.1\;A.$
 
1.1) Déterminer la quantité de charge qui la traverse en une minute.
 
1.2) Déterminer dans ce cas le nombre d'électrons qui ont traversé l'ampoule.
 
1.3) On alimente cette ampoule avec une pile sur laquelle on trouve l'inscription $"1200\;mAh"$
 
Que signifie cette inscription ? Déterminer le temps de fonctionnement de l'ampoule-t-elle ?
 
2) Une batterie de voiture est marquée $50\;Ah$, elle est complètement chargée
 
2.1) Combien de temps pourra-t-elle alimenter les 4 lampes montées en parallèle des feux de stationnement, sans être rechargé. On sait que chaque lampe est parcourue par un courant de $0.5\;A$
 
2.2) La batterie est à nouveau chargée. Après avoir laissé les 4 lampes allumées pendant $12\;h$, combien de temps peut-on faire fonctionner le démarreur de la voiture qui consomme $300\;A\ ?$ (sans recharger la batterie et en éteignant les lampes)

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 


 
Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Généralités sur le courant électrique - 2nd S

Classe: 
Seconde
 

Exercice 1

Compléter le texte ci-dessous avec des mots de la liste suivante : négative, positive, électrons, ions, cations, anion.
 
Indication : Un mot peut ne pas être utilisé ou être utilisé plusieurs fois.
 
Dans les métaux, la conduction du courant électrique est assurée par les $\ldots\ldots$ qui se déplacent de la borne $\ldots\ldots$ du générateur vers sa borne $\ldots\ldots.$
 
Une solution ionique est constituée de deux sortes d'ions : Les ions chargés positivement sont appelés des $\ldots\ldots$ et les ions chargés négativement sont appelés des $\ldots\ldots.$
 
Dans une solution ionique, le courant électrique est dû à un double déplacement des $\ldots\ldots.$
 
Les cations sont attirés par l'électrode reliée à la borne $\ldots\ldots$ du générateur et les $\ldots\ldots$ sont attirés par l'électrode qui est reliée à la borne $\ldots\ldots$ du générateur
 

Exercice 2

1) Réaliser le schéma de ce montage en utilisant les symboles normalisés

 

 
2) Ces schémas correspondent-ils à des circuits électrique fonctionnel ? Justifier

 

 
 

Exercice 3

A partir des éléments dessinés ci-dessous, réaliser les branchements :
 
1) pour que les lampes soient montées en série.
 
2) pour que les lampes soient montées en parallèle.

 

 

Exercice 4

Analyse d'un montage à trois lampes

 

 
1) Schématiser le montage ci-dessus
 
2) Pour connaître tous les courant où faut-il placer le minimum d'ampèremètres ?
 
3) La lampe $L_{1}$ vient à griller ; les lampes $L_{2}\ $ et $\ L_{3}$ éclairent-elles ?
 
4) La lampe $L_{2}$ vient à griller ; les lampes $L_{1}\ $ et $\ L_{3}$ éclairent-elles ?
 

Exercice 5

Les dipôles $D_{1}\;,\ D_{2}\;,\ D_{3}\;,\ D_{4}\ $ et $\ D_{5}$ ne sont pas des générateurs.

 

 
Choisir les affirmations exactes :
 
1.1) Le courant électrique est un mouvement de porteurs de charges.
 
1.2) Les charges en mouvement dans un circuit sont toujours des électrons.
 
1.3) A l'extérieur du générateur, les électrons circulent de la borne $-$ vers la borne $+.$
 
1.4) Le courant sort du générateur par la borne verticale située à droite sur ce schéma.
 
2.1) Les dipôles $D_{4}\ $ et $\ D_{6}$ sont en série.
 
2.2) Les dipôles $D_{4}\ $ et $\ D_{6}$ sont en parallèle.
 
2.3) Les dipôles $D_{4}\ $ et $\ D_{6}$ ne sont ni l'un ni l'autre.
 
2.4) Les dipôles $D_{1}\ $ et $\ D_{2}$ sont en série.
 
3.1) Il y a dans ce circuit 2 nœuds.
 
3.2) Il y a dans ce circuit 6 nœuds.
 
3.3) Il y a dans ce circuit 2 branches en dérivation.
 
3.4) Il y a dans ce circuit 3 branches en dérivation.
 

Exercice 6 

L'électrolyse est un processus de conversion d'énergie électrique en énergie chimique. En effet, cette méthode consiste à faire passer du courant électrique dans une solution aqueuse afin de transformer la matière (réaction chimique) au niveau des électrodes. Cette technique est utilisée pour "plaquer" les bijoux.
 
Une bague en métal est plongée dans une solution de chlorure d'argent reliée à un générateur pour être plaquée en argent :

 

 
1) Indiquer quelles solutions aqueuses conduisent le courant électrique.
 
2) Préciser la nature du courant électrique dans les solutions.
 
3) Donner la formule chimique de la solution de chlorure d'argent.
 
Sur quelle électrode (positive ou négative) doit-on placer la bague pour qu'elle se recouvre d'argent ?
 
Justifier
 

Exercice 7

1) Schématiser un circuit comprenant, en série, un générateur, une lampe, un ampèremètre, et un électrolyseur (vous ferez le dessin de l'électrolyseur en faisant apparaître les électrodes)
 
2) Comment schématise-t-on un électrolyseur ?
 
3) On place successivement dans l'électrolyseur : une solution de sulfate de cuivre, une solution de glucose, une solution d'eau déminéralisée et une solution d'eau minérale
 
a) Quel est le but de cette expérience ?
 
b) Présenter les résultats des observations dans un tableau
 
c) Ajouter une ligne au tableau et donner l'interprétation des observations
 
5) On place dans l'électrolyseur une solution de chlorure de zinc :
 
a) Sur le schéma, indiquer en rouge le sens du courant
 
b) Sur le schéma, indiquer en bleu le sens des ions positifs
 
c) Sur le schéma, indiquer en noir le sens des électrons libres
 
d) Sur le schéma, indiquer en vert le sens des ions négatif
 

Exercice 8

Un élève de seconde, réalise l'expérience suivante avec différents solides puis reporte ses résultats dans un tableau
 
Schéma de l'expérience :

 

 
Tableau de résultats :
$$\begin{array}{|l|c|c|}\hline\text{solide}&\text{état de la}&\text{solide conducteur}\\&\text{lampe}&\text{ou isolant}\\ \hline\text{fer}&\text{allumée}&\\ \hline\text{bois}&\text{éteinte}&\\ \hline\text{aluminium}&\text{allumée}&\\ \hline\text{cuivre}&\text{allumée}&\\ \hline\text{papier}&\text{éteinte}&\\ \hline\text{argent}&\text{allumée}&\\ \hline\text{verre}&\text{éteinte}&\\ \hline\end{array}$$
 
1) Compléter la dernière colonne du tableau en indiquant si le solide est conducteur ou isolant du courant électrique
 
2) D'après ces résultats, est-ce que tous les solides conduisent le courant électrique ?
 
3) Cette expérience montre que les métaux ont une propriété commune. Quelle est cette propriété ?
 

Exercice 9

Deux circuits électriques sont décrits ci-dessous, on doit proposer un schéma pour chacun.
 
1) Le premier circuit électrique contient un générateur, un interrupteur, une lampe et une résistance et fonctionne ainsi :
 
L'interrupteur commande la lampe et la résistance simultanément (ensemble),
 
Si la lampe est grillée, la résistance continue de chauffer
 
1.1) Tracer le schéma
 
1.2) Expliquer pourquoi la résistance continue de chauffer lorsque la lampe est grillée.
 
2) Le deuxième circuit électrique contenant un générateur, un interrupteur, un moteur et une $DEL$ et fonctionne ainsi :
 
L'interrupteur commande le moteur et la $DEL$ simultanément (ensemble),
 
Si le moteur est détruit, la $DEL$ ne brille plus.
 
2.1) Tracer le schéma
 
2.2) Expliquer pourquoi la $DEL$ ne brille plus lorsque le moteur est détruit
 

Exercice 10

Observez les circuits électriques ci-dessous et répondez aux questions en justifiant toutes vos réponses.

 

 
1) Dans quel circuit n'y a-t-il pas de courant électrique qui circule ?
 
2) Indiquer le sens de circulation du courant électrique dans les autres circuits.
 
3) Quels sont les circuits en série ? Parmi ces circuits, quels sont les deux dans lesquels la lampe éclaire de la même façon ?
 
4) Quels sont les circuits qui comportent des dérivations ?
 
5) Dans le circuit 7, placez un interrupteur permettant d'allumer la lampe indépendamment des autres dipôles. Placez un 2e interrupteur permettant de commander la résistance et le moteur en même temps indépendamment de la lampe.
 
Dans quels circuits la lampe éclaire-t-elle le plus
 

Exercice 11

Dans chacun des exercices ci-dessous, relever les affirmations justes et modifier (si possible) celles qui sont fausses ou incomplètes.
 
1) Qu'est-ce que le courant électrique ?
 
a) Dans un métal, le courant électrique est dû à un déplacement d'ensemble d'électrons libres (ou électrons de conduction).
 
b) La vitesse de ce déplacement d'ensemble est de l'ordre de 10 kilomètres par heure.
 
c) Les électrons libres sont des électrons qui sont très liés aux noyaux des atomes métalliques.
 
d) Dans une solution conductrice (électrolyte), le courant électrique est dû à un déplacement d'espèces ioniques négatives (anions).
 
2) Quel est le rôle du générateur ?
 
a) Le générateur injecte dans le circuit les électrons de conduction.
 
b) Le générateur impose la mise en mouvement des électrons de conduction.
 
c) Le générateur délivre au circuit la tension électrique nécessaire à la mise en mouvement des électrons de conduction.
 
d) Le courant électrique circule de la borne positive du générateur vers sa borne négative.

 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

 

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Dipôles passifs - 2nd S

Classe: 
Seconde
 

Exercice 1

1) Représenter l'allure de la caractéristique intensité-tension d'un dipôle :
 
a) dipôle symétrique passif.
 
b) dipôle asymétrique passif.
 
c) dipôle actif.
 
2) Comment varie la résistance d'un fil conducteur :
 
a) avec sa section.
 
b) avec sa longueur.
 

Exercice 2

On donne les caractéristiques intensité-tension respectives des dipôles $D_{1}\;,\ D_{2}\ $ et $\ D_{3}.$

 

 
Compléter le tableau suivant :
 
$$\begin{array}{|l|c|c|c|}\hline\text{Dipôle}&D_{1}&D_{2}&D_{3}\\ \hline\text{Symétrique/Asymétrique}&&&\\ \hline\text{Linéaire/Non linéaire}&&&\\ \hline\text{Actif/Passif}&&&\\ \hline \end{array}$$

Exercice 3

On réalise le montage suivant :

 

 
1) L'ampèremètre affiche $7.13\;mA$ et le voltmètre indique $3.29\;V$
 
Quelle est la résistance $X$ du conducteur ohmique placé entre $A\ $ et $\ B\ ?$
 
2) On déplace le curseur du rhéostat de sorte que le voltmètre affiche $2.03\;V$
 
Quelle est alors l'indication de l'ampèremètre ?
 
3) On déplace le curseur du rhéostat de sorte que l'ampèremètre indique $5.12\;mA$
 
Quelle est alors l'indication affichée par le voltmètre ?
 

Exercice 4

On a relevé quelques points de fonctionnement d'une lampe à incandescence à filament métallique, normalement utilisé sous une tension de $6\;V$
 
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|}\hline U(V)&0.05&0.1&0.3&0.4&0.6&0.8&2&3&4&5&6&7\\ \hline I(mA)&25&50&100&111&129&148&240&295&345&395&435&475\\ \hline \end{array}$$
 
1) Tracer la caractéristique intensité tension de la lampe.
 
2) Déterminer, pour chaque point de fonctionnement la résistance $R$ de la lampe.
 
Représenter graphiquement la relation $R=f(U.I)$
 
Que peut-on dire de la variation de la résistance $R$ du filament avec la température ?
 
3) Il est possible de linéariser la caractéristique entre les points de fonctionnement $(3\;V\;,\ 295\;mA)\ $ et $\ (7\;V\;,\ 475\;mA)$
 
Déterminer la relation affine qui décrit approximativement le fonctionnement de la lampe dans ce domaine d'utilisation
 

Exercice 5

On considère la caractéristique intensité tension d'un dipôle
 
1) Représenter un schéma du montage qui nous a permis de tracer cette caractéristique
 
2) Préciser en justifiant la réponse, la nature du dipôle étudié, déterminer sa résistance

 

 
 

Exercice 6

On réalise un circuit électrique simple avec une pile dont la tension entre ses bornes est $U=12\;V$ et un résistor de résistance $R=100\Omega$ qui supporte une intensité maximale de $100\;mA.$
 
1) Ne risque-t-on pas d'endommager $R\ ?$ Justifier.
 
2) Quelle résistance minimale $R'$ faut-il mettre en série avec $R$ dans le circuit pour pouvoir fermer sans dommage l'interrupteur.
 
3) On branche $R\ $ et $\ R''$ en parallèle, $R''$ inconnue, et les deux en série avec $R'$ minimale aux bornes du générateur.
 
a) Déterminer la valeur de $R''$ pour que l'intensité du courant soit égale à $0.12\;A$
 
b) Déterminer l'intensité du courant qui traverse $R'$ en déduire celui qui traverse $R.$
 

Exercice 7

On fournit la caractéristique d'un conducteur ohmique

 

 
1) Expliquer pourquoi l'observation de ce graphe permet d'affirmer que le dipôle AB est un conducteur ohmique.
 
2) Faire le schéma conventionnel du dipôle AB en plaçant les deux points $A\ $ et $\ B$, la flèche tension $U_{_{AB}}$ et le courant $I.$
 
3) Calculer la résistance du conducteur ohmique à partir de sa caractéristique.
 
4)
4.1) Quelle est la tension aux bornes du conducteur ohmique lorsqu'il est traversé par un courant de $15\;mA\ ?$
 
4.2) Quelle est l'intensité du courant qui traverse le conducteur ohmique lorsqu'il est soumis à une tension de $4\;V\ ?$
 
5) Le professeur a conseillé à l'élève de ne pas alimenter le dipôle sous une tension supérieure à $10\;V.$
 
Quelle est l'intensité maximale que peut supporter le composant ?
 

Exercice 8


 
Un diviseur de tension est composé de deux conducteurs ohmiques $R_{1}\ $ et $\ R_{2}$ montés en série. 
 
Il est alimenté par une tension $U_{_{AB}}$ (tension d'entrée $U_{e}$) et la tension $U_{_{CB}}$ (tension de sortie $U_{s}$) peut être appliquée aux bornes d'un appareil dans lequel elle fera circuler un courant.
 
1) Le diviseur de tension est à vide. Aucun appareil n'est branché entre $C\ $ et $\ B.$
 
1.1) Exprimer en fonction de $U_{e}\;,\ R_{1}\ $ et $\ R_{2}$ l'intensité $I$ du courant qui circule dans le circuit.
 
1.2) En déduire l'expression de la tension de sortie $U_{s}$ en fonction de $U_{e}\;,\ R_{1}\ $ et $\ R_{2}.$
 
1.3) Applications numériques :

$U_{e}=6.0\;V\;,\ R_{1}=2.2\;k\Omega\ $ et $\ R_{2}=4.7\;k\Omega$
 
Calculer les valeurs de $I$ et de $U_{s}.$
 
2) Le diviseur de tension alimente maintenant un conducteur ohmique dont la résistance $R=1.0\;k\Omega$ (le diviseur de tension est dit en charge).
 
2.1) Représenter le schéma du circuit réalisé.
 
2.2) Déterminer la résistance équivalente $R_{e}$ à l'association des conducteurs ohmiques de résistances $R_{2}\ $ et $\ R.$
 
2.3) Déterminer la résistance équivalente $R'_{e}$ à l'ensemble du circuit $R_{1}\;,\ R_{2}\ $ et $\ R$, c'est à dire au dipôle $AB.$
 
2.4) En déduire les intensités des courants dans les conducteurs de résistances $R_{1}\;,\ R_{2}\ $ et $\ R.$
 
2.5) Montrer que la tension de sortie est alors $U'_{s}$ différente de $U_{s}$
 

Exercice 9

Soient les deux dipôles résistors $R_{1}=10\Omega\ $ et $\ R_{2}=20\Omega.$
 
1) Dans le premier circuit ci-dessous, l'ampèremètre indique un courant d'intensité $I=0.2\;A$

 

 
a) Le circuit est-il en série ou en dérivation ?
 
b) Représenter le branchement des voltmètres permettant la mesure des tensions $U_{1}$ aux bornes de $R_{1}$ et $U_{2}$ aux bornes de $R_{2}.$
 
c) Rappeler la loi d'Ohm relative à un résistor.
 
d) Calculer les tensions $U_{1}\ $ et $\ U_{2}.$
 
e) En déduire, en précisant la loi utilisée, la tension aux bornes du générateur.
 
f) Calculer la résistance équivalente à cette association de $R_{1}\ $ et $\ R_{2}$
 
2) On considère que la tension aux bornes du générateur reste constante. On réalise avec les mêmes dipôles le deuxième circuit suivant :

 

 
a) Les résistors dans ce deuxième circuit sont-ils associés en série ou en dérivation ?
 
En déduire $R'_{eq}$ la résistance équivalente à cette association de $R_{1}\ $ et $\ R_{2}$
 
b) Combien de voltmètres faut-il utiliser pour mesurer la tension $U'_{1}$ aux bornes de $R_{1}$ et $U'_{2}$ aux bornes de $R_{2}\ ?$
 
Préciser la valeur de chacune de ces deux tensions
 
c) Calculer l'intensité du courant $I_{1}$ traversant $R_{1}$
 
d) Calculer l'intensité du courant $I_{2}$ traversant $R_{2}$
 
e) En déduire l'intensité $I'$ du courant mesurée par l'ampèremètre en précisant la loi utilisée.
 
f) Calculer le rapport $\left(\dfrac{U_{\text{Générateur}}}{I'}\right)$ et le comparer avec la résistance $R'_{eq}$
 
3) Comparer les intensités du courant $I\ $ et $\ I'.$ 
 
En déduire une comparaison entre les intensités du courant débité par le même générateur dans un circuit en série et un circuit en dérivation comportant les mêmes dipôles
 

Exercice 10

Un circuit électrique comporte un générateur de tension continue et trois conducteurs ohmiques de résistance $R_{1}\;,\ R_{2}\ $ et $\ R_{3}$ (voir schéma). On donne $R_{3}=220\Omega.$
 
1) Recopier le schéma ci-dessous, y placer le sens conventionnel du courant électrique
 
L'intensité mesurée dans la branche $PN$ vaut : $I=69.5\;mA$

 

 
2) Calculer le nombre d'électrons traversant une section de la branche $PN$ pendant une seconde.
 
3) Représenter les tensions positives aux bornes de chacun des dipôles. Justifier.
 
4) La tension électrique aux bornes du générateur est de $6.20\;V.$ Déterminer les intensités $I_{1}\ $ et $\ I_{2}$ des courants circulant dans les branches $ABC\ $ et $\ DE.$ Justifier
 
5) La tension électrique aux bornes du conducteur ohmique de résistance $R_{1}$ est de $4.13\;V$
 
Déterminer les résistances $R_{1}\ $ et $\ R_{2}$ des conducteurs ohmiques de la branche $ABC.$
 
Données : $e=1.6\;10^{-19}\;C$
 

Exercice 11

On se propose de déterminer la caractéristique d'un dipôle inconnu $D$
 
1) Rappeler la définition de la caractéristique d'un dipôle. Quels sont les appareils de mesure nécessaires à sa détermination.
 
2) Représenter le schéma du montage électrique correspondant avec les appareils de mesure 
 
3) Les résultats des mesures sont regroupés dans le tableau suivant
 
$$\begin{array}{|l|c|c|c|c|c|c|c|c|}\hline U(V)&0&1&1.5&2&3.5&5&7&8\\ \hline I(mA)&0&2.1&3.2&4.2&7.4&10.0&14.9&17\\ \hline\end{array}$$
 
Tracer la représentation graphique $U=f(I)$ sur papier millimétré $(1\;cm$ pour $0.5\;V$ et $1\;cm$ pour $1\;mA).$
 
4) Qu'obtient-on comme courbe ? Qu'en déduit-on sur la nature du dipôle $D.$ 
 
Justifier en rappelant la loi appropriée.
 
5) Déterminer la valeur de la grandeur caractérisant le dipôle $D$
 

Exercice 12

Si une diode Zener est parfois utilisée pour protéger un dispositif des variations de tension, il arrive qu'il faille protéger la diode Zener elle-même. 
 
C'est le but du dispositif de la figure ci-dessous figure 2
 
Caractéristiques de la diode à jonction 
 
$D_{1}\ :\ I_{_{FM}}=1\;A\;;\ U_{s}\approx 0\;V\;;\ U_{_{RM}}=100\;V.$
 
Caractéristiques de la diode Zener
 
$D_{2}\ :\ I_{_{FM}}=100\;mA\;;\ U_{s}\approx 0\;V\;;\ U_{_{RZ}}=8\;V\;;\ I_{_{RM}}=60\;mA$
 
Les deux diodes sont considérées comme idéales. La tension $U_{_{AC}}$ appliquée aux bornes du circuit vaut $+12\ V$, soit $-12\;V$
 
1) La tension $U_{_{AC}}$ vaut $+12\;V.$ Quel est le rôle de $D_{1}\ ?$
 
Calculer la résistance $R_{2}$ minimale pour que la diode $D_{2}$ soit protégée. 
 
La diode $D_{1}$ est-elle alors protégée elle aussi ?
 
2) La tension $U_{_{AC}}$ vaut $-12\;V.$ Calculer la résistance $R_{1}$ pour que la diode $D_{2}$ soit protégée

 
 

Exercice 13

On considère une $VDR$ que l'on a étudié en convention récepteur; les résultats sont regroupés dans le tableau ci-dessous
 
$$\begin{array}{|c|c|c|c|c|c|}\hline U(\text{en }V)&I(\text{en }A)&U(\text{en }V)&I(\text{en }A)&U(\text{en }V)&I(\text{en }A)\\ \hline0&0&1.4&0.47&2.8&1.12\\ \hline 0.2&0.06&1.6&0.55&3.0&1.23\\ \hline 0.4&0.12&1.8&0.63&3.4&1.16\\ \hline 0.6&0.18&2.0&0.72&3.8&1.71\\ \hline 0.8&0.25&2.2&0.81&4.2&2.03\\ \hline 1.0&0.32&2.4&0.91&4.6&2.47\\ \hline 1.2&0.39&2.6&1.01&5.0&3.51\\ \hline\end{array}$$
 
1) Tracer la caractéristique de la $VDR.$
 
On associe en série cette $VDR$ avec un générateur linéaire de f.é.m $E=4.5\;V$ et de résistance interne $r=3\Omega.$
 
2) Quelle relation existe-t-il entre l'intensité et la tension pour ce générateur ?
 
Tracer la caractéristique de ce générateur.
 
3) Déterminer graphiquement la valeur de l'intensité circulant dans le circuit ainsi que celles des tensions aux bornes de chacun des deux composants.
 
On associe maintenant le générateur précédent ainsi qu'un conducteur ohmique de résistance $R=0.87\Omega$ en parallèle avec la $VDR$ de telle sorte que l'on ait trois branches.
 
4) Déterminer la relation entre l'intensité et la tension pour les deux branches générateur – conducteur $R.$
 
5) Déterminer la valeur de la tension aux bornes de chacun des trois composants ainsi que celles des intensités du courant circulant dans chacune des trois branches
 

Exercice 14

On considère le circuit suivant comportant les 5 résistors $R_{1}\;;\ R_{2}\;;\ R_{3}\;;\ R_{4}\ $ et $\ R_{5}$ :

 

 
$R_{1}=R_{5}=25\Omega\;;\ R_{2}=R_{3}=R_{4}=50\Omega$
 
1) Déterminer la résistance équivalente du dipôle $CD.$
 
2) Déduire la résistance totale du dipôle $AB.$
 
3) Déterminer l'intensité du courant $I.$
 
4) Déduire les intensités $I_{2}\ $ et $\ I_{3}$ passant respectivement par $R_{4}\ $ et $\ (R_{2}+R_{3}).$
 

Exercice 15

Soit le montage suivante :

 

 
1) Représenter $U_{_{AB}}\;,\ U_{_{PN}}\;,\ U_{_{PA}}\;,\ U_{_{CA}}\;,\ U_{_{BN}}\ $ et $\ U_{_{CB}}.$
 
2) Que vaut $U_{_{BN}}\ ?$
 
3) Représenter le sens des courants.
 
4) Calculer $U_{_{PA}}.$
 
5) Calculer $I.$
 
6) Calculer $I_{2}.$
 
7) Calculer $R_{2}.$
 
8) Calculer $R_{1}.$
 
9) Calculer $U_{_{CB}}.$
 
10) Calculer $I_{3}.$
 
11) Calculer $I_{4}.$
 
12) Calculer $R_{5}.$
 
13) Calculer $R_{eq}$ la résistance équivalente aux 5 résistances en 4 étapes rédigées.
 
Données : $U_{_{PN}}=12\;V\;,\ U_{_{AB}}=8\;V\;,\ U_{_{AC}}=6\;V\;,\ R_{3}=200\Omega\;,\ R_{4}=200\Omega\;,\ I_{1}=15\;mA$
 

Exercice 16

Une diode Zener utilisée en inverse est par les mesures suivantes :
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|}\hline U(V)&0&2.0&5.0&5.2&5.5&5.6&5.7&5.8&5.82&5.86&5.90\\ \hline I(mA)&0&0&1.0&2.0&5.0&10&20&30&60&100&150\\ \hline\end{array}$$
 
Cette diode, toujours utilisée en inverse, est branchée avec un générateur de f.é.m $E=6\;V$, d'une résistance interne $r=1.8\Omega$ et avec un conducteur ohmique de résistance $R$
 
1) Tracer la caractéristique courant-tension de cette diode
 
2) Quelle doit la valeur de $R$ pour que la tension aux bornes de la diode soit $5.6\;V$
 
3) Que se passe-t-il en ce moment-là si la tension varie aux bornes de la pile ?
 
Dans quel de tension peut-on considérer que la diode Zener assure une régulation de la tension à ses bornes ?

Déterminer les valeurs correspondantes de $R$

 

Auteur: 
Sidy Mouhamed Ndiaye

Pages