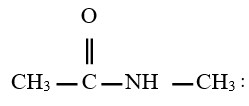Vous êtes ici

Physique

pH d'une solution aqueuse-autoprotolyse de l'eau - produit ionique - indicateurs colorés - Ts

Classe:

Terminale

L'eau très répandue et apparemment très banale, du point de vue de la chimie est cependant, en permanence le siège des réactions chimiques entre ses molécules d'une part et les ions et les molécules des corps dissouts d'un autre part

I. Solutions aqueuses

De nombreuses espèces chimiques peuvent se dissoudre dans l'eau constituant ainsi des solutions aqueuses

1. Définition

Une solution aqueuse est un mélange homogène constitué d'un solvant (l'eau) et un ou plusieurs soluté(s)

2. Concentrations

2.1 Concentrations molaires

2.1.1 Concentration molaire volumique d'une solution

Si le soluté est un corps que l'on dissout dans le solvant la concentration molaire du soluté est définie :

$$C_{A}=\dfrac{n_{A}}{V}$$

$n_{A}$ en moles (mol)

$V$ en litres $(L)$

$C$ en moles par litres $(mol\cdot L^{-1})$

2.1.2 Concentration molaire volumique d'une espèce chimique en solution

La concentration molaire d'une espèce chimique $A$ en solution, notée $[A]$ est définie par le rapport :

$$[A]=\dfrac{n_{A}}{V}$$

$n_{A}$ en moles (mol)

$V$ en litres $(L)$

$[A]$ en moles par litres $(mol\cdot L^{-1})$

Exemple :

Exprimer les concentrations des ions d'une solution aqueuse de sulfate de sodium $Na_{2}SO_{4}$ de concentration $C$

Équation de dissolution :

$Na_{2}SO_{4}\stackrel{H_{2}O}{\longrightarrow}2Na^{+}+SO_{4}^{2-}$

$C$ $2C$ $C$

$\left[Na^{+}\right]=2C$ ; $\left[SO_{4}^{+}\right]=C$

2.2 Concentration massique

C'est la masse d'une substance $A$ dissoute dans un litre de solution

$$C_{m}(A)=\dfrac{m_{A}}{V}$$

$m_{A}$ en grammes $(g)$

$V$ en litres $(L)$

$C_{m}(A)$ en grammes par litres $(g\cdot L^{-1})$

Remarque :

Il existe une entre la concentration molaire et la concentration massique

$C_{m}(A)=C_{A}M_{A}$

II. Autoprotolyse de l'eau

1. Conductibilité électrique de l'eau

L'eau pure conduit légèrement le courant électrique.

Elle contient donc des ions

2. Ionisation partielle de l'eau : autoprotolyse de l'eau

La conductibilité électrique de l'eau pure est due à sa légère ionisation appelée réaction d'autoprotolyse

$H_{2}O\ +\ H_{2}O\ \leftrightarrows\ H_{3}O^{+}\ +\ OH^{-}$

ion hydronium ion hydroxyde

Dans l'eau pure, il y a donc un équilibre entre les ions hydronium et les ions hydroxyde et des molécules d'eau

L'eau pure a donc autant d'ions $H_{3}O^{+}$ et des ions $OH^{-}$

$\boxed{\left[H_{3}O^{+}\right]=\left[OH^{-}\right]}$

3. Le produit ionique de l'eau

La réaction de dissociation est une réaction d'équilibre.

Cet équilibre est caractérisé par une constante $Ke$ appelée produit ionique de l'eau

$\boxed{Ke=\left[H_{3}O^{+}\right]\left[OH^{-}\right]}$

$Ke$ augmente avec la température

$Ke=1.1\cdot 10^{-15}\text{ à }0^{\circ}C$

$Ke=10^{-14}\text{ à }25^{\circ}C$

$Ke=5.5\cdot 10^{-13}\text{ à }100^{\circ}C$

Remarque :

La constante $Ke$ du produit ionique de l'eau est valable non seulement pour l'eau pure, mais aussi toute pour solution aqueuse

II. $pH$ d'une solution

La connaissance de la teneur en ion hydronium seul ou en ion hydroxyde seul suffit pour savoir si une solution est acide

On convient de caractériser l'acidité, la basicité ou la neutralité d'une solution par la concentration en ion hydronium par une grandeur notée $pH$, grandeur liée à la concentration des ions hydroniums

1. Expression du $pH$ d'une solution

Le $pH$ d'une solution est un nombre par lequel on exprime la concentration des ions hydroniums d'une solution

$pH=-\log\left[H_{3}O^{+}\right]$ où $\left[H_{3}O^{+}\right]=10^{-pH}$

$\log$ représente le logarithme décimal

Remarque :

On peut aussi définir le $pOH$

$$\boxed{pOH=-\log\left[OH^{-}\right]}$$

2. Mesure du $pH$ d'une solution

On mesure le $pH$ d'une solution à l'aide d'un appareil appelé $pH-$ mètre

Il est constitué de deux parties :

$-\ $ deux électrodes constituant une pile : une électrode indicatrice de $pH$, le plus souvent une électrode en verre ; l'autre électrode appelée électrode de référence, dont le potentiel est constant

$-\ $ un voltmètre électronique gradué en unités de $pH$ permet de mesurer la tension, fonction affine, entre les électrodes

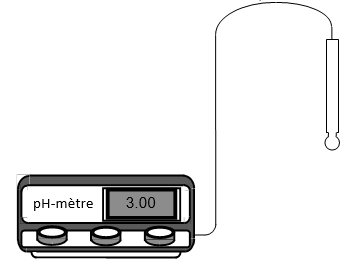
Remarque :

Les deux électrodes peuvent être combinées ou non

3. Caractères acido-basique d'une solution

Si on dissout un composé ionique dans l'eau, ses ions peuvent réagir avec les ions de l'eau, mais le produit ionique de l'eau reste constant

$Ke=\left[H_{3}O^{+}\right]\left[OH^{-}\right]=10^{-14}\text {à }25^{\circ}C$

$\begin{array}{lcl} -\ \text{Si }\left[H_{3}O^{+}\right]>10^{-7}&\Rightarrow&-\log\left[H_{3}O^{+}\right]<-\log\,10^{-7}\\&\Rightarrow& pH<7\;,\text{ la solution est plus acide que l'eau} \end{array}$

$\begin{array}{lcl} -\ \text{Si }\left[H_{3}O^{+}\right]<10^{-7}&\Rightarrow&-\log\left[H_{3}O^{+}\right]>-\log\,10^{-7}\\&\Rightarrow& pH>7\;,\text{ la solution est plus basique que l'eau} \end{array}$

$\begin{array}{lcl} -\ \text{Si }\left[H_{3}O^{+}\right]=10^{-7}&\Rightarrow&-\log\left[H_{3}O^{+}\right]=-\log\,10^{-7}\\&\Rightarrow& pH=7\;,\text{ basicité ou l'acidité de la solution est la même que celle de l'eau} \end{array}$

La solution est dite neutre

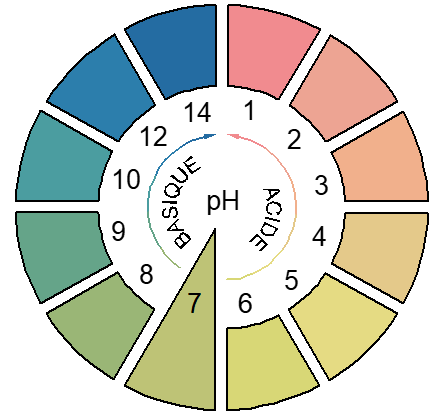
Échelle de $pH$ : Caractère d'une solution :

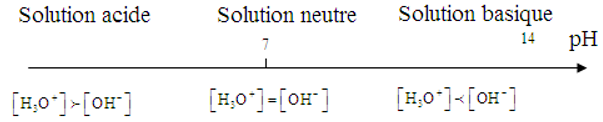
IV. Indicateurs colorés

1. Définition

Les indicateurs colorés sont des substances qui passent progressivement, quand le $pH$ croit, d'une couleur à une autre dans un petit domaine de $pH$ appelé zone de virage de cet indicateur

2. Exemples d'indicateurs colorés

$$\begin{array}{|c|c|c|c|} \hline \text{Indicateur}&\text{Teinte acide}&\text{Zone de virage}&\text{Teinte basique}\\ \hline \text{Hélianthine}&\text{Rouge}&2.4-4.4&\text{jaune}\\ & &\text{Orange}&\\ \hline \text{Phénolphtaléine}&\text{Incolore}&8.2-9.8&\text{Violette}\\ & &\text{Rose}&\\ \hline \text{Bleu de Bromothymol}&\text{Jaune}&6.0-7.6&\text{Bleue}\\ (BBT)& &\text{Verte}&\\ \hline \end{array}$$

3. Utilisation des indicateurs

L'utilisation des indicateurs colorés permet de déterminer une valeur approchée du $pH$ d'une solution.

On ajoute quelques gouttes de l'indicateur coloré dans la solution à étudier et on note la couleur obtenue

On peut aussi utiliser un papier $pH$

Il s'agit du papier préparé à l'aide d'un mélange d'indicateurs colorés et qui prend une couleur bien déterminée lorsqu'il est en contact avec une solution de $pH$ étudiée

Il suffit donc de mettre ce papier en contact avec la solution et de comparer la teinte qu'il prend avec une des teintes donnant le $pH$

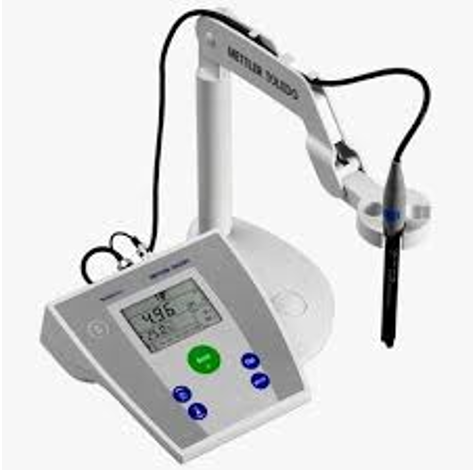
Un $pH-$ mètre

Le $pH-$ mètre est constitué d'une sonde relié à un voltmètre.

La sonde se compose d'une électrode de fer est d'une électrode de référence.

La tension $U$ aux bornes de la sonde plongée dans une solution est une fonction affine du $pH$ : $U= a-b\cdot pH$

Avant toute mesure, il est nécessaire d'étalonner un $pH-$ mètre avec deux solutions étalons de $pH$ connu $($généralement $4$ et $7).$

Cet étalonnage permet de fixer avec précision les valeurs de $'a'$ et $'b'.$

Un $pH$ mètre est précis à $0.05$ unité $pH$ environ.

L'incertitude relative sur la valeur de la concentration en ion oxonium est donc de $10\%$ environ.

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Cinétique chimique - Ts

Classe:

Terminale

En chimie le plus souvent, on se contente d'écrire l'équation-bilan d'une réaction ; cette équation ne renseigne pas sur le caractère lent ou rapide d'une réaction.

Une réaction chimique peut être rapide, lente ou très lente ; sa durée dépend étroitement des conditions expérimentales.

La cinétique chimique est l'étude de l'évolution d'une réaction chimique, possible, au cours du temps.

I. Étude qualitative

1. Réactions rapides

Une réaction rapide se fait quasi-instantanément, dès que les réactifs sont en contact

Exemples :

$-\ $ Réaction entre $I_{2}$ et $S_{2}O_{3}^{2-}$

$-\ $ Réaction entre $H_{2}O_{2}$ et $MnO_{4}^{-}$ en milieu acide

2. Réactions lentes

Une réaction lente peut durer quelques minutes à plusieurs heures

Les produits ne se forment que progressivement

Exemple :

réaction entre $I^{-}$ et $S_{2}O_{3}^{2-}$

Il se forme $I_{2}$ qui colore le mélange réactionnel en jaune puis en brun de plus en plus foncé, au fur et à mesure que le temps passe

3. Réactions très lentes

Le système chimique ne semble pas évoluer au cours du temps.

La réaction peut durer plusieurs mois ou plusieurs années

Exemple :

formation de la rouille

II. Étude quantitative

1. Vitesse de formation ou disparition d'un corps

Dans le cas des réactions lentes, il est possible de suivre l'évolution des réactifs ou des produits au cours du temps

Considérons une réaction du type :

$aA\ +\ bB\ \longrightarrow\ cC\ +\ dD$

Pour suivre l'évolution de cette réaction, on peut :

$-\ $ soit mesurer la quantité des produit $C$ ou $D$ qui apparait en fonction du temps

$-\ $ soit mesurer la quantité des réactifs $A$ ou $B$ qui reste en fonction du temps

$A$ volume constant, on peut suivre expérimentalement la variation de la concentration de $A$ ou $B$ et $C$ ou $D$

1.1 Vitesse moyenne de formation ou de disparition du corps

1.1.1 Vitesse moyenne de formation d'un corps

Soient $\left[C_{i}\right]$ et $\left[C_{f}\right]$ les concentrations molaires du produit $C$ aux instants $t_{i}$ et $t_{f}$

Par définition, la vitesse de formation de $C$ entre les instants $t_{i}$ et $t_{f}$ est :

$$V_{moy}(C)=\dfrac{\left[C_{f}\right]-\left[C_{i}\right]}{t_{f}-t_{i}}=\dfrac{\Delta[C]}{\Delta\,t}=\tan\alpha$$

Cette vitesse moyenne est représentée par le coefficient directeur de la droite $\left(M_{i}M_{f}\right)$ joignant les points $M_{i}$, $M_{f}$ de la courbe d'abscisses $t_{i}$ et $t_{f}$

La vitesse exprime en moles par litre et par seconde $\left(mol\cdot L^{-1}\cdot S^{-1}\right)$

1.1.2 Vitesse moyenne de disparition d'un corps

La vitesse moyenne de disparition du réactif $A$ entre les instants $t_{i}$ et $t_{f}$ caractérise la quantité moyenne de $A$ disparu par unité de temps dans cet intervalle

Elle vaut : $V_{moy}(A)=\dfrac{\left[A_{f}\right]-\left[A_{i}\right]}{t_{f}-t_{i}}=\dfrac{\Delta[A]}{\Delta\,t}=\tan\alpha$

Le signe moins $(-)$ s'explique par le fait $\Delta[A]<0$ alors que la vitesse est toujours positive

2. Vitesse instantanée de formation ou de disparition du corps

2.1 Vitesse instantanée de formation du corps

a) Définition

La vitesse instantanée de formation d'un produit $(C$ ou $D)$ est la dérivée par rapport au temps de sa concentration

$$V_{C}=\dfrac{d[C]}{\mathrm{d}\,t}\ ;\ V_{D}=\dfrac{d[D]}{\mathrm{d}\,t}$$

b) Traduction graphique

La vitesse instantanée de formation du produit $C$ ou $D$ à l'instant $t$ est donnée par le coefficient directeur de la tangente à la courbe au temps $t$ considérée

2.2 Vitesse instantanée de disparition d'un corps

a) Définition

La vitesse instantanée de disparition du réactif $A$ ou $B$ est l'opposé de la dérivée par rapport au temps de sa concentration

$$V_{A}=\dfrac{d[A]}{\mathrm{d}\,t}\ ;\ V_{B}=\dfrac{d[B]}{\mathrm{d}\,t}$$

b) Traduction graphique

La vitesse instantanée de disparition du réactif $A$ ou $B$ à l'instant $t$ est donnée par l'opposé du coefficient directeur de la tangente à la courbe au temps $t$ considéré

Remarque :

Pour une réaction donnée, il est possible de définir une vitesse unique dont la valeur indépendante de l'espèce considéré

Si l'équation-bilan de la réaction s'écrit :

$\boxed{aA\ +\ bB\ \longrightarrow\ cC\ +\ dD}$

La vitesse de réaction est définie par :

$\begin{array}{lcl} V&=&\dfrac{l}{c}\dfrac{d[C]}{\mathrm{d}\,t}\\&=&\dfrac{l}{d}\dfrac{d[D]}{\mathrm{d}\,t}\\&=&\dfrac{l}{a}\dfrac{d[A]}{\mathrm{d}\,t}\\&=&-\dfrac{l}{b}\dfrac{d[B]}{\mathrm{d}\,t}\\&\Rightarrow& V=\dfrac{V_{C}}{c}\\&=&\dfrac{V_{D}}{d}\\&=&\dfrac{V_{A}}{a}\\&=&\dfrac{V_{B}}{b} \end{array}$

3. Temps de demi-réaction

On caractérise souvent la rapidité avec laquelle la réaction se déroule par le temps de demi-réaction

Considérons la réaction d'équation

$$aA\ +\ bB\ \longrightarrow\ cC\ +\ dD$$

Le temps de demi-réaction est la durée nécessaire pour consommer la moitié du réactif limitant initialement présent

$-\ $ Si $A$ est le réactif limitant alors $n_{A}=\dfrac{1}{2}n_{iA}$ pour $t_{1/2}$

$-\ $ Si on opère en milieu liquide ou gazeux à volume constant alors $[A]=\dfrac{1}{2}[A_{i}]$ pour $t_{1/2}$

III. Facteurs cinétiques

Ce sont des grandeurs qui permettent d'influer sur les vitesses de réaction

1. Concentration des réactifs

Il faut un contact entre les réactifs pour que la réaction se fasse

En augmentant leur concentration, on augmente leur chance de se rencontrer : la réaction est plus rapide

$\bullet\ $ La vitesse volumique de réaction augmente quand la concentration des réactifs augmente

$\bullet\ $ Le temps de demi-réaction diminue quand la concentration en réactifs initiale augmente

Application :

$-\ $ Pour stopper une réaction qui a lieu en solution, on ajoute un solvant (l'eau par exemple) pour diluer les réactifs

$-\ $ Au fur et à mesure le temps passe, la concentration des réactifs diminue, donc la vitesse volumique de réaction diminue

2. La température

Quand la température augmente, l'énergie cinétique des réactifs augmente, les chocs entre eux sont plus violents, plus efficaces : la réaction plus rapide

$\bullet\ $ La vitesse volumique de réaction augmente quand la température augmente

$\bullet\ $ Le temps de demi-réaction diminue quand la température augmente

Application :

$-\ $ Pour bloquer une réaction, on ajoute de la glace pour arrêter brutalement le mélange réactionnel : c'est la trempe (opération qui consiste à bloquer une réaction en ajoutant de la glace pour refroidir brutalement le mélange réactionnel)

$-\ $ Pour déclencher une réaction, on utilise une allumette enflammée, une étincelle.

$-\ $ Pour cuire des aliments plus rapidement, on utilise une cocotte-minute $($la température d'ébullition de l'eau est de $120^{\circ}C)$

3. Surface de contact

Si l'un des réactifs est solide, la réaction est plus rapide si on augmente la surface de contact entre le solide et les autres réactifs en solution : on utilise des poudres au lieu de gros morceaux pour augmenter la vitesse volumique d'une réaction

4. Le catalyseur

4.1 Définition

Un catalyseur est une entité chimique, utilisée en faible proportion, capable d'augmenter la vitesse d'une réaction possible spontanément en son absence et sans apparaitre dans l'équation-bilan de la réaction

Remarque :

Lorsqu'une réaction chimique est catalysée par l'un des produits cette réaction ; elle est dite autocatalysée.

Il s'agit d'une autocatalyse

4.2 Caractères généraux de la catalyse

$\bullet\ $ Le catalyseur se trouve inaltérée à la fin de la réaction (puisqu'il n'entre pas dans l'équation-bilan)

$\bullet\ $ Une faible quantité de catalyseur permet, en général, la transformation de quantités importantes de réactifs

$\bullet\ $ Un catalyseur peut avoir une action orientatrice du fait de sa sélectivité

$\bullet\ $ Un catalyseur ne permet, en aucun cas, réaliser des réactions théoriquement impossibles

$\bullet\ $ Un catalyseur ne déplacer un équilibre chimique : il permet de l'atteindre rapidement

Autre définition du catalyseur

Un catalyseur est une espèce chimique qui diminue la durée d'une transformation : il participe à la réaction mais est régénéré en fin de réaction.

Il n'apparaît pas dans l'équation de la réaction

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Les acides carboxyliques et dérivés - Ts

Classe:

Terminale

A. Les acides carboxyliques

I. Généralités

1. Définition

Les acides carboxyliques sont des composés oxygénés dont la chaine carbonée comporte deux atomes d'oxygène

Leur formule générale est :

$\left(C_{n}H_{2n+1}COOH\text{ ou }C_{n}H_{2n}O_{2}\right)$

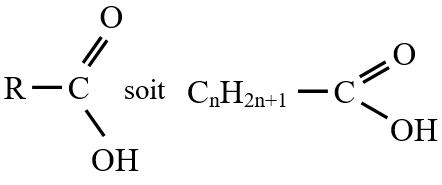
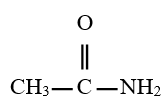
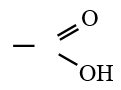est le groupe fonctionnel appelé groupe carboxylique

2. Nomenclature

Le nom de l'acide dérive de celui de l'alcane de même chaine carbonée en remplaçant le « e » par oïque, le tout précédé du mot acide

Le carbone du groupe fonctionnel porte toujours le numéro $1$

Exemples :

$HCOOH$ : Acide méthanoïque

Remarque :

$-\ $ Un composé organique peut posséder deux groupes carboxyles positionnés soit aux extrémités d'une chaine aliphatique, soit sur deux carbones d'un groupe aromatique

Ces diacides sont dénommés dioïques ou dicarboxyliques

Exemples :

$HOOC-COOH$ : Acide éthanedioïque (ou acide oxalique)

$HOOC-\left(CH_{2}\right)_{4}-COOH$ : Acide hexanedioïque (ou acide adipique)

Acide benzène $-1.2-$ dioïque (acide orthophtalique)

Les acides gras sont des acides à chaines linéaires saturées ou non possédant un nombre d'atomes de carbone pair et tel que $4\leq n\leq 22$

$CH_{3}-\left(CH_{2}\right)_{16}-COOH$ : Acide stéarique

$CH_{3}-\left(CH_{2}\right)_{7}-CH=CH-\left(CH_{2}\right)_{7}-COOH$ : Acide oléique

II. Propriétés des acides carboxyliques

1. Propriétés physiques

Dans les conditions ordinaires de température et de pression, tous les acides carboxyliques sont liquides ou solides.

Les acides carboxyliques de $C_{1}$ à $C_{4}$ sont très solubles dans l'eau.

La solubilité dans l'eau décroit quand le nombre d'atomes de carbone augmente

Les acides carboxyliques ont des températures d'ébullition relativement élevées

2. Propriétés chimiques

2.1. Propriétés acides

2.1.1. Action sur l'eau

Les acides carboxyliques sont des acides faibles.

Toutes les solutions aqueuses d'acide carboxylique sont acides

Les acides carboxyliques réagissent sur l'eau : la réaction est limitée par la réaction inverse

$R-COOH\ +\ H_{2}O\ \leftrightarrows\ R-COO^{-}\ +\ H_{3}O^{+}$

acide carboxylique ion carboxylique ion hydronium

Exemple :

$HCOOH\ +\ H_{2}O\ \leftrightarrows\ HCOO^{-}\ +\ H_{3}O^{+}$

acide méthanoique ion méthanoate

2.1.2. Action sur les bases

Une solution aqueuse d'acide carboxylique peut-être dosée par une base forte

L'équation-bilan s'écrit :

$R-COOH+OH^{-}\rightarrow R-COO^{-}+H_{2}O$

Exemple :

$CH_{3}-CH_{2}-COOH+OH^{-}\rightarrow CH_{3}-CH_{2}-COO^{-}+H_{2}O$

acide propanoique ion propanoate

La réaction est totale.

Une indicateur coloré peut servir d'indicateur de fin de réaction

c) Action sur les métaux

Les acides carboxyliques donnent de nombreux sels avec certains métaux (zinc, aluminium...)

La réaction est une oxydoréduction

Exemple :

$2CH_{3}-COOH+Zn\rightarrow\left(CH_{3}CO_{2}\right)_{2}Zn+H_{2}$

2.2. La décarboxylation

La décarboxylation est une élimination du dioxyde de carbone des molécules d'acides

C'est une réaction qui permet de mettre en évidence le groupement carboxyle

Elle se fait, le plus souvent, à température élevée en présence de catalyseur

Les équations-bilans s'écrivent :

$R-COOH\stackrel{Ni\text{ à }200^{\circ}}{\longrightarrow}RH\ +\ CO_{2}$

Alcane

Exemples :

$CH_{3}-COOH\stackrel{Ni\text{ à }200^{\circ}}{\longrightarrow}CH_{4}\ +\ CO_{2}$

$CH_{3}-COOH+HCOOH\stackrel{Al_{2}O_{3}\text{ à }400^{\circ}}{\longrightarrow}CH_{3}-CH_{2}-CHO+CO_{2}+H_{2}O$

Remarques :

$-\ $ Le dernier exemple constitue un cas particulier car la réaction aboutit à la formation d'un aldéhyde

$-\ $ Un diacide peut se « décarboxyler » pour donner un monoacide

La décarboxylation de l'acide propanedioïque, par exemple, peut donner l'acide éthanoïque

L'équation-bilan de la réaction s'écrit :

$HOOC-CH_{2}-COOH\stackrel{140^{\circ}}{\longrightarrow}CH_{3}COOH\ +\ CO_{2}$

B. Les dérivées des acides carboxyliques

La formule générale d'un dérivé de l'acide carboxylique est :

I. Les chlorures d'acyle ou chlorures d'acide

1. Formule générale

Lorsque $Z$ est un atome de chlore, le dérivé d'acide carboxylique est un chlorure d'acyle (ou d'acide) de formule :

2. Nomenclature

Le chlorure d'acyle est appelé chlorure de suivi du nom de l'alcane ayant la même chaine carbonée auquel on remplace la terminaison $« e »$ par oyle

Exemples :

3. Préparation des chlorures d'acyle

Les chlorures d'acyle sont obtenus en traitant les acides carboxyliques par :

$-\ $ le pentachlorure de phosphore $PCl_{5}$

$-\ $ le trichlorure de phosphore $PCl_{3}$

$-\ $ le chlorure de thionyle $SOCl_{2}$

Les équations-bilans s'écrivent :

Soit en résumé :

4. Hydrolyse des chlorures d'acide

Les chlorures d'acyle s'hydrolysent facilement en donnant l'acide carboxylique correspondant.

La réaction est exothermique

Exemple :

$CH_{3}-COCl\ +\ H_{2}O\ \rightarrow\ CH_{3}-COOH\ +\ H_{2}O$

II. Les anhydrides d'acide

1. Formule générale :

Lorsque $Z$ est un groupe

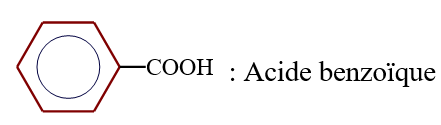
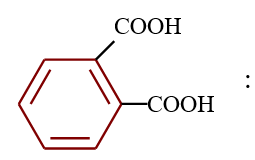
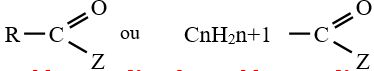
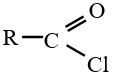
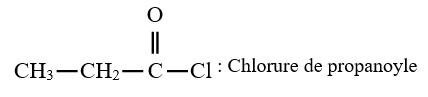
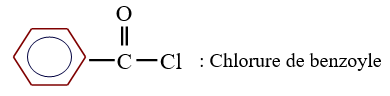
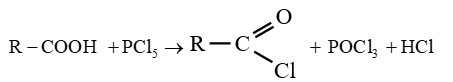
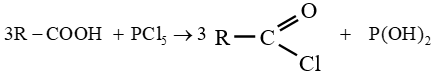
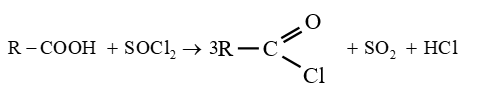
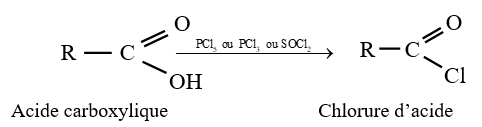
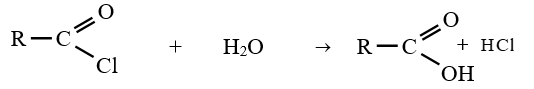
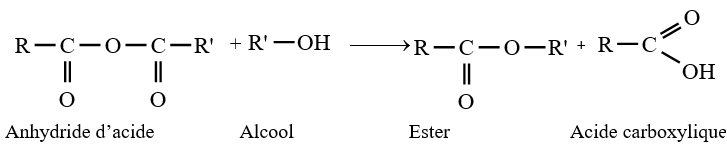
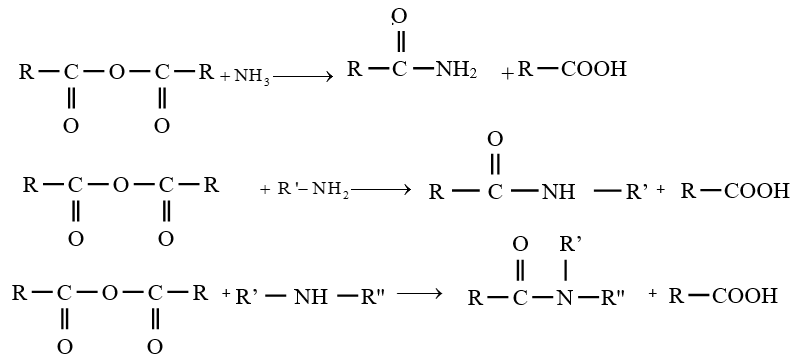
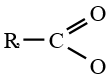le dérivé d'acide carboxylique est un anhydride d'acide de formule générale :

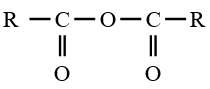$\left(C_{n}H_{2n-3}O_{3}\quad n\geq 2\right)$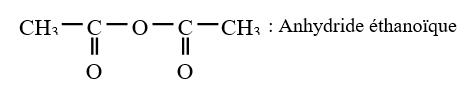

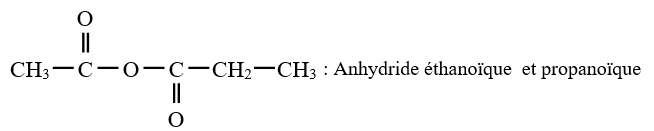
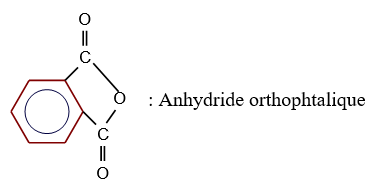
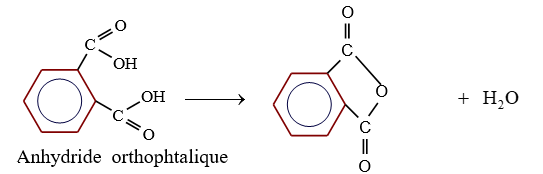
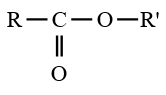2. Nomenclature

L'anhydride d'acide est appelé anhydride, suivi du nom de l'acide carboxylique auquel on élimine le mot acide

Exemples :

3. Préparation des anhydrides d'acide

Les anhydrides d'acide peuvent être obtenus :

3.1 Par élimination à partir d'eau de deux fonctions carboxyliques

3.1.1 Déshydratation intermoléculaire

Un déshydratant énergétique telque pentoxyde de diphosphore $P_{2}O_{5}$ ou decaoxyde de tétraphosphore $P_{4}O_{10}$ permet d'éliminer une molécule d'eau entre deux molécules d'acides carboxyliques.

On parle de déshydratation intermoléculaire

L'équation-bilan de la réaction s'écrit :

Exemple :

3.1.2 Déshydratation intramoléculaire

Dans le cas d'un diacide si les deux groupes carboxyliques sont suffisamment proches de l'un de l'autre, il peut y avoir élimination d'une molécule d'eau à partir d'une seule molécule d'acide.

On parle de déshydratation intramoléculaire

C'est le cas pour l'acide benzène $-1.2-$ dioïque

2.2 Par action d'un chlorure d'acyle sur un acide ou sur un ion carboxylate

Les anhydrides d'acide peuvent obtenus par action d'un chlorure d'acide sur un acide ou sur un ion carboxylate

Les équations-bilans des réactions s'écrivent :

Remarque :

Dans la pratique, les anhydrides d'acide sont surtout préparés par action des chlorures d'acide sur les acides carboxyliques ou les ions carboxylates

III. Les esters

1. Formule générale

Lorsque $Z$ est un groupe $O-R'$, le dérivé d'acide carboxylique est un ester de formule générale :

$\left(C_{n}H_{2n}O_{2}\text{ avec }n\geq 2\right)$

2. Nomenclature

Le nom de l'ester s'obtient en faisant suivre le nom du groupe carboxylate de celui du groupe alkyle $-R$

Exemples :

$CH_{3}-CH_{2}-COO-C_{2}H_{5}$ : Propanoate d'éthyle

3. Estérification

Un ester peut être préparé par plusieurs méthodes :

$-\ $ par action d'un acide carboxylique sur un alcool : on parle d'estérification directe

$-\ $ par action d'un chlorure d'acyle ou d'un anhydride sur un alcool : on parle d'estérification indirecte

3.1 Estérification directe

C'est une réaction entre un acide et un alcool

Il s'agit d'une réaction très lente, athermique, réversible (donc limitée)

L'équation-bilan de la réaction s'écrit :

Exemple :

$CH_{3}-COOH+CH_{3}-CH_{2}-CH_{2}OH\rightarrow CH_{3}-COO-CH_{2}-CH_{2}-CH_{3}+H_{2}O$

$\bullet\ $ Rendement d'une estérification

On appelle rendement d'une transformation chimique le rapport entre la quantité de matière (respectivement la masse) du produit effectivement obtenu et la quantité de matière (respectivement la masse) théorique que l'on obtiendrait si la réaction était totale

$$\boxed{\dfrac{n_{\text{obtenu}}}{n_{\text{max}}}=\dfrac{m_{\text{obtenu}}}{m_{\text{max}}}}$$

Remarque

Le rendement de l'estérification dépend peu du choix de l'acide.

En revanche il dépend beaucoup de la classe de l'alcool

Pour un mélange équimolaire d'acide et d'alcool, ce rendement est de $67\%$ pour un alcool primaire, $60\%$ pour un alcool secondaire et $5\%$ pour un alcool tertiaire

$\bullet\ $ Constante d'estérification

$$\boxed{K_{\text{estérification}}=\dfrac{[\text{ester}][\text{eau}]}{[\text{acide}][\text{alcool}]}}$$

3.2 Estérification indirecte

Si l'estérification directe des alcools par les acides carboxyliques est limitée et lente, en revanche la réaction d'estérification par des chlorures d'acyle ou des anhydrides est totale et rapide

Les équations-bilans des réactions s'écrivent :

Exemples :

$CH_{3}-COCl+CH_{3}OH\rightarrow CH_{3}-COOCH_{3}+HCl$

Chlorure d'éthanoyle méthanol éthanoate de méthyle chlorure d'hydrogène

$\left(CH_{3}-CO\right)_{2}O+CH_{3}-CHOH-CH_{3}\rightarrow CH_{3}-COO-CH\left(CH_{3}\right)-CH_{3}-COOH$

Anhydride acétique Propan $-2-$ ol Acétate de méthyléthyle ou d'isopropyle Acide acétique

4. Cas des polyesters

On peut avoir une réaction d'estérification entre :

$-\ $ un acide carboxylique et un polyalcool

$-\ $ un polyacide et un polyalcool

Exemples :

$-\ $ Les corps gras sont des polyesters plus précisément des triesters du glycérol

L'équation-bilan de la réaction s'écrit :

$-\ $ La réaction de polycondensation entre l'éthane $-1.2-$ diol et le diacide conduit à la formation des chaines de polyesters

$nHO-CH_{2}CH_{2}-OH+nHOOC-C_{6}H_{4}-COOH\rightarrow -\left(O-CO-C_{6}H_{4}-COO-CH_{2}CH_{2}\right)_{n}-\ +\left(2n-1\right)H_{2}O$

Remarque :

Une réaction de polycondensation se distingue d'une polymérisation par le fait que la jonction entre les différents maillons de la macromolécule est accompagnée de la formation d'une molécule annexe

4. Hydrolyse

L'hydrolyse d'un ester est son action sur l'eau : c'est une réaction inverse de l'action de l'acide sur un alcool

Comme l'estérification, c'est une réaction lente et limitée : elle conduit à un équilibre chimique

L'équation-bilan de la réaction s'écrit :

$R-COOR'+H_{2}O\rightarrow R-COOH+R'-OH$

Remarque :

L'estérification et l'hydrolyse constituent une réaction lente et réversible conduisant à un équilibre chimique où les quatre composés coexistent dans des proportions constantes (en fait il s'agit d'un équilibre dynamique durant lequel les deux réactions continuent d'avoir lieu mais avec des vitesses égales)

5. Saponification

Les esters réagissent sur les bases fortes comme l'hydroxyde de sodium $(NaOH)$ ou l'hydroxyde de potassium $(KOH)$

La réaction donne un alcoolate et un carboxylate de potassium ou de sodium

L'équation-bilan de la réaction s'écrit :

$R-CO-O-R'+MOH\rightarrow R-COO^{-}M^{+}+R'-OH$

$\left(M=Na^{+}\;,\ K^{+}\right)$ Carboxylate de $M$ Alcool

(Savon)

La saponification conduit à la formation du savon lorsqu'elle est effectuée avec des esters particuliers

La saponification d'un triglycéride (corps gras) par l'hydroxyde de sodium par exemple donne le glycérol et un carboxylate de sodium

IV. Les amides

1. Formule générale

Lorsque $Z$ est un groupe fig571 le dérivé d'acide carboxylique est un amide de formule générale : fig572 $(R$ et $R'$ pouvant être des atomes d'hydrogène ou des groupes alkyles$)$

2. Nomenclature

Le nom d'un amide dérive de celui de l'alcane de même de chaine carbonée en remplaçant la terminaison $« e »$ par amide

Exemples :

Ethanamide

$N$, $N-$ diéthylbenzanamide

$N-$ éthyléthanamide

$N$, éthyl $-N-$ propyl $-2-$ méthylpropanamide

3. Préparation des amides

Les amides peuvent être obtenus à partir des acides

L'action de :

$-\ $ l'ammoniac, d'une amine primaire ou secondaire conduit à la formation d'un carboxylate d'ammonium ou alkylammonium

Ce carboxylate porté à haute température se déshydrate avec formation d'un amide

Ces réactions sont lentes et réversibles conduisant à un équilibre chimique ; ce qui limite les rendements

$-\ $ l'action de l'ammoniac ou d'une amine sur le chlorure d'acyle

La réaction d'un chlorure d'acyle sur l'ammoniac ou amine primaire ou secondaire est rapide et totale

Exemple :

$-\ $ les amides peuvent être obtenus à partir des anhydrides d'acide.

La réaction est totale et rapide

Les équations-bilans des réactions s'écrivent :

4. Les polyamides

Il s'agit des macromolécules formées par la répétition d'un motif élémentaire comportant la fonction amide

Ils sont obtenus par des réactions de polycondensation mettant en jeu un diacide et une diamine, soit aminoacide

Exemple :

Le « nylon $6-6$ » est un polyamide, produit de la réaction de polycondensation entre le chlorure d'hexanedioyle et l'hexane $-1.6-$ diamine

$nCOCl-\left(CH_{2}\right)_{4}-COCl+nH_{2}N-\left(CH_{2}\right)_{6}-NH_{2}\rightarrow\left(-CO-\left(CH_{2}\right)_{4}-CO-HN-\left(CH_{2}\right)_{6}-NH\right)_{n}-\ +2nHCl$

Remarque :

L'appellation du « nylon $6-6$ » précise que la réaction de polycondensation fait intervenir deux molécules renfermant chacune six atomes de carbone

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Les amines - Ts

Classe:

Terminale

I. Généralités

1. Définition

Les amines sont des composés azotés dont la chaine carbonée comporte au moins un atome d'azote

Leur formule générale est :

est le groupe fonctionnel des amines

2. Les classes d'amine

La classe d'une amine est liée au nombre de groupe alkyle (ou aryle) portés par l'atome d'azote

Il existe trois classes d'amines :

$-\ $ les amines primaires : $R-NH_{2}$

$-\ $ les amines secondaires : $R-NH-R'$

$-\ $ les amines tertiaires : $R-NR'-R''$

$R\;,\ R'\text{ et }R''$ peuvent être identiques ou différents.

Si l'un d'eux est au moins un groupe aryle $\left(C_{6}H_{5^{-}}\right)$, il s'agit d'une amine benzénique (on dit aussi aromatique)

3. Nomenclature

a) Cas des amines aliphatiques

$-\ $ Les amines primaires sont nommées en ajoutant la terminaison amine éventuellement précédée du numéro de l'atome de carbone portant le groupe caractéristique entre tirets

Exemples :

$CH_{3}-CH_{2}-NH_{2}$ : Éthanamide ou éthylamine

$CH_{3}-CH\left(NH_{2}\right)-CH_{3}$ : propan $-2-$ amine

$CH_{3}-CH_{2}-CH_{2}-CH\left(CH_{3}\right)-CH_{2}-CH_{2}NH_{2}$ : $3-$ méthylhéxan $-1-$ amine

$-\ $ Les amines secondaires et tertiaires sont constituées comme dérivant de l'amine primaire correspondant à la chaine carbonée la plus longue

Le nom de cette amine est précédé du nom ou des noms des substituants sur l'atome d'azote énuméré dans l'ordre alphabétique et précédé du préfixe $N-$

Pour les amines secondaires et tertiaires, lorsque les substituants alkyles sont identiques, on ajoute le suffixe « amine » au nom du radical alkyle privé du « e » final et précédé du suffixe multiplicatif adéquat

Exemples :

$CH_{3}-CH_{2}-CH_{2}-NH-CH_{3}$ : $N-$ méthylpropane $-1-$ amine

$CH_{3}-CH_{2}-NH-CH_{2}-CH_{3}$ : $N-$éthyléthanamine ou diéthylamine

$CH_{3}-CH\left(C_{6}H_{5}\right)-CH_{2}-NH-CH_{2}-CH_{3}$ : $N-$ éthyl $-2-$ phénylpropanamine

$CH_{3}-CH_{2}-CH_{2}-N\left(CH_{3}\right)-CH_{2}-CH_{3}$ : $N-$ éthyl $-N-$ méthylpropanamine

$CH_{3}-CH_{2}-N\left(C_{2}H_{5}\right)-CH_{2}-CH_{2}-CH_{3}$ : $N\;,\ N-$ diéthyl léthanamine ou triéthylamine

b) Cas des amines aromatiques

Pour les amines aromatiques nous donnerons quelques exemples

$C_{6}H_{5}-NH_{2}$ : Phénylamine ou aniline

$C_{6}H_{5}-NH-C_{6}H_{5}$ : Diphénylamine

$C_{6}H_{5}-N\left(CH_{3}\right)_{2}$ : $N\;,\ N-$ diméthylaniline

II. Propriétés des amines

1. Propriétés basiques d'une amine :

a) Ionisation dans l'eau

L'action des amines sur l'eau est limitée, elle se fait avec libération de l'ion hydroxyde $OH^{-}$

$R-NH_{2}+H_{2}O\longrightarrow R-NH_{3}^{+}+OH^{-}$

$R-NH-R'+H_{2}O\longrightarrow R-NH_{2}^{+}-R'+OH^{-}$

$R-NR'-R'+H_{2}O\longrightarrow R-NH^{+}R'-R''+OH^{-}$

b) Action des amines sur quelques ions métalliques

Les solutions d'ammoniac et d'amines aliphatiques donnent des propriétés avec certains ions métalliques tels que :

$-\ $ les ions $Cu^{2+}$

$-\ $ les ions $Fe^{2+}\;,\ Fe^{3+}\;,\ Al^{3+}\ldots$

2. Réaction d'alkylation

On appelle alkylation toute réaction au cours de laquelle un groupe alkyle se fixe sur une molécule

Les équations-bilans s'écrivent :

$NH_{3}+R-X\ \rightarrow\ R-NH_{2}+HX$

$R_{1}-NH-R_{2}+R-X\ \rightarrow\ R_{1}-NR-R_{2}+HX$

$R_{1}-NR_{3}-R_{2}+R-X\ \rightarrow\ \left[ R_{1}-NRR_{3}-R_{2}\right]^{+}+X^{-}$

$\left(X=Cl\;,\ Br\;,\ I\ldots\right)$

Exemple :

$CH_{3}-CH\left(CH_{3}\right)-CH_{2}Br+NH_{3}\ \rightarrow\ CH_{3}-CH\left(CH_{3}\right)-CH_{2}NH_{2}+HBr$ : $2-$ méthylpropan $-1-$ amine

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Les alcools - Ts

Classe:

Terminale

I. Généralités

1. Définition

Un alcool est un composé organique oxygéné qui comporte un groupe hydroxyle fixé sur un atome de carbone tétragonal.

Leur formule générale est : $R-OH$

soit $C_{n}H_{2n+1}OH$ où $OH$ est le groupe fonctionnel des alcools appelé groupe hydroxyle

2. Nomenclature

a) Cas des monoalcools à chaine carbonée saturée

Le nom de l'alcool dérive de celui d'un alcane de même chaine carbonée en remplaçant la terminaison $e$ par $ol$ précédé du numéro le plus petit du carbone porteur du groupe hydroxyle

Exemples :

$CH_{3}-CH_{2}-CH_{2}OH$ : propan$-1-$ol

$CH_{3}-CH\left(CH_{3}\right)-CHOH-CH_{3}$ : $3-$méthylbutan$-2-$ol

Remarque :

Un carbone asymétrique est un carbone tétragonal lié à quatre atomes ou groupes d'atomes différents.

On le repère habituellement par un astérisque $(\ast)$

Exemple :

b) Cas des polyols

On fait précéder le suffixe du préfixe multiplicatif adéquat (di, tri, tétra, penta...) précédé des numéros des atomes de carbone portant les groupes d'hydroxydes séparés par des virgules, l'ensemble étant mis entre tirets

Exemples :

$CH_{2}OH-CH_{2}OH$ : éthane$-1.2-$diol

$CH_{2}OH-CHOH-CH_{2}OH$ : propane$-1\;,\ 2\;,\ 3-$triol ou glycérol

$CH_{3}-CHOH\left(CH_{3}\right)-CHOH\left(CH_{3}\right)-CH_{3}$ : $2.3-$diméthylbutane$-2.3-$diol

3. Les classes d'alcool

La classe d'alcool est lié au nombre de groupe(s) d'alkyle(s) porté(s) par le carbone fonctionnel

Il existe trois classes d'alcools :

$-\ $ les alcools primaires : leur carbone fonctionnel est lié à un atome de carbone

$R-CH_{2}OH$

Exemples :

$CH_{3}-CH_{2}OH$ : Éthanol

$CH_{3}-CH\left(CH\right)_{3}-CH_{2}OH$ : $2-$méthylpropan$-1-$ol

$-\ $ les alcools secondaires : leur carbone fonctionnel est lié à deux atomes de carbone

$R-CHOH-R'$

Exemple :

$CH_{3}-CH_{2}-CHOH-CH_{3}$ : butan$-2-$ol

$-\ $ les alcools tertiaires : leur carbone fonctionnel est lié à trois atomes de carbone

$R-COHR'-R''$

Exemple :

$\left(CH_{3}\right)_{2}-COH-CH_{2}-CH_{3}$ : $2-$méthylbutan$-2-$ol

II. Propriétés des alcools

1. Les propriétés physiques

Dans les conditions ordinaires de température et de pression $(25^{\circ}C$ ; $1\,atm)$ les alcools son liquides jusqu'à $C_{12}.$

Au de $C_{12}$ ils sont solides

Les alcools en $C_{4}$ sont assez solubles dans l'eau.

La solubilité diminue lorsque le nombre d'atomes de carbone augmente

Les alcools à très grands nombres de carbone sont pratiquement insolubles dans l'eau

2. Les propriétés chimiques :

2.1. Action du sodium

Les alcools réagissent sur le sodium métallique en donnant un dégagement de dihydrogène et un alcoolate

L'équation-bilan de la réaction s'écrit :

$$\boxed{R-OH\ +\ Na\ \rightarrow\ RO^{-}\ +\ Na^{+}\ +\ \dfrac{1}{2}H_{2}}$$

2.2. Oxydation des alcools

2.2.1. Oxydation dans le dioxygène

a) Oxydation brutale ou combustion

Comme toute substance organique, les alcools en présence d'un excès de dioxygène ou d'air peuvent subir une combustion complète

La combustion des alcools est une réaction exothermique

L'équation-bilan de la réaction s'écrit :

$$\boxed{C_{n}H_{2n+1}OH\ +\ \dfrac{3n}{2}O_{2}\ \rightarrow\ nCO_{2}\ +\ (n+1)H_{2}O}$$

Cette réaction explique l'emploi des alcools comme combustible ou carburants

b) Oxydation ménagée des alcools

Lorsque l'oxydation d'un alcool se fait sans destruction de la chaine carbonée, on dit qu'il y a oxydation ménagée

$\bullet\ $ Un alcool primaire est d'abord oxydé en aldéhyde ; ensuite en acide carboxylique :

$$R-CH_{2}OH\ +\ \dfrac{1}{2}O_{2}\ \stackrel{Pt\ ou\ Cu}{\longrightarrow}\ R-CHO\ +\ H_{2}O$$

$$R-CHO\ +\ \dfrac{1}{2}O_{2}\ \stackrel{Pt\ ou\ Cu}{\longrightarrow}\ R-COOH$$

Remarque :

$-\ $ Le réactif de Schiff qui rosit met en évidence la formation d'un aldéhyde

$-\ $ Le bleu de bromothymol qui vire en jaune met en évidence la formation d'un acide

$\bullet\ $ Un alcool secondaire est oxydé en cétone

$$R-CHOH-R'\ +\ \dfrac{1}{2}O_{2}\ \stackrel{Pt\ ou\ Cu}{\longrightarrow}\ R-CO-R'\ +\ H_{2}O$$

$\bullet\ $ L'alcool tertiaire ne subit pas l'oxydation ménagée car le carbone fonctionnel n'est pas lié à un atome d'hydrogène

2.2.2. Oxydation ménagée en solution aqueuse

Les alcools peuvent subir l'oxydation ménagée en solution aqueuse si cette oxydation est réalisée par les ions usuels $($ion dichromate $Cr_{2}O_{7}^{2-}$, ion permanganate $MnO_{4}^{-}$ en milieu acide$)$

L'oxydation d'un alcool primaire donne un aldéhyde lorsque l'oxydant est en défaut en acide carboxylique lorsque l'oxydant est en excès

De manière générale, les couples rédox mis en jeu sont :

$\ast\ \ RCHO|R-CH_{2}OH\ ;\ RCOOH|RCHO\ ;\ RCOOH|R-CH_{2}OH|R-CO-R'|R-CHOH-R'$

$\ast\ \ Cr_{2}O_{7}^{2-}|Cr^{3+}\ :\ Cr_{2}O_{7}^{2-}\ +\ 14H^{+}\ +\ 6e\ \leftrightarrows\ 2Cr^{3+}\ +\ 7H_{2}O$

rouge verte

$\ast\ \ MnO_{4}^{-}|Mn^{2+}\ :\ MnO_{4}^{-}\ +\ 8H^{+}\ +\ 5e\ \leftrightarrows\ Mn^{2+}\ +\ 4H_{2}O$

violette incolore

Exemple :

oxydation du propan$-2-$ol par les ions dichromates en milieu sulfurique :

$\left\lbrace\begin{array}{l}\left(CH_{3}-CHOH-CH_{3}\ \rightarrow\ CH_{3}-CO-CH_{3}+2H^{+}+2e\right)\\ Cr_{2}O_{7}^{2-}+14H^{+}+6e\ \rightarrow\ 2Cr^{3+}+7H_{2}O\end{array}\right.$

Demi-équations électroniques :

Équation-bilan :

$3CH_{3}-CHOH-CH_{3}+Cr_{2}O_{7}^{2-}+8H^{+}\ \rightarrow\ CH_{3}-CO-CH_{3}+2Cr^{3+}+7H_{2}O$

2.3. Déshydratation des alcools

2.3.1. Déshydratation intramoléculaire

Elle conduit à un alcène

Exemple :

$CH_{3}-CHOH-CH_{3}\stackrel{Al_{2}O_{3}\text{ à }400^{\circ}C}{\longrightarrow}CH_{3}-CH=CH_{2}+H_{2}O$

De manière générale, la déshydratation catalytique à la température élevée conduit à des alcènes, que l'alcool soit primaire, secondaire ou tertiaire

Les alcools tertiaires se déshydratent plus facilement $($dès $200^{\circ}C)$

3.1. Déshydratation intermoléculaire

Elle conduit à un éther-oxyde.

Elle se produit à une température moins élevée

$R-OH+HO-R'\stackrel{Al_{2}O_{3}\text{ à }250^{\circ}C}{\longrightarrow}R-O-R'+H_{2}O$

Exemples :

$CH_{3}-OH+HO-CH_{3}\stackrel{Al_{2}O_{3}\text{ à }250^{\circ}C}{\longrightarrow}CH_{3}-O-CH_{3}+H_{2}O$ oxyde de diméthyle

$CH_{3}-OH+HO-CH_{2}-CH_{3}\stackrel{Al_{2}O_{3}\text{ à }250^{\circ}C}{\longrightarrow}CH_{3}-O-CH_{2}-CH_{3}+H_{2}O$ oxyde de méthyle d'éthyle ou méthoxyéthane

3.2. Estérification

La réaction d'estérification est la réaction d'un acide carboxylique avec un alcool

Elle donne naissance à une naissance à un ester et de l'eau

La réaction d'estérification est lente, athermique et réversible (elle conduit à un équilibre chimique)

$R-COOH\ +\ HO-R'\leftrightarrows R-COO-R'\ +\ H_{2}O$

acide carboxylique alcool ester eau

Exemple :

$HCOOH\ +\ HO-CH_{2}-CH_{3}\leftrightarrows HCOO-CH_{2}-CH_{3}\ +\ H_{2}O$

acide méthanoique éthanol méthanoate d'éthyle eau

3.3. Hydrolyse

La réaction d'estérification est limitée par la réaction d'hydrolyse

La réaction d'hydrolyse d'un ester est son action sur l'eau.

Elle donne naissance à un acide carboxylique et un alcool

$R-COO-R'\ +\ H_{2}O\leftrightarrows R-COOH\ +\ HO-R'$

ester eau acide carboxylique alcool

Estérification et hydrolyse d'un ester sont des réactions inverses

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Force et champ électrostatiques - 1er s

Classe:

Première

Exercice 1 : pendule et force électrostatique

Une bille de masse $m=20\,g$ est suspendu à un fil de longueur $l=10\,cm.$

La bille porte une charge électrique $q$ que l'on souhaite déterminer.

En approchant horizontalement une tige isolante qui porte à son extrémité une charge $q'=+10^{-6}C$, la bille est attirée par la tige et le fil fait un angle $\alpha=20^{\circ}$ par rapport à la verticale.

Les charges $q$ et $q'$ sont situés à une distance $d=2\,cm.$

1) Faire le bilan des forces qui s'exercent sur la bille et les représenter

2) Écrire la condition d'équilibre

3) Déterminer l'intensité de la force électrostatique.

4) En déduire la charge $q$ portée par la bille. $\left(k=1/\left(4\pi\varepsilon_{0}\right)=9.0\cdot 10^{9}N\cdot m^{2}\cdot C^{-2}\right)$

Exercice 2

On place aux points $A$ et $B$ deux boules métalliques identiques $\left(B_{1}\right)$ et $\left(B_{2}\right)$ supposées ponctuelles.

La distance entre $A$ et $B$ est égale à $2a.$

La boule $\left(B_{1}\right)$ porte la charge $-q$ et la boule $\left(B_{2}\right)$ porte la charge $+q$ $(q>0).$

On note $O$ milieu du segment $[AB]$ et $(\Delta)$ la médiatrice de $[AB]$ contenue dans le plan de la figure.

Soit $M$ un point de $(\Delta)$ distant de $h$ du point $O.$ (figure 1)

1.1. Définir la ligne de champ.

Représenter le spectre électrique des deux charges placées en $A$ et $B.$

1.2. Représenter les vecteurs champs électriques $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ créés respectivement par $B_{1}$ et $B_{2}$ au point $M.$

1.3. Exprimer la valeur de $E_{A}$ et de $E_{B}$ en fonction de $K$, $q$, $a$ et $h.$

Montrer que $E_{A}=E_{B}\cdot K=9\cdot 10^{9}\quad u.s.i$

2. On notera $\overrightarrow{E}_{M}$ le champ électrique créé par les deux boules $\left(B_{1}\right)$ et $\left(B_{2}\right)$ au point $M.$

2.1. Déterminer les coordonnées $E_{Mx}$ et $E_{My}$ du vecteur $\overrightarrow{E}_{M}$ dans le repère orthonormé $(M\;,\ \vec{i}\;,\ \vec{j})$ en fonction de $K$, $q$, $a$ et $h.$

2.2. Montrer que :

$$\overrightarrow{E}_{M}=-\dfrac{2K|q|\cos\alpha}{\left(a^{2}+h^{2}\right)}\overrightarrow{i}\;,\text{ avec }\cos\alpha=\dfrac{a}{\sqrt{a^{2}+h^{2}}}$$

2.3. Déduire la valeur de $\overrightarrow{E}_{M}$ au point $O.$

On donne $a=10\,cm\;,\ h=17.33\,cm\text{ et }q=0.3\mu C.$

Exercice 3

Deux charges électriques ponctuelles sont placées aux points $A$ et $B$ distants de $10\,cm.$

La charge placée en $A$ vaut $q_{A}=-3\cdot 10^{-9}C$ celle placée en $B$ vaut $q_{B}=4\cdot10^{-9} C.$

1. Énoncer la loi de Coulomb.

2.1. Déterminer les caractéristiques de la force exercée par $A$ sur $B$ et la force exercée par $B$ sur $A.$

2.2. Représenter $\overrightarrow{F}_{B/A}$ et $\overrightarrow{F}_{A/B}$

3. Déterminer les caractéristiques du vecteur champ électrostatique $\overrightarrow{E}$ créé par ces deux charges électriques en ces deux cas, puis les représenter.

3.1. Au milieu $O$ de segment $AB.$

3.2. En un point $M$ de la médiatrice de $AB$, situé à $5\,cm$ de $O.$

4. Quelles sont les caractéristiques d'un champ électrique uniforme (donner un schéma de spectre de champ)

Exercice 4

Trois pendules électrostatiques sont formés de trois petites sphères identiques $A$, $B$ et $C$, supposées ponctuelles, de même masse $m=10.0\,g$, suspendues par des fils de masses négligeables à un support horizontal de telle façon que leurs points d'attache respectifs $A'$, $B'$ et ce sont régulièrement espacés : $A'B'=B'C'$ (voir Figure ci-dessous).

Les deux fils supportant les sphères $A$ et $C$ sont de même longueur $l$, égale à $25.0\,cm$, et forment tous les deux un angle $\alpha$ avec la verticale.

Le fil supportant la sphère $B$ est vertical et d'une longueur $l'$ telle que les centres de $A$, $B$ et $C$ sont alignés dans un même plan horizontal.

Les sphères $A$ et $C$ portent chacune la même charge : $q=+200\,nC$

La sphère $B$ porte une charge $q'$ de valeur double de celle de $q.$

Données :

Distance $d$ entre les centres de $A$ et $B$ $($égale à la distance entre les centres de $B$ et $C)$ : $d=10.0\,cm.$

Accélération de la pesanteur : $g=9.81\,m\cdot s^{-2}.$

Interaction de Coulomb : $k=9.00\cdot10\,u\ S.I$

Interaction de Newton : $G=6.67\cdot10^{-11}u\ S.I$

On néglige les actions de l'air, ainsi que les interactions gravitationnelles entre les sphères.

1. Quel est le signe de $q'$ ?

Justifier.

2. On s'intéresse à l'équilibre de $A.$

2.1. Faire le bilan des forces qui s'exercent sur $A$, sans faire intervenir, pour simplifier, l'action de $C.$

2.2. Représenter ces forces sur un schéma, sans souci d'échelle mais en respectant leurs directions, leurs sens et leurs points d'application.

2.3. Énoncer la condition d'équilibre de $A.$

2.4. En déduire la valeur de l'angle $\alpha.$

2.5. Déterminer les valeurs des forces qui s'exercent sur $A.$

3. On s'intéresse à l'équilibre de $B.$

3.1. Faire le bilan des forces qui s'exercent sur $B.$

3.2. Représenter ces forces sur un schéma, sans souci d'échelle mais en respectant leurs directions, leurs sens et leurs points d'application.

3.3. Déterminer les valeurs des forces qui s'exercent sur $B.$

Exercice 5

Une tige isolante $AB$ $(AB=20\,cm)$ est inclinée d'un angle $\alpha=30^{\circ}$ avec l'horizontale.

1. On fixe en $A$ une charge $q_{1}=-10\,nC$, en $B$ une charge $q_{2}=10\,nC.$

Déterminer les caractéristiques du vecteur champ électrostatique au point $C$ situé sur la tige $AB$ à $5\,cm$ de $A.$

2. Une petite sphère $(S)$ portant une charge $q=30\,nC$, de masse $m$, peut coulisser sans frottement sur la tige $AB$, elle s'immobilise en $C.$

a) Faire le bilan des forces qui s'exercent sur la sphère $(S)$ ; les représenter.

b) En appliquant la condition d'équilibre de la sphère, calculer la masse $m$ et la valeur de la réaction de la tige.

On donne $g=10\,N\cdot Kg^{-1}.$

3. En maintenant la tige $AB$ horizontalement, la sphère reste-t-elle immobile ?

Si non dans quel sens va-t-elle se déplacer ?

Exercice 6

On donne la constante électrostatique $K=9\cdot10^{9}\ u.s.i.$

Le schéma de la figure 1 représente deux pendules électrostatiques, de même longueur $l=20\,cm$, portant, respectivement, à leurs extrémités libres deux boules supposées ponctuelles $A$ et $B$ de même masse et de charges respectives $q_{A}=-q_{B}=2\mu C.$

Lorsqu'on rapproche les pendules l'un de l'autre, ils prennent la position d'équilibre indiquée sur le schéma de la figure

À l'équilibre, chacun des deux pendules fait un angle $\alpha$ très petit avec $\sin\alpha=0.1.$

La distance séparant les deux points d'attache $O$ et $O'$ des deux pendules est $OO'=14\,cm.$

1. Calculer la distance $AB$ à l'équilibre.

2.1. Représenter toutes les forces exercées sur les boules $A$ et $B$

2.2. Déterminer la valeur de la force de l'interaction électrique existant entre les boules $A$ et $B.$

Exercice 7

Deux points $A$ et $B$ sont situés sur la circonférence d'un cercle de centre $O$ et de rayon $R=6\,cm.$

En $A$ et $B$ on place respectivement deux boules ponctuelles chargées de même charge $q_{A}=q_{B}=2\cdot10^{-7}C$ et de masses négligeables.

1. Représenter les forces électriques $\overrightarrow{F}_{A/B}$ et $\overrightarrow{F}_{B/A}$ qui constituent l'interaction électrique existant entre $q_{A}$ et $q_{B}.$

Donner les caractéristiques de $\overrightarrow{F}_{A/B}$

2.1. Représenter, au point $O$, les vecteurs champs électrostatiques de $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ créés respectivement par les charges $q_{A}$ et $q_{B}.$

Calculer la valeur de $\overrightarrow{E}_{A}$

2.2. Déterminer les caractéristiques du vecteur champ électrostatique $\overrightarrow{E}_{O}=\overrightarrow{E}_{A}+\overrightarrow{E}_{B}$ créé par l'ensemble des deux charges au point $O.$

3. Au point $O$, on place un corps ponctuel $(C)$ de masse $m$ qui porte une charge de valeur absolue $|Q_{0}|=2\cdot10^{-8}C$, il prend une position d'équilibre stable.

3.1. Représenter la force $\overrightarrow{F}$ exercée par $q_{A}$ et $q_{B}$ sur la charge $Q_{0}.$

Quel est le signe de $Q_{0}$ ?

Justifier la réponse.

3.2 Écrire la condition d'équilibre du corps ponctuel $(C).$

Calculer la masse $m$ du corps

Exercice 8

Une sphère de centre $S$ est attachée au point $O$ par un fil isolant de masse négligeable et de longueur $l=40\,cm.$

La sphère, de masse $m=2\cdot10^{-2}kg$, porte une charge $q.$

$$g=10\,N\cdot kg^{-1}$$

1. On la soumet à un champ électrique uniforme $E$, horizontal, orienté comme indique la figure.

Le fil s'incline alors d'un angle $\alpha=10^{\circ}$ par à rapport à la verticale.

En déduire la valeur de la charge $q.$

Intensité du champ électrostatique $E=10^{3}V\cdot m^{-1}$

2. On superpose au champ électrostatique précédent, un autre champ électrostatique uniforme $E'$ vertical.

Quels doivent être le sens et l'intensité du champ $E'$ pour que le fil s'incline sur la verticale d'un angle $\alpha=20^{\circ}$

3. Quelle serait l'inclinaison $\alpha'$ si l'on changeait le sens de $E'$ sans modifier son intensité

Exercice 9

Deux petites sphères métalliques et identiques sont fixées aux extrémités $A$ et $B$ d'une barre.

On a : $AO=OB=l$

Les sphères sont chargées et portent respectivement les charges $q$ et $-q.$

On introduit ce dispositif entre deux plaques parallèles.

Lorsque celles-ci sont branchées à la terre, la barre $AOB$ est parallèle aux plaques, et le fil n'est pas tordu.

Lorsque les plaques sont branchées à la terre, la barre $AOB$ est parallèle aux plaques, et le fil n'est pas tordu.

Lorsque les plaques sont branchées à un générateur haute tension, il existe un champ électrostatique uniforme $\overrightarrow{E}$ perpendiculaire aux plaques.

La barre $AOB$ fait alors un angle $\alpha$ avec la direction précédente et reste horizontale

1. Calculer en fonction de $l$, $\alpha$, $q$ et $E$ le moment des forces électrostatiques par rapport à l'axe de rotation du dispositif.

2. Calculer le moment du poids du système par rapport à l'axe de rotation.

3. Le dispositif étant en équilibre, le fil de torsion exerce des actions mécaniques dont le moment par rapport à l'axe de rotation est proportionnel à l'angle de rotation $\alpha$ :

$|M_{\Delta}|=C\alpha$ Avec $C=13.5\cdot10^{-7}N\cdot m\cdot rad^{-1}.$

Calculer $q$ sachant que : $E=272\,V\cdot m^{-1}$ ; $l=15\,cm$ ; $\alpha=\dfrac{\pi}{6}.$

Exercice 10

En deux points $A$ et $B$ tels que $OA=OB=d$, sont placées deux charges ponctuelles égales $q$ et de même signe.

On se propose de déterminer le champ électrique crée par ces deux charges en un point $M$ tel que $OM=x.$

Établir, en fonction de $x$, $d$ et $q$ ; l'expression du champ électrique crée par les deux charges au point $M$ dans chacun des cas représentés sur les schémas suivants :

1) Le point $M$ se trouve sur le segment $[AB]$ entre les points $O$ et $B$ :

2) Le point $M$ se trouve dans l'alignement de $AB$ à l'extérieur du segment $[AB]$ du côté du point $B$ :

3) Le point $M$ est situé sur la médiatrice du segment $[AB]$ :

Exercice 11

Une charge ponctuelle $Q=-40\,nC$ est placée au sommet $A$ d'un carré $ABCD$ de $2.0\,cm$ de côté

1. Déterminer les caractéristiques (valeur, direction et sens) des champs électriques $\overrightarrow{E}_{B}$ et $\overrightarrow{E}_{C}$ créés par cette

charge aux points $B$ et $C.$

2. Représenter ces champs

3. Représenter quelques lignes de champs autour du point $A.$

4. On place une charge ponctuelle $q=-10\,nC$ au point $C.$

4.1. Déterminer les caractéristiques (valeur, direction et sens) de la force électrique s'exerçant sur cette charge.

4.2. Représenter cette force

4.3. Représenter, à la même échelle, la force électrique qui s'exerce sur la charge $Q.$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur:

Sidy Mouhamed Ndiaye

Série d'exercices : La calorimétrie - 1er s

Classe:

Première

Exercice 1

1) Calculer la quantité de chaleur nécessaire pour élever de $20^{\circ}C$ à $80^{\circ}C$ une masse égale à $1$ tonne d'eau.

2) Si cette énergie calorifique pouvait être transformée en énergie potentielle de pesanteur, à quelle altitude $z$ pourrait-on soulever cette tonne d'eau ?