Exercice 2
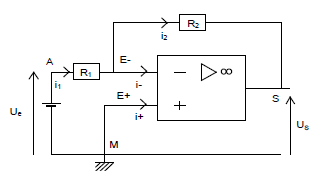
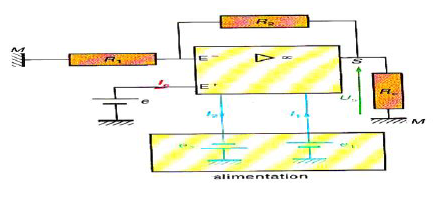
On considère le montage ci-dessus pour lequel l'amplificateur opérationnel (A.O.) est supposé idéal.
La tension de saturation de l'A.O. est $V_{\text{sat}}=15\;V.$
On donne les résistances : $R_{1}=2.2\;k\Omega\;,\ R_{2}=4.7\;k\Omega$
La tension d'entrée est $U_{e}=U_{_{AM}}=1.5\;V.$
1) Un A.O. est considéré comme idéal si :
$-\ $ le courant $i^{-}$ entrant par l'entrée inverseuse $E^{-}$ est nul ;
$-\ $ le courant $i^{+}$ entrant par l'entrée non inverseuse $E^{+}$ est nul ;
$-\ $ la tension entre les entrées $E^{+}\ $ et $\ E^{-}$ est nulle en régime linéaire, cette tension est notée $u_{d}.$
2.1) Montrons qu'avec ce montage un même courant traverse $R_{1}\ $ et $\ R_{2}.$
Le point $E^{-}$ est un nœud du circuit. La loi des nœuds s'écrit :
$$i_{1}=i_{2}+i^{-}$$
L'A.O. étant idéal alors, $i^{-}=0$
Par suite, $i_{1}=i_{2}.$ Les intensités $i_{1}\ $ et $\ i_{2}$ sont donc égales.
2.2) Établissons que, dans les conditions considérées, la tension de sortie $U_{s}=U_{_{SM}}$ est donnée par :
$$U_{s}=-\dfrac{R_{2}}{R_{1}}U_{e}$$
La loi d'additivité des tensions à l'entrée s'écrit :
$$U_{e}=U_{AM}=U_{AE^{-}}+U_{E^{-}E^{+}}+U_{E^{+}M}$$
Avec :
$U_{AE^{-}}=R_{1}.i$
$U_{E^{-}E^{+}}=-u_{d}=0$ puisque l'A.O. est idéal
$U_{E^{+}M}=0$, il ne passe aucun courant dans cette branche (l'A.O. est idéal) et il s'agit d'un simple fil.
La tension $U_{e}$ est donc :
$$U_{e}=R_{1}.i$$
De même la tension de sortie $U_{s}$ a pour expression :
$$U_{s}=U_{SM}=U_{SE^{-}}+U_{E^{-}E^{+}}+U_{E^{+}M}$$
Comme $U_{SE^{-}}=-U_{E^{-}S}=-R_{2}.i\;,\ U_{E^{-}E^{+}}=0\ $ et $\ U_{E^{+}M}=0$ alors :
$$U_{s}=-R_{2}.i$$
De l'expression de $U_{e} $on tire :
$$i=\dfrac{U_{e}}{R_{1}}\ \Rightarrow\ U_{s}=-\dfrac{R_{2}}{R_{1}}U_{e}$$
2.3) Justifions le nom de montage amplificateur inverseur donné à ce montage.
Avec ce montage la résistance $R_{2}$ supérieure à $R_{1}$, la valeur absolue de $U_{s}$ est supérieure à celle de $U_{e}.$
Le montage est dit montage amplificateur.
Avec ce montage, les tensions d'entrée et de sortie sont de signes contraires. Le montage est dit montage amplificateur inverseur.
2.4) Calcul de la tension de sortie.
Soit : $U_{s}=-\dfrac{R_{2}}{R_{1}}U_{e}$
A.N : $U_{s}=-\dfrac{4.7\times 1.5}{2.2}=-3.2$
Donc, $\boxed{U_{s}=-3.2\;V}$
3) Entre $A\ $ et $\ M$, à l'entrée du montage précédent, on remplace la pile par un générateur de tension réglable.
Compléter le tableau ci-dessous en précisant, pour chaque valeur de la tension d'entrée $U_{e}$ la valeur correspondante de la tension de sortie $U_{s}.$
La relation entre $U_{s}\ $ et $\ U_{e}$ établie s'applique tant que la tension de sortie de l'A.O. vérifie :
$$-V_{sat}\leq U_{s}\leq +V_{sat}$$
Pour $U_{e}=-4.0\;V$ alors : $U_{s}=-\dfrac{4.7\times(-4)}{2.2}=8.5$
On obtient le tableau suivant :
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|}\hline U_{e}(V)&-10&-8.0&-4.0&-2.0&0.0&2.0&4.0&8.0&10\\ \hline U_{s}(V)&15&15&8.5&4.3&0.0&-4.3&-8.5&-15&-15\\ \hline\end{array}$$
Exercice 3
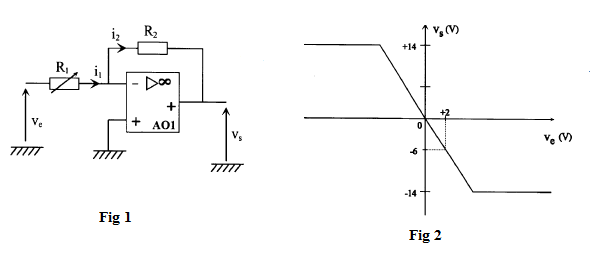
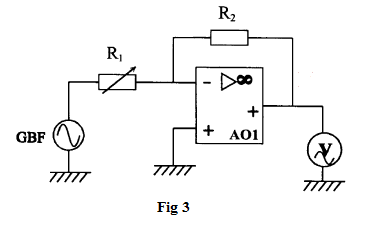
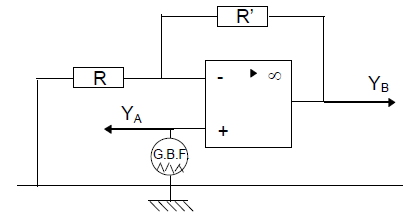
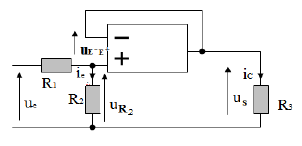
Le montage étudié dans cette partie est représenté sur la figure 1.
L'amplificateur opérationnel $AO_{1}$ utilisé est considéré comme parfait.
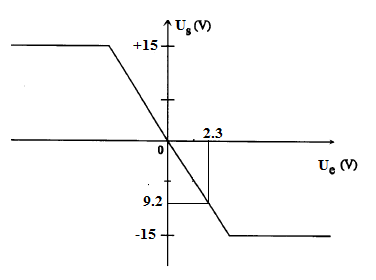
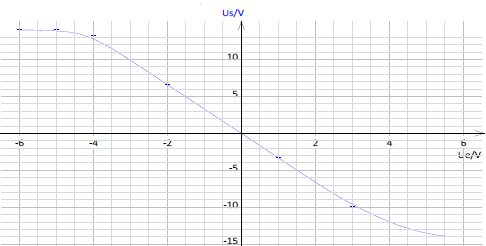
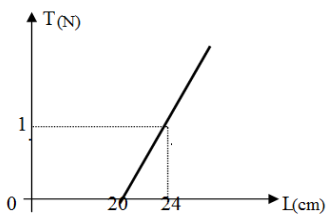
La caractéristique $V_{s}=f(V_{e})$ du montage est représentée sur la figure 2.
La résistance $R_{1}$ est ajustable et $R_{2}=10\;k\Omega.$
1) Montrons qu'en régime linéaire l'amplification du montage peut s'exprimer sous la forme :
$$A=\dfrac{V_{s}}{V_{e}}=-\dfrac{R_{2}}{R_{1}}$$
La loi d'additivité des tensions à l'entrée s'écrit :
$\begin{array}{rcl} V_{e}=V_{AM}&=&V_{AE^{-}}+V_{E^{-}E^{+}}+V_{E^{+}M}\\ \\&=&R_{1}.i+0+0\\ \\&=&R_{1}.i\end{array}$
De même la tension de sortie $V_{s}$ a pour expression :
$\begin{array}{rcl} V_{s}=V_{SM}&=&V_{SE^{-}}+V_{E^{-}E^{+}}+V_{E^{+}M}\\ \\&=&-R_{2}.i_{2}+0+0\\ \\&=&-R_{2}.i_{2}\end{array}$
La loi des nœuds en E-s'écrit :
$$i_{1}=i_{2}+i^{-}$$
Or, $i^{-}=0$ donc, $i_{1}=i_{2}$
L'amplification $A$ du montage peut alors s'écrire :
$\begin{array}{rcl} A&=&\dfrac{V_{s}}{V_{e}}\\ \\&=&\dfrac{-R_{2}.i_{2}}{R_{1}.i_{1}}\quad\text{or, }\ i_{1}=i_{2}\\ \\&=&\dfrac{-R_{2}.i_{1}}{R_{1}.i_{1}}\\ \\&=&-\dfrac{R_{2}}{R_{1}}\end{array}$
Ainsi, $\boxed{A=-\dfrac{R_{2}}{R_{1}}}$
2) En utilisant le résultat précédent et la caractéristique de la figure 2, déterminons la valeur donnée à la résistance $R_{1}.$
On a : $-\dfrac{R_{2}}{R_{1}}=\dfrac{V_{s}}{V_{e}}\ \Rightarrow\ R_{1}=-\dfrac{V_{e}}{V_{s}}R_{2}$
A.N : $R_{1}=-\dfrac{2}{-6}\times 10=3.3$
D'où, $\boxed{R_{1}=3.3\;kV}$
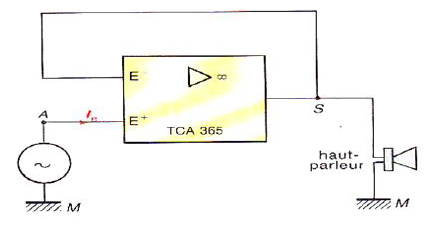
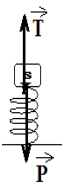
3) On applique à l'entrée du montage une tension sinusoïdale de valeur efficace $V_{_{E}}=2.0\;V.$
Un voltmètre est utilisé en en position $AC$ conformément à la figure 3.
Soit $V_{s}$ l'indication de cet appareil.
De la relation $\dfrac{V_{s}}{V_{e}}=-\dfrac{R_{2}}{R_{1}}$, on tire : $V_{s}=-\dfrac{R_{2}}{R_{1}}V_{e}$
A.N : $V_{s}=-\dfrac{10}{3.3}\times 2.0=-6.1$
Donc, $\boxed{V_{s}=-6.1\;kV}$
Exercice 4
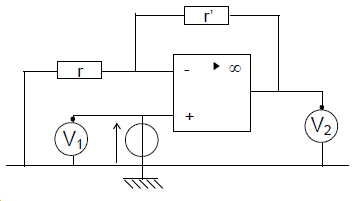
On réalise avec le même montage deux séries de mesures :
La caractéristique $U_{s}=f(U_{e})$ du montage est représentée sur la figure ci-dessous.
$\centerdot\ $ première série : le voltmètre $n^{\circ}1$ indique $2.3\;V$ et le voltmètre $n^{\circ}2$ affiche $9.2\;V$ ;
$\centerdot\ $ deuxième série : le voltmètre $n^{\circ}1$ indique $4.1\;V$ et le voltmètre $n^{\circ}2$ affiche $13.6\;V$
1) La tension mesurée par le voltmètre $n^{\circ}1$ est la tension à l'entrée.
2) La tension mesurée par le voltmètre $n^{\circ}2$ est la tension à la sortie.
3) Le coefficient d'amplification du montage
La valeur $U=13.6\;V$ est plus proche de la tension de saturation donc, la première série de mesure convient.
Ainsi, $A=-\dfrac{V_{2}}{V_{1}}=-\dfrac{9.2}{2.3}=-4$
D'où, $\boxed{A=-4}$
4) La tension de saturation du montage est : $$U_{sat}=15\;V$$
Exercice 5
$R_{1}=10\;k\Omega\;;\quad R_{2}=33\;k\Omega$
Pour ce montage, le coefficient d'amplification vaut : $A=-\dfrac{R_{2}}{R_{1}}$ et la tension de saturation $\pm 14\;V$
1) On appelle $U_{e}$ la tension d'entrée du montage et $U_{s}$, la tension de sortie.
Reportons sur le montage les flèches tension $U_{e}\ $ et $\ U_{s}$ (voir figure)
2) Calculons $A.$
On a : $A=-\dfrac{R_{2}}{R_{1}}=-\dfrac{33}{10}=-3.3$
Ainsi, $\boxed{A=-3.3}$
Lorsque le montage amplificateur fonctionne en régime linéaire, établissons la relation qui existe entre la tension de sortie $U_{s}$ et la tension d'entrée $U_{e}.$
La loi d'additivité des tensions à l'entrée s'écrit :
$$U_{s}=U_{R_{2}}+U_{E^{-}E^{+}}$$
Or, $U_{E^{-}E^{+}}=0$ donc,
$$U_{s}=-R_{2}.i_{2}$$
La loi des nœuds en $E^{-}$ s'écrit :
$$i_{1}=i_{2}+i^{-}=i_{2}+0$$
Ce qui entraine : $i_{1}=i_{2}.$ Par suite,
$$U_{s}=-R_{2}.i_{1}$$
Ainsi, $\dfrac{U_{s}}{U_{e}}=-\dfrac{R_{2}.i_{1}}{R_{1}.i_{1}}=-\dfrac{R_{2}}{R_{1}}$
Par conséquent, $\boxed{U_{s}=-\dfrac{R_{2}}{R_{1}}U_{e}}$
3) Complétons le tableau de valeurs :
Soit : $A=\dfrac{U_{s}}{U_{e}}\ \Rightarrow\ U_{s}=A.U_{e}$
Ainsi, pour $U_{e}=-4\;V$ alors $U_{s}=-3.3\times(-4)=13.2$
$$\begin{array}{|l|c|c|c|c|c|c|c|}\hline U_{e}(V)&-6&-4&-2&0&1&3&5\\ \hline U_{s}(V)&14&13.2&6.6&0&-3.3&-9.9&-14\\ \hline\end{array}$$
4) Construisons le graphique de la fonction $U_{s}=f(U_{e})$ ;
5) A partir de cette courbe, on remarque :
$-\ \ $ les valeurs de $U_{e}$ pour lesquelles le régime de fonctionnement est appelé linéaire sont :
$$13.2\;V\;;\quad 6.6\;V\;;\quad 0\;V\;;\quad -3.3\;V\quad \text{ et }\quad -9.9\;V$$
$-\ \ $ les valeurs de $U_{e}$ pour lesquelles le régime de fonctionnement est dit saturé sont :
$$-6\;V\ \text{ et }\ 5\;V$$
Exercice 6
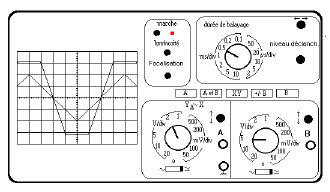
On réalise le montage suivant et on observe les deux oscillogrammes ci-dessous :
Déterminons :
1) la tension de saturation :
En observant les deux oscillogrammes ci-dessous, on obtient : $U_{sat}=3.2\times 5=16$
D'où, $\boxed{U_{sat}=16\;V}$
2) le coefficient d'amplification du montage.
Soit : $U_{s}=3\times 5=15\;V\ $ et $\ U_{e}=1\times 2=2\;V$
Alors, $A=\dfrac{U_{s}}{U_{e}}=\dfrac{15}{2}=7.5$
Ainsi, $\boxed{A=7.5}$
Exercice 7
1) Rappel des caractéristiques d'un A.O. idéal.
$-\ $ le courant $i^{-}$ entrant par l'entrée inverseuse $E^{-}$ est nul ;
$-\ $ le courant $i^{+}$ entrant par l'entrée non inverseuse $E^{+}$ est nul ;
$-\ $ la tension entre les entrées $E^{+}\ $ et $\ E^{-}$ est nulle en régime linéaire
2) Relation simple qui existe entre la tension $U_{e}$ et la tension $U_{s}$
$$U_{e}=U_{s}$$
Exercice 8
A l'aide d'un amplificateur opérationnel alimenté par un générateur $(e_{1}\;,\ 0\;,\ -e_{2})$, nous avons réalisé le montage de la figure ci-dessous
1) En supposant l'$A.O.$ idéal $(I^{+}=I^{-}=0\;;\ V_{_{E^{+}}}-V_{_{E^{-}}}=0)$ montrons que :
$$\dfrac{U_{s}}{e}=\dfrac{R_{1}+R_{2}}{R_{1}}$$
La loi d'additivité des tensions à l'entrée s'écrit :
$$e=U_{R_{1}}+U_{E^{+}E^{-}}$$
Or, $U_{E^{+}E^{-}}=0$ donc, $e=U_{R_{1}}=R_{1}.i_{1}$
La loi d'additivité des tensions à la sortie s'écrit :
$$U_{s}=U_{SM}=U_{R_{2}}+U_{R_{1}}=R_{2}.i_{2}+R_{1}.i_{1}$$
La loi des nœuds en $E^{-}$ s'écrit :
$$i_{1}=i_{2}+i^{-}=i_{2}+0$$
Ce qui entraine : $i_{1}=i_{2}.$ Par suite,
$$U_{s}=(R_{2}+R_{1}).i_{1}$$
Ainsi, $\dfrac{U_{s}}{e}=\dfrac{(R_{2}+R_{1}).i_{1}}{R_{1}.i_{1}}=\dfrac{R_{2}+R_{1}}{R_{1}}$
D'où, $\boxed{\dfrac{U_{s}}{e}=\dfrac{R_{1}+R_{2}}{R_{1}}}$
Application numérique : $R_{1}=10\;k\Omega\;;\quad R_{2}=100\;k\Omega$
Par suite, $\dfrac{U_{s}}{e}=\dfrac{10+100}{10}=11$
2) Avec un $A.O.\ 741$, on a relevé les mesures suivantes :
$I_{e}=0.004\;\mu A\;;\ e=0.48\;V\;;\ U_{s}=5.4\;V$
$R_{c}=2000\Omega\;;\ e_{1}=15.13\;V\;;\ I_{1}=4.23\;mA\;;\ e_{2}=15.10\;V\;;\ I_{2}=1.50\;mA$
Calculons le rapport expérimental $\dfrac{U_{s}}{e}.$
Soit : $\dfrac{U_{s}}{e}=\dfrac{5.4}{0.48}=11$ donc, $\dfrac{U_{s}}{e}=11$
Et par conséquent, $\dfrac{U_{s}}{e}=\dfrac{R_{1}+R_{2}}{R_{1}}$
Exercice 9
Pour le montage de la figure ci-dessous, on donne :
$R_{1}=10\;k\Omega\;;\ R_{2}=4.7\;k\Omega\ $ et $\ R_{3}=2.2\;k\Omega$
De plus, la mesure de $i_{c}$ a donné : $i_{c}=2.5\;mA$
1) L'ampli opérationnel fonctionne en régime linéaire car la sortie est bouclée sur l'entrée inverseuse
2) Calcul de l'intensité $i_{e}$ du courant dans la résistance $R_{2}.$
La loi d'additivité des tensions à la sortie s'écrit :
$\begin{array}{rcl} U_{s}=U_{E^{-}E^{+}}+U_{R_{2}}&\Rightarrow&R_{3}.i_{c}=0+R_{2}.i_{e}\\ \\&\Rightarrow&i_{e}=\dfrac{R_{3}}{R_{2}}i_{c}\\ \\&\Rightarrow&i_{e}=\dfrac{2.2}{4.7}\times 2.5\\ \\&\Rightarrow&i_{e}=1.2\end{array}$
Ainsi, $\boxed{i_{e}=1.2\;mA}$
3) calculons la tension d'entrée $u_{e}.$
Soit : $U_{e}=(R_{1}+R_{2}).i_{e}$
A.N : $U_{e}=(10+4.7)\times 10^{3}\times 1.2\cdot 10^{-3}=17.6$
Ainsi, $\boxed{U_{e}=17.6\;V}$