Physique

Série d'exercices : Travail de la force électrostatique-Énergie potentielle électrostatique - 1er s

Classe: 
Première
 

Exercice 1

Deux plaques $P_{1}$ et $P_{2}$, planes et parallèles, entre lesquelles règne un vide poussé, sont distantes de $d=10cm$
 
Elles sont respectivement reliées aux pôles $+$ et $–$ d'un générateur tension qui délivre une tension continue $U=500V$
 
1. Quels sont, la direction, le sens et l'intensité du champ électrique $\overrightarrow{E}$, supposé uniforme, qui règne dans le domaine situé $D$ entre les deux plaques ?
 
2. Sur l'axe $XOX'$ perpendiculaire aux plaques, dont l'origine $O$ est sur $P_{1}$ et est orienté de $P_{1}$ vers $P_{2}$, on place les points $M$ et $N$ d'abscisses $X_{M}=2cm$ et $X_{N}=7cm$
 
Calculer les d.d.p $V_{O}-V_{M}$ ; $V_{O}-V_{N}$ et $V_{M}-V_{N}$
 
3. Un électron pénètre dans le domaine $D$, au point $R$, avec une vitesse nulle
 
3.1 Donner les caractéristiques de la force électrostatique $\overrightarrow{F}$ qui s'exerce sur lui
 
3.2 Quelle est la vitesse de l'électron à son passage en $N$, $M$, puis en $O$
 
4. Calculer le travail $W(\overrightarrow{F})$ de la force lorsque l'électron déplace de $N$ à $M$
 
On donne : 
 
$m_{e}=9.1\cdot10^{-31}kg$ ; 
 
charge élémentaire : $e=1.6\cdot10^{-1}$
 
 

Exercice 2

On maintient une $U_{AC}=640V$ entre la cathode $C$ et l'anode $A$ d'un canon à électrons. 
 
La vitesse de sortie des électrons de la cathode est supposée nulle. 
 
La distance $CA=l=5cm$ ; la masse de l'électron $m=9.1\cdot10^{-31}Kg$, la charge élémentaire $e=1.6\cdot10^{-19}C$ ; on néglige le poids de l'électron.
 
 
1.1 Déterminer les caractéristiques du vecteur champ électrostatique entre $C$ et $A.$
 
1.2 Calculer le travail de la force électrostatique appliquée à un électron pour aller de $C$ à $A$
 
2. Les électrons arrivent au point $O$, avec une vitesse $V=V_{A}$, entre deux plaques conductrices $P$ et $N$ identiques, horizontales, distantes de $d=5cm$ et symétriques par rapport à la direction $xx'.$
 
Lorsqu'on établit une tension $U_{PN}=1000\,v$, les électrons sortent du champ électrostatique entre $P$ et $N$ en un point $M$ tel que $OM=d'=2\,cm.$ 
 
Calculer la tension $U_{OM}.$
 
3. Calculer l'énergie potentielle électrostatique d'un électron en $O$ puis en $M$, en prenant comme référence la plaque négative $N.$
 
4. Déterminer le travail de la force électrostatique s'exerçant sur un électron pour aller de $O$ à $M$ en fonction de la variation de l'énergie potentielle électrostatique.
 
5. Calculer :
 
5.1 L'énergie cinétique de sortie $E_{CM}$ de l'électron en $M.$
 
5.2 La vitesse de l'électron $V_{M}$ au point $M.$

Exercice 3

On considère une particule de charge $q$ négative $(q=-2e)$ et de masse $m=3\cdot210^{-27}kg.$ 
 
Cette particule, initialement au point $A$ de potentiel $V_{A}=-2.0V$ se dirige vers le point $B$ de potentiel $V_{B}=3.0V.$
 
Ce déplacement se fait à l'air libre dans un champ électrique uniforme $E$ et à la surface de la Terre, dans le champ de pesanteur uniforme $g.$
 
1. Faire l'inventaire des forces que subit cette particule au cours de son déplacement de $A$ vers $B.$ (On n'en négligera aucune à cette question).
 
2. Parmi ces forces, quelles sont celles que l'on qualifie de « conservatives » ?
 
3. En supposant que la trajectoire de la particule est rectiligne, donner l'expression du travail de la force de frottement de l'air $f$, supposée constante entre $A$ et $B$, en fonction de $AB$ et $f.$
 
 
On suppose à présent qu'il règne un vide parfait entre ces deux armatures.
 
4. Quel est le signe de la charge électrique de l'armature haute ? 
 
Justifier.
 
5. Représenter, sans tenir compte de leur norme, le champ électrique $E$ et le champ de pesanteur $g$ sur la figure ci-contre.
 
6. Donner l'expression du travail de la force électrique $F_{e}$, puis du poids $P$, en fonction de $m$, $q$, $V_{A}$, $V_{B}$, $g$, $\alpha$ et $AB.$
 
7. Préciser pour chacune de ces forces si leur travail est moteur ou résistant.
 
8. Calculer le travail de ces forces sur le trajet $AB=1.8m$ et conclure que l'on peut négliger l'énergie potentielle de pesanteur de la particule. 
 
Alors, on ne prend en compte que l'énergie potentielle électrique.
 
On rappelle l'expression de l'énergie potentielle électrique : $E_{Pe}=q\cdot U_{AB}$
 
9. Déduire de la conclusion précédente l'expression de l'énergie mécanique de la particule au point $A$ en fonction de sa vitesse $v_{A}$ et des grandeurs $V_{A}$, $q$, et $m.$
 
10. Même question au point $B$ en fonction de la vitesse $v_{B}$ et des grandeurs $V_{B}$, $q$, et $m.$
 
11. Justifier pourquoi l'énergie mécanique se conserve.
 
12. En déduire la vitesse $v_{B}$ de la particule sachant que $v_{A}=0.53 m\cdot s^{-1}$
 
Données : 
 
charge élémentaire $e=1.6\cdot10^{-19}C$ ; 
 
Champ de pesanteur $g=9.8N/kg$ ; 
 
$\alpha=30^{\circ}$ ; 
 
$E=\dfrac{U}{d}$ ;
 
$U_{AB}=V_{A}-V_{B}$
 
Exercice 4 : Travail d'une force électrostatique
 
Deux armatures métalliques $P_{A}$ et $P_{B}$, parallèles entre elles et distantes de $d$, sont reliées aux bornes d'un générateur de tension continue. 
 
Entre ces deux armatures règne un champ électrostatique $\overrightarrow{E}$ uniforme.
 
1. Donner l'expression du travail de la force électrostatique $\overrightarrow{E}$ qui s'exerce sur une particule de charge $q$ se déplaçant d'un point $A$ de l'armature $P_{A}$ à un point $B$ de l'armature $P_{B}.$ 
 
L'exprimer en fonction de $E$, $AB$ et $q.$
 
2. Montrer que le travail de cette force s'écrit : $W_{AB}(\overrightarrow{F})=q\cdot U_{AB}.$
 
3. Calculer sa valeur dans le cas d'un noyau d'hélium $He^{2+}$ se déplaçant de $A$ à $B.$
 
Données : 
 
$e=1.60\times 10^{-19}C$ ; $U_{AB}=400\,V$

Exercice 5

Une particule $\alpha$ (noyau d'hélium), produite par une source radioactive, est émise au voisinage d'un point $A.$
 
La valeur de sa vitesse en $A$ est négligeable devant celle qu'elle peut atteindre en $B.$
 
Entre les points $A$ et $B$ règne un champ électrostatique uniforme qui permet l'accélération de la particule. 
 
Le poids et les frottements sont négligeables lors de ce mouvement.
 
1. Quelle est la charge $q_{\alpha}$ de la particule $\alpha$ ?
 
2. Établir l'expression du travail de la force électrostatique s'appliquant sur la particule $\alpha$ se déplaçant entre $A$ et $B.$ 
 
Exprimer ce travail en fonction $q\alpha$, $V_{A}$ et $V_{B}.$ 
 
$(V_{A}$ et $V_{B}$ sont les potentiels respectifs aux points $A$ et $B.)$
 
3. En déduire l'expression de la variation d'énergie potentielle électrique entre $A$ et $B.$
 
4. L'énergie mécanique se conserve-elle ? 
 
Justifier.
 
5.1 À partir des réponses précédentes, exprimer la différence de potentiel $V_{A}-V_{B}$ en fonction de $v_{B}$, $m_{\alpha}$ et $q_{\alpha}$
 
5.2 Calculer cette valeur sachant que la vitesse en $B$ a pour valeur $v_{B}=1.00\cdot10^{3}km\cdot s^{-1}.$
 
Données : 
 
$e=1.60\cdot10^{-19}C$ ; $m_{\alpha}=6.70\times 10^{-27}kg.$
 
 

Exercice 6

Au voisinage de la Terre, près du sol, il existe un champ électrostatique uniforme, vertical et dirigé vers le sol. 
 
Sa norme varie linéairement avec l'altitude selon la loi $E=a+bz$ entre les altitudes $z=0$ et $z=1\ 400m.$
 
1) Sachant que pour $z=0$, $E=100V\cdot m^{-1}$ et que pour $z=1\ 400m$, $E=20V\cdot m^{-1}$, déterminer les constantes $a$ et $b.$ 
 
Quelles sont leurs unités ?
 
Représenter graphiquement $E$ en fonction de $z.$
 
2) Par une méthode graphique, déterminer le travail des forces électriques s'exerçant sur une charge de $10^{-10}C$ se déplaçant de l'altitude $O$ à l'altitude $z.$ 
 
En déduire le potentiel électrostatique d'un point situé à l'altitude $h$ si l'on prend comme référence la surface terrestre.
 
3) Un ion $H^{+}$ est formé à l'altitude $z=1\ 400m.$ 
 
Le champ de pesanteur est supposé uniforme, d'intensité $g=10m\cdot s^{-2}.$
 
Calculer l'énergie potentielle de pesanteur et l'énergie potentielle électrostatique de cet ion. 
 
Les comparer.
 
Si l'ion part de l'altitude $z=1400m$ avec une vitesse nulle, quelle sera sa vitesse à l'arrivée sur le sol (on négligera toutes les autres interactions) ?

Exercice 7

La sphère, supposée petite et chargée positivement, d'un pendule électrostatique est en équilibre en un point $O$ situé entre deux plaques $P$ et $N$ conductrices, parallèles et distantes de $d=15cm.$ 
 
Les plaques sont initialement neutres. 
 
On applique une tension $U_{PN}=1\ 500V$ entre les deux plaques. 
 
La sphère chargée adopte, après quelques oscillations, une nouvelle position d'équilibre $A.$
 
1) Calculer la charge $q$ du pendule si, à l'équilibre, l'angle $\alpha$ que fait le fil de suspension avec la verticale vaut $30^{\circ}$ ; la sphère est attirée du côté de la plaque négative $N.$
 
2) Le point $O$ est pris comme point de référence $\alpha$ est l'angle que fait le fil du pendule avec la verticale lorsque la sphère est attirée par la plaque $N.$ 
 
Pour $\alpha\in\left[0\;,\ \dfrac{\pi}{2}\right[$, exprimer en fonction de $\alpha$ l'énergie potentielle de pesanteur $\mathcal{E}_{pg}$ et l'énergie potentielle électrostatique $\mathcal{E}_{pe}.$
 
Représenter graphiquement $\mathcal{E}_{pg}$ et $\mathcal{E}_{pe}$ en fonction de $\alpha.$
 
En déduire la représentation graphique de la somme $\mathcal{E}_{p}$ de ces énergies potentielles.
 
Pour quelle valeur de $\alpha$ cette somme est-elle minimale ? 
 
Conclure.
 
Données : 
 
masse de la sphère : $m=0.5g$ ; 
 
longueur du fil : $l=20m$ ; $g=10m\cdot s^{-2}$

Exercice 8

Un générateur maintient une tension $U=200V$ entre deux plaques conductrices parallèles situées dans le vide.
 
1) Un électron quitte la plaque négative pour être capté par la plaque positive. 
 
Calculer le travail de la force électrostatique qui s'exerce sur cet électron (en joules et en électronvolts).
 
2) La distance séparant les plaques est $d=2cm.$
 
Caractériser le champ électrostatique en tout point de l'espace compris entre les plaques.
 
3) On écarte les plaques, toujours parallèles, à $d'=4cm$ ; la tension de $200V$ est maintenue.
 
Reprendre les questions précédentes. 
 
Conclure.
 
4) Les plaques sont déplacées de façon quelconque et ne sont plus parallèles.
 
Peut-on toujours calculer simplement le travail de la force électrostatique qui s'exerce sur l'électron allant de la plaque positive à la plaque négative ?

Exercice 9

Une d.d.p $V_{1}-V_{2}=100V$ est appliquée entre deux grilles métalliques planes, parallèles, $G_{1}$ et $G_{2}.$ 
 
Entre ces deux grilles règne un champ électrostatique uniforme ; il est nul en dehors de cette zone. 
 
Des électrons, émis par un canon à électrons suivant les lignes de champ, traversent la grille $G_{1}$ avec la vitesse $V_{1}.$
 
1) Quelle est la vitesse $V_{1}$ minimale des électrons qui parviennent à traverser la grille $G_{2}$ ?
 
2) Quelle est la vitesse $V_{2}$ d'un électron traversant $G_{2}$ après avoir traversé $G_{1}$ avec la vitesse $V_{1}=9\cdot10^{6}m\cdot s^{-1}$ ?
 
3) Dans les conditions de la deuxième question, un électron rencontre un neutron immobile se trouvant au voisinage de $G_{2}.$ 
 
Le choc est élastique, et l'électron repart avec une vitesse de sens opposé . 
 
Avec quelle vitesse retraverse-t-il $G_{1}$ ?
 
On fera les approximations légitimes.
 
Données : 
 
$m_{e}=9.1\cdot10^{-31}kg$ ; $m_{n}=1\ 840m_{e}.$
 
On indique qu'au cours d'un choc élastique il y a conservation de l'énergie cinétique et conservation de la quantité de mouvement du système (électrons, neutron).

Exercice 10

Deux plaques métalliques verticales parallèles $A$ et $B$ séparées d'une distance $d=3.45cm$ sont portées aux potentiels $V_{A}=-500V$ et $V_{B}=+500V.$ 
 
Ces deux plaques forment un condensateur plan.
 
On rappelle que la tension $U_{AB}=V_{A}-V_{B}$, et on donnera un nombre correct de chiffres significatifs
 
1. Donner les caractéristiques (sens, direction et valeur) du champ électrique entre les armatures du condensateur et dessiner quelques lignes de champs
 
2. On insère entre les $2$ plaques un fil de masse négligeable auquel est accrochée une petite boule de masse $m=2.5g.$ 
 
Initialement la boule ne porte pas de charges électriques et le pendule ainsi formé est vertical.
 
On apporte ensuite à la boule une charge $q=-0.50\mu C.$ 
 
Le pendule s'incline alors d'un angle $\alpha30^{\circ}$ vers la droite par rapport à la position précédente.
 
2.1 Sur une autre figure, dessiner le pendule incliné en équilibre ainsi que les forces exercées sur la boule.
 
2.2 Calculer l'intensité du champ électrique pour que le fil s'incline d'un angle $\alpha=30^{\circ}$ vers la droite par rapport à la verticale.
 
On prendra $g=10m\cdot s^{-2}$
 
2.3 De quel angle le fil s'incline-t-il par rapport à la verticale Si le champ a une valeur de $1.0\cdot10^{4}V\cdot m^{-1}$ ? 
 
On prendra $g=10 m\cdot s^{-2}.$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : Réactions nucléaires - Ts

Classe: 
Terminale
 

Exercice 1

Données :
 
Unité de masse atomique : $u=1.660 54\times 10^{-27}kg$ 
 
Énergie de masse de l'unité de masse atomique : $E=931.5MeV$, $c=3.0\cdot10^{8}m\cdot s^{-1}.$
$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Nom du noyau}&\text{Radon}&\text{Radium}&\text{Hélium}&\text{Neutron}&\text{Proton}&\text{Électron}\\ \text{ou de la particule}& & & & & &\\ \hline \text{Symbole}&_{86}^{222}Rn&_{88}^{226}Ra&_{2}^{4}He&_{0}^{1}n&_{1}^{1}p&_{-1}^{0}e\\ \hline \text{Masse (en u)}&221.970&225.977&4.001&1.009&1.007&5.49\times10^{-4}\\ \hline \end{array}$$
 
1. Désintégration du radium
 
L'air contient du radon $222$ en quantité plus ou moins importante. 
 
Ce gaz radioactif naturel est issu des roches contenant de l'uranium et du radium. 
 
Le radon se forme par désintégration du radium $($lui-même issu de la famille radioactive de l'uranium $238)$, selon l'équation de réaction nucléaire suivante : 
 
$_{88}^{226}Ra\ \rightarrow\ _{86}^{222}Rn\ +\ _{2}^{4}He$
 
1.1 Quel est le type de radioactivité correspondant à cette réaction de désintégration ? 
 
Justifier votre réponse.
 
1.2 Défaut de masse
 
Donner l'expression littérale du défaut de masse $\Delta\,m$ du noyau de symbole $_{Z}^{A}X$ et de masse $m_{X}$
 
Calculer le défaut de masse du noyau de radium $Ra.$ 
 
L'exprimer en unité de masse atomique $u.$
 
1.3 Écrire la relation d'équivalence masse-énergie.
 
1.4 Le défaut de masse $\Delta\,m$ $(Rn)$ du noyau de radon $Rn$ vaut $3.04\times 10^{-27}\,kg$
 
Définir l'énergie de liaison $E_{1}$ d'un noyau. 
 
Calculer, en joule, l'énergie de liaison $E_{1}(Rn)$ du noyau de radon.
 
Vérifier que cette énergie de liaison vaut $1.71\times10^{3}MeV.$
 
En déduire l'énergie de liaison par nucléon $\dfrac{E_{1}}{A}$ du noyau de radon. 
 
Exprimer ce résultat en $MeV\cdot nucléon^{-1}.$
 
1.5 Bilan énergétique
 
Établir littéralement la variation d'énergie $\Delta\,E$ de la réaction $(1)$ en fonction de $m_{Ra}$, $m_{Rn}$ et $m_{He}$ masses respectives des noyaux de radium, de radon et d'hélium. 
 
Exprimer $\Delta\,E$ en joule $m_{X}.$

Exercice 2 Radioactivité et médecine

La médecine désigne l'ensemble des applications ou des substances radioactivités sont associées au diagnostic et à la thérapie.
 
Depuis des années $1930$, la médecine nucléaire progresse grâces à la découverte et à la maîtrise de nouveaux isotopes.
 
La radiothérapie vise à administrer un radio pharmaceutique dont les rayonnements ionisants sont destinés à traiter un organe cible dans un but curatif ou palliatif. 
 
Ainsi on utilise du rhénium $186$ dans le but de soulager la maladie rhumatoïde et du phosphore $32$ pour réduire la production excessive de globules rouges dans la moelle osseuse.
 
La première partie de cet exercice traite de l'utilisation du rhénium $186$ et la seconde partie de l'utilisation du phosphate $32.$ 
 
On s'intéresse à l'aspect physique des phénomènes, les aspects biologique ne sont pas pris en compte.
 
Données :
 
$-\ $ temps de demi-vie du rhénium $186$ : $t_{1/2}\left(_{Z}^{186}Re\right)=3.7\,j$ (jours) ;
 
$-\ $ masse molaire du rhénium $186$ : $M\left(_{Z}^{186}Re\right)=186\,g\cdot mol^{-1}$ ;
 
$-\ $ constantes radioactives : $\lambda\left(_{Z}^{186}Re\right)=2.2\cdot10^{-6}\,s^{-1}$ ;
 
$\lambda\left(_{15}^{32}P\right)=5.6\cdot10^{-7}\,s^{-1}$ ;
 
$-\ $ masse de quelque noyaux et particules : $m\left(_{15}^{32}P\right)=5.30803\cdot10^{-26}\,kg$ ;
 
$m\left(_{16}^{32}S\right)=5.30763\cdot10^{-26}\,kg$ ;
 
$m\left(_{-1}^{0}e\right)=9.1\cdot10^{-31}\,kg$ ; 
 
$-\ $ célérité de la lumière dans le vide : $c=3.0\cdot10^{8}\,m\cdot s^{-1}$ ; 
 
$-\ $ constante d'Avogadro : $N_{A}=6.0\cdot10^{23}\,mol^{-1}$
 
$-\ $ électron-volt : $1eV=1.6\cdot10^{-19}\,j.$
 
1) Injectionnintra-articulaire d'une solution
 
contenant du rhénium $186$
 
1.1 Le rhénium $186$ $(\ )$ est un noyau radio actif $\beta^{-}.$ 
 
Sur le diagramme $(N\;,\ Z)$ de la figure 3 ci-dessous ou $N$ représente le nombre de neutrons et $Z$ le nombre de protons, la courbe tracée permet de situer la vallée de stabilité des isotopes. 
 
 
Le point représentatif du noyau de rhénium $186$ est placé au-dessus de cette courbe.
 
1.1.1 Déduire de ce diagramme si cet isotope radio actif possède un excès de neutron(s) ou un excès de proton(s) par rapport à un isotope stable du même élément.
 
1.1.2 Quel nom porte la particule émise au cours d'une désintégration
 
1.2.3 Écrire l'équation de la désintégration du noyau de rhénium $186$ noté $\left(_{Z}^{186}Re\right)$ sachant que le noyau fils obtenu correspond à un isotope de l'osmium noté $\left(_{76}^{A}Os\right).$
 
En énonçant les lois utilisées, déterminer les valeurs de $A$ et de $Z.$ 
 
On admet que le noyau fils obtenu lors de cette transformation n'est pas dans un étant excité.
 
2. Injection intraveineuse d'une solution contenant du phosphore $32$
 
Carte d'identité du phosphore $32$ (tableau)
$$\begin{array}{|c|c|} \hline \text{nom de l'isotope}&\text{Phosphore }32\\ \hline \text{symbole}&_{15}^{32}P\\ \hline \text{type de radioactivité}&\beta^{-}\\ \hline \text{énergie du rayonnement}&1.7\,MeV\\ \text{émis}&\\ \hline \text{équation de la}&_{15}^{32}P\ \rightarrow\ _{16}^{32}S\ +\ _{-1}^{0}e\\ \text{désintégration}&\\ \hline \text{demi-vie}&14\text{ jours}\\ \hline \end{array}$$
 
l'injection en voie veineuse d'une solution contenant du phosphore $32$ radio actif permet dans certains cas de traiter une production excessive de globules rouges au niveau des cellules de la moelle osseuses.
 
2.1 Donner la composition du noyau de phosphore $32.$
 
2.2 A l'aide des masse données en début d'exercice et de la carte d'identité du phosphore $32$, vérifier par un calcule la valeur $E$ de l'énergie du rayonnement émis par la désintégration du phosphore $32.$ $Non\ faisable\ pour\ l'instant\;!$
 
2.3 Pour la très grande majorité d'entre eux, les noyaux fils obtenus de cette transformation ne sont pas dans un état excité.
 
A quel type de rayonnement particulièrement pénétrant le patient n'est-il pas exposé ?
 
2.4 Rappeler la loi de décroissance du nombre  $N(t)$ de noyaux radioactifs d'un échantillon en fonction de $\lambda$ et $N_{0}$ $($nombre de noyaux radio actifs à la date $t=0.)$
 
2.5 Définir le temps le temps de demi-vie radioactive $t_{1/2}$ et établir la relation qui existe entre la demi-vie et la constante de désintégration radio active $\lambda.$
 
2.6 Vérifier, par un calcul, la valeur approchée du temps de demi-vie proposée dans la carte d'identité ci-dessus.

Exercice 3

1. Temps de demi-vie
 
Le thorium $^{230}Th$ est utilisé dans la datation des coraux et concrétions carbonatées ainsi que dans la datation des sédiments marins et lacustres.
 
Dans un échantillon de $«$ thorium $230\ »$, on appelle $N(t)$ le nombre de noyaux de thorium présents à chaque date $t$ et $N_{0}$ celui des noyaux présents à la date $t_{0}=0\;an.$
 
On a représenté ci-dessous la courbe donnant le rapport $\dfrac{N(t)}{N_{0}}$
 
 
1.1 Le noyau $^{230}Th$ est un émetteur $\alpha$ et se désintègre pour donner du $_{88}Ra.$ 
 
Indiquer ce que représente $\alpha$ et écrire l'équation de la réaction nucléaire correspondante, en précisant les lois utilisées (le noyau de radium est obtenu dans un état non excité)
 
1.2 Donner la définition du temps de demi-vie $$t_{1/2}.$
 
Vérifier que sa valeur est de $7.5\times10^{4}$ années en expliquant succinctement la méthode utilisée.
 
1.3 Donner l'expression mathématique de la loi de décroissance radioactive et calculer la constante radioactive en année$^{-}.$
 
1.4 Parmi ces grandeurs :
 
l'âge de l'échantillon de noyaux la quantité initiale de noyaux. 
 
La température la nature des noyaux
 
Quelle est la seule grandeur qui fait varier le temps de demi-vie ?
 
1.5 Le thorium $^{230}Th$ fait partie de la famille radioactive de l'uranium $^{238}U.$ 
 
Une famille radioactive est composée d'un ensemble de noyaux radioactifs, tous issus d'un noyau initial instable qui, de père en fils, par désintégrations successives conduisent à un noyau stable, ici le $«$ plomb $206\ ».$ 
 
L' $«$ uranium $238\ »$, dissous à l'état de traces dans l'eau de mer, produit des atomes de $«$ thorium $230»$ suivant les réactions nucléaires suivantes :
$$_{92}^{238}U\ \rightarrow\ _{90}^{234}Th\ \rightarrow\ _{91}^{234}Pa\ \rightarrow\ _{Z_{4}}^{234}U\ \rightarrow\ _{Z_{5}}^{230}Th$$
 
Donner les valeurs de $Z_{4}$ et $Z_{5}$, en les justifiant, et indiquer le type de radioactivité pour les deux premières transformations.
 
1.6 Au début de leur formation, les concrétions carbonatées des coraux contiennent de l' $«$ uranium $238\ »$ et pas de $«$ thorium $230\ ».$ 
 
La méthode de datation de ces carbonates repose sur le rapport des nombres de noyaux : $N^{230}Th/N^{238}U.$ 
 
Ce rapport augmente au cours du temps jusqu'à $«$ l'équilibre séculaire $».$
 
Celui-ci correspond à l'état où les deux populations des noyaux d' $«$ uranium $238\ »$ et de $«$ thorium $230\ »$ ont même activité.
 
1.6.1 L'activité $A(t)$ d'une population de noyaux identiques est définie ici par :
$$A(t)=-\dfrac{\mathrm{d}N(t)}{\mathrm{d}t}$$
 
En vous aidant de la question 1.3 
 
Démontrer que $A(t)=\lambda\cdot N(t)$ pour une population de noyaux donnée.
 
1.6.2 En déduire, qu'à l'équilibre séculaire, le rapport $N^{230}Th/N^{238}U$ est constant

Exercice 4

A. Le plutonium $_{94}^{241}Pu$ est radioactif $\beta^{-}$, il donne l'américium $_{Z}^{A}Am.$
 
1) Écrire l'équation de la réaction nucléaire correspondante. 
 
Préciser les lois utilisées.
 
2) Déterminer la composition de chacun des deux noyaux $(Pu$ et $Am).$ 
 
Déduire l'origine de la particule émise $(\beta^{-}).$
 
B. le noyau $_{Z}^{A}Am$ d'américium est radioactif $\alpha.$ 
 
Il se désintègre en donnant un noyau de neptunium $(Np)$ dans son état fondamental.
 
1) Écrire l'équation de cette désintégration.
 
2) Montrer que cette réaction libère une énergie $W.$ 
 
Calculer $($en $Mev)$ l'énergie $W$ libérée par la désintégration d'un noyau d'américium.
 
On donne : 
 
$m_{\alpha}=4.0015\,u$, 
 
$m_{Am}=241.0567\,u$, 
 
$m_{Np}=237.0480\,u$, 
 
$1\,u=931.5,Mev\cdot c^{-2}$
 
3) Le noyau $_{94}^{241}Am$ est supposé au repos. 
 
D'après les lois de conservation on montre que :
 
$m_{\alpha}\cdot E_{C\alpha}=m_{Np}\cdot E_{C_{Np}}$
 
On admet que l'énergie $W$ libérée par cette désintégration est communiquée totalement aux particules formées sous forme d'énergie cinétique. 
 
$W=E_{C\alpha}+E_{C_{Np}}$
 
Calculer $($en $Mev)$ $E_{C\alpha}$ et $E_{C_{Np}}.$
 
4) A une date $t_{0}=0s$, on dispose d'un échantillon contenant $N_{0}$ noyaux d'américium $_{95}^{241}Am.$
 
A différents dates $t$, on mesure, à l'aide d'un compteur de Geiger, son activité A. 
 
On obtient la courbe représentée ci-dessous : $-Ln(A)=f(t)$
 
a) Définir l'activité d'une substance radioactive, donner son unité.
 
En utilisant la loi de décroissance radioactive : $N=N_{0}\cdot e^{-\lambda\,t}$, 
 
Montrer que $-Ln(A)=\lambda\,t=–Ln(A_{0}).$
 
b) Déterminer graphiquement :
 
$-\ $ La valeur de la constante radioactive $\lambda$ de $_{95}^{241}Am.$ 
 
Déduire sa période $T.$
 
$-\ $ L'activité $A_{0}$ de l'échantillon d'américium $_{95}^{241}Am.$ 
 
Déduire $N_{0}.$
 
$-\ $ L'activité actuelle. 
 
Calculer l'âge de l'échantillon d'américium.
 
 

Exercice 5 : L'age de la terre

La détermination de l'âge de la Terre a commencé vers le $XVI^{ième}$ siècle, on
l'estimait alors autour de $5\ 000$ ans. 
 
Au $XIX^{ième}$ siècle, des scientifiques admettaient un âge d'environ $100$ millions d'années.
 
La découverte de la radioactivité, par $H.$
 
Becquerel en $1896$, bouleversa toutes les données connues.
 
La datation à l'uranium-plomb permit de déterminer assez précisément l'âge de la Terre.
 
Nous proposons de comprendre cette technique de datation.
 

I. Étude de la famille uranium $238$ $–$ plomb $206$

Le noyau d'uranium $238$, naturellement radioactif, se transforme en un noyau de plomb $206$, stable, par une série de désintégrations successives. 
 
Nous allons étudier ce processus.
 
$($On ne tiendra pas compte de l'émission $\gamma).$
 
1) Dans la première étape, un noyau d'uranium $_{92}^{238}U$ subit une radioactivité $\alpha.$ 
 
Le noyau fils est du thorium $($symbole $Th).$
 
a) Qu'est-ce qu'un noyau radioactif ?
 
b) Écrire l'équation de la réaction nucléaire en précisant les règles utilisées.
 
c) Calculer l'énergie libérée au cours de cette désintégration en joule puis en $Mev.$ 
 
On donne :
$$\begin{array}{|c|c|c|c|} \hline \text{Symbole du noyau}&_{92}^{238}U&_{2}^{4}He&_{Z}^{A}Th\\ \hline \text{Masse du noyau (en u)}&238.0508&4.0015&234.0436\\ \hline \end{array}$$
 
$1\,u=1.66\cdot10^{-27}Kg$ et $1\,ev=1.6\cdot10^{-19}J.$
 
2) Dans la deuxième étape, le noyau de thorium $234$ se transforme en un noyau de protactinium $_{91}^{234}Pa.$ 
 
L'équation de la réaction nucléaire est : $_{90}^{234}Th\ \rightarrow\ _{91}^{234}Pa\ +\ _{-1}^{0}e$
 
a) Donner le type de radioactivité correspondant à cette transformation et préciser son origine.
 
b) L'équation globale du processus de transformation d'un noyau d'uranium $238$ en un noyau de plomb $206$ est : $_{92}^{238}U\ \rightarrow\ _{82}^{206}Pb\ +\ x\;_{-1}^{0}e\ +\ y\;_{2}^{4}He$
 
Déterminer, en justifiant, le nombre de désintégrations $\alpha$ et $\beta^{-}$ de ce processus.

II. Géochronologie :

On a constaté d'une part, que les minéraux d'une même couche géologique, donc du même âge, contiennent de l'uranium $238$ et du plomb $206$ en proportions remarquablement constantes, et d'autre part que la quantité de plomb dans un minéral augmente proportionnellement à son âge relatif.
 
Si on mesure la quantité de plomb $206$ dans un échantillon de roche ancienne, en considérant qu'il n'y en avait pas initialement, on peut déterminer l'âge du minéral à partir de la courbe de décroissance radioactive du nombre de noyaux d'uranium $238.$
 
Étudions un échantillon de roche ancienne dont l'âge, noté terre, correspond à celui de la Terre.
 
1) On considère la courbe de décroissance radioactive du nombre $N_{U}(t)$ de noyaux d'uranium $238$ dans un échantillon de roche ancienne. (figure 1).
 
Sachant que $\mathrm{d}N_{U}$ est le nombre de noyaux qui se désintègrent pendant l'intervalle de temps $\mathrm{d}t.$
 
a) Prélever à partir du graphe, la quantité initiale $N_{U}(0)$ de noyaux d'uranium.
 
b) Montrer que $N_{U}(t)$ vérifie l'équation différentielle $\dfrac{\mathrm{d}N_{U}}{\mathrm{d}t}+\lambda\,N_{U}=0$ avec $\lambda$ est la constante radioactive de l'uranium $238.$
 
c) Sachant que la solution de l'équation différentielle précédente s'écrit sous la forme $N_{U}(t)=B\cdot e^{-t/\tau}$, montrer que $B=N_{U}(0)$ et que $\lambda=\dfrac{1}{\tau}$
 
d) Déterminer à partir du graphe la constante de temps $\tau$ de l'uranium $238.$
 
e) Définir la demie-vie $T$ et établir une relation entre $T$ et $\tau.$ 
 
Calculer $T.$ 
 
Retrouver la valeur de $T$ graphiquement.
 
2) La détermination du nombre de noyaux d'uranium $238$ est effectuée à l'aide d'un compteur de Geiger Müller qui mesure l'activité d'un échantillon d'une substance radioactive.
 
a) Définir l'activité radioactive. 
 
Calculer, en becquerel, l'activité initiale de l'uranium $238.$
 
$($une année$=365.25\cdot24.3600\,s=3.15\cdot10^{7}s.)$
 
b) Déterminer graphiquement et par calcul l'activité de l'uranium à $t=15\cdot10^{9}$ années.
 
3) La quantité de plomb mesurée dans la roche à la date $t_{Terre}$, notée $N_{Pb}(t_{Terre})$, est égale à $2.5\cdot10^{12}$ atomes.
 
a) Établir la relation entre $N_{U}(t_{Terre})$, $N_{U}(0)$ et $N_{Pb}(t_{Terre}).$
 
Calculer la quantité $N_{U}(t_{Terre})$ de noyaux d'uranium.
 
b) Déterminer l'âge $t_{Terre}$ de la Terre.

Exercice 6 Fusion Deutérium Tritium

La fusion nucléaire, c'est le Diable et le Bon Dieu !
 
Le Bon Dieu dans les étoiles où elle fait naître tous les atomes, jusqu'à ceux de la vie. 
 
Mais le Diable sur Terre où elle fut utilisée à fabriquer des bombes qui pourraient tout anéantir, à commencer par la vie.
 
Mais alors que le diable de la destruction thermonucléaire semble rentrer dans sa boîte, la fusion nucléaire contrôlée dans les réacteurs civils ouvre des perspectives de développement économique durable à très long terme.
 
Paul-Henri Rebut,
 
L'énergie des étoiles-la fusion nucléaire contrôlée Éditions Odile Jacob $1999$ (dos de couverture).
 
Notations utilisées :
$-\ $ Particules ou noyaux $_{Z}^{A}X$ : $_{1}^{1}H$, $_{2}^{4}He$, $_{-1}^{0}e$, $_{0}^{1}n$, $_{1}^{1}p.$ 
 
$-\ $ Masse de la particule ou du noyau $_{Z}^{A}X$ : $m\left(_{Z}^{A}X\right).$
 
$-\ $ Énergie de liaison du noyau $$_{Z}^{A}X$ : $E_{\ell}\left(_{Z}^{A}X\right).$
 
1) Isotopie
 
1) a) Qu'appelle-t-on isotopes ?
 
1) b) Dans la littérature scientifique, on mentionne souvent :
 
$-\ $ le deutérium $D$ dont le noyau contient $1$ proton et $1$ neutron ;
 
$-\ $ le tritium $T$ dont le noyau contient $1$ proton et $2$ neutrons.
 
Comment doit-on noter $($dans la notation $_{Z}^{A}X)$ les noyaux $D$ et $T$ ? 
 
A quel élément chimique appartiennent-ils ?
 
2) Radioactivité
 
2) a) Qu'est-ce qu'un noyau radioactif ?
 
2) b) Le tritium $T$ est radioactif $\beta^{-}.$ 
 
Écrire l'équation de la désintégration de $T$ $($en utilisant la notation $_{Z}^{A}X).$
 
2) c) Le tritium $T$ a une demie-vie $_{1/2}=12$ ans. 
 
Que signifie cette affirmation ?
 
3) Fusion de noyaux
 
3) a) Qu'appelle-t-on réaction nucléaire de fusion ?
 
3) b) En utilisant la notation $_{Z}^{A}X.$, écrire l'équation nucléaire de la fusion $DT$, c'est-à-dire de la fusion entre un noyau de deutérium et un noyau de tritium, au cours de laquelle se forme un noyau d'hélium $_{2}^{4}He.$
 
Exprimer l'énergie $\Delta\,E$ qui peut être libérée par cette réaction en fonction des énergies de masse $E_{m}\left(_{Z}^{A}X\right)$ des particules (ou des noyaux) qui interviennent.
 
3) c) Exprimer la masse $m\left(_{Z}^{A}X\right)$ du noyau $_{Z}^{A}X$ en fonction de $m_{p}$, $m_{n}$, $Z$, $A$ et de l'énergie de liaison $E_{\ell}\left(_{Z}^{A}X\right).$
 
Pour la réaction de fusion envisagée, en déduire l'expression de $\Delta\,E$ en fonction des énergies de liaison.
 
3) d) On donne les valeurs des énergies de liaison des noyaux suivants :
 
$-\ \ E_{\ell}(D)=2.224\,Me\,V$ ;
 
$-\ \ E_{\ell}(T)=8.481\,Me\,V$ ;
 
$-\ \ E_{\ell}(42He)=28.29\,Me\,V.$
 
Calculer numériquement la valeur de $\Delta\,E.$
 
4) Conditions de la fusion $DT$
 
La fusion n'a lieu que si les deux noyaux sont en contact.
 
4) a) Les noyaux $D$ et $T$ se repoussent. 
 
Pourquoi ?
 
4) b) Pour que la fusion ait lieu, il faut que les noyaux $D$ et $T$ entrent en contact. 
 
Celui-ci n'est possible que si l'agitation thermique, c'est-à-dire l'énergie cinétique $E_{C}$ des noyaux, est suffisamment.

Exercice 7 Temps caractéristiques en physique

Les parties $1$, $2$ et $3$ de cet exercice sont indépendantes, toutefois l'objectif de cette étude expérimentale consiste, pour trois systèmes différents :
 
$\bullet\ $ d'une part à étudier un « temps » défini comme « temps caractéristique »
 
$\bullet\ $ d'autre part, à observer l'influence éventuelle sur ce temps caractéristique :
 
des grandeurs caractéristiques ; de conditions initiales ; et de paramètres extérieurs.
 
Pour chacun des phénomènes, les grandeurs caractéristiques, les conditions initiales et les paramètres extérieurs envisagés sont précisés dans le tableau de données.
 
Un échantillon de matière radioactive est placé dans la chambre d'un photomultiplicateur.
 
Un détecteur, associé au photomultiplicateur, mesure un nombre d'événements, pendant une durée $\Delta\,t$ déterminée.
 
On trace la courbe d'évolution du nombre d'événements mesuré par seconde $($noté $x)$, au cours du temps.
 
Soit $x_{0}$ la valeur de $x$ à l'instant choisi pour origine des dates.
 
On réalise des mesures avec des échantillons de radon $_{86}^{220}Rn$ et de radon $_{86}^{222}Rn$ qui sont des émetteurs $\alpha.$
 
Le tableau ci-dessous résume les conditions expérimentales de cette étude :
$$\begin{array}{|c|c|c|c|} \hline &\text{Expérience 1}&\text{Expérience 2}&\text{Expérience 3}\\ \hline \text{Grandeurs caractéristiques du système :}&\text{radon }220&\text{radon }220&\text{radon }222\\ \text{nature du noyau}& & &\\ \hline \text{Conditions initiales :}&N_{0}&N'_{0}&N''_{0}\\ \text{population initialede noyaux radioactifs}& & &\\ N_{0}\neq N'_{0}\neq N''_{0}& & &\\ \text{Paramètres extérieurs}&\text{Aucune modification}&\text{Aucune modification}&\text{Aucune modification}\\\text{des paramètres extérieurs}&\text{des paramètres extérieurs}&\text{des paramètres extérieurs}&\text{des paramètres extérieurs}\\\hline \text{Temps caractéristique}&t_{1/2}=55.5\,s&t_{1/2}=55.5\,s&t_{1/2}= ?\text{(déterminé à la question 1.3.)}\\ \hline\end{array}$$
 
Les courbes correspondant à cette étude et donnant l'évolution de $x$ au cours du temps sont représentées en annexe
 
1) Définir le temps de demi-vie (ou demi-vie).
 
2) La loi de décroissance radioactive s'écrit sous la forme $N=N_{0}\cdot e^{-\lambda\,t}$ où : $N$ est le nombre de noyaux radioactifs présents à l'instant de date $t$, $N_{0}$ est le nombre de noyaux radioactifs présents à l'instant choisi pour origine des dates $t_{0}=0\,s$, $\lambda$ est la constante radioactive. 
 
En utilisant la définition du temps de demi-vie, établir l'expression de $\lambda$ en fonction de $t_{1/2}.$
 
3) Dans le cas de l'expérience 3, déterminer graphiquement la valeur du temps de demi-vie.
 
La détermination devra apparaître clairement sur la courbe (3) de l'annexe
 
Pour cette détermination, on admettra que le nombre d'événements détectés par seconde, à l'instant de date $t$, est proportionnel au nombre de noyaux radioactifs présents dans l'échantillon, à cette même date.
 
Pour déterminer le temps de demi-vie, on peut alors utiliser la courbe $x=f(t)$ de la même façon que celle représentant le nombre de noyaux radioactifs présents dans l'échantillon en fonction du temps.
 
4) En justifiant les réponses à partir des données du tableau et du résultat obtenu à la question
 
5) Préciser :
 
$-\ $ Si les grandeurs caractéristiques ont une influence sur la valeur du temps de demi-vie ;
 
$-\ $ Si les conditions initiales ont une influence sur la valeur du temps de demi-vie.
 
 

Exercice 8

Tableaux de données :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline \text{Particule}&\text{Neutron}&\text{Hydrogène}&\text{Hydrogène}&\text{Hydrogène}&\text{Hélium}&\text{Hélium}&\text{Uranium}&\text{Xénon}&\text{Strontium}\\ \text{ou Noyau}& &1\text{ ou proton}&2\text{ ou Deutérium}&3\text{ ou Tritium}&3&4&235&  &\\ \hline \text{Symbole}&_{0}^{1}n&_{1}^{1}H&_{1}^{2}H&_{1}^{3}H&_{2}^{3}H&_{2}^{4}H&_{92}^{235}U&_{54}^{A}Xe&_{Z}^{94}Sr\\ \hline \text{Masse en }u&1.00866&1.00728&2.01355&3.01550&3.01493&4.00150&234.9942&138.8892&93.8945\\ \hline \end{array}$$
 
$$\begin{array}{|c|c|} \hline \text{Unité de masse atomique}&u=1.66\times 10^{-27}kg\\ \hline \text{Énergie de masse de l'unité de masse atomique}&E=931.5\,MeV\\ \hline \text{Électronvolt}&1\,eV=1.60\times 10^{-19}J\\ \hline \text{Vitesse de la lumière dans le vide}&c=3.00\times 10^{8}m\cdot s^{-1}\\ \hline \text{Nombre d'Avogadro}&N=6.02\cdot 10^{23} \\ \hline \end{array}$$

I. La combustion du butane $C_{4}H_{8}$ (gaz de ville) :

L'énergie dégagée au cours de la combustion complète d'une mole de butane est $Q=2878\cdot10^{3}J$ ça veut dire que la combustion complète de $56\,g$ de butane dégage une énergie de $2878\cdot10^{3}J.$

II. Fission nucléaire

Une centrale nucléaire est une usine de production d'électricité. 
 
Actuellement ces centrales utilisent la chaleur libérée par des réactions de fission de l'uranium $235$ qui constitue le "combustible nucléaire". 
 
Cette chaleur transforme de l'eau en vapeur. 
 
La pression de la vapeur permet de faire tourner à grande vitesse une turbine qui entraîne un alternateur produisant l'électricité.
 
Certains produits de fission sont des noyaux radioactifs à forte activité et dont la demi-vie peut être très longue.
 
1) Définir le terme demi-vie.
 
2) Le bombardement d'un noyau d'uranium $235$ par un neutron peut produire un noyau de strontium et un noyau de xénon selon l'équation suivante :
$$_{92}^{235}U\ +\ _{0}^{1}n\ \rightarrow\ _{Z}^{94}Sr\ +\ _{54}^{A}Xe\ +\ 3_{0}^{1}n$$
 
a) Déterminer les valeurs des nombres $A$ et $Z.$
 
b) Calculer en $MeV$ puis en joule l'énergie libérée par la fission d'un noyau d'uranium $235.$
 
Déduire L'énergie libérée en joule par la fission d'une mole d'uranium $235.$
 
c) Quelle est la masse de butane qu'on doit utiliser au cours d'une combustion complète pour produire la même quantité d'énergie libérée lors de la fission de $235\,g$ d'uranium $^{235}U.$

III. Fusion nucléaire

La fusion est la source d'énergie du soleil et des autres étoiles.
 
Pour obtenir une réaction de fusion, il faut rapprocher suffisamment deux noyaux qui se repoussent, puisqu'ils sont tous deux chargés positivement. 
 
Une certaine énergie est donc indispensable pour franchir cette barrière et arriver dans la zone, très proche du noyau, où se manifestent les forces nucléaires capables de l'emporter sur la répulsion électrostatique.
 
La réaction de fusion la plus accessible est la réaction impliquant le deutérium et le tritium.
 
C'est sur cette réaction que se concentrent les recherches concernant la fusion contrôlée.
 
La demi-vie du tritium consommé au cours de cette réaction n'est que de quelques années.
 
De plus il y a très peu de déchets radioactifs générés par la fusion et l'essentiel est retenu dans les structures de l'installation.
 
1. Le deutérium de symbole $_{1}^{2}H$ et le tritium de symbole $_{1}^{3}H$ sont deux isotopes de l'hydrogène.
 
1.1 Définir le terme de noyaux isotopes.
 
1.2 Donner la composition de ces deux noyaux.
 
2. Qu'appelle-t-on réaction de fusion ?
 
3. Écrire l'équation de la réaction nucléaire entre un noyau de Deutérium et un noyau de Tritium sachant que cette réaction libère un neutron et un noyau noté $_{Z}^{A}X.$
 
Préciser la nature du noyau $_{Z}^{A}X.$
 
4. Montrer que l'énergie libérée au cours de cette réaction de fusion est de $17.6\,MeV.$ 
 
Quelle est l'énergie libérée par la fusion d'une mole de tritium.
 
5. Quelle est la masse de butane qu'on doit utiliser au cours d'une combustion complète pour produire la même quantité d'énergie libérée lors de la fusion d'une mole de tritium.
 
6. A-t-on intérêt d'implanter en Tunisie un réacteur nucléaire. 
 
Citer les avantages et les inconvénients.

Exercice 9

On donne pour tout l'exercice : 
 
$m(Bi)=210.0535\,U$
 
$M(Po)=210.0362\,u$ ; 
 
$M(Pb)=206.0295\,u$ ; 
 
$m_{\alpha}=4.0015\,u$ ; 
 
$m_{n}=1.0086\,u$ ; 
 
$m_{p}=1.0072\,u$
 
$1\,Mev=1.6\cdot10^{-13}J$ ; 
 
$1\,u=1.66\cdot10^{-27}kg=931.5\,Mev$ ; 
 
$1$ jour$=86400\,s.$
 
Les parties $A$ et $B$ sont indépendantes.
 
A. un isotope du bismuth $_{Z}^{A}Bi$ est radioactif émetteur $\beta^{-}$ sa désintégration donne un noyau de polonium $_{84}^{210}Po.$
 
1) a) Écrire l'équation de la réaction nucléaire de désintégration du bismuth en précisant les lois utilisées.
 
b) Cette désintégration est-elle provoquée ou spontanée ? 
 
Justifier la réponse.
 
c) Quelle est l'origine de la particule $\beta^{-}$ émise.
 
2) a) Calculer, en $Mev.$ nucléon$^{-1}$, l'énergie de liaison par nucléon $E_{1}$ du noyau de bismuth utilisé.
 
b) Sachant que l'énergie de liaison du noyau de polonium est $E_{l_{2}}=1539.02\,Mev$, comparer la stabilité des noyaux de $_{Z}^{A}Bi$ et de $_{84}^{210}Po.$
 
3) A l'instant initial $t=0$, on considère un échantillon de bismuth de masse $m_{0}=1\,g$, soit $m(t)$ la masse du bismuth restant à la date $t$ $(t$ exprimée en jours$).$
 
a) donner l'expression du nombre de noyaux $N$ existant dans un échantillon de masse $m$ de bismuth en fonction de $m$, $M$ (masse molaire du bismuth) et $N$ (nombre d'Avogadro).
 
b) En appliquant la loi de décroissance radioactive, exprimer $m(t)$ en fonction de $m_{0}$, de la constante de désintégration radioactive $\lambda$ et de $t.$
 
c) Donner la définition de la période radioactive $T$ du bismuth puis calculer sa valeur (en jours) sachant que $m(t+10)=\dfrac{m(t)}{4}$ $(t$ : en jours$).$
 
d) Quelle est la masse restante de bismuth à la date $t=18$ jours.
 
e) Définir l'activité d'une substance radioactive. 
 
Déterminer l'activité radioactive $A_{0}$ de l'échantillon à la date $t=0$, puis déduire l'activité $A$ à la date $t=18$ jours $($il faut donner $A$ et $A_{0}$ en $B_{q})$
 
B. Le polonium $_{84}^{210}Po$ est radioactif émetteur $\alpha.$
 
1) Écrire l'équation de la réaction de désintégration $\alpha$ du $_{84}^{210}Po$ sachant qu'il conduit à un isotope du plomb $P_{b}.$
 
2) Calculer, en $Mev$, l'énergie $E$ libérée par cette réaction nucléaire.
 
3) En admettant que l'énergie $E$ libérée est répartie entre la particule $\alpha$ et le noyau de plomb sous forme d'énergie cinétique et que le rapport des énergies cinétiques de $\alpha$ et de $P_{b}$ est égal à l'inverse du rapport de leurs masses $\left(\dfrac{E_{C_{\alpha}}}{E_{C_{Pb}}}=\dfrac{m_{Pb}}{m\alpha}\right).$
 
Calculer en $Mev$ l'énergie cinétique de la particule $\alpha$ émise et celle $E_{C_{Pb}}$ du noyau de plomb, puis déduire la vitesse $v_{\alpha}$ de la particule $\alpha.$
 
4) En réalité, la particule $\alpha$ émise possède une énergie cinétique $E'_{C_{\alpha}}$ tel que $E'_{C_{\alpha}}<E_{C_{\alpha}}.$
 
a) Expliquer brièvement cette différence.
 
b) Sachant que l'énergie du photon $\lambda$ émis est $W_{\lambda}=0.918\,Mev$, déduire la valeur de $E'_{C_{\alpha}}$ et la longueur d'onde du photon $\lambda.$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Niveaux d'énergie de l'atome - Ts

Classe: 
Terminale
 

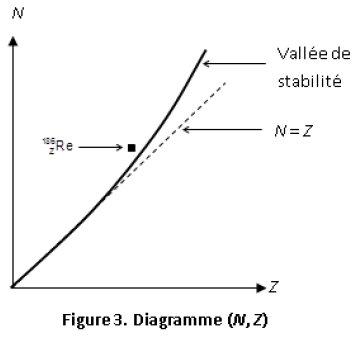
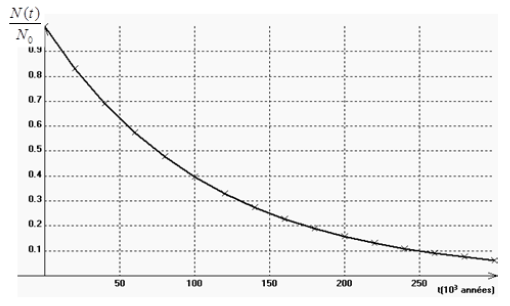
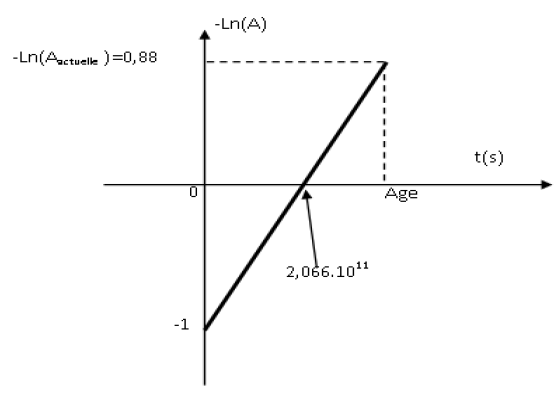
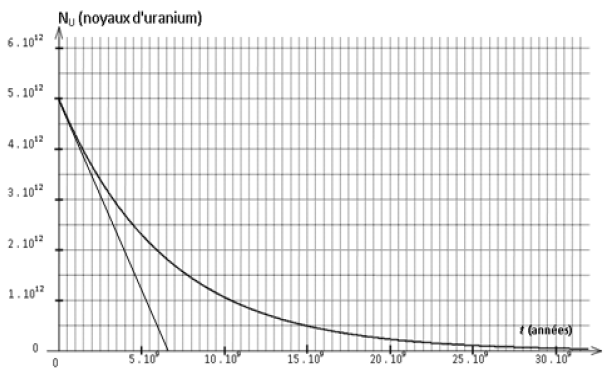
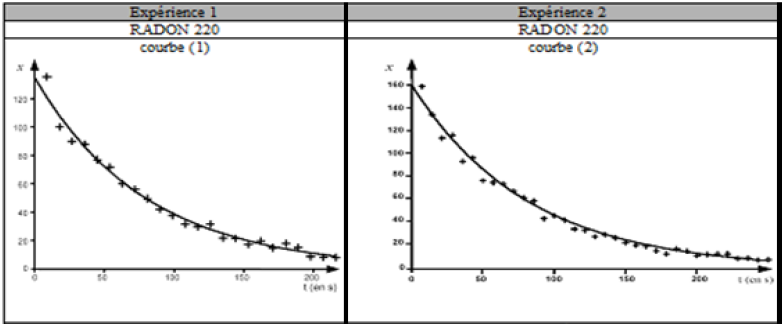
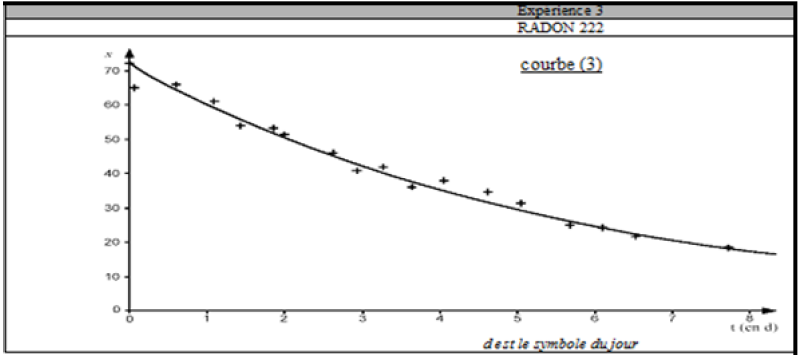
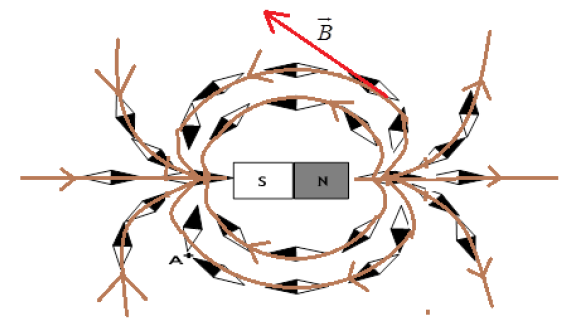
Exercice 1

Les énergies des différents niveaux, exprimés en électron-volt, sont données par la formule :
 
$E_{n}=\dfrac{-13.6}{n^{2}}$
 
1) Calculer les énergies correspondant à $n=1\;,\ 2\;,\ 3$ et $\infty$ et représenter le diagramme des niveaux d'énergie de l'atome d'hydrogène.
 
2) Quelle est l'énergie minimale que l'on doit fournir à un atome d'hydrogène pour qu'il passe de l'état fondamental à un état excité ? 
 
La transcrire sur le diagramme.
 
3) Cette énergie est apportée à l'atome par une radiation lumineuse monochromatique.
 
Calculer sa longueur d'onde.
 
4) Calculer la longueur d'onde de la radiation susceptible d'ioniser l'atome d'hydrogène

Exercice 2

1) Rutherford a décrit l'atome d'hydrogène par le modèle planétaire : 
 
l'électron a un mouvement circulaire, de rayon $r$, autour d'un noyau constitué de proton.
 
La force électrique subie l'électron est dirigée selon la droite proton-électron, attractive de valeur $F=\dfrac{ke^{2}}{r^{2}}$
 
La force gravitationnelle est négligeable devant cette force
 
a) Montrer que le mouvement de l'électron est uniforme
 
b) Établir l'expression de la vitesse $v$ en fonction de $k$, $e$, $r$ et $m$
 
c) Exprimer son énergie cinétique en fonction de ces mêmes paramètres.
 
d) Exprimer en énergie mécanique $E$ en fonction de $k$, $e$ et $r$ sachant que son énergie potentielle est : $E_{p}=-\dfrac{ke^{2}}{r}$
 
Quelle est sa limite quand $r$ tend vers l'infini
 
2) Différents faits expérimentaux ont conduit Niels Bohr à formuler l'hypothèse suivante :
 
l'électron ne se déplacer que sur certains cercles dont les rayons $r_{n}$ obéissent à la loi :
 
$v_{n}r_{n}=\dfrac{nK}{m}$ ; $K$ constante universelle : 
 
$K=1.054\cdot10^{-34}J\cdot s$
 
$n$ : nombre entier $n\geq 1$ ; 
 
$v_{n}$ vitesse de l'électron sur le cercle de rayon $r_{n}$
 
a) Déterminer l'expression de $r_{n}$ en fonction des constantes $k$, $K$, $m$, $e$ et $n.$ 
 
Exprimer $r_{n}$ en fonction de $r_{1}.$ 
 
Calculer $r_{1}$
 
b) Déterminer l'expression de $E_{n}$, énergie mécanique de l'électron sur le cercle de rayon $r_{n}$, en fonction des mêmes paramètres
 
Exprimer $E_{n}$ en fonction de $E_{1}$
 
c) Calculer $E_{1}$ et $E_{2}$ en électronvolts. 
 
Quelle cause peut faire passer l'énergie de l'électron de $E_{1}$ à $E_{2}.$
 
$m_{e}=9.109\cdot10^{-31}Kg$ ; 
 
$e=1.602\cdot10^{-19}$ ; 
 
$k=9.000\cdot10^{9}SI$
 
 

Exercice 3 L'atome d'hydrogène

Diagramme d'énergie de l'atome d'hydrogène obtenu à partir de la formule : $E_{n}=-\dfrac{13.6}{n^{2}}(en\ eV)$
 
 
1) Quel est le nom du nombre noté $"n"$ qui apparaît dans le diagramme ?
 
2) Quant dit-on qu'un atome est dans son état fondamental ? 
 
Quel est l'état fondamental de l'atome d'hydrogène ? 
 
Le noter sur schéma.
 
3) Considérons une population d'atomes d'hydrogène au repos, sans apport d'énergie de la part extérieur.
 
Dans quel état se trouvent les atomes (ou du moins l'immense majorité) ?
 
4) Que représente le niveau noté : $n=\infty$ ? 
 
Noter son nom sur le schéma.
 
5) Quelle énergie minimale, en $eV$, faut-il fournir à un atome d'hydrogène pour l'ioniser lorsqu'il est dans son état fondamental ?
 
6) Un atome d'hydrogène à la configuration électronique telle que : $n=3$
 
$\bullet\ $ Est-il dans son état fondamental ? 
 
Comment s'appelle un tel état?
 
$\bullet\ $ Le représenter par un petit point sur le diagramme précédent
 
7) L'atome d'hydrogène peut-il se trouver dans un état situé entre les niveau $n=1$ et $n=2$ ?
 
8) L'atome d'hydrogène est excité sur le niveau : $n=3$ 
 
$\bullet\ $ Comment peut-on exciter cet atome ?
 
$\bullet\ $ Montrons qu'en se dés-excitant vers le niveau $2$, il émet un photon de longueur d'onde : $\lambda=656.1\,nm.$
 
Cette radiation est-elle située dans les $X$, les $UV$, le visible ou $l'IR$ ?
 
$\bullet\ $ Représenter par un flèche, sur le diagramme précédent, la transition correspondant à cette dés excitation.
 
9) Une radiation émise par l'atome d'hydrogène a une égale à : $E+2.54eV$
 
$\bullet\ $ cette radiation émise par l'atome d'hydrogène fait partie de la série de balmer $($retour au niveau $n=2.)$
 
Déterminer la transition électronique correspondant à l'émission de cette radiation.
 
La noter sur le schéma.
 
$\bullet\ $ Calculer la longueur d'onde correspondante.
 
10) Une lampe à décharge à hydrogène émet-elle un spectre continu de radiation ou un spectre discontinu ?

Exercice 4

Données : 
 
célérité de la lumière dans le vide : $3\cdot10^{8}m/s$ ; 
 
constante de Planck : $h=6.62\cdot10^{-34}\,js$ ; 
 
charge élémentaire : $e=1.6\cdot10^{-19}C$ ; 
 
masse de l'électron $m=9\cdot10^{-31}\,Kg.$
 
La figure représente un diagramme très simplifié des niveaux d'énergie de l'atome de lithium de numéro atomique $Z=3$, de formule électronique $K^{2}L^{1}.$
 
 
On considère les quatre transitions représentées sur le diagramme.
 
Les longueurs d'ondes correspondantes sont : 
 
$\lambda1_{1}=671\,nm$ ; 
 
$\lambda_{2}=812\,nm$ ; 
 
$\lambda_{3}=323\,nm$ et 
 
$\lambda_{4}=610\,nm.$
 
1) Expliquer brièvement niveau d'énergie et spectres de raies.
 
2) Montrer qu'entre l'énergie $E(en\ eV)$ d'un photon et sa longueur d'onde $\lambda$ il existe la relation $E=\dfrac{1240}{\lambda}.$
 
$\lambda$ étant exprimé en $nm$ et $E$ en $eV.$
 
$-\ $ Déterminer l'énergie $(eV)$ des photons émis lors de chacune des $4$ transitions.
 
3) L'énergie du niveau $I$ vaut $E_{1}=-5.39\,eV.$ 
 
C'est l'énergie de l'électron externe dans son état fondamental. 
 
Affecter l'énergie $E_{i}(eV)$ à chaque niveau du diagramme.
 
Pour quelle valeur de la longueur d'onde des radiations incidentes les atomes de lithium subiront-ils une ionisation à partir de l'état fondamental ?

Exercice 5 : Niveaux d'énergie de l'atome d'hydrogène

On s'intéresse dans ce qui suit aux niveaux d'énergie des atomes d'hydrogène et de sodium, tous deux éléments de la première colonne du tableau de classification périodique. 
 
1. Les niveaux d'énergie de l'atome d'hydrogène sont donnés par la relation : $E_{n}=-\dfrac{13.6}{n^{2}}$ où $E_{n}$ en $eV$ et $n$ un entier naturel non nul.
 
1.1 Déterminer l'énergie minimale en $eV$, qu'il faut fournir à l'atome d'hydrogène pour l'ioniser dans les cas suivants :
 
1.1.1 L'atome d'hydrogène est initialement à son état fondamental $(n=1)$
 
1.1.2 L'atome d'hydrogène est à l'état excité correspondant au niveau d'énergie $(n=2).$
 
1.2 Faire le schéma du diagramme des niveaux d'énergie de l'atome d'hydrogène en utilisant l'échelle :
 
$1\,cm$ pour $1eV.$ 
 
On ne représentera que les six premiers niveaux.
 
2. On donne ci-dessous le diagramme simplifié des niveaux d'énergie de l'a tome de sodium (l'échelle n'est pas respectée).
 
 
L'état fondamental correspond au niveau d'énergie $E_{1}.$ 
 
Les niveaux d'énergie $E_{2}$ et $E_{3}$ correspondant à des états excités.
 
2.1 Lorsque l'atome passe de $E_{2}$ à $E_{1}$ il émet une radiation de longueur d'onde $\lambda_{1}=589\,nm$ ; lorsqu'il passe de $E_{3}$ à $E_{2}$, il émet une radiation de longueur d'onde $\lambda=568.8nm.$
 
En expliquant le raisonnement, calculer la différence d'énergie $(E_{3}-E_{1})$ en $eV.$
 
2.2 Lorsque l'atome, initialement dans son état fondamental, est éclairé par un faisceau monochromatique de longueur d'onde $\lambda$ convenable, il peut directement passer du niveau d'énergie $E_{1}$ au niveau d'énergie $E_{3}.$
 
Exprimer la longueur d'onde $\lambda$ de ce faisceau en fonction des longueurs d'onde $\lambda_{1}$ et $\lambda_{2}.$ 
 
Faire l'application numérique

Exercice 6

La mécanique quantique montre que l'état fondamental de l'atome d'hydrogène est caractérisé par une énergie $E_{1}=-13.6ev$ et chaque niveau excité $n>1$ est définie par une énergie $E_{n}=-\dfrac{E_{0}}{n^{2}}$ $(n$ est un entier naturel positif$)$ avec $E_{0}=13.6ev.$
 
1) A quoi correspond l'énergie $E_{0}$ ?
 
2) Quelle relation simple existe entre l'énergie de transition $\Delta\,E$ d'un niveau $n$ à un niveau $p$ et la longueur d'onde du photon émis ou absorbé. 
 
(Traiter chaque cas à part)
 
3) a) Montrer que pour une transition d'un niveau $p$ à un niveau $n$ tel que $p>n$, on peut écrire la relation $\dfrac{1}{\lambda}=R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right).$
 
b) Vérifier que $R_{H}$ (appelée constante de Rydberg) vaut $R_{H}=1.10\cdot10^{+7}\,m^{-1}$
 
c) Dans la série de Balmer $($le retour au niveau $n=2)$ l'atome $H$ émet $1$ spectre contenant $4$ raies visibles, on se propose de calculer deux longueurs d'ondes de $2$ raies de ce spectre correspondant à $p=3(\lambda_{3.2})$ et $p=4(\lambda_{4.2}).$ 
 
Sans faire de calcul, et en utilisant $\Delta\,E$, comparer $\lambda_{3.2}$ et $\lambda_{4.2}$ puis calculer leurs valeurs.
 
4) L'atome $H$ est dans son état fondamental $(n=1)$, on l'excite à l'aide d'un photon incident d'énergie $W=130.8\,ev.$ 
 
Que se passe-t-il ? 
 
Calculer $(en\ ev)$ l'énergie cinétique $E_{c}$ de l'électron de $H$ éjecté.
 
5) si l'atome entre en choc inélastique avec un électron ayant une énergie cinétique égale $11ev$, que se passe-t-il ?

Exercice 7

Données :
 
charge élémentaire : $e=1.6\cdot10^{-19}C$ 
 
Constante de Planck : $h=6.62\cdot10^{-34}J\cdot s$
 
célérité de la lumière dans le vide : $c=3\cdot10^{8}m\cdot s^{-1}$
 
$1eV=1.6\cdot10^{-19}J$ 
 
$1nm=10^{-9}m$
 
Le spectre de l'atome d'hydrogène est obtenu par décharge électrique dans un tube contenant du dihydrogène sous faible pression. 
 
Deux électrodes situées à chaque extrémité du tube permettent d'appliquer une différence de potentiel.
 
Lorsque les paramètres (d.d.p, température, pression) sont correctement fixés, on observe l'émission de lumière dont l'analyse est faite à l'aide d'un spectroscope.
 
Le spectre obtenu est constitué, dans sa partie visible, de quatre raies notées $H_{\alpha}$ $H_{\beta}$ $H_{\lambda}$ $H_{\delta}$ de longueurs d'onde respectives dans le vide : 
 
$656.27\,nm$ ; 
 
$486.13\,nm$ ; 
 
$434,05\,nm$ ; 
 
$410.17\,nm.$
 
 
Spectre d'émission de l'atome d'hydrogène
 
1. Sachant que les couleurs des raies émises sont bleue, indigo, rouge et violette, restituer à chaque radiation sa couleur.
 
2. En 1885, le physicien suisse Balmer, remarque que les longueurs d'onde $\lambda$ de ces quatre radiations satisfont à une relation empirique :
$$\lambda=\lambda_{0}\dfrac{n^{2}}{n^{2}-4}$$
 
$\lambda_{0}=367.7nm$, $n$ est un nombre entier naturel non nul $(n\in\mathbb{N^{\ast}})$
 
2.1 Indiquer la plus petite valeur possible de $n.$ 
 
En déduire la longueur d'onde de la raie correspondante.
 
2.2 Quelles valeurs doit prendre $n$ pour retrouver les autres raies visibles du spectre ?
 
3. Les niveaux d'énergie quantifiés de l'atome d'hydrogène sont donnés par la relation :
 
$E_{n}=-\dfrac{E_{0}}{n^{2}}(eV)\quad\left\lbrace\begin{array}{lcl} E_{0}&=&13.6\,eV\\ n&\text{est}&\text{un nombre entier naturel non nul.} \end{array}\right.$
 
Pour $n=1$ l'énergie de l'atome est minimale, l'atome est dans son état fondamental.
 
Pour toutes les autres valeurs de $n(n\geq 2)$, l'atome est dans un état excité.
 
3.1 Expliquer brièvement le terme “ niveau d'énergie quantifié ”.
 
Que représente $E_{0}$ pour l'atome d'hydrogène ?
 
3.2 Établir, en fonction de $n$, la fréquence $v_{n\;,\ 2}$ $($exprimée en $Hz)$ des radiations émises lorsque cet atome passe d'un état excité $n>2$ à l'état excité $n=2.$
 
3.3 Retrouver l'expression empirique de Balmer :
$$\lambda=\lambda_{0}\dfrac{n^{2}}{n^{2}-4}$$
 
$\lambda$ étant exprimée en $nm.$
 
A quelle transition correspond l'émission de la radiation de longueur d'onde $\lambda_{0}$ ? 
 
Justifier la réponse.
 
3.4 Tracer le diagramme représentant les transitions entre les différents niveaux d'énergie de l'atome d'hydrogène pour les quatre raies $H_{\alpha}$, $H_{\beta}$, $H_{\lambda}$, $H_{\delta}$ de la série de Balmer.
 
4.1 Quelle est l'énergie cinétique minimale d'un électron projectile capable de provoquer par choc l'excitation d'un atome d'hydrogène de son état fondamental à son deuxième état excité ?
 
4.2 Sous quelle tension minimale cet électron projectile, initialement au repos, a-t-il été accéléré ?
 
4.3 L'atome d'hydrogène précédemment excité revient à son état fondamental avec émission de deux photons. 
 
Déterminer les longueurs d'onde de ces deux photons.

Exercice 8 

Données :
 
$h=6.62\times10^{-34}J\cdot s$ ; 
 
$c=3.00\times10^{8}m\cdot s^{-1}$ 
 
et $e=1.60\times10^{-19}C$
 
Les lampes à vapeur de lithium contiennent de la vapeur de lithium à très faible pression. 
 
Cette vapeur est excitée par un faisceau d'électrons qui traverse le tube. 
 
Les atomes de lithium absorbent l'énergie des électrons. 
 
L'énergie est restituée lors du retour à l'état fondamental sous forme de radiations lumineuses.
 
On représente le diagramme des niveaux d'énergie de l'atome de lithium (figure 1) de numéro atomique $Z=3.$ 

 
L'analyse du spectre d'émission d'une lampe à vapeur de lithium révèle la présence de raies de longueur d'onde $\lambda$ bien définie.
 
On donne le spectre d'émission et le spectre d'absorption de l'atome de lithium (figure 2).

 
1) Préciser le spectre d'émission de l'atome de lithium et le spectre d'absorption.
 
2) Représenter le schéma du montage qui permet d'obtenir le spectre d'émission.
 
3) A l'aide du spectre d'émission, interpréter la quantification de l'énergie de l'atome de lithium.
 
4) L'énergie du l'état fondamental vaut $E_{1}=-5.39eV.$ 
 
(C'est l'énergie de l'électron de la couche externe dans son état fondamental).
 
a) Prélever les valeurs des longueurs d'onde $\lambda_{1}$ ; $\lambda_{2}$ et $\lambda_{3}$
 
b) Montrer que la longueur d'onde $\lambda$ du photon émis lors d'une transition du niveau $n$ au niveau $p(n>p)$ est $\lambda=\dfrac{1241}{E_{n}-E_{p}}$ avec $\lambda$ en $nm$ et $E_{n}-E_{p}$ en $ev.$
 
c) trouver les valeurs d'énergie des autres niveaux sachant que la longueur d'onde du photon émis lors d'une transition du niveau :
 
$\bullet\ \ 3$ au niveau est égale à $812nm.$
 
$\bullet\ \ 4$ au niveau est égale à $323nm.$
 
5) définir l'énergie d'ionisation de l'atome de lithium. 
 
Donner sa valeur.
 
6) L'atome de sodium, considéré maintenant à l'état fondamental, reçoit une radiation lumineuse dont le quantum d'énergie a une longueur d'onde $\lambda$ égale à :
 
a) $220nm.$
 
b) $300nm$

Exercice 9

Dans le spectre d'émission de l'atome d'hydrogène on trouve les quatre raies suivantes, caractérisées par leur longueur d'onde :
 
$\lambda_{1}=410\,nm$ (violet), 
 
$\lambda_{2}=434.1\,nm$ (indigo), 
 
$\lambda_{3}=486.1\,nm$ (bleu) et 
 
$\lambda_{4}=656.3\,nm$ (rouge). 
 
On donne le diagramme des niveaux d'énergie de l'atome d'hydrogène.
 
1) Justifier la discontinuité du spectre d'émission.
 
a) Que signifie l'état fondamental de l'atome ?
 
b) Définir l'énergie d'ionisation de l'atome d'hydrogène. 
 
Donner sa valeur.
 
2) a) Calculer la longueur d'onde maximale $\lambda_{max}$ correspondant à la transition de l'électron d'un niveau $n>2$ au niveau $2.$ 
 
Déduire que $\lambda_{max}=\lambda_{4}.$
 
b) A quelle transition correspond chacune des radiations de longueur d'onde $\lambda_{1}$, $\lambda_{2}$ et $\lambda_{3}.$
 
3) a) L'atome d'hydrogène est dans son niveau d'énergie $E_{2}\ (n=2)$, reçoit un photon incident de longueur d'onde $\lambda=486.1\,nm.$ 
 
Ce photon est-il absorbé ? 
 
justifier sans calcul.
 
b) L'atome d'hydrogène est dans son état fondamental, reçoit :
 
$\bullet\ $ Un photon d'énergie $11\,ev.$
 
$\bullet\ $ Un électron incident d'énergie cinétique $11\,ev.$
 
$\bullet\ $ Un photon d'énergie $14.3\,ev.$
 
Dire, en le justifiant ce qui se passe dans chaque cas (dans le cas où l'atome est ionisé donner l'énergie cinétique de l'électron émis).

Exercice 10 Étoile Vega et son spectre

L'étoile Véga se trouve dans la constellation de la Lyre. 
 
Elle émet de la lumière que l'on peut décomposer. 
 
On obtient un spectre dont voici sa représentation :
 
La première raie à $x=0\,cm$ correspond à la longueur d'onde $\lambda=400\,nm$ et la dernière raie correspondant à $x=8.5\,cm$ est la longueur d'onde $\lambda=700\,nm.$
 
A chaque raie correspond une abscisse $x$ sur l'axe orienté. 
 
La longueur d'onde $\lambda$ est fonction affine de $x$ de la forme $\lambda=ax+b.$
 
1) Quelle est la nature du spectre ?
 
2) En déduire si l'étoile possède une atmosphère.
 
3) Tracer, rapidement, avec seulement $2$ points, $\lambda$ en fonction de $x.$
 
4) En déduire le coefficient directeur de la droite ainsi que son ordonnée à l'origine. Donner alors l'équation numérique de $\lambda=ax+b$
 
5) A l'aide de l'équation numérique trouver les valeurs des longueurs d'onde émises par l'étoile.
 
6) Y-a-t-il de l'hydrogène ou de l'hélium dans l'étoile Véga ? 
 
Conclure.
 
Données :
 
$-\ $ longueurs d'onde en $nm$ émise par l'élément $H$ : $398\ –\ 410\ -\ 434\ -\ 486$
 
$-\ $ longueurs d'onde en $nm$ émise par l'élément $He$ : $380\ –\ 403\ –\ 414\ -\ 447$

Exercice 11

On donne les spectres de deux éléments, le titane et le nickel, ainsi que le spectre d'une étoile. 
 
Ces spectres ont été réalisés dans les mêmes conditions et les réglages du spectroscope étaient les mêmes.
 
1) Quel nom donne-t-on aux spectres des deux éléments ?
 
2) Expliquer l'allure du spectre de l'étoile en utilisant les mots ou les expressions suivantes : spectre (ou fond) continu ; raies d'absorption.
 
3) La comparaison du spectre de l'étoile et des spectres de chaque élément permet de faire une affirmation relative à la composition chimique de l'étoile. 
 
Laquelle ?

Exercice 12

L'énergie des niveaux de l'atome $H$ est donnée par $E_{n}=-\dfrac{13.6}{n^{2}}(eV)$, avec $n$ entier non nul.
 
1. Représenter les $6$ premiers niveaux sur un diagramme à l'échelle $1\,cm$ pour $1eV.$ 
 
Ajouter le niveau $E=0eV$ correspondant à l'atome ionisé.
 
2. Calculer la longueur d'onde $\lambda$ d'un photon capable de provoquer la transition de l'atome $H$ de son niveau fondamental au niveau $n=3.$
 
Représenter cette transition sur le diagramme précédent.
 
3. Calculer la longueur d'onde correspondant à la transition du niveau $3$ au niveau $2.$ 
 
Donner le résultat en $nm.$ 
 
Cette transition correspond-elle à un photon émis ou absorbé ?
 
4. Cet atome étant de nouveau dans son état fondamental, il absorbe un photon de longueur d'onde égal à $8.5\cdot10^{-8}m.$ 
 
Comparer cette énergie à celle du niveau fondamental.
 
Montrer alors que l'électron est arraché à l'atome. Comment nomme-t-on ce phénomène ?
 
5. Quelle est l'énergie d'ionisation de l'atome d'hydrogène ?
 
6. Établir l'expression littérale de la longueur d'onde des radiations émises lorsque cet atome passe d'un état excité tel que $n>2$ à l'état $n=2$ correspondants à la série nommée série de Balmer.
 
7. L'analyse du spectre d'émission de l'atome d'hydrogène révèle la présence de radiations de longueur d'onde : $656\,nm\left(H_{\alpha}\right)$, $486\,nm\left(H_{\beta}\right)$, $434\,nm\left(H_{\lambda}\right)$, $410\,nm\left(H_{\sigma}\right)$
 
7.1. Déterminer à quelles transitions correspondent ces radiations de la série de Balmer.
 
7.2. Représenter ces transitions sur le diagramme des niveaux d'énergie de l'hydrogène.
 
8. Un photon d'énergie $7eV$ arrive sur un atome d'hydrogène. 
 
Que se passe-t-il si l'atome est
 
a) dans l'état fondamental 
 
b) dans l'état excité $n=2.$
 
9. Un gaz d'hydrogène atomique est porté à la température $2500\,K.$ On admet que les atomes d'hydrogène se trouvent dans leur état fondamental. Parmi les photons suivants dont on donne l'énergie quels sont ceux qui sont susceptibles d'être absorbés par les atomes : $8.5eV$, $10.2eV$, $13.2eV$, $13.4eV$, $14.5eV.$

Exercice 13

Dans le spectre d'émission de l'hydrogène, on trouve les trois raies suivantes caractérisées par leur longueur d'onde $\lambda_{1}=434.1\,nm$, $$\lambda_{2}=486.1\,nm$, $\lambda_{3}=656.3\,nm.$
 
1. A quel domaine du spectre électromagnétique appartiennent ces rayonnements lumineux ?
 
2. Calculer en $eV$, les énergies des photons de longueurs d'onde $\lambda_{1}=434.1\,nm$, $\lambda_{2}=486.1\,nm$, $\lambda_{3}=656.3\,nm.$
 
3. Justifier la discontinuité du spectre d'émission.
 
4. Donner le diagramme des niveaux d'énergie de l'atome d'hydrogène.
 
Donner l'expression des énergies des niveaux d'énergies, en calculant numériquement les énergies des niveaux $E_{i}$ de $i=1$ à $6.$
 
5. Sur le diagramme, noter quel est l'état fondamental, les états excités, l'énergie d'ionisation.
 
6. Montrer que les trois raies étudiées correspondent à des transitions qui ramènent l'atome d'hydrogène excité au même état.
 
7. Quelle doit être l'énergie du photon pour faire passer l'atome d'hydrogène du niveau $n=1$ à $n=4$ ?

Exercice 14

La mécanique quantique montre que l'état fondamental de l'atome d'hydrogène est caractérisé par une énergie $E_{1}=-13.6ev$ et chaque niveau excité $n>1$ est définie par une énergie $E_{n}=-\dfrac{E_{n}}{n^{2}}$ $(n$ est un entier naturel positif$)$ Avec $E_{0}=13.6eV.$
 
1. A quoi correspond l'énergie $E_{0}$ ?
 
2. Quelle relation simple existe entre l'énergie de transition $\Delta E$ d'un niveau $n$ à un niveau p et la longueur d'onde du photon émis ou absorbé. (Traiter chaque cas à part)
 
3.1. Montrer que pour une transition d'un niveau $p$ à un niveau $n$ tel que $p>n$, on peut écrire la relation $\dfrac{1}{2}=R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right).$
 
3.2. Vérifier que $R_{H}$ (appelée constante de Rydberg) vaut $R_{H}=1.10\cdot10^{+7}m^{-1}$
 
3.3. Dans la série de Balmer $($le retour au niveau $n=2)$ l'atome $H$ émet $1$ spectre contenant $4$ raies visibles, on se propose de calculer deux longueurs d'ondes de $2$ raies de ce spectre correspondant à $p=3$ $(\lambda_{3.2})$ et $p=4$ $(\lambda_{4.2})$
 
Sans faire de calcul, et en utilisant $\Delta E$, comparer $(\lambda_{3.2})$ et $(\lambda_{4.2})$ puis calculer leurs valeurs.
 
4. L'atome $H$ est dans son état fondamental $(n=1)$, on l'excite à l'aide d'un photon incident d'énergie $W=13.8eV.$ 
 
Que se passe-t-il ? 
 
Calculer $($en $eV)$ l'énergie cinétique $E_{c}$ de l'électron de $H$ éjecté.
 
5. si l'atome entre en choc inélastique avec un électron ayant une énergie cinétique égale $11eV$, que se passe-t-il ?

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Solution des exercices : Généralité sur les champs magnétique - champs magnétiques des courants - Ts

Classe: 
Terminale
 

Exercice 1

1) Représentation du spectre de l'aimant
 
 
2) a) Calcul de l'intensité du champ magnétique au point $A$
 
$B=\dfrac{1m\,T\times227\,mV}{20\,mV}\Rightarrow\;B=11.35\,mT$
 
b) Tracé le vecteur champ magnétique au point $A.$ (Voir figure)

Exercice 2

1) Tracé du spectre de l'aimant en $U$ entre les deux pôles
 
 
2) Orientation des lignes de champ. (Voir figure)
 
3) Identification des pôles de l'aimant. (Voir figure)
 
4) Le vecteur $\overrightarrow{B}$ dans cette région de l'espace champ magnétique est constant.
 
Un tel champ magnétique est appelé champ magnétique uniforme.

Exercice 3

1) Identification des pôles du solénoïde.
 
 
 
2) Calcul de la norme du champ magnétique créé au centre de ce solénoïde.
 
$\begin{array}{lcl} B&=&\mu_{0}\dfrac{N}{L}I\\&=&4\pi\cdot10^{-7}\dfrac{N}{L}I\\&=&4\pi\cdot110^{-7}\times\dfrac{2000}{50\cdot10^{-2}}\times1.5\\\Rightarrow B&=&7.5\cdot10^{-3}T \end{array}$
 
3) Représentation du vecteur champ magnétique au centre du solénoïde. (Voir figure)
 
4) Représentation le vecteur champ magnétique en $A$ (Voir figure).

Exercice 4

 
1) Représentation du vecteur champ magnétique en $M$, lorsque les deux pôles en regard sont de même nom.
 
$\overrightarrow{B}=\overrightarrow{B_{1}}+\overrightarrow{B_{2}}=\overrightarrow{0}$
 
2) Représentation du vecteur champ magnétique en $M$, lorsque les deux pôles sont de noms différents.
 
$\overrightarrow{B}=\overrightarrow{B_{1}}+\overrightarrow{B_{2}}$
 
Or $\overrightarrow{B_{1}}=\overrightarrow{B_{2}}\Rightarrow\;\overrightarrow{B}=2\overrightarrow{B_{1}}$ ;
 
$B=2\times20\Rightarrow\;B=40\,mT$
 
3) La norme du champ magnétique créé par la bobine
 
Premier cas : 
 
$\begin{array}{lcl} \overrightarrow{B}&=&\overrightarrow{B_{1}}+\overrightarrow{B_{2}}\\\Rightarrow B&=&B_{1}+B_{2}\\\Rightarrow B_{2}&=&B-B_{1}\\&=&60-20\\\Rightarrow B_{2}&=&40\,mT \end{array}$

Deuxième cas : 
 
$\begin{array}{lcl} \overrightarrow{B}&=&\overrightarrow{B_{1}}+\overrightarrow{B_{2}}\\\Rightarrow B&=&B_{1}-B_{2}\\\Rightarrow B_{2}&=&B+B_{1}\\&=&60+20\\\Rightarrow B_{2}&=&80\,mT \end{array}$
 
Sens du courant voir figure.

Exercice 5

1) Représentation des vecteurs champs magnétique créés en $M$ par chacune des deux sources.
 
 
2) Représentation du vecteur champ magnétique résultant. Voir figure
 
Détermination de la norme du vecteur champ magnétique
 
$\begin{array}{lcl} \overrightarrow{B}&=&\overrightarrow{B_{1}}+\overrightarrow{B_{2}}\\\Rightarrow B^{2}&=&B_{1}^{2}+B_{2}^{2}+2B_{1}^{2}B_{2}^{2}\cos\left(\overrightarrow{B_{1}}\;,\ \overrightarrow{B_{2}}\right)\\\Rightarrow B&=&\sqrt{B_{1}^{2}+B_{2}^{2}+2B_{1}^{2}B_{2}^{2}\cos\left(\overrightarrow{B_{1}}\;,\ \overrightarrow{B_{2}}\right)}\\B&=&\sqrt{2^{2}+4^{2}+2\times 2\times 4\cos 60^{\circ}}\\\Rightarrow B&=&5.3\,mT \end{array}$

Exercice 6

 
1) Représentation du vecteur induction magnétique $B_{1}$ au centre de $S_{1}.$ (Voir figure)
 
Expression de l'intensité du vecteur induction magnétique $B_{1}$ en fonction de $n_{1}$ et $I_{1}.$
 
$B_{1}=4\pi\cdot10^{-7}n_{1}I_{1}$
 
2) Sens de $I_{2}$ pour que le vecteur induction $B_{2}$ crée au centre de $S_{2}$ ait le même sens que l'axe $(y'y).$ (Voir figure)
 
3) Une petite aiguille aimantée, placée au centre $O$ des deux solénoïdes prend une direction $\alpha$ avec l'axe $(x'x).$
 
3) a) Schéma dans lequel sont représentés les vecteurs $B_{1}$, $B_{2}$ et l'aiguille.
 
b) Expression du rapport $\dfrac{n_{2}}{n_{1}}$ en fonction de $\alpha$, $I_{1}$ et $I_{2}.$
 
$\begin{array}{lcl} \tan\alpha&=&\dfrac{B_{2}}{B_{1}}\\&=&\dfrac{4\pi\cdot10^{-7}n_{2}I_{2}}{4\pi\cdot10^{-7}n_{1}I_{1}}\\\Rightarrow \dfrac{n_{2}}{n_{1}}&=&\dfrac{I_{1}}{I_{2}}\tan\alpha \end{array}$
 
 
c) Calcul de $n_{1}$ et $n_{2}$
 
$\tan\alpha=\dfrac{n_{2}I_{2}}{n_{1}I_{1}}\Rightarrow\;n_{1}=\dfrac{n_{2}I_{2}}{I_{1}\tan\alpha}$
 
$\begin{array}{lcl} n_{1}+n_{2}&=&500\\\Rightarrow\dfrac{n_{2}I_{2}}{I_{1}\tan\alpha}+n_{2}&=&500\\\Rightarrow\,n_{2}\left(\dfrac{I_{2}}{I_{1}\tan\alpha}+1\right)&=&500\\\Rightarrow n_{2}&=&\dfrac{500}{\dfrac{I_{2}}{I_{1}\tan\alpha}}+1\\\Rightarrow n_{2}&=&\dfrac{500}{\dfrac{1}{2\tan 63.2^{\circ}}}+1\\\Rightarrow n_{2}&=&399\,spires\cdot m^{-1}\\\Rightarrow n_{1}&=&500-399\\\Rightarrow n_{1}&=&101\,spires\cdot m^{-1} \end{array}$
 
Valeur du champ résultant en $O.$
 
$\begin{array}{lcl} B&=&\dfrac{B_{1}}{\cos\alpha}\\&=&\dfrac{4\pi\cdot10^{-7}n_{1}I_{1}}{\cos\alpha}\\&=&\dfrac{4\pi\cdot10^{-7}\times101\times2}{\cos 63.2^{\circ}}\\\Rightarrow B&=&0.56\,mT \end{array}$

Exercice 7

1) Représentation le vecteur $\overrightarrow{B_{H}}$ composante horizontale du champ géomagnétique.
 
 
 
 
 
 
 
2) Représentation du vecteur $\overrightarrow{B_{S}}$ du champ magnétique crée par le courant électrique $i$ au centre $O$ du solénoïde.
 
 
 
 
 
 
 
Déduction des faces nord et sud du solénoïde. (Voir figure)
 
3) a) Détermination de l'équation numérique de la courbe $\tan\alpha=f(i).$
 
 
 
La courbe représentant $\tan\alpha=f(i)$ est une droite qui passe par l'origine d'équation de la forme :
 
$\begin{array}{lcl} \tan\alpha&=&ai\\ \text{avec }a&=&\dfrac{\Delta\tan\alpha}{\Delta\,i}\\&=&\dfrac{25-0}{2-0}\\\Rightarrow a&=&12.5\\\Rightarrow\tan\alpha&=&12.5\,i \end{array}$ 
 
b) Représentation des vecteurs $\overrightarrow{B_{H}}$ et $\overrightarrow{B_{S}}$
 
 
 
c) Relation entre la valeur de $B_{H}$ et $B_{S}$ et $\alpha$
 
$\tan\alpha=\dfrac{B_{S}}{B_{H}}\Rightarrow\;B_{H}=\dfrac{B_{S}}{\tan\alpha}$
 
4) Valeur de la composante horizontale $B_{H}$ du champ géomagnétique.
 
$\begin{array}{lcl} \tan\alpha&=&\dfrac{B_{S}}{B_{H}}\\\Rightarrow B_{H}&=&\dfrac{B_{S}}{\tan\alpha}\\&=&\dfrac{4\pi\cdot10^{-7}ni}{12.5i}\\&=&\dfrac{4\pi\cdot10^{-7}n}{12.5}\\&=&\dfrac{4\pi\cdot10^{-7}\times200}{12.5}\\\Rightarrow B_{H}&=&2.0\cdot10^{-5}T \end{array}$

Exercice 8

Partie I

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&11&14&17&20\\ \hline B_{S}(mT)&3.3&3.3&3.3&3.3&3.2&2.8&2.1\\ \hline \end{array}$$
 
1) Tracé les variations de $B$ en fonction de $x$ sur toute la longueur du solénoïde
 
 
 
2) Le champ magnétique à l'intérieur de la bobine est uniforme.
 
3) Calcul de l'intensité $I$ du courant qui traverse la bobine.
 
$\begin{array}{lcl} B&=&4\pi\cdot10^{-7}\dfrac{N}{L}I\\\Rightarrow I&=&\dfrac{B}{4\pi\cdot10^{-7}N}\\&=&\dfrac{3.3\cdot10^{-3}}{4\pi\cdot10^{-7}\times250}\\\Rightarrow I&=&10.5\,A \end{array}$
 
4) Détermination de la longueur du solénoïde sur laquelle la valeur du champ magnétique reste supérieure à $90\%$ de sa valeur maximale
 
$\begin{array}{lcl} B&\geq& 90\%B_{max}\\\Rightarrow B&\geq&\dfrac{90}{100}\times 3.3\\\Rightarrow B&\geq&2.97\,mT\\\Rightarrow x&=&13.8\,cm \end{array}$

Partie II

1) Sens du courant dans les spires pour que le champ crée par la bobine soit dirigé vers la droite. (Voir figure)
 
 
 
2) Schéma représentant les vecteurs champs créés par le solénoïde $\overrightarrow{B_{S}}$ ; par la Terre $\overrightarrow{B_{H}}$, et le champ résultant.
 
 
 
3) Calcul de la nouvelle valeur de $B_{S}$
 
$\begin{array}{lcl} \tan\alpha&=&\dfrac{B_{S}}{B_{H}}\\\Rightarrow B_{S}&=&B_{H}\tan\alpha\\&=&2.0\cdot10^{-5}\times\tan 14.3^{\circ}\\\Rightarrow B_{S}&=&5.1\cdot10^{-6}T \end{array}$
 

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices Effet photoélectrique - Ts

Classe: 
Terminale
 

Exercice 1

Une surface métallique est éclairé par la lumière $UV$ de longueur d'onde $\lambda=0.150\mu m.$
 
Elle émet des électrons dont l'énergie cinétique maximale à $4.8eV.$
 
a) Calculer le travail d'extraction $W_{0}$
 
b) Quelle est la nature du métal ?
$$\begin{array}{|c|c|} \hline \text{Métal}&\text{Seuil photoélectrique }\lambda_{0}(\mu m)\\ \hline Zn&0.35\\ \hline Al&0.365\\ \hline Na&0.50\\ \hline K&0.55\\ \hline Sr&0.60\\ \hline Cs&0.66\\ \hline \end{array}$$
 
c) Quelle tension serait nécessaire pour arrêter cette émission
 
d) Pour augmenter la vitesse maximale d'émission, faut-il changer sa longueur d'onde ?

Exercice 2

1) Décrire une cellule photoélectrique dite cellule photoémissive à vide
 
Dessiner un schéma de montage à réaliser pour mettre en évidence l'effet photoélectrique en utilisant cette cellule
 
2) La longueur d'onde correspondante au seuil photoélectrique d'une photocathode émissive au césium est $\lambda_{0}=0.66\cdot10^{-6}m$
 
a) Quelle est en joules et en $eV$ l'énergie d'extraction $W_{0}$ d'un électron ?
 
Exprimer cette énergie en $eV$
 
b) La couche de césium reçoit une radiation monochromatique de longueur d'onde $\lambda=0.44\cdot10^{-6}m$
 
Déterminer l'énergie cinétique maximale $E_{c}$ d'un électron émis au niveau de la cathode. 
 
L'exprimer en joules puis en $eV.$

Exercice 3

On utilise une cellule photoélectrique au césium
 
Pour différentes radiations incidentes, on mesure la tension qui annule le courant photoélectrique (Tension d'arrêt)
 
 
Les résultats sont les suivants :
$$\begin{array}{|c|c|c|c|c|} \hline \lambda(\mu m)&0.60&0.50&0.40&0.30\\ \hline U(V)&0.19&0.60&1.22&2.26\\ \hline \end{array}$$
 
1) Exprimer l'énergie cinétique de l'électron au départ de la couche photoémissive en fonction de la fréquence $ѵ$ et du travail d'extraction $W_{0}$
 
2) Faire le schéma du montage utilisé
 
Exprimer la tension d'arrêt en fonction de $ѵ$ et $W_{0}$
 
3) Calculer les fréquences $ѵ$ des radiations utilisées
 
4) Tracer la courbe représentant la fonction $U=f(ѵ)$ et en déduire la fréquence $ѵ_{0}$ du seuil photoélectrique du césium, ainsi que la longueur d'onde $\lambda_{0}$ correspondante

Exercice 4

On réalise le montage suivant avec une cellule photoémissive à vide éclairée par une lumière monochromatique de fréquence (schéma)
 
Pour chaque valeur de $ѵ_{i}$, la tension $U_{CA}$ entre cathode et anode est réglée à la valeur $U_{0}$ juste nécessaire pour l'intensité $i$ traversant la cellule. 
 
Le voltmètre indique alors $U_{0}$
 
On obtient les valeurs suivantes :
$$\begin{array}{|c|c|c|c|c|c|} \hline V(Hz)&6\cdot10^{14}&7\cdot10^{14}&8\cdot10^{14}&9\cdot10^{14}&10\cdot10^{14}\\ \hline U_{0}(V)&0.4&0.8&1.24&1.66&2.08\\ \hline \end{array}$$
 
1) Rappeler : l'expression de l'énergie d'un photon de fréquence $ѵ$ ; l'expression de l'énergie maximale des électrons émis par la cathode en fonction de $U_{0}$
 
En déduire la relation existant entre $ѵ$, $U_{0}$, $h$ (constante de Planck), $e$ et $W_{0}$ travail d'extraction correspondant à la cellule utilisée
 
2) Faire la représentation graphique des variations de $U_{0}$ en fonction de $ѵ$
 
Abscisses : $1cm$ pour $1014Hz$ ; 
 
ordonnées : $1cm$ pour $0.2V$
 
En déduire le seuil de fréquence $ѵ_{0}$ de la cellule, la constante de Planck $h$ et $W_{0}$ (exprimé en électron-volt)

Exercice 5

La charge de l'électron est $-e=-1.6\cdot10^{-19}C.$
 
On éclaire une cellule photoélectrique par un faisceau lumineux monochromatique de fréquence $ѵ$ et on mesure le potentiel d'arrêt $U_{0}$ de la cellule.
 
1) Faire un schéma du montage utilisé
 
2) On répète l'opération en utilisant diverses radiations et on obtient les résultats suivants :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline V(Hz)&5.18\cdot10^{14}&5.49\cdot10^{14}&5.88\cdot10^{14}&6.17\cdot10^{14}&6.41\cdot10^{14}&6.78\cdot10^{14}&6.91\cdot10^{14}&7.31\cdot10^{14}\\ \hline U_{0}(V)&0.042&0.171&0.332&0.452&0.56&0.706&0.758&0.924\\ \hline \end{array}$$
 
Tracer sur papier millimétré, le graphe $U_{0}=f(ѵ)$ en utilisant les échelles suivantes : $10cm$ pour $1V$ ; $2cm$ pour $1014Hz.$
 
3) Rappeler la relation entre le potentiel d'arrêt, le travail d'extraction $W_{0}$, d'un électron du métal de la cathode et l'énergie des photons incidents
 
4) Déterminer à l'aide du graphique :
 
a) La constante de Planck
 
b) Le travail d'extraction d'un électron du métal de la cathode.
 
5) Citer autre phénomène qui, comme l'effet photoélectrique la nature corpusculaire de la lumière. 
 
Quelle caractéristique du photon met-il en évidence

Exercice 6

La courbe de la figure ci-dessous représente les variations de $|U_{0}|$ en fonction de $\dfrac{1}{\lambda}$
 
 
$|U_{0}|$ désigne la valeur absolue du potentiel d'arrêt d'une cellule photoélectrique et $\lambda$, la longueur d'onde de la radiation monochromatique qui éclaire la cathode de la cellule.
 
1) Déterminer graphiquement l'équation de la courbe représentant $|U_{0}|=f\left(\dfrac{1}{\lambda}\right)$
 
2) a) Établir la relation entre le potentiel d'arrêt $U_{0}$, le travail d'extraction $W_{0}$ d'un électron du métal de la cathode et l'énergie $W$ d'un photon incident. 
 
En déduire l'expression de $|U_{0}|$ en fonction de
b) En identifiant la relation précédente à celle trouvée graphiquement dans la première question, déterminer une valeur approchée de la constante de Planck $h$ et calculer $W_{0}.$
 
3) On éclaire maintenant la cellule photoélectrique par une lumière monochromatique de longueur d'onde $\lambda=0.588\mu m.$
 
a) Calculer, dans le système international d'unités, l'énergie $W$ et la quantité de mouvement $\|\overrightarrow{P}\|$ en $MeV\cdot c^{-1}$
 
b) A l'aide de la courbe représentant $|U_{0}|=\left(\dfrac{1}{\lambda}\right)$, calculer le potentiel d'arrêt $U_{0}$ correspondant et en déduire la valeur de l'énergie cinétique maximale des électrons émis par la cathode.
 
c) En supposant relativiste toute particule animée, dans un repère galiléen, d'une vitesse supérieure à $0.14c$, montrer que l'énergie cinétique d'une telle particule doit être supérieure à une fraction minimale $x$ de son énergie au repos. 
 
Calculer $x.$ 
 
En déduire si les électrons émis par la cathode sont relativistes ou non.
 
d) Calculer alors la vitesse maximale d'émission d'un électron par la cathode. 
 
On donne :
 
$\ast\ $ La célérité de la lumière dans le vide : $c=3\cdot10^{8}m\cdot s^{-1}$
 
$\ast\ $ La masse d'un électron : $m=9.1\cdot10^{-19}C.$
 
$\ast\ $ La constante de Planck : $h=6.62\cdot10^{-34}Js$

Exercice 7

Une cellule photoélectrique comporte une cathode $(C)$ constituée d'une surface métallique dont l'énergie d'extraction est $W_{0}=2.5eV.$
 
Un dispositif expérimental permet d'éclairer $(C)$ avec l'une des radiations de longueur d'onde : $623.6nm$ ; $413.7nm$ ; $560.0nm$ ; $451.4nm.$
 
1) Quelle est la valeur $\lambda_{0}$ de la longueur d'onde du seuil photoélectrique ?
 
2) Parmi les quatre radiations monochromatiques considérées, deux seulement de longueur d'onde $\lambda_{1}$ et $\lambda_{2}$ peuvent extraire des électrons du métal et leur communiquer une énergie cinétique.
 
a) Donner les valeurs de $\lambda_{1}$ et $\lambda_{2}$ ?
 
b) Montrer que l'expression du potentiel d'arrêt s'écrit $U_{0}=-\dfrac{E_{c}}{e}$ où $E_{c}$ est l'énergie cinétique de l'électron émis et $(-e)$ sa charge électrique.
 
c) Calculer la valeur du potentiel d'arrêt correspondant à chacune des deux radiations de longueur d'onde $\lambda_{1}$ et $\lambda_{2}$ capables d'extraire un électron du métal et lui communiquer une énergie cinétique.
 
3) On éclaire simultanément la cathode $(C)$ par les des deux radiations de longueur d'onde $\lambda_{1}$ et $\lambda_{2}.$
 
Déterminer, en le justifiant, la valeur du potentiel d'arrêt correspondant à cette expérience. 
 
Données : 
 
constante de Planck $h=6.62\cdot10^{-34}J\cdot s$
 
charge d'un électron $-e=-1.6\cdot10^{-19}C$ 
 
célérité de la lumière $c=3\cdot10^{8}m\cdot s$
 
$-11nm=10^{-9} m.$
 
$1eV=1.6\cdot10^{-19}J$
 

 $\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Interférences lumineuses - Ts

Classe: 
Terminale
 

Exercice 1

Deux fentes $F_{1}$ et $F_{2}$ distantes de $a=2mm$ émettent de la lumière provenant d'une même fente $F$ Elles produisent un système d'interférences lumineuses sur un écran placé à la distance $D=2m$ des fentes. 
 
La lumière de la source $F$ contient deux radiations monochromatiques, de longueur d'onde $\gamma_{1}=0.60\mu m$ et $\gamma_{2}=0.48\mu m.$ 
 
L'interfrange $i$ (distance séparant les milieux de deux franges sombres ou de deux brillantes consécutive) est lié à $\gamma$ par la relation $i=\gamma\dfrac{D}{a}$
 
1) Représenter à l'échelle $5$, sur une largeur de $15cm$ :
 
a) la figure d'interférences obtenue avec la radiation de longueur d'onde $\gamma_{1}$
 
b) la figure d'interférences obtenue avec la radiation de longueur d'onde $\gamma_{2}$
 
c) la figure d'interférences obtenue avec la lumière émise par la source $F$
 
2) Qu'observerait-on si la source Fémettait de la lumière blanche

Exercice 2

A l'aide d'un dispositif interférentiel, on crée deux sources lumineuses $S_{1}$ et $S_{2}$ synchrones et cohérentes distantes de $a.$ 
 
Quand le dispositif est éclairé par une source de lumière monochromatique de longueur d'onde $\gamma=0.6\mu m$, on observe des franges d'interférence sur l'écran $E$ placé à $D=2.5m$ de $S_{1}$ et $S_{2}$
 
1) Établir l'expression de la différence de marche au point $M$ de l'écran
 
2) Déterminer la distance entre les deux sources pour que la distance entre les milieux de la $6^{e}$ et $9^{e}$ frange brillante située de part et d'autre de la frange centrale numérotée $0$ soit égale à $1.5cm$
 
3) Déterminer la nature de la frange en un point $P$ de $E$ distant de $2.5mm$ de la frange centrale

Exercice 3

Deux fentes $F_{1}$ et $F_{2}$ sont éclairées par une fente source en lumière monochromatique rouge de longueur d'onde $\gamma=0.64\mu m$ et se comportent comme deux sources synchrones et en phase. 
 
La figure d'interférence est observée sur un écran. 
 
On considère un point $M$ sur un écran situé à la distance $d_{1}$ de $F_{1}$ et $d_{2}$ de $F_{2}$ (schéma)
 
1) Les vibrations lumineuses issues des fentes $F_{1}$ et $F_{2}$ sont-elles en phase ?
 
(Justifier les réponses)
 
2) La vibration lumineuse émise par la fente $F_{1}$ arrive en $M$ avec un certain retard.
 
Exprimer ce retard en fonction de $d_{1}$ et de la vitesse $c$ de la lumière dans l'air
 
3) Même question pour la vibration lumineuse issue de la fente $F_{2}$
 
4) En déduire à quelles conditions le point $M$ sera sur frange brillante ; sur une frange sombre $5.$ 
 
Que peut-on dire des points $M$ suivants :
 
$-\ $ $M$ est tel que $d_{2}-d_{1}=0$
 
$-\ $ $M$ est tel que $d_{2}-d_{1}=3.20\mu m$
 
$-\ $ $M$ est tel que $d_{2}-d_{1}=2.24\mu m$

Exercice 4

La lumière serait de nature contradictoire. 
 
Si une théorie permet d'expliquer de nombreux phénomènes, elle peut s'avérer insuffisante pour en comprendre d'autres.
 
Le but de cet exercice est de montrer que, selon l'expérience réalisée, un des aspects du comportement de la lumière. 
 
A cet effet on réalise le dispositif ci-dessous :
 
 
1) Dispositif expérimental
 
$(S)$ est une source de lumière qui éclaire deux fentes fines, verticales distantes de $a=1.5mm.$ 
 
La source $(S)$ est équidistante des deux fentes. 
 
$(E)$ est un écran opaque vertical placé à une distance $D=2m$ du plan des fentes.
 
a) Quel phénomène se produit à la sortie de chaque fente ? 
 
Quel aspect de la lumière permet-il de mettre en évidence ?
 
b) Justifier l'utilisation d'une source unique pour éclairer les deux dentes.
 
c) Reproduire le schéma et représenter la marche des faisceaux lumineux issus des fentes $F_{1}$ et $F_{2}.$ 
 
Hachurer le champ où l'on peut observer le phénomène d'interférence.
 
2) La source $(S)$ émet une lumière monochromatique de longueur d'onde $\gamma.$
 
a) Qu'observe-t-on sur l'écran ? 
 
Préciser la direction des franges et la nature de la frange centrale qui se forme en $O.$
 
b) Pour déterminer la longueur d'onde $\gamma$, on compte $5$ franges brillantes de part et d'autres de la frange centrale occupant ensemble une largeur $l=8mm.$
 
En déduire la valeur de $\gamma.$
 
3) La source précédente $(S)$ est remplacée par une source $(S')$ qui émet simultanément deux radiations monochromatiques de longueur d'onde $\gamma_{1}=0.60\mu m$, et $\gamma_{2}=0.54\mu m.$ 
 
Il se produit une superposition des systèmes de franges formées par les deux radiations.
 
A quelle distance $x$ du point $O$ se produit la première coïncidence de franges brillantes ?

Exercice 5

Un pinceau de lumière monochromatique émis par un laser hélium-néon éclaire deux fentes parallèles séparées par une distance $a=05mm.$ 
 
Un écran est placé perpendiculairement au pinceau lumineux à une distance $D2m$ du plan des fentes. 
 
Dessiner le dispositif expérimental.
 
1) Interpréter la formation des franges brillantes et obscures.
 
2) Définir et calculer la différence de marche aux $2$ fentes d'un point $M$ de l'écran, pour en déduire la position des franges brillantes et obscures
 
3) Préciser la nature de la frange centrale appartenant au plan médiateur des $2$ fentes.
 
4) Définir et calculer l'interfrange. 
 
Quelle est l'influence des différents paramètres sur l'interfrange ? 
 
Comment doit-on modifier la distance entre les $2$ fentes pour obtenir des franges plus espacées ?
 
5) Calculer la longueur d'onde et la fréquence de la lumière émise par le laser, sachant que $6$ franges sont espacées de $12.7mm.$
 
6) Est-ce que la longueur d'onde ou la fréquence change (ou aucune des deux), si le rayon lumineux se propage dans le verre ? 
 
Calculer les nouvelles valeurs. 
 
$($On sait que dans le verre la célérité de la lumière vaut $200000km/s.)$

Exercice 6

Une lumière monochromatique, issue d'une fente $F$, tombe sur un écran $E$ percé de deux fentes $F_{1}$ et $F_{2}$ parallèle à $F.$ 
 
Un dispositif spécial permet de faire varier la distance entre les fentes $F_{1}$ et $F_{2}$ $(F_{1}F_{2}=a)$ qui reste toute fois située à égale distance de $F.$
 
1) On dispose un écran $K$, parallèle à $E$ et à une distance $d$ de celui-ci. 
 
Qu'observe-t-on sur l'écran $K$
 
2) La longueur d'onde de la lumière monochromatique est $\gamma.$
 
On mesure dans le plan $K$ l'intervalle $L$ séparant $N$ franges brillantes consécutives.
 
Établir la formule donnant $a$ en fonction de $\gamma$, $N$, $d$ et $L$ (On supposera établie la formule de l'interfrange)
 
Calculer $a$ lorsque $\gamma=0.55\mu m$, $L=7.2mm$, $N=7$ et $d=1.20m$
 
3) On augmente l'intervalle $a=F_{1}F_{2}$
 
Qu'en résulte-il sur le phénomène observé sur l'écran ?
 
D'autre part on remarque que pour un interfrange inférieur à $0.2mm$, l'observation du phénomène devient très difficile à l'œil nu.
 
Quelle sera la valeur limite $a'$ de la distance $F_{1}F_{2}$ séparant les deux fentes ?
 
4) Combien observe-t-on de franges brillantes sur l'intervalle $L=7.2mm$ de l'écran $K$ quand $a=a'$ ? 
 
La mesure de l'intervalle est faite à partir d'une frange brillante

Exercice 7

1) Soit la distance de deux fentes fines et parallèles $F$ et $F'$ dans l'expérience de Young. 
 
On éclaire $F$ et $F'$ par une fente lumineuse parallèle aux précédentes et à égale distance de chacune d'elle. 
 
soit $\gamma$ la longueur d'onde dans le vide de la lumière monochromatique employée. 
 
On observe dans l'air des franges d'interférences sur un écran $(P)$ parallèle au plan des deux fentes et situé à une distance $d$ de ses fentes. 
 
Soit la largeur de $N$ interfranges consécutifs (on prendra comme plan de figure un plan perpendiculaire au plan $(FF')$
 
1.1 Établir la relation donnant $\gamma$ en fonction de $a$, $d$, $i$ et $N.$

AN : 

$a=2.00\,mm$ ; $1=4.00\,mm$ ; $N=12$ et $d=1.00m.$ 
 
Calculer $\gamma$
 
1.2 Quelle serait la nouvelle longueur $l$ du même nombre $N$ d'interfranges si tout le dispositif était plongé dans un milieu d'indice par rapport à l'air

A.N : 

$n_{o}=1.30$
 
1.3 Le système étant placé dans l'air, on recouvre la fente $F$ du côté de l'écran par un verre à faces parallèles d'épaisseur $e$ et d'indice $n=1.52.$ 
 
Qu'observe-t-on sur l'écran.
 
Expliquer le phénomène.
 
Calculer $e$ si le déplacement de la frange centre est $X=4.40mm$
 
1.4 On place sur $F$ une autre lame d'épaisseur $e'$ et d'indice $n'$ ; le système de franges obtenu est alors identique à celui réalité avant la mise en place des deux lames. 
 
Donner en fonction de $e$, $n$ et $n'$ l'expression de $e'$
 
Calculer $e'$ si $n'=1.402.$ 
 
Le dispositif est celui de la question 1., mais la source émet deux radiation : $\gamma=0.550\mu m$ et $\gamma=0.650\mu m.$
 
On observe simultanément les deux franges.
 
Déterminer dans le plan $(p)$, la plus petite distance par rapport à la frange centrale ou les milieux de deux franges brillantes correspondant aux deux radiation coïncident.

Exercice 8

La source $F$ n'est plus monochromatique, mais des filtres permettent d'obtenir des radiations monochromatiques différentes (voir figure). 
 
 
Pour chaque radiation, on mesure la longueur d'onde correspondant à $6$ interfranges $i$ $(i$ est la distance séparant le milieu de deux franges brillantes consécutives ou de deux franges sombres consécutives$)$ (voir figure).
 
 
1) Pourquoi mesure-t-on la distance correspondant à $6$ interfranges plutôt que celle mesurant $1$ interfrange ?
 
2) On a obtenu les résultats suivants. 
 
Compléter le tableau.
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Couleur}& & & & &\\ \hline 6i&14.1&15.6&17.4&18.3&19.5\\ \hline \gamma(\mu m)&0.47&0.52&0.58&0.61&00.65\\ \hline  \end{array}$$
 
3) Tracer la courbe représentative de la fonction $i=f(\gamma).$
 
4) La relation $i=\gamma\dfrac{D}{a}$ est-elle en accord avec la courbe obtenue précédemment ?
 
5) Comment faudrait-il modifier le dispositif expérimental pour obtenir des mesures avec une plus grande précision ?
 
6) Quelle serait la valeur de l'interfrange obtenu avec une radiation de longueur d'onde $0.50\mu m$ ?
 
7) On dispose d'une source monochromatique de longueur d'onde inconnue. 
 
Comment feriez vous expérimentalement pour la déterminer.

Exercice 9

On réalise une expérience d'interférences lumineuses avec le dispositif d'Young, en utilisant une lumière monochromatique de longueur d'onde $\gamma\,l=0.52\mu m.$ 
 
La fente-source $F$ éclaire deux fentes fines identiques $F_{1}$ et $F_{2}$ situées dans un plan vertical et distantes de $F_{1}F_{2}=a=2mm.$
 
Un écran d'observation $(E)$ est placé à $150cm$ du plan contenant $F_{1}$ et $F_{2}$ et parallèlement à celui-ci.
 
1) a) Décrire et expliquer le phénomène observé sur l'écran $(E).$
 
b) Quelle conclusion peut-on en tirer quant à la nature de la lumière ?
 
2) Définir et calculer l'interfrange $i.$
 
3) La frange centrale brillante est d'ordre zéro.
 
Calculer la distance séparant la troisième frange brillante à gauche de la frange centrale et la deuxième frange noire à droite de cette frange centrale.
 
La fente-source $F$ émet maintenant une radiation monochromatique de longueur d'onde $\gamma_{2}=0.65\mu m.$
 
4) A quelle distance de cette fente-source $F$ doit-on placer l'écran d'observation $(E)$ pour que l'interfrange $i'$ obtenu avec ce dispositif soit égal à l'interfrange $i$ de la question 2 ? 
 
La distance entre la fente-source $F$ et le plan contenant $F_{1}$ et $F_{2}$ est égale à $50cm.$
 
5) La fente-source $F$ émet simultanément les deux radiations de longueurs d'onde $\gamma_{1}=0.52\mu m$ et $\gamma_{2}=0.65\mu m.$
 
On remet l'écran $(E)$ à la position où il est distant de $150cm$ du plan contenant $\gamma_{2}=0.65\mu m.$
 
On remet l'écran $(E)$ à la position où il est distant de $150cm$ du plan contenant $F_{1}$ et $F_{2}.$
 
6) A quelle distance de la frange centrale aura lieu la première coïncidence des franges brillantes des deux systèmes de franges obtenus.

Exercice 10 

Le dispositif des fontes d'YOUNG schématisé sur la figure 1 permet de réaliser une expérience de mise en évidence d'interférences lumineuses.
 
 
La source $(S)$ émet une lumière monochromatique de longueur d'onde $\gamma=0.6\cdot10^{-6}m$ 
 
$(P)$ est un plan opaque comportant deux fentes fines $S_{1}$ et $S_{2}$ distantes de $a=1\,mm$ et assimilables à deux sources ponctuelles monochromatique symétriques par rapport à un point $I$ milieu de $S_{1}S_{2}.$
 
Un écran $(E)$ est disposé parallèlement à $(P)$ et à une distance $D=2\,m$ de celui-ci.
 
On observe des interférences lumineuses dans la représenté hachurée sur le schéma où les deux faisceaux issus de $S_{1}$ et $S_{2}$ couvrent une partie commune. 
 
L'intersection de cette zone hachurée avec l'écran $(E)$ est un ensemble de franges brillantes équidistantes ayant la couleur de lumière monochromatique. 
 
Deux franges brillantes successives sont séparées par une frange sombre, et la frange centrale en $O$ est brillante. 
 
Un point $M$ du champ d'interférence est repéré par son abscisse $x=OM$ 
 
Lorsque $M$ appartient à une frange brillante, il vérifie la relation $MS_{2}-MS_{1}=k\gamma$ $($avec $k$ entier$).$ 
 
Par contre s'il appartient à une frange sombre il vérifie la relation $MS_{2}-MS_{1}=(2k+1)\dfrac{\gamma}{2}$ $($avec $k$ entier$).$
 
1) a) Montrer que la différence de marche a pour expression $(MS_{2}-MS_{1})=\dfrac{ax}{D}$
 
b) En déduire l'expression de l'abscisse $x$ d'un point $M$ de l'écran en fonction de $\gamma$, $D$ et $a$ : 
 
$-\ $ Lorsqu'il appartient à une frange brillante
 
$-\ $ Lorsqu'il appartient à une frange sombre.
 
2) a) Déterminer l'expression de l'interfrange $i$ en fonction de $\gamma$, $D$ et $a.$ 
 
Calculer $i.$
 
b) Préciser, en le justifiant, la nature (brillante ou sombre) de la frange d'abscisse $x=-4.2mm.$
 
3) On apporte les changements suivants au dispositif expérimental de la figure 1 :
 
$-\ $ On supprime la source $(S)$ et le plan opaque $(P)$
 
$-\ $ à l'emplacement des deux sources secondaires $S_{1}$ et $S_{2}$ on dispose de deux sources $S'_{1}$ et $S'_{2}$ totalement indépendantes, émettant chacune la lumière monochromatique de longueur d'onde $l=0.6\cdot10^{-6}m.$ (figure 2) 
 
 
On n'observe d'interférences lumineuses. 
 
Expliquer pourquoi ?
 
4) Citer un dispositif, autre que les fentes d'YOUNG, permettant de réaliser une expérience de mise en évidence d'interférences lumineuses :
 
$-\ $ on tracera la marche des rayons lumineux 
 
$-\ $ et on hachurera la zone où les deux faisceaux lumineux, issus des deux sources secondaires, couvrent une partie commune correspondant aux interférences lumineuse.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Devoir n° 1 - Physique chimie - 2nd S

Classe: 
Seconde
 

Exercice 1

Modou explique à Fatou comment on fabrique du " Café Touba " : il lui indique les trois $(3)$ étapes que comprend cette préparation.
 
$1^{ière}$ étape : mettre de l'eau dans une cafetière, porter l'eau à l'ébullition puis ajouter la poudre de " Café Touba " et attendre quelle minutes.
 
$2^{ième}$ étape : Faire passer le mélange obtenu à travers un tissu pour recueillir la partie liquide.
 
$3^{ième}$ étape : Ajouter du sucre à volonté et remuer à l'aide d'une cuillère. 
 
Le " Café Touba " est prêt.
 
1) Quel type de mélange obtient-on à la fin de la ère étape ?
 
2) Quelle est la méthode de séparation utilisée dans la $2^{ième}$ étapes ?
 
3) Comment appelle-t-on, en chimie, le liquide obtenu ; est-ce un corps pur ?
 
4) Quel type de mélange obtient-on à la fin de la $3^{ième}$ étape ? 
 
Justifier votre réponse

Exercice 2

Le carbone est le constituant essentiel de la matière vivante.
 
Il est présent dans toutes les molécules organiques.
 
Un atome de carbone, de symbole $C$, a $12$ nucléons son noyau. 
 
La charge électrique de son nuage électronique est $q=-6e.$
 
1) Pourquoi peut-on dire que le noyau contient $6$ protons ? 
 
justifier.
 
2) Exprimer puis calculer la charge de son noyau.
 
3) Donner le symbole de son noyau.
 
4) Énoncer les réglés de remplissage des électrons sur les couches électroniques puis donner la structure électronique de l'atome de carbone.
 
5) Calculer la valeur approchée de la masse de l'atome de carbone et celle de son noyau
 
Données :
 
$m_{p}=m_{n}=1.7\cdot 10^{-27}kg$, 
 
masse de l'électron : $m_{e}=9.1\cdot10^{-31}kg$, 
 
charge élémentaire : $e=1.6\cdot10^{-19}C$
 
6) Pourquoi peut-on dire que la masse de l'atome est quasiment la même que celle du noyau de l'atome ? 
 
Justifier votre réponse par un calcul. 
 
7) Donner le nombre d'atomes de carbone contenus dans un échantillon de masse $m=1.00\,g.$

Exercice 3  Position de rencontre de deux mobiles

Les équations horaires des mouvements de deux mobiles $A$ et $B$ en mouvement sur une route droite munie d'un axe $(x'0x)$ sont :
 
$x_{A}=20t-10$
 
$x_{B}=-10t+90$ avec $x_{A}$ et $x_{B}$ en mètres et $t$ en secondes.
 
1) Déterminer, en justifiant la réponse, la nature du mouvement de chacun des deux mobiles.
 
2) Quelle est la position de chaque mobile à l'origine du temps $(t=0s)$ ?
 
3) Quelle distance sépare les deux mobiles à l'origine du temps ?
 
4) Dans quel sens se déplace chaque mobile ? 
 
Et avec quelle vitesse ?
 
5) Déterminer l'instant de rencontre des deux mobiles.
 
6) En déduire la position de rencontre des deux mobiles

Exercice 4

Les questions 1, 2 et 3 sont indépendantes
 
1. Définir les termes suivants : 
 
force, système, force extérieure, force intérieure
 
2. Dire si les propositions suivantes sont vraies ou fausses. 
 
Corriger celles qui sont fausses.
 
2.1 Les actions de contact peuvent être ponctuelles ou réparties.
 
2.2 L'action du vent sur la voile du véliplanchiste est une action à distance.
 
2.3 L'unité légale de la force est le kilogramme, de symbole $kg.$
 
2.4 La valeur d'une force se mesure avec un dynamomètre
 
3. Trouver la résultante des forces suivantes (méthode géométrique puis analytique) agissant sur un corps au point $O.$
 
L'intensité de la force $\overrightarrow{F_{1}}$ est égale à $1200N$, celle de $\overrightarrow{F_{2}}$ à $900N$ et celle de $\overrightarrow{F_{3}}$ à $300N.$ 
 
Les directions et sens sont indiqués sur la figure à l'échelle : $1cm\longrightarrow 300N.$

N.B : 

Pour la détermination géométrique veuillez travailler directement sur la figure 
 
$$\text{Durée : }3\text{ heures}$$
 
Auteur: 
Sidy Ndiaye

Devoir n° 1 - Physique chimie - Ts

Classe: 
Terminale
 

Exercice 1 Alcools et dérivés

1) Un alcool saturé non cyclique dénommé $A$ a pour composition centésimale massique $68.2\%$ de carbone et $13.6\%$ d'hydrogène. 
 
Déterminer sa formule brute.
 
2) L'oxydation du composé $A$ par le permanganate de potassium en excès produit les composés $B$ et $C.$
 
$C$ donne une teinte rose au papier $pH.$ 
 
$B$, chauffé avec de la liqueur de Fehling, fait apparaître un précipité rouge, et par ailleurs précipite la $2.4-DNPH.$
 
a) Conclure sur la nature des produits $A$, $B$, et $C$
 
b) Donner les différentes formules semi-développées possibles de $A.$
 
3) Pour préciser la nature du composé $A$, on réalise l'addition d'une molécule d'eau sur un alcène $D.$
 
Cette réaction donne un produit majoritaire $E$ et également le composé $A$ minoritaire.
 
a) Sachant qu'un atome de carbone de $D$ porte trois liaisons simples carbone-carbone, donner les noms et les formules des composés $A$, $B$, $C$, $D$ et $E.$
 
b) Écrire l'équation de la réaction d'addition sur $D$ produisant $E.$
 
4) Dans un montage à reflux, on chauffe un mélange équimolaire de $A$ et d'acide éthanoïque. 
 
Dans le ballon, on a introduit $3.3\,mL$ d'alcool $A$ de densité $0.8.$ 
 
Après avoir stoppé la réaction, on dose l'acide éthanoïque restant dans le ballon par une solution d'hydroxyde de sodium de concentration $C_{b}=0.1\,mol\cdot L^{-1}.$ 
 
L'équivalence est atteinte pour un volume de base ajouté $V_{b}=150\,mL.$
 
a) Écrire l'équation de la réaction ayant eu lieu entre $A$ et l'acide éthanoïque.
 
b) Calculer le rendement de cette réaction.
 
c) Quelle est la masse du produit formé ?
 
d) La réaction a-t-elle atteint la limite communément admise pour une telle réaction ?
 
Données : 
 
masses molaires en $g\cdot mol^{-1}$ : $C$ : $12$ ; $O$ : $16$ ; $H$ : $1$

Exercice 2 Deux méthodes de synthèse d'un esterI.

Au cours d'une séance de travaux pratiques, on réalise la synthèse d'un ester, l'éthanoate de pentyle, par deux méthodes, afin de montrer que le contrôle de l'évolution d'un système chimique peut s'effectuer par changement de l'un des réactifs.
 
La méthode $n_{01}$ consiste à faire réagir de l'acide éthanoïque avec une quantité stœchiométrique de pentan $-1-$ ol.
 
La méthode $n_{02}$ consiste à faire réagir de l'anhydride éthanoïque avec une quantité stœchiométrique de pentan $-1-$ ol.
 
a) Écrire les formules semi-développées de l'acide éthanoïque, du pentan $-1-$ ol et de l'anhydride éthanoïque. 
 
Entourer les groupes caractéristiques et nommer les familles des composés correspondantes.
 
b) Écrire les équations chimiques des deux réactions envisagées.
 
c) Déterminer les volumes d'acide carboxylique et d'anhydride d'acide, notés $V_{1}$ et $V_{2}$, nécessaires à la préparation d'un mélange stœchiométrique avec $50\,mL$ de pentan $-1-$ ol.
 
II. Sur le protocole de $TP$, on peut lire :
 
Méthode $n_{01}$ 
 
$-\ $ dans un ballon introduire $50\,mL$ de pentan $-1-$ ol, le volume $V_{1}$ d'acide éthanoïque calculé précédemment et $1\,mL$ d'acide sulfurique. 
 
Ajouter quelques billes de verre (ou pierre ponce) et chauffer à reflux pendant $1$ heure.
 
Méthode $n_{02}$ 
 
$-\ $ dans un ballon bien sec, introduire $50\,mL$ de pentan $-1-$ ol. 
 
Sous la hotte, verser, avec beaucoup de précautions et lentement, en agitant après chaque ajout, le volume $V_{2}$ d'anhydride éthanoïque calculé précédemment.
 
Ajouter quelques billes de verre et chauffer à reflux pendant $20$ minutes.
 
a) Quel est le rôle de l'acide sulfurique ajouté dans la méthode $n_{01}$ ?
 
b) Quel est le rôle des billes de verre ?
 
c) Pourquoi réalise-t-on l'expérience à chaud ?
 
d) Donner le schéma annoté du chauffage à reflux
 
III. Après refroidissement des deux ballons, on verse chaque mélange réactionnel dans de l'eau, on agite, puis on transvase dans une ampoule à décanter. 
 
Quelle que soit la méthode de préparation utilisée, on observe dans les deux ampoules deux couches de liquides non miscibles, dont l'une est l'ester. 
 
Après traitement de la phase convenable, on pèse la masse d'ester formée : 
 
méthode $n_{01}$ : $m_{1}=30\,g$ ; 
 
méthode $n_{02}$ : $m_{2}=52\,g$
 
a) Faire un schéma du contenu de l'ampoule à décanter dans le cadre de la méthode $n_{01}.$ 
 
On justifiera la position des deux phases.
 
b) Calculer le rendement dans chaque cas.
 
c) Quelle est la méthode la plus avantageuse en terme de rendement ?
 
d) Pour la méthode $n_{01}$, on peut éliminer l'eau formée du mélange réactionnel et ainsi obtenir l'ester avec un meilleur rendement. 
 
Justifier ce résultat en utilisant le tableau des données ci-dessous. 
 
Pour quelle raison le rendement est-il meilleur ?
 
Données:
$$\begin{array}{|c|c|c|c|} \hline &\text{Masse volumique en }g\cdot cm^{-3}&\text{Masse molaire}&\text{Température d’ébullition}\\ & &\text{moléculaire en }g\cdot mol^{-1}&TE\\ \hline \text{Pentan}-1-ol&0.81&88&118\\ \hline \text{Acide éthanoïque}&1.05&60&117\\ \hline \text{Anhydride éthanoïque}&1.08&102&\\ \hline \text{Ester}&0.87&130&143\\ \hline \end{array}$$

Exercice 3

Une piste $ABCD$ est formée d'une partie $AB$ rectiligne qui fait un angle $\alpha$ avec la verticale, une partie $BC$ ayant la forme d'un arc de cercle de centre $O$ et de rayon $r$, et enfin une partie $CD$ verticale (voir fig). 
 
 
Données : 
 
$\alpha=60^{\circ}$, 
 
$g=10\,m/s^{2}$, 
 
$BO=CO=r=1m$, 
 
$OD=2m.$
 
Un solide S de masse $m=200\,g$ est lancé de $A$ vers $B$ avec une vitesse $V_{A}.$
 
1. Déterminer la nature du mouvement de $A$ à $B.$ 
 
Les frottements sont assimilables à une force $f=mg/4$ $($les frottements n'existent qu'entre $A$ et $B$ seulement$.)$
 
2. Calculer la vitesse minimale avec laquelle il faut lancer le solide $S$ du point $A$ pour qu'il arrive en $B$ avec une vitesse nulle.
 
3. Le solide $S$ descend de $B$ vers $C$ sans vitesse initiale.
 
3.1 Donner l'expression de sa vitesse en $M$ en fonction de $g$, $r$ et $(OB\;,\ OM)=30^{\circ}$
 
3.2 Trouver l'expression de la réaction $R$ en $M$ de la piste en fonction de $g$, $m$ et $8.$ 
 
La calculer.
 
4. Donner les caractéristiques de la vitesse du solide $S$ en $C.$
 
5. Le solide $S$ quitte la piste à $t=0$ et arrive au sol au point $E.$
 
6. Donner l'équation de la trajectoire du solide dans le repère $(O\ ;\ x\ ;\ y).$
 
Déterminer les coordonnées du point de chute $E.$

Exercice 4

« Les personnages et les situations de ce récit étant purement fictifs, toute ressemblance avec des personnes ou des situations existantes ou ayant existé ne saurait être que fortuite.»
 
 
$-\ $ Afin d'améliorer son saut, l'athlète, qui suit des études en Terminale S, visualise grâce à une vidéo le saut effectué lors de son dernier entraînement Figure 1
 
$-\ $ Elle souhaite connaître la distance $d$ qui sépare son pied d'appel de l'aplomb de la barre pour éviter de retomber sur la barre ou de faire tomber la barre après le franchissement de celle-ci.
 
$-\ $ D'après ce qu'elle a vu dans son cours de physique, elle va essayer d'appliquer les lois du mouvement d'un projectile dans le champ de pesanteur.
 
L'angle entre le vecteur vitesse $\overrightarrow{V_{0}}$ et le plan horizontal du sol est noté $\alpha.$
 
Hypothèses simplificatrices proposées par son professeur de sciences physiques :
 
$-\ $ Les frottements avec l'air seront négligés
 
$-\ $ La poussée d'Archimède sera négligée.
 
$-\ $ Seul sera étudié le mouvement du centre de gravité $G$ de l'athlète.
 
$-\ $ Le mouvement du centre de gravité $G$ se fera dans un plan
 
$-\ $ Le champ de pesanteur est constant et égal à $g=9.80\,m\cdot s^{-2}.$
 
$-\ $ Le schéma de la situation est donné sur la figure 2 (l'échelle n'est pas respectée).

I. Force(s) exercées sur l'athlète pendant son saut

1) Préciser le référentiel à utiliser ainsi que le système.
 
2) En utilisant les hypothèses simplificatrices, quelle(s) est (sont) le(s) force(s) qui s'applique(nt) sur l'athlète ?

II. Équation de la trajectoire

1) Rappeler à l'athlète l'énoncé de la deuxième loi de Newton.
 
2) En appliquant la deuxième loi de Newton, déterminer les équations horaires du mouvement de $G.$
 
3) Montrer que l'équation de la trajectoire peut se mettre sous la forme $y(x)=Ax^{2}+Bx+C.$ 
 
On donnera Les expressions littérales de $A$, $B$ et $C$ et on précisera leurs unités respectives (si elles existent).

III. Calcul de la vitesse initiale

La barre est placée à une hauteur $H=1.78\,m$ ; le centre d'inertie de l'athlète est tel que $h=1.00\,m$
 
L'angle $\alpha$ est égal à $60^{\circ}.$
 
1) Montrer que la vitesse initiale $V_{0}$ peut se mettre sous la forme que $V_{0}=\sqrt{\dfrac{2g(H-h)}{\cos\alpha}}$ 
 
2) Calculer la vitesse initiale $V_{0}$, d'abord en $m/s$ puis en $km/h$, dans les conditions indiquées.
 
3) La valeur trouvée pour la vitesse initiale est-elle aberrante ?

IV. Calcul de la distance $d$

1) Montrer que la distance $d=\dfrac{2g(H-h)}{\tan\alpha}$
 
2) Calculer la distance $d$ pour $H=1.78\,m$ ; $h=1.00\,m$ et $\alpha=60^{\circ}$
 
3) La valeur trouvée pour la distance $d$ est-elle aberrante ?

V. Franchissement de la barre

1) Son entraîneur lui conseille d'éloigner sa prise d'appel de la barre quand celle-ci est placée plus haute.
 
L'expression précédente de $d$ confirme-t-elle ce conseil ?
 
L'athlète est-elle sûr de franchir la barre ? 
 
Que doit-elle modifier dans le cas contraire

Exercice 5

Un faisceau d'électrons homocinétiques pénètre en $O$ entre les plaques horizontales $P$ et $N$ d'un condensateur plan, avec une vitesse initiale $V_{O}$ de norme $V_{O}=8\times 106ms^{-1}$ (voir figure ci-dessous). 
 
 
La tension entre les plaques est $U=V_{P}-V_{N}$, la plaque $P$ étant au potentiel le plus élevé
 
1) En appliquant le théorème du centre d'inertie, exprimé dans le repère orthonormé les équations horaires du mouvement d'un électron dans le champ. 
 
On négligera le poids de l'électron devant la force électrique.  
 
2) En l'équation de la trajectoire des électrons dans le champ et préciser sa nature
 
Quelle valeur maximale doit avoir $U$ pour que les électrons sortent du champ sans heurter les plaques ? 
  
3) Cette condition étant réalisée, on recueille les électrons sur un écran $(\mathfrak{C})$ placé à une distance $L=36\,cm$ du centre $I$ des plaques. 
 
Soit $Y$ l'ordonnée du point d'impact des électrons sur l'écran. 
 
Calculer le rapport  
 
4) Citer une application de la déviation d'un faisceau d'électron dans un champ électrique uniforme.   
 
Données : 
 
Distance entre les plaques : $d=5\,cm.$ 
 
Longueur des plaques : $l=10\,cm$
$$\text{Durée : }04\text{ heures}$$
 
Auteur: 
Sidy Ndiaye

Devoir n° 3 - Physique chimie - TL2

Classe: 
Terminale
 

Exercice 1

Lire attentivement ce texte et répondre aux questions
 
Les réseaux de distribution livrent directement l'électricité chez les consommateurs finaux. 
 
Les lignes électriques sont à une tension de $20\ 000$ volts, augmentant la déperdition énergétique unitaire mais sur de courtes distances. 
 
Des postes de transformation sont placés à l'interconnexion des réseaux de transport et de distribution.
 
Certains moyens de production d'électricité décentralisés (éoliennes, panneaux photovoltaïques chez un particulier) peuvent être directement raccordés au réseau de distribution et ne passent pas par le réseau de transport. 
 
On parle de production locale pour cette raison.
 
Lors du transport et de la distribution d'électricité, le courant est le plus souvent triphasé. 
 
Il y a trois câbles conducteurs par circuit pour optimiser l'acheminement de l'électricité et minimiser les pertes en lignes
 
1.1 Donner un titre à ce texte
 
1.2 Définir les mots soulignés
 
1.3 Expliquer l'intérêt du courant triphasé
 
1.4 Quelles sont les particularités des certains moyens de production d'électricité décentralisés ?

Exercice 2

2.1 Compléter les phrases suivantes avec cette liste de mots en les soulignant : thermodurcissable, chlorure, incinération, hydrogène, air, recyclage, thermoplastiques, thermique, indice, stockage des déchets, polymère, motifs, thermique
 
2.1.1 Le degré ou ........... de polymérisation d'un ............... est le nombre moyen de ................ que comporte ses macromolécules.
 
2.1.2 Les polymères qui à froid retrouvent leur forme initiale après déformation, sont dits .................. alors que dans les mêmes conditions les ............. restent durs. 
 
Ceux qui à chaud se ramollissent sont dits .................
 
2.1.3 Les matières plastiques, une fois utilisées posent un problème de ................
 
Ainsi pour lutter contre cette pollution visuelle ; deux méthodes sont essentiellement utilisées le ............... et l'...................
 
La première offre une seconde vie à la matière. 
 
Par contre la seconde est une source d'énergie............... dont le seul inconvénient est de rejeter dans l'.............. des gaz polluants tel que le................d'................ pour le polychlorure de vinyle.
 
2.2 Choisir la ou les bonne(s) réponse(s)
 
2.2.1 Le transport de l'énergie électrique se fait à haute tension
 
a) pour augmenter la puissance transportée
 
b) pour diminuer l'intensité des courants de ligne
 
c) pour diminuer les pertes en ligne
 
2.2.2 Une utilisation domestique dispose d'une tension entre phase et neutre :
 
a) la valeur efficace vaut $230V$
 
b) la valeur efficace vaut $400V$
 
c) la fréquence est égale à $50Hz$
 
2.2.3 Un transformateur fonctionne :
 
a) pour des tensions continues
               
b) pour des tensions sinusoïdales
               
c) pour des tensions continues et sinusoïdales

Exercice 3

La peinture est un matériau fluide, qui, après application en couche mince sur un support, donne, par un processus physique ou chimique, un film mince adhérent protecteur et ou décoratif.
 
Elle est constituée de quatre grandes familles
 
$-\ $ le liant : il apporte les principales propriétés au revêtement,
 
$-\ $ les solvants : ils donnent la fluidité à la peinture pour permettre la fabrication et l'application ; la formation du film se faisant après leur élimination.
 
$-\ $ les additifs : ils modifient ou ajoutent certaines propriétés de la peinture (fongicide, insecticide, ...).
 
$-\ $ les matières pulvérulentes
 
$-\ $ les pigments : ils apportent la couleur et l'opacité,
 
$-\ $ les matières de charge : ils permettent d'ajouter le renforcement mécanique du contrôle du brillant.
 
Les peintures polymères, à base de résine alkyde, ou glycérophtalique sont devenues courantes.
 
Données : 
 
$M_{C}=12g\cdot mol^{–1}$ ;
 
$M_{H}=1g\cdot mol^{–1}$ et 
 
$M_{O}=16g\cdot mol^{–1}$
 
3.1 Définir le terme : monomère.
 
3.2 La masse molaire de la résine alkyde est de $33.3kg\cdot mol^{–1}.$
 
Son degré de polymérisation est de $150.$
 
3.2.1 En déduire la masse molaire moléculaire du monomère correspondant.
 
3.2.2 Sa composition centésimale massique est : 
 
$\%C=59.5\%$ de carbone, 
 
$\%O=36\%$ d'oxygène et le reste d'hydrogène.
 
En déduire la formule brute de la résine.
 
3.3 La réaction chimique faisant intervenir le styrène-butadiène est
 
$a(C_{8}H_{8})+b(C_{4}H_{6})\longrightarrow {(C_{28}H_{30})}n$
 
3.3.1 Donner les expressions de $a$ et $b$ en fonction de $n.$
 
3.2.1 Rappeler ce qu'est une polymérisation.

Exercice 4

Une installation de chauffage électrique est composée de $4$ radiateurs montés en parallèle :
 
$-\ $ un radiateur d'une puissance de $1.5kW$ ;
 
$-\ $ deux radiateurs d'une puissance de $1kW$ chacun ;
 
$-\ $ un radiateur d'une puissance de $750W.$
 
La tension d'alimentation est de $220V$ et un fusible de $20A$ protège l'installation.
 
4.1 Calculer :
 
4.1.1 La puissance de l'installation
 
4.1.2 L'intensité du courant absorbé par l'installation quand tous les radiateurs fonctionnent.
 
4.1.3 L'énergie absorbée par ces $4$ radiateurs après $2h\ 30\,min$ de fonctionnement.
 
4.2 Peut-on ajouter un radiateur supplémentaire de $1000W$ à cette installation ? 
 
Justifier la réponse.
 
Auteur: 
Sidy Mouhamed Ndiaye

Composition du premier semestre de sciences physiques

EXERCICE1

Notre planète est entourée d'une couche d'air dont la plus grande partie est répartie sur une épaisseur d’une dizaine de kilomètres. On appelle pression atmosphérique la pression qu'exerce cette couche d'air sur les corps à la surface de la Terre. Le symbole de la pression est $P$. La pression atmosphérique est une donnée précieuse pour la météorologie car les mouvements des masses d'air en altitude sont responsables de l'évolution du climat. La mesure de la pression atmosphérique est donc nécessaire pour prévoir les conditions climatiques. L'unité légale de la pression est le pascal (symbole : $Pa$). La pression atmosphérique est mesurée par un appareil de mesure : le baromètre. Certains baromètres sont gradués en hectopascals (symbole : $hPa$) ou en millibars (symbole : mbar). D'autres baromètres sont gradués en hauteur de colonne de mercure (symbole : $mm Hg$).
1.1. Quel instrument de mesure est cité dans ce texte ?
1.2. Que mesure cet instrument ?
1.3. Quel est le symbole de la pression ?
1.4. Quelle est l'unité de pression dans le système international ? Quel est son symbole ?
1.5. Donner les autres unités de pression citées dans le texte. Donner le symbole de chacune, de ces unités.
1.6. Convertir un hectopascal en pascal.
1.7. A part les laboratoires de météorologie, dans quels lieux trouve – t – on des appareils qui permettent de mesurer la pression ? Qui les utilisent ?

EXERCICE2

On considère les mesures suivantes :

$A = 26000 x 10^{ 5} m$ $B = 450 x 10^{– 7} m$ $C = 606 x 10 m$
$D = 0,0108 x 10^{ – 4} m$ $E = 0,019 x 10 ^{4} m$ $ F = 0,0170x 10^{– 7} m$

1)- Ecrire ces mesures en utilisant la notation scientifique tout en conservant la précision.
2)- Indiquer le nombre de chiffres significatifs pour chaque mesure.
3)- Donner un ordre de grandeur pour chaque mesure.
4)- Placer ces ordres de grandeurs sur une échelle adaptée. Que peut-on dire de cette échelle ? Justifier.

Pages